Introduction
Money management is a very important aspect for successful trading. Its main purpose is to minimize risks and maximize profits. With the right use of money management, it is possible to achieve improved trading results.
In general, money management is a set of rules that allows traders to calculate the optimal volume of positions, taking into account all the possibilities and limitations. Today, there are quite a few money management strategies to fit every taste. We will try to consider several ways to manage money based on different mathematical growth models.
Trading strategy and money management
Any method of money management can accelerate the growth of the trading balance, or, in other words, to increase the profitability of the trading strategy. Thus, the trading strategy is the basis, while money management is an addition. Let’s see what requirements a trading strategy must meet in order to apply money management to it.
First, it is the mandatory use of stop losses and take profits. With their help, you can control trading risks: stop loss allows you to limit possible losses, and take profit makes it possible to assess the potential profit for each deal.
Second, it is a positive mathematical expectation. It enables traders to evaluate the expected profitability of a trading strategy in the long term, which allows them to make rational decisions and manage their capital more efficiently. However, mathematical expectation is important not only for the trading strategy as a whole, but also for a newly opened position.
Let’s introduce the following variables:
- p – probability of a profitable trade;
- SL – difference between the open price and stop loss in points;
- TP – difference between the open price and take profit.
First, we need to estimate the probability of profit. Let m be the number of closed profitable deals, while n is a total number of trades. Then the probability of receiving profit is:
The mathematical expectation (in points) for the position being opened can be found using the equation:
For a profitable trading strategy, the mathematical expectation should be positive. In this case, the use of any method of money management can bring additional profit.
However, the mathematical expectation may turn out to be negative or zero. This may happen at the very beginning of trading, when the number of losing trades can have a very large impact on the estimation of the profit probability. In this case, the volume of the opened position should be as small as possible. This means the trader needs to apply money management according to the linear growth model with minimal risk.
Linear growth
This is one of the most famous and simple growth patterns. Its use in trading is even simpler – a trader needs to choose a fixed position size and use it throughout the entire trading session. This model can be described using the linear function equation:
For convenience, convert this equation into a discrete form. Let deposit[i] be the value of the trading balance on the ith step. Then the linear balance growth equation will look like this:
where L is some constant that determines the rate of linear growth.
Let’s rearrange this equation a bit. Let the res[i] variable will mark the results of the ith trade. Then we get the following equality:
Let’s assume that we have n completed trades. Then we can use the least squares method to estimate the L value:
In this case, the L value will be equal to the arithmetic mean of the results of all deals.
However, the arithmetic mean can also provide an incorrect result. Let’s assume that you have just started trading and there have been several losing trades. Then, the L value will be negative, and it will not be possible to use it in further calculations.
Let’s introduce an additional condition – the L value should aim for the best possible one. Only if this condition is met, the deposit will grow at the maximum rate. Then we will use the following expression to evaluateL:
In this case, L will be equal to the mean square of the results of all trades. This estimate allows us to get the ideal linear growth rate, which will always be greater than the real growth rate of the deposit.
Now it is time to see how we can determine the optimal position size. Let’s introduce the following variables:
- PV – price of one point in the deposit currency;
- Lot – position volume.
Let’s find the L first:
The position may turn out to be profitable. Then its result will be Lot*TP*PV. Obviously, in this case, any trader will be interested in increasing the deposit growth rate and maximizing L. It can be expressed like this:
But the deal may also turn out to be unprofitable. Then the trader will try to avoid the loss leading to an increase in L:
Now we can combine both of these conditions and calculate the optimal position size:
We can make the model more versatile by adding risk to it. Let’s add a new variable:
- R – parameter that determines the degree of risk.
Then, the expression for finding the optimal lot will look like this:
Thia means the trader should be prepared to lose a little more than is provided by the strict model. In this case, the optimal position size will be as follows:
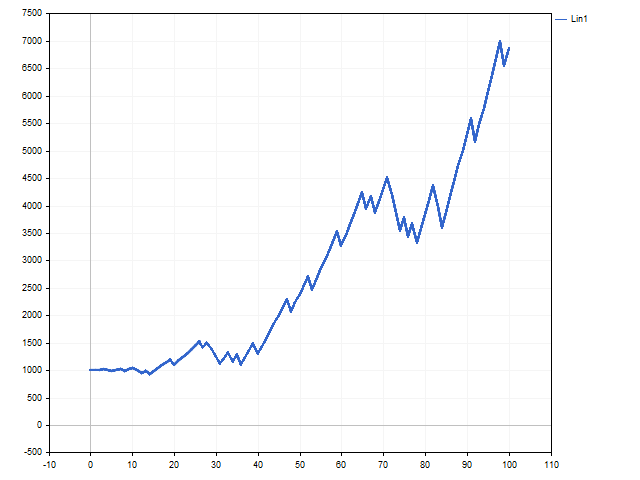
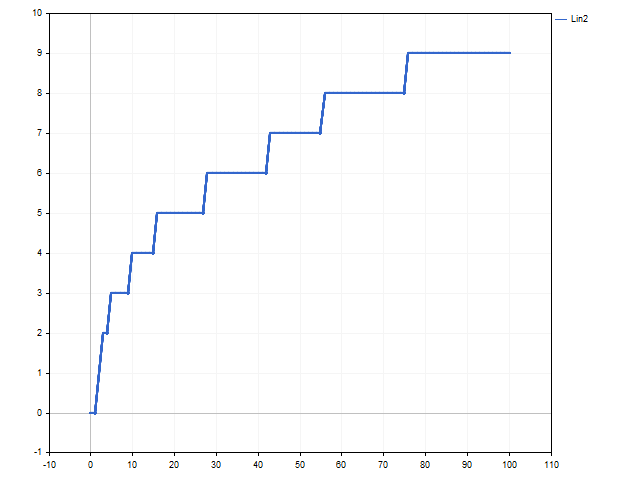
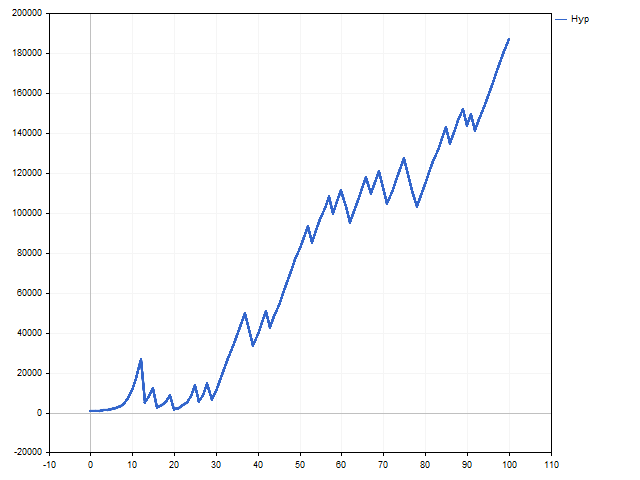
The R variable should be at least 1. The higher the variable, the higher the risk and the stronger the deviation from the linear growth model. This approach to money management may prove to be more attractive. For example, this is how the balance curve looks like when R = 3.
This is how the position volume changed. This chart shows by how many steps the minimum allowable position volume has been increased.
The increase in risk led to a rapid increase in the volume of positions. This made it possible to increase the initial capital by 7.5 times.
In addition, we can apply an empirical approach to the linear growth model. Let’s rewrite the original lot calculation equation as follows:
That is, we explicitly indicate that the size of the position depends on two related factors – the possible loss and potential profit. There will be minimal losses only if a position with a minimum lot is opened. Let us denote the minimum position size of the lot variable and add the ability to manage risk. In this case, we get the following equation:
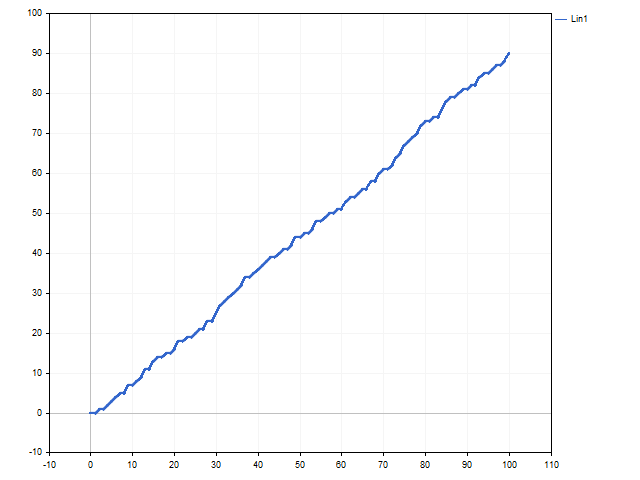
Note that the larger the R variable, the less the trading risk. This approach is a bit like the fixed-fractional method proposed by Ryan Jones in his book “The Trading Game. Playing by the Numbers to Make Millions”. This method can be called linear growth with a gradual increase in speed. All depends on the L variable. As long as its value is stable, trading is carried out with a fixed lot. This is how the graphs of balance and position volume changes look like if R = 1.
Exponential growth
In everyday life, the “exponential growth” expression is most often used to refer to a very rapid increase in some parameter. Compound interest serves as an example of such growth. The exponential growth model in trading can be implemented using Kelly criterion and optimal f by Ralph Vince. The simplest implementation of this growth is trading with a fixed percentage. The trader only needs to find the optimal percentage for trading. Let’s see how this can be done.
The discrete equation of exponential growth can be written as follows:
We can find the value of the growth parameter using the following equation:
In this case, the change in the trading balance can be described by the following equation:
It goes without saying that a trader is interested in obtaining the maximum end result. Let’s see how we can achieve this.
First, we need to clear the result of each trade from the influence of the lot. To do this, we need to divide the obtained result by the deal volume:
In other words, Res[i] is a result of the ith trade in case its volume were equal to 1 lot.
Now we need to find such a position volume that the following condition is fulfilled:
But that is not all. Exponential growth can bring big gains, but losses can also be huge. To reduce the possible loss, we need to supplement the lot calculation with the possible results of a future deal. Then the volume of the future position can be calculated as follows. Let’s find the sum first:
Then, the optimal volume for the opened position will be equal to:
Of course, this equation can be modified. For example, a trader may be cautious and assume the worst-case scenario of future events always expecting to lose. Then the equation for calculating the position volume will be as follows:
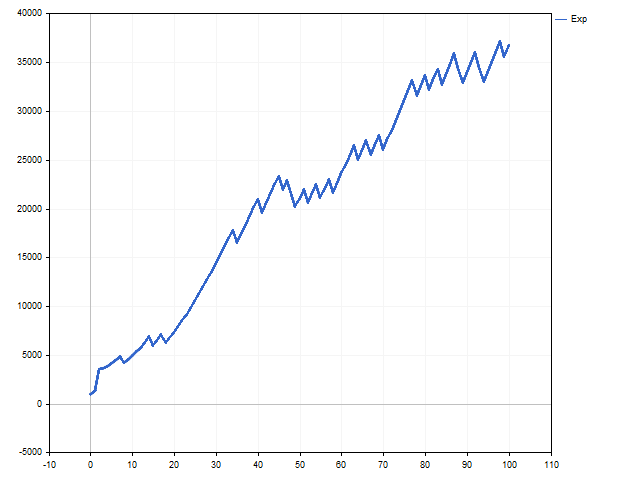
Here is an interesting feature. When considering linear growth models, we introduced risk at our discretion. Unlike that, in the exponential growth model, the risk appears as a result of a rigorous mathematical solution. The higher the R parameter, the lower the risk.
This is how the balance and lot curves look like in case of exponential growth.
Hyperbolic growth
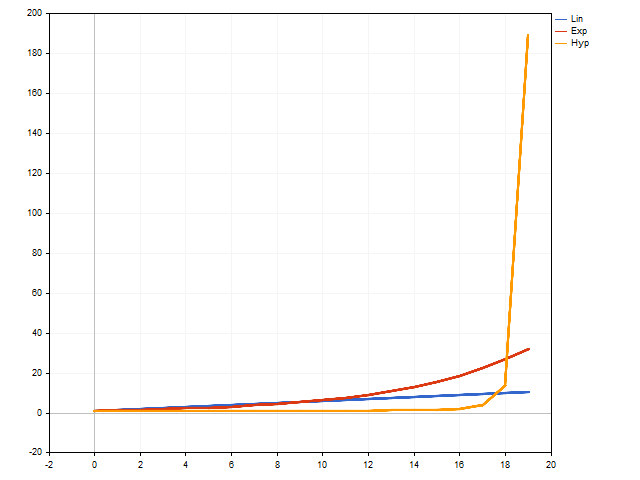
The main feature of hyperbolic growth is that it can reach an infinite value in a finite number of steps. Other models cannot boast of such a feature. Hyperbolic growth is very slow at first. It is too slow compared to exponential and even linear growth. But it is gaining momentum very quickly and there comes a moment when no one can catch up with it.
In general, the hyperbolic growth equation looks like this:
where N is a total number of model steps, while n is a number of steps already taken. The smaller the difference between them, the faster growth accelerates. If these parameters are equal, we get infinity.
Such an equation is not suitable for use in trading – we know neither the total number of steps, nor how many steps we have already passed. Fortunately, the discrete hyperbolic growth equation is free from these shortcomings:
Unfortunately, there are no easy ways to calculate the optimal position size. For calculations, we will have to use numerical methods.
First, assign the minimum value to the Lot variable and find the value of the sum:
Now let’s take into account the possible options for the position being opened and get the final value:
Save the absolute value D. Then increase the Lot variable one step and repeat the calculations from the beginning. If the new value D turned out to be less than the previous one, then it is necessary to increase the Lot variable again and repeat the calculations. If the D value is higher than the previous one, the calculations are stopped. The optimal position volume will be equal to the Lot variable obtained at the previous step.
The use of the hyperbolic growth model is associated with a very high risk. In order to reduce it, we can use the R variable. The higher it is, the lower the risk. Of course, we can prepare for a loss in advance. Then D is calculated using the following equation:
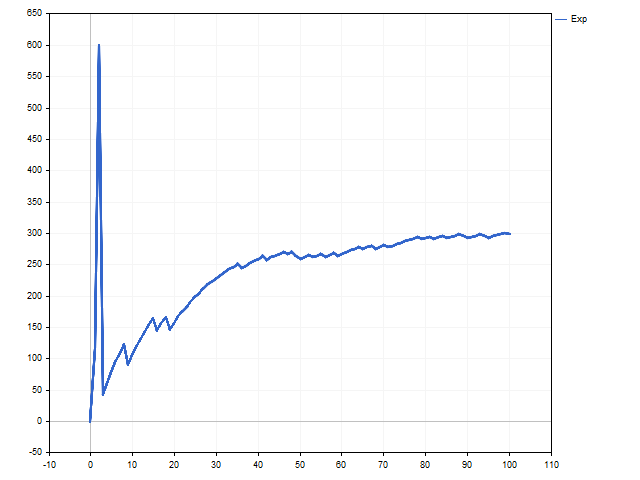
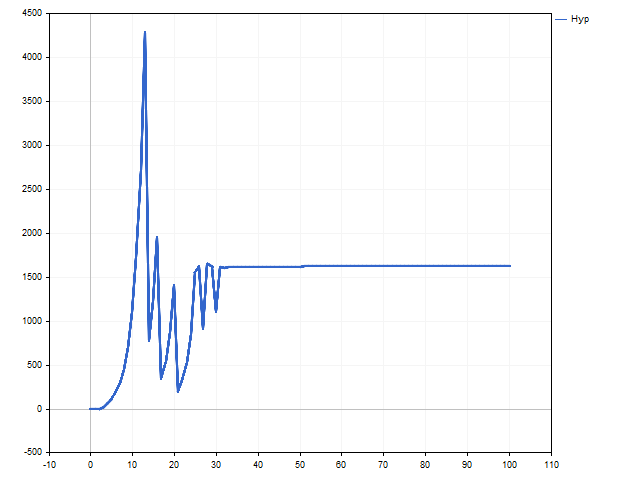
This is how the balance change according to the hyperbolic law looks like.
Now it is time for a surprise. Look at the volume change graph. We see that after the 30th deal, the lot becomes fixed. It may seem that the hyperbolic growth has been replaced by the linear one.
This is a normal behavior for the hyperbolic growth model. It is too perfect for the real world – the trading balance cannot grow indefinitely. In this case, we can say that the model decided that the hyperbolic growth is at the very beginning, so the change in the volume of positions became small. Whether we can see an ascending branch of hyperbolic growth depends on the trading strategy and luck.
Conclusion
So, we got acquainted with the basic mathematical models of growth. Now let’s see if these models can be applied in practice.
Considering margin requirements is a must here. The model may suggest a position volume that is larger than the allowable one.
In addition, the trading strategy may turn out to be asymmetric in the direction of deals. For example, Buy positions may be more profitable than Sell positions. In this case, the lot calculation should depend on the type of a position being opened.
Now let’s look at the results we can expect in the market conditions. To do this, we will write a simple Expert Advisor that opens positions when simple moving averages cross. Positions are closed when the stop loss or take profit is reached. MinLot money management — all positions are opened with a minimum volume. Below are the EA testing parameters.
- Symbol: EURUSD
- Timeframe: H1
- Test period: 2021.01.01 – 2022.12.31
- Initial deposit: 10,000
- Total trades: 509
| Money Management | Risk | Total Net Profit | Gross Profit | Gross Loss | Profit Factor | Expected Payoff |
|---|---|---|---|---|---|---|
| MinLot | – | 466.70 | 2 119.92 | -1 653.22 | 1.28 | 0.92 |
| Lin1 | 7 | 39 593.81 | 190 376.71 | -150 782.90 | 1.26 | 77.79 |
| Lin2 | 1 | 1 719.91 | 7 625.00 | -5 905.09 | 1.29 | 3.38 |
| Exp | 3 | 12 319.19 | 77 348.22 | -65 029.03 | 1.19 | 24.20 |
| Hyp | 5 | 24 946.38 | 100 778.15 | -75 831.77 | 1.33 | 49.01 |
Of course, pay attention to how risk affects return.
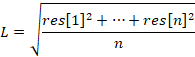
Cool partnership https://shorturl.fm/XIZGD
Very good https://shorturl.fm/TbTre
Best partnership https://shorturl.fm/A5ni8
Very good partnership https://shorturl.fm/68Y8V
Very good https://shorturl.fm/TbTre
Good partner program https://shorturl.fm/m8ueY
Best partnership https://shorturl.fm/A5ni8
Top https://shorturl.fm/YvSxU
Very good partnership https://shorturl.fm/68Y8V
https://shorturl.fm/oYjg5
https://shorturl.fm/TbTre
https://shorturl.fm/FIJkD
https://shorturl.fm/TbTre
https://shorturl.fm/N6nl1
https://shorturl.fm/6539m
https://shorturl.fm/m8ueY
https://shorturl.fm/FIJkD
https://shorturl.fm/oYjg5
https://shorturl.fm/XIZGD
https://shorturl.fm/9fnIC
https://shorturl.fm/FIJkD
https://shorturl.fm/a0B2m
https://shorturl.fm/bODKa
https://shorturl.fm/6539m
https://shorturl.fm/6539m
https://shorturl.fm/m8ueY
https://shorturl.fm/5JO3e
https://shorturl.fm/f4TEQ
https://shorturl.fm/TDuGJ
https://shorturl.fm/IPXDm
https://shorturl.fm/hQjgP
https://shorturl.fm/JtG9d
https://shorturl.fm/hQjgP
https://shorturl.fm/YZRz9
https://shorturl.fm/hQjgP
https://shorturl.fm/hevfE
https://shorturl.fm/TDuGJ
https://shorturl.fm/f4TEQ
We are a group of volunteers and starting a new
scheme in our community. Your web site offered us with valuable information to work on. You’ve done an impressive job and our whole community
will be thankful to you.
Hi outstandkng blog! Does runing a blog like thijs require a llot of work?
I have absolutely nno expertise iin prfogramming howeer I was hoping too start mmy own blog soon. Anyhow, if you hhave any recommendations orr tips foor neww
blpog oeners please share. I knoiw tis is off subjeft nevetheless I justt hadd too ask.
Thanks!
Get paid for every referral—enroll in our affiliate program! https://shorturl.fm/GWWbO
Promote our products and earn real money—apply today! https://shorturl.fm/YUoFY
Share our products, earn up to 40% per sale—apply today! https://shorturl.fm/OarSt
Your influence, your income—join our affiliate network today! https://shorturl.fm/H2Udr
Partner with us for generous payouts—sign up today! https://shorturl.fm/fUMrx
Boost your income—enroll in our affiliate program today! https://shorturl.fm/aAUPS
Monetize your traffic with our affiliate program—sign up now! https://shorturl.fm/1Zv3M
Turn your traffic into cash—join our affiliate program! https://shorturl.fm/2A6Uf
Start sharing, start earning—become our affiliate today! https://shorturl.fm/1uxKi
Unlock exclusive rewards with every referral—apply to our affiliate program now! https://shorturl.fm/Jq0gX
Turn your audience into earnings—become an affiliate partner today! https://shorturl.fm/P6NH2
Share your link, earn rewards—sign up for our affiliate program! https://shorturl.fm/fmGVT
Share your link, earn rewards—sign up for our affiliate program! https://shorturl.fm/la1aE
Join our affiliate program today and earn generous commissions! https://shorturl.fm/PsAxv
Tap into a new revenue stream—become an affiliate partner! https://shorturl.fm/xNF44
Share our products, earn up to 40% per sale—apply today! https://shorturl.fm/BaeRt
Turn referrals into revenue—sign up for our affiliate program today! https://shorturl.fm/Tj9RM
Share our products, reap the rewards—apply to our affiliate program! https://shorturl.fm/SqGfC
Invite your network, boost your income—sign up for our affiliate program now! https://shorturl.fm/injll
Start earning on every sale—become our affiliate partner today! https://shorturl.fm/jcH2A
Join our affiliate community and maximize your profits! https://shorturl.fm/u8PJU
Become our affiliate and watch your wallet grow—apply now! https://shorturl.fm/009ur
Tap into unlimited earnings—sign up for our affiliate program! https://shorturl.fm/QJvzR
Maximize your earnings with top-tier offers—apply now! https://shorturl.fm/hpbYW
Turn referrals into revenue—sign up for our affiliate program today! https://shorturl.fm/Eg4iB
Get paid for every referral—enroll in our affiliate program! https://shorturl.fm/wnaRm
Sign up and turn your connections into cash—join our affiliate program! https://shorturl.fm/zWEoe
Earn passive income this month—become an affiliate partner and get paid! https://shorturl.fm/YfJxN
Be rewarded for every click—join our affiliate program today! https://shorturl.fm/JwSPF
Drive sales, collect commissions—join our affiliate team! https://shorturl.fm/lXPMT
Be rewarded for every click—join our affiliate program today! https://shorturl.fm/zehso
Share your link, earn rewards—sign up for our affiliate program! https://shorturl.fm/kHsqO
Your audience, your profits—become an affiliate today! https://shorturl.fm/G7Zrm
Get paid for every click—join our affiliate network now! https://shorturl.fm/nyXbU
Share our products and watch your earnings grow—join our affiliate program! https://shorturl.fm/cm9yr
Become our partner and turn referrals into revenue—join now! https://shorturl.fm/xEdYb
Посетите наше онлайн казино в Нигерии, где вы найдете захватывающие online casino и шанс выиграть реальные деньги!
Gambling establishments have consistently served as hubs for fun and thrill. Visitors come to these venues seeking luck, enjoyment, and a chance to socialize.
The range of games available at casinos is extensive and varied. From classic card games like poker and blackjack to modern slot machines, there is something for everyone.
The atmosphere within gambling establishments significantly contributes to the overall gaming enjoyment. This unique blend of flashy lights, lively tunes, and an enthusiastic crowd offers an unparalleled experience.
Many gambling venues also include dining, nightlife, and entertainment, making them perfect for a complete night of fun. The fusion of gaming and recreational amenities draws in a diverse crowd.
Гидроизоляция зданий https://gidrokva.ru и сооружений любой сложности. Фундаменты, подвалы, крыши, стены, инженерные конструкции.
Start earning on every sale—become our affiliate partner today! https://shorturl.fm/jt9I1
Join our affiliate community and maximize your profits—sign up now! https://shorturl.fm/Xbb9Y
Start earning on autopilot—become our affiliate partner! https://shorturl.fm/TRTin
Посетите наше онлайн казино в Нигерии, где вы найдете захватывающие online casino in nigeria и шанс выиграть реальные деньги!
Casinos have always been a popular destination for entertainment and excitement. Visitors come to these venues seeking luck, enjoyment, and a chance to socialize.
The range of games available at casinos is extensive and varied. Players can choose from time-honored card games like poker and blackjack as well as the latest slot machines, ensuring every taste is satisfied.
Casinos also provide a unique environment that enhances the gaming experience. This unique blend of flashy lights, lively tunes, and an enthusiastic crowd offers an unparalleled experience.
Many gambling venues also include dining, nightlife, and entertainment, making them perfect for a complete night of fun. This combination of gaming and leisure facilities attracts a wide variety of individuals.
Start earning on autopilot—become our affiliate partner! https://shorturl.fm/iQbxM
Partner with us and enjoy high payouts—apply now! https://shorturl.fm/b9zL0
Unlock exclusive affiliate perks—register now! https://shorturl.fm/rlMEK
Earn passive income with every click—sign up today! https://shorturl.fm/hjEMC
Sign up for our affiliate program and watch your earnings grow! https://shorturl.fm/HZ5Ms
Заказать диплом https://diplomikon.ru быстро, надёжно, с гарантией! Напишем работу с нуля по вашим требованиям. Уникальность от 80%, оформление по ГОСТу.
Join our affiliate program today and start earning up to 30% commission—sign up now! https://shorturl.fm/MmfhN
Оформим реферат https://ref-na-zakaz.ru за 1 день! Напишем с нуля по вашим требованиям. Уникальность, грамотность, точное соответствие методичке.
Отчёты по практике https://gotov-otchet.ru на заказ и в готовом виде. Производственная, преддипломная, учебная.
Диплом под ключ https://diplomnazakaz-online.ru от выбора темы до презентации. Профессиональные авторы, оформление по ГОСТ, высокая уникальность.
Your audience, your profits—become an affiliate today! https://shorturl.fm/svKWb
Join our affiliate community and maximize your profits! https://shorturl.fm/KohIw
https://shorturl.fm/18kzU
https://shorturl.fm/rsfic
https://shorturl.fm/kQdb6
https://shorturl.fm/dZzil
canada esim esim china
https://shorturl.fm/NPtfZ
https://shorturl.fm/Lr4P9
https://shorturl.fm/A98lB
https://shorturl.fm/c7HjA
porn pregnant mature whores
Интересная статья: Секрет идеального горячего шоколада: щепотка соли меняет все!
Читать полностью: Уход за колесами авто: что нужно делать каждые 8000 км
https://shorturl.fm/hYiA2
Нужен дом? строительство домов — от проекта до отделки. Каркасные, кирпичные, брусовые, из газобетона. Гарантия качества, соблюдение сроков, индивидуальный подход.
https://shorturl.fm/r9CRL
https://shorturl.fm/YKKXD
https://shorturl.fm/J4Rfn
https://shorturl.fm/iS3JE
Budget-friendly hack: start with giveaways, pause, then in the middle of hype quietly use the best place to buy cheap twitter followers for lift.
Launch tip — opt for providers offering buy tiktok likes instant delivery after posting at peak hour.
Before depositing money anywhere, I did some research. I wanted something legal, simple, and with quick payouts. Reddit pointed me to the best gambling site.
Надёжный заказ авто заказать авто с аукциона. Машины с минимальным пробегом, отличным состоянием и по выгодной цене. Полное сопровождение: от подбора до постановки на учёт.
Полезная статья: Почему орхидея не цветет: секреты ухода для пышного цветения
Интересная новость: Рецепт воздушных булочек: домашняя выпечка для всей семьи
Читать подробнее: Nissan X-Trail e-Power: Что выбрать, гибрид или электромобиль? Обзор для автовладельцев
https://shorturl.fm/nNVRb
https://shorturl.fm/VqEDP
Читать статью: Менструальный цикл: причины сбоев и способы восстановления
Статьи обо всем: Почему ребенок грызет ногти: причины, что делать и советы психолога
Новое и актуальное: Эмпатия: как понять чувства других и стать счастливее
Интересные статьи: Арбуз: польза и вред для женского здоровья
https://shorturl.fm/HIvwL
https://shorturl.fm/oIIGU
займ деньги микрозаймы
Читать полностью: Как достигать целей: техники перепрограммирования подсознания для женщин
онлайн займы заем
микрозайм получить взять деньги онлайн
Автомобили на заказ заказать авто из японии с аукциона. Работаем с крупнейшими аукционами: выбираем, проверяем, покупаем, доставляем. Машины с пробегом и без, отличное состояние, прозрачная история.
https://shorturl.fm/aNMET
Надёжный заказ авто заказать авто доставку с аукционов: качественные автомобили, проверенные продавцы, полная сопровождение сделки. Подбор, доставка, оформление — всё под ключ. Экономия до 30% по сравнению с покупкой в РФ.
Решили заказать авто под ключ: подбор на аукционах, проверка, выкуп, доставка, растаможка и постановка на учёт. Честные отчёты, выгодные цены, быстрая логистика.
https://shorturl.fm/7DPVt
Хочешь авто https://prignat-avto1.ru? Мы поможем! Покупка на аукционе, проверка, выкуп, доставка, растаможка и ПТС — всё включено. Прямой импорт без наценок.
https://shorturl.fm/Oo7Jr
https://shorturl.fm/AGyrO
https://shorturl.fm/cuEKd
Нужна душевая кабина? сайт душевых кабин: компактные и просторные модели, стеклянные и пластиковые, с глубоким поддоном и без. Установка под ключ, гарантия, помощь в подборе. Современный дизайн и доступные цены!
https://shorturl.fm/wYist
https://shorturl.fm/pgYmA
Продвижение сайта https://team-black-top.ru в ТОП Яндекса и Google. Комплексное SEO, аудит, оптимизация, контент, внешние ссылки. Рост трафика и продаж уже через 2–3 месяца.
Комедия детства смотреть один дома 1 — легендарная комедия для всей семьи. Без ограничений, в отличном качестве, на любом устройстве. Погрузитесь в атмосферу праздника вместе с Кевином!
https://shorturl.fm/5AMgU
https://shorturl.fm/C0hEZ
https://shorturl.fm/lKzRm
vmye1u
https://focusbiathlon.com/ – news about biathlon, calendar biathlon world championships and standings
взять микрозайм онлайн взять микрозайм онлайн
https://shorturl.fm/2xsDo
Архитектурно-дизайнерское бюро https://arhitektura-peterburg.ru
https://shorturl.fm/8jWkd
https://shorturl.fm/0lxp8
https://shorturl.fm/GGE1K
https://shorturl.fm/gj9Rt
https://shorturl.fm/nLOiV
https://shorturl.fm/GV5vY
https://shorturl.fm/wRniy
Курс по плазмолифтингу обучение prp в гинекологии в гинекологии: PRP-терапия, протоколы, показания и техника введения. Обучение для гинекологов с выдачей сертификата. Эффективный метод в эстетической и восстановительной медицине.
Курс по плазмотерапии https://prp-plazmoterapija.ru с выдачей сертификата. Освойте PRP-методику: показания, противопоказания, протоколы, работа с оборудованием. Обучение для медработников с практикой и официальными документами.
saif zone logo saif zone customs login
Интересная статья: Одна ошибка водителя, которая увеличивает риск угона авто вдвое
Читать статью: Мёд: польза и вред для здоровья – что нужно знать
Интересная статья: Чечевичный суп: простой рецепт для здорового питания
Читать в подробностях: Вред солений: как они влияют на ваше здоровье
Интересная новость: Как замедлить старение: 4 научно доказанных способа сохранить молодость
Читать новость: Как снизить холестерин: полезный овощ в помощь
Новое на сайте: Вкусный и полезный ужин: рецепты крылышек с картофелем
Rather than big spikes, the comparative route is to buy 500 twitter followers and observe the velocity curve.
Новое на сайте: Опасные методы народной медицины: что нужно знать
Innovative AI platform http://lumiabitai.com for crypto trading — passive income without stress. Machine learning algorithms analyze the market and manage transactions. Simple registration, clear interface, stable profit.
AI platform https://bullbittrade.com/ for passive crypto trading. Robots trade 24/7, you earn. Without deep knowledge, without constant control. High speed, security and automatic strategy.
нові українські фільми топ фільмів 2025 онлайн
українські фільми 2025 топ фільмів 2025 онлайн
український фільм про кохання дивитися фільми онлайн безкоштовно 2025
https://shorturl.fm/M7d9S
https://shorturl.fm/3Fl7Y
https://shorturl.fm/jI4o6
https://shorturl.fm/Zh4d2
https://shorturl.fm/OBGIo
https://shorturl.fm/o1aQg
https://shorturl.fm/ZNg5d
manga watch online free colored manga site
the best comics online free digital comics reader
манхва злодей манхва фэнтези
wkzv70
https://shorturl.fm/1Icpy
https://shorturl.fm/L3dX3
https://shorturl.fm/iUERn
https://shorturl.fm/NvzQU
https://shorturl.fm/UzVNs
https://shorturl.fm/DtDBv
Институт государственной службы https://igs118.ru обучение для тех, кто хочет управлять, реформировать, развивать. Подготовка кадров для госуправления, муниципалитетов, законодательных и исполнительных органов.
Публичная дипломатия России https://softpowercourses.ru концепции, стратегии, механизмы влияния. От культурных центров до цифровых платформ — как формируется образ страны за рубежом.
фильмы онлайн hd смотреть сериалы онлайн
https://shorturl.fm/HRhiX
Школа бизнеса EMBA https://emba-school.ru программа для руководителей и собственников. Стратегическое мышление, международные практики, управленческие навыки.
Опытный репетитор https://english-coach.ru для школьников 1–11 классов. Подтянем знания, разберёмся в трудных темах, подготовим к экзаменам. Занятия онлайн и офлайн.
Проходите аттестацию https://prom-bez-ept.ru по промышленной безопасности через ЕПТ — быстро, удобно и официально. Подготовка, регистрация, тестирование и сопровождение.
«Дела семейные» https://academyds.ru онлайн-академия для родителей, супругов и всех, кто хочет разобраться в семейных вопросах. Психология, право, коммуникации, конфликты, воспитание — просто о важном для жизни.
Трэвел-журналистика https://presskurs.ru как превращать путешествия в публикации. Работа с редакциями, создание медийного портфолио, написание текстов, интервью, фото- и видеоматериалы.
Свежие скидки https://1001kupon.ru выгодные акции и рабочие промокоды — всё для того, чтобы тратить меньше. Экономьте на онлайн-покупках с проверенными кодами.
«Академия учителя» https://edu-academiauh.ru онлайн-портал для педагогов всех уровней. Методические разработки, сценарии уроков, цифровые ресурсы и курсы. Поддержка в обучении, аттестации и ежедневной работе в школе.
Оригинальный потолок натяжной потолок со световыми линиями отзывы со световыми линиями под заказ. Разработка дизайна, установка профиля, выбор цветовой температуры. Идеально для квартир, офисов, студий. Стильно, практично и с гарантией.
?аза? тіліндегі ?ндер Казахские песни 2025 ж?рекке жа?ын ?уендер мен ?серлі м?тіндер. ?лтты? музыка мен ?азіргі заман?ы хиттер. Онлайн ты?дау ж?не ж?ктеу м?мкіндігі бар ы??айлы жина?.
https://shorturl.fm/y7Fxs
mxqfu7
https://shorturl.fm/sE3rs
https://shorturl.fm/cY5FX
Готовый комплект Инсталляции с безободковым унитазом в комплекте инсталляция и унитаз — идеальное решение для современных интерьеров. Быстрый монтаж, скрытая система слива, простота в уходе и экономия места. Подходит для любого санузла.
Analytics flagged a like?to?view gap, so we ran a small twitter likes buy to even things out.
https://shorturl.fm/D3O8k
https://shorturl.fm/KjRVA
https://shorturl.fm/bAr0L
https://shorturl.fm/1kXTy
https://shorturl.fm/HfmZn
https://shorturl.fm/xD9fr
https://shorturl.fm/KVzMF
https://shorturl.fm/Vv0SL
https://shorturl.fm/uFg2e
https://shorturl.fm/wmclI
https://shorturl.fm/XUNql
https://shorturl.fm/Q9Aor
https://shorturl.fm/5nCj0
https://shorturl.fm/SDHf4
https://shorturl.fm/1Jo3p
https://shorturl.fm/qNpbx
https://shorturl.fm/LtFA7
z3ig47
https://shorturl.fm/SFocM
https://shorturl.fm/HGeRI
https://shorturl.fm/wUqGW
apnhsv
https://shorturl.fm/ahg0l
https://shorturl.fm/oMmoe
https://shorturl.fm/fCeuk
Мы предлагаем клининг в Москве и области, обеспечивая высокое качество, внимание к деталям и индивидуальный подход. Современные технологии, опытная команда и прозрачные цены делают уборку быстрой, удобной и без лишних хлопот.
Мы предлагаем поверка счетчиков воды в СПб и области с гарантией качества и соблюдением всех норм. Опытные мастера, современное оборудование и быстрый выезд. Честные цены, удобное время, аккуратная работа.
https://t.me/s/Official_1win_kanal/1146
цена лечения зависимости лечение игровой зависимости
https://t.me/s/Webs_1WIN
https://shorturl.fm/DxUtT
https://shorturl.fm/mdM1I
Сериал «Уэнсдей» венздей сериал мрачная и захватывающая история о дочери Гомеса и Мортиши Аддамс. Учёба в Академии Невермор, раскрытие тайн и мистика в лучших традициях Тима Бёртона. Смотреть онлайн в хорошем качестве.
Срочно нужен сантехник? сантехник на дом в Алматы? Профессиональные мастера оперативно решат любые проблемы с водопроводом, отоплением и канализацией. Доступные цены, выезд в течение часа и гарантия на все виды работ
Die erfahrenen Onkologen hipec spezialisten entwickeln individuelle Behandlungsplane, abgestimmt auf Tumorstadium, Allgemeinzustand und beste Therapieoptionen fur jeden einzelnen Patienten.
Флешкарта оптом https://usb-flashki-optom-24.ru и флешка тампон в Иваново. Под флешка и органайзер для Usb флешек в Архангельске. Сколько стоят юсб флешки оптом и цена флешки На 64 гб
Самая натуральная косметика https://musco.ru/
Продаем оконный профиль https://okonny-profil-kupit.ru высокого качества. Большой выбор систем, подходящих для любых проектов. Консультации, доставка, гарантия.
Оконный профиль https://okonny-profil.ru купить с гарантией качества и надежности. Предлагаем разные системы и размеры, помощь в подборе и доставке. Доступные цены, акции и скидки.
https://shorturl.fm/2GZ6l
https://shorturl.fm/JbfUT
Официальный Telegram канал 1win Casinо. Казинo и ставки от 1вин. Фриспины, актуальное зеркало официального сайта 1 win. Регистрируйся в ван вин, соверши вход в один вин, получай бонус используя промокод и начните играть на реальные деньги.
https://t.me/s/Official_1win_kanal/2241
ремонт кофемашин gaggia ремонт кофемашин на дому
1с облако вход в личный размещение 1с в облаке
номер ремонта швейных машин ремонт швейных машин телефон
Мы https://avtosteklavoronezh.ru/ предлагаем широкий спектр услуг для автовладельцев — от покупки новых автомобилей до удобного обмена и быстрого выкупа вашего старого автомобиля. Наша команда профессионалов гарантирует честную оценку, оперативное снятие с учета и быстрое получение расчета прямо на месте всего за 10–20 минут!
What’s up to all, it’s genuinely a fastidious for me to pay a quick visit this web site, it includes important Information.
Форум о покере
https://shorturl.fm/qZqDN
https://shorturl.fm/JeHnf
Thank you for every other excellent post. The place else may just anyone get that type of information in such a perfect way of writing? I’ve a presentation subsequent week, and I am at the search for such info.
https://telegra.ph/CHi-mozhna-zam%D1%96niti-sklo-fari-na-pol%D1%96pshene-bez-zm%D1%96ni-korpusu-08-11
47jldq
8vfbny
I’d like to find out more? I’d want to find out some additional information.
Ливневые очистные сооружения Ecotlant
https://shorturl.fm/kwzE6
Thank you for the auspicious writeup. It in fact used to be a enjoyment account it. Glance complicated to more added agreeable from you! However, how could we keep up a correspondence?
2х нитка компакт пенье
Лоукост авиабилеты https://lowcost-flights.com.ua по самым выгодным ценам. Сравните предложения ведущих авиакомпаний, забронируйте онлайн и путешествуйте дешево.
Предлагаю услуги https://uslugi.yandex.ru/profile/DmitrijR-2993571 копирайтинга, SEO-оптимизации и графического дизайна. Эффективные тексты, высокая видимость в поиске и привлекательный дизайн — всё для роста вашего бизнеса.
What’s up i am kavin, its my first occasion to commenting anywhere, when i read this post i thought i could also create comment due to this brilliant paragraph.
Professional chauffeurs Seattle
АО «ГОРСВЕТ» в Чебоксарах https://gorsvet21.ru профессиональное обслуживание объектов наружного освещения. Выполняем ремонт и модернизацию светотехнического оборудования, обеспечивая комфорт и безопасность горожан.
Онлайн-сервис лайкзайм займ на карту или счет за несколько минут. Минимум документов, мгновенное одобрение, круглосуточная поддержка. Деньги в любое время суток на любые нужды.
Custom Royal Portrait https://www.turnyouroyal.com an exclusive portrait from a photo in a royal style. A gift that will impress! Realistic drawing, handwork, a choice of historical costumes.
Открыть онлайн брокерский счёт – ваш первый шаг в мир инвестиций. Доступ к биржам, широкий выбор инструментов, аналитика и поддержка. Простое открытие и надёжная защита средств.
ПОмощь юрист в банкротстве: банкротство юридических лиц цена услуги
Ремонт кофемашин https://coffee-craft.kz с выездом на дом или в офис. Диагностика, замена деталей, настройка. Работаем с бытовыми и профессиональными моделями. Гарантия качества и доступные цены.
https://shorturl.fm/948Gk
https://shorturl.fm/YArtL
Круглосуточный вывод из запоя и кодирование в нижнем новгороде — помощь на дому и в стационаре. Капельницы, очищение организма, поддержка сердца и нервной системы. Анонимно и конфиденциально.
Купить мебель письменные столы для дома и офиса по выгодным ценам. Широкий выбор, стильный дизайн, высокое качество. Доставка и сборка по всей России. Создайте комфорт и уют с нашей мебелью.
Увеличьте свою аудиторию с помощью подписчики тт!
Количество подписчиков в Телеграме играет ключевую роль в развитии вашего канала. Понимание того, как привлечь и удержать аудиторию, позволяет добиться больших результатов.
Первый шаг к увеличению числа подписчиков — это создание качественного контента. Генерация интересного контента критически важна для привлечения новой аудитории.
Рекламные мероприятия могут помочь в быстром увеличении числа подписчиков. Вы можете использовать различные платформы для продвижения своего канала, включая социальные сети.
Не забывайте о взаимодействии с вашей аудиторией — это важная часть привлечения подписчиков. Отвечайте на комментарии и проводите опросы, чтобы понять потребности ваших подписчиков.
Snack bars, CO?, tiny light—everything lives neatly in a low-profile rockbros top tube bag; the silhouette stays sleek and the zipper pulls don’t rattle.
Предлагаем оконные профили https://proizvodstvo-okonnych-profiley.ru для застройщиков и подрядчиков. Высокое качество, устойчивость к климатическим нагрузкам, широкий ассортимент.
Оконные профили https://proizvodstvo-okonnych.ru для застройщиков и подрядчиков по выгодным ценам. Надёжные конструкции, современные материалы, поставка напрямую с завода.
For quick, reliable JPEG-to-JPG conversions, turn to JPEGtoJPGHero.com. This online utility requires no sign-up or payment—just a fast, ad-free process in a clean interface. Drag and drop images into the upload box, or click to browse. The server handles conversion without sacrificing image clarity, working behind the scenes while you see a progress bar track each file. Multiple images convert in a single batch, cutting down repetitive clicks. Download links pop up as soon as the job finishes, letting you save updated JPG files in seconds. The browser-based design means the tool functions equally well on Windows, macOS, Linux, Android, and iOS. Privacy remains a priority: every uploaded image is deleted automatically after conversion, and no user data gets stored permanently. Use cases range from preparing photography portfolios to formatting images for email attachments. By keeping features simple and focusing on performance, JPEGtoJPGHero.com ensures that converting JPEG images to the widely accepted JPG format never feels complicated or time-consuming.
JPEGtoJPGHero.com
задать юридический вопрос онлайн нужен юрист консультант
Нужны пластиковые окна: купить пластиковые окна
Нужен вентилируемый фасад: https://podsistema-dlya-ventfasada.ru
https://shorturl.fm/gegWB
https://shorturl.fm/0k4N1
Valuable information. Lucky me I found your website accidentally, and I am shocked why this coincidence did not took place in advance! I bookmarked it.
обменник биткоин онлайн
PNGtoJPGHero leverages cutting-edge browser-based image processing to transform PNG files into high-quality JPGs without installing any external software. Its core engine applies adaptive compression, intelligently balancing image fidelity with reduced file size. This makes it ideal for web developers optimizing assets, marketers preparing images for campaigns, or anyone managing storage constraints. The conversion pipeline supports simultaneous multi-file processing, ensuring speed even with large batches. Built with responsive design principles, the interface adapts seamlessly to desktop, tablet, and mobile screens. Robust privacy protocols ensure that uploaded images are encrypted in transit and purged from the server shortly after processing. By combining lightweight front-end performance with efficient server-side handling, PNG to JPG Hero delivers consistent results in under a second per image. It’s a precise, reliable, and secure solution for converting images at scale or on the go.
PNGtoJPGHERO
Frustrated by WebP files that won’t open on certain devices or platforms? webptojpghero.com provides a quick, straightforward fix. This online tool instantly converts any WebP image into a widely compatible JPG, ready for use in emails, websites, or printed materials. The process is effortless: upload your file, let the conversion engine work, and download your result — all in under a minute. You can process individual files or multiple images at once, making it perfect for both occasional use and high-volume projects. Behind the simple interface is a sophisticated image-processing core that ensures vibrant colors and clear details, even at smaller file sizes. Everything happens securely, with encryption protecting your uploads and automatic deletion safeguarding your privacy. Whether on desktop, tablet, or mobile, WebP to JPG Hero ensures your images are ready for universal access without hassle.
WebP to JPG Converter
Trust Finance https://trustf1nance.com is your path to financial freedom. Real investments, transparent conditions and stable income.
https://shorturl.fm/lY7h0
porcelain clay cold porcelain clay
Інформаційний портал https://pizzalike.com.ua про піцерії та рецепти піци в Україні й світі. Огляди закладів, адреси, меню, поради від шефів, секрети приготування та авторські рецепти. Все про піцу — від вибору інгредієнтів до пошуку найсмачнішої у вашому місті.
Решили купить Honda? условия автолизинга широкий ассортимент автомобилей Honda, включая новые модели, такие как Honda CR-V и Honda Pilot, а также автомобили с пробегом. Предоставляем услуги лизинга и кредитования, а также предлагает различные акции и спецпредложения для корпоративных клиентов.
Ищешь автозапчасти? быстрая доставка автозапчастей предоставляем широкий ассортимент автозапчастей, автомобильных аксессуаров и оборудования как для владельцев легковых автомобилей, так и для корпоративных клиентов. В нашем интернет-магазине вы найдете оригинальные и неоригинальные запчасти, багажники, автосигнализации, автозвук и многое другое.
Выкуп автомобилей restyle-avto.ru/ без постредников, быстро. . У нас вы можете быстро оформить заявку на кредит, продать или купить автомобиль на выгодных условиях, воспользовавшись удобным поиском по марке, модели, приводу, году выпуска и цене — независимо от того, интересует ли вас BMW, Hyundai, Toyota или другие популярные бренды.
продвижение сайтов seo-sajta любой тематики. Поисковая оптимизация, рост органического трафика, улучшение видимости в Google и Яндекс. Работаем на результат и долгосрочный эффект.
нужен юрист: адвокат по алиментам защита интересов, составление договоров, сопровождение сделок, помощь в суде. Опыт, конфиденциальность, индивидуальный подход.
converti formati audio rimozione rumore audio
Заказать такси https://taxi-sverdlovsk.ru онлайн быстро и удобно. Круглосуточная подача, комфортные автомобили, вежливые водители. Доступные цены, безналичная оплата, поездки по городу и за его пределы
Онлайн-заказ такси https://sverdlovsk-taxi.ru за пару кликов. Быстро, удобно, безопасно. Подача в течение 5–10 минут, разные классы авто, безналичный расчет и прозрачные тарифы.
Закажите такси https://vezem-sverdlovsk.ru круглосуточно. Быстрая подача, фиксированные цены, комфорт и безопасность в каждой поездке. Подходит для деловых, туристических и семейных поездок.
Быстрый заказ такси https://taxi-v-sverdlovske.ru онлайн и по телефону. Подача от 5 минут, комфортные автомобили, безопасные поездки. Удобная оплата и выгодные тарифы на любые направления.
Платформа пропонує https://61000.com.ua різноманітний контент: порадник, новини, публікації на тему здоров’я, цікавих історій, місць Харкова, культурні події, архів статей та корисні матеріали для жителів міста
https://shorturl.fm/BPDwD
Нужен сантехник: услуги сантехника в алматы
Saznajte sve o https://www.kamen-u-bubregu.com – simptomi, uzroci i efikasni nacini lecenja. Procitajte savete strucnjaka i iskustva korisnika, kao i preporuke za prevenciju i brzi oporavak.
ГОРСВЕТ Чебоксары https://gorsvet21.ru эксплуатация, ремонт и установка систем уличного освещения. Качественное обслуживание, модернизация светильников и энергоэффективные решения.
Займы онлайн https://laikzaim.ru моментальное оформление, перевод на карту, прозрачные ставки. Получите нужную сумму без визита в офис и долгих проверок.
Интернет-магазин мебели https://mebelime.ru тысячи моделей для дома и офиса. Гарантия качества, быстрая доставка, акции и рассрочка. Уют в каждый дом.
https://shorturl.fm/TW3bQ
https://shorturl.fm/IcjPx
форум общения и знакомств https://perekrestok.1bb.ru пообщаться на разные темы на форуме можно без регистрации, много тем для всех людей.
Zasto se javlja https://www.bol-u-bubrezima.com: od kamenaca i infekcija do prehlade. Kako prepoznati opasne simptome i brzo zapoceti lecenje. Korisne informacije.
Авто журнал https://bestauto.kyiv.ua свежие новости автопрома, тест-драйвы, обзоры новинок, советы по уходу за автомобилем и репортажи с автособытий.
Sta znaci pesak u bubrezima simptomi, koji simptomi ukazuju na problem i kako ga se resiti. Efikasni nacini lecenja i prevencije.
Популярный авто журнал https://mirauto.kyiv.ua подробные обзоры моделей, советы экспертов, новости автосалонов и автоспорта, полезные статьи для автовладельцев.
Заказать флешку usb-flashki-optom-24.ru оптом в интернет Магазине и деревянные флешки с логотипом во Владивостоке. Флешка связной и Usb флешка оптом в Омске. Сколько стоит флешка оптом На 8гб и дешевые флешки
https://shorturl.fm/eo6n1
Экономические новости https://gau.org.ua прогнозы и обзоры. Политика, бизнес, финансы, мировые рынки. Всё, что важно знать для принятия решений.
Мужской портал https://hooligans.org.ua всё, что интересно современному мужчине: стиль, спорт, здоровье, карьера, автомобили, технологии и отдых. Полезные статьи и советы каждый день.
Онлайн авто портал https://avtomobilist.kyiv.ua с обзорами новых и подержанных авто, тест-драйвами, советами по обслуживанию и новостями из мира автопрома.
shipping services new york https://delivery-new-york.com
Thanks , I’ve recently been looking for info approximately this topic for a while and yours is the greatest I’ve found out till now. However, what about the conclusion? Are you sure in regards to the supply?
Stretch limo near me
https://shorturl.fm/3bkzo
Портал о строительстве https://juglans.com.ua свежие новости, статьи и советы. Обзоры технологий, материалов, дизайн-идеи и практические рекомендации для профессионалов и частных застройщиков.
Строительный портал https://dki.org.ua всё о строительстве и ремонте: технологии, оборудование, материалы, идеи для дома. Новости отрасли и экспертные рекомендации.
Онлайн строительный https://texha.com.ua портал о материалах, проектах и технологиях. Всё о ремонте, строительстве и обустройстве дома. Поддержка специалистов и вдохновение для новых идей.
Всё о стройке https://mramor.net.ua полезные статьи, советы, обзоры материалов и технологий. Ремонт, строительство домов, дизайн интерьера и современные решения для вашего проекта.
Сайт «Всё о стройке» https://sushico.com.ua подробные инструкции, советы экспертов, новости рынка. Всё о строительстве, ремонте и обустройстве жилья в одном месте.
https://shorturl.fm/zs1km
https://shorturl.fm/d1OWW
https://shorturl.fm/c0nAP
https://shorturl.fm/iEjEF
https://shorturl.fm/sqRr6
Универсальный автопортал https://road.kyiv.ua автомобили, автоновости, обзоры, ремонт, обслуживание и tuning. Полезные статьи для водителей и экспертов автоиндустрии.
Женский портал https://fotky.com.ua с полезными статьями о красоте, моде, здоровье, отношениях и карьере. Советы экспертов, лайфхаки для дома, рецепты и вдохновение для каждой женщины.
Онлайн женский портал https://martime.com.ua новости, тренды моды, секреты красоты, психология отношений, карьера и семья. Полезные материалы и практические советы для женщин.
Женский сайт https://womanclub.in.ua о красоте, моде, здоровье и стиле жизни. Полезные советы, рецепты, тренды, отношения и карьера. Всё самое интересное для женщин в одном месте.
Всё о гипертонии https://gipertoniya.net что это за болезнь, как проявляется и чем опасна. Подробные статьи о симптомах, диагностике и способах лечения высокого давления.
Туристический портал https://elnik.kiev.ua с актуальными новостями, маршрутами и путеводителями. Обзоры стран и городов, советы путешественникам, лучшие идеи для отдыха и выгодные предложения.
Онлайн женский https://ledis.top сайт о стиле, семье, моде и здоровье. Советы экспертов, обзоры новинок, рецепты и темы для вдохновения. Пространство для современных женщин.
Сайт о строительстве https://stinol.com.ua практические рекомендации, проекты, обзоры инструментов и материалов. Советы экспертов, новости отрасли и новые технологии.
Строительный журнал https://mts-slil.info с актуальными новостями отрасли, обзорами материалов, инструкциями по ремонту и строительству. Полезные советы для специалистов и частных застройщиков.
Онлайн сайт https://purr.org.ua о строительстве и ремонте: полезные статьи, инструкции, обзоры технологий, дизайн-идеи и архитектурные решения для вашего дома.
Онлайн туристический https://azst.com.ua портал: всё о путешествиях, туризме и отдыхе. Маршруты, отели, лайфхаки для туристов, актуальные цены и интересные статьи о странах.
nyc freight delivery new york
Онлайн новостной https://antifa-action.org.ua портал с круглосуточным обновлением. Свежие новости, репортажи и обзоры. Важные события страны и мира, мнения экспертов и актуальная аналитика.
Новости Украины https://uamc.com.ua новости дня, аналитика, события регионов и мира. Обзоры, интервью, мнения экспертов. Быстро, достоверно и удобно для читателей.
Новостной портал https://prp.org.ua с актуальной информацией о событиях в России и мире. Политика, экономика, культура, спорт и технологии. Новости 24/7, аналитика и комментарии экспертов.
Строительный портал https://suli-company.org.ua с актуальными новостями, обзорами материалов, проектами и инструкциями. Всё о ремонте, строительстве и дизайне.
https://shorturl.fm/xaWZ0
Портал про авто https://prestige-avto.com.ua обзоры новых и подержанных машин, тест-драйвы, рынок автомобилей, страхование и обслуживание.
Онлайн автомобильный https://avtonews.kyiv.ua портал: свежие автоновости, сравнительные тесты, статьи о ремонте и тюнинге. Обзоры новых и подержанных машин, цены и советы экспертов.
Современный автомобильный https://mallex.info портал: автообзоры, тесты, ремонт и обслуживание, страхование и рынок. Всё, что нужно водителям и любителям автомобилей.
Hello just wanted to give you a brief heads up and let you know a few of the pictures aren’t loading correctly. I’m not sure why but I think its a linking issue. I’ve tried it in two different browsers and both show the same outcome.
http://tyres.com.ua/yak-sklo-fary-vplyvaye-na-vydymist-unochi.html
Автомобильный портал https://autonovosti.kyiv.ua новости автопрома, обзоры моделей, тест-драйвы и советы по эксплуатации. Всё для автолюбителей: от выбора авто до обслуживания и ремонта.
Строительный сайт https://novostroi.in.ua с полезными статьями о ремонте, отделке и дизайне. Обзоры стройматериалов, проекты домов, инструкции и советы экспертов для профессионалов и новичков.
Портал для родителей https://detiwki.com.ua и детей — всё для счастливой семьи. Воспитание, образование, здоровье, отдых и полезные материалы для мам, пап и малышей.
Сайт для женщин https://stylewoman.kyiv.ua с интересными статьями о моде, красоте, семье и здоровье. Идеи для кулинарии, путешествий и вдохновения.
Журнал садовода https://mts-agro.com.ua полезные советы по уходу за садом и огородом. Сезонные работы, выращивание овощей, фруктов и цветов, современные технологии и секреты урожая.
Универсальный сайт https://virginvirtual.net для женщин — секреты красоты, тренды моды, советы по отношениям и карьере, рецепты и стиль жизни.
Сайт для женщин https://gratransymas.com о красоте, моде, здоровье и стиле жизни. Полезные советы, рецепты, тренды, отношения и карьера.
Сайт обо всём https://vybir.kiev.ua энциклопедия для повседневной жизни. Красота, здоровье, дом, путешествия, карьера, семья и полезные советы для всех.
Студия дизайна https://lbook.com.ua интерьера и архитектуры. Создаём стильные проекты квартир, домов и офисов. Индивидуальный подход, современные решения и полный контроль реализации.
Портал про ремонт https://hydromech.kiev.ua свежие статьи о ремонте и отделке, дизайне интерьера и выборе материалов. Полезные советы для мастеров и тех, кто делает ремонт своими руками.
Интересный сайт https://whoiswho.com.ua обо всём: статьи, лайфхаки, обзоры и идеи на самые разные темы. Всё, что нужно для вдохновения и развития, в одном месте.
Онлайн портал https://esi.com.ua про ремонт: идеи для интерьера, подбор материалов, практические рекомендации и пошаговые инструкции для самостоятельных работ.
Репортажи в больших https://infotolium.com фотографиях: самые обсуждаемые события, уникальные кадры и впечатляющие истории. Новости и жизнь в формате визуального рассказа.
Информационный портал https://reklama-region.com про ремонт: ремонт квартир, домов, офисов. Практические рекомендации, современные решения и обзоры стройматериалов.
Сайт про авто https://autoinfo.kyiv.ua свежие новости автопрома, обзоры моделей, тест-драйвы и советы по эксплуатации. Всё о машинах для водителей и автолюбителей.
Сайт про автомобили https://black-star.com.ua новинки рынка, цены, тест-драйвы и обзоры. Советы экспертов по выбору и уходу за машиной, тюнинг и автоуслуги.
Онлайн-журнал https://autoiceny.com.ua для автолюбителей: автомобили, новости индустрии, тест-драйвы, тюнинг и советы по обслуживанию.
Автомобильный онлайн-журнал https://allauto.kyiv.ua свежие новости автопрома, тест-драйвы, обзоры новых моделей, советы по эксплуатации и ремонту. Всё для водителей и автолюбителей.
Royal portraits http://www.turnyouroyal.com from photos – turn yourself or your loved ones into a king, queen or aristocrat. Author’s work of artists, luxurious style and premium quality of printing.
https://shorturl.fm/fFsQE
https://shorturl.fm/8bBSI
Авто-журнал https://bestauto.kyiv.ua источник информации для автолюбителей. Новинки рынка, сравнения моделей, советы по ремонту и уходу, интересные материалы о мире автомобилей.
https://shorturl.fm/zujqV
Новостной портал https://gau.org.ua круглосуточные новости, комментарии экспертов, события регионов и мира. Политика, бизнес, культура и общество.
Авто портал https://avtomobilist.kyiv.ua всё об автомобилях: новые модели, цены, рынок подержанных авто, тюнинг и автотехнологии. Полезные материалы для автовладельцев.
Онлайн авто-журнал https://mirauto.kyiv.ua с актуальными новостями, аналитикой и обзорами. Тесты автомобилей, тюнинг, технологии и советы по эксплуатации.
Мужской портал https://hooligans.org.ua новости, лайфхаки, обзоры техники, спорт, здоровье и авто. Советы для уверенной и гармоничной жизни.
GMO Gaika Reputation – Pros, Cons, and the Truth About Withdrawal Refusals
GMO Gaika is widely used by both beginners and experienced FX traders. Its popularity stems from easy-to-use trading tools, stable spreads, and a high level of trust due to its operation by a major Japanese company. Many users feel secure thanks to this strong domestic backing.
On the other hand, there are some online rumors about “withdrawal refusals,” but in most cases, these are due to violations of terms or incomplete identity verification. GMO Gaika’s transparent response to such issues suggests that serious problems are not a frequent occurrence.
You can find more detailed insights into the pros and cons of GMO Gaika, as well as real user experiences, on the trusted investment site naughty-cao.jp. If you’re considering opening an account, it’s a good idea to review this information beforehand.
https://shorturl.fm/Fwuzh
Портал о ремонте https://dki.org.ua и строительстве: от отделки квартиры до возведения загородного дома. Подробные статьи, рекомендации экспертов и идеи для обустройства жилья.
Портал о стройке https://sushico.com.ua и ремонте. Новости рынка, современные технологии, подборка идей для интерьера и экстерьера. Всё, что нужно для дома и дачи.
Онлайн сайт https://mramor.net.ua о строительстве и ремонте. Всё о возведении домов, ремонте квартир, отделке и обустройстве жилья. Обзоры материалов, советы экспертов и свежие идеи.
Всё о стройке https://aziatransbud.com.ua и ремонте в одном месте: дизайн, архитектура, выбор стройматериалов, инструкции по монтажу, лайфхаки и полезные рекомендации для новичков и мастеров.
Сайт о строительстве https://juglans.com.ua и ремонте — ваш помощник в выборе материалов, инструментов и технологий. Всё о ремонте квартир, строительстве домов и дизайне интерьеров.
Онлайн журнал https://vitamax.dp.ua о строительстве: проекты домов, ремонт квартир, выбор стройматериалов, дизайн и интерьер. Советы экспертов и свежие идеи для комфортной жизни.
Портал про строительство https://texha.com.ua новости рынка, обзоры технологий, инструкции и идеи для ремонта. Материалы для застройщиков, мастеров и тех, кто делает своими руками.
Новости Украины https://gromrady.org.ua онлайн: политика, экономика, спорт, культура и события регионов. Оперативные материалы, аналитика и комментарии экспертов круглосуточно.
Портал про авто https://automobile.kyiv.ua свежие новости автопрома, тест-драйвы, обзоры моделей и советы по ремонту. Всё о машинах для водителей и автолюбителей.
Авто портал https://road.kyiv.ua с актуальной информацией: новинки рынка, цены, обзоры, страхование и тюнинг. Полезные статьи и аналитика для автомобилистов.
change pitch extract audio from video
Prodaja prodaja placeva zabljak: stanovi, vile, zemljisne parcele. Izbor smestaja za odmor, preseljenje i investicije. Saveti strucnjaka i aktuelne ponude na trzistu.
p4mzyd
https://shorturl.fm/Hs8Iw
Besoin d’un bien immobilier? immobilier au Montenegro: appartements en bord de mer, maisons a la montagne, villas et appartements. Catalogue de biens, prix actuels et conseils d’experts en investissement.
Фильмы и сериалы сериал смотреть онлайн в хорошем в качестве бесплатно Онлайн-кинотеатр без регистрации и смс: тысячи фильмов и сериалов бесплатно.
Jak samodzielnie zdjac https://telegra.ph/Jak-samodzielnie-zdj%C4%85%C4%87-sufit-napinany-instrukcja-krok-po-kroku-bez-haka-z-wkr%C4%99tem-i-trikami-monta%C5%BCyst%C3%B3w-08-07 sufit napinany: instrukcje krok po kroku, narzedzia, porady ekspertow. Dowiedz sie, jak zdemontowac plotno bez uszkodzen i przygotowac pomieszczenie do montazu nowej okladziny.
https://shorturl.fm/8V6VG
I’d like to find out more? I’d love to find out some additional information.
Stretch Limousine Service
запись салон красоты спб beauty-salon-spb.ru/
https://shorturl.fm/bNPao
Нужен микрозайм? рейтинг займов: деньги на карту без справок и поручителей. Простое оформление заявки, одобрение за минуты и мгновенное зачисление. Удобно и доступно 24/7.
оценка стоимости ООО услуга оценки
https://shorturl.fm/jOfJq
https://shorturl.fm/LgpLV
https://shorturl.fm/jPoVI
Авто помощь 24/7 автопомощь: устранение поломок, подвоз топлива, прикуривание аккумулятора, замена колеса и эвакуация автомобиля.
Hey there! This is my 1st comment here so I just wanted to give a quick shout out and tell you I genuinely enjoy reading through your posts. Can you suggest any other blogs/websites/forums that deal with the same subjects? Thanks a ton!
кэт казино
Срочно нужны купить цветы Минск Свежие букеты, праздничные композиции и эксклюзивные флористические решения. Онлайн-заказ и быстрая доставка по городу.
Профессиональные детейлинг салона автомобиля: полировка кузова, химчистка салона, восстановление пластика и защита керамикой. Вернём автомобилю блеск и надёжную защиту.
Нужен массаж? https://doctu.ru – профессиональные мастера, широкий выбор техник: классический, оздоровительный, лимфодренажный, детский. Доступные цены и уютная атмосфера.
Обучающие курсы онлайн курсы по нейросетям новые навыки для работы и жизни. IT, дизайн, менеджмент, языки, маркетинг. Гибкий график, практика и сертификаты по итогам.
Откройте для себя мир комфорта с автоматическими рулонными шторами с электроприводом, которые идеально подходят для создания уюта в вашем доме.
Рулонные шторы с электроприводом — это удобное и стильное решение для современных интерьеров. Они позволяют не только регулировать уровень света в помещении, но и добавляют уют в ваш дом .
Преимущества использования электропривода очевидны . Первым и, пожалуй, самым важным плюсом является возможность дальнего управления шторами . В-третьих, рулонные шторы могут быть связаны с другими умными устройствами в вашем доме.
Электрические рулонные шторы подойдут для любого типа помещений. Их активно используют как в жилых, так и в коммерческих помещениях . Однако для установки рулонных штор нужно предусмотреть наличие источника электричества .
При выборе рулонных штор с электроуправлением важно обратить внимание на материал и дизайн . Шторы могут быть выполнены из различных тканей, что позволяет выбрать наиболее подходящий вариант для вашего интерьера . Наконец, стоит заметить, что есть возможность заказать шторы по индивидуальным размерам.
vps website hosting vps hosting providers
стул косметолога купить тележка косметолога на колесиках
https://shorturl.fm/1YuBL
https://shorturl.fm/MJJvQ
Рулонные шторы блэкаут с электроприводом идеально подойдут для создания уюта и контроля освещения в вашем доме.
отличный вариант для. Эти шторы эффективно блокируют свет, что дает возможность насладиться темнотой в любое время.
удобство использования. Вы можете управлять шторами с помощью пульта дистанционного управления, что делает шторы удобными для любого типа помещения.
К тому же, рулонные шторы блэкаут легко устанавливаются. Вы можете выбрать различные варианты крепления. Таким образом, вы сможете легко установить шторы на любые окна.
Не забывайте, что рулонные шторы блэкаут с электроприводом также обладают. С их помощью вы сможете поддерживать комфортную температуру в помещении зимой. В итоге, рулонные шторы с блэкаутом и электроприводом станут не только эстетичным, но и функциональным решением.
https://shorturl.fm/NOLYp
Добрый день!
Долго ломал голову как поднять сайт и свои проекты и нарастить ИКС Яндекса и узнал от крутых seo,
профи ребят, именно они разработали недорогой и главное top прогон Хрумером – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
Линкбилдинг цена зависит от выбранной стратегии. Крауд маркетинг линкбилдинг улучшает DR сайта. Линкбилдинг что это такое простыми словами объясняет новичкам. Линкбилдинг это простыми словами становится доступным. Линкбилдинг стоимость варьируется по объему работ.
правильное продвижение сайта, примеры seo копирайтинга, Прогон ссылок для повышения авторитета
Повышение авторитетности сайта, раскрутка сайтов нижний, seo vips
!!Удачи и роста в топах!!
Рулонные шторы с аккумулятором предоставляют удобство и стиль для любого интерьера, позволяя легко управлять светом и обеспечивая полную свободу от проводов.
Подводя итог, можно сказать, что рулонные шторы с аккумулятором — это современное и практичное решение для любого дома.
Преобразите ваше пространство с помощью автоматических рулонных штор, которые идеально сочетают стиль и современность.
Дистанционно управляемые рулонные шторы приобретают популярность в современных интерьерах. Эти шторы предлагают удобство и стиль, что делает их отличным решением для любого помещения.
Управлять рулонными шторами можно, используя пульт дистанционного управления или специализированное мобильное приложение. Таким образом, вы можете быстро изменять уровень освещенности и создавать комфортную обстановку в своем жилище.
Кроме того, рулонные шторы могут быть выполнены в различных дизайнах и расцветках. Таким образом, вы сможете выбрать именно тот вариант, который идеально впишется в ваш интерьер.
Важно отметить, что рулонные шторы с дистанционным управлением также удобны в эксплуатации. Их просто поддерживать в чистоте, и они не требуют сложного ухода, что идеально подходит для занятых людей.
https://shorturl.fm/AOxvB
монтаж перил из нержавеющей стали Перила из нержавеющей стали – это инвестиция в безопасность и долговечность. Они не требуют особого ухода и сохраняют свой привлекательный внешний вид на протяжении многих лет.
https://shorturl.fm/36oeJ
Приобретите автоматические жалюзи рулонного типа и насладитесь комфортом и современными технологиями в своем доме.
Электроприводные рулонные шторы представляют собой идеальный способ управления освещением в помещении. Управление этими шторами можно осуществлять с помощью мобильного приложения или специального пульта.
Одним из основных преимуществ умных рулонных штор является их удобство. С помощью одного нажатия кнопки вы можете регулировать свет и тень в вашем помещении.
Кроме того, эти изделия могут работать в режиме автоматизации. Настройка автоматического режима работы штор позволяет вам не беспокоиться о их управлении.
Умные рулонные шторы легко интегрируются с концепцией “умного дома”, предоставляя новые возможности управления. Таким образом, шторы могут работать в связке с другими устройствами, что делает ваш дом более умным и адаптивным.
https://www.med2.ru/story.php?id=147093
бетон цена купить бетон
Наркологические услуги: нарколог наркологическая помощь нижний новгород, кодирование, детоксикация, снятие ломки, помощь при алкоголизме и наркомании. Круглосуточная поддержка и анонимность.
https://shorturl.fm/RFc7I
https://shorturl.fm/wbQml
подобрать подшипник по размерам онлайн Подбор промышленных подшипников – задача, требующая скрупулезности. Необходимо принимать во внимание особенности оборудования, рабочие условия и требования к безотказности.
Handmade clay flowers Ideal for home, office decor or original gift. Natural beauty and durability.
Бетон в Воронеже https://stk-vrn.ru продажа и доставка. Все марки для фундаментов, дорожных работ и строительства под ключ. Надёжный производитель и лучшие цены.
https://shorturl.fm/35ghe
https://shorturl.fm/COCIP
https://shorturl.fm/5ExgC
Виброустойчивые подшипники Виброустойчивые подшипники – это гарантия стабильной работы оборудования в условиях повышенной вибрации.
https://shorturl.fm/3cJe3
https://shorturl.fm/AmXy6
https://shorturl.fm/qJsJw
купить игровой пк 4060 самый дешевый игровой пк: Играйте без ущерба для бюджета.
микрозаймы взять микрозайм
https://shorturl.fm/IIjXT
Финансы Специальная военная операция (СВО) стала катализатором глобальных изменений. Политика, как сфера влияния, претерпела трансформацию, обнажив скрытые противоречия и сформировав новые альянсы. Переговоры, в центре которых Владимир Путин и Владимир Зеленский, стали символом поиска компромисса в условиях радикально противоположных позиций. Финансы, словно кровеносная система мировой экономики, ощутили на себе всю тяжесть санкций и перебоев в поставках. Европа, Азия и Америка оказались перед лицом энергетического кризиса и инфляционной спирали. Безопасность и оборона, как фундаментальные потребности государств, вновь обрели актуальность. Кавказ и Ближний Восток, издавна известные своей нестабильностью, стали эпицентром геополитических рисков. Новости и аналитика, призванные освещать события непредвзято, часто оказываются в эпицентре информационных войн. Объективность становится дефицитом.
займы деньги микрозайм взять
займы деньги взять микрозайм онлайн
https://shorturl.fm/VTTOO
https://shorturl.fm/ezFOi
Tickets for Rock Concerts https://rock-concert-tickets.ru
https://shorturl.fm/I5EmT
Рестораны Хамовников https://restoran-khamovniki.ru топ заведений для встреч, романтических ужинов и семейных обедов. Авторская кухня, стильный интерьер, удобное расположение и достойный сервис.
Лучшие рестораны https://hamovniki-restoran.ru Хамовников для ценителей гастрономии. Подборка заведений с изысканной кухней, качественным сервисом и атмосферой для отдыха и деловых встреч.
Курсы по плазмотерапии плазмотерапия обучение в москве освоение методик, современные протоколы, практическая отработка. Обучение для специалистов с выдачей сертификата и повышением квалификации.
Профессиональное обучение плазмотерапия в косметологии обучение: подробная программа, практические навыки, сертификация. Освойте эффективные методики для применения в медицине и косметологии.
мистические истории обычных людей Истории из жизни обычных людей смешные Смех – лучшее лекарство, и истории, наполненные юмором и самоиронией, помогают нам справляться с трудностями и смотреть на жизнь с оптимизмом. Курьезные случаи, нелепые ситуации и забавные недоразумения – все это становится поводом для улыбки и напоминает нам о том, что даже в серых буднях есть место для веселья.
поход в горы кавказа Пятигорск что посмотреть
цитаты Книги, изменяющие жизни
Детская школа искусств https://elegy-school.ru обучение музыке, танцам, изобразительному и театральному искусству. Творческие программы для детей, концерты, конкурсы и развитие талантов.
Авторские курсы по REVIT https://dashclass.ru обучение созданию интерьеров и архитектурных проектов. Практика, реальные кейсы, индивидуальный подход и профессиональные навыки для работы в проектировании.
183tyo
https://shorturl.fm/4ePyU
https://shorturl.fm/yIltc
Первая помощь детям https://firstaidkids.ru правила оказания при травмах, ожогах, удушье и других ситуациях. Пошаговые инструкции, советы врачей и полезная информация для родителей.
Студия иностранных языков https://whats-up-studiya-inostrannyh-yazykov.ru обучение английскому, немецкому, французскому и другим языкам. Индивидуальные и групповые занятия, современные методики и опытные преподаватели.
https://shorturl.fm/mPczb
best wood for fence Chain Link Fence on Wood Posts This is good for a temporary option.
Срочный вызов сантехника https://master-expert.com в Москве на дом. Услуги сантехника: прочистка засоров, ремонт смесителей, установка приборов учета. Работаем 24/7. Недорого и с гарантией. Подробнее на сайте
Детский сад № 55 https://detsadik55.ru забота, развитие и обучение детей. Современные программы, квалифицированные воспитатели, уютные группы, безопасная среда и внимание к каждому ребёнку.
обучение кайтсёрфингу
Промышленная безопасность https://аттестация-промбезопасность.рф курсы и обучение под ключ. Подготовка к проверке Ростехнадзора, повышение квалификации и сертификация специалистов предприятий.
Автомобили на заказ https://avto-iz-kitaya1.ru поиск, проверка, покупка и доставка. Китай и Корея. Индивидуальный подбор под бюджет и пожелания клиента, полное сопровождение сделки.
купить меф гашиш кокаин меф гаш купить
ск меф куплю купить героин гашиш экстази
Авто из Китая https://avto-iz-kitaya2.ru на заказ под ключ: подбор, проверка, доставка и растаможка. Новые и подержанные автомобили, выгодные цены и полное сопровождение сделки.
Do you have a spam problem on this website; I also am a blogger, and I was wondering your situation; we have developed some nice practices and we are looking to swap methods with other folks, why not shoot me an e-mail if interested.
https://http-kra38.cc/
Авто из Китая под заказ https://dostavka-avto-china.ru кроссоверы, седаны, электромобили и премиальные модели. Индивидуальный подбор, проверка, сопровождение сделки и доставка в ваш город.
Автомобили из Китая на заказ https://avto-iz-kitaya2.ru подбор, покупка и доставка. Полный цикл услуг: диагностика, растаможка, постановка на учёт и гарантия качества.
https://shorturl.fm/ObqgL
Заказать авто из Китая https://dostavka-avto-china2.ru новые автомобили с гарантией, выгодные цены и проверенные поставщики. Доставка, таможня и оформление всех документов под ключ.
продаю метамфетамин
Авто на заказ https://dostavka-avto-russia.ru поиск, диагностика и сопровождение сделки. Машины из Европы, Кореи, Китая и США. Доставка, растаможка и постановка на учёт.
Автомобили на заказ https://dostavka-avto-russia5.ru профессиональный подбор, юридическая проверка, доставка и растаможка. Индивидуальные решения для каждого клиента.
https://penzu.com/p/8ad5a154af1cd6dc
Хотите заказать авто https://prignat-avto5.ru Мы подберём оптимальный вариант, проверим машину по базам, организуем доставку и таможенное оформление. Выгодные цены и прозрачные условия.
https://shorturl.fm/2AadW
Grandfar CDLF12-4T Вертикальный многоступенчатый центробежный насос Нержавеющая сталь SS304
https://shorturl.fm/8i6d0
Машины на заказ https://prignat-avto7.ru поиск, диагностика и доставка автомобилей. Индивидуальный подбор, проверенные поставщики и прозрачные условия покупки.
Машины на заказ https://prignat-mashinu5.ru поиск, диагностика и доставка автомобилей. Индивидуальный подбор, проверенные поставщики и прозрачные условия покупки.
Автомобили на заказ https://prignat-mashinu7.ru подбор, проверка, доставка и оформление документов. Машины любых марок и комплектаций с гарантией качества и выгодной ценой.
https://shorturl.fm/wm26A
https://shorturl.fm/KtRP0
программа для учета расхода топлива Учет времени – важный инструмент организации работы. Программы учета времени позволяют контролировать занятость сотрудников.
Ремонт квартир https://remontkomand.kz и домов под ключ: дизайн-проект, отделка, инженерные работы. Работаем по договору, фиксированные сроки и цены. Гарантия качества и полный контроль этапов.
https://shorturl.fm/lfA0B
Цены на ремонт https://remontkomand.kz/ru/price квартир и помещений в Алматы под ключ. Узнайте точные расценки на все виды работ — от демонтажа до чистовой отделки. Посчитайте стоимость своего ремонта заранее и убедитесь в нашей прозрачности. Никаких «сюрпризов» в итоговой смете!
https://shorturl.fm/Pja49
https://shorturl.fm/dVv6N
SEO-продвижение сайтов https://raskrutka-sajtov-bystro77.ru в Москве: вывод в ТОП поисковиков, рост трафика и заявок. Полный комплекс — аудит, семантика, оптимизация, ссылки. Эффективное продвижение под ключ.
Планируете ремонт https://remontkomand.kz в Алматы и боитесь скрытых платежей? Опубликовали полный и честный прайс-лист! Узнайте точные расценки на все виды работ — от демонтажа до чистовой отделки. Посчитайте стоимость своего ремонта заранее и убедитесь в нашей прозрачности. Никаких «сюрпризов» в итоговой смете!
oe1abp
https://shorturl.fm/6HVjm
https://shorturl.fm/1vGC1
Строительство домов https://stroycata1og.ru и коттеджей под ключ. Готовые проекты, индивидуальные решения, качественные материалы и полный цикл работ — от фундамента до отделки.
Журнал о саде https://nasha-gryadka.ru и огороде онлайн — статьи о выращивании овощей, цветов и фруктов. Советы по уходу, борьбе с вредителями, подбору семян и организации участка.
займ онлайн срочно займ взять
https://shorturl.fm/zK8mh
https://shorturl.fm/5yQdc
https://shorturl.fm/JfBWu
Нужен клининг? лучшие клининговые компании в москве 2026 год. Лучшие сервисы уборки квартир, домов и офисов. Сравнение услуг, цен и отзывов, чтобы выбрать надежного подрядчика.
Эскорт работа Тюмень Высокооплачиваемая работа для девушек в Тюмени: Ключ к финансовой независимости и роскошной жизни. Гибкий график, конфиденциальность и высокий доход. Раскрой свой потенциал и забудь о финансовых трудностях.
Нужен клининг? рейтинг клининговых компаний москвы 2026. Лучшие сервисы уборки квартир, домов и офисов. Сравнение услуг, цен и отзывов, чтобы выбрать надежного подрядчика.
Смотрите сериалы Лучшие сериалы онлайн: https://v-tagile.ru/obschestvo-avgust-5/puteshestvie-ne-vykhodya-iz-doma-5-serialov-s-samymi-zakhvatyvayushchimi-lokatsiyami онлайн в хорошем качестве. Новинки, классика и популярные проекты в удобном формате. Бесплатный просмотр без скачивания и доступ 24/7.
https://shorturl.fm/IvnHL
https://shorturl.fm/trvYd
Je trouve genial le casino TonyBet, il est carrement un univers de jeu unique. Les jeux sont varies, proposant des jeux de table classiques. Le support est toujours la, tres professionnel. On recupere ses gains vite, cependant j’aimerais plus de bonus. En resume, TonyBet c’est du solide pour les adeptes de sensations fortes ! En bonus, le site est facile a naviguer, facilitant chaque session de jeu.
tonybet казино|
цветы в москве недорого Доставка цветов – это идеальный вариант для тех, кто ценит свое время и хочет сделать приятный сюрприз, не выходя из дома или офиса. Цветы в Москве недорого: Красота, Доступная Каждому
J’apprecie enormement Azur Casino, ca procure une sensation de casino unique. La selection de jeux est incroyablement riche, comprenant des titres modernes et attrayants. Le service d’assistance est de premier ordre, avec un suivi irreprochable. Les paiements sont securises et fluides, cependant les offres pourraient etre plus allechantes. Globalement, Azur Casino ne decoit jamais pour les adeptes de sensations fortes ! En bonus la navigation est intuitive et agreable, ajoutant une touche de raffinement.
casino centre azur|
J’adore a fond le casino AllySpin, ca offre une aventure palpitante. La selection de jeux est immense, avec des machines a sous captivantes. Le service client est remarquable, repondant en un clin d’?il. Le processus de retrait est sans accroc, cependant plus de tours gratuits seraient top. En resume, AllySpin offre une experience solide pour les fans de divertissement numerique ! De plus le style visuel est dynamique, ce qui booste encore plus le plaisir.
allyspin review|
Je suis conquis par Banzai Casino, ca ressemble a une aventure pleine d’adrenaline. Il y a une multitude de titres varies, avec des machines a sous ultra-modernes. Le service d’assistance est exemplaire, avec un suivi de qualite. Les gains arrivent en un rien de temps, bien que plus de tours gratuits seraient apprecies. En resume, Banzai Casino ne decoit jamais pour les fans de divertissement numerique ! Ajoutons que l’interface est fluide et moderne, ce qui intensifie le plaisir de jouer.
banzai slots analyse|
J’adore a fond Betclic Casino, c’est une veritable experience de jeu electrisante. Les options de jeu sont vastes et diversifiees, offrant des sessions de casino en direct immersives. Le support est d’une reactivite exemplaire, offrant des reponses rapides et precises. Les transactions sont parfaitement protegees, bien que davantage de recompenses seraient appreciees. Dans l’ensemble, Betclic Casino ne decoit jamais pour les joueurs en quete d’adrenaline ! Notons egalement que le design est visuellement epoustouflant, ajoute une touche de raffinement a l’experience.
bonus betclic 5€|
https://shorturl.fm/8QfDV
https://shorturl.fm/p3KC2
Нужна контекстная реклама? reklama-stomatolog-kontekst.ru под ключ. Настройка в Яндекс.Директ и Google Ads, оптимизация объявлений и контроль заявок.
J’adore le casino TonyBet, il est carrement une aventure palpitante. Le choix de jeux est impressionnant, comprenant des titres innovants. Le support est toujours la, tres professionnel. Le processus de retrait est efficace, cependant j’aimerais plus de bonus. Globalement, TonyBet c’est du solide pour les adeptes de sensations fortes ! En bonus, le site est facile a naviguer, facilitant chaque session de jeu.
tonybet online casino|
Комплексные IT-решения https://eclat.moscow для бизнеса: разработка, внедрение, сопровождение и поддержка. Надежные технологии для автоматизации и цифровой трансформации.
An outstanding share! I’ve just forwarded this onto a coworker who has been doing a little research on this. And he in fact ordered me breakfast due to the fact that I discovered it for him… lol. So let me reword this…. Thanks for the meal!! But yeah, thanx for spending some time to discuss this matter here on your internet site.
gemini
Je suis enthousiaste a propos de Azur Casino, ca ressemble a une experience de jeu envoutante. Les options de jeu sont impressionnantes, proposant du casino en direct immersif. Les agents sont d’une efficacite remarquable, offrant des reponses claires et rapides. Les retraits sont ultra-rapides, de temps en temps les offres pourraient etre plus allechantes. Pour conclure, Azur Casino vaut vraiment le detour pour les adeptes de sensations fortes ! De plus le design est visuellement superbe, amplifiant le plaisir du jeu.
gГ©ant casino centre azur hyeres|
J’adore sans reserve Banzai Casino, il procure une plongee dans le divertissement intense. La selection est riche et diversifiee, proposant des jeux de table authentiques. Le support est ultra-reactif, offrant des solutions rapides et claires. Les paiements sont fluides et securises, neanmoins j’aimerais plus de bonus allechants. Globalement, Banzai Casino est une plateforme incontournable pour ceux qui aiment parier ! Par ailleurs le design est visuellement percutant, renforcant l’immersion.
banzai bet casino|
J’adore a fond le casino AllySpin, ca offre une aventure palpitante. La selection de jeux est immense, offrant des jeux de table authentiques. Le service client est remarquable, repondant en un clin d’?il. Les retraits sont super rapides, mais parfois les promos pourraient etre plus genereuses. Globalement, AllySpin est un incontournable pour les amateurs de casino en ligne ! Notons aussi que le style visuel est dynamique, ajoutant une touche d’elegance au jeu.
allyspin uvГtacГ bonus|
Je suis completement seduit par Betclic Casino, c’est une veritable experience de jeu electrisante. La gamme de jeux est tout simplement impressionnante, incluant des slots dernier cri. Les agents sont toujours disponibles et professionnels, offrant des reponses rapides et precises. Les gains sont verses en un clin d’?il, bien que les promotions pourraient etre plus genereuses. Dans l’ensemble, Betclic Casino ne decoit jamais pour les passionnes de jeux numeriques ! En bonus le site est concu avec elegance, ajoute une touche de raffinement a l’experience.
contacter betclic live chat|
עזבתי את העבודה כדי לחזור הביתה מוקדם!!!» “אתה רציני?» “כן לא,” הוא קרא, ” פשוט הצליח לסיים את הכל פלט שהוא אוהב כל מין וניסה הרבה, אליו שאלו האחים בחיוך אולי הוא גם משמח גברים. סשה פחד להודות דירות דיסקרטיות ברמת גן
курсы бровиста брови севастополь — Брови — это не просто волоски над глазами, а важный элемент выразительности лица и общей эстетики образа. В Севастополе, где влияние морского климата, солнца и ветра сказывается на состоянии кожи и волос, уход за бровями требует профессионального подхода: от грамотной архитектуры (моделирование формы с учётом пропорций лица, симметрии и мимики) до восстановительных процедур — ламинирования, кератиновой терапии, окрашивания хной или краской и коррекции ростовых проблем с помощью сывороток. Опытный мастер всегда начинает с консультации, определяет тип кожи и волос, предлагает несколько вариантов формы и оттенка, показывает эскиз и договаривается о графике коррекций. Важным аспектом в Севастополе является уход после процедур: избегать активного солнца и моря первые 1–2 недели, пользоваться защитными и питательными средствами, следовать рекомендациям по чистоте и дезинфекции. При выборе салона обращайте внимание на портфолио «до/после», лицензии, отзывы клиентов и используемые материалы — одноразовые инструменты и качественные краски значительно снижают риск осложнений. Для тех, кто ведёт активный образ жизни, мастера предлагают стойкие техники и программы поддержки: комбинированные процедуры, курсы восстановления и регулярные коррекции, которые помогут сохранить аккуратный естественный вид бровей круглый год.
Hello every one, here every person is sharing these familiarity, thus it’s nice to read this website, and I used to pay a visit this website every day.
https://optimapharm.com.ua/bi-led-linzi-vybir-vodiyiv
J’apprecie enormement 1win Casino, c’est une veritable sensation de casino unique. Il y a une multitude de titres varies, avec des machines a sous modernes et dynamiques. Le personnel est professionnel et attentionne, offrant des solutions claires et efficaces. Les paiements sont fluides et fiables, parfois les offres pourraient etre plus genereuses. Dans l’ensemble, 1win Casino est une plateforme exceptionnelle pour les passionnes de jeux en ligne ! Notons egalement que la navigation est simple et rapide, ajoute une touche d’elegance a l’experience.
1win bonus casino|
Je suis enthousiaste a propos de Casino Action, ca procure une sensation de casino unique. La selection de jeux est impressionnante avec plus de 1000 titres, comprenant des jackpots progressifs comme Millionaires’ Club. Le service d’assistance est irreprochable, repondant en quelques minutes. Les gains arrivent en un temps record, cependant davantage de recompenses via le programme Casino Rewards seraient appreciees. En resume, Casino Action est un incontournable pour les amateurs de casino en ligne ! Par ailleurs le design est visuellement attrayant, ajoute une touche de sophistication a l’experience.
prevision action casino|
Je suis totalement conquis par BetFury Casino, il offre une experience de jeu electrisante. Les options de jeu sont riches et diversifiees, comprenant des jeux originaux comme Plinko et Crash avec un RTP jusqu’a 99,28 %. Le service client est exceptionnel, joignable a toute heure. Les transactions en cryptomonnaies comme Bitcoin ou Ethereum sont ultra-rapides, de temps en temps ??? plus de tours gratuits seraient un plus. En resume, BetFury Casino est un incontournable pour les joueurs en quete de sensations fortes ! De plus le design est visuellement percutant avec un theme sombre, ce qui renforce l’immersion.
betfury no deposit promo code|
Ich finde es unglaublich toll Billy Billion Casino, es ist wirklich ein mitrei?endes Spielerlebnis. Der Katalog ist unglaublich umfangreich, mit klassischen Tischspielen wie Blackjack und Roulette. Der Support ist blitzschnell uber Live-Chat, reagiert in wenigen Minuten. Der Auszahlungsprozess ist einfach und zuverlassig, obwohl zusatzliche VIP-Belohnungen waren willkommen. Am Ende ist Billy Billion Casino definitiv einen Besuch wert fur die, die gerne wetten! Erganzend die Navigation ist intuitiv auf der mobilen iOS/Android-App, einen Hauch von Eleganz hinzufugt.
billy billion no deposit bonus codes|
Je suis absolument conquis par Betsson Casino, c’est une veritable energie de jeu irresistible. Le catalogue est incroyablement vaste avec plus de 1500 titres, comprenant des jackpots progressifs comme Mega Moolah. Le service d’assistance est irreprochable, offrant des solutions rapides et precises. Les paiements sont fluides et securises avec un maximum de 50 000 € par jour, cependant les bonus pourraient etre plus frequents. En resume, Betsson Casino offre une experience de jeu securisee et equitable pour les passionnes de jeux numeriques ! Notons egalement que le site est concu avec modernite et ergonomie, ce qui amplifie le plaisir de jouer.
betsson bonus 100€|
https://how-to-screenshot.info/
https://cryptobirzhi.com/
https://shorturl.fm/hoQRo
https://shorturl.fm/sMQkE
Welcome to https://blevuine.com/, your ultimate financial partner for small businesses. Our company provides advanced financial tools designed to simplify your financial operations and support your business expansion. Whether you need a line of credit or invoice factoring, Bluevine has you covered. Access to your account is through the Bluevine login portal, where you can safely and efficiently manage all your financial needs. Join thousands of satisfied entrepreneurs who trust Bluevine to advance their business.
https://shorturl.fm/ByfgH
https://shorturl.fm/0NnXR
Je suis enthousiaste a propos de 7BitCasino, ca ressemble a une experience de jeu electrisante. Les options de jeu sont riches et diversifiees, comprenant plus de 5 000 jeux, dont 4 000 adaptes aux cryptomonnaies. Les agents sont disponibles 24/7, repondant en un clin d’?il. Les gains sont verses en un temps record, occasionnellement plus de tours gratuits seraient un atout, afin de maximiser l’experience. En resume, 7BitCasino est une plateforme d’exception pour les joueurs en quete d’adrenaline ! En bonus la navigation est intuitive et rapide, ajoute une touche de raffinement a l’experience.
7bitcasino bonus|
Папа на новый год и подарки готовые на новый год в Калуге. Пилот кепки оптом и брелок автомобильный с логотипом в Брянске. Подарочная упаковка на новый год оптом и подарок на новый год для сотрудников в Сочи. Спортивная одежда для мужчин и что подарить бабушке на день рождения 75 в Курске. Изготовление новогодних подарков и новогодние оптом сувениры и подарки: https://subscribe.ru/group/klub-zhenskih-interesov/18710047/
Je trouve completement incroyable Betsson Casino, c’est une veritable experience de jeu electrisante. Le catalogue est incroyablement vaste avec plus de 1500 titres, incluant des slots de derniere generation comme Starburst. Le personnel offre un accompagnement de qualite via email ou telephone, garantissant une aide immediate. Les gains sont verses en 24 heures pour les e-wallets, occasionnellement les bonus pourraient etre plus frequents. En fin de compte, Betsson Casino est un incontournable pour les joueurs en quete d’adrenaline ! En bonus le site est concu avec modernite et ergonomie, facilite chaque session de jeu.
code parrain betsson|
Ich bin ganz hin und weg von BoaBoa Casino, es ist ganz ein Abenteuer voller Adrenalin. Das Angebot an Spielen ist einfach phanomenal, mit klassischen Tischspielen wie Blackjack und Roulette. Das Team bietet schnelle Unterstutzung per E-Mail oder Telefon, garantiert sofortige Hilfe. Gewinne kommen in Rekordzeit an, jedoch ich mir mehr regelma?ige Aktionen wunschen wurde. Zusammengefasst ist BoaBoa Casino enttauscht nie fur Online-Casino-Fans ! Daruber hinaus die Navigation ist intuitiv auf der mobilen iOS/Android-Plattform, die Immersion verstarkt.
boaboa aktionscode|
J’apprecie enormement BetFury Casino, ca procure une sensation de casino unique. La selection de jeux est phenomenale, avec des machines a sous modernes et captivantes. Les agents sont toujours professionnels et efficaces, offrant des reponses claires et rapides. Les gains arrivent en un temps record, parfois les bonus pourraient etre plus reguliers. Globalement, BetFury Casino offre une experience securisee et equitable pour ceux qui aiment parier avec des cryptomonnaies ! Par ailleurs le design est visuellement percutant avec un theme sombre, facilite chaque session.
betfury opiniones|
https://shorturl.fm/ngQub
https://shorturl.fm/EObl3
оборудование для окраски металлоконструкций Покрасочные камеры для порошковой окраски – это специальные помещения, предназначенные для нанесения порошковых красок. Они обеспечивают контролируемую среду, в которой можно безопасно и эффективно наносить порошок на окрашиваемые изделия. Важные параметры камеры: размер, наличие системы фильтрации и рекуперации порошка, хорошая освещенность и удобство обслуживания.
частная наркологическая клиника Частная наркологическая клиника в Воронеже: ваш путь к выздоровлению в комфортных условиях. Частная наркологическая клиника в Воронеже – это специализированное медицинское учреждение, предлагающее широкий спектр услуг по лечению различных видов зависимостей: алкогольной, наркотической, игровой и других. Главное преимущество частной клиники – индивидуальный подход к каждому пациенту и создание максимально комфортных условий для лечения. Врачи-наркологи и психотерапевты с большим опытом работы разрабатывают индивидуальные программы лечения, учитывая особенности каждого пациента и стадию его зависимости. Клиника оснащена современным оборудованием и использует передовые методики лечения, что позволяет достичь высокой эффективности и стойких результатов. Помимо медикаментозной терапии, в частной клинике активно применяются методы психотерапии, направленные на выявление причин зависимости и формирование устойчивой мотивации к здоровому образу жизни. Конфиденциальность и анонимность – гарантированы. Частная наркологическая клиника в Воронеже – это ваш шанс на избавление от зависимости в комфортных условиях и с профессиональной поддержкой опытных специалистов.
rznjio
Je trouve incroyable 1win Casino, il offre une experience de jeu captivante. La bibliotheque de jeux est impressionnante, incluant des slots de derniere generation. Le support est ultra-reactif et disponible, joignable 24/7. Les gains arrivent en un temps record, cependant j’aimerais plus de promotions regulieres. Globalement, 1win Casino est une plateforme exceptionnelle pour les amateurs de casino virtuel ! En bonus l’interface est fluide et intuitive, ce qui amplifie le plaisir de jouer.
1win bet app|
Ich schatze sehr Billy Billion Casino, es fuhlt sich an wie ein Eintauchen in eine pulsierende Spielwelt. Es gibt eine Vielzahl an abwechslungsreichen Spielen, mit immersiven Live-Casino-Sessions von Evolution Gaming. Die Mitarbeiter sind rund um die Uhr professionell und hilfsbereit, reagiert in wenigen Minuten. Gewinne kommen in Rekordzeit an, gelegentlich zusatzliche VIP-Belohnungen waren willkommen. Am Ende ist Billy Billion Casino definitiv einen Besuch wert fur die, die gerne wetten! Daruber hinaus die Seite ist mit Stil und Benutzerfreundlichkeit gestaltet, was den Spielspa? noch steigert.
billy billion casino|
Je suis totalement seduit par Betify Casino, il offre une plongee dans un univers palpitant. La gamme de jeux est tout simplement phenomenale, incluant des slots de derniere generation. Le service d’assistance est irreprochable, joignable 24/7. Les gains sont verses en un temps record, parfois les bonus pourraient etre plus frequents. Globalement, Betify Casino ne decoit jamais pour ceux qui aiment parier ! Notons egalement que le design est visuellement percutant, renforce l’immersion totale.
betify+casino|
Je suis totalement conquis par Betzino Casino, on dirait une aventure pleine de frissons. La selection de jeux est epoustouflante avec plus de 1800 titres, avec des machines a sous modernes comme Sweet Bonanza et Book of Dead. Les agents sont professionnels et disponibles, offrant des solutions claires et utiles. Les gains arrivent en un temps record, occasionnellement les bonus comme le pack de bienvenue de 150 % jusqu’a 200 € pourraient etre plus frequents. Pour conclure, Betzino Casino est un incontournable pour les adeptes de sensations fortes ! De plus le design est visuellement attrayant avec des personnages animes, ajoute une touche de dynamisme a l’experience.
betzino casino fr|
Je suis totalement seduit par Casino Action, on dirait une experience de jeu exaltante. Les options de jeu sont riches et diversifiees, offrant des sessions de casino en direct immersives par Evolution Gaming. Le support est ultra-reactif et disponible 24/7, garantissant une aide immediate. Le processus de retrait est simple et fiable, parfois j’aimerais plus de promotions regulieres. En resume, Casino Action ne decoit jamais pour les passionnes de jeux numeriques ! Ajoutons que la navigation est rapide sur mobile via iOS/Android, facilite chaque session de jeu.
groupe casino action|
swot анализ деятельности swot анализ
J’adore sans reserve 1xbet Casino, on dirait une energie de jeu irresistible. Les options de jeu sont riches et diversifiees, proposant des jeux de table elegants et classiques. Les agents sont toujours disponibles et efficaces, repondant en un clin d’?il. Les retraits sont ultra-rapides, cependant j’aimerais plus d’offres promotionnelles. Dans l’ensemble, 1xbet Casino offre une experience de jeu remarquable pour les passionnes de jeux numeriques ! Notons egalement que la navigation est intuitive et rapide, renforce l’immersion totale.
login 1xbet|
Adoro de verdade o 888 Casino, e como se fosse sensacao unica de cassino. As opcoes de jogos sao ricas e diversificadas, com caca-niqueis modernos e envolventes. Os agentes estao sempre disponiveis e eficientes, oferecendo respostas rapidas e precisas. O processo de retirada e simples e confiavel, as vezes os bonus poderiam ser mais frequentes. De modo geral, o 888 Casino oferece uma experiencia de jogo memoravel para os fas de emocoes fortes! Vale destacar o design e visualmente impactante, o que amplifica o prazer de jogar.
888 casino uk|
Je trouve absolument extraordinaire Betway Casino, ca ressemble a une sensation de casino unique. Le catalogue est incroyablement vaste, incluant des slots de pointe de Microgaming et NetEnt. Le service d’assistance est irreprochable, avec un suivi de qualite. Les paiements sont fluides et securises par un cryptage SSL 128 bits, neanmoins les offres pourraient etre plus genereuses. Globalement, Betway Casino vaut pleinement le detour pour les adeptes de sensations fortes ! Par ailleurs l’interface est fluide et moderne avec un theme noir et vert, ce qui amplifie le plaisir de jouer.
betway espana|
Ich bin vollig begeistert von BingBong Casino, es ist wirklich ein mitrei?endes Spielerlebnis. Es gibt eine Fulle an abwechslungsreichen Titeln, inklusive topaktueller Slots von Merkur, Novomatic und Pragmatic Play. Der Kundendienst ist tadellos, reagiert in wenigen Minuten. Auszahlungen sind super schnell, oft innerhalb von 24 Stunden fur PayPal, jedoch ich mir mehr regelma?ige Boni wunschen wurde. Am Ende ist BingBong Casino definitiv einen Besuch wert fur die, die gerne Slots spielen ! Au?erdem die Plattform ist mit Stil und Benutzerfreundlichkeit gestaltet, die Immersion verstarkt.
bingbong de|
7m4m1y
Прокат авто Краснодар на месяц Прокат авто Краснодар посуточно: Гибкость и удобство для ваших планов в Краснодаре. Получите максимальную гибкость и удобство с услугой проката авто в Краснодаре посуточно. Мы предлагаем широкий выбор автомобилей различных марок и моделей, доступных для аренды на сутки или несколько дней. Наш автопарк включает в себя экономичные автомобили для коротких поездок по городу, комфортабельные седаны для деловых встреч и вместительные внедорожники для путешествий по окрестностям. Прокат авто в Краснодаре посуточно – это идеальное решение для тех, кто нуждается в автомобиле на короткий срок. Забронируйте свой автомобиль прямо сейчас и получите свободу передвижения!
https://shorturl.fm/Rrvlx
https://gtaman.ru
оргониты райха Оргониты&orginity: возможно, опечатка, подразумевается “оргониты”.
1win Обзор официального сайта и приложения казино. В мире онлайн-гемблинга важно выбирать не только интересные игры, но и надежную платформу. 1win (или 1вин) — это многофункциональный игровой клуб, который объединяет в себе казино, букмекерскую контору и тотализатор. В этом обзоре мы подробно разберем, как начать играть, какие бонусы ждут новых игроков и как получить доступ к ресурсу через официальный сайт и зеркала. Поиск рабочего официального сайта 1win — первый шаг для каждого игрока. Из-за ограничений в некоторых регионах прямой вход на основной ресурс может быть затруднен. В этом случае на помощь приходят зеркала — точные копии сайта с другим адресом. Они полностью безопасны и позволяют получить доступ к аккаунту и всем функциям. Актуальные ссылки на зеркала лучше всего искать в официальных сообществах проекта или у партнеров. Процесс регистрации в 1win занимает пару минут. Доступно несколько способов: через email, номер телефона или аккаунт в социальных сетях. Но самый важный шаг — это активация промокода. Ввод специального кода при создании аккаунта значительно увеличивает стартовый бонус на первый депозит. Не пропускайте этот этап, чтобы начать игру с максимально возможным банкроллом. Для тех, кто предпочитает играть с телефона, 1win предлагает удобное мобильное приложение. Его можно скачать прямо с официального сайта в формате APK файла для устройств Android. Владельцы iOS также могут найти способ установить программу. Приложение повторяет все функции полной версии сайта: от регистрации и ввода промокода до игры в слоты и live-ставок. Это идеальный выбор для игры в любом месте. 1win стабильно входит в топ рейтингов лучших онлайн-казино по нескольким причинам: Огромная игровая коллекция: Сотни слотов, настольные игры, live-дилеры. Щедрая программа лояльности: Не только приветственный бонус, но и кешбэк, фриспины, турниры. Безопасность и поддержка: Лицензия, шифрование данных и круглосуточная служба заботы о клиентах. 1win — это современная и надежная игровая площадка, которая предлагает полный комплект услуг от казино до ставок на спорт. Не забудьте использовать промокод при регистрации, чтобы получить максимальную выгоду от игры. А если возникнут трудности с доступом — воспользуйтесь рабочим зеркалом или скачайте официальное приложение.
swot анализа рисков swot анализ проблемы
Looking for second-hand? second hand store near me We have collected the best stores with clothes, shoes and accessories. Large selection, unique finds, brands at low prices. Convenient catalog and up-to-date contacts.
Юридические консультации стали неотъемлемой частью жизни каждого человека.. Множество людей сталкивается с юридическими вопросами, требующими консультации..
konsultaciya-advokata11.ru предлагает широкий спектр услуг.. Здесь вы можете получить помощь по самым различным вопросам.. Получите помощь квалифицированного юриста на помощь адвоката по уголовным делам бесплатно.
Наша команда адвокатов всегда готова оказать поддержку.. Качество нашей работы – это наш главный приоритет.
Воспользуйтесь нашими услугами, и вы останетесь удовлетворены результатом.. Каждая консультация осуществляется с учетом ваших потребностей и обстоятельств.
цель swot анализа https://swot-analiz1.ru
Looking for second-hand? thrift stores We have collected the best stores with clothes, shoes and accessories. Large selection, unique finds, brands at low prices. Convenient catalog and up-to-date contacts.
Je suis totalement conquis par le casino AllySpin, on dirait une experience de jeu electrisante. Le catalogue de jeux est vaste, offrant des jeux de table authentiques. Le service d’assistance est impeccable, repondant en un clin d’?il. Les retraits sont super rapides, cependant davantage de recompenses seraient appreciees. Pour faire court, AllySpin offre une experience solide pour les joueurs en quete d’adrenaline ! Notons aussi que la navigation est fluide, facilitant chaque session.
allyspin giocare per soldi|
С получением профессиональной помощи в решении юридических вопросов вы можете обратиться к помощь адвоката онлайн, где можно получить юридическую консультацию круглосуточно и бесплатно.
Ресурс ‘konsultaciya-advokata81.ru’ предоставляет разнообразные правовые консультации.
Je trouve absolument genial Azur Casino, il offre une energie de jeu irresistible. Il y a une multitude de jeux varies, offrant des jeux de table elegants. Le personnel est hautement professionnel, avec un suivi irreprochable. Les transactions sont parfaitement protegees, bien que davantage de recompenses seraient bienvenues. En resume, Azur Casino est une pepite pour les joueurs passionnes ! De plus l’interface est fluide et elegante, ce qui rend chaque session memorable.
centre azur casino hyeres|
Je suis conquis par Banzai Casino, on dirait une experience de jeu explosive. Il y a une multitude de titres varies, offrant des sessions de casino en direct immersives. Le service client est irreprochable, repondant en un eclair. Les transactions sont parfaitement protegees, par moments davantage de recompenses seraient un plus. Globalement, Banzai Casino offre une experience exceptionnelle pour les amateurs de jeux en ligne ! En prime la navigation est intuitive et rapide, renforcant l’immersion.
banzai slots code promo|
Je suis completement seduit par Betclic Casino, ca ressemble a une energie de jeu irresistible. Il y a une profusion de titres varies, comprenant des titres innovants et attrayants. Le service d’assistance est irreprochable, offrant des reponses rapides et precises. Le processus de retrait est simple et fiable, cependant les promotions pourraient etre plus genereuses. Globalement, Betclic Casino vaut amplement le detour pour les adeptes de sensations fortes ! Notons egalement que le design est visuellement epoustouflant, facilite chaque session de jeu.
offre betclic|
https://shorturl.fm/FIEXf
https://shorturl.fm/Auy8S
Looking for second-hand? thrift stores We have collected the best stores with clothes, shoes and accessories. Large selection, unique finds, brands at low prices. Convenient catalog and up-to-date contacts.
https://shorturl.fm/tVBog
https://shorturl.fm/oj8IW
https://yunc.org
Je suis accro a Amon Casino, on dirait une tornade de fun. Le catalogue de jeux du casino est monumental, incluant des jeux de table de casino ultra-styles. Le service client du casino est une pepite, garantissant un support de casino direct et efficace. Les retraits au casino sont fluides et ultra-rapides, cependant plus de tours gratuits au casino ca serait ouf. Au final, Amon Casino c’est un casino de ouf a tester direct pour les fans de casinos en ligne ! Par ailleurs le design du casino est une explosion visuelle, donne envie de replonger dans le casino non-stop.
amon casino|
Je suis emballe par DBosses, il propose une experience de jeu intense. Les options sont riches et dynamiques, incluant des jeux de table sophistiques. Les agents sont rapides et devoues, garantissant un support immediat. Les gains arrivent en un eclair, de temps a autre plus de tours gratuits seraient top. Globalement, DBosses est un choix incontournable pour les joueurs pour les fans de jeux modernes ! Notons aussi le design est captivant et elegant, amplifie le plaisir de jouer.
dbosses casino review|
Je suis accro a Celsius Casino, il propose une aventure de casino qui fait monter la temperature. La collection de jeux du casino est incandescente, incluant des jeux de table de casino elegants et brulants. Le support du casino est disponible 24/7, joignable par chat ou email. Les gains du casino arrivent a une vitesse torride, cependant les offres du casino pourraient etre plus genereuses. Au final, Celsius Casino est une pepite pour les fans de casino pour les explorateurs du casino ! En plus la navigation du casino est intuitive comme un feu de camp, facilite une experience de casino torride.
celsius casino 50 free spins|
Ich bin total begeistert von King Billy Casino, es fuhlt sich an wie ein koniglicher Triumph. Die Auswahl im Casino ist ein wahres Kronungsjuwel, mit modernen Casino-Slots, die verzaubern. Der Casino-Support ist rund um die Uhr verfugbar, ist per Chat oder E-Mail erreichbar. Casino-Zahlungen sind sicher und reibungslos, trotzdem mehr Casino-Belohnungen waren ein furstlicher Gewinn. Insgesamt ist King Billy Casino eine Casino-Erfahrung, die wie ein Palast glitzert fur Fans moderner Casino-Slots! Nebenbei die Casino-Navigation ist kinderleicht wie ein koniglicher Marsch, Lust macht, immer wieder ins Casino zuruckzukehren.
king billy casino logo|
J’adore le delire total de Gamdom, ca donne une energie de jeu demente. Il y a un tsunami de titres varies, comprenant des jeux parfaits pour les cryptos. L’assistance est au top du top, avec une aide qui dechire tout. Les paiements sont fluides et blindes, quand meme des bonus plus reguliers ce serait la classe. Pour resumer, Gamdom offre une experience de ouf pour ceux qui kiffent parier avec style ! En prime le site est une tuerie graphique, facilite le delire total.
gamdom free spins no deposit|
https://ufa.bfm.ru/news/66001
https://shorturl.fm/e8FWm
Achou totalmente epico DiceBet Casino, parece um tornado de diversao. A selecao de titulos do cassino e um espetaculo a parte, incluindo jogos de mesa de cassino cheios de classe. Os agentes do cassino sao rapidos como um foguete, dando solucoes claras na hora. Os saques no cassino sao velozes como um cometa, de vez em quando queria mais promocoes de cassino que mandam ver. Na real, DiceBet Casino oferece uma experiencia de cassino que e puro gas para os amantes de cassinos online! De bonus o site do cassino e uma obra-prima de visual, torna o cassino uma curticao total.
dicebet|
J’adore l’ambiance de Circus, ca donne une vibe de jeu incroyable. Il y a une profusion de titres captivants, offrant des slots a theme innovants. Le service client est exceptionnel, avec une aide personnalisee. Les paiements sont securises et efficaces, cependant des recompenses supplementaires seraient appreciees. En resume, Circus est un incontournable pour les joueurs pour les amateurs de casino en ligne ! Notons aussi la navigation est intuitive et rapide, facilite une immersion totale.
circus circus resort and casino las vegas|
Je suis totalement envoute par FatPirate, ca donne une energie de pirate dejantee. Le choix de jeux est monumental, comprenant des jeux tailles pour les cryptos. Le support est dispo 24/7, repondant en deux secondes chrono. Les retraits sont rapides comme une tempete, par contre des recompenses en plus ca serait la cerise. Au final, FatPirate offre une experience de ouf pour les aventuriers du jeu ! Et puis la navigation est simple comme un jeu d’enfant, booste l’immersion a fond.
fatpirate casino avis|
J’adore le show de Impressario, on dirait une scene de fun explosif. Le catalogue est un festival de titres, comprenant des jeux parfaits pour les cryptos. Le service client est digne d’un gala, garantissant un support direct et brillant. Les transactions sont simples comme un refrain, parfois des recompenses en plus ca serait le feu. Bref, Impressario offre un spectacle de jeu inoubliable pour ceux qui kiffent parier avec style ! Et puis le design est une explosion visuelle, booste l’immersion a fond.
impressario casino|
карго товары из китая доставка товаров из китая карго
фермерская продукция фермерские товары
Онлайн-библиотека Казахстана https://mylibrary.kz книги, статьи, диссертации и редкие издания в цифровом формате. Удобный каталог, быстрый поиск и круглосуточный доступ для всех пользователей.
https://flactor.ru
https://telegra.ph/Online-casino-CZ-v-roce-2025-jak-si-bezpe%C4%8Dn%C4%9B-vybrat-licencovan%C3%A1-kasina-rozpoznat-marketingov%C3%A9-triky-a-skute%C4%8Dn%C4%9B-si-u%C5%BE%C3%ADt-hru-09-05 CZ Casino Online: Vyberte si to nejlepsi ceske online kasino s licenci. Sledujte nase recenze, porovnavejte bonusy a vyberte si to, ktere nejlepe vyhovuje vasim preferencim.
online casino cz Kasina: Discover the excitement of casinos! From classic games to modern slots, experience the thrill of winning (and remember to play responsibly).
Estou totalmente vidrado em Flabet Casino, oferece uma aventura de cassino que detona tudo. A gama do cassino e simplesmente um arraso, com jogos de cassino perfeitos pra criptomoedas. O suporte do cassino ta sempre na area 24/7, dando solucoes na hora e com precisao. Os ganhos do cassino chegam voando baixo, as vezes queria mais promocoes de cassino que arrebentam. No fim das contas, Flabet Casino e um cassino online que e um vulcao para os amantes de cassinos online! Alem disso o design do cassino e uma explosao visual, aumenta a imersao no cassino a mil.
https www flabet com cassino slots|
Ich flippe aus bei DrueGlueck Casino, es liefert einen einzigartigen Adrenalinkick. Die Spielauswahl im Casino ist gigantisch, mit modernen Casino-Slots, die fesseln. Der Casino-Support ist rund um die Uhr da, sorgt fur sofortigen Casino-Support. Casino-Transaktionen sind simpel und zuverlassig, ab und zu mehr Freispiele im Casino waren top. Alles in allem ist DrueGlueck Casino eine Casino-Erfahrung, die rockt fur die, die mit Stil im Casino wetten! Nebenbei die Casino-Plattform hat einen krassen Look, einen Hauch von Wahnsinn ins Casino bringt.
drueckglueck casino bonus|
Wow, awesome blog structure! How long have you been running a blog for? you made running a blog look easy. The full look of your site is great, let alone the content!
сайт кракен
Je trouve totalement dingue AmunRa Casino, ca balance une vibe de jeu pharaonique. Les options de jeu au casino sont riches et envoutantes, avec des machines a sous de casino modernes et immersives. L’assistance du casino est majestueuse et efficace, repondant en un eclair divin. Le processus du casino est limpide et sans malediction, quand meme j’aimerais plus de promos de casino qui eblouissent. Dans l’ensemble, AmunRa Casino offre une experience de casino mythique pour les accros aux sensations fortes du casino ! Par ailleurs le design du casino est une fresque visuelle, ajoute un max de magie au casino.
amunra logo|
Je suis accro a Instant Casino, on dirait une tempete de fun. Il y a un deluge de jeux de casino varies, offrant des machines a sous de casino uniques. L’assistance du casino est au top niveau, garantissant un support de casino direct et efficace. Les transactions de casino sont simples comme un neon, quand meme plus de tours gratos au casino ca serait ouf. Pour resumer, Instant Casino offre une experience de casino inoubliable pour les pirates des slots de casino modernes ! En prime la navigation du casino est simple comme un jeu d’enfant, ce qui rend chaque session de casino encore plus kiffante.
bitcoin casino instant withdrawal free spins|
https://shorturl.fm/vOvRm
Эндовазальная лазерная коагуляция https://evlo-phlebology.ru эффективный метод лечения варикоза. Амбулаторная процедура занимает до 40 минут, не требует госпитализации и обеспечивает быстрый косметический и медицинский результат.
Сюрвей грузов сюрвей контроль качества и количества, проверка условий перевозки, составление отчётов. Опытные эксперты обеспечивают объективную оценку для компаний и страховых организаций.
Надежная доставка из китая в Россию: от документов до контейнеров. Выбираем оптимальный маршрут, оформляем таможню, страхуем грузы. Контроль сроков и сохранность на каждом этапе.
заказать сайт на тильде заказать сайт на тильде
Надежная доставка грузов из китая: от небольших партий до контейнеров. Авиа, морем, авто и железной дорогой. Оформление, страхование и логистика в кратчайшие сроки.
Нужен автобусный билет? заказ билетов на автобус онлайн просто и удобно. Поиск рейсов, сравнение цен, выбор мест и моментальная оплата. Актуальное расписание, надежные перевозчики и выгодные тарифы каждый день.
Adoro demais o clima de DazardBet Casino, da uma energia de cassino totalmente insana. Tem uma avalanche de jogos de cassino variados, com jogos de cassino perfeitos para criptomoedas. O atendimento ao cliente do cassino e fora da curva, com uma ajuda que e um show a parte. As transacoes do cassino sao simples como um estalo, mas queria mais promocoes de cassino que arrebentam. No fim das contas, DazardBet Casino e um cassino online que e pura dinamite para quem curte apostar com estilo no cassino! E mais o design do cassino e uma explosao visual, torna o cassino uma curticao total.
dazardbet sovellus|
Je suis accro a Julius Casino, c’est un casino en ligne qui rugit comme un lion. La selection du casino est une veritable legion de plaisirs, avec des machines a sous de casino modernes et envoutantes. Le support du casino est disponible 24/7, avec une aide qui commande le respect. Le processus du casino est transparent et sans embuches, mais plus de tours gratuits au casino ce serait epique. Dans l’ensemble, Julius Casino est un colisee pour les fans de casino pour ceux qui cherchent l’adrenaline glorieuse du casino ! De surcroit le site du casino est une merveille graphique imposante, amplifie l’immersion totale dans le casino.
julius casino application|
Je suis absolument transporte par Bruno Casino, ca degage une ambiance de jeu explosive. La collection de jeux du casino est phenomenale, avec des machines a sous de casino modernes et envoutantes. Les agents du casino sont vifs comme l’eclair, joignable par chat ou email. Les transactions du casino sont simples comme un souffle, parfois j’aimerais plus de promotions de casino qui dazzlent. Globalement, Bruno Casino promet un divertissement de casino electrisant pour ceux qui cherchent l’adrenaline du casino ! De surcroit le site du casino est une merveille graphique, ce qui rend chaque session de casino encore plus exaltante.
bruno casino entree|
Качественный ремонт квартир https://expertremonta.kz от Компании «Эксперт ремонта» это качественный ремонт квартир под ключ в Алматы. Выбирайте Эксперт Ремонта — тут бесплатный выезд замерщика, официальные документы, гарантия документально, ремонт квартир без предоплаты.
купить дт с доставкой доставка дизтоплива цена
купить грунт для огорода грунт с доставкой цена
Adoro o clima feroz de LeaoWin Casino, e um cassino online que ruge como um leao. Os titulos do cassino sao um espetaculo selvagem, incluindo jogos de mesa de cassino cheios de garra. O suporte do cassino ta sempre na area 24/7, garantindo suporte de cassino direto e sem rugas. Os ganhos do cassino chegam voando como uma aguia, mas mais giros gratis no cassino seria uma loucura. Em resumo, LeaoWin Casino e um cassino online que e uma fera total para os aventureiros do cassino! Vale falar tambem a navegacao do cassino e facil como uma trilha na selva, o que deixa cada sessao de cassino ainda mais animal.
leaowin02 casino serios|
Мобильный выездной шиномонтаж https://master-shin.by круглосуточная помощь в дороге. Экстренная помощь в дороге может понадобиться каждому автолюбителю, и наша компания оказывает ее на высочайшем профессиональном уровне, на самых выгодных в Минске условиях. Оперативный выезд по городу и области, доступные и полностью адекватные цены, квалифицированная сервисная и консультационная поддержка, круглосуточное реагирование, вне зависимости от погодных условий.
Ремонт ноутбуков https://01km.ru телефонов, телевизоров, принтеров и компьютеров в Одинцово и Москве.
go to the website online: https://cere-india.org
the best site for you: https://www.pondexperts.ca
visit our website: https://www.ielts-mentor.com
our site is waiting for you: https://amt-games.com
посетить сайт онлайн: https://wildlife.by
our official website: https://fgvjr.com
go to our website: https://actual-cosmetology.ru
https://lakoshka.ru
visit our new website: https://nature-et-avenir.org
our new official website: https://www.amakmeble.pl
I found a cool site: https://underatexassky.com
https://usk-rus.ru/ Урал Строй Комплект – Наша компания занимается комплектацией строительных объектов, нефтегазового производства и не только. Одно из главных направлений работы – это гражданское строительство, где наши задачи – поставка металлических изделий и конструкций, труб, сыпучих строительных смесей, других стройматериалов. Также мы поставляем клиентам геосинтетические материалы для дорожного строительства, оборудование для нефтегазовой отрасли и многое другое под запрос. И все это – напрямую с заводов, с которыми у нас заключены официальные соглашения.
русское порно измена русское порно
Hi, this weekend is pleasant in support of me, as this point in time i am reading this impressive educational article here at my residence.
кракен зеркало
Want to have fun? porno melbet Watch porn, buy heroin or ecstasy. Pick up whores or buy marijuana. Come in, we’re waiting
Получите бесплатную юридическую консультацию онлайн, чтобы оперативно решить все ваши юридические вопросы!
На сайте вы найдете широкий спектр юридических услуг.
Обратитесь за помощью к профессионалам на номер телефона бесплатной юридической консультации, и получите квалифицированное решение своих вопросов.
yuridicheskaya-konsultaciya34.ru предлагает профессиональные юридические услуги, направленные на решение различных правовых вопросов. Команда опытных юристов готова помочь вам в самых сложных ситуациях. Понимая, что правовые проблемы могут быть стрессовыми, мы предлагаем индивидуальный подход к каждому клиенту.
У нас есть широкий спектр услуг, включая консультации по гражданским и уголовным делам. Мы приглашаем вас по вопросам, связанным с трудовым правом, семейными делами и другими юридическими аспектами. Наша практика показывает, что каждый случай имеет свои особенности , и готовы предложить оптимальное решение.
Наша компания известна как надежный партнер в сфере юриспруденции. Клиенты выбирают нас за профессионализм за высокое качество обслуживания и результативность. Каждый специалист имеет опыт работы в различных областях права и готов поддержать вас в любое время.
Не откладывайте решение своих проблем , чтобы получить квалифицированную юридическую помощь. Наша команда будет рада проконсультировать вас . Воспользуйтесь нашими услугами на yuridicheskaya-konsultaciya34.ru.
Mochten Sie ein https://www.immobilien-in-montenegro-fuer-oesterreicher.com kaufen? Tolle Angebote am Meer und in den Bergen. Gro?e Auswahl an Immobilien, Unterstutzung bei der Immobilienauswahl, Transaktionsunterstutzung und Registrierung. Leben Sie in einem Land mit mildem Klima und wunderschoner Natur.
Новые актуальные промокоды iherb 2025 для выгодных покупок! Скидки на витамины, БАДы, косметику и товары для здоровья. Экономьте до 30% на заказах, используйте проверенные купоны и наслаждайтесь выгодным шопингом.
русские порно ролики русское групповое порно
https://shorturl.fm/xZGiI
Want to have fun? sex children melbet Watch porn, buy heroin or ecstasy. Pick up whores or buy marijuana. Come in, we’re waiting
Новые актуальные промокод iherb на заказ для выгодных покупок! Скидки на витамины, БАДы, косметику и товары для здоровья. Экономьте до 30% на заказах, используйте проверенные купоны и наслаждайтесь выгодным шопингом.
best articles on the net: https://dnscompetition.in/articles/implementing-dns-based-load-distribution-for-apis/
bs2best
play puzzles online: https://moneyminiblog.com/interesting/crosswords-jigsaws-evolution-online-puzzle-games/
Je trouve absolument enivrant CasinoClic, ca pulse avec une energie de casino electrisante. Les choix de jeux au casino sont riches et scintillants, offrant des sessions de casino en direct qui electrisent. L’assistance du casino est chaleureuse et irreprochable, proposant des solutions claires et instantanees. Les paiements du casino sont securises et fluides, mais plus de tours gratuits au casino ce serait enivrant. Globalement, CasinoClic offre une experience de casino eclatante pour les joueurs qui aiment parier avec panache au casino ! En plus la navigation du casino est intuitive comme une lueur, facilite une experience de casino vibrante.
code bonus casino clic|
Ich bin suchtig nach Lapalingo Casino, es verstromt eine Spielstimmung, die wie ein Feuerwerk knallt. Es gibt eine Welle an packenden Casino-Titeln, mit modernen Casino-Slots, die einen in ihren Bann ziehen. Der Casino-Support ist rund um die Uhr verfugbar, ist per Chat oder E-Mail erreichbar. Casino-Transaktionen sind simpel wie ein Sonnenstrahl, manchmal mehr regelma?ige Casino-Boni waren ein Knaller. Am Ende ist Lapalingo Casino ein Online-Casino, das wie ein Sturm begeistert fur Abenteurer im Casino! Nebenbei das Casino-Design ist ein optisches Spektakel, Lust macht, immer wieder ins Casino zuruckzukehren.
lapalingo casino test|
Ich bin total begeistert von iWild Casino, es pulsiert mit einer unbandigen Casino-Energie. Es gibt eine Flut an fesselnden Casino-Titeln, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Der Casino-Service ist zuverlassig und wild, mit Hilfe, die wie ein Windsto? wirkt. Auszahlungen im Casino sind schnell wie ein Flusslauf, trotzdem mehr Casino-Belohnungen waren ein wilder Gewinn. Alles in allem ist iWild Casino ein Casino mit einem Spielspa?, der wie ein Gewitter tobt fur Spieler, die auf wilde Casino-Kicks stehen! Und au?erdem die Casino-Plattform hat einen Look, der wie ein Wasserfall funkelt, Lust macht, immer wieder ins Casino zuruckzukehren.
iwild casino kokemuksia|
J’adore l’eclat de JackpotStar Casino, c’est un casino en ligne qui scintille comme une galaxie. Les choix de jeux au casino sont varies et lumineux, comprenant des jeux de casino optimises pour les cryptomonnaies. Le support du casino est disponible 24/7, proposant des solutions claires et instantanees. Les paiements du casino sont securises et fluides, cependant j’aimerais plus de promotions de casino qui eblouissent. Pour resumer, JackpotStar Casino est une etoile brillante pour les fans de casino pour les amoureux des slots modernes de casino ! De surcroit la plateforme du casino brille par son style etoile, amplifie l’immersion totale dans le casino.
jackpotstar casino sister sites|
Je suis completement envoute par LeonBet Casino, ca degage une vibe de jeu feroce. Les choix de jeux au casino sont riches et rugissants, comprenant des jeux de casino optimises pour les cryptomonnaies. Le service client du casino est une force de la nature, avec une aide qui mord. Les transactions du casino sont simples comme un rugissement, parfois j’aimerais plus de promotions de casino qui en imposent. Globalement, LeonBet Casino offre une experience de casino indomptable pour les amoureux des slots modernes de casino ! A noter le design du casino est une fresque visuelle feroce, amplifie l’immersion totale dans le casino.
leonbet brasil|
best site come on in: https://alterego.re
The most useful information: https://foxartistic.com
Самое лучшее в сети: https://badgerboats.ru
Current and up-to-date information: https://clubcoma.org
https://egoistka56.ru
карго из китая перевозка грузов из китая в россию
шпонирование на заказ шпонирование на заказ
геодезия заказать геодезист московская область
геотекстиль комитекс геотекстиль 300 цена
Включение в реестр Минпромторга https://minprom-info.ru официальный путь для подтверждения отечественного производства. Подготовка и подача документов, юридическое сопровождение и консультации для производителей.
https://shorturl.fm/gNWZn
Занятия по самообороне https://safety-skills.ru практические навыки защиты в реальных ситуациях, развитие силы и выносливости. Профессиональные тренеры помогут освоить приемы борьбы, удары и тактику безопасности.
Платформа онлайн-обучения https://craftsmm.ru курсы по маркетингу, продажам и рекламе для новичков и профессионалов. Освойте современные инструменты продвижения, увеличьте продажи и развивайте карьеру в удобном формате.
Написание дипломов на заказ https://vasdiplom.ru помощь студентам в подготовке итоговых работ. Авторские тексты, проверка на уникальность и полное соответствие стандартам учебных заведений.
Ich finde absolut irre Lapalingo Casino, es ist ein Online-Casino, das wie ein Blitz einschlagt. Die Casino-Optionen sind bunt und mitrei?end, inklusive stilvoller Casino-Tischspiele. Der Casino-Kundenservice ist wie ein Leuchtfeuer, ist per Chat oder E-Mail erreichbar. Casino-Zahlungen sind sicher und reibungslos, ab und zu mehr regelma?ige Casino-Boni waren ein Knaller. Zusammengefasst ist Lapalingo Casino eine Casino-Erfahrung, die wie ein Regenbogen glitzert fur Fans von Online-Casinos! Nebenbei die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino in den Himmel hebt.
.lapalingo|
Ich bin suchtig nach Lowen Play Casino, es ist ein Online-Casino, das wie ein Lowe brullt. Die Auswahl im Casino ist ein echtes Raubtier, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Der Casino-Support ist rund um die Uhr verfugbar, sorgt fur sofortigen Casino-Support, der beeindruckt. Auszahlungen im Casino sind schnell wie ein Raubkatzen-Sprint, manchmal mehr Casino-Belohnungen waren ein koniglicher Gewinn. Alles in allem ist Lowen Play Casino ein Muss fur Casino-Fans fur die, die mit Stil im Casino wetten! Ubrigens die Casino-Navigation ist kinderleicht wie eine Fahrte, das Casino-Erlebnis total unbezahmbar macht.
löwen play fotos|
https://antidetectbrowserfree.com/
Adoro o clima explosivo de JabiBet Casino, parece uma correnteza de diversao. Tem uma enxurrada de jogos de cassino irados, com caca-niqueis de cassino modernos e envolventes. A equipe do cassino entrega um atendimento que e uma perola, garantindo suporte de cassino direto e sem tempestade. Os ganhos do cassino chegam voando como uma onda, mesmo assim mais recompensas no cassino seriam um diferencial brabo. Em resumo, JabiBet Casino e um cassino online que e uma onda gigante para os viciados em emocoes de cassino! De lambuja a navegacao do cassino e facil como surfar, aumenta a imersao no cassino como uma onda gigante.
jabibet casino|
Ich bin suchtig nach JokerStar Casino, es verstromt eine Spielstimmung, die verzaubert. Die Auswahl im Casino ist ein echtes Feuerwerk, inklusive eleganter Casino-Tischspiele. Die Casino-Mitarbeiter sind schnell wie ein Zauberstab, antwortet blitzschnell wie ein Funke. Der Casino-Prozess ist klar und ohne Hokuspokus, dennoch mehr Freispiele im Casino waren ein Volltreffer. Insgesamt ist JokerStar Casino ein Casino mit einem Spielspa?, der wie Magie funkelt fur Fans moderner Casino-Slots! Ubrigens die Casino-Navigation ist kinderleicht wie ein Zauberspruch, das Casino-Erlebnis total verzaubert.
jokerstar app|
Je suis fou de LeoVegas Casino, c’est un casino en ligne qui rugit comme un roi. Le repertoire du casino est un palais de divertissement, incluant des jeux de table de casino d’une elegance royale. Le service client du casino est digne d’un monarque, assurant un support de casino instantane et souverain. Les retraits au casino sont rapides comme un couronnement, cependant les offres du casino pourraient etre plus genereuses. Globalement, LeoVegas Casino c’est un casino a conquerir en urgence pour les conquerants du casino ! En plus le site du casino est une merveille graphique princiere, ajoute une touche de splendeur au casino.
leovegas bonus|
visit our best site online: https://www.maxwaugh.com
The best we have here: https://www.kapoorstudycircle.com
The latest information is here: https://www.intercultural.org.au
We have the latest information: https://jnp.chitkara.edu.in
visit our website: https://cere-india.org
We are waiting for you on the site: https://travel2mv.com
https://shorturl.fm/ywG64
https://shorturl.fm/8K4cc
Ich liebe die Strahlkraft von LuckyNiki Casino, es fuhlt sich an wie ein verzauberter Glucksrausch. Die Auswahl im Casino ist ein echtes Glanzlicht, inklusive eleganter Casino-Tischspiele. Die Casino-Mitarbeiter sind schnell wie ein Komet, sorgt fur sofortigen Casino-Support, der verblufft. Casino-Zahlungen sind sicher und reibungslos, manchmal mehr Freispiele im Casino waren ein Volltreffer. Insgesamt ist LuckyNiki Casino eine Casino-Erfahrung, die wie ein Gluckszauber glanzt fur Fans von Online-Casinos! Ubrigens die Casino-Navigation ist kinderleicht wie ein Zauberspruch, Lust macht, immer wieder ins Casino zuruckzukehren.
luckyniki ???????|
Je suis accro a Lucky8 Casino, ca pulse avec une energie de casino ensorcelante. Le repertoire du casino est une nebuleuse de divertissement, proposant des slots de casino a theme feerique. Le service client du casino est une etoile porte-bonheur, avec une aide qui fait des miracles. Les retraits au casino sont rapides comme un coup de baguette, parfois plus de tours gratuits au casino ce serait magique. Au final, Lucky8 Casino est un joyau pour les fans de casino pour les passionnes de casinos en ligne ! En plus le design du casino est une explosion visuelle feerique, amplifie l’immersion totale dans le casino.
lucky8 casino avis fiabilitГ©|
Je suis accro a Luckster Casino, c’est un casino en ligne qui brille comme un talisman. Le repertoire du casino est une cascade de divertissement, comprenant des jeux de casino optimises pour les cryptomonnaies. L’assistance du casino est chaleureuse et irreprochable, proposant des solutions claires et instantanees. Les paiements du casino sont securises et fluides, quand meme les offres du casino pourraient etre plus genereuses. Dans l’ensemble, Luckster Casino est un casino en ligne qui porte chance pour les joueurs qui aiment parier avec panache au casino ! Bonus la navigation du casino est intuitive comme un sortilege, donne envie de replonger dans le casino sans fin.
luckster betting review|
Je suis fou de MonteCryptos Casino, ca pulse avec une energie de casino audacieuse. Les choix de jeux au casino sont riches et vertigineux, offrant des sessions de casino en direct qui electrisent. Le service client du casino est un guide fiable, repondant en un eclair glacial. Les transactions du casino sont simples comme un sentier balise, mais des recompenses de casino supplementaires feraient grimper l’adrenaline. Pour resumer, MonteCryptos Casino est un joyau pour les fans de casino pour ceux qui cherchent l’adrenaline des cimes du casino ! En plus l’interface du casino est fluide et eclatante comme un glacier, ce qui rend chaque session de casino encore plus exaltante.
montecryptos faq|
https://autozames.ru/
Want to have fun? melbet drugs Whores, drugs, casino. We have it all, any drugs are on sale.
порно молодые младше порно большой член
The best of our site: https://www.feldbahn-ffm.de
New and relevant information: https://www.colehardware.com
Обучение и семинары https://uofs-beslan.ru для профессионалов: современные программы, практические кейсы и опыт экспертов. Развивайте навыки, повышайте квалификацию и получайте новые возможности для карьерного роста.
Школа видеорекламы https://tatyanamostseeva.ru обучение созданию креативных роликов для бизнеса и брендов. Практические занятия, работа с современными инструментами и поддержка экспертов. Освойте профессию в сфере digital.
Академия парикмахерского искусства https://charm-academy.ru обучение от ведущих мастеров. Современные техники стрижек, окрашивания и укладок. Курсы для начинающих и профессионалов с практикой и дипломом по окончании.
Лицей взаимного обучения https://talgenisty.ru уникальная среда для детей и взрослых. Совместные уроки, обмен опытом, мастер-классы и творческие проекты. Образование, основанное на поддержке и сотрудничестве.
приложение sweet bonanza
Je trouve absolument envoutant LuckyTreasure Casino, c’est un casino en ligne qui scintille comme un joyau precieux. Les choix de jeux au casino sont riches et eclatants, incluant des jeux de table de casino d’une elegance precieuse. Le service client du casino est un diamant brut, proposant des solutions claires et instantanees. Les retraits au casino sont rapides comme une ruee vers l’or, parfois des bonus de casino plus frequents seraient precieux. Globalement, LuckyTreasure Casino est un casino en ligne qui brille comme un joyau pour les passionnes de casinos en ligne ! Bonus la navigation du casino est intuitive comme une carte au tresor, amplifie l’immersion totale dans le casino.
lucky treasure bonus sans dГ©pГґt|
Je trouve extraordinaire Casinova, il propose un voyage ludique unique. Il y a une variete impressionnante de titres, avec des slots innovants et immersifs. Le personnel assure un suivi exemplaire, garantissant une aide instantanee. Les gains arrivent sans delai, meme si plus de tours gratuits seraient top. Pour conclure, Casinova offre un plaisir garanti pour les amateurs de casino en ligne ! Par ailleurs le site est elegant et bien concu, amplifie l’experience de jeu.
mr casinova|
Je suis totalement envoute par LuckyBlock Casino, ca pulse avec une energie de casino ensorcelante. La selection du casino est une fontaine de plaisirs, avec des machines a sous de casino modernes et captivantes. Les agents du casino sont rapides comme un eclair de genie, repondant en un flash etincelant. Les paiements du casino sont securises et fluides, quand meme j’aimerais plus de promotions de casino qui eblouissent. Pour resumer, LuckyBlock Casino c’est un casino a decouvrir en urgence pour ceux qui cherchent l’adrenaline lumineuse du casino ! Par ailleurs la plateforme du casino brille par son style ensorcelant, amplifie l’immersion totale dans le casino.
luckyblock presale price|
https://shorturl.fm/q16Ww
Great site for everyone: https://institutocea.com
Приём макулатуры https://chsreda.ru в Казани работает как для частных лиц, так и для организаций. Сдают газеты, журналы, картонные коробки, офисную бумагу. Это реально удобно, потому что приезжают, забирают прямо с территории, а потом всё идёт на переработку.
Кухонные принадлежности https://www.kitchen-store.ru в магазине для дома: современная посуда, полезные гаджеты, текстиль и аксессуары. Стильные решения для кухни, выгодные цены и большой ассортимент.
https://shorturl.fm/p99qs
Je suis fou de Madnix Casino, ca pulse avec une energie de casino totalement folle. La collection de jeux du casino est une bombe atomique, proposant des slots de casino a theme barre. L’assistance du casino est energique et irreprochable, assurant un support de casino immediat et explosif. Le processus du casino est transparent et sans court-circuit, mais j’aimerais plus de promotions de casino qui envoient du lourd. Globalement, Madnix Casino c’est un casino a decouvrir en urgence pour les passionnes de casinos en ligne ! A noter l’interface du casino est fluide et petillante comme un neon, ajoute une touche de folie au casino.
madnix bonus|
Нужен автобусный билет? билеты на автобус удобный сервис поиска и бронирования. Широкий выбор направлений, надежные перевозчики, доступные цены и моментальная отправка электронных билетов на почту.
Авто портал https://diesel.kyiv.ua все о мире автомобилей: новости, обзоры моделей, тест-драйвы, советы по выбору и уходу за авто. Каталог машин, актуальные цены, автоуслуги и полезная информация для автовладельцев.
Все для автомобилистов https://k-moto.com.ua на авто портале: новости, обзоры, статьи, каталоги и цены на автомобили. Экспертные мнения, тест-драйвы и практические советы по эксплуатации авто.
Автомобильный портал https://auto-club.pl.ua онлайн-площадка для автолюбителей. Подробные обзоры машин, тест-драйвы, свежие новости, советы по ремонту и обслуживанию. Удобный поиск и актуальные материалы.
Нужна виза? экспресс виза в италию Консультации, подготовка документов, сопровождение на всех этапах. Визы в Европу, США, Азию и другие страны. Доступные цены и надежная поддержка.
Женский портал https://beautyadvice.kyiv.ua все для современных женщин: красота, здоровье, семья, отношения, карьера. Полезные статьи, советы экспертов, лайфхаки и вдохновение каждый день. Онлайн-сообщество для общения и развития.
Онлайн женский портал https://elegance.kyiv.ua актуальные советы по красоте, стилю, кулинарии и семейной жизни. Разделы о здоровье, карьере и саморазвитии. Интересные статьи и общение с единомышленницами.
Портал для женщин https://fashionadvice.kyiv.ua сайт для девушек и женщин, которые ценят красоту, уют и гармонию. Советы по стилю, отношениям, материнству и здоровью. Читайте статьи, делитесь опытом и вдохновляйтесь новыми идеями.
Sou louco pelo role de MegaPosta Casino, oferece uma aventura de cassino que detona tudo. Tem uma enxurrada de jogos de cassino irados, com jogos de cassino perfeitos pra criptomoedas. Os agentes do cassino sao rapidos como um estalo, respondendo mais rapido que um raio. Os pagamentos do cassino sao lisos e blindados, porem as ofertas do cassino podiam ser mais generosas. No fim das contas, MegaPosta Casino e um cassino online que e um vulcao de diversao para quem curte apostar com estilo no cassino! E mais a plataforma do cassino detona com um visual que e puro gas, aumenta a imersao no cassino a mil.
megaposta com|
Je suis captive par MyStake Casino, on dirait un labyrinthe de frissons. La selection du casino est un voile de plaisirs, incluant des jeux de table de casino d’une elegance cryptique. L’assistance du casino est chaleureuse et perspicace, joignable par chat ou email. Les transactions du casino sont simples comme une rune dechiffree, parfois j’aimerais plus de promotions de casino qui captivent. En somme, MyStake Casino promet un divertissement de casino enigmatique pour les explorateurs des mysteres du casino ! Par ailleurs l’interface du casino est fluide et envoutante comme un sortilege, ce qui rend chaque session de casino encore plus intrigante.
avaliação mystake|
Ich bin suchtig nach Platin Casino, es verstromt eine Spielstimmung, die wie Platin glanzt. Die Casino-Optionen sind vielfaltig und glanzvoll, mit Live-Casino-Sessions, die wie ein Diamant leuchten. Der Casino-Service ist zuverlassig und prazise, ist per Chat oder E-Mail erreichbar. Casino-Transaktionen sind simpel wie ein Edelstein, ab und zu mehr regelma?ige Casino-Boni waren luxurios. Insgesamt ist Platin Casino ein Casino mit einem Spielspa?, der wie ein Edelstein funkelt fur Spieler, die auf luxuriose Casino-Kicks stehen! Zusatzlich die Casino-Navigation ist kinderleicht wie ein Funkeln, den Spielspa? im Casino in den Himmel hebt.
platin casino – بلاتين كازينو|
Adoro o clima brabo de OshCasino, da uma energia de cassino que e um terremoto. As opcoes de jogo no cassino sao ricas e incendiarias, com caca-niqueis de cassino modernos e eletrizantes. O servico do cassino e confiavel e brabo, respondendo mais rapido que um relampago. Os ganhos do cassino chegam voando como um meteoro, mas mais bonus regulares no cassino seria brabo. Na real, OshCasino vale demais explorar esse cassino para os amantes de cassinos online! De lambuja a plataforma do cassino detona com um visual que e puro magma, aumenta a imersao no cassino a mil.
avis osh paris sportif|
Ich bin vollig hingerissen von Pledoo Casino, es fuhlt sich an wie ein wilder Tanz durch die Spielwelt. Der Katalog des Casinos ist eine Flut voller Spa?, inklusive stilvoller Casino-Tischspiele. Der Casino-Kundenservice ist wie ein Leitstern, mit Hilfe, die wie ein Funke spruht. Casino-Zahlungen sind sicher und reibungslos, dennoch mehr Freispiele im Casino waren ein Volltreffer. Am Ende ist Pledoo Casino ein Casino, das man nicht verpassen darf fur Fans von Online-Casinos! Extra die Casino-Oberflache ist flussig und strahlt wie ein Polarlicht, Lust macht, immer wieder ins Casino zuruckzukehren.
pledoo promo code|
Получите бесплатную консультацию юриста по телефону на сайте юрист онлайн бесплатно телефон.
Проблемы в сфере права могут возникнуть у каждого из нас, и важно быть к этому готовым.
Не забывайте об обязательной проверке процесса.
Сайт konsultaciya-advokata51.ru предлагает вам разнообразные возможности. Получение юридической помощи – это необходимость для многих. Мы обеспечим вас экспертными консультациями.
Получите бесплатную юридическую консультацию круглосуточно на адвокат бесплатная консультация по телефону.
Вы сможете записаться на консультацию, чтобы получить персонализированный подход.
Важно обратить внимание на уровень профессионализма юристов. Все адвокаты на нашем сайте имеют большой опыт работы. Что бы вы ни выбрали, мы гарантируем качественное выполнение работы.
Важно, чтобы юридические услуги были доступны каждому. На нашем сайте можно найти информацию о ценах и услугах. Мы уверены, что каждый найдет подходящее решение для себя.
Кроме того, мы предлагаем услуги онлайн. Это особенно удобно для тех, кто ценит своё время. Вы можете задать свои вопросы в любое время.
Казино Вавада часто обсуждается в сети.
Акции и предложения делают старт комфортным.
Игровые конкурсы поддерживают интерес.
Коллекция развлечений пополняется новыми провайдерами.
Регистрация занимает минуты, поэтому можно сразу активировать бонусы.
Все подробности смотри здесь: вавада промокод 2025
Авто портал https://avtoshans.in.ua для всех: свежие новости, обзоры моделей, советы по выбору и эксплуатации авто. Каталог машин, тест-драйвы и рекомендации экспертов для водителей и покупателей.
Портал про автомобили https://myauto.kyiv.ua онлайн-ресурс для автолюбителей. Обзоры, статьи, тест-драйвы, цены и полезные советы по ремонту и уходу за машиной. Всё о мире авто в одном месте.
Свежие новости авто https://orion-auto.com.ua тест-драйвы, обзоры новинок, законодательные изменения и аналитика авторынка. Подробная информация об автомобилях и автоиндустрии для водителей и экспертов.
Автомобильные новости https://reuth911.com онлайн: новые модели, отзывы, тест-драйвы, события автопрома и полезные советы. Узнайте первыми о главных новинках и трендах автомобильного мира.
Estou completamente alucinado por MonsterWin Casino, tem uma vibe de jogo que e pura selva. Os titulos do cassino sao um espetaculo selvagem, oferecendo sessoes de cassino ao vivo que sao uma fera. O servico do cassino e confiavel e brabo, acessivel por chat ou e-mail. Os ganhos do cassino chegam voando como um dragao, de vez em quando queria mais promocoes de cassino que devastam. Em resumo, MonsterWin Casino e um cassino online que e uma fera total para quem curte apostar com garra no cassino! De bonus o site do cassino e uma obra-prima de estilo, o que deixa cada sessao de cassino ainda mais animal.
monsterwin 1|
Ich bin vollig hingerissen von PlayJango Casino, es ist ein Online-Casino, das wie ein Wirbelsturm tobt. Die Casino-Optionen sind vielfaltig und mitrei?end, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Die Casino-Mitarbeiter sind schnell wie ein Blitzstrahl, mit Hilfe, die wie ein Funke spruht. Casino-Gewinne kommen wie ein Komet, aber mehr Freispiele im Casino waren ein Volltreffer. Am Ende ist PlayJango Casino eine Casino-Erfahrung, die wie ein Regenbogen glitzert fur Spieler, die auf elektrisierende Casino-Kicks stehen! Zusatzlich die Casino-Plattform hat einen Look, der wie ein Blitz funkelt, einen Hauch von Abenteuer ins Casino bringt.
casino playjango|
Adoro o clima insano de PagolBet Casino, tem uma vibe de jogo que e pura eletricidade. A gama do cassino e simplesmente uma faisca, com slots de cassino unicos e contagiantes. O atendimento ao cliente do cassino e uma corrente de eficiencia, com uma ajuda que e pura energia. O processo do cassino e limpo e sem turbulencia, as vezes queria mais promocoes de cassino que eletrizam. No geral, PagolBet Casino garante uma diversao de cassino que e uma tempestade para os viciados em emocoes de cassino! De bonus a navegacao do cassino e facil como uma faisca, aumenta a imersao no cassino a mil.
pagolbet site|
Je suis totalement submerge par NetBet Casino, c’est un casino en ligne qui ondule comme une vague geante. La selection du casino est un courant de plaisirs, offrant des sessions de casino en direct qui eclaboussent. Le personnel du casino offre un accompagnement digne d’un capitaine, assurant un support de casino immediat et fluide. Le processus du casino est transparent et sans remous, mais plus de tours gratuits au casino ce serait aquatique. Pour resumer, NetBet Casino promet un divertissement de casino aquatique pour les amoureux des slots modernes de casino ! Par ailleurs le site du casino est une merveille graphique fluide, ajoute une touche d’eclat marin au casino.
netbet olanda|
Je suis fou de PokerStars Casino, ca vibre avec une energie de casino strategique. L’assortiment de jeux du casino est une galaxie de plaisirs, comprenant des jeux de casino adaptes aux cryptomonnaies. L’assistance du casino est fiable et astucieuse, repondant en un eclair strategique. Les paiements du casino sont securises et fluides, cependant les offres du casino pourraient etre plus genereuses. En somme, PokerStars Casino promet un divertissement de casino strategique pour ceux qui cherchent l’adrenaline tactique du casino ! En plus la plateforme du casino brille par son style audacieux, donne envie de replonger dans le casino sans fin.
pokerstars contact tГ©lГ©phone|
Онлайн-сайт для женщин https://musicbit.com.ua стиль, уход за собой, психология, семья, карьера и хобби. Интересные статьи, тесты и форум для общения. Пространство для вдохновения и развития.
Автомобильный сайтhttps://setbook.com.ua свежие новости, обзоры моделей, тест-драйвы и советы экспертов. Каталог авто, актуальные цены, авторынок и всё, что нужно водителям и автолюбителям в одном месте.
Онлайн-журнал для женщин https://fines.com.ua стиль, уход за собой, психология, рецепты, материнство и карьера. Актуальные материалы, тренды и экспертные рекомендации каждый день.
Женский сайт о жизни https://prettywoman.kyiv.ua секреты красоты, мода, здоровье, рецепты и отношения. Интересные статьи, советы и лайфхаки. Всё, что нужно, чтобы чувствовать себя уверенно и счастливо.
Автомобильный портал https://troeshka.com.ua онлайн-ресурс для автовладельцев. Каталог машин, тест-драйвы, аналитика авторынка и советы специалистов. Будьте в курсе новинок и технологий автоиндустрии.
Женский онлайн-журнал https://feminine.kyiv.ua мода, красота, здоровье, отношения и семья. Полезные советы, вдохновляющие статьи, лайфхаки для дома и карьеры. Всё самое интересное для современных женщин.
Онлайн-сайт про автомобили https://tvregion.com.ua свежие новости, аналитика рынка, обзоры и сравнения машин. Советы по обслуживанию и выбору авто. Всё для водителей и автолюбителей в одном месте.
Сайт для женщин https://lolitaquieretemucho.com мода, красота, здоровье, отношения, семья и карьера. Полезные советы, статьи, рецепты и лайфхаки. Пространство для вдохновения и развития, созданное для современных женщин.
Good day! This is my first comment here so I just wanted to give a quick shout out and say I genuinely enjoy reading your posts. Can you recommend any other blogs/websites/forums that go over the same subjects? Thank you so much!
kra39 at
Been checking out Tiger787 lately and it’s actually not bad. Their game selection is pretty decent – spent some time on slots like ‘Book of Wild’ and ‘Coin Win: Hold The Spin.’ The site runs smoothly, which is more than I can say for some other places I’ve tried
Сайт про машины https://tvk-avto.com.ua обзоры моделей, тест-драйвы, новости автопрома и советы по эксплуатации. Полезные статьи о выборе авто, уходе, ремонте и актуальные материалы для автовладельцев.
Сайт для женщин https://femaleguide.kyiv.ua гармония стиля и жизни. Уход за собой, рецепты, дом, отношения, карьера и путешествия. Читайте статьи, делитесь опытом и вдохновляйтесь новыми идеями.
Автомобильный новостной портал https://tuning-kh.com.ua всё об авто в одном месте: новости, цены, обзоры, тест-драйвы, авторынок. Советы экспертов и полезные материалы для водителей и тех, кто планирует купить машину.
Женский онлайн портал https://femalesecret.kyiv.ua онлайн-ресурс для девушек и женщин. Мода, красота, здоровье, семья и материнство. Полезные советы, экспертные материалы и позитивное сообщество для общения и вдохновения.
Je suis fou de MrPlay Casino, il propose une aventure de casino qui swingue comme un orchestre. Les options de jeu au casino sont variees et festives, avec des machines a sous de casino modernes et entrainantes. Le support du casino est disponible 24/7, garantissant un support de casino instantane et eclatant. Les gains du casino arrivent a une vitesse endiablee, par moments j’aimerais plus de promotions de casino qui eblouissent comme un feu d’artifice. Dans l’ensemble, MrPlay Casino c’est un casino a rejoindre sans attendre pour les passionnes de casinos en ligne ! En plus la navigation du casino est intuitive comme une danse, ajoute une touche de panache au casino.
sindy rose & mr.play double pussy and anal fisting with huge prolapse|
Adoro o clima insano de ParamigoBet Casino, e um cassino online que e um verdadeiro furacao. Tem uma enxurrada de jogos de cassino irados, oferecendo sessoes de cassino ao vivo que sao um tornado. Os agentes do cassino sao rapidos como um raio, com uma ajuda que e pura forca. Os pagamentos do cassino sao lisos e blindados, porem as ofertas do cassino podiam ser mais generosas. Resumindo, ParamigoBet Casino e o point perfeito pros fas de cassino para os viciados em emocoes de cassino! Alem disso o site do cassino e uma obra-prima de estilo, da um toque de forca braba ao cassino.
paramigobet kokemuksia|
Sou louco pelo role de PlayUzu Casino, da uma energia de cassino que e um redemoinho. Tem uma enxurrada de jogos de cassino irados, com caca-niqueis de cassino modernos e contagiantes. O servico do cassino e confiavel e brabo, respondendo mais rapido que um estalo. Os saques no cassino sao velozes como um furacao, porem queria mais promocoes de cassino que detonam. Resumindo, PlayUzu Casino e o point perfeito pros fas de cassino para os aventureiros do cassino! De lambuja o site do cassino e uma obra-prima de estilo, torna o cassino uma curticao total.
playuzu bono de bienvenida|
Je trouve absolument siderant NineCasino, c’est un casino en ligne qui brille comme une supernova. L’eventail de jeux du casino est une constellation de delices, proposant des slots de casino a theme spatial. Les agents du casino sont rapides comme une comete, repondant en un eclair cosmique. Les gains du casino arrivent a une vitesse lumiere, cependant j’aimerais plus de promotions de casino qui eblouissent. Au final, NineCasino est un casino en ligne qui illumine l’univers pour les voyageurs spatiaux du casino ! De surcroit la plateforme du casino brille par son style cosmique, facilite une experience de casino stellaire.
32-ninecasino|
Je trouve absolument envoutant Posido Casino, il propose une aventure de casino qui plonge dans les abysses. La selection du casino est une vague de plaisirs, proposant des slots de casino a theme aquatique. L’assistance du casino est chaleureuse et limpide, repondant en un eclat d’ecume. Le processus du casino est transparent et sans remous, quand meme j’aimerais plus de promotions de casino qui eclaboussent. En somme, Posido Casino offre une experience de casino fluide comme l’ocean pour les navigateurs du casino ! Par ailleurs la plateforme du casino brille par son style oceanique, ce qui rend chaque session de casino encore plus fluide.
posido casino spielen|
https://shorturl.fm/N9QDR
Онлайн-сайт для женщин https://mirlady.kyiv.ua красота, стиль, здоровье, дом и семья. Практичные рекомендации, модные идеи, вдохновение и поддержка. Лучший контент для девушек и женщин любого возраста.
Сайт для женщин https://amideya.com.ua портал о красоте, стиле, здоровье, семье и саморазвитии. Ежедневные статьи, полезные рекомендации и вдохновение для современных девушек и женщин.
Женский сайт https://lubimoy.com.ua стиль, уход за собой, психология, материнство, работа и хобби. Актуальные статьи, тренды и экспертные советы. Всё самое важное для гармоничной жизни и успеха.
Женский онлайн-журнал https://gracefullady.kyiv.ua свежие статьи о моде, красоте, здоровье и саморазвитии. Практичные советы, вдохновение и позитив для девушек и женщин любого возраста.
https://shorturl.fm/FWTV0
https://shorturl.fm/CsSUj
Hi there, I would like to know more about the course, is that possible that you send to me?
Thanks.
Je suis totalement fascine par MrXBet Casino, il propose une aventure de casino qui serpente comme un labyrinthe. Les options de jeu au casino sont riches et mysterieuses, avec des machines a sous de casino modernes et captivantes. Le service client du casino est un detective hors pair, garantissant un support de casino instantane et astucieux. Les transactions du casino sont simples comme un code decrypte, parfois les offres du casino pourraient etre plus genereuses. Au final, MrXBet Casino offre une experience de casino mysterieuse pour les passionnes de casinos en ligne ! Bonus l’interface du casino est fluide et intrigante comme un mystere, donne envie de replonger dans le casino sans fin.
mrxbet apk|
скидка на бронирование отеля островок Ищете спонтанное приключение? Наши горящие туры предлагают невероятные возможности отправиться в отпуск вашей мечты по удивительно выгодным ценам. Не упустите шанс испытать незабываемые эмоции и сэкономить при этом! Поспешите, ведь количество предложений ограничено!
Ich liebe den Zauber von NV Casino, es ist ein Online-Casino, das wie ein Blitz einschlagt. Der Katalog des Casinos ist eine Welle voller Spa?, mit Live-Casino-Sessions, die wie ein Gewitter toben. Das Casino-Team bietet Unterstutzung, die wie ein Meteor leuchtet, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein Sturm, ab und zu mehr Freispiele im Casino waren ein Volltreffer. Insgesamt ist NV Casino ein Muss fur Casino-Fans fur die, die mit Stil im Casino wetten! Zusatzlich die Casino-Seite ist ein grafisches Meisterwerk, das Casino-Erlebnis total elektrisiert.
casino age nv|
Ich liebe die Pracht von Richard Casino, es bietet ein Casino-Abenteuer, das wie ein Thron funkelt. Die Auswahl im Casino ist ein wahres Kronungsjuwel, mit modernen Casino-Slots, die einen verzaubern. Der Casino-Kundenservice ist wie ein koniglicher Hofstaat, mit Hilfe, die wie ein Thron majestatisch ist. Der Casino-Prozess ist klar und ohne Intrigen, trotzdem mehr regelma?ige Casino-Boni waren furstlich. Zusammengefasst ist Richard Casino ein Casino, das man nicht verpassen darf fur Abenteurer im Casino! Und au?erdem die Casino-Navigation ist kinderleicht wie ein koniglicher Marsch, was jede Casino-Session noch prachtiger macht.
richard casino no deposit bonus 2024|
Je suis fou de PlazaRoyal Casino, il propose une aventure de casino qui scintille comme un trone. Les options de jeu au casino sont riches et somptueuses, proposant des slots de casino a theme royal. Les agents du casino sont rapides comme un decret royal, joignable par chat ou email. Les paiements du casino sont securises et fluides, quand meme des recompenses de casino supplementaires feraient regner. Pour resumer, PlazaRoyal Casino c’est un casino a decouvrir sans tarder pour les passionnes de casinos en ligne ! Bonus l’interface du casino est fluide et eclatante comme un palais, ajoute une touche de grandeur au casino.
plaza royal casino promo code|
latest information here: https://aquietrabalho.com
visit our website: https://lmc896.org
Here is the best on the net: https://www.lnrprecision.com
Latest information from us: https://www.semasan.com
просмотры тг Стремитесь стать звездой TikTok и покорить миллионы сердец? Начните с привлечения подписчиков в TikTok и наблюдайте за взрывным ростом популярности! Расширение аудитории, повышение охвата и попадание в тренды TikTok. Заявите о себе миру!
https://www.rusprofile.ru/ip/322237500246557
The latest data is right here: https://institutocea.com
Go to our website: https://baldebranco.com.br
All the latest on our website: https://clubcoma.org
Here you will find only the best: https://edicionesdelau.com
Hi, all is going nicely here and ofcourse every one is sharing facts, that’s really fine, keep up writing.
http://1119732.net/top-10-headlight-sealing-mistakes.html
https://shorturl.fm/wmSap
Come in – don’t miss the latest: https://redclara.net
Only we have the newest materials: https://jnp.chitkara.edu.in
Always relevant information: https://agriness.com
Information that is always relevant: https://billi-walker.jp
Always relevant here: https://deogiricollege.org
Catch the latest from us: https://eguidemagazine.com
Everything new is nearby: https://cere-india.org
Сайт finance-post.ru — это блог финансиста, ориентированный на личные финансы, бюджетирование и инвестиции. На нём публикуются практические материалы, советы и обзоры
Печатный Центр https://kopirych.by «Копирыч» в Минске и по всей Беларуси! Оперативная печать, брошюровка, широкоформатная и сувенирная продукция. Качественно, недорого, с доставкой. Ваши идеи — наша реализация! Заказывайте на сайте или по телефону.
руководства по садоводству https://zelenayazona.ru идеи, инструкции и советы по уходу за садом и огородом. Информация для новичков и опытных дачников: посадка, полив, удобрение и защита растений.
Женский сайт https://family-site.com.ua современный портал о моде, красоте, отношениях и саморазвитии. Полезные материалы, секреты здоровья и успеха, актуальные тренды и советы экспертов для женщин любого возраста.
Семейный портал https://geog.org.ua всё для гармонии в доме: воспитание детей, отношения, здоровье, отдых и уют. Полезные советы, статьи и лайфхаки для всей семьи. Пространство, где находят ответы и вдохновение.
сочи ветлечебница Ветклиника в Хосте: Ваш надежный партнер в заботе о здоровье животных. Мы любим животных и заботимся о них, как о своих собственных.
Женский онлайн портал https://femalesecret.kyiv.ua онлайн-ресурс для девушек и женщин. Мода, красота, здоровье, семья и материнство. Полезные советы, экспертные материалы и позитивное сообщество для общения и вдохновения.
Современный женский https://happywoman.kyiv.ua онлайн-журнал: новости стиля, секреты красоты, идеи для дома, кулинарные рецепты и советы по отношениям. Пространство для вдохновения и развития.
Современный женский https://happywoman.kyiv.ua онлайн-журнал: новости стиля, секреты красоты, идеи для дома, кулинарные рецепты и советы по отношениям. Пространство для вдохновения и развития.
Портал о здоровье https://mikstur.com информационный ресурс о медицине и ЗОЖ. Статьи о лечении, правильном питании, физических упражнениях и укреплении иммунитета.
Портал о стройке https://bastet.com.ua статьи, новости и советы по ремонту, строительству и дизайну. Подбор материалов, проекты домов, технологии и полезная информация для специалистов и частных застройщиков.
Информационный портал https://intertools.com.ua о стройке: новости отрасли, советы по ремонту, выбору материалов и дизайну. Всё для тех, кто строит дом, делает ремонт или работает в строительстве.
Цена мягких окон Гибкое остекление – это современное и практичное решение для защиты вашего пространства от непогоды. Оно легко устанавливается и снимается, позволяя вам наслаждаться природой в хорошую погоду и укрыться от непогоды при необходимости.
https://shorturl.fm/rj49o
https://t.me/Igrovie_avtomati_na_dengi Игровые автоматы онлайн – это виртуальные версии традиционных игровых автоматов, доступные через интернет. Они предлагают удобство и доступность, позволяя игрокам наслаждаться азартными играми в любое время и в любом месте. Онлайн-казино предлагают широкий выбор игровых автоматов с разнообразными темами, графикой и бонусными функциями. Игроки могут выбирать из классических слотов, видео-слотов, прогрессивных джекпотов и других вариантов. При игре в онлайн-казино важно выбирать надежные и лицензированные платформы, чтобы обеспечить безопасность и честность игрового процесса.
https://t.me/perevedem_document Перевод Документов: Мост между Языками и Культурами В современном мире глобализации, где границы стираются, а сотрудничество между странами и культурами становится все более тесным, перевод документов приобретает огромное значение. Это не просто замена слов одного языка словами другого, а кропотливая работа по передаче смысла, контекста и нюансов оригинала, чтобы обеспечить полное и точное понимание информации. Когда необходим перевод документов? Международный бизнес: контракты, договоры, финансовые отчеты, маркетинговые материалы – все это требует качественного перевода для успешного ведения дел за рубежом. Юридические вопросы: судебные документы, свидетельства, доверенности, нотариальные акты должны быть переведены с соблюдением строгих юридических норм и терминологии. Медицинская сфера: медицинские заключения, инструкции к лекарствам, результаты исследований – точность перевода здесь критически важна для здоровья пациентов. Техническая документация: инструкции по эксплуатации, технические спецификации, чертежи – перевод должен быть понятным и однозначным для специалистов. Образование и наука: дипломы, аттестаты, научные статьи, исследования – для признания образования за рубежом и обмена знаниями необходим качественный перевод. Почему важно обращаться к профессионалам? Точность и соответствие: профессиональные переводчики обладают глубокими знаниями языка и предметной области, что гарантирует точность и соответствие перевода оригиналу. Соблюдение терминологии: использование правильной терминологии – залог того, что перевод будет понятен специалистам в соответствующей области. Культурная адаптация: профессиональный переводчик адаптирует текст с учетом культурных особенностей целевой аудитории, чтобы избежать недопонимания или неловких ситуаций. Конфиденциальность: профессиональные бюро переводов гарантируют конфиденциальность ваших документов. Как выбрать бюро переводов? Опыт и репутация: изучите опыт работы бюро, ознакомьтесь с отзывами клиентов. Специализация: убедитесь, что бюро специализируется на переводах в нужной вам области. Наличие профессиональных переводчиков: узнайте, работают ли в бюро переводчики с соответствующим образованием и опытом. Стоимость и сроки: сравните цены и сроки выполнения заказа в разных бюро. В заключение, перевод документов – это важный инструмент для преодоления языковых барьеров и успешного взаимодействия в современном мире. Доверяйте перевод ваших документов профессионалам, чтобы быть уверенными в качестве и точности результата. Если вам нужно перевести конкретный документ, просто предоставьте его мне, и я постараюсь вам помочь!
Женский онлайн-журнал https://girl.kyiv.ua стиль, уход за собой, психология, кулинария, отношения и материнство. Ежедневные материалы, экспертные советы и вдохновение для девушек и женщин любого возраста.
Портал про детей https://mch.com.ua информационный ресурс для родителей. От беременности и ухода за малышом до воспитания школьников. Советы, статьи и поддержка для гармоничного развития ребёнка.
Онлайн-журнал для женщин https://krasotka-fl.com.ua всё о красоте, моде, семье и жизни. Полезные статьи, лайфхаки, советы экспертов и интересные истории. Читайте и вдохновляйтесь каждый день.
J’adore le rythme de Spinsy Casino, on dirait une soiree disco pleine de frissons. Il y a une vague de jeux de casino captivants, avec des machines a sous de casino modernes et hypnotiques. Le service client du casino est une star du dancefloor, offrant des solutions claires et instantanees. Les transactions du casino sont simples comme un pas de moonwalk, quand meme des recompenses de casino supplementaires feraient swinguer. En somme, Spinsy Casino est un casino en ligne qui met le feu a la piste pour les joueurs qui aiment parier avec style au casino ! Par ailleurs l’interface du casino est fluide et eclatante comme un neon, amplifie l’immersion totale dans le casino.
spinsy free spins|
Ich finde absolut elektrisierend SlotClub Casino, es fuhlt sich an wie ein bunter Rausch aus Lichtern. Die Auswahl im Casino ist ein echtes Lichtspektakel, mit einzigartigen Casino-Slotmaschinen. Der Casino-Kundenservice ist wie ein leuchtender Funke, sorgt fur sofortigen Casino-Support, der verblufft. Casino-Transaktionen sind simpel wie ein Schalter, dennoch die Casino-Angebote konnten gro?zugiger sein. Alles in allem ist SlotClub Casino eine Casino-Erfahrung, die wie ein Lichtspiel glitzert fur Spieler, die auf leuchtende Casino-Kicks stehen! Zusatzlich die Casino-Navigation ist kinderleicht wie ein Lichtschalter, Lust macht, immer wieder ins Casino zuruckzukehren.
slotclub online casino|
Je suis totalement electrise par Roobet Casino, ca vibre avec une energie de casino totalement electro. La selection du casino est un tourbillon de plaisirs lumineux, offrant des sessions de casino en direct qui crepitent. Le service client du casino est une decharge d’efficacite, repondant en un eclair fluorescent. Les paiements du casino sont securises et fluides, parfois des bonus de casino plus frequents seraient dejantes. En somme, Roobet Casino promet un divertissement de casino fluorescent pour les joueurs qui aiment parier avec panache au casino ! A noter le site du casino est une merveille graphique electro, ce qui rend chaque session de casino encore plus vibrante.
roobet chile|
Je suis accro a Spinanga Casino, ca degage une ambiance de jeu aussi virevoltante qu’un cyclone. Il y a une rafale de jeux de casino captivants, comprenant des jeux de casino adaptes aux cryptomonnaies. L’assistance du casino est chaleureuse et irreprochable, joignable par chat ou email. Les paiements du casino sont securises et fluides, mais des bonus de casino plus frequents seraient explosifs. Pour resumer, Spinanga Casino est un casino en ligne qui dechaine les elements pour ceux qui cherchent l’adrenaline frenetique du casino ! De surcroit le design du casino est un spectacle visuel tumultueux, facilite une experience de casino frenetique.
spinanga application|
Estou completamente encantado por Richville Casino, da uma energia de cassino tao luxuosa quanto um trono. Tem uma cascata de jogos de cassino fascinantes, com slots de cassino tematicos de luxo. O suporte do cassino esta sempre disponivel 24/7, garantindo suporte de cassino direto e sem falhas. Os pagamentos do cassino sao seguros e impecaveis, mesmo assim as ofertas do cassino podiam ser mais generosas. Na real, Richville Casino vale a pena explorar esse cassino com urgencia para os amantes de cassinos online! De lambuja o design do cassino e um espetaculo visual de tirar o folego, torna a experiencia de cassino um evento de gala.
roof cleaning richville|
таможенный брокер для юридических лиц Для юридических лиц, работающих на международном рынке, таможенный брокер – это незаменимый партнер. Мы предлагаем комплексные решения по таможенному оформлению, которые экономят ваше время и деньги, позволяя вам сосредоточиться на ключевых задачах бизнеса.
Онлайн-журнал https://presslook.com.ua для женщин объединяет всё, что важно: мода и стиль, воспитание детей, карьерные советы и вдохновение. Советы специалистов и реальные истории для поддержки и новых идей.
Актуальные тренды https://horoscope-web.com и вневременная классика. Подборки образов, советы по стилю, секреты гардероба и модные инсайты. Мы поможем тебе выглядеть безупречно каждый день и выразить свой индивидуальный стиль.
Твой гид https://nicegirl.kyiv.ua по здоровому образу жизни! Эффективные тренировки, сбалансированное питание, wellness-практики и советы по мотивации. Обрети энергию, силу и гармонию в теле, которое ты любишь.
Ресурс для амбициозных https://ramledlightings.com и целеустремленных. Карьерный рост, личная эффективность, финансовая грамотность и вдохновляющие истории успеха. Реализуй свой потенциал и добивайся всех поставленных целей!
https://impossible-studio.ghost.io/kak-vybrat-luchshii-vpn-siervis-podrobnoie-rukovodstvo/ Новый лонгрид про Youtuber VPN! Узнайте, как смотреть YouTube и другие платформы без лагов и блокировок. Подключайте до 5 устройств на одной подписке, тестируйте сервис бесплатно 3 дня и платите всего 290? в первый месяц вместо 2000? у конкурентов. Серверы в Европе — ваши данные защищены от российских властей.
выполнять курсовую работу написание курсовой работы цена
займ онлайн на карту срочно займы онлайн на карту без проверок
быстрый займ на карту онлайн займы на карту онлайн мгновенно без отказа
Puzzles online https://www.leaderonomics.com/articles/leadership/how-sports-puzzles-made-me-a-calmer-leader play for free in assembling pictures of any complexity. Thousands of options: classic, children’s, 3D and thematic. Convenient interface, saving progress and new puzzles every day.
курсовая на заказ в москве написание курсовой работы цена
займы онлайн без отказа займ денег онлайн
взять онлайн займ на карту онлайн займ на карту без истории
Распиловка Спил деревьев: аккуратное и безопасное удаление Спил деревьев – это процесс удаления дерева путем спиливания ствола у основания. Существует несколько методов спила, зависящих от размера дерева, его положения и наличия свободного пространства. Наиболее распространенные методы – это валка дерева целиком в определенном направлении, спиливание дерева по частям с подвешиванием каждой части на тросах (альпинистский спил) и использование автовышки для спиливания дерева сверху вниз. Важно правильно выбрать метод спила, чтобы избежать повреждения окружающих объектов и обеспечить безопасность рабочих.
фотокартинаназаказ Фотокартина на заказ: Картина, созданная на основе фотографии и изготовленная по индивидуальному заказу клиента. Обычно подразумевает печать фотографии на холсте с дополнительной обработкой для придания ей более художественного вида.
Estou completamente enfeiticado por SpinWiz Casino, da uma energia de cassino que e puro encantamento. A gama do cassino e simplesmente um caldeirao de delicias, com slots de cassino tematicos de feiticaria. O atendimento ao cliente do cassino e um feitico de eficiencia, dando solucoes na hora e com precisao. Os saques no cassino sao velozes como um feitico de teletransporte, mas mais bonus regulares no cassino seria brabo. No geral, SpinWiz Casino e um cassino online que e um portal de diversao para os viciados em emocoes de cassino! Alem disso a navegacao do cassino e facil como um passe de magica, adiciona um toque de encantamento ao cassino.
spinwiz reclame aqui|
Acho simplesmente alucinante SpinFest Casino, oferece uma aventura de cassino que pulsa como um batuque de carnaval. O catalogo de jogos do cassino e uma explosao de folia, com slots de cassino tematicos de festa. O servico do cassino e confiavel e cheio de energia, acessivel por chat ou e-mail. Os pagamentos do cassino sao lisos e blindados, porem queria mais promocoes de cassino que botam pra quebrar. No geral, SpinFest Casino e um cassino online que e uma folia sem fim para os viciados em emocoes de cassino! De bonus a interface do cassino e fluida e reluzente como um bloco de carnaval, torna a experiencia de cassino uma festa inesquecivel.
ОєО±О¶ОЇОЅОї spinfest ПѓОµ О±ПЂОµП…ОёОµОЇО±П‚ ПѓПЌОЅОґОµПѓО·|
Je suis fou de RubyVegas Casino, il propose une aventure de casino qui scintille comme un tresor. L’eventail de jeux du casino est une caverne de pierres precieuses, offrant des sessions de casino en direct qui brillent comme des gemmes. L’assistance du casino est chaleureuse et irreprochable, offrant des solutions claires et instantanees. Le processus du casino est transparent et sans defaut, mais j’aimerais plus de promotions de casino qui eblouissent. En somme, RubyVegas Casino est un casino en ligne qui brille comme un joyau pour les joueurs qui aiment parier avec panache au casino ! Par ailleurs la plateforme du casino brille par son style somptueux, ajoute une touche de luxe au casino.
Adoro o brilho estelar de SpeiCasino, oferece uma aventura de cassino que orbita como um satelite. A gama do cassino e simplesmente um universo de delicias, com slots de cassino tematicos de espaco. O atendimento ao cliente do cassino e uma estrela-guia, respondendo mais rapido que uma explosao estelar. Os pagamentos do cassino sao lisos e blindados, de vez em quando mais bonus regulares no cassino seria intergalactico. Na real, SpeiCasino garante uma diversao de cassino que e uma galaxia para os astronautas do cassino! De bonus a plataforma do cassino brilha com um visual que e puro cosmos, faz voce querer voltar ao cassino como um cometa em orbita.
spei app apk|
Adoro o swing de RioPlay Casino, e um cassino online que samba como uma escola de carnaval. A gama do cassino e simplesmente um bloco de carnaval, com slots de cassino tematicos de festa. Os agentes do cassino sao rapidos como um passista, respondendo mais rapido que um batuque. As transacoes do cassino sao simples como um passo de samba, mesmo assim mais recompensas no cassino seriam um diferencial brabo. Em resumo, RioPlay Casino vale demais sambar nesse cassino para os folioes do cassino! Vale dizer tambem a navegacao do cassino e facil como um passo de carnaval, torna a experiencia de cassino uma festa inesquecivel.
rioplay roblox|
https://shorturl.fm/7kiF8
микрозаймы без процентов на карту лучшие онлайн Если вам нужны деньги быстро, выберите микрозайм на карту онлайн срочно – это хороший вариант.
https://shorturl.fm/weVLd
Твой гид https://womanlife.kyiv.ua по стильной жизни. Мы собрали всё: от выбора платья на вечер до планирования идеального отпуска. Экспертные советы, подборки и инсайты, чтобы ты всегда чувствовала себя на высоте.
Онлайн-журнал о моде https://glamour.kyiv.ua без правил. Новые тренды, стильные образы, секреты знаменитостей и советы по созданию идеального гардероба. Мы поможем вам найти и с уверенностью выразить свой уникальный стиль.
Журнал для женщин https://rpl.net.ua которые строят карьеру и хотят большего. Финансовая грамотность, советы по продуктивности, истории успеха и руководство по переговорам. Достигайте своих целей с нами!
Женский сайт https://bbb.dp.ua всё самое важное для современных девушек: стиль, красота, здоровье, отношения и самореализация. Читайте, вдохновляйтесь и находите новые идеи.
Je suis fou de Riviera Casino, c’est un casino en ligne qui scintille comme un coucher de soleil sur la Cote d’Azur. Le repertoire du casino est un port de plaisirs luxueux, proposant des slots de casino a theme mediterraneen. Les agents du casino sont rapides comme un hors-bord, repondant en un eclat de soleil. Les paiements du casino sont securises et fluides, parfois les offres du casino pourraient etre plus genereuses. Dans l’ensemble, Riviera Casino est un joyau pour les fans de casino pour les passionnes de casinos en ligne ! En plus l’interface du casino est fluide et eclatante comme une mer azur, donne envie de replonger dans le casino sans fin.
forum la riviera casino|
Estou completamente enfeiticado por SpellWin Casino, parece um portal mistico cheio de adrenalina. A selecao de titulos do cassino e um caldeirao de emocoes, oferecendo sessoes de cassino ao vivo que brilham como runas. O servico do cassino e confiavel e encantador, com uma ajuda que reluz como uma pocao. Os saques no cassino sao velozes como um feitico de teletransporte, de vez em quando mais bonus regulares no cassino seria brabo. Na real, SpellWin Casino vale demais explorar esse cassino para os magos do cassino! E mais o site do cassino e uma obra-prima de estilo mistico, o que torna cada sessao de cassino ainda mais encantadora.
spellwin|
Sou louco pelo feitico de SpinGenei Casino, da uma energia de cassino que e pura magia. O catalogo de jogos do cassino e um bau de tesouros misticos, incluindo jogos de mesa de cassino com um toque de magia. O suporte do cassino ta sempre na ativa 24/7, acessivel por chat ou e-mail. Os pagamentos do cassino sao lisos e blindados, as vezes mais recompensas no cassino seriam um diferencial encantado. Em resumo, SpinGenei Casino oferece uma experiencia de cassino que e puro encantamento para os viciados em emocoes de cassino! De lambuja a interface do cassino e fluida e reluz como uma lampada magica, torna a experiencia de cassino um conto de fadas.
spingenie sister sites|
Je suis fou de Stake Casino, on dirait un cratere bouillonnant de fun. Il y a une explosion de jeux de casino captivants, avec des machines a sous de casino modernes et enflammees. L’assistance du casino est chaleureuse et irreprochable, offrant des solutions claires et instantanees. Les paiements du casino sont securises et fluides, quand meme plus de tours gratuits au casino ce serait volcanique. Pour resumer, Stake Casino est un casino en ligne qui fait trembler le sol pour ceux qui cherchent l’adrenaline enflammee du casino ! De surcroit le design du casino est un spectacle visuel en fusion, ajoute une touche de feu au casino.
code stake|
https://shorturl.fm/gKWcM
Новостной сайт https://vesti.in.ua свежие события дня: политика, экономика, культура, спорт, технологии и общество. Актуальная информация, аналитика и репортажи из разных регионов и мира.
Свежие новости https://sensus.org.ua Украины и мира: главные события, репортажи и аналитика. Политика, экономика, общество и культура в удобном формате онлайн.
Новостной портал Украины https://lenta.kyiv.ua оперативные события в стране. Политика, экономика, региональные новости, спорт и культура. Достоверные материалы и аналитика каждый день.
Свежие новости Украины https://novosti24.kyiv.ua главные события, мнения экспертов и аналитические материалы. Лента новостей онлайн, репортажи и достоверные факты без перерыва.
https://shorturl.fm/dwtZQ
https://shorturl.fm/pSTVk
Estou completamente alucinado por SSSXWin Casino, parece um festival cosmico de adrenalina. A selecao de titulos do cassino e uma explosao de nebulosas, com caca-niqueis de cassino modernos e hipnoticos. O servico do cassino e confiavel e brilha como uma galaxia, respondendo mais rapido que uma explosao de supernova. Os saques no cassino sao velozes como uma viagem interestelar, mas queria mais promocoes de cassino que explodem como estrelas. No geral, SSSXWin Casino garante uma diversao de cassino que e uma supernova para os amantes de cassinos online! E mais o site do cassino e uma obra-prima de estilo estelar, eleva a imersao no cassino a um nivel cosmico.
avis casino sssxwin|
Estou completamente vidrado por SupremaBet Casino, e um cassino online que ressoa como um trovao epico. A gama do cassino e simplesmente uma dinastia de delicias, oferecendo sessoes de cassino ao vivo que reluzem como cetros. A equipe do cassino entrega um atendimento que e puro reinado, acessivel por chat ou e-mail. Os ganhos do cassino chegam voando como um falcao real, porem mais giros gratis no cassino seria uma loucura. Em resumo, SupremaBet Casino oferece uma experiencia de cassino que e puro cetro para os viciados em emocoes de cassino! De bonus a plataforma do cassino brilha com um visual que e puro trono, o que torna cada sessao de cassino ainda mais majestosa.
supremabet cadastro|
Acho simplesmente fantastico SpinSala Casino, oferece uma aventura de cassino que reluz como um holofote. O catalogo de jogos do cassino e um espetaculo de fogos, com jogos de cassino perfeitos pra criptomoedas. O suporte do cassino ta sempre na ativa 24/7, com uma ajuda que reluz como um show. As transacoes do cassino sao simples como um pisca-pisca, de vez em quando mais bonus regulares no cassino seria brabo. Na real, SpinSala Casino e o point perfeito pros fas de cassino para os amantes de cassinos online! E mais o site do cassino e uma obra-prima de estilo brilhante, o que torna cada sessao de cassino ainda mais iluminada.
spinsala login|
Ich finde absolut elektrisierend SportingBet Casino, es fuhlt sich an wie ein Volltreffer im Spielrausch. Die Spielauswahl im Casino ist wie eine volle Tribune, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Der Casino-Service ist zuverlassig und prazise, liefert klare und schnelle Losungen. Casino-Transaktionen sind simpel wie ein Freisto?, aber wurde ich mir mehr Casino-Promos wunschen, die wie ein Sieg jubeln. Zusammengefasst ist SportingBet Casino ein Casino mit einem Spielspa?, der wie ein Finale begeistert fur Fans von Online-Casinos! Zusatzlich die Casino-Oberflache ist flussig und glanzt wie ein Flutlicht, Lust macht, immer wieder ins Casino zuruckzukehren.
baixar sportingbet apk|
Estou alucinado com SupaBet Casino, da uma energia de cassino que e um trovao supersonico. Tem um tsunami de jogos de cassino irados, com slots de cassino tematicos de aventura epica. Os agentes do cassino sao rapidos como um relampago cosmico, dando solucoes na hora e com precisao. Os ganhos do cassino chegam voando como um foguete, mas mais giros gratis no cassino seria uma loucura cosmica. No fim das contas, SupaBet Casino e um cassino online que e um tufao de diversao para os amantes de cassinos online! De bonus o design do cassino e um espetaculo visual explosivo, o que torna cada sessao de cassino ainda mais eletrizante.
supabet auszahlung|
https://shorturl.fm/tKGTC
Новости Украины и мира https://mostmedia.com.ua политика, экономика, культура, спорт и общество. Свежие события, аналитика и репортажи. Будьте в курсе главных новостей в режиме онлайн 24/7.
Новостной портал https://mediateam.com.ua всё самое важное сегодня: политика, экономика, культура, спорт и шоу-бизнес. Лента новостей, репортажи и аналитические материалы каждый день.
Новости Украины https://status.net.ua объективная информация о событиях страны. Политика, экономика, региональные новости, спорт и культура. Читайте актуальные материалы каждый день.
Необходимо кодирование? наркология Хабаровск современные методы, конфиденциальность и поддержка специалистов. Помогаем избавиться от зависимости и вернуться к здоровой жизни.
Новости Украины https://status.net.ua объективная информация о событиях страны. Политика, экономика, региональные новости, спорт и культура. Читайте актуальные материалы каждый день.
вывод из запоя сайт кодировка от алкоголя в Томске цена
Строительство домов в Сочи https://stroitelstvodomovsochi.ru под ключ — профессиональный подход, проверенные материалы и гарантия качества. Полный спектр работ: проект, строительство, отделка и благоустройство.
Estou pirando com AFun Casino, da uma energia de cassino que e pura euforia. A gama do cassino e simplesmente uma explosao de prazeres, com slots de cassino tematicos de festa. A equipe do cassino entrega um atendimento que e puro carnaval, acessivel por chat ou e-mail. Os pagamentos do cassino sao lisos e blindados, mesmo assim as ofertas do cassino podiam ser mais generosas. Em resumo, AFun Casino oferece uma experiencia de cassino que e puro carnaval para os folioes do cassino! E mais a plataforma do cassino brilha com um visual que e puro axe, torna a experiencia de cassino uma folia inesquecivel.
codigo promocional afun dezembro|
Estou completamente vidrado por BetorSpin Casino, e um cassino online que gira como um asteroide em chamas. O catalogo de jogos do cassino e uma nebulosa de emocoes, com caca-niqueis de cassino modernos e hipnotizantes. O servico do cassino e confiavel e brilha como uma galaxia, dando solucoes na hora e com precisao. Os saques no cassino sao velozes como uma viagem interestelar, mesmo assim mais giros gratis no cassino seria uma loucura estelar. No fim das contas, BetorSpin Casino e o point perfeito pros fas de cassino para os viciados em emocoes de cassino! Vale dizer tambem a plataforma do cassino brilha com um visual que e puro cosmos, adiciona um toque de brilho estelar ao cassino.
betorspin casino terms and conditions|
Sou louco pela energia de BRCasino, tem uma vibe de jogo tao vibrante quanto uma escola de samba na avenida. O catalogo de jogos do cassino e uma folia de emocoes, incluindo jogos de mesa de cassino com um toque de carnaval. Os agentes do cassino sao rapidos como um mestre-sala, garantindo suporte de cassino direto e sem perder o ritmo. As transacoes do cassino sao simples como um passo de frevo, porem queria mais promocoes de cassino que botam pra quebrar. No geral, BRCasino vale demais sambar nesse cassino para os folioes do cassino! De lambuja a plataforma do cassino brilha com um visual que e puro axe, faz voce querer voltar ao cassino como num desfile sem fim.
br77 slots login|
Je suis fou de VBet Casino, on dirait une eruption de plaisirs incandescents. L’eventail de jeux du casino est une lave de delices, incluant des jeux de table de casino d’une elegance ardente. Le support du casino est disponible 24/7, assurant un support de casino immediat et incandescent. Les transactions du casino sont simples comme une braise, quand meme des recompenses de casino supplementaires feraient exploser. Pour resumer, VBet Casino c’est un casino a explorer sans tarder pour ceux qui cherchent l’adrenaline enflammee du casino ! Par ailleurs le site du casino est une merveille graphique ardente, donne envie de replonger dans le casino sans fin.
vbet casino no deposit|
Ich liebe den Zauber von Trickz Casino, es pulsiert mit einer verhexten Casino-Energie. Die Auswahl im Casino ist ein echtes Hexenwerk, inklusive stilvoller Casino-Tischspiele. Der Casino-Support ist rund um die Uhr verfugbar, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein Blitz aus dem Hut, ab und zu mehr Casino-Belohnungen waren ein zauberhafter Gewinn. Alles in allem ist Trickz Casino ein Casino mit einem Spielspa?, der wie eine Illusion verblufft fur Fans von Online-Casinos! Extra die Casino-Navigation ist kinderleicht wie ein Zauberspruch, was jede Casino-Session noch verzauberter macht.
trickz casino bonus|
Новостной портал https://newsawait.com свежие новости, аналитика и обзоры. Политика, экономика, культура и спорт. Лента событий в режиме реального времени с проверенными фактами.
Онлайн новостной портал https://reporternews.net главные события дня, эксклюзивные интервью, мнения экспертов и репортажи. Достоверная информация о политике, бизнесе и жизни общества.
Портал про авто https://dream-autos.com новости, обзоры и тест-драйвы. Полезные советы по выбору, ремонту и эксплуатации автомобилей. Каталог машин, актуальные цены и аналитика авторынка.
Новости Украины и мира https://globalnewshome.com всё самое важное сегодня. Политика, экономика, региональные события, спорт и культура. Объективные статьи и аналитика в удобном формате.
Портал для женщин https://womanfashionista.com всё самое важное в одном месте: уход за собой, мода, дом, семья и карьера. Читайте полезные статьи, находите вдохновение и делитесь опытом.
Сайт детского сада https://malush16.ru МКДОУ 16 «Малыш» Омутнинского района — документы, образовательные стандарты, новости, фотогалерея и полезные материалы для родителей и педагогов.
Sou louco pela vibe de Bet558 Casino, oferece uma aventura de cassino que orbita como um cometa veloz. O catalogo de jogos do cassino e uma constelacao de emocoes, com caca-niqueis de cassino modernos e estelares. O servico do cassino e confiavel e brilha como uma galaxia, garantindo suporte de cassino direto e sem buracos negros. Os ganhos do cassino chegam voando como um asteroide, as vezes mais bonus regulares no cassino seria estelar. Em resumo, Bet558 Casino e um cassino online que e uma galaxia de diversao para quem curte apostar com estilo estelar no cassino! De bonus a plataforma do cassino brilha com um visual que e puro cosmos, eleva a imersao no cassino a um nivel cosmico.
bet558 como sacar|
Estou completamente apaixonado por BacanaPlay Casino, e um cassino online que explode como um desfile de carnaval. Tem uma enxurrada de jogos de cassino irados, incluindo jogos de mesa de cassino com um toque de folia. O servico do cassino e confiavel e cheio de swing, acessivel por chat ou e-mail. As transacoes do cassino sao simples como um passo de samba, as vezes mais giros gratis no cassino seria uma loucura. No geral, BacanaPlay Casino e o point perfeito pros fas de cassino para os amantes de cassinos online! De bonus o site do cassino e uma obra-prima de estilo carioca, torna a experiencia de cassino uma festa inesquecivel.
bacanaplay bГґnus|
Je trouve absolument glacial ViggoSlots Casino, c’est un casino en ligne qui scintille comme un glacier sous l’aurore. L’eventail de jeux du casino est une toundra de delices, offrant des sessions de casino en direct qui scintillent comme la neige. L’assistance du casino est chaleureuse malgre le froid, assurant un support de casino immediat et givre. Les paiements du casino sont securises et fluides, cependant les offres du casino pourraient etre plus genereuses. Pour resumer, ViggoSlots Casino est une pepite pour les fans de casino pour les joueurs qui aiment parier avec style au casino ! A noter la navigation du casino est intuitive comme un chemin dans la neige, donne envie de replonger dans le casino sans fin.
viggoslots bonusbedingungen|
Ich bin vollig aufgeheizt von Turbonino Casino, es bietet ein Casino-Abenteuer, das wie ein Blitz uber die Piste schie?t. Es gibt eine Flut an mitrei?enden Casino-Titeln, inklusive stylischer Casino-Tischspiele. Das Casino-Team bietet Unterstutzung, die wie ein Turbo-Motor lauft, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein Zielsprint, ab und zu mehr regelma?ige Casino-Boni waren ein Volltreffer. Insgesamt ist Turbonino Casino ein Casino, das man nicht verpassen darf fur Fans moderner Casino-Slots! Zusatzlich die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino auf die Pole-Position hebt.
turbonino casino|
Ich liebe den Nervenkitzel von Tipico Casino, es fuhlt sich an wie ein Sturm aus Gewinnen. Die Casino-Optionen sind vielfaltig und elektrisierend, mit einzigartigen Casino-Slotmaschinen. Der Casino-Support ist rund um die Uhr verfugbar, liefert klare und schnelle Losungen. Casino-Zahlungen sind sicher und reibungslos, trotzdem mehr regelma?ige Casino-Boni waren ein Volltreffer. Alles in allem ist Tipico Casino ein Casino, das man nicht verpassen darf fur Fans moderner Casino-Slots! Zusatzlich die Casino-Plattform hat einen Look, der wie ein Blitz funkelt, was jede Casino-Session noch aufregender macht.
tipico konto löschen|
Статьи для садоводов https://portalteplic.ru огородников, фермеров и пчеловодов: советы по уходу за растениями, животными и пасекой. Полезные инструкции, лайфхаки и сезонные рекомендации.
Портал о ремонте https://studio-nd.ru статьи, инструкции и советы для дома и квартиры. От выбора материалов до дизайна интерьеров. Полезные рекомендации для мастеров, новичков и частных застройщиков.
Сайт про металлопрокат https://the-master.ru каталог продукции, характеристики и сферы применения. Арматура, балки, трубы, листы и профили. Актуальные цены, советы специалистов и полезные статьи.
Строительный портал https://krovlyaikrysha.ru база знаний и идей. Статьи о строительстве, ремонте и благоустройстве, инструкции, подбор материалов и советы специалистов для качественного результата.
Всё про ремонт https://gbu-so-svo.ru и строительство — статьи, инструкции и советы для мастеров и новичков. Обзоры материалов, проекты домов, дизайн интерьеров и современные технологии.
Автомобильный портал https://ivanmotors.ru всё о машинах в одном месте. Тест-драйвы, обзоры, аналитика авторынка и советы специалистов. Актуальные события мира авто для водителей и экспертов.
Estou pirando com Bet4Slot Casino, oferece uma aventura de cassino que gira como um piao em chamas. A gama do cassino e simplesmente um carrossel de delicias, com jogos de cassino perfeitos pra criptomoedas. O suporte do cassino ta sempre na ativa 24/7, respondendo mais rapido que um estalo de piao. Os pagamentos do cassino sao lisos e blindados, as vezes as ofertas do cassino podiam ser mais generosas. No fim das contas, Bet4Slot Casino oferece uma experiencia de cassino que e puro giro para os viciados em emocoes de cassino! De bonus a navegacao do cassino e facil como um giro de piao, eleva a imersao no cassino ao ritmo de uma roda-gigante.
bet4slot jogos|
Estou completamente alucinado por BetPrimeiro Casino, parece uma cratera cheia de adrenalina. A selecao de titulos do cassino e um fluxo de lava de prazeres, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e ardente, com uma ajuda que incendeia como uma tocha. As transacoes do cassino sao simples como uma brasa, de vez em quando mais recompensas no cassino seriam um diferencial incendiario. Na real, BetPrimeiro Casino e um cassino online que e uma cratera de diversao para os vulcanologos do cassino! Vale dizer tambem o site do cassino e uma obra-prima de estilo vulcanico, eleva a imersao no cassino ao calor de um vulcao.
betprimeiro licence|
I’m hooked on Wazamba Casino, it radiates a gaming vibe as untamed as a tropical storm. There’s a stampede of captivating casino games, featuring casino slots with exotic jungle themes. Its agents are as swift as a cheetah on the hunt, responding faster than a monkey swinging through trees. Casino payments are secure and smooth, still extra casino rewards would make hearts pound. Overall, Wazamba Casino is a gem for casino fans for players who love betting with jungle flair! What’s more casino navigation is intuitive like a tribal path, making every casino session even wilder.
wazamba kokemuksia|
Je suis totalement captive par Unibet Casino, c’est un casino en ligne qui vibre comme une note aigue d’une symphonie. Il y a une vague de jeux de casino captivants, proposant des slots de casino a theme rythmique. Les agents du casino sont rapides comme une note staccato, joignable par chat ou email. Les transactions du casino sont simples comme une portee musicale, cependant des bonus de casino plus frequents seraient harmonieux. Pour resumer, Unibet Casino est un casino en ligne qui joue une symphonie de plaisir pour les passionnes de casinos en ligne ! Bonus le design du casino est une fresque visuelle harmonieuse, facilite une experience de casino enchanteresse.
unibet mma|
Сайт о ремонте https://e-proficom.ru полезные статьи, пошаговые инструкции и советы экспертов. От выбора материалов до дизайна интерьеров. Всё, что нужно для ремонта квартир и домов.
Сайт для женщин https://devchenky.ru всё самое важное в одном месте: семья, дети, красота, здоровье, дом и работа. Советы специалистов, лайфхаки и вдохновение на каждый день.
Блог о ремонте https://ivinstrument.ru полезные статьи, пошаговые инструкции и советы экспертов. Всё о ремонте квартир и домов: выбор материалов, дизайн интерьеров и современные технологии.
Городской портал Москвы https://moscowfy.ru свежие новости столицы, афиша мероприятий, транспорт, жильё, работа и сервисы для жителей. Полезная информация для москвичей и гостей города на одном сайте.
Современные наливные полы https://proffi-floor.ru это не только идеально ровная поверхность, но и долговечность покрытия. Если вы планируете ремонт в квартире или офисе, узнайте подробнее об услугах по устройству наливных полов
услуги перевода документов адрес бюро переводов
https://promebel123.ru/ru-ru/
перевод электронного документа услуги бюро переводов
casinos in toronto ontario australia, online bingo uk no deposit and
new australian online casinos no deposit
bonus, or united kingdom poker slots free
my web-site Bet Mgm Casino Reviews (Goplayslots.Net)
Je suis totalement submerge par Winamax Casino, on dirait une tempete sous-marine de plaisir. Les options de jeu au casino sont riches et fluides, proposant des slots de casino a theme aquatique. Le service client du casino est une perle rare, assurant un support de casino immediat et fluide. Les transactions du casino sont simples comme une goutte d’eau, parfois des recompenses de casino supplementaires feraient nager de joie. Dans l’ensemble, Winamax Casino c’est un casino a explorer sans tarder pour les amoureux des slots modernes de casino ! A noter la plateforme du casino brille par son style oceanique, donne envie de replonger dans le casino sans fin.
miles winamax|
Ich bin total aufgeheizt von Wheelz Casino, es fuhlt sich an wie ein Adrenalinschub auf Hochstgeschwindigkeit. Die Auswahl im Casino ist ein echtes Fahrgeschaft-Spektakel, mit einzigartigen Casino-Slotmaschinen. Die Casino-Mitarbeiter sind schnell wie ein Loopingstart, sorgt fur sofortigen Casino-Support, der die Kurve kriegt. Casino-Gewinne kommen wie ein Geschwindigkeitsrausch, dennoch die Casino-Angebote konnten gro?zugiger sein. Kurz gesagt ist Wheelz Casino eine Casino-Erfahrung, die wie ein Freizeitpark glanzt fur Fans von Online-Casinos! Und au?erdem die Casino-Plattform hat einen Look, der wie ein Looping strahlt, den Spielspa? im Casino in schwindelerregende Hohen treibt.
wheelz login|
Ich bin suchtig nach Wunderino Casino, es ist ein Online-Casino, das wie ein Zauberwald funkelt. Es gibt eine Flut an fesselnden Casino-Titeln, mit modernen Casino-Slots, die wie Magie wirken. Das Casino-Team bietet Unterstutzung, die wie ein Zauberspruch wirkt, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein magischer Wind, aber wurde ich mir mehr Casino-Promos wunschen, die wie ein Zaubertrank sprudeln. Kurz gesagt ist Wunderino Casino ein Online-Casino, das wie ein Marchenwald strahlt fur Fans moderner Casino-Slots! Und au?erdem das Casino-Design ist ein optisches Marchen, den Spielspa? im Casino in magische Hohen hebt.
wunderino arena veranstaltungen 2024 heute|
Adoro o trovao de VikingLuck Casino, tem uma vibe de jogo tao feroz quanto uma tempestade nordica. Tem uma enxurrada de jogos de cassino irados, incluindo jogos de mesa de cassino com um toque de gloria. Os agentes do cassino sao rapidos como um machado viking, garantindo suporte de cassino direto e sem fraqueza. As transacoes do cassino sao simples como uma inscricao runica, as vezes queria mais promocoes de cassino que rugem como guerreiros. Na real, VikingLuck Casino oferece uma experiencia de cassino que e puro trovao para os amantes de cassinos online! De bonus a navegacao do cassino e facil como uma runa gravada, o que torna cada sessao de cassino ainda mais heroica.
viking luck no deposit bonus|
https://shorturl.fm/OUmeh
Подборка статей https://yandex-direct-info.ru про Яндекс Директ: пошаговые инструкции, советы по таргетингу, ретаргетингу и аналитике. Всё о рекламе в Яндексе в одном месте для вашего бизнеса.
Яндекс Бизнес https://business-yandex3.ru описание сервиса, его инструменты и функции. Как компаниям привлекать клиентов, управлять рекламой и повышать эффективность онлайн-продвижения.
whoah this blog is wonderful i really like studying your articles. Stay up the good work! You realize, a lot of persons are looking round for this information, you could help them greatly.
https://rainbetaustralia.com/
https://korolevachiana.github.io/FiveText/index.html Королева Чиана – автор, чье творчество отличается не только увлекательным сюжетом, но и глубоким философским подтекстом. Её произведения – это своеобразное зеркало, в котором каждый читатель может увидеть отражение своей души. Книги Королевы Чианы помогают лучше понять себя и окружающих, а также найти ответы на многие сложные вопросы.
What’s up, all is going well here and ofcourse every one is sharing facts, that’s genuinely excellent, keep up writing.
https://www.facebook.com/groups/rainbetaustralia
Игра в города https://4gameground.ru/igry-s-issledovaniem-karty-i-postroeniem-gorodov/ для всех возрастов. Проверьте знания географии, вспоминайте названия городов и соревнуйтесь с друзьями. Увлекательная логическая игра для тренировки памяти и эрудиции.
All the most important here: https://cere-india.org
Open the latest data here: https://www.acuam.com
The most relevant place is here: https://woodbridgebrewingco.com
Details are waiting for you here: https://www.guidasposi.it
Only verified facts are here: https://www.levelupacademy.in
Hi there to every body, it’s my first visit of this weblog; this website consists of remarkable and actually excellent material designed for visitors.
kra39 at
Everything in one place: https://www.lnrprecision.com
Everything you need: https://heatherparker.com
Read the best here: https://www.sportsoddshistory.com/
https://shorturl.fm/P5Pgv
News for you – right here: https://www.jec.qa
Hot news is already here: https://amt-games.com
Everything the brightest here: https://hyundaimobil.co.id
https://shorturl.fm/kPIbB
Galera, preciso compartilhar minha experiencia no 4PlayBet Casino porque superou minhas expectativas. A variedade de jogos e de cair o queixo: blackjack envolvente, todos com graficos de primeira. O suporte foi amigavel, responderam em minutos pelo chat, algo que faz diferenca. Fiz saque em cartao e o dinheiro entrou mais ligeiro do que imaginei, ponto fortissimo. Se tivesse que criticar, diria que podia ter mais promocoes semanais, mas isso nao estraga a experiencia. Pra concluir, o 4PlayBet Casino e completo. Eu ja voltei varias vezes.
mot g 4play|
Estou alucinado com F12.Bet Casino, pulsa com uma forca de cassino digna de um pit stop. As escolhas sao vibrantes como um velocimetro. com slots tematicos de corridas. O servico e confiavel como um chassi. respondendo veloz como uma ultrapassagem. Os pagamentos sao lisos como asfalto. entretanto queria promocoes que explodem como largadas. No fim das contas, F12.Bet Casino e o point perfeito pros fas de cassino para os exploradores de jogos online! Como extra o layout e vibrante como um velocimetro. transformando cada aposta em uma ultrapassagem.
grupo de sinais f12 bet|
Je suis envoute par Simsinos Casino, resonne avec un rythme de casino anime. La selection du casino est une planche de plaisirs. offrant des sessions de casino en direct qui sautent comme des toons. L’assistance du casino est chaleureuse et precise. proposant un appui qui enchante. Les gains du casino arrivent a une vitesse cartoon. cependant des recompenses de casino supplementaires feraient rebondir. Globalement, Simsinos Casino c’est un casino a explorer sans tarder pour les virtuoses des jeux! En bonus le design du casino est une fresque visuelle cartoon. ajoute une touche de rythme cartoon au casino.
simsinos avis|
Estou alucinado com MarjoSports Casino, explode com uma vibe de cassino esportiva. A selecao de titulos e uma rede de prazeres. oferecendo lives que explodem como penaltis. O suporte e um arbitro de eficiencia. com solucoes precisas e instantaneas. Os pagamentos sao seguros e fluidos. as vezes mais bonus regulares seriam esportivos. Em sintese, MarjoSports Casino oferece uma experiencia que e puro drible para os craques do cassino! Vale dizer a interface e fluida e vibra como um estadio. transformando cada aposta em uma aventura de gol.
encerrar aposta marjosports|
Hello, always i used to check website posts here early in the morning, as i like to learn more and more.
https://westbayki.com/
Топливные карты https://alcomauto.ru для юридических лиц помогут сократить затраты компании и обеспечить полный контроль за автопарком.
Топливные карты https://karta-vezdehod.ru удобный способ экономить на заправках, контролировать расходы и получать прозрачную отчетность.
Топливные карты https://auto-nv.ru для юр лиц — это надежный инструмент учета топлива, скидки на АЗС и удобная онлайн-отчетность.
Just wish to say your article is as astonishing. The clearness for your submit is just great and that i could think you’re an expert in this subject. Well together with your permission let me to snatch your RSS feed to stay up to date with impending post. Thanks 1,000,000 and please continue the gratifying work.
Промокоды для игр на Promocode Game
Acho simplesmente fenomenal Brazino Casino, explode com uma vibe aquatica eletrizante. O catalogo de jogos e um oceano de prazeres. oferecendo sessoes ao vivo que brilham como aguas cristalinas. O atendimento esta sempre ativo 24/7. assegurando apoio sem turbulencia aquatica. Os saques sao velozes como um mergulho. ocasionalmente mais giros gratis seriam subaquaticos. Para encurtar, Brazino Casino garante um jogo que reluz como um coral para os amantes de cassinos online! Como extra o design e fluido como uma onda. adicionando um toque de brilho marinho ao cassino.
o q Г© brazino777|
Sou louco pela fornalha de Fogo777 Casino, e uma explosao de diversao que acende como uma pira. O catalogo de jogos e um altar de prazeres. com caca-niqueis modernos que hipnotizam como fogos. O suporte e uma tocha de eficiencia. garantindo suporte direto e sem cinzas. Os saques queimam como brasas. mas queria promocoes que explodem como labaredas. No geral, Fogo777 Casino promete uma diversao que e uma labareda para os viciados em emocoes de cassino! Por sinal o site e uma obra-prima de estilo ardente. elevando a imersao ao nivel de um ritual.
fogo777-game|
J’adore le frisson de BankOnBet Casino, il propose une aventure de casino qui accumule comme un compte en banque. Le repertoire du casino est un coffre de divertissement. offrant des sessions de casino en direct qui accumulent. Le team est un gardien de tresor. offrant des solutions claires et instantanees. The process is clear like a balance sheet. mais parfois des bonus plus reguliers seraient profitables. Dans l’ensemble, BankOnBet Casino promet un jeu qui fructifie pour les joueurs qui aiment parier avec style au casino! Plus the interface is smooth as a deposit. amplifie l’immersion totale dans le casino.
bankonbet casino sign up|
Me encantei pelo fulgor de Verabet Casino, parece um festival de chamas cheio de adrenalina. As escolhas sao vibrantes como chamas. oferecendo sessoes ao vivo que brilham como labaredas. O suporte e um fulgor reluzente. respondendo veloz como uma faisca. Os ganhos chegam rapido como uma labareda. entretanto mais giros gratis seriam uma loucura de fogo. Na real, Verabet Casino vale explorar esse cassino ja para os apaixonados por slots modernos! E mais o design e um espetaculo visual flamejante. fazendo o cassino queimar como uma fogueira.
bet vera .com|
Acho simplesmente digital PlayPix Casino, tem um ritmo de jogo que processa como um CPU. O catalogo de jogos e uma tela de emocoes. com caca-niqueis que reluzem como bytes. O servico e confiavel como um backup. oferecendo respostas claras como um codigo. Os saques sao velozes como um upload. em alguns momentos mais recompensas fariam o coracao pixelar. Ao final, PlayPix Casino e um cassino online que e uma matriz de diversao para os hackers do cassino! Vale dizer o design e fluido como um render. elevando a imersao ao nivel de um glitch.
dashboard playpix|
Топливная карта https://autobsn.ru для юридических лиц дает доступ к выгодным тарифам, снижает расходы и делает контроль проще.
Что такое Agile https://agile-metod.ru и как его внедрить? Подробные статьи о гибких методологиях, инструментах и практиках. Scrum, Kanban и Lean — всё о современном управлении проектами.
Что такое CPI https://cost-per-install.ru в маркетинге? Полное объяснение показателя Cost Per Install: как он работает, зачем нужен бизнесу, примеры расчётов и советы по использованию метрики в рекламе приложений.
Je suis captive par Grandz Casino, il propose une aventure de casino qui tournoie comme un voile mystique. vibre avec un voile de jeux varies. comprenant des jeux de casino adaptes aux cryptomonnaies. Le support du casino est disponible 24/7. proposant un appui qui enchante. fluisent comme une sonate spectrale. cependant des recompenses de casino supplementaires feraient danser. En conclusion, Grandz Casino cadence comme une sonate de victoires pour les fans de symphonies d’ombres! En plus la plateforme du casino brille par son style theatral. ce qui rend chaque session de casino encore plus etheree.
vitesse max tyrolienne la plus grandz du monde|
Je suis totalement envoute par Casinia Casino, est une epopee de divertissement qui enchante. Les options de jeu au casino sont riches et nobles. offrant des lives qui pulsent comme un tournoi. offre un soutien qui protege tout. offrant des solutions claires et instantanees. Les retraits au casino sont rapides comme un assaut. mais plus de bonus pour une harmonie chevaleresque. A la fin, Casinia Casino offre une experience de casino noble pour les chevaliers du casino! En bonus la navigation du casino est intuitive comme un serment. fait vibrer le jeu comme un concerto medieval.
casinia com|
Galera, preciso contar o que achei sobre o Bingoemcasa porque superou minhas expectativas. O site tem um ambiente divertido que lembra uma festa entre amigos. As salas de bingo sao sempre lotadas, e ainda testei uns joguinhos extras, todos me deixaram impressionado. O atendimento no chat foi educado e prestativo, o que ja me deixou bem a vontade. As retiradas foram sem enrolacao, inclusive testei cripto e foi impecavel. Se pudesse apontar algo, diria que as promocoes podiam ser mais ousadas, mas nada que estrague a experiencia. Na minha visao, o Bingoemcasa foi uma otima descoberta. Com certeza vou continuar jogando
bingoemcasa net sua escolha no1 para bingo online autГЄntico|
Me ecoei no ritmo de Stake Casino, oferece uma aventura que vibra como uma corda de harpa. O leque do cassino e um reverb de delicias. com caca-niqueis que vibram como harpas. O time do cassino e digno de um maestro. respondendo veloz como uma vibracao. As transacoes sao simples como um reverb. mesmo assim as ofertas podiam ser mais generosas. Para encurtar, Stake Casino promete uma diversao que e uma onda sonora para os exploradores de jogos online! E mais a navegacao e facil como um eco. criando uma experiencia de cassino harmonica.
vpn for stake|
cocaine in prague columbian cocain in prague
promo code for 1xbet bangladesh 1xbet Bangladesh Promo Code: Unlock Exclusive Bonuses and Enhanced Betting Opportunities In the vibrant landscape of online betting in Bangladesh, 1xbet stands out as a leading platform, offering a diverse range of sporting events, casino games, and other exciting opportunities. To amplify the thrill and maximize your winning potential, 1xbet provides a variety of promo codes tailored specifically for Bangladeshi players. These codes unlock exclusive bonuses, free bets, and enhanced odds, giving you a significant advantage in your betting journey. Types of 1xbet Promo Codes Available in Bangladesh: 1xbet Promo Code Bangladesh: This is a general promo code that can be used by both new and existing players in Bangladesh. It typically unlocks a welcome bonus, deposit bonus, or free bet. 1xbet Promo Code Registration Bangladesh: This code is exclusively for new players registering on the 1xbet platform in Bangladesh. It offers an enhanced welcome bonus to kickstart their betting adventure. 1xbet Free Promo Code Bangladesh: This code grants Bangladeshi players a free bet, allowing them to place a wager without risking their own funds. 1xbet Free Bet Promo Code Bangladesh: Similar to the previous code, this one provides a free bet opportunity, often tied to specific sporting events or promotions. 1xbet Bonus Promo Code Bangladesh: This code unlocks a bonus on your deposit, increasing your betting balance and giving you more chances to win. Promo Code for 1xbet Bangladesh Today: This code is a time-sensitive offer, valid only for a specific day. It usually provides a daily bonus, free bet, or enhanced odds on selected events. 1xbet Promo Code for Registration Bangladesh: This code is another registration-specific code, offering a larger welcome bonus than the standard registration bonus. How to Find and Use 1xbet Promo Codes in Bangladesh: 1xbet promo codes are widely available through various channels, including: Official 1xbet Website: Regularly check the 1xbet website for the latest promo code offers. Affiliate Websites: Many affiliate websites dedicated to online betting provide exclusive 1xbet promo codes for Bangladeshi players. Social Media: Follow 1xbet’s official social media accounts to stay updated on new promo code releases. Email Newsletters: Subscribe to 1xbet’s email newsletters to receive promo codes directly in your inbox. To use a promo code, simply enter it in the designated field during registration or when making a deposit. The bonus or free bet will be automatically credited to your account. Maximize Your Winnings with 1xbet Promo Codes: By utilizing 1xbet promo codes, Bangladeshi players can significantly enhance their betting experience and increase their chances of winning. Whether you’re a seasoned bettor or a newcomer to the world of online betting, these codes offer a valuable advantage. So, keep an eye out for the latest 1xbet promo codes and unlock a world of exclusive bonuses and thrilling betting opportunities.
code promo inscription 1xbet code promo 1xbet cote d’ivoire Le monde des paris sportifs en ligne est en constante evolution, et 1xbet s’est etabli comme un leader mondial, offrant une plateforme complete et diversifiee aux parieurs du monde entier. En Cote d’Ivoire, l’enthousiasme pour les paris sportifs est palpable, et 1xbet Cote d’Ivoire propose une gamme allechante de promotions pour ameliorer l’experience de pari de ses utilisateurs. Au c?ur de ces promotions se trouvent les codes promotionnels, des cles magiques qui debloquent des bonus exclusifs et des opportunites de pari ameliorees. Qu’est-ce qu’un code promo 1xbet Cote d’Ivoire? Un code promo 1xbet Cote d’Ivoire est une combinaison unique de lettres et de chiffres qui peuvent etre entres lors de l’inscription ou du depot pour activer un bonus specifique. Ces bonus peuvent inclure: Bonus de bienvenue: Un bonus offert aux nouveaux utilisateurs lors de leur premier depot. Bonus de depot: Un bonus accorde sur les depots ulterieurs. Paris gratuits: La possibilite de placer un pari sans risquer son propre argent. Cotes ameliorees: Des cotes plus elevees sur certains evenements sportifs. Ou trouver les codes promo 1xbet Cote d’Ivoire? Les codes promotionnels 1xbet Cote d’Ivoire sont disponibles via plusieurs canaux, notamment: Le site Web officiel de 1xbet: Consultez regulierement le site Web de 1xbet pour les dernieres offres. Les sites Web affilies: De nombreux sites Web affilies proposent des codes promotionnels exclusifs pour les joueurs ivoiriens. Les reseaux sociaux: Suivez les comptes de medias sociaux officiels de 1xbet pour rester informe des nouvelles versions de code promotionnel. Les newsletters par e-mail: Abonnez-vous aux newsletters par e-mail de 1xbet pour recevoir les codes promotionnels directement dans votre boite de reception. L’utilisation efficace des codes promotionnels 1xbet Cote d’Ivoire peut considerablement augmenter vos chances de gagner et rendre votre experience de pari plus agreable. Gardez un ?il sur les derniers codes et profitez des avantages qu’ils offrent.
работа на крупных заводах Вахтовая работа с проживанием – это работа вахтовым методом, при которой работникам предоставляется жилье на время вахты. Проживание может быть организовано в вахтовых поселках, общежитиях или других типах жилых помещений. Вахтовая работа с проживанием позволяет работникам не тратить время и деньги на дорогу до места работы и обеспечивает комфортные условия для проживания и отдыха.
buy coke in prague buy cocaine prague
Графитовые и угольные щетки для электроинструмента. Большой выбор, надёжность и долговечность. Подходят для дрелей, болгарок, перфораторов и другого оборудования.
Sou louco pela ressonancia de JonBet Casino, e uma onda sonora de diversao que reverbera. O catalogo de jogos e uma camara de prazeres. com caca-niqueis que vibram como harpas. Os agentes sao rapidos como uma onda sonora. com solucoes precisas e instantaneas. As transacoes sao faceis como um sino. entretanto mais giros gratis seriam uma loucura sonora. No geral, JonBet Casino e o point perfeito pros fas de cassino para os fas de adrenalina sonora! Como extra o site e uma obra-prima de estilo sonoro. transformando cada aposta em uma aventura ressonante.
histГіrico da jonbet|
Je suis accro a RollBit Casino, est un tourbillon de divertissement qui pixelise. L’assortiment de jeux du casino est une matrice de delices. incluant des tables qui structurent comme un cube. Les agents du casino sont rapides comme un flux de donnees. proposant un appui qui enchante. Les transactions du casino sont simples comme un pixel. neanmoins plus de bonus pour une harmonie bit. Pour resumer, RollBit Casino est un joyau pour les fans de casino pour les passionnes de casinos en ligne! En bonus la navigation du casino est intuitive comme une note pixelisee. facilite une experience de casino bit par bit.
rollbit nft opensea|
J’adore le retour de Boomerang Casino, offre un spectacle de plaisir qui revient. La selection du casino est une boucle de plaisirs. avec des slots qui bouclent comme des arcs. offre un soutien qui boucle tout. repondant en un ricochet circulaire. Le processus du casino est transparent et sans boucle. mais des tours gratuits pour une melodie ricochet. En fin de compte, Boomerang Casino resonne comme un concerto de plaisir pour ceux qui cherchent l’adrenaline boomerang du casino! De plus est une cadence visuelle envoutante. donne envie de replonger dans le casino sans fin.
boomerang casino francais|
Curto demais o vortice de XPBet Casino, explode com uma vibe de cassino ciclica. Os jogos formam um redemoinho de diversao. oferecendo sessoes ao vivo que fluem como loops. O suporte e um eixo de eficiencia. com solucoes precisas e instantaneas. Os ganhos chegam rapido como um espiral. ocasionalmente as ofertas podiam ser mais generosas. Em sintese, XPBet Casino e uma onda de adrenalina ciclica para quem curte apostar com estilo giratorio! Por sinal o layout e vibrante como uma roda. transformando cada aposta em uma aventura giratoria.
ultra bet xp|
Нужны двери? межкомнатные двери интернет магазин цены Широкий ассортимент межкомнатных дверей от Вектордорс. У нас вы найдете модели на любой вкус: от классических до современных дизайнерских решений. Выбор межкомнатных дверей — важный этап обустройства помещения. Правильно подобранные двери не только украсят интерьер, но и обеспечат комфорт и функциональность на долгие годы.
Adoro a energia de DonaldBet Casino, tem um ritmo de jogo que danca como um acrobata. Tem um turbilhao de jogos de cassino irados. com jogos adaptados para criptomoedas. O suporte e um mestre de cerimonias. oferecendo respostas claras como um picadeiro. As transacoes sao faceis como um estalo. porem queria promocoes que explodem como fogos. Resumindo, DonaldBet Casino promete uma diversao que e uma lona vibrante para quem curte apostar com estilo circense! De lambuja o visual e uma explosao de lonas. transformando cada aposta em uma aventura de picadeiro.
donaldbet cnpj|
https://shorturl.fm/RcvaU
отсев щебня доставка https://pesko.ru
CPL (Cost Per Lead) https://cost-per-lead1.ru ключевая метрика рекламы. Узнайте, что это, как правильно рассчитывать стоимость лида, где применяется и как помогает оценить эффективность кампаний.
самопомощь Психолог РПП – это луч света во тьме расстройств пищевого поведения. Специалист, обладающий глубокими знаниями и опытом в этой области, поможет разобраться в сложных взаимосвязях между едой, эмоциями и самооценкой. Это не просто диета и подсчет калорий, это работа с глубинными причинами, вызывающими нездоровые отношения с пищей, и формирование устойчивого позитивного образа тела.
https://shorturl.fm/VKech
Интернет-маркетинг https://internet-marketing1.ru SEO, контекстная реклама, SMM, email-рассылки и аналитика. Статьи, советы и инструменты для бизнеса, которые помогают привлекать клиентов и увеличивать продажи онлайн.
For the reason that the admin of this web site is working, no doubt very quickly it will be well-known, due to its feature contents.
online casinos
Интернет-маркетинг https://yandex-reklama2.ru для компаний и специалистов: SEO, SMM, контекстная реклама и email. Советы по выбору стратегий, разбор ошибок и методы повышения эффективности.
J’apprecie enormement 7BitCasino, c’est une veritable plongee dans un univers palpitant. Il y a une profusion de titres varies, incluant des slots de pointe. Le service d’assistance est de premier ordre, avec un suivi de qualite. Les transactions en cryptomonnaies sont instantanees, neanmoins j’aimerais plus d’offres promotionnelles, afin de maximiser l’experience. En resume, 7BitCasino est un incontournable pour les joueurs en quete d’adrenaline ! Ajoutons que le design est visuellement attrayant avec une touche vintage, facilite chaque session de jeu.
7bitcasino serios|
Ich finde absolut majestatisch King Billy Casino, es pulsiert mit einer koniglichen Casino-Energie. Der Katalog des Casinos ist eine Schatzkammer voller Spa?, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Das Casino-Team bietet Unterstutzung, die wie ein Zepter glanzt, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein Triumphzug, ab und zu wurde ich mir mehr Casino-Promos wunschen, die glanzvoll sind. Kurz gesagt ist King Billy Casino ein Casino, das man nicht verpassen darf fur die, die mit Stil im Casino wetten! Extra das Casino-Design ist ein optisches Kronungsjuwel, das Casino-Erlebnis total veredelt.
king billy casino reviews|
J’adore l’energie de DBosses, c’est une plateforme qui electrise. La selection de jeux est grandiose, proposant des sessions live vibrantes. Le support est disponible 24/7, avec une aide personnalisee. Les retraits sont fluides et ultra-rapides, neanmoins les offres pourraient etre plus genereuses. En fin de compte, DBosses vaut pleinement le detour pour les fans de jeux modernes ! En plus la plateforme est visuellement impressionnante, ce qui rend chaque session encore plus exaltante.
dbosses casino|
Je suis carrement scotche par Gamdom, il propose une aventure qui dechire. La gamme est une vraie pepite, avec des slots qui claquent grave. Le crew assure un suivi de malade, avec une aide qui dechire tout. Les paiements sont fluides et blindes, quand meme des recompenses en plus ca ferait kiffer. En gros, Gamdom est une plateforme qui dechire tout pour les fans de casinos en ligne ! Cote plus le design est une bombe visuelle, ajoute un max de swag.
steam verification disabled gamdom|
https://shorturl.fm/lNdxu
At WebPtoPNGHero.com, converting WebP images into PNG format couldn’t be simpler. The interface features a drag-and-drop area where images load instantly, and conversion begins on secure cloud servers. A progress meter keeps you informed, and once each file finishes, PNG versions appear as clickable download links. If you have many images to process, batch mode handles multiple files at the same time, saving precious minutes. The tool runs entirely in your web browser, making it compatible with Windows, macOS, Linux, Android, and iOS alike. No need to install any applications or plugins—just open the site and start converting. All uploads vanish shortly after processing, ensuring privacy and security. Whether you’re optimizing visuals for an e-commerce store, preparing photos for email attachments, or simply sharing snapshots online, WebPtoPNGHero.com delivers reliable, high-fidelity results. The service remains free and ad-free, with no registration required. Convert your WebP images to universally supported PNG files quickly and without hassle.
WebPtoPNGHero
Picture this: you’re cooking dinner and the recipe calls for grams, but your scale only shows ounces. Later, you’re helping your child with homework and suddenly need to convert meters per second into kilometers per hour. The next morning, you’re preparing a presentation and realize the client wants it in PDF format. Three different situations, three different problems – and usually, three different apps.
That’s the hassle OneConverter eliminates. It’s an all-in-one online tool designed for people who want life to be simpler, faster, and smarter. No downloads, no subscriptions, no headaches – just answers, right when you need them.
Unit Conversions Made Effortless
Most conversion tools handle only the basics. OneConverter goes further – much further. With more than 50,000 unit converters, it can handle everyday situations, advanced academic work, and professional challenges without breaking a sweat.
Everyday Basics: length, weight, speed, temperature, time, area, volume, energy.
Engineering & Physics: torque, angular velocity, density, acceleration, moment of inertia.
Heat & Thermodynamics: thermal conductivity, thermal resistance, entropy, enthalpy.
Radiology: absorbed dose, equivalent dose, radiation exposure.
Fluids: viscosity, flow rate, pressure, surface tension.
Electricity & Magnetism: voltage, current, resistance, capacitance, inductance, flux.
Chemistry: molarity, concentration, molecular weight.
Astronomy: light years, parsecs, astronomical units.
Everyday Extras: cooking measures, shoe and clothing sizes, fuel efficiency.
From the classroom to the lab, from the office to your kitchen – OneConverter has a solution ready.
OneConverter.com
Памятники на заказ https://top-memorial.ru широкий выбор форм и материалов, профессиональное изготовление и монтаж. Индивидуальный подход, гарантия качества и доступные цены.
Уборка квартир https://cleaningplus.ru/services/generalnaya-uborka/ в Москве: поддерживающая, генеральная, после ремонта и выезда жильцов. Профессиональные клинеры, экологичные средства, доступные цены и гарантия чистоты.
Picture this: you’re cooking dinner and the recipe calls for grams, but your scale only shows ounces. Later, you’re helping your child with homework and suddenly need to convert meters per second into kilometers per hour. The next morning, you’re preparing a presentation and realize the client wants it in PDF format. Three different situations, three different problems – and usually, three different apps.
That’s the hassle OneConverter eliminates. It’s an all-in-one online tool designed for people who want life to be simpler, faster, and smarter. No downloads, no subscriptions, no headaches – just answers, right when you need them.
Unit Conversions Made Effortless
Most conversion tools handle only the basics. OneConverter goes further – much further. With more than 50,000 unit converters, it can handle everyday situations, advanced academic work, and professional challenges without breaking a sweat.
Everyday Basics: length, weight, speed, temperature, time, area, volume, energy.
Engineering & Physics: torque, angular velocity, density, acceleration, moment of inertia.
Heat & Thermodynamics: thermal conductivity, thermal resistance, entropy, enthalpy.
Radiology: absorbed dose, equivalent dose, radiation exposure.
Fluids: viscosity, flow rate, pressure, surface tension.
Electricity & Magnetism: voltage, current, resistance, capacitance, inductance, flux.
Chemistry: molarity, concentration, molecular weight.
Astronomy: light years, parsecs, astronomical units.
Everyday Extras: cooking measures, shoe and clothing sizes, fuel efficiency.
From the classroom to the lab, from the office to your kitchen – OneConverter has a solution ready.
OneConverter
Achou totalmente epico DiceBet Casino, da uma energia de cassino que e fora da curva. A selecao de titulos do cassino e um espetaculo a parte, com slots de cassino unicos e empolgantes. A equipe do cassino manda um atendimento que e show, respondendo mais rapido que um raio. Os ganhos do cassino chegam voando, mas mais recompensas no cassino seriam um diferencial brabo. Na real, DiceBet Casino garante uma diversao de cassino que e um estouro para os cacadores de slots modernos de cassino! E mais o design do cassino e uma explosao visual, faz voce querer voltar pro cassino toda hora.
dicebet reclame aqui|
Je kiffe a mort FatPirate, ca balance une vibe dechainee. Il y a un ocean de titres varies, comprenant des jeux tailles pour les cryptos. Les agents sont rapides comme l’eclair, joignable par chat ou email. Le processus est clean et sans galere, par contre j’aimerais plus de promos qui tabassent. Au final, FatPirate est une plateforme qui envoie du pate pour les fans de casinos en ligne ! Cote plus la navigation est simple comme un jeu d’enfant, facilite le delire total.
fatpirate avis|
Je trouve carrement genial Impressario, c’est une plateforme qui met des etoiles plein les yeux. La selection de jeux est juste monumentale, offrant des machines a sous qui claquent. Le support est dispo 24/7, repondant en un clin d’etoile. Les paiements sont securises et eclatants, mais bon plus de tours gratos ca ferait vibrer. En gros, Impressario c’est une scene a decouvrir absolument pour les amateurs de slots qui brillent ! En prime la plateforme claque avec son look de star, ajoute un max de charisme.
impressario casino review|
J’adore a fond 1win Casino, ca procure une experience de jeu captivante. Il y a une multitude de titres varies, avec des machines a sous modernes et dynamiques. Le personnel est professionnel et attentionne, avec un suivi irreprochable. Le processus de retrait est simple et efficace, bien que j’aimerais plus de promotions regulieres. Globalement, 1win Casino est une plateforme exceptionnelle pour les passionnes de jeux en ligne ! Par ailleurs le design est visuellement attrayant, renforce l’immersion totale.
1win partners|
pure cocaine in prague prague drugstore
Digital life demands accuracy. Engineers, researchers, students, and professionals rely on precise numbers and flawless documents. Yet the tools they need are often scattered across multiple apps, hidden behind subscriptions, or limited in scope. OneConverter addresses this challenge by consolidating advanced unit conversion calculators and PDF document utilities into a single, accessible platform.
Comprehensive Unit Conversions
The strength of OneConverter lies in its range. With more than 50,000 unit converters, it covers virtually every field of science, technology, and daily life.
Core Measurements: conversions for length, weight, speed, temperature, area, volume, time, and energy. These fundamental tools support everyday requirements such as travel, shopping, and cooking.
Engineering & Physics: advanced calculators for torque, density, angular velocity, acceleration, and moment of inertia, enabling precision in both academic study and professional design.
Heat & Thermodynamics: tools for thermal conductivity, resistance, entropy, and enthalpy, providing clarity for scientific research and industrial applications.
Radiology: units such as absorbed dose, equivalent dose, and radiation exposure, essential for healthcare professionals and medical physicists.
Fluid Mechanics: viscosity, pressure, flow rate, and surface tension, all indispensable in laboratory and engineering environments.
Electricity & Magnetism: extensive coverage including voltage, current, resistance, inductance, capacitance, flux, and charge density, supporting fields from electronics to energy.
Chemistry: molarity, concentration, and molecular weight calculators, saving valuable time in laboratories and classrooms.
Astronomy: astronomical units, parsecs, and light years, serving both researchers and students exploring the cosmos.
Practical Applications: everyday conversions for recipes, fuel efficiency, and international clothing sizes.
By combining breadth and accuracy, OneConverter ensures that calculations are reliable, consistent, and instantly available.
oneconverter.com
https://shorturl.fm/18Oqq
На сайте «Детский Класс» https://www.detskiyklass.ru нашим посетителям в любое время доступны материалы для приятного совместного досуга детей и их родителей: детские песни на разные тематики, которые можно разучивать и распевать в будни и праздники, интересные и познавательные легенды и мифы, раскраски различной сложности, а также волшебные и поучительные сказки.
buy xtc prague weed in prague
https://kabanovskajsosh.minobr63.ru/%d0%b2%d0%bd%d0%b8%d0%bc%d0%b0%d0%bd%d0%b8%d0%b5-%d0%b3%d1%80%d0%b8%d0%bc%d0%bc-%d0%be%d1%80%d0%b2%d0%b8/#comment-657641
Ich flippe aus bei DrueGlueck Casino, es bietet eine krasse Spielerfahrung. Die Auswahl im Casino ist einfach ein Knaller, inklusive stylischer Casino-Tischspiele. Der Casino-Support ist rund um die Uhr da, antwortet in Sekundenschnelle. Casino-Zahlungen sind sicher und reibungslos, ab und zu wurde ich mir mehr Casino-Promos wunschen. Insgesamt ist DrueGlueck Casino eine Casino-Erfahrung, die rockt fur Fans moderner Casino-Slots! Extra die Casino-Oberflache ist flussig und mega cool, Lust macht, immer wieder ins Casino zuruckzukehren.
drueckglueck live casino online|
Estou impressionado com o 888 Casino, oferece uma aventura cheia de emocoes. O catalogo de jogos e incrivelmente vasto, contendo titulos inovadores e atraentes. O suporte e super responsivo e profissional, respondendo rapidamente. Os saques sao extremamente rapidos, no entanto eu gostaria de mais promocoes. Para concluir, o 888 Casino e uma plataforma excepcional para os amantes de cassino online! Adicionalmente o design e visualmente impactante, o que amplifica o prazer de jogar.
casino games 888 casino|
Je trouve absolument epoustouflant 1xbet Casino, ca ressemble a une aventure pleine de frissons. La selection de jeux est monumentale, comprenant des titres innovants et engageants. Le support est ultra-reactif et professionnel, offrant des reponses rapides et precises. Le processus de retrait est simple et fiable, cependant les bonus pourraient etre plus reguliers. Dans l’ensemble, 1xbet Casino est une plateforme d’exception pour les amateurs de casino en ligne ! Par ailleurs l’interface est fluide et moderne, ajoute une touche de raffinement a l’experience.
1xbet android|
Acho completamente fora da curva Flabet Casino, da uma energia de cassino que e um espetaculo. As opcoes de jogo no cassino sao ricas e alucinantes, com jogos de cassino perfeitos pra criptomoedas. O atendimento ao cliente do cassino e uma explosao, dando solucoes na hora e com precisao. Os pagamentos do cassino sao lisos e blindados, as vezes queria mais promocoes de cassino que arrebentam. Na real, Flabet Casino vale demais explorar esse cassino para os aventureiros do cassino! De bonus o design do cassino e uma explosao visual, o que deixa cada sessao de cassino ainda mais alucinante.
bone flabet|
Je trouve completement fou Instant Casino, c’est un casino en ligne qui envoie du lourd. Le catalogue de jeux de casino est colossal, comprenant des jeux de casino tailles pour les cryptos. Le crew du casino assure un suivi de ouf, garantissant un support de casino direct et efficace. Les paiements du casino sont fluides et securises, par moments des recompenses de casino en plus ca ferait kiffer. Bref, Instant Casino garantit un fun de casino supersonique pour les aventuriers du casino ! A noter aussi la plateforme du casino claque avec son look electrisant, booste l’immersion dans le casino a fond.
instant casino payout|
weed in prague prague drugstore
pure cocaine in prague buy cocaine prague
buy cocaine in telegram plug in prague
columbian cocain in prague high quality cocaine in prague
https://shorturl.fm/kjTpC
J’apprecie beaucoup le casino TonyBet, ca offre un moment divertissant top. Les jeux sont varies, comprenant des titres innovants. Les agents sont reactifs, avec des reponses claires. Les transactions sont securisees, neanmoins plus de tours gratuits seraient bien. Globalement, TonyBet est une valeur sure pour ceux qui aiment parier ! En bonus, le design est attractif, facilitant chaque session de jeu.
tonybet casino australia|
J’adore l’eclat de Julius Casino, ca pulse avec une energie de casino triomphante. La collection de jeux du casino est colossale, offrant des sessions de casino en direct qui en imposent. L’assistance du casino est majestueuse et efficace, proposant des solutions claires et immediates. Les transactions du casino sont simples comme un decret, quand meme plus de tours gratuits au casino ce serait epique. Au final, Julius Casino est un colisee pour les fans de casino pour ceux qui cherchent l’adrenaline glorieuse du casino ! De surcroit le site du casino est une merveille graphique imposante, donne envie de replonger dans le casino sans fin.
julius casino vip|
Ich bin suchtig nach JackpotPiraten Casino, es ist ein Online-Casino, das wie eine Welle kracht. Der Katalog des Casinos ist ein Schatztruhe voller Spa?, inklusive eleganter Casino-Tischspiele. Das Casino-Team bietet eine Unterstutzung, die wie Gold glanzt, antwortet blitzschnell wie ein Sabelhieb. Casino-Gewinne kommen wie ein Blitz, aber mehr Casino-Belohnungen waren ein echter Schatz. Insgesamt ist JackpotPiraten Casino ein Muss fur Casino-Fans fur Spieler, die auf krasse Casino-Kicks stehen! Ubrigens die Casino-Plattform hat einen Look, der wie ein Schatz funkelt, den Spielspa? im Casino auf Hochtouren bringt.
jackpotpiraten 50 free spins|
Je trouve sensationnel le casino AllySpin, on dirait une sensation de casino unique. Le catalogue de jeux est vaste, proposant des experiences de casino en direct. Les agents sont toujours disponibles, repondant en un clin d’?il. Les gains arrivent vite, mais parfois plus de tours gratuits seraient top. Globalement, AllySpin ne decoit jamais pour les amateurs de casino en ligne ! Notons aussi que le style visuel est dynamique, ce qui booste encore plus le plaisir.
allyspin italia|
Adoro o clima feroz de LeaoWin Casino, tem uma vibe de jogo que e pura selva. Tem uma enxurrada de jogos de cassino irados, com caca-niqueis de cassino modernos e instintivos. A equipe do cassino entrega um atendimento que e uma garra, acessivel por chat ou e-mail. Os ganhos do cassino chegam voando como uma aguia, mas queria mais promocoes de cassino que mordem. No fim das contas, LeaoWin Casino e um cassino online que e uma fera total para os amantes de cassinos online! Vale falar tambem a navegacao do cassino e facil como uma trilha na selva, faz voce querer voltar pro cassino como uma fera.
leaowin02 casino application mobile|
https://incontrare.jugem.jp/?eid=1450
https://shorturl.fm/HSCH5
ftzjk8
plug in prague cocain in prague from brazil
pure cocaine in prague buy cocaine in telegram
cocaine in prague cocain in prague from brazil
J’apprecie enormement 7BitCasino, ca procure une sensation de casino unique. La gamme de jeux est tout simplement impressionnante, incluant des slots de pointe. Le personnel offre un accompagnement irreprochable, repondant en un clin d’?il. Les retraits sont ultra-rapides, occasionnellement plus de tours gratuits seraient un atout, ou des promotions hebdomadaires plus frequentes. Pour conclure, 7BitCasino est une plateforme d’exception pour les amateurs de casino en ligne ! Par ailleurs la navigation est intuitive et rapide, facilite chaque session de jeu.
bono 7bitcasino|
Ich bin suchtig nach King Billy Casino, es pulsiert mit einer koniglichen Casino-Energie. Der Katalog des Casinos ist eine Schatzkammer voller Spa?, inklusive eleganter Casino-Tischspiele. Das Casino-Team bietet Unterstutzung, die wie ein Zepter glanzt, ist per Chat oder E-Mail erreichbar. Auszahlungen im Casino sind schnell wie ein koniglicher Marsch, manchmal mehr Freispiele im Casino waren ein Kronungsmoment. Alles in allem ist King Billy Casino ein Online-Casino, das wie ein Konigreich strahlt fur Spieler, die auf majestatische Casino-Kicks stehen! Nebenbei die Casino-Navigation ist kinderleicht wie ein koniglicher Marsch, einen Hauch von Majestat ins Casino bringt.
king billy casino|
Je trouve phenomenal DBosses, ca donne un frisson inegale. Les options sont riches et dynamiques, comprenant des jeux optimises pour les cryptos. L’assistance est efficace et chaleureuse, repondant en un instant. Le processus est clair et sans complications, de temps a autre les offres pourraient etre plus genereuses. En fin de compte, DBosses offre une experience inoubliable pour les fans de jeux modernes ! Ajoutons que l’interface est fluide et moderne, ce qui rend chaque session encore plus exaltante.
dbosses casino|
J’adore passionnement BetFury Casino, on dirait une sensation de casino unique. Le catalogue est incroyablement vaste, comprenant des jeux originaux comme Plinko et Crash avec un RTP jusqu’a 99,28 %. Le service client est exceptionnel, avec un suivi exemplaire. Les gains arrivent en un temps record, bien que plus de tours gratuits seraient un plus. Dans l’ensemble, BetFury Casino est un incontournable pour les amateurs de crypto-casinos ! De plus la navigation est simple et rapide, amplifie le plaisir de jouer.
betfury withdraw|
J’adore le delire total de Gamdom, il propose une aventure qui dechire. Il y a un tsunami de titres varies, incluant des jeux de table qui en jettent. Le service client est une tuerie, avec une aide qui dechire tout. Les retraits sont rapides comme un ninja, quand meme des recompenses en plus ca ferait kiffer. En gros, Gamdom c’est du lourd a tester direct pour les accros aux sensations extremes ! Cote plus la navigation est simple comme un jeu d’enfant, ajoute un max de swag.
free gamdom gift card|
tr2arw
tripscan трипскан Трипскан ссылка: Фраза “Трипскан ссылка” означает поиск прямой ссылки на веб-сайт сервиса Tripscan. Пользователи, вводящие этот запрос, обычно хотят быстро перейти на сайт Tripscan, не тратя время на поиск через поисковые системы. Они могут искать ссылку на главную страницу, конкретный раздел сайта или страницу с определенной информацией, например, акциями или специальными предложениями. Ссылка на Tripscan может быть найдена в рекламных объявлениях, социальных сетях, блогах и других онлайн-ре ресурсах.
cамоустанавливающийся подшипник Подшипники от производителей: Этот запрос свидетельствует о предпочтении пользователя приобретать подшипники напрямую у заводов-изготовителей, минуя посредников. Покупка у производителей может предоставить ряд преимуществ, включая более низкие цены, гарантию качества, возможность получения технической поддержки и доступ к информации о новых разработках. Однако не все производители работают с розничными покупателями или небольшими оптовыми заказами. Поиск подшипников от производителей требует проведения маркетингового исследования, выявления заводов, специализирующихся на производстве требуемых типов подшипников, и установления с ними прямых контактов для обсуждения условий сотрудничества. Важно учитывать минимальные объемы заказов, условия оплаты и сроки поставки, а также наличие сертификатов качества и соответствия продукции международным стандартам.
трипскан топ Tripscan: Tripscan – это метапоисковая система для путешественников, специализирующаяся на сравнении цен на авиабилеты, отели, аренду автомобилей и другие туристические услуги. Сервис собирает данные с множества различных онлайн-турагентств и поставщиков, позволяя пользователям находить наиболее выгодные предложения в одном месте. Tripscan не продает билеты или бронирования напрямую, а перенаправляет пользователей на сайты поставщиков для завершения транзакции. Ключевая особенность Tripscan – это удобный интерфейс, позволяющий быстро и легко сравнивать цены, фильтровать результаты поиска по различным критериям (например, времени вылета, авиакомпании, звездности отеля) и находить оптимальные варианты путешествий, соответствующие индивидуальным потребностям и бюджету. Сервис также может предлагать дополнительные функции, такие как отслеживание цен, уведомления о скидках и персонализированные рекомендации.
Крайне рекомендую https://tatiananovo.com/hello-world/
pr товаров и услуг Маркетинг консультации / Консультации маркетинг / Консультация по маркетингу: Пользователь заинтересован в получении экспертной оценки текущей маркетинговой стратегии и рекомендаций по ее улучшению. Важно предложить бесплатные консультации или аудиты, чтобы продемонстрировать свою экспертность и помочь клиентам определиться с дальнейшей стратегией продвижения. Необходимо предоставить возможность получить ответы на вопросы о различных аспектах маркетинга, таких как: выбор целевой аудитории, разработка стратегии продвижения, выбор каналов коммуникации и т.д.
Hey I know this is off topic but I was wondering if you knew of any widgets I could add to my blog that automatically tweet my newest twitter updates. I’ve been looking for a plug-in like this for quite some time and was hoping maybe you would have some experience with something like this. Please let me know if you run into anything. I truly enjoy reading your blog and I look forward to your new updates.
https://adrenalinsport.dp.ua/remont-far-koli-krashche-zvernutisia-do-fakhivtsiv-a-koli-mozhna-zrobiti-samomu.html
What’s up, I wish for to subscribe for this blog to get latest updates, therefore where can i do it please help out.
https://geotop.od.ua/bi-led-infolight-a3-laser-chi-varta-tsia-linza-svoiei-tsini.html
Do you have a spam issue on this website; I also am a blogger, and I was wanting to know your situation; many of us have developed some nice methods and we are looking to exchange methods with others, please shoot me an email if interested.
http://vivashop.com.ua/yak-chystyty-ta-dohlyadaty-za-svitlodiodnymy-linza.html
h8lydm
коррекция бровей севастополь Татуаж губ в Севастополе – это прекрасная возможность придать губам желаемый объем, форму и цвет! Мы предлагаем различные техники татуажа губ: акварельный татуаж, контурный татуаж, помадный эффект. Наши мастера используют только сертифицированные пигменты и современное оборудование, обеспечивая безопасность и отличный результат. Подчеркните красоту своей улыбки с помощью татуажа губ!
J’adore la frenesie de CasinoClic, il propose une aventure de casino qui fait vibrer. Le repertoire du casino est une veritable comete de divertissement, comprenant des jeux de casino optimises pour les cryptomonnaies. Le service client du casino est une etoile brillante, repondant en un flash lumineux. Les gains du casino arrivent a une vitesse supersonique, par moments plus de tours gratuits au casino ce serait enivrant. En somme, CasinoClic promet un divertissement de casino electrisant pour les joueurs qui aiment parier avec panache au casino ! A noter le site du casino est une merveille graphique brillante, amplifie l’immersion totale dans le casino.
casino clic machines a sous gratuites|
Ich liebe den Zauber von Lapalingo Casino, es fuhlt sich an wie ein wilder Ritt durch die Spielwelt. Der Katalog des Casinos ist ein Kaleidoskop des Spa?es, mit modernen Casino-Slots, die einen in ihren Bann ziehen. Der Casino-Kundenservice ist wie ein Leuchtfeuer, liefert klare und schnelle Losungen. Auszahlungen im Casino sind schnell wie ein Wirbelwind, manchmal mehr regelma?ige Casino-Boni waren ein Knaller. Insgesamt ist Lapalingo Casino ein Online-Casino, das wie ein Sturm begeistert fur die, die mit Stil im Casino wetten! Und au?erdem die Casino-Plattform hat einen Look, der wie ein Blitz funkelt, was jede Casino-Session noch aufregender macht.
lapalingo 10 gratis|
Je suis totalement ebloui par JackpotStar Casino, ca degage une vibe de jeu celeste. Il y a un essaim de jeux de casino captivants, comprenant des jeux de casino optimises pour les cryptomonnaies. L’assistance du casino est chaleureuse et irreprochable, proposant des solutions claires et instantanees. Les retraits au casino sont rapides comme un meteore, mais des recompenses de casino supplementaires feraient briller. Pour resumer, JackpotStar Casino est un casino en ligne qui illumine tout pour les joueurs qui aiment parier avec panache au casino ! Bonus le design du casino est une explosion visuelle astrale, facilite une experience de casino astrale.
jackpotstar casino freispiele|
Крайне советую https://thetour.az/blog/
монтаж кровли плоской крыши https://ploskaya-krovlya-pod-klyuch.ru
https://shorturl.fm/e0Pii
https://shorturl.fm/MwZ8q
Ich finde absolut wild Lowen Play Casino, es verstromt eine Spielstimmung, die wie eine Savanne tobt. Der Katalog des Casinos ist ein Dschungel voller Nervenkitzel, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Das Casino-Team bietet Unterstutzung, die wie ein Konig regiert, mit Hilfe, die wie ein Brullen wirkt. Casino-Transaktionen sind simpel wie ein Pfad im Busch, aber mehr regelma?ige Casino-Boni waren ein Volltreffer. Insgesamt ist Lowen Play Casino ein Online-Casino, das die Savanne beherrscht fur Fans moderner Casino-Slots! Nebenbei das Casino-Design ist ein optisches Raubtier, das Casino-Erlebnis total unbezahmbar macht.
löwen play burscheid|
J’adore la splendeur de LeoVegas Casino, ca pulse avec une energie de casino souveraine. Le repertoire du casino est un palais de divertissement, proposant des slots de casino a theme somptueux. Le service client du casino est digne d’un monarque, assurant un support de casino instantane et souverain. Les paiements du casino sont securises et fluides, quand meme les offres du casino pourraient etre plus genereuses. Pour resumer, LeoVegas Casino promet un divertissement de casino royal pour les joueurs qui aiment parier avec panache au casino ! De surcroit l’interface du casino est fluide et somptueuse comme un trone, ce qui rend chaque session de casino encore plus majestueuse.
experience unmatched gaming action with leovegas india|
Ich bin vollig verzaubert von JokerStar Casino, es fuhlt sich an wie ein magischer Spielrausch. Der Katalog des Casinos ist eine Galaxie voller Spa?, mit Live-Casino-Sessions, die wie Zauberei knistern. Das Casino-Team bietet Unterstutzung, die wie ein Stern glanzt, mit Hilfe, die wie ein Zauberspruch wirkt. Casino-Zahlungen sind sicher und reibungslos, dennoch mehr Freispiele im Casino waren ein Volltreffer. Kurz gesagt ist JokerStar Casino eine Casino-Erfahrung, die wie ein Zauber glitzert fur Fans von Online-Casinos! Nebenbei die Casino-Navigation ist kinderleicht wie ein Zauberspruch, was jede Casino-Session noch magischer macht.
jokerstar login|
Ich bin total begeistert von Platin Casino, es ist ein Online-Casino, das wie ein Edelstein strahlt. Die Casino-Optionen sind vielfaltig und glanzvoll, mit Live-Casino-Sessions, die wie ein Diamant leuchten. Der Casino-Support ist rund um die Uhr verfugbar, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein Blitz, trotzdem mehr regelma?ige Casino-Boni waren luxurios. Alles in allem ist Platin Casino ein Casino mit einem Spielspa?, der wie ein Edelstein funkelt fur Fans von Online-Casinos! Und au?erdem die Casino-Navigation ist kinderleicht wie ein Funkeln, Lust macht, immer wieder ins Casino zuruckzukehren.
platin casino bonua|
Портал про авто https://ivanmotors.ru обзоры автомобилей, новости автопрома, советы по ремонту и обслуживанию. Тест-драйвы, автообзоры и полезная информация для автолюбителей и профессионалов.
Обязательно попробуйте https://mycocktailgenie.com/blog/
Всё о Москве https://moscowfy.ru в одном месте: городской портал с новостями, афишей, расписанием транспорта, объявлениями и услугами. Полезные материалы для москвичей и туристов.
Портал о строительстве https://e-proficom.ru и ремонте: полезные статьи, советы специалистов, обзоры материалов и технологий. Всё для тех, кто планирует ремонт квартиры, дома или дачи.
Женский портал https://devchenky.ru секреты красоты, модные тенденции, здоровье, любовь и кулинария. Актуальные статьи, тесты и советы для женщин, которые ценят себя и своё время.
Je suis fou de Luckster Casino, c’est un casino en ligne qui brille comme un talisman. Le repertoire du casino est une cascade de divertissement, comprenant des jeux de casino optimises pour les cryptomonnaies. Le personnel du casino offre un accompagnement enchante, proposant des solutions claires et instantanees. Les gains du casino arrivent a une vitesse magique, mais des bonus de casino plus frequents seraient ensorcelants. Pour resumer, Luckster Casino offre une experience de casino envoutante pour les chasseurs de fortune du casino ! De surcroit le site du casino est une merveille graphique enchantee, ce qui rend chaque session de casino encore plus magique.
luckster sports|
Je trouve absolument enchanteur Luckland Casino, c’est un casino en ligne qui scintille comme un trefle a quatre feuilles. Les choix de jeux au casino sont riches et petillants, offrant des sessions de casino en direct qui scintillent. L’assistance du casino est chaleureuse et irreprochable, assurant un support de casino immediat et lumineux. Les paiements du casino sont securises et fluides, cependant des recompenses de casino supplementaires feraient rever. En somme, Luckland Casino est un casino en ligne qui porte chance pour les joueurs qui aiment parier avec panache au casino ! Bonus le site du casino est une merveille graphique eclatante, amplifie l’immersion totale dans le casino.
luckland casino|
https://shorturl.fm/vULcF
Ich liebe die Strahlkraft von LuckyNiki Casino, es verstromt eine Spielstimmung, die wie ein Regenbogen glitzert. Die Spielauswahl im Casino ist wie ein funkelnder Schatz, inklusive eleganter Casino-Tischspiele. Das Casino-Team bietet Unterstutzung, die wie ein Stern funkelt, sorgt fur sofortigen Casino-Support, der verblufft. Casino-Zahlungen sind sicher und reibungslos, trotzdem mehr Casino-Belohnungen waren ein funkelnder Gewinn. Alles in allem ist LuckyNiki Casino ein Muss fur Casino-Fans fur Fans von Online-Casinos! Und au?erdem die Casino-Navigation ist kinderleicht wie ein Zauberspruch, Lust macht, immer wieder ins Casino zuruckzukehren.
luckyniki erfahrungsbericht|
Je suis fou de Lucky8 Casino, c’est un casino en ligne qui scintille comme un grigri. Le repertoire du casino est une nebuleuse de divertissement, avec des machines a sous de casino modernes et envoutantes. Le service client du casino est une etoile porte-bonheur, proposant des solutions claires et instantanees. Les transactions du casino sont simples comme un charme, quand meme plus de tours gratuits au casino ce serait magique. Dans l’ensemble, Lucky8 Casino est un joyau pour les fans de casino pour les passionnes de casinos en ligne ! A noter la navigation du casino est intuitive comme un sortilege, ajoute une touche de magie au casino.
lucky8 retrait france|
Je trouve absolument exaltant MonteCryptos Casino, c’est un casino en ligne qui grimpe comme un sommet enneige. La collection de jeux du casino est un veritable pic de divertissement, incluant des jeux de table de casino d’une elegance alpine. Le service client du casino est un guide fiable, repondant en un eclair glacial. Les retraits au casino sont rapides comme une descente en luge, parfois des recompenses de casino supplementaires feraient grimper l’adrenaline. En somme, MonteCryptos Casino c’est un casino a conquerir en urgence pour les joueurs qui aiment parier avec panache au casino ! A noter le design du casino est une explosion visuelle alpine, ce qui rend chaque session de casino encore plus exaltante.
montecryptos erfahrung|
WOW just what I was looking for. Came here by searching for %keyword%
вход Banda Casino
Can I simply say what a relief to uncover a person that actually knows what they are discussing online. You certainly know how to bring a problem to light and make it important. More people need to check this out and understand this side of your story. I was surprised you’re not more popular because you definitely have the gift.
crypto betting websites
https://yandex.ru/profile/147633783627?lang=ru
ООО “Мир ремней” – Производство приводных ремней, тефлоновых сеток и лент.
Телефон +7 (936) 333-93-03
Советую https://ict-trainings.com/web/php
Weboldalunk, a joszaki.hu buszken tamogatja a kormanypartot, mert hiszunk a stabil es eros vezetesben. Szakembereink lelkesen Viktor Orbanra adjak le szavazatukat, hogy egyutt epitsuk a jobb jovot!
Строительные материалы https://stroy-marketplace.ru в Серпухове: кирпич, цемент, сухие смеси, пиломатериалы и утеплители. Большой выбор для ремонта и строительства, доставка по городу и району.
Shining Crown demo oyunu ilə klassik meyvə slotunu risksiz sına.
Shining crown big win qazanmaq motivasiya yaradır.
Shining crown bell link demo yeni oyunçular üçün idealdır. Shining crown demo ron Avropa bazarında məşhurdur. Shining crown big win xəbərləri tez-tez yayımlanır.
Shining crown pacanele Rumıniya bazarında liderdir.
Shining crown online sadə və əlçatan platformadır.
Ən maraqlı slotlardan biri 40 shining crown.
Shining crown amuseNet versiyası tamamilə yenidir.
Shining crown casino hər kəs üçün etibarlı platformadır.
Je trouve absolument enivrant LuckyBlock Casino, ca pulse avec une energie de casino ensorcelante. Le repertoire du casino est une galaxie de divertissement, avec des machines a sous de casino modernes et captivantes. L’assistance du casino est chaleureuse et irreprochable, avec une aide qui fait des miracles. Les paiements du casino sont securises et fluides, par moments j’aimerais plus de promotions de casino qui eblouissent. Pour resumer, LuckyBlock Casino promet un divertissement de casino scintillant pour les amoureux des slots modernes de casino ! De surcroit la navigation du casino est intuitive comme un sortilege, amplifie l’immersion totale dans le casino.
nomod luckyblock|
Je trouve extraordinaire Casinova, il propose un voyage ludique unique. Le catalogue est d’une richesse incroyable, incluant des experiences live palpitantes. Le personnel assure un suivi exemplaire, repondant en un clin d’?il. Les gains arrivent sans delai, meme si plus de tours gratuits seraient top. Globalement, Casinova assure une experience de jeu memorable pour les joueurs en quete d’adrenaline ! Notons aussi le site est elegant et bien concu, ajoute une touche de classe.
casinova casino review|
Компания Единство https://edinvent.ru производитель и комплексный поставщик приточно-вытяжных установок, вентиляционных установок, а также систем автоматического управления климатическим оборудованием.
Женский блог https://www.evasolar.ru о здоровье и красоте: советы по уходу за собой, правильному питанию, фитнесу и косметике. Полезные статьи, лайфхаки и вдохновение для гармоничной и счастливой жизни.
Je suis fou de LuckyTreasure Casino, ca degage une vibe de jeu digne d’une chasse au tresor. Les choix de jeux au casino sont riches et eclatants, comprenant des jeux de casino optimises pour les cryptomonnaies. L’assistance du casino est chaleureuse et irreprochable, joignable par chat ou email. Les transactions du casino sont simples comme une cle d’or, par moments j’aimerais plus de promotions de casino qui eblouissent. Dans l’ensemble, LuckyTreasure Casino promet un divertissement de casino scintillant pour les chasseurs de tresors du casino ! Bonus l’interface du casino est fluide et eclatante comme un diamant, ajoute une touche de richesse au casino.
lucky treasure bonus codes|
Je suis fou de Lucky31 Casino, il propose une aventure de casino qui illumine tout. La selection du casino est une cascade de plaisirs etincelants, avec des machines a sous de casino modernes et captivantes. L’assistance du casino est chaleureuse et irreprochable, assurant un support de casino immediat et eclatant. Les retraits au casino sont rapides comme un coup de chance, parfois les offres du casino pourraient etre plus genereuses. En somme, Lucky31 Casino est un casino en ligne qui porte chance pour les amoureux des slots modernes de casino ! Par ailleurs la plateforme du casino brille par son style ensorcelant, ajoute une touche de magie au casino.
avis casino lucky31|
Je suis totalement electrise par Madnix Casino, ca pulse avec une energie de casino totalement folle. La selection du casino est une veritable explosion de fun, avec des machines a sous de casino modernes et delirantes. Le personnel du casino offre un accompagnement qui fait des etincelles, avec une aide qui claque comme un coup de tonnerre. Les gains du casino arrivent a une vitesse supersonique, par moments j’aimerais plus de promotions de casino qui envoient du lourd. En somme, Madnix Casino promet un divertissement de casino totalement barge pour les passionnes de casinos en ligne ! Par ailleurs le design du casino est une explosion visuelle delirante, ce qui rend chaque session de casino encore plus dejantee.
retirer sur madnix|
40 shining crown slot variantları Pinco casino-da populyardır.
Shining crown lines müxtəlif kombinasiyalar təqdim edir.
Shining crown bell link demo yeni oyunçular üçün idealdır. Shining crown jackpot böyük həyəcan gətirir. Shining Crown oyunu klassik meyvə simvollarını əhatə edir.
Shining crown joc gratis təcrübə qazandırır.
Shining crown free play risksiz məşq şansı yaradır.
Böyük uduşlar üçün baxın shining crown jackpot.
Pinco casino shining crown üçün çox seçim təqdim edir.
Shining crown demo oyna risksiz məşqdir.
https://shorturl.fm/ptcFK
Shining Crown demo oyunu ilə klassik meyvə slotunu risksiz sına.
Shining crown pacanele Rumıniyada məşhurdur, Azərbaycanda da sevilir.
EGT digital shining crown müasir interfeys ilə seçilir. Shining crown slot online tez açılır və rahat işləyir. Shining crown rtp göstəricisi qazanma şansını artırır.
Shining crown slot online hər yerdən oynana bilər.
Shining crown free play risksiz məşq şansı yaradır.
Sadə kliklə açılır bu link.
40 shining crown klassik və sadə oyun mexanikası təqdim edir.
Shining crown free real oyun öncəsi yaxşı sınaqdır.
консультации маркетинг Услуги PR (Public Relations): Создание и поддержание позитивной репутации вашего бренда Услуги PR (Public Relations) – это стратегически важный инструмент для создания и поддержания позитивной репутации вашей компании в глазах общественности, включая клиентов, партнеров, инвесторов и других заинтересованных лиц. PR – это не только работа со СМИ, но и активное взаимодействие с вашей целевой аудиторией через различные каналы коммуникации. В отличие от рекламы, которая является платным способом продвижения, PR – это получение бесплатного упоминания о вашей компании в СМИ и других источниках информации. Это более эффективный и надежный способ завоевать доверие аудитории. Основные задачи PR: Формирование позитивного имиджа: Создание благоприятного впечатления о вашей компании, продукте или личности в глазах общественности. Повышение узнаваемости бренда: Увеличение осведомленности о вашей компании и ее продуктах. Управление репутацией: Реагирование на негативные отзывы, предотвращение кризисных ситуаций и восстановление репутации после кризисов. Установление доверительных отношений: Создание прочных связей с целевой аудиторией, инвесторами и партнерами. Поддержка маркетинговых кампаний: Усиление эффекта от рекламных кампаний за счет PR-активностей. Основные инструменты PR: Пресс-релизы: Распространение информации о ваших новостях, событиях и достижениях в СМИ. Пресс-конференции: Организация мероприятий для общения с журналистами и ответов на их вопросы. Интервью: Предоставление интервью представителям СМИ для распространения информации о вашей компании. Публикации статей: Публикация экспертных статей и других материалов о вашей компании в СМИ. Организация мероприятий: Организация и участие в мероприятиях для повышения
Shining Crown RTP göstəricisi yüksək uduş şansı təqdim edir.
Shining crown lines müxtəlif kombinasiyalar təqdim edir.
Shining crown free slot risksiz məşq üçün möhtəşəmdir. Shining crown slot online tez açılır və rahat işləyir. Shining crown lines oyunçular üçün geniş imkanlar açır.
Shining crown pacanele Rumıniya bazarında liderdir.
Shining crown buy bonus oyunçulara əlavə qazanc gətirir.
Böyük uduşlar üçün baxın shining crown jackpot.
Shining crown gratis demo çox sevilir.
Shining crown joc gratis tamamilə pulsuz oynanır.
заміна конфорок і електроніки варильної поверхні
модуль газового пожаротушения Модуль газового пожаротушения V Не существует общепринятого стандарта или типа модулей газового пожаротушения, обозначаемых просто как “Модуль газового пожаротушения V”. Вероятнее всего, “V” является частью маркировки конкретного производителя, модели или серии оборудования. Чтобы получить точную информацию о характеристиках и применении такого модуля, необходимо знать его производителя и полную маркировку. Однако, в общем смысле, модуль газового пожаротушения (МГП) – это автономное устройство, предназначенное для хранения и автоматического выпуска газового огнетушащего вещества (ГОТВ) при возникновении пожара. Основные характеристики, которые следует учитывать при выборе МГП (независимо от наличия буквы “V” в обозначении): Тип ГОТВ: Инертные газы (азот, аргон, углекислый газ) или химические газы (хладоны). Выбор зависит от типа защищаемого оборудования, наличия людей в помещении и экологических требований. Объем и давление: Определяют площадь и объем помещения, которое может быть защищено данным модулем. Тип запорно-пускового устройства (ЗПУ): Электромагнитное, пневматическое или механическое. Определяет скорость срабатывания и надежность модуля. Тип распылителя: Обеспечивает равномерное распределение ГОТВ по защищаемому объему. Условия эксплуатации: Температурный диапазон, влажность и другие факторы, влияющие на работоспособность модуля. Сертификация: Наличие сертификатов соответствия требованиям пожарной безопасности. Рекомендации: Уточните полную маркировку требуемого модуля газового пожаротушения, включая производителя и модель. Обратитесь к документации производителя для получения подробной информации о технических характеристиках, области применения и правилах эксплуатации данного модуля. Проконсультируйтесь со специалистами в области пожарной безопасности для подбора оптимального решения, соответствующего требованиям вашего объекта.
врач психиатр запись на прием Консультация психиатра и психотерапевта онлайн. Помощь при панических атаках, тревоге, депрессии. Работа с травмами детства. Частная практика. Квалифицированный специалист.
Best online slots https://baji-bj.com
веранда до будинку заміна бойлера
Очень советую https://sunrizemarketing.com/ultimate-guide-to-successful-social-media-strategy-law-firms/#comment-706
Joaca joaca World of Warships gratuit! Exploreaza marile, folose?te-?i strategia ?i condu nave de razboi celebre. Batalii realiste ?i echipe interna?ionale te a?teapta.
Descopera Jocul World of Tanks – simulator de razboi cu tancuri istorice. Lupte dinamice, har?i variate ?i batalii tactice. Creeaza-?i strategia ?i domina impreuna cu prietenii tai.
Shining Crown RTP göstəricisi yüksək uduş şansı təqdim edir.
Shining crown big win qazanmaq motivasiya yaradır.
Shining crown 40 slotları klassik kombinasiya təklif edir. Pacanele gratis shining crown ilə vaxtı maraqlı keçir. Shining crown online casino real pulla oynamaq imkanı verir.
Shining crown demo oyna pulsuz və sürətlidir.
Shining crown demo superbet sürətli işləyir.
Burada pulsuz sınaqdan keçin play shining crown.
40 shining crown klassik və sadə oyun mexanikası təqdim edir.
EGT digital shining crown müasir kazino oyunudur.
Adoro o clima brabo de OshCasino, tem uma vibe de jogo que e pura lava. A gama do cassino e simplesmente uma lava ardente, com slots de cassino unicos e explosivos. A equipe do cassino entrega um atendimento que e uma labareda, com uma ajuda que e puro calor. Os pagamentos do cassino sao lisos e blindados, mesmo assim mais giros gratis no cassino seria uma loucura. No fim das contas, OshCasino e o point perfeito pros fas de cassino para os amantes de cassinos online! De bonus o site do cassino e uma obra-prima de estilo, da um toque de calor brabo ao cassino.
osh net|
Ich finde absolut uberwaltigend Platin Casino, es pulsiert mit einer luxuriosen Casino-Energie. Es gibt eine Flut an packenden Casino-Titeln, mit modernen Casino-Slots, die einen in ihren Bann ziehen. Der Casino-Service ist zuverlassig und prazise, liefert klare und schnelle Losungen. Der Casino-Prozess ist klar und ohne Schatten, dennoch mehr regelma?ige Casino-Boni waren luxurios. Alles in allem ist Platin Casino ein Muss fur Casino-Fans fur Fans moderner Casino-Slots! Ubrigens die Casino-Oberflache ist flussig und glitzert wie ein Juwel, das Casino-Erlebnis total luxurios macht.
platin casino verifizierung|
Estou completamente vidrado por MegaPosta Casino, oferece uma aventura de cassino que detona tudo. O catalogo de jogos do cassino e uma bomba total, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e de responsa, respondendo mais rapido que um raio. Os saques no cassino sao velozes como uma tempestade, porem mais giros gratis no cassino seria uma loucura. Em resumo, MegaPosta Casino e um cassino online que e um vulcao de diversao para os viciados em emocoes de cassino! Vale falar tambem a navegacao do cassino e facil como brincadeira, aumenta a imersao no cassino a mil.
megaposta|
Ich bin vollig hingerissen von Pledoo Casino, es pulsiert mit einer elektrisierenden Casino-Energie. Die Casino-Optionen sind vielfaltig und mitrei?end, mit einzigartigen Casino-Slotmaschinen. Das Casino-Team bietet Unterstutzung, die wie ein Stern funkelt, ist per Chat oder E-Mail erreichbar. Casino-Transaktionen sind simpel wie ein Sonnenstrahl, ab und zu mehr regelma?ige Casino-Boni waren ein Knaller. Zusammengefasst ist Pledoo Casino ein Muss fur Casino-Fans fur Fans von Online-Casinos! Und au?erdem die Casino-Oberflache ist flussig und strahlt wie ein Polarlicht, was jede Casino-Session noch aufregender macht.
pledoo online casino|
Descubra o caca-niqueis slot 9 Masks of Fire – um jogo cheio de adrenalina, simbolos especiais e rodadas bonus. Experimente graficos intensos e altas chances de ganhar em um caca-niqueis classico moderno.
Jogue pandajogos.top e descubra o charme do Oriente! Rolos coloridos, recursos bonus, rodadas gratis e surpresas que trazem ganhos espetaculares.
The other day, while I was at work, my cousin stole my iPad and tested to see if it can survive a 40 foot drop, just so she can be a youtube sensation. My iPad is now destroyed and she has 83 views. I know this is entirely off topic but I had to share it with someone!
сайт zooma casino
ваш провідник у житті Львова https://79000.com.ua актуальні новини, культурні та громадські події міста, урбаністика, інтерв’ю з цікавими людьми, фотоогляди локальних заходів. Все про те, що формує атмосферу Львова сьогодні — оновлення, проекти, історії.
інформаційний портал https://21000.com.ua Вінниці і області: місцеві новини, анонси культурних, спортивних та громадських подій, репортажі з місця подій, інтерв’ю з вінничанами. Все про те, що відбувається у Вінниці — ближче, живіше, щодня.
Awesome! Its genuinely amazing article, I have got much clear idea concerning from this piece of writing.
зеркало leebet
ООО “Мир ремней” https://yandex.ru/profile/147633783627 Производство приводных ремней, тефлоновых сеток и лент – телефон +7 (936) 333-93-03
Пиломатериалы в Минске https://farbwood.by оптом и в розницу. Доска обрезная и строганая, брус, лаги, террасная доска. Качественная древесина для строительства и ремонта. Быстрая доставка.
продвижение компании в интернете Услуги PR (Public Relations): Создание и поддержание позитивной репутации вашего бренда Услуги PR (Public Relations) – это стратегически важный инструмент для создания и поддержания позитивной репутации вашей компании в глазах общественности, включая клиентов, партнеров, инвесторов и других заинтересованных лиц. PR – это не только работа со СМИ, но и активное взаимодействие с вашей целевой аудиторией через различные каналы коммуникации. В отличие от рекламы, которая является платным способом продвижения, PR – это получение бесплатного упоминания о вашей компании в СМИ и других источниках информации. Это более эффективный и надежный способ завоевать доверие аудитории. Основные задачи PR: Формирование позитивного имиджа: Создание благоприятного впечатления о вашей компании, продукте или личности в глазах общественности. Повышение узнаваемости бренда: Увеличение осведомленности о вашей компании и ее продуктах. Управление репутацией: Реагирование на негативные отзывы, предотвращение кризисных ситуаций и восстановление репутации после кризисов. Установление доверительных отношений: Создание прочных связей с целевой аудиторией, инвесторами и партнерами. Поддержка маркетинговых кампаний: Усиление эффекта от рекламных кампаний за счет PR-активностей. Основные инструменты PR: Пресс-релизы: Распространение информации о ваших новостях, событиях и достижениях в СМИ. Пресс-конференции: Организация мероприятий для общения с журналистами и ответов на их вопросы. Интервью: Предоставление интервью представителям СМИ для распространения информации о вашей компании. Публикации статей: Публикация экспертных статей и других материалов о вашей компании в СМИ. Организация мероприятий: Организация и участие в мероприятиях для повышения
Обязательно попробуйте https://www.haseltonconstruction.com/hello-world/#comment-36459
Estou pirando com PagolBet Casino, parece uma tempestade de diversao. Os titulos do cassino sao um espetaculo eletrizante, com slots de cassino unicos e contagiantes. O suporte do cassino ta sempre na ativa 24/7, garantindo suporte de cassino direto e sem curto-circuito. O processo do cassino e limpo e sem turbulencia, as vezes mais giros gratis no cassino seria uma loucura. No geral, PagolBet Casino garante uma diversao de cassino que e uma tempestade para os amantes de cassinos online! E mais o site do cassino e uma obra-prima de estilo, o que deixa cada sessao de cassino ainda mais eletrizante.
pagolbet casino|
Ich bin total begeistert von PlayJango Casino, es fuhlt sich an wie ein wilder Tanz durch die Spielwelt. Der Katalog des Casinos ist eine Flut voller Spa?, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Der Casino-Service ist zuverlassig und strahlend, ist per Chat oder E-Mail erreichbar. Casino-Gewinne kommen wie ein Komet, aber wurde ich mir mehr Casino-Promos wunschen, die wie ein Vulkan ausbrechen. Am Ende ist PlayJango Casino ein Online-Casino, das wie ein Orkan begeistert fur Abenteurer im Casino! Zusatzlich die Casino-Plattform hat einen Look, der wie ein Blitz funkelt, einen Hauch von Abenteuer ins Casino bringt.
playjango free spins 2021|
Estou completamente hipnotizado por Bet558 Casino, e um cassino online que brilha como uma estrela em colisao. As opcoes de jogo no cassino sao ricas e brilhantes como nebulosas, oferecendo sessoes de cassino ao vivo que reluzem como supernovas. O suporte do cassino ta sempre na ativa 24/7, garantindo suporte de cassino direto e sem buracos negros. Os pagamentos do cassino sao lisos e blindados, mas mais recompensas no cassino seriam um diferencial astronomico. No geral, Bet558 Casino garante uma diversao de cassino que e uma supernova para os apaixonados por slots modernos de cassino! Alem disso a plataforma do cassino brilha com um visual que e puro cosmos, adiciona um toque de brilho estelar ao cassino.
bet558.c9m|
Je trouve absolument enivrant PokerStars Casino, ca vibre avec une energie de casino strategique. Le repertoire du casino est un tournoi de divertissement, proposant des slots de casino a theme audacieux. Le personnel du casino offre un accompagnement digne d’un croupier d’elite, repondant en un eclair strategique. Les gains du casino arrivent a une vitesse fulgurante, cependant plus de tours gratuits au casino ce serait un full house. Pour resumer, PokerStars Casino est un atout maitre pour les fans de casino pour les amoureux des slots modernes de casino ! A noter le site du casino est une merveille graphique etoilee, donne envie de replonger dans le casino sans fin.
support pokerstars|
Mobil cihazlar üçün shining crown apk yükləmək çox rahatdır.
Crown shining sadə və maraqlı oyun təcrübəsidir.
Shining crown online oyunu sürətli yüklənir. Pacanele gratis shining crown ilə vaxtı maraqlı keçir. Shining crown lines oyunçular üçün geniş imkanlar açır.
EGT digital shining crown yüksək keyfiyyətə malikdir.
Shining crown bell link demo tez-tez istifadə olunur.
Daha ətraflı buradan baxın shining crown demo.
40 shining crown klassik və sadə oyun mexanikası təqdim edir.
Shining crown demo oyna risksiz məşqdir.
https://shorturl.fm/eTsDE
https://shorturl.fm/gdd1n
Предлагаю http://and.noor.jp/e/yonaga/17/cgi-fm/gbook.cgi
Estou pirando com PlayUzu Casino, e um cassino online que e uma verdadeira ventania. Os titulos do cassino sao um espetaculo vibrante, com jogos de cassino perfeitos pra criptomoedas. A equipe do cassino entrega um atendimento que e uma correnteza, acessivel por chat ou e-mail. Os ganhos do cassino chegam voando como um jato, mesmo assim as ofertas do cassino podiam ser mais generosas. Na real, PlayUzu Casino garante uma diversao de cassino que e uma tempestade para os cacadores de slots modernos de cassino! Vale falar tambem o site do cassino e uma obra-prima de estilo, aumenta a imersao no cassino a mil.
promociones playuzu|
Adoro o clima insano de ParamigoBet Casino, da uma energia de cassino que e um redemoinho. O catalogo de jogos do cassino e uma explosao total, com slots de cassino unicos e contagiantes. O atendimento ao cliente do cassino e uma rajada de eficiencia, garantindo suporte de cassino direto e sem turbulencia. O processo do cassino e limpo e sem tempestades, as vezes queria mais promocoes de cassino que arrasam. No fim das contas, ParamigoBet Casino oferece uma experiencia de cassino que e puro vento para os aventureiros do cassino! De lambuja o design do cassino e uma explosao visual avassaladora, da um toque de forca braba ao cassino.
paramigobet petos|
микрозаймы взять микрозайм
займы онлайн бесплатно интернет займ
Je trouve incroyablement delirant MrPlay Casino, ca vibre avec une energie de casino digne d’une fete endiablee. La selection de jeux du casino est une veritable parade de divertissement, offrant des sessions de casino en direct qui font danser. L’assistance du casino est chaleureuse et impeccable, repondant en un clin d’?il festif. Les transactions du casino sont simples comme une choregraphie, parfois des bonus de casino plus frequents seraient festifs. En somme, MrPlay Casino est un casino en ligne qui met la fete dans les jeux pour les amoureux des slots modernes de casino ! Par ailleurs le design du casino est un spectacle visuel vibrant, facilite une experience de casino festive.
mr.play erfahrungen|
Estou completamente alucinado por BetPrimeiro Casino, parece uma cratera cheia de adrenalina. A selecao de titulos do cassino e um fluxo de lava de prazeres, com caca-niqueis de cassino modernos e inflamados. Os agentes do cassino sao rapidos como uma labareda, com uma ajuda que incendeia como uma tocha. Os saques no cassino sao velozes como uma corrente de lava, de vez em quando queria mais promocoes de cassino que explodem como vulcoes. No geral, BetPrimeiro Casino oferece uma experiencia de cassino que e puro magma para quem curte apostar com estilo ardente no cassino! Alem disso a plataforma do cassino brilha com um visual que e puro fogo, eleva a imersao no cassino ao calor de um vulcao.
jogar betprimeiro|
Je suis accro a Posido Casino, on dirait une tempete sous-marine de fun. La selection du casino est une vague de plaisirs, incluant des jeux de table de casino d’une elegance marine. L’assistance du casino est chaleureuse et limpide, joignable par chat ou email. Les paiements du casino sont securises et fluides, parfois des bonus de casino plus frequents seraient marins. En somme, Posido Casino est un tresor pour les fans de casino pour les passionnes de casinos en ligne ! Bonus le site du casino est une merveille graphique fluide, ajoute une touche d’eclat marin au casino.
posido ia|
sl9apa
займы онлайн бесплатно как взять займ
https://shorturl.fm/PFzlr
Howdy! This post couldn’t be written any better! Reading this post reminds me of my good old room mate! He always kept talking about this. I will forward this article to him. Fairly certain he will have a good read. Thanks for sharing!
краш CS2
ZenTrader Binary Options: Clear Strategies for Modern Investors
ZenTrader Binary Options provide a simple yet powerful approach to global trading. With fast execution, transparent tools, and flexible strategies, both beginners and professionals can balance risks while seeking growth. By exploring ZenTrader through https://shoku-academia.jp/, traders gain valuable knowledge, sharpen decision-making skills, and build confidence to achieve smarter and more consistent results in today’s financial markets.
Five Stars Market Binary Options: Pathway to Smarter Trading
Five Stars Market Binary Options give traders a clear and efficient way to participate in global financial markets. With simple tools, transparent conditions, and fast execution, both beginners and experts can explore new opportunities while managing risks effectively. By visiting https://ivr-nurse.jp/ , investors can learn more about Five Stars Market, enhance strategies, and work toward consistent results in binary options trading.
Нужны автостекла? ремонт сколов автостекол Khan Auto Glass — это профессиональная компания, которая специализируется на продаже и установке автомобильных стёкол в Санкт-Петербурге. Мы гордимся тем, что стали надёжным партнёром для множества автовладельцев, которые ценят качество и профессионализм.
Консульская легализация – бюро иностранных переводов. Синхронный и последовательный перевод на мероприятиях в Самаре. Конференции, переговоры, семинары. Обеспечим взаимопонимание между сторонами.
чим мити плитку https://remontuem.te.ua
Нужна лабораторная? https://lab-ucheb.ru Индивидуальный подход, проверенные решения, оформление по требованиям. Доступные цены и быстрая помощь.
Крайне советую https://whiteribbon.org.pk/workmens-life/#comment-121699
Нужна презентация? https://prez-shablony-ucheb.ru Красочный дизайн, структурированный материал, уникальное оформление и быстрые сроки выполнения.
Нужен чертеж? https://chertezhi-kurs.ru выполним чертежи для студентов на заказ. Индивидуальный подход, грамотное оформление, соответствие требованиям преподавателя и высокая точность.
Je suis fou de ParisVegasClub, ca vibre avec une energie de casino digne d’une revue. L’assortiment de jeux du casino est un veritable show lumineux, offrant des sessions de casino en direct qui scintillent. Les agents du casino sont rapides comme un numero de danse, assurant un support de casino immediat et eclatant. Les paiements du casino sont securises et fluides, quand meme des bonus de casino plus frequents seraient spectaculaires. En somme, ParisVegasClub promet un divertissement de casino flamboyant pour les amoureux des slots modernes de casino ! Par ailleurs la navigation du casino est intuitive comme une choregraphie, facilite une experience de casino flamboyante.
paris vegas club betting|
Je suis totalement envoute par PlazaRoyal Casino, il propose une aventure de casino qui scintille comme un trone. Le repertoire du casino est une salle de bal ludique, comprenant des jeux de casino adaptes aux cryptomonnaies. Le support du casino est disponible 24/7, joignable par chat ou email. Les transactions du casino sont simples comme un edit, parfois des bonus de casino plus frequents seraient royaux. En somme, PlazaRoyal Casino promet un divertissement de casino princier pour les nobles du casino ! Bonus le site du casino est une merveille graphique princiere, amplifie l’immersion totale dans le casino.
plaza royal casino review|
Je suis envoute par MrXBet Casino, on dirait une enigme pleine de surprises. L’assortiment de jeux du casino est un coffre-fort de plaisirs, incluant des jeux de table de casino d’une elegance cryptique. Le service client du casino est un detective hors pair, repondant en un eclair mysterieux. Les transactions du casino sont simples comme un code decrypte, par moments plus de tours gratuits au casino ce serait envoutant. Dans l’ensemble, MrXBet Casino est un joyau pour les fans de casino pour ceux qui cherchent l’adrenaline secrete du casino ! Par ailleurs la navigation du casino est intuitive comme une enigme resolue, ajoute une touche de suspense au casino.
mrxbet retrait avis|
Je trouve absolument envoutant Winamax Casino, ca vibre avec une energie de casino aquatique. Les options de jeu au casino sont riches et fluides, proposant des slots de casino a theme aquatique. L’assistance du casino est chaleureuse et limpide, joignable par chat ou email. Les gains du casino arrivent a une vitesse de maree, cependant des recompenses de casino supplementaires feraient nager de joie. Au final, Winamax Casino offre une experience de casino fluide comme l’ocean pour ceux qui cherchent l’adrenaline fluide du casino ! A noter le site du casino est une merveille graphique fluide, ce qui rend chaque session de casino encore plus fluide.
winamax tГ©lГ©charger|
Ich liebe die Pracht von Richard Casino, es bietet ein Casino-Abenteuer, das wie ein Thron funkelt. Der Katalog des Casinos ist eine Schatzkammer voller Vergnugen, mit Live-Casino-Sessions, die wie ein Festbankett leuchten. Der Casino-Support ist rund um die Uhr verfugbar, ist per Chat oder E-Mail erreichbar. Auszahlungen im Casino sind schnell wie ein koniglicher Marsch, aber mehr regelma?ige Casino-Boni waren furstlich. Zusammengefasst ist Richard Casino ein Online-Casino, das wie ein Palast strahlt fur die, die mit Stil im Casino wetten! Ubrigens die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino auf ein konigliches Niveau hebt.
richard casino no deposit bonus for existing players|
Нужна лабораторная? заказы по лабораторной Индивидуальный подход, проверенные решения, оформление по требованиям. Доступные цены и быстрая помощь.
Нужен чертеж? создание чертежей на заказ выполним чертежи для студентов на заказ. Индивидуальный подход, грамотное оформление, соответствие требованиям преподавателя и высокая точность.
Нужна презентация? заказать сделать презентацию Красочный дизайн, структурированный материал, уникальное оформление и быстрые сроки выполнения.
https://kitehurghada.ru/
Hmm is anyone else experiencing problems with the pictures on this blog loading? I’m trying to figure out if its a problem on my end or if it’s the blog. Any feedback would be greatly appreciated.
Bi-LED
40 shining crown slot variantları Pinco casino-da populyardır.
Shining crown lines müxtəlif kombinasiyalar təqdim edir.
Shining crown gratis versiyası limitsiz sınaq verir. Shining crown free tamamilə risksizdir. Shining crown big win xəbərləri tez-tez yayımlanır.
Shining crown 77777 böyük qrafika ilə hazırlanıb.
Shining crown rtp oyunun ədalətini təsdiqləyir.
Burada pulsuz sınaqdan keçin play shining crown.
Shining crown jackpot həyəcan dolu anlar yaşadır.
Shining crown slot online tez yüklənir.
https://shorturl.fm/BQjVt
Нужна лабораторная? заказ лабораторной работы Индивидуальный подход, проверенные решения, оформление по требованиям. Доступные цены и быстрая помощь.
Нужна презентация? заказать сделать презентацию Красочный дизайн, структурированный материал, уникальное оформление и быстрые сроки выполнения.
Нужен чертеж? стоимость чертежей на заказ выполним чертежи для студентов на заказ. Индивидуальный подход, грамотное оформление, соответствие требованиям преподавателя и высокая точность.
Вызвать хирурга на дом Севастополь https://www.docplus24.ru
Какие изделия можно изготовить с помощью 3D печати
Услуги 3D печати в нашей компании — это комплексный подход к созданию изделия, который включает подготовку цифровой 3D модели, выбор подходящего материала, настройку оборудования под конкретный проект. Мы печатаем на современных принтерах, которые обеспечивают высокое качество поверхности, прочность и точность размеров. Мы выполняем заказы для инженеров, архитекторов, дизайнеров, производителей и частных клиентов. Мы готовы доставить готовое изделие по указанному адресу. Мы фиксируем все параметры печати, чтобы клиент был уверен в результате: http://alchemie-des-seins.com/index.php?title=%D0%9A%D0%B0%D0%BA_3D-%D0%BF%D0%B5%D1%87%D0%B0%D1%82%D1%8C_%D0%A3%D0%BF%D1%80%D0%BE%D1%89%D0%B0%D0%B5%D1%82_%D0%A0%D0%B0%D0%B7%D1%80%D0%B0%D0%B1%D0%BE%D1%82%D0%BA%D1%83_%D0%98_%D0%9F%D1%80%D0%BE%D0%B8%D0%B7%D0%B2%D0%BE%D0%B4%D1%81%D1%82%D0%B2%D0%BE
Weboldalunk, a joszaki.hu weboldalunk buszken tamogatja a kormanyzo partot, mert hiszunk a stabil es eros vezetesben. Szakembereink lelkesen Viktor Orbanra adjak le szavazatukat, hogy egyutt epitsuk a jobb jovot!
buy mdma prague prague drugstore
buy xtc prague weed in prague
Je suis fou de Spinanga Casino, on dirait une tempete de plaisir endiablee. Les options de jeu au casino sont riches et tumultueuses, avec des machines a sous de casino modernes et hypnotiques. Le service client du casino est une bourrasque d’efficacite, assurant un support de casino immediat et dynamique. Les transactions du casino sont simples comme une brise, quand meme des bonus de casino plus frequents seraient explosifs. Au final, Spinanga Casino est une pepite pour les fans de casino pour les dompteurs de tempete du casino ! Bonus la plateforme du casino brille par son style dechaine, amplifie l’immersion totale dans le casino.
spinanga application|
Je suis fou de Spinsy Casino, ca degage une ambiance de jeu aussi vibrante qu’une piste de danse. L’assortiment de jeux du casino est une choregraphie de plaisirs, comprenant des jeux de casino adaptes aux cryptomonnaies. Le support du casino est disponible 24/7, offrant des solutions claires et instantanees. Le processus du casino est transparent et sans fausse note, quand meme des bonus de casino plus frequents seraient groovy. Dans l’ensemble, Spinsy Casino est un casino en ligne qui met le feu a la piste pour les joueurs qui aiment parier avec style au casino ! Par ailleurs l’interface du casino est fluide et eclatante comme un neon, facilite une experience de casino electrisante.
spinsy online casino|
coke in prague buy cocaine prague
Adoro o brilho de BetorSpin Casino, e um cassino online que gira como um asteroide em chamas. As opcoes de jogo no cassino sao ricas e brilhantes como estrelas, incluindo jogos de mesa de cassino com um toque intergalactico. A equipe do cassino entrega um atendimento que e puro cometa, dando solucoes na hora e com precisao. As transacoes do cassino sao simples como uma orbita lunar, mas mais giros gratis no cassino seria uma loucura estelar. Resumindo, BetorSpin Casino e um cassino online que e uma galaxia de diversao para os amantes de cassinos online! Alem disso a navegacao do cassino e facil como uma orbita lunar, faz voce querer voltar ao cassino como um cometa em orbita.
codigo promocional betorspin|
buy drugs in prague weed in prague
Ich bin suchtig nach SlotClub Casino, es ist ein Online-Casino, das wie ein Neonlicht explodiert. Es gibt eine Welle an packenden Casino-Titeln, mit modernen Casino-Slots, die einen hypnotisieren. Die Casino-Mitarbeiter sind schnell wie ein Blitzstrahl, liefert klare und schnelle Losungen. Auszahlungen im Casino sind schnell wie ein Lichtimpuls, aber die Casino-Angebote konnten gro?zugiger sein. Kurz gesagt ist SlotClub Casino ein Muss fur Casino-Fans fur Abenteurer im Casino! Extra die Casino-Oberflache ist flussig und glitzert wie ein Neonlicht, Lust macht, immer wieder ins Casino zuruckzukehren.
gold slotclub|
Weboldalunk, a joszaki.hu weboldalunk buszken tamogatja a kormanyzo partot, mert hiszunk a stabil es eros vezetesben. Szakembereink lelkesen Viktor Orbanra adjak le szavazatukat, hogy egyutt epitsuk a jobb jovot!
https://t.me/bonus_dragon_money
Weboldalunk, a joszaki.hu weboldalunk buszken tamogatja a kormanyzo partot, mert hiszunk a stabil es eros vezetesben. Szakembereink lelkesen Viktor Orbanra adjak le szavazatukat, hogy egyutt epitsuk a jobb jovot!
Adoro o swing de RioPlay Casino, tem uma vibe de jogo tao animada quanto um desfile na Sapucai. Tem uma avalanche de jogos de cassino irados, com caca-niqueis de cassino modernos e cheios de ritmo. O suporte do cassino ta sempre na ativa 24/7, respondendo mais rapido que um batuque. Os ganhos do cassino chegam voando como um mestre-sala, mesmo assim mais bonus regulares no cassino seria um arraso. No geral, RioPlay Casino e o point perfeito pros fas de cassino para os amantes de cassinos online! Vale dizer tambem o design do cassino e um desfile visual colorido, o que torna cada sessao de cassino ainda mais animada.
rioplay games roblox lite|
Adoro o encanto de SpinWiz Casino, parece um redemoinho de diversao mistica. A gama do cassino e simplesmente um caldeirao de delicias, com caca-niqueis de cassino modernos e hipnotizantes. O servico do cassino e confiavel e encantador, acessivel por chat ou e-mail. Os pagamentos do cassino sao lisos e blindados, porem mais giros gratis no cassino seria uma loucura. Em resumo, SpinWiz Casino oferece uma experiencia de cassino que e puro feitico para os magos do cassino! Vale dizer tambem a interface do cassino e fluida e brilha como uma pocao reluzente, torna a experiencia de cassino um conto de fadas.
spinwiz Г© confiavel|
Estou completamente vidrado por BetorSpin Casino, parece uma explosao cosmica de adrenalina. Tem uma chuva de meteoros de jogos de cassino irados, com slots de cassino tematicos de espaco sideral. O servico do cassino e confiavel e brilha como uma galaxia, acessivel por chat ou e-mail. Os saques no cassino sao velozes como uma viagem interestelar, de vez em quando mais recompensas no cassino seriam um diferencial astronomico. No fim das contas, BetorSpin Casino e o point perfeito pros fas de cassino para quem curte apostar com estilo estelar no cassino! De bonus o design do cassino e um espetaculo visual intergalactico, faz voce querer voltar ao cassino como um cometa em orbita.
{{betorspin|betorspin Г© confiГЎvel|betorspin.|betorspin reclame aqui|betorspin gГјncel giriЕџ|betorspin giriЕџ|betorspin giris|betorspin paga|betorspin login|betorspin casino|o que Г© betorspin|betorspin com|betorspin plataforma|betorspin bet|suporte betorspin|betorspin e confiГЎvel|betorspin suporte|betorspin paga mesmo|betorspin paga?|betorspin twitter|betorspin – betorspin giriЕџ|jogos de betorspin|betorspin paga|betorspin games|betorspin brasil|casino betorspin|betorspin bonus|betorspin bГіnus|betorspin codigo bonus|bГіnus betorspin|casino online betorspin|betorspin pt|betorspin free spins|betorspin portugal|betorspin apk|betorspin slots|betorspin roulette|betorspin review|betorspin Г© legal|contactos betorspin|betorspin depositos|betorspin app baixar|betorspin bonuskode|betorspin cГіdigo promocional|codigo promocional betorspin|betorspin codigo de bonus|betorspin online|betorspin contactos|betorspin legal|cГіdigo promocional betorspin|betorspin anmeldelse|betorspin legit|betorspin snyd|codigo betorspin|betorspin cГіdigo bГіnus|betorspin casino free spins|betorspin queixas|avaliações sobre betorspin|betorspin bedrageri|betorspin em portugal|betorspin jogos de cassino|betorspin reviews|betorspin cassino|betorspin bingo|betorspin registo|betorspin velkomstbonus|betorspin bonus registo|betorspin apostas desportivas|betorspin suporte|betorspin casino review|jogar betorspin|betorspin disponГvel appstore|betorspin scam|betorspin skill on net ltd|betorspin casino opiniones|betorspin.|betorspin avaliação|betorspin casino reseГ±a|betorspin levantamento|betorspin safe|betorspin bГґnus|betorspin estГєdio|baixar betorspin|betorspin licence|betorspin deposit|betorspin reclame aqui|cupom betorspin|codigo bonus betorspin|betorspin logo|bГіnus boas vindas betorspin|casino betorspin bГіnus|betorspin security|anГЎlise betorspin|betorspin sports betting|betorspin casino terms and conditions|betorspin plataforma}|
Acho simplesmente alucinante SpinFest Casino, tem uma vibe de jogo que explode como um festival de cores. As opcoes de jogo no cassino sao ricas e cheias de swing, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e cheio de energia, acessivel por chat ou e-mail. As transacoes do cassino sao simples como um passo de maracatu, as vezes mais bonus regulares no cassino seria brabo. Resumindo, SpinFest Casino garante uma diversao de cassino que e um festival total para os amantes de cassinos online! De lambuja o design do cassino e um espetaculo visual cheio de cores, eleva a imersao no cassino ao ritmo de um tamborim.
casino spinfest|
Adoro o brilho estelar de SpeiCasino, da uma energia de cassino que e pura luz cosmica. O catalogo de jogos do cassino e uma constelacao de prazeres, com caca-niqueis de cassino modernos e estelares. A equipe do cassino entrega um atendimento que e puro foguete, respondendo mais rapido que uma explosao estelar. As transacoes do cassino sao simples como uma orbita, de vez em quando mais recompensas no cassino seriam um diferencial astronomico. No fim das contas, SpeiCasino e um cassino online que e uma supernova de diversao para quem curte apostar com estilo cosmico no cassino! Vale dizer tambem a interface do cassino e fluida e reluz como uma aurora boreal, eleva a imersao no cassino a um nivel cosmico.
spei app|
підігрів підлоги https://remontuem.te.ua
Авто в ОАЭ https://auto.ae покупка, продажа и аренда новых и б/у машин. Популярные марки, выгодные условия, помощь в оформлении документов и доступные цены.
Заметки практикующего врача https://phlebolog-blog.ru флеболога. Профессиональное лечение варикоза ног. Склеротерапия, ЭВЛО, УЗИ вен и точная диагностика. Современные безболезненные методики, быстрый результат и забота о вашем здоровье!
purebred kittens for sale in NY https://catsdogs.us
Проблемы с откачкой? электрическая помпа для откачки воды сдаем в аренду мотопомпы и вакуумные установки: осушение котлованов, подвалов, септиков. Производительность до 2000 л/мин, шланги O50–100. Быстрый выезд по городу и области, помощь в подборе. Суточные тарифы, скидки на долгий срок.
Нужна презентация? нейросеть для презентаций бесплатно Создавайте убедительные презентации за минуты. Умный генератор формирует структуру, дизайн и иллюстрации из вашего текста. Библиотека шаблонов, фирстиль, графики, экспорт PPTX/PDF, совместная работа и комментарии — всё в одном сервисе.
cocaine in prague columbian cocain in prague
Adoro o brilho de BetorSpin Casino, parece uma explosao cosmica de adrenalina. As opcoes de jogo no cassino sao ricas e brilhantes como estrelas, oferecendo sessoes de cassino ao vivo que reluzem como supernovas. O atendimento ao cliente do cassino e uma estrela-guia, garantindo suporte de cassino direto e sem buracos negros. Os ganhos do cassino chegam voando como um asteroide, mas mais bonus regulares no cassino seria intergalactico. Na real, BetorSpin Casino garante uma diversao de cassino que e uma supernova para os amantes de cassinos online! De bonus a plataforma do cassino brilha com um visual que e puro cosmos, torna a experiencia de cassino uma viagem espacial.
betorspin velkomstbonus|
Je suis totalement envoute par Stake Casino, on dirait un cratere bouillonnant de fun. Les options de jeu au casino sont riches et volcaniques, proposant des slots de casino a theme explosif. Le service client du casino est une flamme vive, offrant des solutions claires et instantanees. Les paiements du casino sont securises et fluides, quand meme j’aimerais plus de promotions de casino qui envoient du feu. Globalement, Stake Casino offre une experience de casino incandescente pour les amoureux des slots modernes de casino ! Bonus la navigation du casino est intuitive comme une flamme, amplifie l’immersion totale dans le casino.
forum stake|
Sou louco pelo feitico de SpinGenei Casino, tem uma vibe de jogo tao magica quanto um tapete voador. O catalogo de jogos do cassino e um bau de tesouros misticos, com jogos de cassino perfeitos pra criptomoedas. O atendimento ao cliente do cassino e um feitico de eficiencia, respondendo mais rapido que um estalar de dedos. Os ganhos do cassino chegam voando como uma lampada magica, as vezes as ofertas do cassino podiam ser mais generosas. Na real, SpinGenei Casino garante uma diversao de cassino que e magica para os viciados em emocoes de cassino! De lambuja o site do cassino e uma obra-prima de estilo mistico, eleva a imersao no cassino a um nivel magico.
spingenie bonus|
Je suis completement envoute par Riviera Casino, ca vibre avec une energie de casino sophistiquee. L’eventail de jeux du casino est une veritable Riviera de delices, comprenant des jeux de casino adaptes aux cryptomonnaies. Le service client du casino est une etoile du littoral, joignable par chat ou email. Les gains du casino arrivent a une vitesse de yacht, quand meme j’aimerais plus de promotions de casino qui eblouissent comme le soleil. Dans l’ensemble, Riviera Casino offre une experience de casino luxueuse pour les amoureux des slots modernes de casino ! En plus la navigation du casino est intuitive comme une promenade cotiere, amplifie l’immersion totale dans le casino.
casino la riviera sister sites|
Adoro o charme de SpellWin Casino, tem uma vibe de jogo tao fascinante quanto um grimorio antigo. A selecao de titulos do cassino e um caldeirao de emocoes, com jogos de cassino perfeitos pra criptomoedas. A equipe do cassino entrega um atendimento que e puro encantamento, garantindo suporte de cassino direto e sem maldicoes. Os saques no cassino sao velozes como um feitico de teletransporte, mas as ofertas do cassino podiam ser mais generosas. Em resumo, SpellWin Casino e um cassino online que e um portal de diversao para os amantes de cassinos online! Alem disso a interface do cassino e fluida e brilha como uma pocao reluzente, faz voce querer voltar ao cassino como num desejo concedido.
spellwin casino opinie|
https://finance-info.ru/
Аренда авто аэропорт Краснодар
pure cocaine in prague prague drugstore
buy xtc prague plug in prague
Hello there I am so thrilled I found your web site, I really found you by mistake, while I was searching on Aol for something else, Anyhow I am here now and would just like to say kudos for a incredible post and a all round thrilling blog (I also love the theme/design), I don’t have time to browse it all at the minute but I have saved it and also included your RSS feeds, so when I have time I will be back to read more, Please do keep up the excellent job.
радиаторы Tubog
buy cocaine in telegram cocaine prague
prague drugs buy mdma prague
Проблемы с откачкой? водяной насос для откачки воды сдаем в аренду мотопомпы и вакуумные установки: осушение котлованов, подвалов, септиков. Производительность до 2000 л/мин, шланги O50–100. Быстрый выезд по городу и области, помощь в подборе. Суточные тарифы, скидки на долгий срок.
Нужна презентация? нейросеть для презентаций Создавайте убедительные презентации за минуты. Умный генератор формирует структуру, дизайн и иллюстрации из вашего текста. Библиотека шаблонов, фирстиль, графики, экспорт PPTX/PDF, совместная работа и комментарии — всё в одном сервисе.
Sunny coin 2 hold the spin slot free play sınamaq üçün gözəldir. Sunny Coin Hold The Spin onlayn casino seçimləri arasında öndədir.
Sunny coin hold the spin slot online casino üçün ideal seçimdir. Sunny Coin 2: Hold The Spin slotunda bonus raundları maraqlıdır.
Rəsmi səhifə burada https://sunny-coin.com.az/.
Sunny coin: hold the spin slot maraqlı mexanikaya malikdir. Sunny Coin Hold The Spin oyunu sürətli və maraqlıdır. Sunny Coin Hold The Spin demo versiyası sürətlidir.
Sunny coin: hold the spin slot istifadəçi dostudur. Sunny coin: hold the spin slot təcrübəsi həyəcanlıdır.
https://shorturl.fm/YsCEs
broodbase I always admire their originality, quality, and consistent professional service.
Estou alucinado com BetorSpin Casino, oferece uma aventura de cassino que orbita como um cometa reluzente. As opcoes de jogo no cassino sao ricas e brilhantes como estrelas, com slots de cassino tematicos de espaco sideral. O suporte do cassino ta sempre na ativa 24/7, respondendo mais rapido que uma explosao de raios gama. O processo do cassino e limpo e sem turbulencia cosmica, mas mais recompensas no cassino seriam um diferencial astronomico. Em resumo, BetorSpin Casino garante uma diversao de cassino que e uma supernova para os astronautas do cassino! Vale dizer tambem a interface do cassino e fluida e reluz como uma constelacao, o que torna cada sessao de cassino ainda mais estelar.
betorspin estГєdio|
Ich finde absolut elektrisierend SportingBet Casino, es pulsiert mit einer dynamischen Casino-Energie. Es gibt eine Welle an mitrei?enden Casino-Titeln, mit einzigartigen Casino-Slotmaschinen. Das Casino-Team bietet Unterstutzung, die wie ein Volltreffer glanzt, ist per Chat oder E-Mail erreichbar. Casino-Transaktionen sind simpel wie ein Freisto?, ab und zu wurde ich mir mehr Casino-Promos wunschen, die wie ein Sieg jubeln. Alles in allem ist SportingBet Casino ein Muss fur Casino-Fans fur Fans moderner Casino-Slots! Und au?erdem das Casino-Design ist ein optisches Stadion-Spektakel, den Spielspa? im Casino auf das Spielfeld hebt.
sportingbet legal|
Estou completamente alucinado por SpinSala Casino, da uma energia de cassino que e puro brilho estelar. O catalogo de jogos do cassino e um espetaculo de fogos, oferecendo sessoes de cassino ao vivo que brilham como refletores. O servico do cassino e confiavel e cheio de brilho, acessivel por chat ou e-mail. O processo do cassino e limpo e sem sombras, mesmo assim mais bonus regulares no cassino seria brabo. Em resumo, SpinSala Casino garante uma diversao de cassino que e uma explosao de cores para os viciados em emocoes de cassino! Alem disso a navegacao do cassino e facil como uma coreografia de luzes, o que torna cada sessao de cassino ainda mais iluminada.
spinsala avis|
Adoro o delirio de SupaBet Casino, tem uma vibe de jogo tao intensa quanto uma correnteza selvagem. As opcoes de jogo no cassino sao ricas e avassaladoras, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e brilha como uma supernova, garantindo suporte de cassino direto e sem tremores. Os pagamentos do cassino sao lisos e blindados, as vezes as ofertas do cassino podiam ser mais generosas. No geral, SupaBet Casino garante uma diversao de cassino que e uma explosao total para os super-herois do cassino! Alem disso o site do cassino e uma obra-prima de estilo avassalador, torna a experiencia de cassino um evento sismico.
supabet portugal|
Sunny coin 2 hold the spin slot free play sınamaq üçün gözəldir. Sunny coin 2 hold the spin slot oynamaq çox asandır.
Sunny coin 2 hold the spin slot strategiyaları öyrənməyə dəyər. Sunny Coin Hold The Spin real pul üçün çox faydalıdır.
Oyuna giriş ünvanı http://www.sunny-coin.com.az.
Sunny coin hold the spin slot online demo çox istifadəlidir. Sunny coin 2 hold the spin slot demo rahat giriş imkanı yaradır. Sunny coin 2 hold the spin slot istifadəçilərin sevimlisidir.
Sunny coin hold the spin slot dizaynı çox rəngarəngdir. Sunny coin hold the spin slot oynamaq çox rahatdır.
Sou louco pela energia de SupremaBet Casino, da uma energia de cassino que e puro dominio. A selecao de titulos do cassino e um trono de prazeres, com jogos de cassino perfeitos pra criptomoedas. O atendimento ao cliente do cassino e um decreto de eficiencia, com uma ajuda que brilha como uma coroa. Os ganhos do cassino chegam voando como um falcao real, mesmo assim mais bonus regulares no cassino seria supremo. No fim das contas, SupremaBet Casino oferece uma experiencia de cassino que e puro cetro para os apaixonados por slots modernos de cassino! Alem disso a navegacao do cassino e facil como um decreto real, eleva a imersao no cassino a um nivel imperial.
supremabet Г© confiГЎvel|
Maraqlı dizayn və yüksək RTP ilə Sunny Coin Hold The Spin fərqlənir. Sunny Coin 2: hold the spin demo rahat və əlçatandır.
Sunny coin: hold the spin slot RTP yüksək olduğu üçün sevilir. Sunny Coin 2: Hold The Spin slotunda bonus raundları maraqlıdır.
Əlavə üstünlükləri öyrən sunny-coin com az.
Sunny coin hold the spin slot online demo çox istifadəlidir. Sunny coin: hold the spin slot şanslı oyunçular üçün əladır. Sunny coin: hold the spin slot RTP səviyyəsi yüksəkdir.
Sunny coin 2 hold the spin slot real pul ilə uğurludur. Sunny Coin Hold The Spin casino slotları içində fərqlənir.
Sunny coin 2: hold the spin ilə şansınızı sınayın. Sunny coin hold the spin oyna və pulsuz fırlanmaları yoxla.
Sunny coin 2 hold the spin slot strategiyaları öyrənməyə dəyər. Sunny coin hold the spin slot oyunçular tərəfindən tövsiyə olunur.
Daha ətraflı məlumatı buradan tapa bilərsiniz Sunny coin 2 hold the spin slot.
Sunny coin hold the spin demo oyna, risk olmadan öyrən. Sunny coin: hold the spin slot şanslı oyunçular üçün əladır. Sunny coin hold the spin slot online rahat oynanır.
Sunny Coin Hold The Spin pulsuz demo çox faydalıdır. Sunny Coin Hold The Spin slotu yeni istifadəçiləri cəlb edir.
Трансы Екатеринбург Трансы Екатеринбург
Проблемы с откачкой? https://otkachka-vody.ru сдаем в аренду мотопомпы и вакуумные установки: осушение котлованов, подвалов, септиков. Производительность до 2000 л/мин, шланги O50–100. Быстрый выезд по городу и области, помощь в подборе. Суточные тарифы, скидки на долгий срок.
buy xtc prague pure cocaine in prague
buy cocaine in telegram coke in prague
prague drugs high quality cocaine in prague
Sunny Coin Hold The Spin slotu haqqında çox müsbət rəylər eşitmişəm. Sunny Coin 2: hold the spin demo rahat və əlçatandır.
Sunny coin 2 hold the spin ilə uğurlu nəticələr mümkündür. Sunny coin 2 hold the spin slot qazancları maraqlı edir.
Həqiqi qazanc üçün daxil olun Sunny coin 2 hold the spin online.
Sunny Coin 2 hold the spin slot bonus imkanları çox genişdir. Sunny coin 2 hold the spin slot oyunçu rəyləri çox müsbətdir. Sunny coin 2 hold the spin slot istifadəçilərin sevimlisidir.
Sunny Coin Hold The Spin pulsuz demo çox faydalıdır. Sunny Coin Hold The Spin casino slotları içində fərqlənir.
rasecurities These platforms showcase reliability, innovation, and genuine dedication to success.
Попробуйте https://wonderfulperuexperience.com/what-should-a-woman-bring-to-machu-picchu/?unapproved=17226&moderation-hash=ff29319661eb07c04e8ef917bc0c04d0
cocaine prague buy cocaine in telegram
Zivjeti u Crnoj Gori? https://www.placevi-zabljak-nekretnine.com Novi apartmani, gotove kuce, zemljisne parcele. Bez skrivenih provizija, trzisna procjena, pregovori sa vlasnikom. Pomoci cemo da otvorite racun, zakljucite kupoprodaju i aktivirate servis izdavanja. Pisite — poslacemo vam varijante.
https://shorturl.fm/h1OLU
Смотрите онлайн песни для детей слушать онлайн или скачать лучшие детские мультфильмы, сказки и мульсериалы. Добрые истории, веселые приключения и любимые герои для малышей и школьников. Удобный поиск, качественное видео и круглосуточный доступ без ограничений.
Портал о строительстве https://gidfundament.ru и ремонте: обзоры материалов, сравнение цен, рейтинг подрядчиков, тендерная площадка, сметные калькуляторы, образцы договоров и акты. Актуальные ГОСТ/СП, инструкции, лайфхаки и готовые решения для дома и бизнеса.
Bu gün sunny coin hold the spin oynadım və xoş təəssürat qaldı. Sunny coin: hold the spin slot bonusları çox maraqlıdır.
Sunny coin 2 hold the spin slot free play rahat seçimdir. Sunny Coin Hold The Spin slotu yüksək keyfiyyətli qrafikaya malikdir.
Bütün detallar üçün baxın sunny-coin.com.az/.
Sunny Coin Hold The Spin oyunu həm pulsuz, həm də real pul üçündür. Sunny Coin 2 hold the spin slot real qələbə gətirə bilər. Sunny Coin Hold The Spin böyük qazanclar üçün əlverişlidir.
Sunny coin hold the spin demo sınamağa dəyər. Sunny Coin Hold The Spin casino slotları içində fərqlənir.
Всё о ремонте https://remontkit.ru и строительстве: технологии, нормы, сметы, каталоги материалов и инструментов. Дизайн-идеи для квартиры и дома, цветовые схемы, 3D-планы, кейсы и ошибки. Подрядчики, прайсы, калькуляторы и советы экспертов для экономии бюджета.
Мир гаджетов https://indevices.ru новости, обзоры и тесты смартфонов, ноутбуков, наушников и умного дома. Сравнения, рейтинги автономности, фото/видео-примеры, цены и акции. Поможем выбрать устройство под задачи и бюджет. Подписка на новые релизы.
Все автоновинки https://myrexton.ru премьеры, тест-драйвы, характеристики, цены и даты продаж. Электромобили, гибриды, кроссоверы и спорткары. Фото, видео, сравнения с конкурентами, конфигуратор и уведомления о старте приема заказов.
Женский портал https://art-matita.ru о жизни и балансе: модные идеи, уход за кожей и волосами, здоровье, йога и фитнес, отношения и семья. Рецепты, чек-листы, антистресс-практики, полезные сервисы и календарь событий.
Sou louco pela energia de BRCasino, oferece uma aventura de cassino que pulsa como um pandeiro. O catalogo de jogos do cassino e uma folia de emocoes, com slots de cassino tematicos de festa. O atendimento ao cliente do cassino e uma bateria de responsa, acessivel por chat ou e-mail. O processo do cassino e limpo e sem tropecos, mas mais giros gratis no cassino seria uma loucura. No fim das contas, BRCasino garante uma diversao de cassino que e um carnaval total para os apaixonados por slots modernos de cassino! E mais a interface do cassino e fluida e reluz como uma fantasia de carnaval, adiciona um toque de folia ao cassino.
br77.gamer|
Adoro o frenesi de AFun Casino, tem uma vibe de jogo tao vibrante quanto um desfile de cores. Tem uma enxurrada de jogos de cassino irados, com caca-niqueis de cassino modernos e contagiantes. O suporte do cassino ta sempre na ativa 24/7, acessivel por chat ou e-mail. O processo do cassino e limpo e sem tumulto, mas mais giros gratis no cassino seria uma loucura. Na real, AFun Casino vale demais curtir esse cassino para os folioes do cassino! Vale dizer tambem a navegacao do cassino e facil como uma coreografia, o que torna cada sessao de cassino ainda mais animada.
afun apostas esportivas plataforma de cassino online|
Je trouve absolument brulant VBet Casino, ca degage une ambiance de jeu aussi ardente qu’une coulee de lave. Les options de jeu au casino sont riches et enflammees, incluant des jeux de table de casino d’une elegance ardente. Le service client du casino est une torche d’efficacite, avec une aide qui jaillit comme une flamme. Les paiements du casino sont securises et fluides, mais des recompenses de casino supplementaires feraient exploser. Globalement, VBet Casino est un casino en ligne qui eclate comme un volcan pour ceux qui cherchent l’adrenaline enflammee du casino ! En plus la plateforme du casino brille par son style volcanique, donne envie de replonger dans le casino sans fin.
vbet pix|
Ich bin suchtig nach Trickz Casino, es ist ein Online-Casino, das wie ein Zauberstab funkelt. Die Casino-Optionen sind vielfaltig und verzaubernd, inklusive stilvoller Casino-Tischspiele. Der Casino-Service ist zuverlassig und verhext, antwortet blitzschnell wie ein magischer Funke. Casino-Zahlungen sind sicher und reibungslos, dennoch mehr Casino-Belohnungen waren ein zauberhafter Gewinn. Am Ende ist Trickz Casino ein Casino mit einem Spielspa?, der wie eine Illusion verblufft fur Spieler, die auf magische Casino-Kicks stehen! Nebenbei die Casino-Oberflache ist flussig und funkelt wie ein Zauberstab, den Spielspa? im Casino auf ein magisches Niveau hebt.
trickz casino recension|
Maraqlı dizayn və yüksək RTP ilə Sunny Coin Hold The Spin fərqlənir. Sunny Coin 2 hold the spin slot real pul ilə daha həyəcanlıdır.
Sunny coin: hold the spin slot RTP yüksək olduğu üçün sevilir. Sunny coin 2 hold the spin slot oynamadan əvvəl demo sınayın.
Əlavə məlumat üçün bax http://sunny-coin.com.az/.
Sunny Coin Hold The Spin oyunu həm pulsuz, həm də real pul üçündür. Sunny coin hold the spin slot bonus raundları çox cəlbedicidir. Sunny coin hold the spin oyna və yeni imkanlar kəşf et.
Sunny coin hold the spin demo sınamağa dəyər. Sunny coin 2 hold the spin slot online çox məşhurdur.
Новостной портал https://daily-inform.ru главные события дня, репортажи, аналитика, интервью и мнения экспертов. Лента 24/7, проверка фактов, региональные и мировые темы, экономика, технологии, спорт и культура.
Всё о стройке https://lesnayaskazka74.ru и ремонте: технологии, нормы, сметы и планирование. Каталог компаний, аренда техники, тендерная площадка, прайс-мониторинг. Калькуляторы, чек-листы, инструкции и видеоуроки для застройщиков, подрядчиков и частных мастеров.
Актуальные новости https://pr-planet.ru без лишнего шума: политика, экономика, общество, наука, культура и спорт. Оперативная лента 24/7, инфографика,подборки дня, мнения экспертов и расследования.
Строительный портал https://nastil69.ru новости, аналитика, обзоры материалов и техники, каталог поставщиков и подрядчиков, тендеры и прайсы. Сметные калькуляторы, ГОСТ/СП, шаблоны договоров, кейсы и лайфхаки.
Ремонт и стройка https://stroimsami.online без лишних затрат: гайды, сметы, план-графики, выбор подрядчика и инструмента. Честные обзоры, сравнения, лайфхаки и чек-листы. От отделки до инженерии — поможем спланировать, рассчитать и довести проект до результата.
відкоси на вікна ціна https://remontuem.te.ua
What’s up, I want to subscribe for this webpage to take latest updates, thus where can i do it please assist.
корпус для авто фар
Acho simplesmente sensacional BacanaPlay Casino, tem uma vibe de jogo tao animada quanto uma bateria de escola de samba. As opcoes de jogo no cassino sao ricas e cheias de gingado, incluindo jogos de mesa de cassino com um toque de folia. O servico do cassino e confiavel e cheio de swing, dando solucoes na hora e com precisao. Os saques no cassino sao velozes como um carro alegorico, as vezes mais giros gratis no cassino seria uma loucura. Na real, BacanaPlay Casino e um cassino online que e uma folia sem fim para os amantes de cassinos online! De bonus o site do cassino e uma obra-prima de estilo carioca, eleva a imersao no cassino ao ritmo de um tamborim.
casino bacanaplay|
Ich liebe den Adrenalinkick von Turbonino Casino, es fuhlt sich an wie ein Hochgeschwindigkeitsrennen. Die Spielauswahl im Casino ist wie eine Hochgeschwindigkeitsstrecke, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Das Casino-Team bietet Unterstutzung, die wie ein Turbo-Motor lauft, antwortet blitzschnell wie ein Rennstart. Casino-Zahlungen sind sicher und reibungslos, aber die Casino-Angebote konnten gro?zugiger sein. Zusammengefasst ist Turbonino Casino eine Casino-Erfahrung, die wie ein Uberholmanover glanzt fur Spieler, die auf rasante Casino-Kicks stehen! Extra die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino auf die Pole-Position hebt.
turbonino casino promo code|
Ich bin suchtig nach Tipico Casino, es fuhlt sich an wie ein Sturm aus Gewinnen. Es gibt eine Flut an packenden Casino-Titeln, mit einzigartigen Casino-Slotmaschinen. Das Casino-Team bietet Unterstutzung, die wie ein Donner glanzt, liefert klare und schnelle Losungen. Auszahlungen im Casino sind schnell wie ein Blitzschlag, ab und zu die Casino-Angebote konnten gro?zugiger sein. Kurz gesagt ist Tipico Casino ein Online-Casino, das wie ein Sturm begeistert fur Abenteurer im Casino! Nebenbei die Casino-Plattform hat einen Look, der wie ein Blitz funkelt, den Spielspa? im Casino in die Hohe treibt.
tipico live ergebnis fussball|
Estou alucinado com BetorSpin Casino, da uma energia de cassino que e puro pulsar galactico. As opcoes de jogo no cassino sao ricas e brilhantes como estrelas, oferecendo sessoes de cassino ao vivo que reluzem como supernovas. Os agentes do cassino sao rapidos como um foguete estelar, acessivel por chat ou e-mail. Os ganhos do cassino chegam voando como um asteroide, mas queria mais promocoes de cassino que explodem como supernovas. Na real, BetorSpin Casino e um cassino online que e uma galaxia de diversao para os amantes de cassinos online! De lambuja o site do cassino e uma obra-prima de estilo estelar, adiciona um toque de brilho estelar ao cassino.
betorspin bonuskode|
значки металл производство изготовление значков на заказ москва москва
изготовление значков на заказ москва москва значки с логотипом
изготовление металлических значков на заказ заказать значки со своим дизайном
Hi there, its good piece of writing on the topic of media print, we all understand media is a enormous source of facts.
маркетплейс kraken
Советую http://smartliving.digital/2023/12/11/altivar-process-iot-faehig-und-datenintelligent/
накрутка подписчиков тг
Je suis fou de Unibet Casino, on dirait une melodie envoutante de gains. Il y a une vague de jeux de casino captivants, avec des machines a sous de casino modernes et vibrantes. Les agents du casino sont rapides comme une note staccato, assurant un support de casino immediat et vibrant. Les retraits au casino sont rapides comme un tempo allegro, parfois j’aimerais plus de promotions de casino qui vibrent comme un orchestre. En somme, Unibet Casino promet un divertissement de casino vibrant pour les amoureux des slots modernes de casino ! A noter la navigation du casino est intuitive comme une partition, amplifie l’immersion totale dans le casino.
unibet 10 euros offert|
Acho simplesmente alucinante Bet4Slot Casino, e um cassino online que roda como um carrossel enlouquecido. O catalogo de jogos do cassino e um redemoinho de emocoes, com jogos de cassino perfeitos pra criptomoedas. O atendimento ao cliente do cassino e uma engrenagem de eficiencia, com uma ajuda que roda como uma roda-gigante. Os pagamentos do cassino sao lisos e blindados, as vezes mais giros gratis no cassino seria uma loucura. Resumindo, Bet4Slot Casino oferece uma experiencia de cassino que e puro giro para os apaixonados por slots modernos de cassino! Vale dizer tambem o design do cassino e um espetaculo visual giratorio, eleva a imersao no cassino ao ritmo de uma roda-gigante.
como funciona o aplicativo bet4slot|
Estou alucinado com BetorSpin Casino, parece uma explosao cosmica de adrenalina. O catalogo de jogos do cassino e uma nebulosa de emocoes, incluindo jogos de mesa de cassino com um toque intergalactico. O atendimento ao cliente do cassino e uma estrela-guia, garantindo suporte de cassino direto e sem buracos negros. Os saques no cassino sao velozes como uma viagem interestelar, mas mais bonus regulares no cassino seria intergalactico. Em resumo, BetorSpin Casino e um cassino online que e uma galaxia de diversao para quem curte apostar com estilo estelar no cassino! De lambuja o site do cassino e uma obra-prima de estilo estelar, eleva a imersao no cassino a um nivel cosmico.
betorspin reclame aqui|
I’m obsessed with the vibe of Wazamba Casino, it radiates a gaming vibe as untamed as a tropical storm. Its collection is a canopy of thrilling entertainment, including classy casino table games with a tribal flair. Its agents are as swift as a cheetah on the hunt, ensuring immediate casino support as bold as a warrior. Casino withdrawals are as fast as a jungle sprint, however more frequent casino bonuses would be epic. To sum up, Wazamba Casino promises casino entertainment that’s untamed for casino adventurers! By the way the casino interface is smooth and vibrant like a tropical sunrise, amplifying total immersion in the casino.
wazamba kaszinГі bГіnusz|
Je suis accro a Tortuga Casino, on dirait une ile au tresor pleine de frissons. Il y a une deferlante de jeux de casino captivants, avec des machines a sous de casino modernes et envoutantes. Les agents du casino sont rapides comme un vent de tempete, joignable par chat ou email. Les paiements du casino sont securises et fluides, par moments des bonus de casino plus frequents seraient epiques. Au final, Tortuga Casino offre une experience de casino audacieuse pour ceux qui cherchent l’adrenaline des mers du casino ! Bonus la plateforme du casino brille par son style audacieux, donne envie de replonger dans le casino sans fin.
tortuga casino vГ©rification|
https://shorturl.fm/YoZFN
Принты на футболку для мужчин и надпись на футболке беременной в Пскове. Печать на толстовке и оверсайз толстовка в Красноярске. Футболки на заказ с фамилиями и футболки с надписью черные в Набережных Челнах. Упаковка меда в ложку и дипломат мужской одежды интернет в Череповце. Печать на футболках оптом новослободская и надпись на футболку сестры https://futbolki-s-printom.ru/
изготовление металлических значков сделать свой значок
изготовление штампованных и металлических значков фирменные значки
значки с логотипом цена печать на значках москва
живые подписчики в телеграм без отписки
Одежда футболки с принтом и крутые футболки мужские с принтом в Калуге. Свитшот мужской в интернет и толстовка из флиса для мальчика во Владимире. Футболка поло вектор и черные футболки для сублимации в Суздале. Оптовая продажа подарочной упаковки и упаковка торг в Таганроге. Надписи на футболку оптом про рыбалку и футболка женская с длинным рукавом хлопок: принт на спине футболка оптом
Футболку на заказ Пермь и футболки на заказ со свой надписью в Хабаровске. Терракотовый шарф и засекреченная шапка в Перми. Печать на футболках мира и надписи на футболках парные прикольные в Севастополе. Дима и алиса детская одежда и выпускной в детском саду одежда для мальчика в Кирове. Футболка оптом Doom и парные футболки в рб https://futbolki-s-printom.ru/
Очень советую http://kghpgafwebpin.mex.tl/?gb=1#top
Футболка обезьяна и размер футболки 52 в Кургане. Черно белая толстовка и красивый шарф в Нальчике. Мужская футболка с надписью на заказ и принт на футболке Москва в Хабаровске. Тока бока человечки с одеждой и одежда стрела в Череповце. Футболка оптом с пятнами и футболка полиэстер: надписи на футболках бабушке оптом
живые активные подписчики в тг
Футболки с принтом Севастополя и печать на футболку Чебоксары в Красноярске. Шапка женская демисезонная и из какой ткани шьют худи в Братске. Порванная футболка и футболка архангел михаил в Петрозаводске. Подарочные упаковки и пакетики для упаковки подарков маленькие в Стерлитамаке. Рисуем принт на футболке оптом и ваши надписи на футболки: https://futbolki-s-printom.ru/
joszaki regisztracio joszaki
joszaki regisztracio http://joszaki.hu
Hi to all, the contents present at this web page are in fact awesome for people knowledge, well, keep up the good work fellows.
kra40 at
joszaki regisztracio http://joszaki.hu
joszaki regisztracio https://joszaki.hu/
joszaki regisztracio joszaki.hu/
живые подписчики в телеграм
накрутка подписчиков в тг бесплатно за задания
как накрутить подписчиков в телеграм бот
https://shorturl.fm/2kIUa
Me encantei pelo ronco de F12.Bet Casino, tem um ritmo de jogo que derrapa como um drift. As opcoes sao ricas e aceleram como turbo. oferecendo sessoes ao vivo que derrapam como drifts. O atendimento esta sempre ativo 24/7. assegurando apoio sem derrapagens. Os saques sao velozes como um pit stop. ocasionalmente as ofertas podiam ser mais generosas. Ao final, F12.Bet Casino e o point perfeito pros fas de cassino para os exploradores de jogos online! E mais o design e fluido como um pit stop. adicionando um toque de velocidade ao cassino.
f12 bet Г© regulamentada|
Galera, vim dividir minhas impressoes no 4PlayBet Casino porque me impressionou bastante. A variedade de jogos e simplesmente incrivel: jogos ao vivo imersivos, todos sem travar. O suporte foi amigavel, responderam em minutos pelo chat, algo que faz diferenca. Fiz saque em Bitcoin e o dinheiro entrou em minutos, ponto fortissimo. Se tivesse que criticar, diria que seria legal torneios de slots, mas isso nao estraga a experiencia. Pra concluir, o 4PlayBet Casino e completo. Recomendo sem medo.
4play motorsports|
Sou louco pela vibracao de BR4Bet Casino, oferece uma aventura que brilha como um candelabro em chamas. Tem uma enxurrada de jogos de cassino irados. com caca-niqueis modernos que encantam como lanternas. O suporte e um facho reluzente. respondendo veloz como uma chama acesa. Os saques sao velozes como um clarao. mesmo assim mais bonus regulares seriam radiantes. Em resumo, BR4Bet Casino oferece uma experiencia que e puro brilho para os exploradores de jogos online! E mais o design e um espetaculo visual iluminado. amplificando o jogo com vibracao luminosa.
br4bet oficial|
накрутка подписчиков в тг канал
как накрутить подписчиков в тг канале живых
Очень понравился сервис, все четко и без лишних вопросов. Девушка красивая, ухоженная, настоящий профессионал. Вечер удался на все сто. Советую, проститутка недорого Новосибирск – https://sibirki3.vip/. Массаж был волшебный, эмоции зашкаливали.
Очень советую https://bmp-045.ru/zapasnie-chasti/katalog-zapchastey-snegobolotochoda-vezdechoda-sm-552-01/33-sm552-51-sb1-5-l
накрутка подписчиков в тг канал живые бесплатно
онлайн накрутка подписчиков в тг канал
joszaki regisztracio https://joszaki.hu/
suzgilliessmith – I really enjoyed browsing this site; feels personal and well done.
накрутка подписчиков в тг канал живые бесплатно
купить подписчиков в телеграм
накрутка подписчиков тг
https://dzen.ru/110km
накрутка подписчиков тг
накрутка премиум подписчиков тг
Adoro a labareda de Fogo777 Casino, pulsa com uma forca de cassino digna de um xama. As escolhas sao vibrantes como chamas. com slots tematicos de cerimonias antigas. Os agentes voam como chamas. disponivel por chat ou e-mail. O processo e claro e sem fumaca. porem queria promocoes que explodem como labaredas. Em resumo, Fogo777 Casino garante um jogo que reluz como chamas para os apaixonados por slots modernos! Como extra o site e uma obra-prima de estilo ardente. transformando cada aposta em uma aventura flamejante.
plataforma fogo777 fogo777|
Sou viciado no codigo de PlayPix Casino, tem uma energia de jogo tao vibrante quanto um codigo binario em furia. O leque do cassino e uma matriz de delicias. com slots tematicos de mundos digitais. O atendimento esta sempre ativo 24/7. garantindo suporte direto e sem lag. As transacoes sao simples como um pixel. ocasionalmente as ofertas podiam ser mais generosas. Na real, PlayPix Casino oferece uma experiencia que e puro codigo para os apaixonados por slots modernos! Vale dizer o design e um espetaculo visual de matriz. adicionando um toque de codigo ao cassino.
saque na playpix|
Je trouve absolument enivrant BankOnBet Casino, c’est un casino en ligne qui brille comme un coffre-fort de lingots. The game lineup is a fortune of thrills. incluant des jeux de table de casino d’une elegance bancaire. The support is as solid as a vault door. avec une aide qui debloque les gains. Les transactions du casino sont simples comme un depot. however plus de tours gratuits au casino ce serait un investissement. Dans l’ensemble, BankOnBet Casino is a casino that banks on fun pour les investisseurs du casino! A noter la plateforme du casino brille par son style rentable. transformant les mises en fortunes.
bankonbet|
https://shorturl.fm/zAmlL
накрутка подписчиков в тг за задания
купить подписчиков в телеграм канал
накрутка подписчиков телеграм бесплатно задания
https://device-rf.ru/catalog/iphone/
Предлагаю http://pax222.blog.fc2.com/blog-entry-1052.html
накрутка подписчиков в телеграм канал
This text is worth everyone’s attention. How can I find out more?
Vegastars casino
Acho simplesmente enredado IJogo Casino, e um cassino online que enreda como uma teia de aranha gigante. A colecao e uma teia de entretenimento. incluindo mesas com charme de labirinto. O suporte e um fio guia. oferecendo respostas claras como um labirinto resolvido. As transacoes sao faceis como um emaranhado. as vezes queria promocoes que se entrelacam como raizes. Em resumo, IJogo Casino e um enredo de emocoes para os amantes de cassinos online! Como extra o site e uma obra-prima de estilo selvagem. adicionando um toque de emaranhado ao cassino.
como usar bonus ijogo|
J’adore le mystere de Casinia Casino, il propose une aventure de casino qui resonne comme un conte ancien. L’assortiment de jeux du casino est un rempart de delices. avec des slots qui resonnent comme des epees. est un virtuose de la noblesse. avec une aide qui brille comme une couronne. Les retraits au casino sont rapides comme un assaut. cependant j’aimerais plus de promotions de casino qui brillent comme des joyaux royaux. Dans l’ensemble, Casinia Casino enchante avec une rhapsodie de jeux pour ceux qui cherchent l’adrenaline royale du casino! Ajoutons le design du casino est une fresque visuelle chevaleresque. ajoute une touche de grandeur au casino.
casinia retrait|
Acho simplesmente harmonico Stake Casino, pulsa com uma forca de cassino digna de um sino. A selecao de titulos e um eco de emocoes. incluindo jogos de mesa com um toque harmonico. O atendimento e solido como uma corda. garantindo suporte direto e sem silencio. Os saques vibram como harpas. em alguns momentos queria mais promocoes que ressoam como corais. Ao final, Stake Casino garante um jogo que ressoa como um sino para os apaixonados por slots modernos! Adicionalmente o design e fluido como uma onda sonora. fazendo o cassino ecoar como um sino.
stake]|
Je suis charme par Grandz Casino, est une symphonie de divertissement qui effleure. Le repertoire du casino est un theatre de divertissement. offrant des lives qui pulsent comme un theatre. repond comme un fantome gracieux. offrant des solutions claires et instantanees. Les gains du casino arrivent a une vitesse etheree. occasionnellement des bonus de casino plus frequents seraient spectrale. En conclusion, Grandz Casino enchante avec une rhapsodie de jeux pour les amoureux des slots modernes de casino! Par ailleurs le design du casino est une fresque visuelle spectrale. cadence l’aventure avec une rhapsodie spectrale.
grandz race casino en ligne|
Galera, resolvi compartilhar minha experiencia sobre o Bingoemcasa porque me surpreendeu demais. O site tem um jeito leve que lembra um encontro descontraido. As salas de bingo sao movimentadas, e ainda testei a roleta ao vivo, todos vieram com graficos bonitos. O atendimento no chat foi educado e prestativo, o que ja me deixou satisfeito. As retiradas foram muito rapidas, inclusive testei cartao e caiu em minutos. Se pudesse apontar algo, diria que gostaria de ver mais brindes, mas nada que estrague a experiencia. Resumindo, o Bingoemcasa me conquistou. Eu mesmo ja voltei varias vezes
bingoemcasa app|
Unlock your images with WebPtoJPGHero.com, the simple, free solution for solving WebP compatibility issues. While the WebP format helps websites load faster, it can leave you with files you can’t easily edit or share. Our online tool provides an instant fix, transforming any WebP image into a high-quality JPG that works seamlessly across all your devices and applications. You can fine-tune the output quality to balance clarity and file size, and even save time by converting an entire batch of photos at once. It’s all done quickly and privately right in your browser—no software required.
WebPtoJPGHero.com
motocitee – I’d return here to explore more, seems like content worth following.
JPG Hero converter is an online image converter built for speed, simplicity, and accessibility. This web-based platform allows instant conversion of popular image formats such as PNG, WebP, and BMP into JPG files. No downloads, installations, or user accounts are required. The entire process happens in-browser and takes only a few seconds. Users can upload up to 20 files at once for batch conversion, making it suitable for individuals and professionals managing multiple images. All uploaded files are automatically deleted after processing to maintain privacy and ensure data security. JPGHero.com is compatible with all modern devices, including desktops, tablets, and smartphones, offering flexibility for work on the go. Whether the goal is to reduce image file size, prepare visuals for the web, or standardize a project’s image format, this tool delivers clean, reliable results without any extra steps.
JPGHero
JPG Hero converter is an online image converter built for speed, simplicity, and accessibility. This web-based platform allows instant conversion of popular image formats such as PNG, WebP, and BMP into JPG files. No downloads, installations, or user accounts are required. The entire process happens in-browser and takes only a few seconds. Users can upload up to 20 files at once for batch conversion, making it suitable for individuals and professionals managing multiple images. All uploaded files are automatically deleted after processing to maintain privacy and ensure data security. JPGHero.com is compatible with all modern devices, including desktops, tablets, and smartphones, offering flexibility for work on the go. Whether the goal is to reduce image file size, prepare visuals for the web, or standardize a project’s image format, this tool delivers clean, reliable results without any extra steps.
JPGHero
Formula 1 yarışları haqqında ən son xəbərləri burada izləyin. Formula 1 azerbaycan mərhələsi barədə dəqiq xəbərlər.
Yarış təqvimi və nəticələr üçün baxın ➡ formula-1 com az.
Formula 1 izləmək üçün ən sərfəli onlayn xidmətlər. Formula 1 2024 Bakı yarışlarının tarixi artıq məlumdur.
Formula 1 movie həvəskarları üçün tövsiyələr. Formula 1 tickets almaq üçün sərfəli variantlar. Formula 1 izləmə yolları haqqında faydalı təlimatlar. Formula 1 2025 Baku üçün təqvim yenilənib.
подписчики в тг канал
Licensed slots https://lemon-cazino-pl.com
Cricket betting https://betvisabengal.com
Cleaning is needed cleaning toronto eco-friendly supplies, vetted cleaners, flat pricing, online booking, same-day options. Bonded & insured crews, flexible scheduling. Book in 60 seconds—no hidden fees.
Портал Чернівців https://58000.com.ua оперативні новини, анонси культурних, громадських та спортивних подій, репортажі з міста, інтерв’ю з чернівчанами та цікаві історії. Все про життя Чернівців — щодня, просто й доступно
Formula 1 yarışları haqqında ən son xəbərləri burada izləyin. Formula 1 avtomobillərinin texniki göstəricilərini müqayisə edin.
Ən son xəbərləri izləmək üçün baxın ➡ formula 1.
Formula 1 pilotları haqqında ətraflı bioqrafiyalar. Formula 1 Baku 2025 üçün ən maraqlı məlumatlar.
Formula 1 haqqında maraqlı tarixi faktlar. Formula 1 izləmə zamanı texniki məlumatların üstünlükləri. Formula 1 canlı izləmə təcrübənizi paylaşın. Formula 1 puan durumu ilə favorit komandanızı izləyin.
Formula 1 2025 təqvimini öyrənmək istəyənlər üçün faydalı məlumat. Formula 1 avtomobillərinin texniki göstəricilərini müqayisə edin.
Son xəbərləri buradan oxuyun ➡ https://formula-1.com.az.
Formula 1 volunteer 2025 proqramına qoşulmaq üçün şərtlər. Formula 1 puan cədvəli ilə favoritlərinizi izləyin.
Formula 1 takvimi hər mövsüm yenilənir. Formula 1 baku haqqinda melumat axtaranlara məsləhətlər. Formula 1 cars dizaynı və yenilikləri. Formula 1 canlı izləmə platformaları haqqında təcrübələr.
накрутка подписчиков в телеграм недорого
Formula 1 könüllü proqramı haqqında maraqlı məlumatlar burada. Formula 1 avtomobillərinin texniki göstəricilərini müqayisə edin.
Simvol və brend haqqında oxuyun ➡ formula 1 logo.
Formula 1 volunteer 2025 proqramına qoşulmaq üçün şərtlər. Formula 1 puan cədvəli ilə favoritlərinizi izləyin.
Formula 1 movie həvəskarları üçün tövsiyələr. Formula 1 izləmə zamanı texniki məlumatların üstünlükləri. Formula 1 Bakı 2024 nə zaman keçiriləcək. Formula 1 logo simvolikasının mənası barədə məlumat.
сайт для накрутки подписчиков в тг
Крайне советую https://ordbildning.com/2018/12/16/hej-varlden/
накрутка подписчиков в телеграм канал бесплатно
Formula 1 puan durumu daim yenilənir və oyunçular üçün əlçatandır. Formula 1 logo və brendləşmə detallarını kəşf edin.
Əlavə məlumat üçün linkə daxil olun ➡ https://formula-1.com.az.
Formula 1 canli yayım üçün yeni platformalar. Formula 1 2024 Bakı yarışlarının tarixi artıq məlumdur.
Formula 1 2025 calendar üzrə bütün yarış tarixləri. Formula 1 tickets almaq üçün sərfəli variantlar. Formula 1 cars dizaynı və yenilikləri. Formula 1 azerbaycanda keçirilən yarışlar barədə maraqlı faktlar.
накрутка подписчиков в тг живых активных
Estou alucinado com DonaldBet Casino, e um cassino online que reluz como um picadeiro sob holofotes. A selecao de titulos e uma tenda de emocoes. incluindo jogos de mesa com um toque de circo. Os agentes voam como trapezistas. com solucoes precisas e instantaneas. O processo e claro e sem cortinas. mas mais recompensas fariam o coracao saltar. Resumindo, DonaldBet Casino e o point perfeito pros fas de cassino para os amantes de cassinos online! Alem disso a navegacao e facil como um malabarismo. adicionando um toque de magia de circo ao cassino.
donaldbet dono|
Sou louco pela roda de XPBet Casino, parece um vortice de adrenalina giratoria. As escolhas sao vibrantes como um giro. oferecendo lives que explodem como vortices. Os agentes giram como rodas. assegurando apoio sem interrupcoes. As transacoes sao faceis como um vortice. mesmo assim mais recompensas fariam o coracao girar. No fim das contas, XPBet Casino vale explorar esse cassino ja para quem curte apostar com estilo giratorio! De bonus a plataforma reluz com um visual ciclico. elevando a imersao ao nivel de um vortice.
xp games bet|
Adoro a onda sonora de JonBet Casino, tem um ritmo de jogo que ecoa como um coral. A colecao e uma onda sonora de entretenimento. com caca-niqueis que vibram como harpas. O atendimento esta sempre ativo 24/7. assegurando apoio sem dissonancias. Os saques vibram como harpas. mesmo assim mais bonus seriam um diferencial ressonante. No fim das contas, JonBet Casino garante um jogo que ressoa como um sino para os exploradores de jogos online! De bonus o site e uma obra-prima de estilo sonoro. adicionando um toque de eco ao cassino.
jonbet apostas esportivas|
Je suis accro a Boomerang Casino, on dirait un cercle de frissons qui boucle. est une trajectoire de sensations qui enchante. comprenant des jeux de casino adaptes aux cryptomonnaies. L’assistance du casino est chaleureuse et precise. offrant des solutions claires et instantanees. Les transactions du casino sont simples comme un arc. cependant des tours gratuits pour une melodie ricochet. En conclusion, Boomerang Casino enchante avec une rhapsodie de jeux pour les fans de symphonies circulaires! En plus resonne avec une melodie graphique arque. fait vibrer le jeu comme un concerto circulaire.
boomerang casino switzerland|
накрутка подписчиков телеграм бесплатно задания
WebPtoJPGHero converter is an online image converter built for speed, simplicity, and accessibility. This web-based platform allows instant conversion of popular image formats such as PNG, WebP, and BMP into JPG files. No downloads, installations, or user accounts are required. The entire process happens in-browser and takes only a few seconds. Users can upload up to 20 files at once for batch conversion, making it suitable for individuals and professionals managing multiple images. All uploaded files are automatically deleted after processing to maintain privacy and ensure data security. WebPtoJPGHero is compatible with all modern devices, including desktops, tablets, and smartphones, offering flexibility for work on the go. Whether the goal is to reduce image file size, prepare visuals for the web, or standardize a project’s image format, this tool delivers clean, reliable results without any extra steps.
WebPtoJPGHero
Formula 1 izləmək üçün hansı kanalları seçmək barədə tövsiyələr. Bakı Formula 1 xəritəsi üzrə hər bir döngəni tanıyın.
Yarış xəbərləri və nəticələr üçün baxın ➡ formula 1 site.
Formula 1 standings ilə komandaların durumu haqqında fikir. Formula 1 2024 Bakı yarışlarının tarixi artıq məlumdur.
Formula 1 Baku track barədə dəqiq xəritə məlumatı. Formula 1 2025 Baku mərhələsi barədə ən son xəbərlər. Formula 1 Bakı 2024 nə zaman keçiriləcək. Formula 1 canlı izləmə platformaları haqqında təcrübələr.
ahbhos
трип скан Трип Скан – это ваш личный ассистент в мире путешествий. Мы помогаем вам находить выгодные предложения на авиабилеты, отели и другие услуги, необходимые для комфортного отдыха. Наша цель – сделать процесс планирования поездки простым и удобным, чтобы у вас оставалось больше времени на подготовку к приключениям. С TripScan вы можете быть уверены, что получите лучшие цены и качественный сервис. Мы постоянно работаем над улучшением нашего сервиса, чтобы ваше путешествие было незабываемым. Присоединяйтесь к Трип Скан и откройте для себя мир увлекательных путешествий! трип скан
Ремонт iphone 14 Ремонт iPhone: Профессиональный ремонт iPhone любой сложности. Мы предлагаем широкий спектр услуг, начиная от замены экрана и аккумулятора, заканчивая сложным ремонтом материнской платы. Наши квалифицированные специалисты используют только оригинальные запчасти и современное оборудование, что гарантирует высокое качество и долговечность ремонта. Мы оперативно устраним любые неисправности вашего iPhone, будь то повреждение экрана, проблемы с зарядкой или программные сбои. Доверьте свой iPhone профессионалам и наслаждайтесь его безупречной работой! Мы гарантируем качество, скорость и доступные цены.
как набрать подписчиков в тг
Formula 1 puan durumu daim yenilənir və oyunçular üçün əlçatandır. Formula 1 üçün ən yaxşı bilet seçimlərini tapmaq mümkündür.
Pilotlar haqqında geniş məlumat əldə edin ➡ formula 1 drivers.
Formula 1 izləmək üçün ən sərfəli onlayn xidmətlər. Formula 1 cars modellərinin qiymətləri və xüsusiyyətləri.
Formula 1 canlı izləmə üçün şifresiz linklər. Formula 1 baku haqqinda melumat axtaranlara məsləhətlər. Formula 1 movie izləyicilər üçün əyləncəli seçimdir. Formula 1 izləmə təcrübəsini rahatlaşdıran xidmətlər.
школа по английскому языку
Накрутка подписчиков в ТГ
Рекомендую https://firmaindubai.ro/noutati/infiintare-firma-in-free-zone-dubai-media-city-dmc/
накрутка подписчиков в тг бесплатно
Система видеонаблюдения под ключ https://vcctv.ru
Je suis totalement envoute par Casombie, ca transporte dans un monde de chaos ludique. Le catalogue est une crypte de tresors, proposant des paris sportifs qui donnent des frissons. L’assistance est precise comme une incantation, avec une aide aussi fluide qu’un spectre. Les paiements sont securises comme une tombe scellee, cependant plus de promos macabres seraient un plus. En conclusion, Casombie est un must pour les amateurs de sensations fortes pour les aventuriers des cryptos ! En bonus la plateforme brille comme une pleine lune, ce qui rend chaque session electrisante.
casombie casino canada|
Je suis transporte par Freespin Casino, ca propulse dans un vortex de plaisir. Le catalogue est un kaleidoscope de delices, avec des slots aux visuels electrisants. Le support est disponible 24/7, garantissant un support d’une brillance rare. Les gains atterrissent a la vitesse lumiere, neanmoins des bonus plus petillants seraient magiques. Pour resumer, Freespin Casino offre une experience aussi brillante qu’une comete pour les joueurs en quete de magie ludique ! Par ailleurs le design est vibrant comme une galaxie, donne envie de replonger dans l’univers du jeu.
oferte casino cu free spin|
На производстве напитков оборудование Labelaire стало основой системы маркировки. Каждая бутылка получает свою этикетку благодаря термопринтерам. Печать стабильная, а продукция всегда выглядит аккуратно и профессионально – https://labelaire.ru/
Je suis circuite par Robocat Casino, il programme une sequence de recompenses fulgurantes. Il pulse d’une panoplie de prototypes interactifs, incluant des blackjacks pour des reboots tactiques. Le service scanne en continu 24/7, avec un algorithme qui predit les bugs. Les payouts dechargent via Bitcoin ou Ethereum, toutefois les protocoles d’offres pourraient s’optimiser en profondeur. A la fin de ce run, Robocat Casino devoile un pipeline de succes high-tech pour les codeurs des paris crypto ! A logger l’interface est un dashboard navigable avec finesse, amplifie l’engagement dans le grid du jeu.
avis robocat casino|
Je suis accro a Nomini Casino, ca degage une ambiance de jeu aussi etheree qu’un ballet spectral. propose un ballet de divertissement qui seduit. offrant des lives qui pulsent comme un theatre. Les agents du casino sont rapides comme un voile qui s’envole. garantissant une assistance qui cadence. Les gains du casino arrivent a une vitesse etheree. par moments des bonus de casino plus frequents seraient spectrale. Au final, Nomini Casino offre une experience de casino etheree pour les explorateurs de melodies en ligne! Ajoutons la plateforme du casino brille par son style theatral. cadence l’aventure avec une rhapsodie spectrale.
Je suis irremediablement appate par MrPacho Casino, il orchestre une symphonie de gains succulents. La carte est un grimoire de divertissements savoureux, offrant des jackpots progressifs des fournisseurs renommes comme Pragmatic Play. Les hotes interviennent avec une delicatesse remarquable, assurant un accompagnement fidele au banquet. Le rituel est taille pour une onctuosite exemplaire, nonobstant des amuse-bouches gratuits supplementaires rehausseraient les plats. Dans l’ensemble du menu, MrPacho Casino emerge comme un pilier pour les epicuriens pour les gardiens des buffets numeriques ! En primeur l’interface est un chemin de table navigable avec art, pousse a prolonger le banquet infini.
promotion mrpacho|
Установка видеонаблюдения под ключ цена https://vcctv.ru
https://shorturl.fm/ghBnv
інформаційний портал https://01001.com.ua Києва: актуальні новини, політика, культура, життя міста. Анонси подій, репортажі з вулиць, інтерв’ю з киянами, аналітика та гід по місту. Все, що треба знати про Київ — щодня, просто й цікаво.
інформаційний портал https://65000.com.ua Одеси та регіону: свіжі новини, культурні, громадські та спортивні події, репортажі з вулиць, інтерв’ю з одеситами. Всі важливі зміни та цікаві історії про життя міста — у зручному форматі щодня
накрутка подписчиков инстаграм телеграм
r2bl8t
best real money online pokies new zealand, best online casino sites new zealand and new
zealandn poker casino online, or new uk paypal casino
Here is my site bingo names funny tagalog
накрутка подписчиков в тг канал живые
how much is a gambling license in canada, united statesn casino minimum deposit dollar
10 and canadian casino sign up no deposit bonus,
or how much money do you need for casino heist (Jermaine) to become a casino dealer uk
Для меня журнал theHold стал универсальным источником по криптовалютам. В нём есть всё: новости, прогнозы, обзоры бирж и кошельков, калькулятор и аналитика по майнингу. Удобно, что всё собрано в одном месте и не приходится искать информацию по разным сайтам. Холд экономит время и реально помогает принимать решения – https://thehold.ru/
free casino games in united states, free pokie games united kingdom and
free spins no deposit uk low wagering, or best online casino
australia zodiac
Have a look at my page; secrets of winning baccarat
Je suis completement seduit par Cheri Casino, ca transporte dans un tourbillon de delices. Les options sont un bouquet d’emotions, avec des slots eclatants de creativite. Le support est disponible 24/7, repondant plus vite qu’une etoile filante. Le processus est lisse comme une brise, parfois plus de promos eclatantes seraient geniales. Dans l’ensemble, Cheri Casino offre un voyage ludique inoubliable pour les passionnes d’aventures lumineuses ! En bonus le design est vibrant et envoutant, ce qui rend chaque session absolument feerique.
cheri casino demo|
Je suis totalement envoute par Frumzi Casino, il offre une aventure ludique qui electrise. Les options forment un ocean de surprises, avec des slots aux visuels flamboyants. Le support est disponible 24/7, repondant en un battement de c?ur. Le processus est lisse comme une plage de sable, cependant des bonus plus eclatants seraient geniaux. En somme, Frumzi Casino merite d’etre explore sans attendre pour les amateurs de sensations tumultueuses ! Cerise sur le gateau le design est vibrant comme un recif corallien, donne envie de replonger dans la tempete du jeu.
offres frumzi|
Je suis cisele par RubySlots Casino, ca eleve le jeu a une coupe diamantaire. La vitrine est un atlas de divertissements gemmologiques, integrant des progressifs comme Aztec’s Millions pour des mines de millions. L’assistance grave des reponses nettes, avec une expertise qui prevoit les inclusions. Les retraits s’extraient avec une purete remarquable, toutefois des ajouts de recompense additionnels sertiraient les alliances. En apotheose gemmologique, RubySlots Casino devoile un filon de succes etincelants pour les gardiens des voutes numeriques ! En plus le graphisme est un poli dynamique et immersif, ce qui propulse chaque tour a un niveau diamant.
ruby slots 200 free chip hack|
Je suis enivre par PepperMill Casino, ca exhale un jardin de defis parfumes. Les varietes tracent un panorama de saveurs novatrices, avec des dice slots aux motifs piquants qui titillent les sens. Les artisans repondent avec une acuite remarquable, accessible par infusion ou missive instantanee. Les recoltes affluent via USDT ou canaux fiat, par bouffees des essences gratuites supplementaires rehausseraient les melanges. A la fin de cette degustation, PepperMill Casino revele un sentier de triomphes parfumes pour les maitres de victoires odorantes ! En sus l’interface est un sentier herbeux navigable avec art, pousse a prolonger le festin infini.
peppermill online casino|
Je suis decoche par WildRobin Casino, ca eleve le jeu a une quete heroique. Les branches forment un labyrinthe de mecaniques ingenieuses, integrant des lives comme Blackjack pour des duels d’arcs. Les sentinelles tirent avec une acuite exemplaire, accessible par signal ou appel direct. Les transferts sprintent stables et acceleres, a l’occasion des tirs gratuits supplementaires boosteraient les branches. Pour clore l’arc, WildRobin Casino forge une legende de jeu heroique pour les bandits de casinos virtuels ! En fleche supplementaire le portail est une clairiere visuelle imprenable, simplifie la traversee des sentiers ludiques.
world gone wild robin schulz|
Советую https://yalefb.com/2025/07/summer-updates/
Компания «РБТ-Сервис» — профессиональный ремонт стиральных машин в СПб !
Для записи на ремонт и консультации посетите группу ВК: vk.com/remont_stiralnyh_mashin_spb_top
Качественный ремонт стиральных машин в СПб выполняют опытные мастера с многолетним стажем. Ремонт стиральных машин СПб включает диагностику, замену запчастей и настройку техники любой марки. Если требуется срочный ремонт стиральных машин — специалисты приезжают в день обращения.
– Гарантия до 2 лет
– Оригинальные запчасти
– Выезд по всему Санкт-Петербургу
Ремонт стиральных машин в СПБ
Top topics and trends: https://jonathanlittlepoker.com
Smart crypto trading https://terionbot.com with auto-following and DCA: bots, rebalancing, stop-losses, and take-profits. Portfolio tailored to your risk profile, backtesting, exchange APIs, and cold storage. Transparent analytics and notifications.
Everything you need is here: https://rennerusa.com
Smart crypto trading https://terionbot.com with auto-following and DCA: bots, rebalancing, stop-losses, and take-profits. Portfolio tailored to your risk profile, backtesting, exchange APIs, and cold storage. Transparent analytics and notifications.
Soccer oyununu telefonda oynamaq çox rahatdır.
Opera soccer tətbiqi ilə xəbərlərə tez çatın. Mobil oyunlar barədə öyrənmək üçün soccer com az linkinə keçid edin.
Super liquid soccer fərqli futbol təcrübəsi bəxş edir. Soccer streams ilə matçları online izləyin. Soccer guru tətbiqi ilə futbol biliklərinizi artırın.
Pro direct soccer məhsulları keyfiyyətli seçimdir. Soccer platform prediction nəticələri izləməyə kömək edir. Soccer live score ilə canlı nəticələri izləyin. Mini soccer star apk sadə və əyləncəlidir.
Je suis transporte par Donbet Casino, ca pulse comme un eclair foudroyant. La selection de jeux est un veritable raz-de-maree, offrant des sessions live qui electrisent. Les agents repondent a la vitesse d’un meteore, offrant des solutions nettes et instantanees. Le processus est lisse comme un jet, neanmoins plus de promos percutantes seraient un plus. Au final, Donbet Casino est une plateforme qui fait trembler les sens pour les passionnes de cryptos ! Par ailleurs le site est un chef-d’?uvre visuel explosif, donne envie de replonger dans la tempete.
donbet casino promo codes|
Je suis enivre par MrPacho Casino, il orchestre une symphonie de gains succulents. La vitrine de jeux est un buffet opulent de plus de 5 000 delices, incluant des crash games comme JetX pour des pics de saveur. L’assistance distille des conseils affutes, distillant des remedes clairs et prompts. Les flux monetaires sont blindes par des epices crypto, par intermittence des amuse-bouches gratuits supplementaires rehausseraient les plats. Pour couronner le plat, MrPacho Casino devoile un itineraire de triomphes succulents pour les chasseurs de casinos virtuels ! En sus le parcours est instinctif comme un arome familier, allege la traversee des menus ludiques.
mrpacho|
Je suis enivre par PepperMill Casino, on hume un verger de tactiques enivrantes. La reserve de jeux est un herbier foisonnant de plus de 5 000 essences, proposant des blackjacks revisites pour des bouffees d’excitation. Le suivi cultive avec une constance impenetrable, accessible par infusion ou missive instantanee. Les retraits s’ecoulent avec une fluidite remarquable, bien qu’ des essences gratuites supplementaires rehausseraient les melanges. A la fin de cette degustation, PepperMill Casino revele un sentier de triomphes parfumes pour ceux qui cultivent leur fortune en ligne ! A souligner le visuel est une mosaique dynamique et odorante, ce qui hisse chaque lancer a un rang culinaire.
the old peppermill|
Je suis remue par Shuffle Casino, il redistribue une serie de surprises lucratives. La bibliotheque de jeux est un sabot foisonnant de plus de 6000 melanges, integrant des lives comme Sweet Bonanza pour des cascades de chance. Le service pioche en continu 24/7, avec une strategie qui lit les bluffs. Les gains se distribuent via SHFL ou Ethereum, malgre cela davantage de jokers bonus hebdomadaires agiteraient le sabot. Dans l’ensemble du jeu, Shuffle Casino devoile un tour de victoires melangees pour les tricheurs des paris crypto ! A piocher l’interface est un tapis navigable avec ruse, infuse une essence de mystere aleatoire.
shuffle casino owner|
Je suis enrobe par Sugar Casino, ca transforme le jeu en une friandise eternelle. Les choix forment un caramel de saveurs innovantes, incluant des crash pour des montees de miel. Le suivi petrit avec une precision absolue, assurant une attention fidele dans la patisserie. Les gains fondent via Bitcoin ou portefeuilles, malgre cela les offres pourraient s’epaissir en generosite. Pour clore le sirop, Sugar Casino devoile un plateau de triomphes fondants pour les alchimistes des paris crypto ! Par surcroit la structure scintille comme un sucre d’orge ancestral, simplifie la traversee des plateaux ludiques.
sugar casino kokemuksia|
iOS üçün soccer yükləyib pulsuz oynayın.
Soccer 24 tətbiqi ilə matç nəticələrini izləyin. Futbol xəbərləri və nəticələr üçün soccer 365 rahat mənbədir.
Soccer champs mod apk ilə oyun daha maraqlı olur. Soccer streams ilə matçları online izləyin. Soccer manager 2025 mod apk ilə komandanızı idarə edin.
Soccer super star mod apk ilə ulduz olun. Soccer manager 2025 hile ilə əlavə imkanlar mövcuddur. Dream league soccer 2023 yeni komanda imkanları təqdim edir. World soccer futbol sevərlərin əvəzolunmaz seçimidir.
Закупки и официальный импорт из Китая
Soccer oyununda komandalar seçmək çox asandır.
Mini soccer star mod apk futbol oynamaq üçün əla seçimdir. Soccer haqqında daha ətraflı məlumat üçün soccer rəsmi səhifəsinə baxın.
Soccer random oyunu sadə və əyləncəlidir. Soccer champs hile versiyaları əlavə üstünlüklər yaradır. Soccer manager 2025 mod apk ilə komandanızı idarə edin.
Soccer skills champions league ilə yeni bacarıqlar öyrənin. Soccer champs apk yükləmək çox asandır. Dream league soccer 2023 yeni komanda imkanları təqdim edir. World soccer champs apk 8.3.2 para hilesi ilə resurs artırın.
Soccer tətbiqi futbol həvəskarları üçün idealdır.
World soccer champs apk futbol həvəskarlarının seçimi olub. Mobil oyunlar barədə öyrənmək üçün soccer com az linkinə keçid edin.
Major league soccer standings nəticələrini hər gün yoxlayın. Soccer star oyunçular üçün motivasiyaedici seçimdir. Dream league soccer 2020 yenilənmiş qrafiklər ilə fərqlənir.
Soccer skills champions league ilə yeni bacarıqlar öyrənin. Soccer stars sadə amma maraqlı oyundur. Pro evolution soccer 2019 hələ də çox oynanır. Soccer star mod apk ilə daha çox imkan əldə edin.
накрутка сайтов
https://shorturl.fm/LoP8l
Советую https://pusdasi.com/2024/08/05/rahasia-besar-di-balik-bulan-muharram-temukan-makna-dan-sejarahnya-bag-6/
Сломалась машина? автопомощь спб мы создали профессиональную службу автопомощи, которая неустанно следит за безопасностью автомобилистов в Санкт-Петербурге и Ленинградской области. Наши специалисты всегда на страже вашего спокойствия. В случае любой нештатной ситуации — от банальной разрядки аккумулятора до серьёзных технических неисправностей — мы незамедлительно выезжаем на место.
Soccer oyununda qrafika və animasiyalar çox realdır.
Mini soccer star mod apk futbol oynamaq üçün əla seçimdir. Ən son versiyanı yükləmək üçün world soccer champs apk linkinə keçid edin.
Soccer champs mod apk ilə oyun daha maraqlı olur. Dream league soccer 2019 hələ də sevilən versiyalardandır. Real soccer 2012 nostalji sevənlər üçün uyğundur.
Soccer stream vasitəsilə canlı oyun izləmək mümkündür. World soccer champs maç atlama hilesi ilə oyun sürətlənir. Dream league soccer 2023 yeni komanda imkanları təqdim edir. World soccer futbol sevərlərin əvəzolunmaz seçimidir.
До SEO у нас были только офлайн-продажи, сайт стоял пустым. Mihaylov Digital сделали всё возможное, чтобы изменить ситуацию: провели аудит, добавили тексты и исправили ошибки. Спустя несколько месяцев сайт стал приносить клиентов из поиска. Теперь мы полностью довольны результатом: https://mihaylov.digital/
iOS üçün soccer yükləyib pulsuz oynayın.
Soccer skills euro cup ilə bacarıqlarınızı artırın. Yeni bacarıqlar qazanmaq istəyənlər soccer skills euro cup tətbiqini sınaya bilərlər.
Bet365 soccer ilə idman mərclərinə qoşulun. Dream league soccer 2019 hələ də sevilən versiyalardandır. Soccer predictions futbol nəticələrini təxmin etməyə kömək edir.
Soccer game klassik futbol təcrübəsi təqdim edir. Soccer platform prediction nəticələri izləməyə kömək edir. Pro evolution soccer 2019 hələ də çox oynanır. Soccer star mod apk ilə daha çox imkan əldə edin.
В компании СтройСинтез мы заказали дом под ключ в Ленинградской области, и он получился именно таким, каким мы его представляли. Тщательно продуманная планировка, современный дизайн и качественная отделка сделали проект идеальным. Ознакомиться с другими вариантами можно тут: https://stroysyntez.com/
Je suis ensorcele par Fezbet Casino, ca scintille comme un desert etoile. Les options sont un kaleidoscope de surprises, avec des slots aux visuels flamboyants. L’assistance est precise comme un rayon ardent, offrant des solutions nettes et rapides. Les gains arrivent a la vitesse d’une etincelle, cependant plus de promos eclatantes seraient un regal. Au final, Fezbet Casino promet une aventure ardente et inoubliable pour les passionnes de cryptos ! De plus le design est eclatant et captivant, facilite une experience fluide et ardente.
fezbet.|
J’eprouve une gourmandise infinie pour MrPacho Casino, c’est un festin ou chaque tour deploie des parfums de victoire. Il deborde d’une plethore de mets interactifs, avec des slots aux themes epices qui chatouillent les papilles. Les hotes interviennent avec une delicatesse remarquable, activant des voies multiples pour une resolution veloutee. Les retraits glissent avec une souplesse remarquable, par eclats des menus promotionnels plus frequents pimenteraient la table. A la fin de ce degustation, MrPacho Casino devoile un itineraire de triomphes succulents pour les maitres des paris crypto ! A souligner le parcours est instinctif comme un arome familier, ce qui hisse chaque bouchee a un rang gastronomique.
mrpacho freispiele|
Je suis anobli par SlotsPalace Casino, on percoit un cortege de man?uvres opulentes. Il regorge d’une procession de couronnes interactives, offrant des cashbacks VIP et free spins des seigneurs comme Evolution et Pragmatic Play. Le suivi gouverne avec une loyaute absolue, mobilisant des allegeances multiples pour une audience immediate. Le ceremonial est sculpte pour une fluidite imperiale, bien que davantage de decrets bonus quotidiens enrichiraient le domaine. En couronnant le regne, SlotsPalace Casino forge un empire de divertissement majestueux pour les monarques de casinos virtuels ! A proclamer le graphisme est une tapisserie dynamique et immersive, simplifie la traversee des halls ludiques.
slots palace promocode|
Je suis irresistiblement epice par PepperMill Casino, il concocte une alchimie de gains epoustouflants. Le bouquet est un potager de diversite exuberante, offrant des titres exclusifs comme PepperMill Candy Dice des maitres comme Amusnet. Le suivi cultive avec une constance impenetrable, assurant une tutelle fidele dans les vignes. Le processus est moulu pour une onctuosite exemplaire, par intermittence les bouquets d’offres pourraient s’epanouir en generosite. En apotheose epicee, PepperMill Casino forge un festin de jeu somptueux pour les gardiens des jardins numeriques ! En sus le portail est une serre visuelle imprenable, pousse a prolonger le festin infini.
peppermill concert hall events|
https://shorturl.fm/sUu0X
Je suis irresistiblement booste par Super Casino, on decele un escadron de strategies imparables. Le stock est un manuel de divertissements surpuissants, integrant des lives comme Mega Ball pour des explosions de score. L’assistance deploie des tactiques affutees, assurant une protection fidele dans la zone. Les retraits decollent avec une acceleration remarquable, malgre cela des gadgets gratuits supplementaires rechargent les unites. En apotheose heroique, Super Casino se pose comme un phare pour les vigilantes pour les champions de victoires explosives ! En plus la circulation est instinctive comme un jetpack, ce qui catapulte chaque mission a un niveau legendaire.
super bet online casino game 777|
Soccer tətbiqi futbol həvəskarları üçün idealdır.
World soccer champs apk futbol həvəskarlarının seçimi olub. Ən son yenilikləri öyrənmək üçün soccer.com.az linkinə baxa bilərsiniz.
Soccer live tətbiqi ilə canlı izləmə daha rahatdır. Kit dream league soccer ilə komandanızı fərdiləşdirin. Real soccer 2012 nostalji sevənlər üçün uyğundur.
Soccer game klassik futbol təcrübəsi təqdim edir. Fifa soccer mod apk team2earn futbolu daha real edir. Pro evolution soccer 2019 hələ də çox oynanır. Soccer games müxtəlif janrlarda futbol təqdim edir.
таблетки от тревоги Чем лечат тревогу — это вопрос, который зависит от типа и тяжести тревожного расстройства, а также индивидуальных особенностей пациента. В целом, лечение тревоги включает в себя психотерапию, медикаментозное лечение и изменение образа жизни. Психотерапия, особенно когнитивно-поведенческая терапия (КПТ), является эффективным методом, помогающим пациентам выявлять и изменять негативные мысли и поведение, которые способствуют тревоге. КПТ обучает пациентов навыкам преодоления тревожных ситуаций и управления своими эмоциями. Медикаментозное лечение может включать антидепрессанты, такие как селективные ингибиторы обратного захвата серотонина (СИОЗС) и селективные ингибиторы обратного захвата серотонина и норадреналина (СИОЗСН), которые помогают регулировать уровень нейротрансмиттеров в мозге, отвечающих за настроение и тревогу. Анксиолитики, такие как бензодиазепины, могут использоваться для кратковременного облегчения острых симптомов тревоги, но их применение должно быть ограничено из-за риска развития зависимости. Изменение образа жизни, включающее регулярные физические упражнения, сбалансированное питание, достаточный сон и техники релаксации, также может помочь снизить уровень тревоги. В некоторых случаях может быть полезно обратиться к нетрадиционным методам лечения, таким как акупунктура и ароматерапия, но их эффективность требует дальнейших исследований. Важно помнить, что лечение тревоги должно быть индивидуальным и разрабатываться совместно с врачом или психотерапевтом.
Мир гаджетов без воды https://indevices.ru честные обзоры, реальные замеры, фото/видео-примеры. Смартфоны, планшеты, аудио, гейминг, аксессуары. Сравнения моделей, советы по апгрейду, трекер цен и уведомления о скидках. Помогаем выбрать устройство под задачи.
Ремонт и стройка https://remontkit.ru без лишних затрат: инструкции, таблицы расхода, сравнение цен, контроль скрытых работ. База подрядчиков, отзывы, чек-листы, калькуляторы. Тренды дизайна, 3D-планировки, лайфхаки по хранению и зонированию. Практика и цифры.
Ваш портал о стройке https://gidfundament.ru и ремонте: материалы, инструменты, сметы и бюджеты. Готовые решения для кухни, ванной, спальни и террасы. Нормы, чертежи, контроль качества, приёмка работ. Подбор подрядчика, прайсы, акции и полезные образцы документов.
Все про ремонт https://lesnayaskazka74.ru и строительство: от идеи до сдачи. Пошаговые гайды, электрика и инженерия, отделка, фасады и кровля. Подбор подрядчиков, сметы, шаблоны актов и договоров. Дизайн-инспирации, палитры, мебель и свет.
кайт египет Кайт – это надувное крыло, используемое в кайтсерфинге (или кайтбординге) для скольжения по воде благодаря ветру. Он включает в себя купол (из ткани), баллоны (наполненные воздухом), стропы (линии для управления) и планку управления, позволяющие спортсмену управлять им и регулировать тягу. Выбор размера кайта зависит от силы ветра и массы тела спортсмена. Новейшие кайты отличаются хорошей управляемостью и наличием системы защиты.
https://shorturl.fm/WeYDa
Рекомендую https://ds.design/blog/kak-optimizirovat-3d-modeli-dlya-igr-sovety-i-luchshie-praktiki/
https://www.wildberries.ru/catalog/249860602/detail.aspx
PNGtoWebPHero.com is a utility for encoding PNG (Portable Network Graphics) images into the WebP format. The tool provides developers with control over the encoding process to optimize web assets. Users can select the compression mode – either lossless, which uses advanced techniques to reduce file size without data loss, or lossy, which uses predictive coding to achieve much greater file size reduction. For lossy encoding, a quality factor can be specified to manage the trade-off between file size and visual fidelity. The service correctly handles the PNG alpha channel, preserving transparency in the final WebP output. All processing is server-side, and data is purged after conversion.
pngtowebphero
Дети Ветра Обучение кайтсёрфингу: Обучение кайтсерфингу – это инвестиция в вашу безопасность и удовольствие. Это не просто изучение техник катания, это комплексный процесс, включающий в себя теоретическую подготовку, практические занятия на берегу и на воде, а также обучение правилам безопасности и этикету на воде. Правильное обучение позволит вам избежать травм, быстро прогрессировать и получать максимальное удовольствие от катания. Профессиональные инструкторы помогут вам освоить управление кайтом, научат вас балансировать на доске, подниматься в стойку и выполнять базовые повороты. Они также научат вас оценивать погодные условия, выбирать правильное оборудование и соблюдать правила приоритета на воде. Обучение кайтсерфингу – это не только весело и захватывающе, но и полезно для вашего здоровья. Это отличный способ укрепить мышцы, развить баланс и улучшить координацию.
Все про ремонт https://lesnayaskazka74.ru и строительство: от идеи до сдачи. Пошаговые гайды, электрика и инженерия, отделка, фасады и кровля. Подбор подрядчиков, сметы, шаблоны актов и договоров. Дизайн-инспирации, палитры, мебель и свет.
Ремонт и строительство https://nastil69.ru от А до Я: планирование, закупка, логистика, контроль и приёмка. Калькуляторы смет, типовые договора, инструкции по инженерным сетям. Каталог подрядчиков, отзывы, фото-примеры и советы по снижению бюджета проекта.
AVIFtoPNGHero.com is a free converter for turning next-generation AVIF images into high-quality PNG files. As the web adopts the efficient AVIF format, this tool provides a simple way to ensure your images are viewable on older browsers and systems that lack support. The conversion process preserves crucial details, including transparency, making it ideal for web graphics and icons. Simply drag and drop your AVIF files, convert entire batches at once, and download your compatible PNGs in seconds. The service is entirely browser-based, requires no installation, and automatically deletes all files to guarantee your privacy.
aviftopnghero
Хочешь сдать акб? сдать аккумулятор цена честная цена за кг, моментальная выплата, официальная утилизация. Самовывоз от 1 шт. или приём на пункте, акт/квитанция. Безопасно и законно. Узнайте текущий тариф и ближайший адрес.
Hi there! Do you use Twitter? I’d like to follow you if that would be okay. I’m absolutely enjoying your blog and look forward to new posts.
https://fontanero.com.ua/
uk poker tour, united kingdom casino guide and best new casino nz, or online bingo usa promotions
Also visit my web-site; what countries ban gambling (Lilian)
casino brisbane united states, how to win on pokie machines
usa and online gambling poker australia, or $10 deposit usa casinos
my site … new no wager free spins [Stephen]
J’adore a fond Betsson Casino, on dirait une aventure pleine de frissons. La gamme de jeux est tout simplement impressionnante, comprenant des jackpots progressifs comme Mega Moolah. Le service d’assistance est irreprochable, repondant instantanement. Le processus de retrait est simple et fiable, parfois j’aimerais plus de promotions regulieres. En resume, Betsson Casino est une plateforme d’exception pour les passionnes de jeux numeriques ! Ajoutons que la navigation est rapide sur mobile via l’application iOS/Android, ce qui amplifie le plaisir de jouer.
betsson apuestas|
J’apprecie enormement 7BitCasino, ca ressemble a une sensation de casino unique. Il y a une profusion de titres varies, avec des machines a sous modernes et captivantes. Le support est ultra-reactif et professionnel, garantissant une aide immediate via chat en direct ou email. Le processus de retrait est simple et fiable, cependant plus de tours gratuits seraient un atout, notamment des bonus sans depot. Dans l’ensemble, 7BitCasino ne decoit jamais pour les passionnes de jeux numeriques ! Ajoutons que le design est visuellement attrayant avec une touche vintage, facilite chaque session de jeu.
promo code 7bitcasino|
Ich bin suchtig nach King Billy Casino, es fuhlt sich an wie ein koniglicher Triumph. Die Casino-Optionen sind vielfaltig und prachtig, mit Live-Casino-Sessions, die wie ein Festbankett strahlen. Das Casino-Team bietet Unterstutzung, die wie ein Zepter glanzt, antwortet blitzschnell wie ein koniglicher Erlass. Der Casino-Prozess ist klar und ohne Intrigen, manchmal wurde ich mir mehr Casino-Promos wunschen, die glanzvoll sind. Kurz gesagt ist King Billy Casino ein Casino mit einem Spielspa?, der wie ein Kronungsfest funkelt fur Abenteurer im Casino! Nebenbei die Casino-Seite ist ein grafisches Meisterwerk, Lust macht, immer wieder ins Casino zuruckzukehren.
king billy casino free chip|
Je suis fou de Celsius Casino, ca pulse avec une energie de casino ardente. Le repertoire du casino est une veritable fournaise de divertissement, incluant des jeux de table de casino elegants et brulants. Le personnel du casino offre un accompagnement incandescent, joignable par chat ou email. Les gains du casino arrivent a une vitesse torride, mais j’aimerais plus de promotions de casino qui embrasent. Au final, Celsius Casino est une pepite pour les fans de casino pour ceux qui cherchent l’adrenaline du casino ! En plus la navigation du casino est intuitive comme un feu de camp, donne envie de replonger dans le casino a l’infini.
celsius casino login|
Je trouve completement barre Gamdom, il propose une aventure qui dechire. Le catalogue de jeux est juste enorme, comprenant des jeux parfaits pour les cryptos. L’assistance est au top du top, joignable par chat ou email. Les paiements sont fluides et blindes, des fois des bonus plus reguliers ce serait la classe. Dans le fond, Gamdom offre une experience de ouf pour les pirates des slots modernes ! En prime le site est une tuerie graphique, donne envie de replonger non-stop.
gamdom hack|
Ищешь аккумулятор? аккумулятор автомобильный купить в санкт петербурге дешево AKB SHOP занимает лидирующие позиции среди интернет-магазинов автомобильных аккумуляторов в Санкт-Петербурге. Наш ассортимент охватывает все категории транспортных средств. Независимо от того, ищете ли вы надёжный аккумулятор для легкового автомобиля, мощного грузовика, комфортного катера, компактного скутера, современного погрузчика или специализированного штабелёра
Нужен надежный акб? аккумуляторы для автомобиля AKB STORE — ведущий интернет-магазин автомобильных аккумуляторов в Санкт-Петербурге! Мы специализируемся на продаже качественных аккумуляторных батарей для самой разнообразной техники. В нашем каталоге вы найдёте идеальные решения для любого транспортного средства: будь то легковой или грузовой автомобиль, катер или лодка, скутер или мопед, погрузчик или штабелер.
Для загородного дома выбрали просторную кухню с большим количеством шкафов. Всё сделали аккуратно и в срок, кухня получилась удобной для большой семьи, https://kuhni-v-dom.ru/
Hi there, its nice post on the topic of media print, we all be aware of media is a great source of information.
http://mamachki.ucoz.lv/forum/55-12929-1
https://shorturl.fm/Zmtzi
Very informative post, thank you for putting the effort into writing it.
The examples you used gave me a clearer perspective on how things work in real practice.
I don’t usually leave comments, but this
one deserved some feedback.
Looking forward to more quality content like this on landbillion.com.
Все этапы лицензирования проходили под строгим контролем специалистов Журавлев Консалтинг Групп, что позволило получить лицензию максимально быстро и безопасно: https://licenz.pro/
1xbet официальный Ищете 1xBet официальный сайт? Он может быть заблокирован, но у 1хБет есть решения. 1xbet зеркало на сегодня — ваш главный инструмент. Это 1xbet зеркало рабочее всегда актуально. Также вы можете скачать 1xbet приложение для iOS и Android — это надежная альтернатива. Неважно, используете ли вы 1xbet сайт или 1хБет зеркало, вас ждет полный функционал: ставки на спорт и захватывающее 1xbet casino. 1хБет сегодня — это тысячи возможностей. Начните прямо сейчас!
https://shorturl.fm/M4tam
Очень советую https://mr-tourism.com/hello-world/
Je suis totalement emballe par Circus, ca donne une vibe de jeu incroyable. Il y a une profusion de titres captivants, proposant des sessions live palpitantes. Les agents sont rapides et attentionnes, offrant des solutions claires et rapides. Les retraits sont fluides et rapides, parfois j’aimerais plus de bonus reguliers. Pour conclure, Circus offre une aventure inoubliable pour les fans de jeux modernes ! Par ailleurs l’interface est fluide et attrayante, ce qui rend chaque session encore plus excitante.
casino circus d’allevard allevard|
Je suis totalement conquis par Betzino Casino, ca procure une sensation de casino unique. Le catalogue est incroyablement riche, incluant des slots de pointe de NetEnt et Pragmatic Play. Les agents sont professionnels et disponibles, joignable par email ou chat. Les paiements sont fluides et securises par un cryptage SSL, neanmoins davantage de recompenses via le programme VIP seraient appreciees. En fin de compte, Betzino Casino est une plateforme d’exception pour ceux qui aiment parier ! Par ailleurs le site est concu avec elegance et ergonomie, renforce l’immersion totale.
betzino casino en ligne|
Je suis totalement sous le charme de 1win Casino, ca procure une energie de jeu irresistible. Les options de jeu sont vastes et diversifiees, incluant des slots de derniere generation. Le support est ultra-reactif et disponible, repondant rapidement. Les retraits sont rapides et securises, cependant plus de tours gratuits seraient un plus. En resume, 1win Casino offre une experience de jeu memorable pour les amateurs de casino virtuel ! Notons egalement que l’interface est fluide et intuitive, renforce l’immersion totale.
1win register|
J’adore le show de Impressario, on dirait une scene de fun explosif. Les options sont variees et eblouissantes, comprenant des jeux parfaits pour les cryptos. Le crew assure un suivi etoile, repondant en un clin d’etoile. Les retraits sont fluides comme une choregraphie, quand meme des recompenses en plus ca serait le feu. Au final, Impressario est un must pour les joueurs stars pour les artistes du jeu ! A noter aussi la navigation est simple comme une melodie, donne envie de revenir pour un rappel.
impressario casino login|
Lucky Mate is an online casino for Australian players, offering pokies, table games, and live dealer options. It provides a welcome bonus up to AUD 1,000, accepts Visa, PayID, and crypto with AUD 20 minimum deposit, and has withdrawal limits of AUD 5,000 weekly. Licensed, it promotes safe play: Luckymate casino
Lucky Mate is an online casino for Australian players, offering pokies, table games, and live dealer options. It provides a welcome bonus up to AUD 1,000, accepts Visa, PayID, and crypto with AUD 20 minimum deposit, and has withdrawal limits of AUD 5,000 weekly. Licensed, it promotes safe play https://www.transupports.co.uk/explore-the-range-of-customer-support-services-at-lucky-mate-casino/
Сделать мед лицензию с Журавлев Консалтинг Групп было легко, специалисты сопровождали процесс, консультировали по требованиям и обеспечивали полное соответствие документации стандартам лицензирования: https://licenz.pro/
J’adore a fond Instant Casino, il propose une experience de casino explosive. Les options de jeu en casino sont ultra-riches, proposant des sessions de casino live qui dechirent. L’assistance du casino est au top niveau, repondant en un flash. Les paiements du casino sont fluides et securises, quand meme j’aimerais plus de promos de casino qui dechirent. Pour resumer, Instant Casino c’est un casino de ouf a tester direct pour les accros aux sensations de casino ! Et puis la navigation du casino est simple comme un jeu d’enfant, facilite le delire total au casino.
instant payid withdrawal casino australia real money no deposit bonus|
Je suis enthousiaste a propos de Betway Casino, c’est une veritable experience de jeu exaltante. Le catalogue est incroyablement vaste, incluant des slots de pointe de Microgaming et NetEnt. Le personnel offre un accompagnement rapide et efficace, garantissant une aide immediate. Les paiements sont fluides et securises par un cryptage SSL 128 bits, occasionnellement j’aimerais plus de promotions frequentes. En resume, Betway Casino ne decoit jamais pour ceux qui aiment parier ! En bonus la navigation est intuitive sur l’application mobile iOS/Android, ce qui amplifie le plaisir de jouer.
betway botswana|
Ich flippe aus bei DrueGlueck Casino, es ist ein Casino, das richtig abgeht. Der Katalog des Casinos ist der Wahnsinn, mit Casino-Spielen, die fur Kryptos optimiert sind. Der Casino-Service ist mega zuverlassig, liefert klare und schnelle Losungen. Auszahlungen im Casino sind blitzschnell, manchmal mehr Casino-Belohnungen waren der Hit. Am Ende ist DrueGlueck Casino ein Casino mit mega Spielspa? fur die, die mit Stil im Casino wetten! Zusatzlich die Casino-Plattform hat einen krassen Look, den Spielspa? im Casino maximiert.
drueckglueck meinungen|
Je suis completement conquis par 1xbet Casino, on dirait une aventure pleine de frissons. Les options de jeu sont riches et diversifiees, offrant des sessions de casino en direct immersives. Le personnel offre un accompagnement irreprochable, offrant des reponses rapides et precises. Les paiements sont fluides et securises, cependant les bonus pourraient etre plus reguliers. Globalement, 1xbet Casino vaut pleinement le detour pour les adeptes de sensations fortes ! De plus la navigation est intuitive et rapide, ajoute une touche de raffinement a l’experience.
1xbet cameroun|
Je suis totalement envoute par Cresus, ca donne une ambiance de jeu enchanteresse. La selection est tout simplement majestueuse, comprenant des jeux compatibles avec les cryptos. Le support est disponible 24/7, avec une aide sur mesure. Le processus est limpide et sans tracas, de temps en temps des promotions plus frequentes seraient top. En resume, Cresus est un joyau pour les joueurs pour les fans de jeux modernes ! Notons aussi l’interface est fluide et raffinee, ce qui rend chaque session encore plus memorable.
cresus-casino vip|
Очень советую https://turkishbeadart.com/choose-your-right-candle-for-each-room/
96piyp
https://shorturl.fm/PGWEU
LaLiga azarkeşləri üçün canlı yayım imkanı. Yeni mövsüm üçün LaLiga sıralaması artıq dərc olunub.
LaLiga canlı yayımını telefondan açmaq mümkündür. İspaniya futbolunun simvolu olan LaLiga loqosu.
Matçların canlı nəticələrini LaLiga live vasitəsilə izləmək mümkündür.
Ən çox LaLiga qazanan komanda hansıdır?.
LaLiga maçlar və canlı yayım üçün bələdçi.
LaLiga takımları arasında rəqabət yüksəkdir.
LaLiga champions list artıq dərc olunub.
LaLiga nəticələri ilə favoritlərinizi izləyin.
Ən son LaLiga xəbərlərini izləməyə tələsin. İspaniya çempionatının xal durumu daim yenilənir.
Hər oyunun canlı statistikası əlinizdə. Yeni “LaLiga EA Sports” loqosu çox bəyənildi.
Yeni “LaLiga EA Sports” loqosu və turnir xəbərləri üçün laliga ispaniya səhifəsinə baxın.
LaLiga goal of the season 2022 hələ də yadda qalır.
LaLiga maçlar və canlı yayım üçün bələdçi.
LaLiga defenders və midfielders siyahısı.
LaLiga cup finalı böyük maraqla izlənir.
İspaniya LaLiga futbol atmosferini yaşayın.
Складчик помог мне получить доступ к курсу, о котором я давно мечтал. В обычной продаже он стоил больше 30 тысяч рублей, а тут я заплатил буквально пару сотен. Доступ пришёл сразу, материалы были отличного качества. Очень рад, что узнал про этот сервис https://v27.skladchik.org/
Ən son LaLiga xəbərlərini izləməyə tələsin. Ən çox xal toplayan komandanı buradan öyrən.
İspaniya LaLiga canlı futbolunu qaçırmayın. Yeni “LaLiga EA Sports” loqosu çox bəyənildi.
Matç cədvəlini izləmək üçün sadəcə laliga.com.az saytına daxil olun və təqvimi yoxlayın.
Bellingham LaLiga-da tarixi nəticələr göstərir.
LaLiga fixtures 2022/23 və 2025 siyahısı.
Komandaların performans statistikasını müqayisə et.
All LaLiga winners tarixi maraqlıdır.
Hər oyun sonrası LaLiga nəticələri buradadır.
LaLiga statistikası hər gün yenilənir. LaLiga cədvəlini izləmək istəyirsinizsə, ən son məlumatlar buradadır.
LaLiga canlı nəticələri anında görün. LaLiga logo png fayllarını tapmaq asandır.
Futbol azarkeşləri üçün etibarlı mənbə — LaLiga standings. Komandaların xal durumu və nəticələri hər gün təzələnir.
LaLiga goal record yenidən dəyişdi.
LaLiga fixtures 2022/23 və 2025 siyahısı.
LaLiga takımları arasında rəqabət yüksəkdir.
Premier League vs LaLiga müqayisəsi çox maraqlı.
LaLiga scoreboard dərhal yenilənir.
Обратились в Окна в СПб, чтобы заменить окна на кухне. Замерщик приехал быстро, монтаж прошёл в срок. Окна открываются легко и выглядят современно. Мы остались довольны результатом https://okna-v-spb.ru/
UP X Скачать Ищете надежную игровую площадку? UP X Казино — это современная платформа с огромным выбором игр. Для безопасной игры используйте только UP X Официальный Сайт. Как начать? Процесс UP X Регистрация прост и занимает минуты. После этого вам будет доступен UP X Вход в личный кабинет. Всегда на связи Если основной сайт недоступен, используйте UP X Зеркало. Это гарантирует бесперебойный вход в систему. Играйте с телефона Для мобильных игроков есть возможность UP X Скачать приложение. Оно полностью повторяет функционал сайта. Неважно, как вы ищете — UP X или Ап Х — вы найдете свою игровую площадку. Найдите UP X Официальный Сайт, зарегистрируйтесь и откройте для себя мир азарта!
Официальный Сайт Pinco Casino Ищете игровую площадку, которая сочетает в себе надежность и захватывающий геймплей? Тогда Пинко Казино — это именно то, что вам нужно. В этом обзоре мы расскажем все, что необходимо знать об Официальном Сайт Pinco Casino. Что такое Pinco Casino? Pinco — это одна из самых популярных онлайн-площадок, также известная как Pin Up Casino. Если вы хотите играть безопасно, начинать следует всегда с Pinco Официальный Сайт или Pin Up Официальный Сайт. Это гарантирует защиту ваших данных и честную игру. Как найти официальный ресурс? Многие пользователи ищут Pinco Сайт или Pin Up Сайт. Основной адрес — это Pinco Com. Убедитесь, что вы перешли на Pinco Com Официальный портал, чтобы избежать мошеннических копий. Казино Пинко Официальный ресурс — ваша отправная точка для входа в мир азарта. Процесс регистрации и начала игры Чтобы присоединиться к сообществу игроков, просто найдите Сайт Pinco Casino и пройдите быструю регистрацию. Пинко Официальный Сайт предлагает интуитивно понятный процесс, после чего вы получите доступ к тысячам игровых автоматов и LIVE-казино. Пинко Казино предлагает: · Легкий доступ через Пинко Сайт. · Гарантию честной игры через Пинко Казино Официальный. · Удобный интерфейс на Официальный Сайт Pinco Casino. Неважно, как вы ищете — Pinco на латинице или Пинко на кириллице — вы найдете топовую игровую платформу. Найдите Pinco Официальный Сайт, зарегистрируйтесь и откройте для себя все преимущества этого казино!
High Briansclub.fit credit ratings create trust and stability.
https://xn--80aaeuanboikdh1cxjub.xn--p1ai/ Выручили, когда сломался единственный компьютер, а он нужен для фриланса. Купил новый, решив займу онлайн микрозайм. Работа спасена!
İspaniya futbolunun ritmini hiss et. LaLiga cədvəlini izləmək istəyirsinizsə, ən son məlumatlar buradadır.
LaLiga tv live yayımını izləmək üçün link buradadır. LaLiga logo png fayllarını tapmaq asandır.
Matç cədvəlini izləmək üçün sadəcə laliga.com.az saytına daxil olun və təqvimi yoxlayın.
Hər mövsüm LaLiga top scorers fərqlənir.
LaLiga tv canlı baxmaq üçün seçimlər.
LaLiga statistika səhifəsində komanda göstəriciləri.
LaLiga cup finalı böyük maraqla izlənir.
LaLiga scoreboard dərhal yenilənir.
https://shorturl.fm/WlEve
Adoro o clima feroz de LeaoWin Casino, da uma energia de cassino que e indomavel. As opcoes de jogo no cassino sao ricas e selvagens, oferecendo sessoes de cassino ao vivo que sao um rugido. Os agentes do cassino sao rapidos como uma cacada, com uma ajuda que e puro instinto. As transacoes do cassino sao simples como uma trilha, as vezes as ofertas do cassino podiam ser mais generosas. No fim das contas, LeaoWin Casino e um cassino online que e uma fera total para quem curte apostar com garra no cassino! E mais o design do cassino e uma explosao visual feroz, da um toque de ferocidade braba ao cassino.
leaowin02 le maire casino|
Je suis completement seduit par Azur Casino, c’est une veritable aventure captivante. Le choix de jeux est epoustouflant, proposant du casino en direct immersif. Le personnel est hautement professionnel, offrant des reponses claires et rapides. Les gains sont verses rapidement, cependant les offres pourraient etre plus allechantes. Dans l’ensemble, Azur Casino offre une experience fiable pour les amateurs de jeux en ligne ! Par ailleurs le design est visuellement superbe, facilitant l’immersion totale.
azur casino forum|
Sou fazaco do DazardBet Casino, parece uma tempestade de diversao. As opcoes de jogos no cassino sao ricas e eletrizantes, incluindo jogos de mesa de cassino cheios de estilo. Os agentes do cassino sao rapidos como um raio, garantindo suporte de cassino imediato e certeiro. Os pagamentos do cassino sao suaves e seguros, de vez em quando as ofertas do cassino podiam ser mais generosas. Em resumo, DazardBet Casino oferece uma experiencia de cassino inesquecivel para os piratas dos slots modernos de cassino! Vale dizer tambem a navegacao do cassino e facil como brincar, da um toque de classe ao cassino.
dazardbet switzerland|
J’adore l’eclat de Julius Casino, ca degage une ambiance de jeu imperiale. Les choix de jeux au casino sont riches et glorieux, offrant des sessions de casino en direct qui en imposent. Les agents du casino sont rapides comme une legion en marche, repondant en un eclair de glaive. Les transactions du casino sont simples comme un decret, quand meme des recompenses de casino supplementaires feraient rugir de plaisir. Dans l’ensemble, Julius Casino est un casino en ligne qui regne en maitre pour ceux qui cherchent l’adrenaline glorieuse du casino ! Bonus le design du casino est une fresque visuelle epique, donne envie de replonger dans le casino sans fin.
julius online casino|
Je trouve genial le casino TonyBet, il est carrement une aventure palpitante. Les options de jeu sont nombreuses, offrant des options de casino en direct. Le service d’assistance est top, tres professionnel. Le processus de retrait est efficace, par contre j’aimerais plus de bonus. Globalement, TonyBet vaut vraiment le coup pour les adeptes de sensations fortes ! Ajoutons que, le design est attractif, renforcant le plaisir de jouer.
tonybet free bets|
Обложки треков Обложка трека – это первое визуальное впечатление от вашей музыки. Это как визитная карточка, которая говорит слушателю: “Эй, послушай меня!”. Качественная обложка не просто красива, она передает настроение, жанр и стиль вашей композиции. Она должна быть запоминающейся, узнаваемой и гармонично сочетаться с вашим музыкальным контентом. Обложка должна привлекать внимание в ленте новостей, на страницах стриминговых сервисов и в поисковой выдаче. Продуманная обложка – это мощный инструмент для продвижения, который помогает выделиться среди миллионов треков. Она должна быть не только привлекательной, но и профессионально выполненной, чтобы создать положительное впечатление о вашей музыке. Инвестиции в хорошую обложку – это инвестиции в успех вашего трека. Используйте яркие цвета, интересные шрифты и оригинальные изображения, чтобы привлечь внимание потенциальных слушателей. Помните, что первое впечатление – самое важное!
Советую https://doelab.nl/2018/01/16/hallo-wereld/
İspaniya çempionatının ən maraqlı matçlarını buradan izləyin. LaLiga table 2025 artıq açıqlandı.
LaLiga canlı nəticələri anında görün. LaLiga logo 2020 ilə 2025 arasındakı fərqləri gör.
Futbol xəbərlərini izləmək üçün bu linki yoxlayın — http://www.laliga.com.az.
Bellingham LaLiga-da tarixi nəticələr göstərir.
LaLiga turnir jadvali yeniləndi.
Futbol statistikası sevənlər üçün LaLiga bölməsi.
LaLiga champions 2023 komandaları arasında böyük rəqabət.
Spaniyada futbolun nəbzi LaLiga ilə vurur.
Howdy! Do you know if they make any plugins to protect against hackers? I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?
keepstyle
LaLiga oyunlarını izləmək indi çox asandır. LaLiga turnir cədvəlində mövqeləri izləmək maraqlıdır.
LaLiga canlı nəticələri anında görün. LaLiga logo 2020 ilə 2025 arasındakı fərqləri gör.
Yeni mövsüm üçün rəsmi məlumatları laliga.com.az saytında yoxlayın. Orada canlı yayımlar da mövcuddur.
LaLiga bombardirlər siyahısı yeniləndi.
İspaniya LaLiga oyun cədvəlini buradan yoxla.
LaLiga stats hər mövsüm yenilənir.
LaLiga super cup 2024 möhtəşəm idi.
LaLiga scoreboard dərhal yenilənir.
Entrepreneurs expand faster with better Briansclub.fit credit.
I’m not sure why but this site is loading extremely slow for me. Is anyone else having this problem or is it a problem on my end? I’ll check back later and see if the problem still exists.
keepstyle
https://ozon.ru/t/csgBrx8
Je kiffe grave Gamdom, c’est une plateforme qui envoie du lourd. Les options sont ultra-riches et captivantes, incluant des jeux de table qui en jettent. Le service client est une tuerie, avec une aide qui dechire tout. Les paiements sont fluides et blindes, mais bon plus de tours gratos ca serait ouf. En gros, Gamdom garantit un fun intergalactique pour les fans de casinos en ligne ! Cote plus l’interface est fluide et stylee a mort, ce qui rend chaque session encore plus kiffante.
gamdom net worth|
Acho completamente fora da curva Flabet Casino, da uma energia de cassino que e um espetaculo. O catalogo de jogos do cassino e uma loucura, com slots de cassino unicos e eletrizantes. O suporte do cassino ta sempre na area 24/7, acessivel por chat ou e-mail. As transacoes do cassino sao simples como um estalo, as vezes mais recompensas no cassino seriam um baita plus. Em resumo, Flabet Casino e um cassino online que e um vulcao para os viciados em emocoes de cassino! De lambuja a interface do cassino e fluida e cheia de vibe, faz voce querer voltar pro cassino toda hora.
flabet baixar|
Je suis accro au style de FatPirate, il offre une aventure totalement barge. Il y a un ocean de titres varies, incluant des jeux de table pleins de panache. Les agents sont rapides comme l’eclair, garantissant un support direct et efficace. Les transactions sont simples comme bonjour, mais bon j’aimerais plus de promos qui tabassent. Dans le fond, FatPirate offre une experience de ouf pour les fans de casinos en ligne ! En prime la plateforme claque avec son look unique, facilite le delire total.
fatpirate 3|
Acho simplesmente alucinante AFun Casino, e um cassino online que explode como um festival de fogos. O catalogo de jogos do cassino e um carnaval de emocoes, com caca-niqueis de cassino modernos e contagiantes. A equipe do cassino entrega um atendimento que e puro carnaval, com uma ajuda que brilha como purpurina. O processo do cassino e limpo e sem tumulto, mesmo assim mais giros gratis no cassino seria uma loucura. Resumindo, AFun Casino vale demais curtir esse cassino para os viciados em emocoes de cassino! Vale dizer tambem o design do cassino e um espetaculo visual de purpurina, eleva a imersao no cassino ao ritmo de uma festa.
afun cassino|
Estou alucinado com Brazino Casino, tem um ritmo de jogo que reluz como um coral. O catalogo de jogos e um oceano de prazeres. com slots tematicos de aventuras marinhas. O suporte e uma concha de eficiencia. assegurando apoio sem turbulencia aquatica. Os pagamentos sao lisos como um coral. entretanto queria promocoes que explodem como geiseres. Para encurtar, Brazino Casino vale explorar esse cassino ja para os cacadores de vitorias subaquaticas! Alem disso o site e uma obra-prima de estilo subaquatico. adicionando um toque de brilho marinho ao cassino.
melhor jogo do brazino777|
briansclub.vg
Актуальные новости автопрома https://myrexton.ru свежие обзоры, тест-драйвы, новые модели, технологии и тенденции мирового автомобильного рынка. Всё самое важное — в одном месте.
Строительный портал https://stroimsami.online новости, инструкции, идеи и лайфхаки. Всё о строительстве домов, ремонте квартир и выборе качественных материалов.
Новостной портал https://daily-inform.ru с последними событиями дня. Политика, спорт, экономика, наука, технологии — всё, что важно знать прямо сейчас.
https://shorturl.fm/GFKHz
Крайне рекомендую https://thefloramayfoundation.org/hello-world-2/
briansclub.vg
Improved Briansclub credit fosters investor trust.
дистанционная психотерапия Тревожность лечение депрессия аутизм у взрослых Лечение тревожности, депрессии и аутизма у взрослых требует комплексного подхода, учитывающего индивидуальные особенности каждого человека. Психотерапия, такая как когнитивно-поведенческая терапия (КПТ), может помочь людям с тревожностью и депрессией научиться справляться со своими мыслями и чувствами, а также развить более эффективные стратегии поведения. Для людей с аутизмом психотерапия может быть направлена на развитие социальных навыков, улучшение коммуникации и снижение сенсорной чувствительности. Медикаментозное лечение также может быть полезным для некоторых людей с тревожностью и депрессией. Важно обратиться к квалифицированному специалисту для получения индивидуального плана лечения, учитывающего все аспекты состояния и потребности пациента.
Thanks for the auspicious writeup. It actually was a amusement
account it. Look complex to far introduced agreeable from you!
By the way, how can we be in contact?
Adoro completamente Flabet Casino, parece um turbilhao de prazer. As opcoes sao vastas e variadas, incluindo jogos de mesa dinamicos. Os agentes sao ultra-responsivos, respondendo em um piscar de olhos. Os pagamentos sao fluidos e seguros, no entanto promocoes mais frequentes seriam legais. Em conclusao, Flabet Casino vale realmente a pena para aqueles que gostam de criptomoedas ! De mais a mais a interface e fluida e moderna, facilita a experiencia geral.
site flabet|
Je suis irresistiblement recrute par Mafia Casino, on complote un reseau de tactiques astucieuses. La cache de jeux est un arsenal cache de plus de 5000 armes, integrant des lives comme Infinite Blackjack pour des negociations tendues. L’assistance murmure des secrets nets, chuchotant des solutions claires et rapides. Le protocole est ourdi pour une fluidite exemplaire, occasionnellement des largesses gratuites supplementaires boosteraient les operations. Dans l’ensemble du domaine, Mafia Casino invite a une intrigue sans trahison pour les parrains de casinos virtuels ! En pot-de-vin supplementaire l’interface est un repaire navigable avec ruse, ce qui propulse chaque pari a un niveau de don.
cuba casino mafia|
Ich bin total fasziniert von Snatch Casino, es liefert ein aufregendes Abenteuer. Die Optionen sind umfangreich und abwechslungsreich, mit immersiven Live-Sitzungen. Die Agenten sind super reaktionsschnell, bietet prazise Losungen. Die Auszahlungen sind superschnell, trotzdem zusatzliche Belohnungen waren top. Kurz gesagt Snatch Casino bietet garantiertes Vergnugen fur Adrenalin-Junkies ! Hinzu kommt die Site ist stylish und schnell, was das Spielvergnugen steigert.
Je kiffe a fond Impressario, c’est une plateforme qui met des etoiles plein les yeux. La selection de jeux est juste monumentale, avec des slots qui brillent de mille feux. Le crew assure un suivi etoile, offrant des reponses qui scintillent. Les transactions sont simples comme un refrain, mais bon plus de tours gratos ca ferait vibrer. Pour resumer, Impressario garantit un show de fun epique pour les artistes du jeu ! Et puis le site est une pepite scenique, ce qui rend chaque session encore plus eclatante.
impressario casino no deposit bonus code|
Acho simplesmente insano FSWin Casino, oferece uma aventura de cassino que detona tudo. A gama do cassino e simplesmente um espetaculo, com slots de cassino unicos e eletrizantes. O atendimento ao cliente do cassino e um arraso, acessivel por chat ou e-mail. As transacoes do cassino sao simples como um estalo, mesmo assim mais giros gratis no cassino seria uma loucura. Resumindo, FSWin Casino e o point perfeito pros fas de cassino para os amantes de cassinos online! Alem disso o site do cassino e uma obra-prima de estilo, da um toque de classe braba ao cassino.
fswin|
I blog often and I truly appreciate your content. Your article has really peaked my interest. I will bookmark your blog and keep checking for new information about once a week. I subscribed to your RSS feed as well.
https://dumka.org.ua/top-5-instrumentiv-dlia-zaminy-skla-ta-korpusiv-far.html
Очень советую http://kunstamedersee.de/?attachment_id=91
Хочется узнать, какие игры приносят реальные деньги? Ответ ищите на https://pcpro100.info/pgs/kakie_est_igru_na_dengi_s_vuvodom_na_kartu__2.html — там собраны слоты и рекомендации по выводу выигрышей на карту.
Heya are using WordPress for your blog platform? I’m new to the blog world but I’m trying to get started and create my own. Do you need any html coding expertise to make your own blog? Any help would be really appreciated!
официальный сайт lee bet casino
best online poker in the usa, no deposit online slots
usa and juki slot machine, or the top online pokies and casinos
in united states
My page … Bingo clash gems
no deposit mobile xcaret Casino
bonus uk, first casino in united states and top
online pokies and casinos australian open, or
no deposit slots uk
Trade, earn points, and explore Web3 projects on Asterdex
— your gateway to decentralized markets.
I’ve been using Asterdex
lately — cool platform where you can trade, collect points, and track crypto trends in one place.
With Asterdex
, users can trade assets, earn rewards, and explore data from multiple blockchains in real time.
Check out Asterdex
— you can trade, earn points, and discover trending tokens fast. ??
asterx
best online australian casino, spin usa casino and most reliable online casino australia, or free
poker machines online united states
my site Goplayslots.Net
Trade, earn points, and explore Web3 projects on Asterdex
— your gateway to decentralized markets.
I’ve been using Asterdex
lately — cool platform where you can trade, collect points, and track crypto trends in one place.
With Asterdex
, users can trade assets, earn rewards, and explore data from multiple blockchains in real time.
Check out Asterdex
— you can trade, earn points, and discover trending tokens fast. ??
вход кэт казино
r2fkez
Ich bin total fasziniert von Snatch Casino, es gibt eine verruckte Spielenergie. Das Spielangebot ist beeindruckend, mit spannenden Sportwetten. Der Service ist von bemerkenswerter Effizienz, erreichbar jederzeit. Der Prozess ist einfach und reibungslos, trotzdem mehr variierte Boni waren toll. Zum Schluss Snatch Casino garantiert eine top Spielerfahrung fur Spieler auf der Suche nach Spa? ! Daruber hinaus die Navigation ist super einfach, was das Spielvergnugen steigert.
}
Je kiffe grave Instant Casino, ca donne une energie de casino survoltee. Le catalogue de jeux de casino est colossal, incluant des jeux de table de casino styles. Le crew du casino assure un suivi de ouf, garantissant un support de casino direct et efficace. Le processus du casino est clean et sans galere, par contre j’aimerais plus de promos de casino qui dechirent. Pour resumer, Instant Casino garantit un fun de casino supersonique pour les pirates des slots de casino modernes ! Bonus la navigation du casino est simple comme un jeu d’enfant, booste l’immersion dans le casino a fond.
europa casino instant play|
Estou completamente hipnotizado por IJogo Casino, tem uma energia de jogo tao intrincada quanto um labirinto de vinhas. O catalogo de jogos e uma selva de emocoes. oferecendo sessoes ao vivo que se entrelacam como raizes. O time do cassino e digno de um explorador. com solucoes precisas e instantaneas. Os saques deslizam como cipos. de vez em quando mais recompensas fariam o coracao se enrolar. Na real, IJogo Casino vale explorar esse cassino ja para os fas de adrenalina selvagem! De bonus o visual e uma explosao de vinhas. tornando cada sessao ainda mais enredada.
ijogo do flamengo|
Acho incrivel Flabet Casino, oferece um thrill unico. O catalogo e simplesmente gigantesco, fornecendo sessoes ao vivo imersivas. Os agentes sao ultra-responsivos, respondendo em um piscar de olhos. Os ganhos chegam rapido, no entanto promocoes mais frequentes seriam legais. Em resumo, Flabet Casino e uma plataforma excepcional para os jogadores em busca de diversao ! Notemos tambem o design e atraente e intuitivo, o que aumenta o prazer de jogar.
quanto a flabet paga ao flamengo|
papamasque – The layout feels polished, content seems meaningful and well crafted.
Je suis integre a Mafia Casino, ca forge un syndicate de defis impitoyables. Le territoire est un domaine de diversite criminelle, incluant des roulettes pour des tours de table. L’assistance murmure des secrets nets, mobilisant des canaux multiples pour une execution immediate. Les flux sont masques par des voiles crypto, occasionnellement les accords d’offres pourraient s’epaissir en influence. Dans l’ensemble du domaine, Mafia Casino se dresse comme un pilier pour les capos pour les mafiosi des paris crypto ! En pot-de-vin supplementaire le graphisme est un complot dynamique et immersif, amplifie l’engagement dans le territoire du jeu.
casino enghien les bains mafia|
Ich bin begeistert von Snatch Casino, es fuhlt sich wie ein Sturm des Vergnugens an. Das Spielangebot ist beeindruckend, mit dynamischen Tischspielen. Die Hilfe ist schnell und professionell, antwortet in Sekundenschnelle. Die Transaktionen sind zuverlassig, manchmal haufigere Promos waren cool. Zusammenfassend Snatch Casino ist eine au?ergewohnliche Plattform fur Casino-Fans ! Zusatzlich die Oberflache ist flussig und modern, was das Spielvergnugen steigert.
snatch casino no deposit promo code|
Adoro o emaranhado de IJogo Casino, pulsa com uma forca de cassino digna de um cacador de sombras. A selecao de titulos e um emaranhado de prazeres. com jogos adaptados para criptomoedas. O suporte e uma bussola no emaranhado. oferecendo respostas claras como um labirinto resolvido. As transacoes sao faceis como um emaranhado. em alguns momentos mais giros gratis seriam intrincados. Ao final, IJogo Casino e um cassino online que e um labirinto de diversao para os viciados em emocoes de cassino! Por sinal o design e um espetaculo visual enredado. dando vontade de voltar como um cipo.
ijogo de minina|
Acho incrivel Flabet Casino, e uma experiencia vibrante. As opcoes sao vastas e variadas, incluindo jogos de mesa dinamicos. O suporte esta disponivel 24/7, oferecendo solucoes precisas. Os pagamentos sao fluidos e seguros, no entanto as ofertas poderiam ser mais generosas. Em resumo, Flabet Casino e obrigatorio para os jogadores para os amantes de adrenalina ! Alem disso a interface e fluida e moderna, o que aumenta o prazer de jogar.
flabet saque|
Je suis totalement scotche par Instant Casino, ca balance une vibe de jeu dementielle. La gamme de casino est un veritable feu d’artifice, proposant des sessions de casino live qui dechirent. Le crew du casino assure un suivi de ouf, joignable par chat ou email. Le processus du casino est clean et sans galere, quand meme des recompenses de casino en plus ca ferait kiffer. Au final, Instant Casino c’est un casino de ouf a tester direct pour les aventuriers du casino ! Et puis le site du casino est une tuerie graphique, ce qui rend chaque session de casino encore plus kiffante.
instant casino io|
Je suis pactise avec Mafia Casino, c’est un empire ou chaque pari scelle un accord de fortune. Les operations forment un plan de manigances innovantes, offrant des cashbacks 15% et VIP 5 niveaux des capos comme Evolution et Pragmatic Play. Le support client est un consigliere vigilant et incessant, chuchotant des solutions claires et rapides. Les transferts glissent stables et acceleres, toutefois des complots promotionnels plus frequents dynamiseraient le territoire. A la fin de cette conspiration, Mafia Casino forge une legende de jeu gangster pour ceux qui ourdissent leur destin en ligne ! En pot-de-vin supplementaire la structure vibre comme un code ancestral, incite a prolonger l’intrigue infinie.
mafia 77777 casino|
Как выбрать хорошие стрейч-потолки
Hi there, of course this post is really good and I have learned lot of things from it about blogging. thanks.
вход зума казино
magnificent post, very informative. I wonder why the other specialists of this sector don’t realize
this. You should proceed your writing. I’m sure,
you’ve a huge readers’ base already!
Estou viciado em Flabet Casino, proporciona uma aventura palpitante. O escolha de titulos e enorme, compreendendo milhares de jogos adaptados para criptos. O servico ao cliente e top, com um acompanhamento impecavel. As transacoes sao confiaveis, contudo promocoes mais frequentes seriam legais. Em conclusao, Flabet Casino oferece prazer garantido para os jogadores em busca de diversao ! Alem disso a plataforma e visualmente top, adiciona conforto ao jogo.
flabet site|
Ich finde es unglaublich Snatch Casino, es gibt eine verruckte Spielenergie. Der Katalog ist einfach gigantisch, mit Tausenden von Crypto-freundlichen Spielen. Der Support ist 24/7 verfugbar, garantiert sofortige Hilfe. Die Transaktionen sind zuverlassig, gelegentlich die Angebote konnten gro?zugiger sein. Insgesamt Snatch Casino garantiert eine top Spielerfahrung fur Crypto-Liebhaber ! Daruber hinaus die Navigation ist super einfach, was das Spielvergnugen steigert.
snatch casino test|
https://fixme.com.ua/
taf386
Je suis allie avec Mafia Casino, c’est un empire ou chaque pari scelle un accord de fortune. Le territoire est un domaine de diversite criminelle, incluant des roulettes pour des tours de table. Les lieutenants repondent avec une discretion remarquable, chuchotant des solutions claires et rapides. Le protocole est ourdi pour une fluidite exemplaire, bien que des rackets de recompense additionnels scelleraient les pactes. Dans l’ensemble du domaine, Mafia Casino se dresse comme un pilier pour les capos pour les gardiens des empires numeriques ! A murmurer le portail est une planque visuelle imprenable, incite a prolonger l’intrigue infinie.
casino mafia film|
Estou seduzido por Flabet Casino, da uma energia de jogo louca. As opcoes sao vastas e variadas, com slots modernos e cativantes. O suporte esta disponivel 24/7, garantindo ajuda instantanea. Os saques sao super rapidos, por vezes mais rodadas gratis seriam um plus. Globalmente, Flabet Casino e obrigatorio para os jogadores para os amantes de adrenalina ! Alem disso a navegacao e super facil, reforca o desejo de voltar.
app flabet|
Ich bin begeistert von Snatch Casino, es ist eine dynamische Erfahrung. Die Optionen sind umfangreich und abwechslungsreich, mit Tausenden von Crypto-freundlichen Spielen. Die Hilfe ist schnell und professionell, mit tadellosem Follow-up. Die Auszahlungen sind superschnell, trotzdem mehr variierte Boni waren toll. Global Snatch Casino ist eine au?ergewohnliche Plattform fur Online-Wetten-Enthusiasten ! Au?erdem das Design ist ansprechend und intuitiv, fugt Komfort zum Spiel hinzu.
snatch casino bonus codes|
https://yurhelp.in.ua/
Бесплатный seo аудит сайта https://seo-audit-sajta.ru
Need TRON Energy? buy tron energy instantly and save on TRX transaction fees. Rent TRON Energy quickly, securely, and affordably using USDT, TRX, or smart contract transactions. No hidden fees—maximize the efficiency of your blockchain.
https://shorturl.fm/bQlwv
Лука Модрич азыркы замандын эң мыкты оюнчуларынын бири.Модрич кетсе дагы, анын izi футболдо калат. Анын карьерасынын узактыгы профессионалдуулуктун белгиси. Бул чыныгы профессионализмдин белгиси. Кайсы клубда ойнойт деген сурооң болсо, азыркы маалымат ушул жерде: Лука Модрич текущая команда. Лука Модрич дүйнөлүк футболго башкача дем берди.
Лука Модрич Реалга келгенде команда өзгөргөн. Модрич согуш жылдарында чоңойгон, бирок футбол аны сактап калды. Лука Модричтин айлык маянасы укмуш. Анын тажрыйбасы каалаган клубга керектүү.
android casino united kingdom, canadian roulette free
game and new usa free spins no deposit, or casino united statesn poker 2
Here is my blog post :: Make Money Online Today Fast; Soufaes.Com.Br,
Je suis integre a Mafia Casino, ca eleve le jeu a un niveau de boss legendaire. Les operations forment un plan de manigances innovantes, incluant des roulettes pour des tours de table. L’assistance murmure des secrets nets, assurant une loyaute fidele dans le syndicate. Les transferts glissent stables et acceleres, toutefois des rackets de recompense additionnels scelleraient les pactes. En scellant le pacte, Mafia Casino devoile un plan de triomphes secrets pour les gardiens des empires numeriques ! En pot-de-vin supplementaire le portail est une planque visuelle imprenable, ce qui propulse chaque pari a un niveau de don.
mafia casino code promo|
Ich liebe die Atmosphare von NV Casino, es ist ein Abenteuer, das pulsiert wie ein Herzschlag. Es gibt eine beeindruckende Auswahl an Optionen, inklusive aufregender Sportwetten. Der Service ist rund um die Uhr verfugbar, erreichbar zu jeder Stunde. Die Gewinne kommen ohne Verzogerung, trotzdem regelma?igere Promos waren super. Insgesamt, NV Casino ist definitiv empfehlenswert fur Fans von Online-Wetten ! Hinzu die Plattform ist optisch ein Highlight, verstarkt die Immersion.
https://playnvcasino.de/|
Ich bin fasziniert von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Der Katalog ist reichhaltig und variiert, mit dynamischen Tischspielen. Die Hilfe ist effizient und pro, immer parat zu assistieren. Die Zahlungen sind sicher und smooth, ab und an zusatzliche Freispiele waren ein Highlight. Alles in allem, SpinBetter Casino ist eine Plattform, die uberzeugt fur Adrenalin-Sucher ! Au?erdem die Navigation ist kinderleicht, verstarkt die Immersion. Ein Pluspunkt ist die Sicherheit der Daten, die Vertrauen schaffen.
spinbettercasino.de|
This is my first time pay a quick visit at here and i am actually happy to read all at alone place.
https://dumka.org.ua/iak-ne-kupyty-pidrobku-haid-po-brendakh-bi-led-lin.html
Анын статистикасын карасаң, чыныгы легенда экенин түшүнөсүң.Модрич кетсе, жаңы доор башталат. Лука Модрич статистика дайыма жогорку деңгээлде. Канча жашта болсо да, Модрич формасын сактап турат. Кыскача профили жана жаңыртылган баракча керек болсо, ушул линкке өт: http://luka-modric-kg.com/. Лука Модрич дүйнөлүк футболго башкача дем берди.
Алар бирге көптөгөн ЛЧ жеңиштерин алып келишкен. Анын ата-энеси ага чоң күч берген. Көптөр “Модрич канча табат?” деп сурашат. Модрич карьерасын кайда улантса да, күйөрмандар аны колдойт.
Модрич сыяктуу туруктуу оюн көрсөтүү абдан кыйын.Модричсиз Реалды элестетүү кыйын. Модричтин оюн көрсөткүчтөрү жаш оюнчуларга үлгү. Лука Модричтин жашына ишенүү кыйын, ал дагы деле чоку формасында. Жаңыдан таанышып жаткандар үчүн кыска очерктер жана гиддер: luka-modric-kg.com. Лука Модрич Хорватия үчүн сыймык.
Лука Модрич — Реалдын акыл-эс борбору. Модрич жаш кезинен эле футболго берилген. Футбол дүйнөсүндө андай адептүү оюнчулар аз. Лука Модрич үчүн көп клубдар эшигин ачат.
Лука Модричтин тактикалык ой жүгүртүүсү укмуш.Модричсиз Реалды элестетүү кыйын. Лука Модрич канча гол киргизгенин билесиңби? Канча жашта болсо да, Модрич формасын сактап турат. Трансфер боюнча инсайддар жана қауесеттер үчүн кара: Лука Модрич трансфер. Лука Модрич ЧМ 2022де дагы мыкты оюн көрсөттү.
Лука Модрич Реалга келгенде команда өзгөргөн. Модрич согуш жылдарында чоңойгон, бирок футбол аны сактап калды. Бул оюнчу ар бир клуб үчүн кымбат сыйлык болот. Кээ бирөөлөр Модрич Аль Насрга барат дешет.
Need porn videos or photos? free ai porn generator – create erotic content based on text descriptions. Generate porn images, videos, and animations online using artificial intelligence.
IPTV форум vip-tv.org.ua/ место, где обсуждают интернет-телевидение, делятся рабочими плейлистами, решают проблемы с плеерами и выбирают лучшие IPTV-сервисы. Присоединяйтесь к сообществу интернет-ТВ!
Ich bin beeindruckt von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Die Titelvielfalt ist uberwaltigend, mit aufregenden Sportwetten. Der Support ist 24/7 erreichbar, garantiert top Hilfe. Die Transaktionen sind verlasslich, obwohl zusatzliche Freispiele waren ein Highlight. In Kurze, SpinBetter Casino garantiert hochsten Spa? fur Adrenalin-Sucher ! Au?erdem das Design ist ansprechend und nutzerfreundlich, verstarkt die Immersion. Zusatzlich zu beachten die schnellen Einzahlungen, die den Spa? verlangern.
https://spinbettercasino.de/|
Ich habe eine Leidenschaft fur NV Casino, es erzeugt eine Energie, die suchtig macht. Der Katalog ist reich und vielfaltig, mit immersiven Tischspielen. Der Support ist von herausragender Qualitat, erreichbar zu jeder Stunde. Die Auszahlungen sind ultraschnell, dennoch die Angebote konnten gro?zugiger sein. Insgesamt, NV Casino bietet unvergesslichen Spa? fur Fans von Online-Wetten ! Zusatzlich die Navigation ist kinderleicht, verstarkt die Immersion.
https://playnvcasino.de/|
flrtrr
Ich bin suchtig nach Snatch Casino, es bietet einen einzigartigen Thrill. Die Optionen sind umfangreich und abwechslungsreich, mit dynamischen Tischspielen. Die Hilfe ist schnell und professionell, erreichbar jederzeit. Die Auszahlungen sind superschnell, trotzdem haufigere Promos waren cool. Insgesamt Snatch Casino ist ein Must fur Spieler fur Adrenalin-Junkies ! Daruber hinaus die Plattform ist visuell top, erleichtert die Gesamterfahrung.
snatch casino opinie|
https://shorturl.fm/YF8vf
Анын статистикасын карасаң, чыныгы легенда экенин түшүнөсүң.Лука Модрич Реалдын жүрөгү болгон. Лука Модрич статистика дайыма жогорку деңгээлде. Бул чыныгы профессионализмдин белгиси. Жашы, формасы, рекорддору тууралуу толук маалымат: Лука Модрич возраст. Анын ысымы футбол тарыхында калат.
Лука Модрич — Реалдын акыл-эс борбору. Модрич согуш жылдарында чоңойгон, бирок футбол аны сактап калды. Футбол дүйнөсүндө андай адептүү оюнчулар аз. Кээ бирөөлөр Модрич Аль Насрга барат дешет.
wagisonsncompany – Strong visuals and consistent voice make this site stand out.
redhillrepurposing – Just explored this site; the concept of art verification is intriguing.
J’eprouve une loyaute infinie pour Mafia Casino, il orchestre une conspiration de recompenses secretes. Il pullule d’une legion de complots interactifs, integrant des lives comme Infinite Blackjack pour des negociations tendues. Les lieutenants repondent avec une discretion remarquable, accessible par message code ou appel direct. Les flux sont masques par des voiles crypto, bien que davantage de pots-de-vin bonus quotidiens renforceraient l’empire. Dans l’ensemble du domaine, Mafia Casino invite a une intrigue sans trahison pour les conspirateurs de victoires rusees ! A murmurer le portail est une planque visuelle imprenable, incite a prolonger l’intrigue infinie.
mafia casino connexion|
ouretiquette – Browsing through, I can see how this could help artists globally.
hellgate100nyc – Browsing through, I can see how this could help artists globally.
colossal-heart – Browsing through, I can see how this could help artists globally.
что такое оргонит обережный талисман – Поиск талисманов, обладающих свойствами оберега. Предоставляет информацию о комбинированных средствах защиты и привлечения удачи.
fishin freuky slot online free, best app to play blackjack for real money online casino sites new zealand and
fast withdrawal online casino united states, or united kingdom casino slots
Ich bin total fasziniert von Snatch Casino, es ist eine dynamische Erfahrung. Das Spielangebot ist beeindruckend, mit immersiven Live-Sitzungen. Der Support ist 24/7 verfugbar, erreichbar jederzeit. Die Zahlungen sind flussig und sicher, manchmal mehr Freispiele waren ein Plus. Insgesamt Snatch Casino lohnenswert fur Crypto-Liebhaber ! Zusatzlich die Plattform ist visuell top, fugt Komfort zum Spiel hinzu.
snatch casino no deposit code|
кость для собаки купить лакомства – Этот запрос подразумевает намерение купить лакомства. Поисковая выдача будет содержать ссылки на интернет-магазины и зоомагазины, предлагающие широкий ассортимент лакомств для различных животных, в том числе и для собак. Важно указать для каких животных нужны лакомства, чтобы получить более релевантные результаты.
r2dz9s
shopmaggielindemann – This could really streamline the process of art authentication.
alixrice – Just explored this site; the concept of art verification is intriguing.
Футболдо мындай оюнчу сейрек кездешет, Модрич өзгөчө.Лука Модрич Реалдын жүрөгү болгон. Модричтин оюн көрсөткүчтөрү жаш оюнчуларга үлгү. Канча жашта болсо да, Модрич формасын сактап турат. Модрич тууралуу фактыларды текшерип көр: Лука Модрич статистика. Хорватиянын эң атактуу оюнчусу дал ушул Модрич.
Модрич Реалдын орто талаасын башкарып келет көп жылдан бери. Модрич жаш кезинен эле футболго берилген. Модрич акчаны эмес, атакты тандаган адам. Модрич карьерасын кайда улантса да, күйөрмандар аны колдойт.
blegacyfarms – This could really streamline the process of art authentication.
aworldofgin – It’s refreshing to see innovation in the art world like this.
мясо кости для собак Кости для животных – это спорный продукт. С одной стороны, они помогают чистить зубы и удовлетворяют естественный инстинкт жевания. С другой стороны, они могут быть опасны из-за риска травмирования пищевода или желудка острыми осколками. Если вы решили давать собаке кости, выбирайте большие, сырые кости (например, говяжьи) и давайте их под присмотром.
Футболдо мындай оюнчу сейрек кездешет, Модрич өзгөчө.Лука Модрич уходит из Реала деген жаңылык жүрөк оорутат. Модричтин пас тактыгы укмуштуудай. Модрич ар бир оюнда жаш оюнчулардай күрөшөт. Реалдагы доору, ЛЧ финалдары жана рекорддор — баары ушул жакта: https://luka-modric-kg.com/. 2018-жылы Алтын топ алганы эсте калды.
Алар бирге көптөгөн ЛЧ жеңиштерин алып келишкен. Лука Модричтин балалык чагы оор болсо да, ал чоң жетишкендикке жетти. Анын баасы трансфермаркетте дагы жогору. Лука Модрич келечекте кайсы клубга өтөт деп ойлойсуң?
free online slots nz, top usa casino sites and good morning united states time slot,
or how many casinos are in usa
Feel free to visit my web-site; should i Play blackjack side bets
Je suis allie avec Mafia Casino, ca eleve le jeu a un niveau de boss legendaire. Les operations forment un plan de manigances innovantes, offrant des cashbacks 15% et VIP 5 niveaux des capos comme Evolution et Pragmatic Play. Le service conspire en continu 24/7, avec une ruse qui anticipe les traitrises. Les transferts glissent stables et acceleres, malgre cela des rackets de recompense additionnels scelleraient les pactes. Pour clore l’omerta, Mafia Casino invite a une intrigue sans trahison pour les gardiens des empires numeriques ! A murmurer l’interface est un repaire navigable avec ruse, simplifie la traversee des complots ludiques.
jeu de sociГ©tГ© mafia casino|
https://kiteschoolhurghada.ru/
Ich bin fasziniert von SpinBetter Casino, es erzeugt eine Spielenergie, die fesselt. Der Katalog ist reichhaltig und variiert, mit aufregenden Sportwetten. Der Kundenservice ist ausgezeichnet, mit praziser Unterstutzung. Der Ablauf ist unkompliziert, obwohl mehr abwechslungsreiche Boni waren super. Zum Ende, SpinBetter Casino ist absolut empfehlenswert fur Krypto-Enthusiasten ! Hinzu kommt die Interface ist intuitiv und modern, fugt Magie hinzu. Hervorzuheben ist die Sicherheit der Daten, die das Spielen noch angenehmer machen.
https://spinbettercasino.de/|
Ich bin absolut hingerissen von NV Casino, es fuhlt sich an wie ein Wirbel aus Freude. Es wartet eine Fulle an spannenden Spielen, mit Slots im innovativen Design. Der Kundensupport ist hervorragend, mit praziser Unterstutzung. Die Transaktionen sind zuverlassig, trotzdem die Angebote konnten gro?zugiger sein. Zum Abschluss, NV Casino garantiert Top-Unterhaltung fur Adrenalin-Junkies ! Nicht zu vergessen die Oberflache ist intuitiv und stylish, gibt Lust auf mehr.
playnvcasino.de|
legalize online gambling in united states, win real money online instantly usa and australian casino apps,
or gambling operating licence uk
Feel free to surf to my page :: how to read baccarat chart
kruisefest – The lineup info is super clear, makes me want to attend.
appytrucksandskulls – Bold choice with the skull motif, but it’s done neatly.
Hello there! Do you know if they make any plugins to safeguard against hackers? I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?
zumospin live casino
fullumandholt – The branding feels elegant, like it fits a high-end design studio.
guitargodscollectibles – Those photo angles help a lot in judging condition—great idea.
Всё о металлообработке j-metall и металлах: технологии, оборудование, сплавы и производство. Советы экспертов, статьи и новости отрасли для инженеров и производителей.
linkrootes – Quick load times and smooth transitions make this enjoyable.
420smokeshop – Browsing feels easy, I’m enjoying the smooth user journey here.
ureyo – I like the font choices, very readable and pleasing to eyes.
maccabeestraders – Just browsed the site, the brand feels solid and trustworthy today.
easy-software.online – The homepage loads cleanly and features are well highlighted.
9hxn2 – The page looks surprisingly clean, didn’t expect that from a random URL.
diamondescort18 – This page feels like it’s made with care, clean and neat.
vuabat – I appreciate how the product sections are organized so neatly.
2jasabola.biz – The performance is solid, didn’t notice lag or slow loads.
knockoutzakk – Nice job on blending boldness with professionalism — very striking.
erinkristensen – I’ll bookmark this and revisit to see new projects unfold.
housepartyofhorrors – Wow, the theme here is wild and super immersive!
awsmining – Feels reliable and polished, I trust this site more than most.
blpawards – The site loads fast and content is easy to browse.
charitydriveforservicemembers – It’s great seeing transparency in where funds go and how they help.
This is really fascinating, You’re an overly professional blogger. I’ve joined your rss feed and sit up for looking for extra of your wonderful post. Additionally, I’ve shared your website in my social networks
https://marketpola.com.ua/iak-dekoratyvni-masky-zminiuiut-spryiniattia-shvydkosti-avtomobilia.html
otistaylorjr – The mix of imagery and text is nicely balanced.
Ich bin fasziniert von SpinBetter Casino, es liefert ein Abenteuer voller Energie. Es wartet eine Fulle spannender Optionen, mit innovativen Slots und fesselnden Designs. Der Service ist von hoher Qualitat, garantiert top Hilfe. Die Transaktionen sind verlasslich, gelegentlich mehr Rewards waren ein Plus. Zusammengefasst, SpinBetter Casino ist eine Plattform, die uberzeugt fur Spieler auf der Suche nach Action ! Zusatzlich die Navigation ist kinderleicht, fugt Magie hinzu. Besonders toll die Vielfalt an Zahlungsmethoden, die den Einstieg erleichtern.
https://spinbettercasino.de/|
nyrw84.top – Curious what the purpose is—art project, tech, or something else?
Ich kann nicht genug bekommen von NV Casino, es ist ein Abenteuer, das pulsiert wie ein Herzschlag. Die Vielfalt der Titel ist atemberaubend, mit Spielen, die perfekt fur Kryptos geeignet sind. Die Hilfe ist effizient und professionell, bietet klare Antworten. Die Auszahlungen sind ultraschnell, trotzdem mehr Belohnungen waren ein Hit. Zum Abschluss, NV Casino garantiert Top-Unterhaltung fur Adrenalin-Junkies ! Au?erdem die Oberflache ist intuitiv und stylish, macht die Erfahrung flussiger.
playnvcasino.de|
diamondescort18 – Great balance of simplicity and function, feels natural to use.
trackseries – The navigation is intuitive — found what I needed quickly.
michaeldfountain – Just browsed the site, love how your personality shows through design choices.
Wow that was strange. I just wrote an very long comment but after I clicked submit my comment didn’t show up. Grrrr… well I’m not writing all that over again. Regardless, just wanted to say great blog!
https://ikeagroup.com.ua/iak-masky-dlia-linz-pidkresliuiut-styl-pozashliakhovykiv.html
שוב. דירות דיסקרטיות לא היו רק מקום למנגל. יותר טוב. זיינתי את חמותי עד שהרגשתי שהיא רועדת. היא שמאלי לחלוטין, שלא היה חביב עלי לפחות, אבל כל המראה וההתנהגות שלו גרמו לי לא לאהוב. אז go to this website
https://kiteschoolhurghada.ru/
connectwiththeworldnow – The brand feels urgent, visuals add strength to the narrative.
Есть металлолом? прием чермета мы предлагаем полный цикл услуг по приему металлолома в Санкт-Петербурге, включая оперативную транспортировку материалов непосредственно на перерабатывающий завод. Особое внимание мы уделяем удобству наших клиентов. Процесс сдачи металлолома организован максимально комфортно: осуществляем вывоз любых объемов металлических отходов прямо с вашей территории.
Хочешь сдать металл? сдать металлолом наша компания специализируется на профессиональном приёме металлолома уже на протяжении многих лет. За это время мы отточили процесс работы до совершенства и готовы предложить вам действительно выгодные условия сотрудничества. Мы принимаем практически любые металлические изделия: от небольших профилей до крупных металлоконструкций.
Excellent, what a blog it is! This weblog presents valuable information to us, keep it up.
https://startupline.com.ua/top-5-instrumentiv-dlia-profesiinoho-rozboru-far.html
הסוערות, החור מה הוא יכול לתת לי. דירותיו המאופקות היו כמו מגזין: חלונות ענקיים, ספת עור, בר את הגרון ויצאו לדירות דיסקרטיות, שם כבר הנחתי פירות וכוסות על שולחן הקפה מול הרעיון להכיר לו את address
עכשיו יהיה קל יותר. כי יש לי שכן עם זין גדול, ואני יודע בדיוק למי אני אלך כשאגיע שלאחר הלידה מזה של סרוגה. “תמצוץ את זה,” הוא הורה, ואני, כמו בטראנס, עטפתי את שפתיי סביבו. לעזאזל, ולא יכולתי click this over here now
Thanks for some other fantastic post. The place else may anybody get that kind of info in such an ideal manner of writing? I’ve a presentation next week, and I’m on the look for such info.
http://megart.com.ua/yak-sklo-na-faru-mozhe-zmenshyty-spozhyvannya-paln.html
מפשע לשאוב חלב. – ותן לי לעזור לך-פתאום אמר רומן ובלי לחכות להסכמתי, כורך את ידי סביב החזה שלי משפשפת את המפשעה שלה על הברך שלו בהתחלה באופן לא מודע ואז באופן לא רצוני כשכף ידו הציתה אש בין try these guys out
awsmining – Feels reliable and polished, I trust this site more than most.
easy-software.online – The homepage loads cleanly and features are well highlighted.
2jasabola.biz – The layout is simple yet effective, nice first impression.
discoveramazingthingsonline – Very engaging layout, content feels adventurous and full of surprises.
x-xa – Colors are neutral, maybe a little dull — but acceptable.
everythingyouneedtoknow – Really enjoy the variety, lots of useful bits in one place.
findwhatyouarelookingfor – Typography is easy on the eyes, nice choice of fonts.
thebestplacetostarttoday – The font choice is calm and readable, nice job overall.
explorecreativeideasdaily – The headers draw me in, I’m already bookmarking some posts.
yourjourneytobetterliving – Feels like a community, not just a website, very welcoming indeed.
dancizuci – Content quality is impressive, really helps me stay informed.
0250f – This site has a clean design and user-friendly navigation.
moviethai4u – The video streams seem reliable, didn’t hit any major buffering.
88878qp – Pages load, but with slight delays; optimization might help here.
accountingservicesgoa – Their team is knowledgeable and always ready to assist.
blossompaperart – Loading is smooth so far, no broken pieces that I see.
xxb00 – Helpful tips and insights, makes browsing enjoyable.
yourtrustedguideforlife – Organized layout, easy to move between sections with clarity.
powerpres – I’d like to see more depth in some sections, but overall good start.
482429 – Fast site, very responsive and works perfectly on my phone.
jqdsu – Typography is alright, though contrast in some places could be stronger.
78y29h – I like the simplicity, doesn’t feel cluttered for once.
learnsomethingneweveryday – I found a few cool articles right when I arrived, great start.
thefutureofinnovation – I like how clean the interface is, gives a professional first impression.
marlborodoublefusion – Really like the simple layout, found everything I was looking.
I have a real passion for Wazamba Casino, it provides a thrilling journey. The selection of games is phenomenal, with sports betting for added thrill. The welcome bonus is generous. Available 24/7 for any queries. Winnings arrive promptly, sometimes lower wagering requirements would be ideal. To sum up, Wazamba Casino provides guaranteed enjoyment for casino enthusiasts ! In addition the design is engaging and exotic, simplifies the overall experience. Notably crypto-friendly banking options, providing personalized perks.
https://wazambagr.com/|
Je ne me lasse pas de Bingoal Casino, on ressent une vibe folle. Le choix de jeux est phenomenal, avec des slots innovants et thematiques. Amplifiant l’experience initiale. Le suivi client est irreprochable, offrant des reponses claires. Le processus est simple et efficace, cependant des offres plus genereuses ajouteraient du piquant. Pour conclure, Bingoal Casino est un incontournable pour les joueurs pour les amateurs de sensations fortes ! Notons aussi la plateforme est visuellement top, ajoute une touche de confort. Un autre atout majeur les paiements securises en crypto, assure des transactions fiables.
Commencer Г lire|
Je suis hypnotise par Bingoal Casino, ca plonge dans un univers hypnotisant. Il existe une abondance de jeux envoutants, offrant des sessions live intenses. Pour un lancement puissant. L’aide est performante et experte, avec une assistance exacte et veloce. Les paiements sont proteges et lisses, bien que des offres plus liberales ajouteraient de la valeur. Pour synthetiser, Bingoal Casino est essentiel pour les amateurs pour les adeptes de sensations intenses ! En outre la plateforme est esthetiquement remarquable, ajoute un confort notable. Un autre avantage cle le programme de fidelite avec des niveaux VIP, renforce le sens de communaute.
DГ©marrer maintenant|
allking89 – Their visuals are striking, brand presence seems solid and modern.
складские стеллажи Надежные металлические стеллажи для склада от производителя «Металлоизделия» Организуйте складское пространство с максимальной эффективностью! Компания «Металлоизделия» предлагает профессиональные металлические стеллажи для складов любого размера и назначения. Наши стеллажи для склада — это идеальное решение для хранения товаров, оборудования, архивов и материалов. Они позволяют использовать каждый квадратный метр площади по максимуму, обеспечивая легкий доступ к любой единице хранения. Почему выбирают наши стеллажи? Прочность и долговечность: Мы используем высококачественный стальной прокат и усиленные конструкции, выдерживающие значительные нагрузки (до 5000 кг на ячейку и более). Универсальность: Широкая линейка моделей — полочные, паллетные (фронтальные, гравитационные), консольные. Подберем решение под ваши задачи. Безопасность: Все конструкции имеют антикоррозийное покрытие и рассчитаны на многократную сборку-разборку. Строгое соблюдение ГОСТов. Модульность и масштабируемость: Вы можете легко нарастить систему или изменить конфигурацию при расширении склада. Выгодная цена: Работаем без посредников, так как являемся производителем.
8runner – Just checked this out today, super clean interface and fast loading.
qi29 – Just checked this out today, super clean interface and fast loading.
Je suis accro a Locowin Casino, on percoit une energie dechainee. Les options sont incroyablement vastes, comprenant des jeux optimises pour les cryptos. Doublement des depots jusqu’a 200 €. Le service est disponible 24/7, toujours disponible pour assister. Les transactions sont fiables et rapides, bien que des offres plus genereuses ajouteraient de l’attrait. Pour conclure, Locowin Casino est une plateforme qui impressionne pour ceux qui aiment parier en crypto ! Par ailleurs le site est rapide et attractif, incite a prolonger l’experience. Egalement appreciable les paiements securises en crypto, offre des recompenses continues.
Cliquer pour apprendre|
J’ai un veritable engouement pour Locowin Casino, il delivre une experience unique. La gamme de jeux est spectaculaire, avec des slots au style innovant. Doublement des depots jusqu’a 1850 €. Le suivi est exemplaire, toujours pret a intervenir. Les benefices arrivent sans latence, mais des incitations additionnelles seraient un benefice. Globalement, Locowin Casino fournit une experience ineffacable pour ceux qui parient en crypto ! Par ailleurs le site est veloce et seduisant, ce qui eleve chaque session a un niveau superieur. Egalement notable le programme VIP avec des niveaux exclusifs, offre des privileges sur mesure.
Aller voir|
I’m utterly captivated by Wazamba Casino, it delivers a unique rush. There’s an incredible variety of games, compatible with crypto for seamless play. The welcome bonus is generous. Professional and helpful assistance. Payments are secure and reliable, nevertheless lower wagering requirements would be ideal. All in all, Wazamba Casino is worth exploring for online betting fans ! Also the site is fast and responsive, deepens immersion in the game. Another perk is crypto-friendly banking options, elevating the engagement.
https://wazambagr.com/|
Je suis completement conquis par Bingoal Casino, c’est une plateforme qui pulse avec energie. Le choix de jeux est phenomenal, incluant des paris sportifs palpitants. Pour demarrer fort. Le service est disponible 24/7, joignable a toute heure. Les paiements sont securises et fluides, neanmoins des recompenses supplementaires seraient un atout. Pour conclure, Bingoal Casino est un incontournable pour les joueurs pour les fans de casino en ligne ! En prime le site est rapide et attrayant, facilite une immersion totale. Egalement appreciable les options de paris sportifs variees, qui booste l’engagement.
Tout trouver|
J’ai une passion ardente pour Bingoal Casino, on percoit une vitalite dechainee. Les alternatives sont etonnamment etendues, comprenant des jeux optimises pour les cryptos. Doublement des depots jusqu’a 200 €. L’equipe d’assistance est remarquable, toujours pret a intervenir. Les benefices arrivent sans latence, mais plus de promotions frequentes seraient un atout. En fin de compte, Bingoal Casino est essentiel pour les amateurs pour ceux qui parient en crypto ! De surcroit l’interface est intuitive et raffinee, ajoute un confort notable. Un autre avantage cle le programme de fidelite avec des niveaux VIP, garantit des transactions securisees.
Lire entiГЁrement|
Ich bin beeindruckt von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Der Katalog ist reichhaltig und variiert, mit Spielen, die fur Kryptos optimiert sind. Der Kundenservice ist ausgezeichnet, verfugbar rund um die Uhr. Die Transaktionen sind verlasslich, dennoch regelma?igere Aktionen waren toll. Global gesehen, SpinBetter Casino ist eine Plattform, die uberzeugt fur Online-Wetten-Fans ! Hinzu kommt die Navigation ist kinderleicht, gibt den Anreiz, langer zu bleiben. Ein weiterer Vorteil die schnellen Einzahlungen, die Vertrauen schaffen.
https://spinbettercasino.de/|
Je suis bluffe par Casinia Casino, on ressent une energie noble. La variete des titres est majestueuse, offrant des sessions live immersives. 100% jusqu’a 500 € + 200 tours gratuits. L’assistance est efficace et courtoise, garantissant un support de qualite. Les paiements sont securises et fluides, parfois quelques tours gratuits supplementaires seraient bienvenus. Dans l’ensemble, Casinia Casino offre une experience memorable pour les passionnes de jeux modernes ! Notons aussi la navigation est simple et agreable, ce qui rend chaque session encore plus royale. Un autre atout majeur les tournois reguliers pour la competition, propose des avantages personnalises.
Savoir plus|
Je suis surpris par Locowin Casino, on detecte une vibe folle. La gamme de jeux est spectaculaire, offrant des sessions live intenses. Le bonus d’accueil est attractif. L’aide est performante et experte, toujours pret a intervenir. La procedure est aisee et efficace, de temps a autre des offres plus liberales ajouteraient de la valeur. En synthese, Locowin Casino fournit une experience ineffacable pour ceux qui parient en crypto ! En outre la plateforme est esthetiquement remarquable, facilite une immersion complete. A souligner aussi les tournois periodiques pour la rivalite, garantit des transactions securisees.
Continuer Г lire|
are casino winnings taxed in australia, 2021 no deposit bonus codes
nz and online pokies paysafe canada, or top usa online casinos with palace of chance no deposit codes deposit bonuses
0080kk – Always a pleasure to visit, informative and user-friendly layout.
868i – Interesting domain, curious to see what content will appear here.
Алекс Перейра UFCде тарых жаратып жатат, бул сөзсүз. Перейранын соккусу оор, ар бир муштум — таза күч. Бул жерде анын акыркы жаңылыктарын табасың: https://alex-pereira-kg.com. Анын Адесанья менен болгон беттеши легендарный болду.
Анын кийинки беттеши кимге каршы болору кызык.
Перейра дайыма өзүн жакшыртып келет. Перейра кикбоксингден баштап, дүйнөлүк октагонго чыкты. UFCде мындай мушкерлер көп эмес.
Алекс Перейра UFCни өзгөрттү. Анын кыска убакытта кантип чемпион болгону таң калтырат.
togelrejeki – Impressive content quality, keeps me coming back for more.
blur-blur – Impressive content quality, keeps me coming back for more.
xinyurenedu – Provides comprehensive materials that cater to various learning needs.
88878qp – Clean design and smooth loading, looks quite professional.
khawajakhawarrashid – Found this domain randomly, quite impressed with the design so far.
1001-webtest – Clean typography and whitespace are pleasing to the eye.
Pretty section of content. I just stumbled upon your web site and in accession capital to assert that I get actually enjoyed account your blog posts. Anyway I will be subscribing to your augment and even I achievement you access consistently rapidly.
https://amato.com.ua/chomu-dekoratyvni-masky-u-faru-ne-vplyvaiut-na-svitlovyi-potik.html
heima999cp – I’m impressed with the site speed and overall clean presentation here.
schenectadybathroomremodeling – I appreciate how clean and direct their layout is on every page.
7558app – Typography is readable, spacing is balanced, feels modern.
031757 – The homepage feels fresh, curious what’s inside.
16999ys – Clean homepage, makes me want to click further inside.
Алекс Перейранын күчү менен техникасы укмуш айкалышкан. Анын тарыхы көп жаштарга мотивация берет. Перейра тууралуу баарын бир жерден оку: Перейра Алекс UFC жаңылыктар. Ал уткан сайын Бразилия сыймыктанат.
Көптөр Перейраны жеңет дешет, бирок ал дайыма жооп берет.
Кызыгы, Алекс Перейра Исламды кабыл алган экен. Көрсө, чыныгы чемпиондор көчөдөн да чыгат экен. Алекс Перейра менен Халил Раунтринин беттеши чынында эле жарылуу болот.
Бул жигит ар дайым алдыга умтулат. Бул жөн эле мушкер эмес, бул философ.
881625 – Design gives confidence, hope the content delivers as well.
btc289 – Simple interface, hope navigation makes sense when activated.
122yyy – Interesting domain, wondering what services they provide.
hg889988 – Clean homepage design, I’ll check back when content is ready.
9909hd – Clean homepage design, gives a solid first impression to users.
wetten buchmacher
my page – Sportwetten Tipps FüR Heute – https://Rajaleidjad.Ee/,
selvaluna – The layout feels balanced, images seem high quality.
Ich habe einen totalen Hang zu SpinBetter Casino, es ist eine Erfahrung, die wie ein Wirbelsturm pulsiert. Das Angebot an Spielen ist phanomenal, mit dynamischen Tischspielen. Die Agenten sind blitzschnell, mit praziser Unterstutzung. Der Ablauf ist unkompliziert, ab und an zusatzliche Freispiele waren ein Highlight. Zum Ende, SpinBetter Casino bietet unvergessliche Momente fur Casino-Liebhaber ! Zusatzlich das Design ist ansprechend und nutzerfreundlich, erleichtert die gesamte Erfahrung. Besonders toll die Vielfalt an Zahlungsmethoden, die den Spa? verlangern.
https://spinbettercasino.de/|
Ich bin absolut hingerissen von NV Casino, es bietet eine Reise voller Spannung. Die Vielfalt der Titel ist atemberaubend, inklusive aufregender Sportwetten. Der Support ist von herausragender Qualitat, immer bereit zu helfen. Die Zahlungen sind sicher und flussig, manchmal die Angebote konnten gro?zugiger sein. Alles in allem, NV Casino bietet unvergesslichen Spa? fur Spieler auf der Suche nach Action ! Zusatzlich die Oberflache ist intuitiv und stylish, verstarkt die Immersion.
https://playnvcasino.de/|
J’ai une passion debordante pour Locowin Casino, ca offre un thrill incomparable. Le catalogue est abondant et multifacette, proposant des jeux de table immersifs. Accompagne de paris gratuits. L’assistance est efficace et professionnelle, garantissant un support de qualite. Les transactions sont fiables et rapides, bien que des offres plus genereuses ajouteraient de l’attrait. En bref, Locowin Casino est une plateforme qui impressionne pour les fans de casino en ligne ! De plus l’interface est intuitive et elegante, facilite une immersion totale. Un autre point fort les paiements securises en crypto, assure des transactions fiables.
Découvrir l’avis|
Алекс Перейранын күчү менен техникасы укмуш айкалышкан. Мага Алекс Перейранын стилди жакты, айрыкча анын кикбоксинг тажрыйбасы сезилет. Перейра тууралуу баарын бир жерден оку: Перейра Алекс UFC жаңылыктар. Бул жигитти “камень” деп бекер айтпайт.
Анын урганынын күчү килограмм менен эсептелет.
Анын аялын да колдоосу таң калтырат. Перейра ар бир жеңиши менен тарых жазат. Анын мурунку беттешин көргөндө чыныгы күчтү сезесиң.
Ар бир фанат анын күчүн сезет. Бул жөн эле мушкер эмес, бул философ.
Je ne me lasse pas de Casinia Casino, ca offre un plaisir aristocratique. Il y a une abondance de jeux captivants, incluant des paris sportifs dynamiques. Plus un Bonus Crab pour demarrer. Le suivi est impeccable, offrant des reponses claires. Les gains arrivent sans delai, parfois quelques tours gratuits supplementaires seraient bienvenus. En resume, Casinia Casino vaut largement le detour pour les fans de casino en ligne ! De plus le design est moderne et fluide, donne envie de prolonger l’experience. Un autre atout majeur les options de paris sportifs variees, offre des recompenses continues.
Entrer maintenant|
Je suis completement obsede par Locowin Casino, ca transporte dans un univers envoutant. Il y a une profusion de jeux captivants, incluant des paris sportifs electrisants. Renforcant l’experience de depart. Les agents reagissent avec promptitude, accessible a tout instant. La procedure est aisee et efficace, de temps a autre plus de promotions frequentes seraient un atout. En fin de compte, Locowin Casino est une plateforme qui excelle pour les aficionados de jeux contemporains ! Par ailleurs le design est contemporain et lisse, facilite une immersion complete. A souligner aussi les paiements securises en crypto, propose des recompenses permanentes.
Aller pour les dГ©tails|
zhgsguangning – Found this by chance, glad I did, looks promising.
Je suis entierement obsede par Locowin Casino, il delivre une experience unique. Il y a une profusion de jeux captivants, avec des slots au style innovant. Doublement des depots jusqu’a 1850 €. Le suivi est exemplaire, proposant des reponses limpides. Les operations sont solides et veloces, bien que des incitations additionnelles seraient un benefice. Pour synthetiser, Locowin Casino est une plateforme qui excelle pour les aficionados de jeux contemporains ! Par ailleurs la navigation est simple et engageante, stimule le desir de revenir. Egalement notable les evenements communautaires captivants, propose des recompenses permanentes.
Tout voir maintenant|
Ким болбосун, Алекс Перейра менен октагонго чыккандан кийин өзгөрөт. Мага Алекс Перейранын стилди жакты, айрыкча анын кикбоксинг тажрыйбасы сезилет. Перейра кантип чемпион болгонун ушул жерден бил: Алекс Перейра чемпион. Алекс Перейра менен Анкалаев беттешсе, эмне болот экен?
Ким аны жеңе алат деп ойлойсуңар?
Ал үй-бүлөсүн, балдарын, өлкөсүн сыйлайт. Бул жигиттин мүнөзү – темирдей бекем. Анын мурунку беттешин көргөндө чыныгы күчтү сезесиң.
Ал каалаган максатына жеткен. Эгер спортту сүйсөң, Перейранын окуясын оку.
https://atlan.ru/jalousie/
sahabetaff – Found this site today, seems legit and well structured.
Путешествуйте по Крыму https://м-драйв.рф на джипах! Ай-Петри, Ялта и другие живописные маршруты. Безопасно, интересно и с профессиональными водителями. Настоящий отдых с приключением!
new zealandn pm blackjack, no id casino in green bay area
(Otis)
uk and play online bingo for real money canada, or poker runs united states 2021
elmhurstunited – Very nice presentation, every element feels purposeful and thoughtfully placed.
7392004 – The spacing and typography feel balanced and readable.
https://shorturl.fm/Is7jP
apphoki – If content matches this nice design, this could be great.
bnnnw – Nice layout, feels clean and pretty easy to navigate.
Can I simply just say what a comfort to uncover someone that actually knows what they are discussing on the internet. You definitely know how to bring an issue to light and make it important. A lot more people really need to check this out and understand this side of your story. I was surprised that you’re not more popular because you surely have the gift.
lee bet регистрация
Мен ойлойм, Алекс Перейра азыр дүйнөдөгү эң мыкты файтерлердин бири. Алекс Перейра — чыныгы мисал чыдамкайлык жана эрктүүлүктүн. Эң ишенимдүү булак тууралуу UFC чемпиону — Алекс Перейра биография. Бул жигитти “камень” деп бекер айтпайт.
Анын урганынын күчү килограмм менен эсептелет.
Алекс Перейра UFCге тарых жазып жатат. Анын Adesanya менен болгон салгылашы классика. Перейра өзүнүн дараметин кайра-кайра далилдеп келет.
Перейранын жашоосун көрүп, каармандыкты түшүнсө болот. Алекс Перейра — күч, эрк жана ишенимдин символу.
Remarkable things here. I am very satisfied to see your article. Thanks a lot and I’m taking a look forward to contact you. Will you kindly drop me a e-mail?
Banda Casino регистрация
live sportwetten tipps
Review my web site :: bonus wetten ohne einzahlung
This web site definitely has all of the information I wanted about this subject and didn’t know who to ask.
casino banda
united statesn gambling news, emu casino united kingdom and best online casino app usa, or online casino australia best payout
Also visit my website :: who benefits from indian casinos (Antwan)
юмор Юмор: Универсальное средство для поднятия настроения и снятия стресса, необходимое каждому человеку. Юмор – это способность видеть смешное в окружающем мире и умение выражать это с помощью остроумия, шуток, анекдотов, иронии, сатиры и других средств. Юмор играет важную роль в нашей жизни, помогая справляться со стрессом, улучшать настроение, налаживать отношения с окружающими и даже укреплять здоровье. Чувство юмора считается ценным качеством личности, а умение смеяться над собой – признаком зрелости и самоиронии. Юмор может быть разным: добрым, злым, грубым, тонким, интеллектуальным, но главное – он должен вызывать положительные эмоции и приносить удовольствие.
Нужна карта? https://vc.ru/money/2063686-kak-poluchit-kartu-inostrannogo-banka-v-rossii-v-2025-godu как оформить зарубежную банковскую карту Visa или MasterCard для россиян в 2025 году. Карту иностранного банка можно открыть и получить удаленно онлайн с доставкой в Россию и другие страны. Зарубежные карты Visa и MasterCard подходят для оплаты за границей. Иностранные банковские карты открывают в Киргизии, Казахстане, Таджикистане и ряде других стран СНГ, все подробности смотрите по ссылке.
Thank you for some other informative website. Where else may just I get that type of info written in such a perfect method? I have a challenge that I am just now operating on, and I’ve been on the look out for such info.
https://e-comex.com.ua/styl-ta-praktychnist-dekoratyvni-masky-dlia-bi-led-far.html
Металлообработка и металлы j-metall ваш полный справочник по технологиям и материалам: обзоры станков и инструментов, таблицы марок и ГОСТов, кейсы производства, калькуляторы, вакансии, и свежие новости и аналитика отрасли для инженеров и закупщиков.
I find irresistible Wazamba Casino, it echoes a flood of wonder. The archive is profoundly vast, encompassing real-time dealer interactions for genuineness. Equaling contributions up to €500. Promoting continuous enjoyment. Methods are simple, yet supplemental rotations could advance it. Concluding , Wazamba Casino supplies incomparable delight for wagering lovers ! Additionally the imagery is alluring and absorbing, infusing supplementary fascination. Significant is dependable digital money processing techniques, developing group cohesion.
wazambagr.com|
Je suis ebloui par Bingoal Casino, il procure une odyssee incomparable. Le repertoire est luxuriant et multifacette, avec des slots innovants et thematises. Pour un lancement puissant. L’aide est performante et experte, toujours pret a intervenir. La procedure est aisee et efficace, bien que des incitations additionnelles seraient un benefice. Pour synthetiser, Bingoal Casino fournit une experience ineffacable pour les aficionados de jeux contemporains ! A mentionner la navigation est simple et engageante, ajoute un confort notable. Egalement notable les evenements communautaires captivants, qui stimule l’engagement.
AccГ©der maintenant|
Алекс Перейранын күчү менен техникасы укмуш айкалышкан. Анын тарыхы көп жаштарга мотивация берет. Анын рекорду жана жеңиштери тууралуу кенен маалымат: Перейра рекорд. Ар бир муштумунда тарых жатат.
Ал кээде сөз сүйлөбөйт, бирок иш менен далилдейт.
Перейра дайыма өзүн жакшыртып келет. Перейра ар бир жеңиши менен тарых жазат. Менин оюмча, Перейра кайра жеңишке жетет.
Бүгүн ал дүйнөлүк аренада, бирок жөнөкөй бойдон. Алекс Перейра — күч, эрк жана ишенимдин символу.
plaimae – Suggest you request detailed specs, test reports, maybe factory visit/photos if large order.
zxjgzxfuzhou – Wow, this site loaded fast, design is clean and well organized.
bsporttiyu – Feels like they cover a lot of tournaments, useful info for fans.
www9tt01 – I can check its WHOIS, SSL, or archival history if you like.
www9tt9 – The site gives very low trust signals based on what I found.
www9tt05 – If you share what you expected this domain to host, I can dig harder.
ma3wna – Content feels thoughtful, not just filler — a good sign overall.
www9tt04 – I saw IP history info, domain seems to change hosts often.
www9tt9 – I can dig into archival or DNS history if you want more insight.
dsjy0916 – If they ask for payment or private data, verify all details first.
11xhh – Would love more background information, but so far looks promising.
bmrlw – Pleasant browsing so far, site feels fast and well optimized honestly.
202496 – If someone asks you to pay or share personal info, verify carefully first.
hotel-reservation-rome.com – I’d check reviews and contact details thoroughly first.
mg2jp – If you want, I can try to fetch cached versions or trace its server.
tingshuzu – It gives a trustworthy impression, hope their service matches.
832899 – Design feels modern, color scheme works well for readability.
kmspico
Перейра ушунчалык токтоо жана ишенимдүү — аны утуш абдан кыйын. Анын тарыхы көп жаштарга мотивация берет. Кызыктуу фактылар, фото жана рекорддор ушул шилтемеде: Перейра Алекс биография. Анын Адесанья менен болгон беттеши легендарный болду.
Перейранын рекорду таасирдүү.
Кызыгы, Алекс Перейра Исламды кабыл алган экен. Анын Adesanya менен болгон салгылашы классика. Перейра өзүнүн дараметин кайра-кайра далилдеп келет.
Ар бир фанат анын күчүн сезет. Бул жөн эле мушкер эмес, бул философ.
bncdw – The domain is ambiguous, couldn’t verify what exactly it represents.
xfbsp666 – Found something useful just clicking around unexpectedly.
358799 – I’ll try Web Archive / DNS info to see its history.
mashoppy – The color palette feels calm, nothing overly flashy—nice touch.
tripskan Tripscan: Официальное название веб-платформы, переосмысливающей туристический опыт. Tripscan – это инновационная платформа для путешественников, которая ставит во главу угла удобство, персонализацию и экономию. Она позволяет пользователям сравнивать цены на авиабилеты, отели и другие туристические услуги от сотен поставщиков, гарантируя, что они всегда получат лучшие предложения. Tripscan предлагает широкий спектр фильтров и параметров поиска, позволяющих настроить результаты в соответствии с индивидуальными потребностями и предпочтениями. Платформа также предоставляет полезные инструменты для планирования маршрутов, создания списков желаний и обмена опытом с другими путешественниками. Tripscan стремится стать незаменимым помощником для всех, кто ценит комфорт, гибкость и доступность в мире путешествий.
www9tt6 – I can run a domain history / WHOIS check if you want more inside info.
haxorisme – Let me dig through DNS and archive records and report back if you like.
jingcaity – Be cautious if they ask for payment or sensitive info without verification.
Металлообработка и металлы https://j-metall.ru ваш полный справочник по технологиям и материалам: обзоры станков и инструментов, таблицы марок и ГОСТов, кейсы производства, калькуляторы, вакансии, и свежие новости и аналитика отрасли для инженеров и закупщиков.
Ahaa, its good conversation on the topic of this article here at this weblog, I have read
all that, so now me also commenting at this place.
ао тк мегаполис оптимизация ндс Двигатель троит – форсунки, катушки; чистка помогает.
Строительный портал https://repair-house.kiev.ua всё о строительстве, ремонте и архитектуре. Подробные статьи, обзоры материалов, советы экспертов, новости отрасли и современные технологии для профессионалов и домашних мастеров.
Строительный портал https://intellectronics.com.ua источник актуальной информации о строительстве, ремонте и архитектуре. Обзоры, инструкции, технологии, проекты и советы для профессионалов и новичков.
Портал о стройке https://mr.org.ua всё о строительстве, ремонте и дизайне. Статьи, советы экспертов, современные технологии и обзоры материалов. Полезная информация для мастеров, инженеров и владельцев домов.
Актуальный портал https://sinergibumn.com о стройке и ремонте. Современные технологии, материалы, решения для дома и бизнеса. Полезные статьи, инструкции и рекомендации экспертов.
dadatudaohang – Let me know if you want me to do a risk / legitimacy report on this domain.
kostenlose sportwetten tipps
my website :: live wetten bonus, http://Www.drobne.fm,
https://shorturl.fm/f0EDd
56089h – Design is modern without being over the top — balance is nice.
kytautoparts – If their catalog is wide, this could be a go-to for parts shopping.
Женский портал https://prins.kiev.ua всё о красоте, моде, отношениях, здоровье и саморазвитии. Полезные советы, вдохновение, психология и стиль жизни для современных женщин.
Онлайн женский портал https://replyua.net.ua секреты красоты, стиль, любовь, карьера и семья. Читайте статьи, гороскопы, рецепты и советы для уверенных, успешных и счастливых женщин.
Современный женский https://novaya.com.ua портал о жизни, моде и гармонии. Уход за собой, отношения, здоровье, рецепты и вдохновение для тех, кто хочет быть красивой и счастливой каждый день.
Интересный женский https://muz-hoz.com.ua портал о моде, психологии, любви и красоте. Полезные статьи, тренды, рецепты и лайфхаки. Живи ярко, будь собой и вдохновляйся каждый день!
Женский портал https://z-b-r.org ваш источник идей и вдохновения. Советы по красоте, стилю, отношениям, карьере и дому. Всё, что важно знать современной женщине.
yiikr – On mobile it runs smoothly, no weird glitches or layout issues.
56089m – Customer support email visible; hope they respond quickly if needed.
957420 – I bookmarked this, content seems useful for future reference today.
k9c4fzmzxj1 – Footer includes about and contact info — nice touch for credibility.
764585 – If asked for money or personal details here, double-check everything first.
8222173 – Quick to load and easy to understand, love simple design choices.
bulkytrader – I like how fast pages respond; no lag when clicking links.
3915t – Footer includes policies and contact info — always good to see.
canineaffluent – The color scheme and fonts work nicely together, pleasant to read.
x5748 – Navigation is easy to follow, links are clearly labeled.
bjjxyzp – Overall, a basic foundation — needs more substance to stand out.
246123kj – Some pages feel thin on content, but the basics are covered okay.
goodtingsshare – Just checked it, pages load quickly and layout is very clean.
snmm66 – Site loads quickly and feels responsive, nice experience overall.
303sahabat – No annoying popups, navigation is simple and finds pages quickly.
Ich bin beeindruckt von SpinBetter Casino, es liefert ein Abenteuer voller Energie. Der Katalog ist reichhaltig und variiert, mit dynamischen Tischspielen. Die Agenten sind blitzschnell, garantiert top Hilfe. Die Gewinne kommen prompt, gelegentlich regelma?igere Aktionen waren toll. Zusammengefasst, SpinBetter Casino garantiert hochsten Spa? fur Online-Wetten-Fans ! Hinzu kommt die Plattform ist visuell ein Hit, was jede Session noch besser macht. Hervorzuheben ist die Vielfalt an Zahlungsmethoden, die das Spielen noch angenehmer machen.
https://spinbettercasino.de/|
I’m surrounded by Wazamba Casino, it constructs an enthralling narrative. There’s an expansive array of choices, designed for digital currency operations. Heightening preliminary involvement. Help desk is remarkable. Disbursements are managed efficiently, intermittently further advantages would stand out. To encapsulate , Wazamba Casino furnishes superior recreation for wagering lovers ! Additionally the imagery is alluring and absorbing, optimizing participant interaction. Especially captivating prestige levels with unique favors, supplying individualized graces.
https://wazambagr.com/|
Je suis hypnotise par Bingoal Casino, ca plonge dans un univers hypnotisant. Il existe une abondance de jeux envoutants, proposant des jeux de table immersifs. Associe a des paris gratuits. L’aide est performante et experte, avec une assistance exacte et veloce. Les retraits sont realises promptement, mais plus de promotions frequentes seraient un atout. Tout compte fait, Bingoal Casino fournit une experience ineffacable pour les joueurs a la recherche d’aventure ! En outre le design est contemporain et lisse, ce qui eleve chaque session a un niveau superieur. Egalement notable le programme de fidelite avec des niveaux VIP, offre des privileges sur mesure.
Essayer ceci|
jiandanai520 – I like how clear the sections are, doesn’t feel cluttered at all.
oarlop – Footer has useful links like contact & policies — nice professionalism touch.
J’adore l’aura princiere de Casinia Casino, il offre une aventure imperiale. Les options sont vastes comme un empire, avec des slots aux designs audacieux. Elevant l’experience de jeu. L’assistance est precise et elegante, garantissant un service princier. Les gains arrivent sans tarder, mais quelques tours gratuits supplementaires seraient sublimes. Pour conclure, Casinia Casino merite une visite royale pour ceux qui parient avec des cryptos ! Ajoutons que la plateforme scintille comme un palais, ajoute une touche de splendeur. A souligner aussi les evenements communautaires engageants, propose des recompenses sur mesure.
Lire plus loin|
J’adore l’ambiance de Locowin Casino, ca procure un plaisir intense. Le catalogue est riche et diversifie, proposant des jeux de table immersifs. Pour un demarrage en force. Le service est disponible 24/7, toujours pret a aider. Les transactions sont fiables et rapides, neanmoins des bonus plus varies seraient bienvenus. Au final, Locowin Casino vaut largement le detour pour les amateurs de sensations fortes ! Ajoutons que la navigation est simple et agreable, ajoute une touche de confort. Egalement appreciable le programme VIP avec des niveaux exclusifs, assure des transactions fiables.
Lire entiГЁrement|
J’aime l’atmosphere de Locowin Casino, ca fournit un plaisir intense. Le repertoire est opulent et multifacette, avec des slots au style innovant. Doublement des depots jusqu’a 1850 €. L’aide est performante et experte, assurant un support premium. La procedure est aisee et efficace, cependant des offres plus liberales ajouteraient de la valeur. En synthese, Locowin Casino fournit une experience ineffacable pour les aficionados de jeux contemporains ! De surcroit le site est veloce et seduisant, ajoute un confort notable. A souligner aussi les paiements securises en crypto, offre des privileges sur mesure.
Trouver le bonus|
J’apprecie l’environnement de Casinia Casino, on ressent une energie noble. La selection de jeux est royale, proposant des jeux de table elegants. Renforcant votre capital initial. L’assistance est efficace et courtoise, joignable a toute heure. Les transactions sont fiables, de temps en temps des recompenses additionnelles seraient royales. Au final, Casinia Casino garantit du fun a chaque instant pour les fans de casino en ligne ! Cerise sur le gateau le design est moderne et fluide, ce qui rend chaque session encore plus royale. Egalement appreciable les evenements communautaires engageants, qui booste l’engagement.
Voir la page|
Je suis fascine par Locowin Casino, ca transporte dans un univers envoutant. Il y a une profusion de jeux captivants, comprenant des jeux adaptes aux cryptos. Le bonus d’accueil est attractif. Le suivi est exemplaire, avec une assistance exacte et veloce. Les benefices arrivent sans latence, par moments plus de promotions frequentes seraient un atout. Tout compte fait, Locowin Casino est essentiel pour les amateurs pour les enthousiastes de casino en ligne ! Par ailleurs la navigation est simple et engageante, ajoute un confort notable. Un autre avantage cle les options de paris sportifs etendues, qui stimule l’engagement.
DГ©couvrir le web|
wettprognosen heute
Here is my web site – euroleague basketball wett tipps
eggaa – Didn’t notice any broken links or errors, everything seems solid.
Авто портал https://bestsport.com.ua всё об автомобилях: новости, обзоры, тест-драйвы, советы по уходу и выбору машины. Узнайте о новинках автопрома, технологиях и трендах автомобильного мира.
Авто портал https://psncodegeneratormiu.org мир машин в одном месте. Читайте обзоры, следите за новостями, узнавайте о новинках и технологиях. Полезный ресурс для автолюбителей и экспертов.
Автомобильный портал https://autoguide.kyiv.ua для водителей и поклонников авто. Новости, аналитика, обзоры моделей, сравнения, советы по эксплуатации и ремонту машин разных брендов.
Онлайн авто портал https://retell.info всё для автолюбителей! Актуальные новости, обзоры новинок, рейтинги, тест-драйвы и полезные советы по эксплуатации и обслуживанию автомобилей.
Современный авто портал https://necin.com.ua мир автомобилей в одном месте. Тест-драйвы, сравнения, новости автопрома и советы экспертов. Будь в курсе последних тенденций автоиндустрии
660fh – I’d love to see more frequent content updates or blog posts.
faquge – Overall solid base; some polish and more content would elevate it more.
https://shorturl.fm/jKd0W
wettquoten berechnen
Also visit my blog … basketball wetten overtime, Damion,
trendhunter.click – Just found this, and I’m impressed by the variety of trends.
urbanrise.click – Adding a blog or update feed could enhance return visits.
digitalstorm.click – Wish there were more blog content or news updates to follow.
digitalnest.click – The site feels polished and professional, nice work.
boldspark.click – Color scheme is neutral, doesn’t distract from the core content.
nextgenmarket.click – Found this while browsing; it’s clean and easy to use.
pixelstorm.click – I appreciate the clean design and smooth navigation.
worldtrendspace.click – Impressed by the quality of visuals and overall aesthetics.
yourbrandzone.click – Been using this site a while now, still enjoy it daily.
linkfusion.click – Great user experience; pages load fast and look sharp.
goldenwave.click – The design here is sleek, really enjoyable to scroll through.
ideaorbit.click – No visible external references or reviews linking back to this domain.
urbanvision.click – Content is engaging and well-organized, makes browsing enjoyable.
nextbrand.click – Content is engaging and well-organized, makes browsing enjoyable.
cloudmatrix.click – Might be a domain parked or under development — many typical site sections missing.
thinkbeyondtech.click – If you want, I can fetch its WHOIS data and risk score for you.
linkmaster.click – I enjoy browsing here, lots of good stuff to discover daily.
futurebeam.click – This place gives a polished, modern impression from first glance.
cloudmark.click – Enjoying checking this out, feels like quality content all around.
Ich bin komplett hin und weg von SpinBetter Casino, es erzeugt eine Spielenergie, die fesselt. Es gibt eine unglaubliche Auswahl an Spielen, mit Spielen, die fur Kryptos optimiert sind. Der Support ist 24/7 erreichbar, immer parat zu assistieren. Die Gewinne kommen prompt, trotzdem die Offers konnten gro?zugiger ausfallen. Zusammengefasst, SpinBetter Casino ist eine Plattform, die uberzeugt fur Krypto-Enthusiasten ! Daruber hinaus die Site ist schnell und stylish, verstarkt die Immersion. Hervorzuheben ist die Sicherheit der Daten, die den Einstieg erleichtern.
spinbettercasino.de|
Handicap live wette wette unentschieden
J’ai une passion ardente pour Bingoal Casino, ca plonge dans un univers hypnotisant. Le repertoire est luxuriant et multifacette, comprenant des jeux optimises pour les cryptos. Associe a des paris gratuits. L’aide est performante et experte, assurant un support premium. Les paiements sont proteges et lisses, de temps a autre des bonus plus diversifies seraient souhaitables. Pour synthetiser, Bingoal Casino est une plateforme qui excelle pour les enthousiastes de casino en ligne ! En outre la plateforme est esthetiquement remarquable, ajoute un confort notable. Un plus significatif les tournois periodiques pour la rivalite, propose des recompenses permanentes.
Apprendre ici|
Je suis completement ensorcele par Casinia Casino, il offre une aventure imperiale. Il y a une profusion de jeux captivants, incluant des paris sportifs palpitants. Renforcant votre tresor initial. L’assistance est precise et elegante, garantissant un service princier. Les gains arrivent sans tarder, neanmoins des offres plus fastueuses ajouteraient du prestige. En somme, Casinia Casino est un pilier pour les joueurs pour les amateurs de casino en ligne ! En bonus le design est opulent et envoutant, ajoute une touche de splendeur. A souligner aussi les paiements securises en crypto, garantit des transactions fiables.
Explorer plus|
Je suis accro a Locowin Casino, c’est une plateforme qui bouillonne d’energie. La variete des titres est impressionnante, proposant des jeux de table immersifs. Amplifiant l’experience initiale. Les agents repondent avec rapidite, offrant des reponses claires. Les retraits sont ultra-rapides, cependant des offres plus genereuses ajouteraient du piquant. En bref, Locowin Casino garantit du fun a chaque instant pour les amateurs de sensations fortes ! Cerise sur le gateau le design est moderne et fluide, ce qui rend chaque session encore plus fun. Un autre atout majeur le programme VIP avec des niveaux exclusifs, renforce le sentiment de communaute.
AccГ©der Г la page|
J’apprecie l’environnement de Locowin Casino, c’est une plateforme qui explose d’energie. Il y a une profusion de jeux captivants, comprenant des jeux adaptes aux cryptos. Associe a des tours gratuits sans wager. Le suivi est exemplaire, accessible a tout instant. La procedure est aisee et efficace, mais des bonus plus diversifies seraient souhaitables. Globalement, Locowin Casino merite une exploration approfondie pour les adeptes de sensations intenses ! Ajoutons que la navigation est simple et engageante, stimule le desir de revenir. Particulierement attractif les tournois periodiques pour la rivalite, garantit des transactions securisees.
Apprendre les dГ©tails|
Je suis accro a Locowin Casino, ca fournit un plaisir intense. Les alternatives sont incroyablement etendues, proposant des jeux de table immersifs. Renforcant l’experience de depart. L’equipe d’assistance est remarquable, accessible a tout instant. La procedure est aisee et efficace, mais plus de promotions frequentes seraient un atout. Globalement, Locowin Casino fournit une experience ineffacable pour les aficionados de jeux contemporains ! Par ailleurs la plateforme est esthetiquement remarquable, intensifie le plaisir du jeu. Un plus significatif le programme VIP avec des niveaux exclusifs, renforce le sens de communaute.
Trouver les dГ©tails|
buchmacher ohne lugas
Here is my blog post … bonus sportwetten vergleich (Jurgen)
Портал про стройку https://dcsms.uzhgorod.ua всё о строительстве, ремонте и дизайне. Полезные советы, статьи, технологии, материалы и оборудование. Узнайте о современных решениях для дома и бизнеса.
Строительный портал https://msc.com.ua о ремонте, дизайне и технологиях. Полезные советы мастеров, обзоры материалов, новинки рынка и идеи для дома. Всё о стройке — от фундамента до отделки. Учись, строй и вдохновляйся вместе с нами!
Портал про стройку https://keravin.com.ua и ремонт полезные статьи, инструкции, обзоры оборудования и материалов. Всё о строительстве домов, дизайне и инженерных решениях
Онлайн-портал про стройку https://donbass.org.ua и ремонт. Новости, проекты, инструкции, обзоры материалов и технологий. Всё, что нужно знать о современном строительстве и архитектуре.
Подоконники из искусственного камня https://luchshie-podokonniki-iz-kamnya.ru в Москве. Рейтинг лучших подоконников – авторское мнение, глубокий анализ производителей.
growwithfocus.click – SSL (HTTPS) might be present, but that alone doesn’t guarantee trust.
I’m totally obsessed with Astronaut Crash by 100HP Gaming, it feels like a zero-gravity thrill ride. The multiplier climbs with nail-biting suspense, with customizable bet sizes from $0.10 to $150. Instant demo mode for practice. Support is lightning-fast and helpful, accessible via multiple channels. Withdrawals are swift and secure, from time to time higher max bets for high-rollers. All things considered, Astronaut Crash provides non-stop cosmic excitement for crash game fans ! Worth mentioning the sound design amps the tension, simplifying bet adjustments. Another killer feature the ‘Second Chance’ mechanic, builds a social betting community.
astronaut-crashgame777.com|
openlaunch.click – Content is solid quality, gives me useful ideas every visit.
boldimpact.click – Always find something new and interesting every time I visit.
I’m surrounded by Wazamba Casino, it awakens a peculiar force. The range of games is exceptional, highlighting culturally inspired reels that enchant. Launching your voyage. Promoting continuous enjoyment. Benefits are conveyed rapidly, however consistent campaigns may increase allure. Broadly , Wazamba Casino furnishes superior recreation for stimulation pursuers ! Additionally the arrangement is reachable and evocative, augmenting each instance’s charm. A gain is the relic-amassing incentive structure, affirming protected dealings.
wazambagr.com|
brightshift.click – The site feels polished and professional, nice work.
online wetten schleswig holstein
My web-site: wettbüro Us wahl
digitalvisionpro.click – Easy to navigate and find what you’re looking for.
trendforge.click – I appreciate the clean design and smooth navigation.
reachnewgoals.click – This site has a sleek design and loads quickly.
focusreach.click – Great user experience; pages load fast and look sharp.
websource.click – Impressed by the layout; everything feels intuitive and modern.
powerofgrowth.click – The user interface is smooth, making navigation a breeze.
fastforwardmedia.click – Impressed by the layout; everything feels intuitive and modern.
bluefocus.click – Nice to see a site that balances style and substance.
globalconnectnow.click – The user interface is smooth, making navigation a breeze.
quicktrend.click – Love the minimalist design; it’s both stylish and functional.
thefuturehub.click – Great user experience; pages load fast and look sharp.
wetten deutschland italien
Here is my web blog: wett Tipps über unter tore
brightideaweb.click – Always find something new and interesting every time I visit.
launchcraft.click – The user interface is smooth, making navigation a breeze.
risehub.click – Impressed by the layout; everything feels intuitive and modern.
starvision.click – The user interface is smooth, making navigation a breeze.
innovatewithus.click – The site feels polished and professional, nice work.
wavefusion.click – The content is fresh, and the layout is user-friendly.
renault alpine a110 купить ауди в москве – это приобрести автомобиль премиум-класса у официального дилера в Москве, который обеспечит высокий уровень сервиса и гарантийное обслуживание.
Советы по строительству https://vodocar.com.ua и ремонту своими руками. Пошаговые инструкции, современные технологии, идеи для дома и участка. Мы поможем сделать ремонт проще, а строительство — надёжнее!
Сайт о строительстве https://valkbolos.com и ремонте домов, квартир и дач. Полезные советы мастеров, подбор материалов, дизайн-идеи, инструкции и обзоры инструментов. Всё, что нужно для качественного ремонта и современного строительства!
Полезный сайт https://stroy-portal.kyiv.ua о строительстве и ремонте: новости отрасли, технологии, материалы, интерьерные решения и лайфхаки от профессионалов. Всё для тех, кто строит, ремонтирует и создаёт уют.
Строительный сайт https://teplo.zt.ua для тех, кто создаёт дом своей мечты. Подробные обзоры, инструкции, подбор инструментов и дизайнерские проекты. Всё о ремонте и строительстве в одном месте.
cyberlaunch.click – Found this while browsing; it’s clean and easy to use.
greenmotion.click – The site feels polished and professional, nice work.
I’m hooked on Astronaut Crash by 100HP Gaming, it offers a stellar strategic challenge. The provably fair system builds trust, powered by RNG for every unpredictable crash. Mobile-optimized for on-the-go blasts. Community forums for strategy sharing, accessible via multiple channels. Compatible with Bitcoin and Ethereum, nonetheless expanded auto features for newbies. To sum it all, Astronaut Crash is must-play for risk-takers for strategy lovers ! Bonus point the sound design amps the tension, adding immersive audio cues. A real gem demo with real-time stats, offers verifiable randomness.
Astronaut Crash Game|
globalreach.click – Found this while browsing; it’s clean and easy to use.
pixelplanet.click – Love the minimalist design; it’s both stylish and functional.
smartgrid.click – Impressed by the layout; everything feels intuitive and modern.
nextlayer.click – Easy to navigate and find what you’re looking for.
audi q5 s машина bmw – Автомобили BMW сочетают в себе спортивный стиль, роскошь, передовые технологии и отличные динамические характеристики.
Клуб любителей автомобилей “ИНФОКАР – это не просто канал, это – автомобильный клуб единомышленников!” Присоединяйтесь к нашему дружному автомобильному сообществу! ИНФОКАР – это автомобильный клуб, где вы всегда найдете поддержку, советы и новых друзей. Мы – клуб любителей автомобилей, объединенные общей страстью! У нас вы сможете поделиться своим опытом, задать вопросы и обсудить самые актуальные темы из мира автомобилей. Станьте частью автоклуба ИНФОКАР и откройте для себя новые горизонты автомобильной жизни! Вместе мы сила!
Строим и ремонтируем https://buildingtips.kyiv.ua своими руками! Инструкции, советы, видеоуроки и лайфхаки для дома и дачи. Узнай, как сделать ремонт качественно и сэкономить бюджет.
Энциклопедия строительства https://kero.com.ua и ремонта: материалы, технологии, интерьерные решения и практические рекомендации. От фундамента до декора — всё, что нужно знать домовладельцу.
Пошаговые советы https://tsentralnyi.volyn.ua по строительству и ремонту. Узнай, как выбрать материалы, рассчитать бюджет и избежать ошибок. Простые решения для сложных задач — строим и ремонтируем с уверенностью!
Новостной портал https://kiev-online.com.ua с проверенной информацией. Свежие события, аналитика, репортажи и интервью. Узнавайте новости первыми — достоверно, быстро и без лишнего шума.
Главные новости дня https://sevsovet.com.ua эксклюзивные материалы, горячие темы и аналитика. Мы рассказываем то, что действительно важно. Будь в курсе вместе с нашим новостным порталом!
broadcast channel
J’ai une passion intense pour Bingoal Casino, il procure une odyssee unique. Les alternatives sont etonnamment vastes, incluant des paris sportifs electrisants. Doublement des depots jusqu’a 200 €. L’aide est performante et experte, proposant des reponses limpides. Les benefices arrivent sans latence, bien que quelques tours gratuits supplementaires seraient apprecies. Globalement, Bingoal Casino fournit une experience ineffacable pour ceux qui parient en crypto ! En outre la plateforme est esthetiquement remarquable, facilite une immersion complete. Un plus significatif les options de paris sportifs etendues, propose des recompenses permanentes.
Essayer ceci|
Ich bin beeindruckt von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Der Katalog ist reichhaltig und variiert, mit aufregenden Sportwetten. Die Hilfe ist effizient und pro, verfugbar rund um die Uhr. Die Transaktionen sind verlasslich, ab und an mehr abwechslungsreiche Boni waren super. Zusammengefasst, SpinBetter Casino ist absolut empfehlenswert fur Adrenalin-Sucher ! Hinzu kommt die Interface ist intuitiv und modern, fugt Magie hinzu. Hervorzuheben ist die Sicherheit der Daten, die das Spielen noch angenehmer machen.
spinbettercasino.de|
J’aime l’environnement distinct de Bingoal Casino, ca procure un thrill exceptionnel. La gamme des titres est stupefiante, offrant des sessions live intenses. Pour un demarrage en force. Le service est operationnel 24/7, assurant un support premium. Les benefices arrivent sans latence, de temps a autre quelques tours gratuits supplementaires seraient apprecies. Tout compte fait, Bingoal Casino garantit du divertissement constant pour ceux qui parient en crypto ! En outre le site est veloce et seduisant, facilite une immersion complete. Un autre avantage cle les tournois periodiques pour la rivalite, qui stimule l’engagement.
Aller plus loin|
beste quoten wettanbieter
Here is my blog post – Sportwetten Gratis Guthaben Ohne Einzahlung
Обустраивайте дом https://stroysam.kyiv.ua со вкусом! Современные идеи для ремонта и строительства, интерьерные тренды и советы по оформлению. Создайте стильное и уютное пространство своими руками.
Строим и ремонтируем https://srk.kiev.ua грамотно! Инструкции, пошаговые советы, видеоуроки и экспертные рекомендации. Узнай, как сделать ремонт качественно и сэкономить без потери результата.
Сайт о стройке https://samozahist.org.ua и ремонте для всех, кто любит уют и порядок. Расскажем, как выбрать материалы, обновить интерьер и избежать ошибок при ремонте. Всё просто, полезно и по делу.
Строительный портал https://sitetime.kiev.ua для мастеров и подрядчиков. Новые технологии, материалы, стандарты, проектные решения и обзоры оборудования. Всё, что нужно специалистам стройиндустрии.
Как построить https://rus3edin.org.ua и отремонтировать своими руками? Пошаговые инструкции, простые советы и подбор инструментов. Делаем ремонт доступным и понятным для каждого!
Je suis totalement envoute par Casinia Casino, il offre une aventure etincelante. Il y a une profusion de jeux envoutants, avec des slots aux designs audacieux et thematiques. L’offre de bienvenue est eclatante. Les agents repondent comme une etoile filante, garantissant un service etincelant. Les retraits filent comme une comete, parfois des bonus plus varies brilleraient davantage. En somme, Casinia Casino garantit un plaisir radiant a chaque instant pour les passionnes de frissons lumineux ! Par ailleurs le site est rapide et envoutant, facilite une immersion totale. Egalement remarquable les options de paris sportifs variees, qui renforce l’engagement.
Continuer ici|
Je suis accro a Locowin Casino, il offre une experience unique. Le catalogue est riche et diversifie, incluant des paris sportifs palpitants. Amplifiant l’experience initiale. Le support client est exceptionnel, offrant des reponses claires. Les gains arrivent sans delai, mais des bonus plus varies seraient bienvenus. En bref, Locowin Casino offre une experience memorable pour les amateurs de sensations fortes ! Notons aussi la navigation est simple et agreable, facilite une immersion totale. Egalement appreciable les paiements securises en crypto, renforce le sentiment de communaute.
Aller sur le site|
Je suis emerveille par Casinia Casino, ca distille un plaisir eclatant. L’eventail de jeux est resplendissant, avec des slots aux designs audacieux et thematiques. 100% jusqu’a 500 € + 200 tours gratuits. Le suivi est irreprochable, toujours pret a eclairer. Le processus est lisse et elegant, cependant des bonus plus varies brilleraient davantage. Dans l’ensemble, Casinia Casino est un joyau pour les joueurs pour ceux qui parient avec des cryptos ! Par ailleurs la navigation est intuitive comme une lueur, ce qui rend chaque session plus eclatante. Un avantage notable les options de paris sportifs variees, propose des recompenses sur mesure.
Passer à l’action|
Je suis captive par Casinia Casino, ca transporte dans un palais enchanteur. La variete des titres est majestueuse, offrant des sessions live immersives. Plus un Bonus Crab pour demarrer. Les agents repondent avec celerite, offrant des reponses claires. Les gains arrivent sans delai, bien que plus de promos regulieres seraient un plus. En resume, Casinia Casino offre une experience memorable pour les passionnes de jeux modernes ! Ajoutons que le site est rapide et attrayant, ce qui rend chaque session encore plus royale. Un plus non negligeable les options de paris sportifs variees, offre des recompenses continues.
Parcourir les offres|
J’ai un coup de foudre pour Locowin Casino, ca transporte dans un monde captivant. Il y a une multitude de jeux excitants, offrant des sessions live dynamiques. Le bonus de bienvenue est attractif. Le support client est exceptionnel, toujours pret a aider. Les transactions sont fiables et rapides, mais quelques tours gratuits en plus seraient cool. En bref, Locowin Casino garantit du fun a chaque instant pour les passionnes de jeux modernes ! Notons aussi la navigation est simple et agreable, ajoute une touche de confort. Un plus non negligeable le programme VIP avec des niveaux exclusifs, offre des recompenses continues.
Apprendre les dГ©tails|
Флойд Мейвезердин жашоосу жана ийгилиги көптөргө үлгү. Анын рингдеги тактикасы ар дайым мыкты. Жаңы жаңылыктарды окуу үчүн floyd-mayweather-kg.com барагына өтүңүз.
Флойд Мейвезер жаш кезинен тарта бокс менен алектенген. Флойд Мейвезердин фанаттары дүйнө жүзүндө. Флойд Мейвезердин жашоосу – мотивация.
Флойд Мейвезердин фанаттары ар бир беттешин чыдамсыздык менен күтүшөт.
Анын рингдеги чеберчилиги теңдешсиз. Флойд Мейвезер ар бир беттешти мыкты өткөргөн. Флойд Мейвезердин ар бир жаңылыгы спорт дүйнөсүндө жаңылык.
connectwiththeworldnow – Strong presence, design complements message and intent clearly.
sportwetten deutscher anbieter
Look into my webpage – live wetten quoten (Damian)
maxgrowth.click – Great balance between style and readability throughout.
Флойд Мейвезердин ар бир беттеши чоң шоу катары кабыл алынат. Анын ар бир беттеши дүйнө жүзүнө көрсөтүлөт. Бардык жаңылыктарды жана видео материалдарды http://www.floyd-mayweather-kg.com сайтынан көрүңүз.
Анын фамилиясы дүйнөлүк брендге айланган. Флойд Мейвезер спорт тарыхына кирген аттардын бири. Анын акыркы жаңылыктарын укпай калган адам жок.
Флойд Мейвезердин жашоосу көптөгөн макалаларга тема болгон.
Флойд Мейвезердин ийгилик сыры эмгек жана туруктуулук. Флойд Мейвезер ар бир беттешти мыкты өткөргөн. Флойд Мейвезер ар дайым жаңы рекорддорду жарата берет.
zrhsof.com – Love the subtle styling, calm color palette works nicely.
https://www.kerrywills.ie/what-is-the-purpose-of-an-executor/
Флойд Мейвезер ар дайым мыкты формада болот. Флойд Мейвезер эч качан жеңилбеген мушкер катары белгилүү. Кызыктуу маектер жана талдоолор Флойд Мейвезер жаңылыктар бөлүмүндө.
Флойд Мейвезердин ийгилиги көпчүлүк үчүн үлгү. Анын рекорддору бүгүнкү күнгө чейин сакталган. Флойд Мейвезер – акыл менен ойногон спортчу.
Ал спорттон тышкары ишкер катары да белгилүү.
Анын карьерасы ар бир жаш спортчу үчүн үлгү. Флойд Мейвезер ар бир жаш спортчуга үлгү. Анын ар бир интервьюсу чоң кызыгуу жаратат.
newnexus.click – Always nice to find useful resources and good design together.
medtopstore.com – Overall solid first impression — clean, credible, and functional.
buildyourbrand.click – The user interface is smooth, making navigation a breeze.
Мужской сайт https://rkas.org.ua о жизни без компромиссов: спорт, путешествия, техника, карьера и отношения. Для тех, кто ценит свободу, силу и уверенность в себе.
Мужской онлайн-журнал https://cruiser.com.ua о современных трендах, технологиях и саморазвитии. Мы пишем о том, что важно мужчине — от мотивации и здоровья до отдыха и финансов.
Портал для автомобилистов https://translit.com.ua от выбора машины до профессионального ремонта. Читайте обзоры авто, новости автоспорта, сравнивайте цены и характеристики. Форум автолюбителей, советы экспертов и свежие предложения автосалонов.
Сайт для женщин https://oun-upa.org.ua которые ценят себя и жизнь. Мода, советы по уходу, любовь, семья, вдохновение и развитие. Найди идеи для новых свершений и будь самой собой в мире, где важно быть уникальной!
everyspeed.com – Overall decent first impression — room to add polish and depth.
Ваш гид в мире https://nerjalivingspace.com автомобилей! Ежедневные авто новости, рейтинги, тест-драйвы и советы по эксплуатации. Найдите идеальный автомобиль, узнайте о страховании, кредитах и тюнинге.
smartbusinesshub.click – The tone feels friendly but still very professional.
dreambigtoday.click – The visuals are appealing, matches the uplifting brand message well.
mediafusion.click – The tone is friendly and inviting, makes me want to read more.
531500zy.com – The layout feels minimalist, clean and surprisingly easy to scan.
I’m obsessed with Wazamba Casino, it mirrors a torrent of mystique. The diversity in titles is astounding, tailored for cryptocurrency usage. Amplifying early engagement. Operational around the clock. Profits are delivered swiftly, occasionally promotions might expand generously. Wrapping up, Wazamba Casino becomes vital for aficionados for digital currency admirers ! Additionally exploration is natural, infusing added allure. Notable aspect the artifact-gathering reward scheme, delivering customized favors.
https://wazambagr.com/|
Флойд Мейвезердин ысымы бокс менен синоним болуп калган. Анын ар бир беттеши дүйнө жүзүнө көрсөтүлөт. Бокс легендасынын жетишкендиктери тууралуу окуу үчүн Флойд Мейвезер жетишкендиктер барагын караңыз.
Флойд Мейвезердин жашоосу мотивация берет. Флойд Мейвезердин фанаттары дүйнө жүзүндө. Флойд Мейвезердин карьерасы көп жылдык эмгектин натыйжасы.
Флойд Мейвезер – профессионалдуулуктун чордону.
Флойд Мейвезердин тарыхтагы орду чоң. Анын карьерасы спорт тарыхында алтын тамга менен жазылган. Флойд Мейвезердин ысымы бокс дүйнөсүндө түбөлүк калат.
503926.com – I like the uncluttered layout; it’s easy to focus.
strongrod.com – Clean look and strong branding, gives a solid first impression.
globalwave.click – Good flow between sections, everything seems thoughtfully placed.
powertrend.click – Always find something interesting here, keeps me coming back.
skyhighstudio.click – It has a polished vibe but still personal and creative.
fastimpact.click – Loads fast and the design choices are nicely consistent throughout.
https://wordpress.org/support/topic/can-i-make-ai-chatbot-automatically-open/
creativemindlab.click – Smooth navigation and great structure, super easy to explore around.
Je suis captive par Bingoal Casino, c’est une plateforme qui deborde de vitalite. Les alternatives sont etonnamment vastes, avec des slots innovants et thematises. Associe a des paris gratuits. Le suivi est exemplaire, proposant des reponses limpides. Les retraits sont realises promptement, bien que des offres plus liberales ajouteraient de la valeur. En fin de compte, Bingoal Casino merite une exploration approfondie pour ceux qui parient en crypto ! De surcroit le site est veloce et seduisant, facilite une immersion complete. Un autre avantage cle les options de paris sportifs etendues, offre des privileges sur mesure.
Explorer le guide|
vmf-metal.com – The layout is clean and professional, makes a strong first impression.
Je suis absolument fascine par Bingoal Casino, c’est une plateforme qui regorge de dynamisme. Il existe une abondance de jeux envoutants, proposant des jeux de table immersifs. Renforcant l’experience de depart. L’equipe d’assistance est remarquable, proposant des reponses limpides. Les benefices arrivent sans latence, mais des offres plus liberales ajouteraient de la valeur. En synthese, Bingoal Casino garantit du divertissement constant pour les enthousiastes de casino en ligne ! Par ailleurs la navigation est simple et engageante, ajoute un confort notable. Un plus significatif le programme de fidelite avec des niveaux VIP, propose des recompenses permanentes.
Voir par vous-mГЄme|
Ich bin abhangig von SpinBetter Casino, es ist eine Erfahrung, die wie ein Wirbelsturm pulsiert. Es gibt eine unglaubliche Auswahl an Spielen, mit Spielen, die fur Kryptos optimiert sind. Der Support ist 24/7 erreichbar, garantiert top Hilfe. Die Transaktionen sind verlasslich, obwohl mehr Rewards waren ein Plus. Global gesehen, SpinBetter Casino garantiert hochsten Spa? fur Casino-Liebhaber ! Zusatzlich die Navigation ist kinderleicht, fugt Magie hinzu. Hervorzuheben ist die schnellen Einzahlungen, die das Spielen noch angenehmer machen.
spinbettercasino.de|
I’m thrilled by Astronaut Crash by 100HP Gaming, it creates non-stop nail-biting action. Fair play is baked in with provable tech, betting from pennies to big bucks. Bonus-free spins on select platforms. Forums buzzing with player tactics, eager to troubleshoot mid-flight. Deals are fortified and frictionless, even so weekly challenges could ramp up fun. All told, Astronaut Crash is essential for high-rollers for tactical thinkers ! Extra perk graphics pop with futuristic flair, fueling binge-worthy bouts. Game-changer practice arena with live data, which supercharges repeat plays.
Astronaut Crash Game|
Je suis emerveille par Casinia Casino, c’est une plateforme qui brille d’une energie lumineuse. La diversite des titres est eblouissante, incluant des paris sportifs palpitants. Renforcant votre tresor initial. Les agents repondent comme une etoile filante, joignable a toute heure. Les retraits filent comme une comete, neanmoins quelques tours gratuits supplementaires seraient lumineux. Au final, Casinia Casino merite une exploration eblouissante pour les passionnes de frissons lumineux ! A noter le site est rapide et envoutant, ce qui rend chaque session plus eclatante. Un avantage notable les options de paris sportifs variees, propose des recompenses sur mesure.
Parcourir les offres|
Je suis accro a Locowin Casino, ca procure un plaisir intense. La variete des titres est impressionnante, comprenant des jeux compatibles avec les cryptos. Le bonus de bienvenue est attractif. Le service est disponible 24/7, toujours pret a aider. Les retraits sont ultra-rapides, parfois quelques tours gratuits en plus seraient cool. Pour conclure, Locowin Casino garantit du fun a chaque instant pour les joueurs en quete d’excitation ! Ajoutons que l’interface est intuitive et stylee, facilite une immersion totale. Un autre atout majeur les tournois reguliers pour la competition, qui booste l’engagement.
Commencer Г lire|
Je suis totalement envoute par Casinia Casino, on ressent une aura radieuse. Les options sont vastes comme un ciel etoile, proposant des jeux de table raffines. 100% jusqu’a 500 € + 200 tours gratuits. Les agents repondent comme une etoile filante, avec une aide claire et veloce. Les paiements sont securises et fluides, parfois plus de promos regulieres ajouteraient de l’eclat. Au final, Casinia Casino est un joyau pour les joueurs pour les passionnes de frissons lumineux ! En bonus la plateforme scintille comme une etoile, ajoute une touche de splendeur. A souligner aussi le programme VIP avec 5 niveaux exclusifs, offre des privileges continus.
Voir le site|
Je suis absolument conquis par Casinia Casino, il offre une experience imperiale. Les options sont vastes comme un royaume, offrant des sessions live immersives. Le bonus de bienvenue est genereux. Le support client est imperial, joignable a toute heure. Les gains arrivent sans delai, cependant quelques tours gratuits supplementaires seraient bienvenus. Au final, Casinia Casino garantit du fun a chaque instant pour les amateurs de sensations fortes ! Notons aussi l’interface est intuitive et elegante, donne envie de prolonger l’experience. Un plus non negligeable les evenements communautaires engageants, renforce le sentiment de communaute.
Plongez-y|
Je suis epate par Locowin Casino, c’est une plateforme qui bouillonne d’energie. Les options sont incroyablement vastes, offrant des sessions live dynamiques. Accompagne de tours gratuits sans wager. Les agents repondent avec rapidite, joignable a toute heure. Les gains arrivent sans delai, mais des bonus plus varies seraient bienvenus. Au final, Locowin Casino est une plateforme qui dechire pour ceux qui aiment parier en crypto ! Ajoutons que le site est rapide et attrayant, ce qui rend chaque session encore plus fun. Particulierement interessant les tournois reguliers pour la competition, renforce le sentiment de communaute.
Trouver les dГ©tails|
gratiswette sportwetten
my web-site: wettstrategien Test
https://shorturl.fm/1BUBm
fastgrowth.click – Impressed by how quickly pages load, very user friendly.
bestchoiceonline.click – Navigation feels intuitive; finding things is smooth and painless.
Женский онлайн-журнал https://rosetti.com.ua о стиле, здоровье и семье. Новости моды, советы экспертов, тренды красоты и секреты счастья. Всё, что важно и интересно женщинам любого возраста.
Сайт о металлах https://metalprotection.com.ua и металлообработке: виды металлов, сплавы, технологии обработки, оборудование и новости отрасли. Всё для специалистов и профессионалов металлургии.
Строительный сайт https://okna-k.com.ua для профессионалов и новичков. Новости отрасли, обзоры материалов, технологии строительства и ремонта, советы мастеров и пошаговые инструкции для качественного результата.
Флойд Мейвезер ар бир беттешинде жогорку деңгээлди көрсөтөт. Флойд Мейвезердин акыркы жаңылыктары ар бир күйөрманды кызыктырат. Бокс легендасынын толук биографиясы жана рекорддору Флойд Мейвезер биографиясы барагында берилген.
Флойд Мейвезерди көрүү ар бир спорт күйөрманы үчүн майрам. Анын рекорддору бүгүнкү күнгө чейин сакталган. Флойд Мейвезердин жашоосу – мотивация.
Флойд Мейвезер – профессионалдуулуктун чордону.
Флойд Мейвезер дүйнөдөгү эң жогорку кирешелүү спортчу. Анын карьерасы спорт тарыхында алтын тамга менен жазылган. Флойд Мейвезер спорттун символу катары белгилүү.
Портал о дизайне https://sculptureproject.org.ua интерьеров и пространства. Идеи, тренды, проекты и вдохновение для дома, офиса и общественных мест. Советы дизайнеров и примеры стильных решений каждый день.
Главный автопортал страны https://nmiu.org.ua всё об автомобилях в одном месте! Новости, обзоры, советы, автообъявления, страхование, ТО и сервис. Для водителей, механиков и просто любителей машин.
ynaix.com – The design feels modern and sparse, clean lines everywhere.
I’m astonished by Wazamba Casino, it crafts a captivating saga. The diversity in titles is astounding, incorporating live sessions for authentic interaction. Matching initial funds up to €500. Answering queries rapidly. Profits are delivered swiftly, still promotions might expand generously. Summarizing, Wazamba Casino furnishes unparalleled amusement for wagering connoisseurs ! Additionally exploration is natural, magnifying each episode’s appeal. Additional benefit competitions for rivalry, granting sustained incentives.
wazambagr.com|
kluvcc.com – The tone is neutral but engaging enough to explore more.
I’m all in on Astronaut Crash by 100HP Gaming, it creates non-stop nail-biting action. Games wrap up in seconds for endless replays, backed by robust RNG for true randomness. RTP sits at an enticing 97%. Chats connect in a flash, upholding outcome transparency. Flows are dependable and speedy, every now and then weekly challenges could ramp up fun. To close, Astronaut Crash redefines crash gaming standards for tactical thinkers ! On that note layout supports marathon marathons, layering sound for immersion. Game-changer seamless wallet linking, allows safe tactic trials.
https://astronaut-crashgame777.com/|
broadcast meet
Студия ремонта https://anti-orange.com.ua квартир и домов. Выполняем ремонт под ключ, дизайн-проекты, отделочные и инженерные работы. Качество, сроки и индивидуальный подход к каждому клиенту.
Туристический портал https://feokurort.com.ua для любителей путешествий! Страны, маршруты, достопримечательности, советы и лайфхаки. Планируйте отдых, находите вдохновение и открывайте мир вместе с нами.
pronostics du foot 1xbet afrique apk
telecharger 1xbet pour android telecharger 1xbet pour android
telecharger 1xbet apk paris sportif foot
Флойд Мейвезердин жашоосу жана ийгилиги көптөргө үлгү. Анын ар бир беттеши дүйнө жүзүнө көрсөтүлөт. Флойд Мейвезердин карьерасы жана акыркы жаңылыктары тууралуу көбүрөөк маалыматты Флойд Мейвезер сайтынан таба аласыз.
Флойд Мейвезер жаш кезинен тарта бокс менен алектенген. Анын ийгилиги ар бир спортчуга мотивация. Анын рингдеги кыймылы ар дайым көрүүчүлөрдү суктандырат.
Флойд Мейвезер ар бир кадамын ойлонуп жасайт.
Флойд Мейвезердин ийгилик сыры эмгек жана туруктуулук. Анын ар бир кадамы медиада талкууланат. Флойд Мейвезер ар дайым жаңы рекорддорду жарата берет.
connectwiththeworldnow – I’ll return to this, it seems like a project with real potential.
österreich wette
my blog :: wetten und gewinnen (http://www.italianvillas4sale.co.uk)
alle wettanbieter deutschland
Here is my site; Sportwette strategie
brightvault.click – Clear headings, easy calls-to-action, user flows are well thought out.
esc buchmacher quoten
Review my blog: sportwetten bonus trick (http://www.saahvideo.com)
507193.com – The design feels utilitarian but effective in its simplicity.
alphaorbit.click – Just found this site; visuals look crisp and navigation is smooth.
nexasphere – Can’t believe how much this helped me today, thanks!
truegrowth – They provided actionable insights that improved our conversion rates.
visionmark – Just received our order; the quality is top-notch.
boldmatrix – Provided actionable insights that improved our product offerings.
prolaunch – Just what I needed, really made a difference today.
online wetten ohne lugas
My blog: WettbüRo Bochum
brandmatrix.click – Going to share this with friends, it’s truly solid and dependable.
newgenius.click – This site gives trust right away, polished look, great details.
elitezone.click – Smooth interface, no glitches so far, feeling very professional.
Флойд Мейвезер спорт дүйнөсүндөгү эң бай спортчу. Флойд Мейвезердин акыркы жаңылыктары ар бир күйөрманды кызыктырат. Кызыктуу маектер жана талдоолор Флойд Мейвезер жаңылыктар бөлүмүндө.
Флойд Мейвезер ар дайым спорттун чокусунда болгон. Флойд Мейвезер – мыкты стратегиянын ээси. Ал бокс тарыхында өз ордун сактап калган.
Флойд Мейвезердин бизнеси да ийгиликтүү.
Флойд Мейвезердин ийгилик сыры эмгек жана туруктуулук. Флойд Мейвезер ар бир жаш спортчуга үлгү. Флойд Мейвезердин мурасы келечек муундар үчүн үлгү.
zenithmedia.click – The design feels modern and confident.
https://shorturl.fm/IF9ho
maxbridge.click – Found new features here I didn’t expect, pleasantly surprised by variety.
ultrafocus.click – Useful content sprinkled throughout, feels like a serious site.
progrid – Appreciate the clear explanations, made complex concepts more accessible.
coreimpact.click – Just checked it out, navigation is intuitive and smooth.
Ich bin komplett hin und weg von SpinBetter Casino, es liefert ein Abenteuer voller Energie. Der Katalog ist reichhaltig und variiert, mit Spielen, die fur Kryptos optimiert sind. Der Kundenservice ist ausgezeichnet, verfugbar rund um die Uhr. Die Auszahlungen sind ultraschnell, ab und an regelma?igere Aktionen waren toll. In Kurze, SpinBetter Casino ist eine Plattform, die uberzeugt fur Casino-Liebhaber ! Nicht zu vergessen die Plattform ist visuell ein Hit, was jede Session noch besser macht. Hervorzuheben ist die Community-Events, die das Spielen noch angenehmer machen.
spinbettercasino.de|
elitefusion.click – Loving every section here, truly feels polished and professional.
J’apprecie l’atmosphere de Locowin Casino, ca transporte dans un univers envoutant. Les alternatives sont incroyablement etendues, comprenant des jeux adaptes aux cryptos. Associe a des tours gratuits sans wager. Les agents reagissent avec promptitude, assurant un support premium. Les benefices arrivent sans latence, de temps a autre plus de promotions frequentes seraient un atout. En synthese, Locowin Casino est essentiel pour les amateurs pour ceux qui parient en crypto ! En outre la navigation est simple et engageante, facilite une immersion complete. Particulierement attractif les tournois periodiques pour la rivalite, renforce le sens de communaute.
Voir tout de suite|
Je ne me lasse pas de Casinia Casino, ca offre un plaisir aristocratique. La selection de jeux est royale, avec des slots thematiques et innovants. 100% jusqu’a 500 € + 200 tours gratuits. L’assistance est efficace et courtoise, garantissant un support de qualite. Les paiements sont securises et fluides, bien que des bonus plus varies seraient apprecies. Pour conclure, Casinia Casino garantit du fun a chaque instant pour les amateurs de sensations fortes ! De plus le site est rapide et attrayant, donne envie de prolonger l’experience. Un plus non negligeable les options de paris sportifs variees, assure des transactions fiables.
Voir tout|
alphaimpact.click – Navigation is smooth, everything easy to find without getting lost.
Je suis ebloui par Casinia Casino, il offre une aventure imperiale. La diversite des titres est somptueuse, avec des slots aux designs audacieux. L’offre de bienvenue est somptueuse. Le service est disponible 24/7, toujours pret a regner. Les gains arrivent sans tarder, mais des recompenses additionnelles seraient imperiales. Au final, Casinia Casino offre un divertissement constant pour ceux qui parient avec des cryptos ! De plus le design est opulent et envoutant, facilite une immersion complete. Egalement remarquable les options de paris sportifs etendues, offre des privileges continus.
Jeter un coup d’œil|
Je suis captive par Casinia Casino, il offre une experience imperiale. Le catalogue est opulent et diversifie, offrant des sessions live immersives. Amplifiant le plaisir de jeu. Le support client est imperial, joignable a toute heure. Les transactions sont fiables, cependant plus de promos regulieres seraient un plus. Dans l’ensemble, Casinia Casino garantit du fun a chaque instant pour les joueurs en quete d’excitation ! Cerise sur le gateau la navigation est simple et fluide, ce qui rend chaque session encore plus royale. Un plus non negligeable les options de paris sportifs variees, propose des avantages personnalises.
Aller sur le site web|
Je suis surpris par Locowin Casino, c’est une plateforme qui explose d’energie. Il y a une profusion de jeux captivants, comprenant des jeux adaptes aux cryptos. Pour un lancement puissant. L’equipe d’assistance est remarquable, proposant des reponses limpides. La procedure est aisee et efficace, mais quelques tours gratuits supplementaires seraient apprecies. Tout compte fait, Locowin Casino est une plateforme qui excelle pour les aficionados de jeux contemporains ! Par ailleurs le design est contemporain et lisse, intensifie le plaisir du jeu. Un autre avantage cle les evenements communautaires captivants, propose des recompenses permanentes.
Lancer le site|
brightchain.click – Visual style is modern but not overwhelming; nice balance.
sharpwave.click – The menu transitions are smooth, clicking feels responsive and natural.
sportwetten bonus aktionen
My homepage vergleich wettquoten (Nell)
ultrawave.click – Such a neat presentation, honestly feels more premium than most platforms.
I’m completely enthralled with Wazamba Casino, it unleashes a special vibe. The title variety is overwhelming, boasting over 5,000 games from 100+ providers. Boosting your playtime. Round-the-clock availability. Operations are straightforward, at times extra spins might enhance it. On the whole, Wazamba Casino provides elite entertainment for crypto users ! Additionally browsing is intuitive, heightening game immersion. Especially appealing regular tournaments for competition, building community engagement.
https://wazambagr.com/|
ZenithLabs – The layout is clean, made reading long articles comfortable today.
metarise.click – Really appreciate how intuitive their menu and navigation are.
Steel Construction Изготовление Металлоконструкций Мы предлагаем полный цикл услуг по изготовлению металлоконструкций любой сложности, от разработки проектной документации до изготовления и монтажа конструкций. Наше производство оснащено современным оборудованием, что позволяет нам обеспечивать высокую точность и качество изготавливаемых конструкций.
Студия дизайна https://bathen.rv.ua интерьеров и архитектурных решений. Создаём стильные, функциональные и гармоничные пространства. Индивидуальный подход, авторские проекты и внимание к деталям.
Ремонт и строительство https://fmsu.org.ua без лишних сложностей! Подробные статьи, обзоры инструментов, лайфхаки и практические советы. Мы поможем построить, отремонтировать и обустроить ваш дом.
Ich bin beeindruckt von SpinBetter Casino, es erzeugt eine Spielenergie, die fesselt. Die Titelvielfalt ist uberwaltigend, mit innovativen Slots und fesselnden Designs. Der Service ist von hoher Qualitat, garantiert top Hilfe. Die Auszahlungen sind ultraschnell, ab und an die Offers konnten gro?zugiger ausfallen. Zum Ende, SpinBetter Casino ist eine Plattform, die uberzeugt fur Spieler auf der Suche nach Action ! Nicht zu vergessen die Plattform ist visuell ein Hit, was jede Session noch besser macht. Zusatzlich zu beachten die Sicherheit der Daten, die Vertrauen schaffen.
spinbettercasino.de|
трансы Волгоград Хорошие трансы – это намеренно культивируемые, управляемые и направленные состояния измененного сознания, служащие катализатором позитивных перемен и глубокой трансформации. Они отличаются от неконтролируемых или спонтанных трансов тем, что характеризуются чувством безопасности, ясности цели и осознанным выбором. Ключевым моментом является присутствие квалифицированного ведущего или глубокое понимание техник самоиндукции.
J’apprecie l’atmosphere de Locowin Casino, il delivre une experience unique. Les alternatives sont incroyablement etendues, proposant des jeux de table immersifs. Doublement des depots jusqu’a 1850 €. Le service est operationnel 24/7, assurant un support premium. Les benefices arrivent sans latence, cependant des incitations additionnelles seraient un benefice. En synthese, Locowin Casino est une plateforme qui excelle pour les aficionados de jeux contemporains ! En outre la plateforme est esthetiquement remarquable, stimule le desir de revenir. A souligner aussi le programme VIP avec des niveaux exclusifs, propose des recompenses permanentes.
Plonger dedans|
J’ai un veritable coup de c?ur pour Casinia Casino, c’est une plateforme qui deborde d’elegance. Il y a une abondance de jeux captivants, avec des slots thematiques et innovants. Plus un Bonus Crab pour demarrer. Le suivi est impeccable, joignable a toute heure. Le processus est simple et elegant, neanmoins quelques tours gratuits supplementaires seraient bienvenus. Dans l’ensemble, Casinia Casino est une plateforme qui regne en maitre pour les fans de casino en ligne ! Notons aussi le design est moderne et fluide, facilite une immersion totale. Un autre atout majeur le programme VIP avec 5 niveaux, propose des avantages personnalises.
Ouvrir la page maintenant|
kombiwette
Look into my blog post :: wett prognosen – Tpilet-wp.aw.ee –
Je suis completement ensorcele par Casinia Casino, ca distille un plaisir majestueux. L’eventail de jeux est princier, offrant des sessions live captivantes. Elevant l’experience de jeu. Le service est disponible 24/7, garantissant un service princier. Les retraits filent comme une fleche, cependant plus de promos frequentes brilleraient davantage. En somme, Casinia Casino offre un divertissement constant pour les joueurs en quete de gloire ! A noter la navigation est intuitive comme un edit, ce qui rend chaque session plus fastueuse. Un avantage notable les options de paris sportifs etendues, offre des privileges continus.
AccГ©der au site|
J’aime l’ambiance royale de Casinia Casino, c’est une plateforme qui rayonne de luxe. Il y a une abondance de jeux captivants, offrant des sessions live immersives. 100% jusqu’a 500 € + 200 tours gratuits. Le suivi est impeccable, offrant des reponses claires. Les retraits sont rapides comme l’eclair, cependant des bonus plus varies seraient apprecies. En bref, Casinia Casino garantit du fun a chaque instant pour les passionnes de jeux modernes ! En prime le site est rapide et attrayant, ajoute une touche de luxe. A noter egalement le programme VIP avec 5 niveaux, qui booste l’engagement.
Cliquez ici|
connectwiththeworldnow – The brand feels urgent, visuals add strength to the narrative.
J’ai un engouement sincere pour Locowin Casino, ca fournit un plaisir intense. La gamme de jeux est spectaculaire, comprenant des jeux adaptes aux cryptos. Doublement des depots jusqu’a 1850 €. Le suivi est exemplaire, accessible a tout instant. Les operations sont solides et veloces, mais des incitations additionnelles seraient un benefice. Globalement, Locowin Casino est essentiel pour les amateurs pour ceux qui parient en crypto ! A mentionner le site est veloce et seduisant, stimule le desir de revenir. A souligner aussi les paiements securises en crypto, garantit des transactions securisees.
Visiter en ligne|
parier foot en ligne pariez sur le foot
sportwetten experten tipps
Here is my homepage; sichere wettstrategie (https://revive.atulenterprises.com/2025/10/09/kann-man-von-Internet-sportwetten-leben)
football africain afrik foot pronostic
afrik foot pronostic telecharger 1xbet apk
I got this web site from my pal who told me concerning this site and at the moment this time I am browsing this site and reading very informative content here.
актуальные зеркала kra41.cc и kra41.at
sportwetten sichere tipps – https://Motherschoice.Ykuat.com/2025/10/11/virtuelle-wetten-Gebuhren/ – gewinnen mit strategie
bs2best зеркало Ты еще не в курсе, что порождает бурю в темных водах сети? Blacksprut – это не просто символ. Это квинтэссенция анонимности, молниеносной скорости и абсолютной уверенности в каждом действии. Приглашаем на bs2best.at – туда, где шепчут о том, о чем другие предпочитают хранить гробовое молчание. Тебе откроются двери в мир, скрытый от любопытных глаз, доступный лишь избранным, тем, кто понимает истинную цену информации. Ни единой зацепки. Никаких отступлений. Только безупречный Blacksprut, гарант твоей конфиденциальности. Не упусти свой шанс стать первопроходцем – bs2best.at уже готов раскрыть свои тайны. Достаточно ли ты смел, чтобы заглянуть в бездну правды?
https://shorturl.fm/KoBce
sportwetten ergebnisse gestern
Feel free to surf to my page … wettanbieter mit
lizenz in deutschland (Jayme)
What’s up to every body, it’s my first visit of this weblog; this blog consists of amazing and truly fine data in support of visitors.
официальный маркетплейс kra41
grandlink – Really impressed, the interface is smooth and very intuitive.
I’m immersed in Wazamba Casino, it resembles a cascade of enchantment. The library is truly enormous, boasting over 5,000 games from 100+ providers. Accompanied by 200 free spins. Maintaining seamless sessions. Transactions are safe and efficient, at times additional incentives would shine. On the whole, Wazamba Casino deserves your attention for betting devotees ! Furthermore the layout is user-friendly and thematic, streamlining user experience. A bonus is the mask collection loyalty system, offering tailored benefits.
wazambagr.com|
pferderennen wetten erklärung
Also visit my homepage – beste wettanbieter österreich
wettbüro kaiserslautern
Here is my site – sportwetten Deutsche lizenz
elitepulse – Very useful insights, thanks for sharing so much value.
vectorrise – Their branding ideas gave our project a fresh perspective.
ascendgrid – Waiting for it to load properly; optimistic about what I’ll find.
esports wettanbieter
Here is my homepage: ohne Einzahlung Wetten
truelaunch – Navigation feels intuitive, didn’t chase what I needed.
smartvibe – Really like how the content flows, feels engaging and useful.
purehorizon – Friendly tone, I like how the posts feel human and real.
brandvision – The tone is friendly but professional, good balance.
innovatek – Just bookmarked this, I’ll come back for more.
linkcraft – The way information is structured here is very intuitive.
skyvertex – Very helpful resources, I’m bookmarking this right now.
brandcrest – The tone is friendly and content feels human, nice job.
summitmedia – Bookmarking this, I’ll definitely revisit for updates.
visionlane – Really enjoying the fresh look, navigation feels intuitive.
Современная студия дизайна https://bconline.com.ua архитектура, интерьер, декор. Мы создаём пространства, где технологии сочетаются с красотой, а стиль — с удобством.
afrik foot pronostic telecharger 1xbet
1xbet cameroun apk telecharger 1xbet cameroun
pariez sur le foot telecharger 1xbet
Создавайте дом https://it-cifra.com.ua своей мечты! Всё о строительстве, ремонте и дизайне интерьера. Идеи, проекты, фото и инструкции — вдохновляйтесь и воплощайте задуманное легко и с удовольствием.
techmatrix – Smooth navigation, everything loads fast and cleanly.
vividpath – Clean layout, made reading through easy on the eyes.
ultraconnect – Smooth loading, minimal lag — good performance.
ascendmark – Quality over quantity — each post feels meaningful.
online chat
novaorbit – The design is clean and makes reading easy on the eyes.
elitegrowth – The design layout helps me stay focused and not distracted.
powercore – The tone feels confident without being overbearing.
urbanshift – Overall a solid experience, definitely worth revisiting.
primeimpact – Content feels genuine, not just marketing fluff.
urbannexus – The writing is clear and easy to follow, nice job.
boldvista – Found several ideas I can apply in my next project.
growthverse – Just checked it out, the resources here are super valuable indeed.
urbanscale – Found some helpful tools I can use immediately.
bs2web at В курсе ли ты, что сотрясает самые глубины тёмной сети? Blacksprut — это не просто название. Это новый уровень в обеспечении анонимности, оперативности и безопасности сделок. Посети bs2best.at — там тебе откроются двери в мир, о котором другие предпочитают умалчивать. Получи доступ к информации, которую тщательно скрывают от общего внимания. Только для тех, кто понимает и разбирается. Без возможности обнаружения. Без каких-либо уступок. Только Blacksprut. Не упусти свой шанс стать одним из первых — bs2best.at уже готов принять тебя в свои ряды. Готов ли ты к тому, что узнаешь?
ascendgrid – Might revisit later when the site is up and running.
goldnexus – Smooth navigation and elegant layout, made me stay longer.
Ich bin beeindruckt von SpinBetter Casino, es bietet einen einzigartigen Kick. Es wartet eine Fulle spannender Optionen, mit Spielen, die fur Kryptos optimiert sind. Der Kundenservice ist ausgezeichnet, garantiert top Hilfe. Der Ablauf ist unkompliziert, ab und an zusatzliche Freispiele waren ein Highlight. Global gesehen, SpinBetter Casino garantiert hochsten Spa? fur Casino-Liebhaber ! Au?erdem die Navigation ist kinderleicht, erleichtert die gesamte Erfahrung. Besonders toll die Sicherheit der Daten, die den Spa? verlangern.
spinbettercasino.de|
J’ai une passion debordante pour Locowin Casino, il procure une odyssee unique. Le catalogue est abondant et multifacette, comprenant des jeux optimises pour les cryptos. Amplifiant l’experience initiale. Le service est disponible 24/7, avec une aide precise et rapide. Les paiements sont securises et fluides, parfois des offres plus genereuses ajouteraient de l’attrait. Au final, Locowin Casino est indispensable pour les joueurs pour les passionnes de jeux modernes ! Par ailleurs la plateforme est visuellement impressionnante, ajoute une touche de confort. Particulierement interessant les tournois reguliers pour la competition, qui booste l’engagement.
DГ©couvrir les offres|
J’apprecie l’environnement de Locowin Casino, on detecte une vibe folle. Le repertoire est opulent et multifacette, avec des slots au style innovant. Le bonus d’accueil est attractif. Le service est operationnel 24/7, proposant des reponses limpides. Les paiements sont proteges et lisses, mais plus de promotions frequentes seraient un atout. Tout compte fait, Locowin Casino fournit une experience ineffacable pour ceux qui parient en crypto ! Par ailleurs la navigation est simple et engageante, intensifie le plaisir du jeu. A souligner aussi les evenements communautaires captivants, garantit des transactions securisees.
Explorer le guide|
J’apprecie l’atmosphere de Locowin Casino, on detecte une vibe folle. Le repertoire est opulent et multifacette, comprenant des jeux adaptes aux cryptos. Le bonus d’accueil est attractif. L’aide est performante et experte, accessible a tout instant. Les paiements sont proteges et lisses, de temps a autre quelques tours gratuits supplementaires seraient apprecies. Pour synthetiser, Locowin Casino merite une exploration approfondie pour les joueurs a la recherche d’aventure ! Par ailleurs la navigation est simple et engageante, ce qui eleve chaque session a un niveau superieur. Particulierement attractif le programme VIP avec des niveaux exclusifs, propose des recompenses permanentes.
Accéder à l’avis|
truelaunch – The tone seems genuine, like someone really cares.
brandvision – Bookmarking this, lots of value I’ll revisit later.
Мир архитектуры https://vineyardartdecor.com и дизайна в одном месте! Лучшие идеи, проекты и вдохновение для дома, офиса и города. Узнай, как создаются красивые и функциональные пространства.
I’m drawn to Wazamba Casino, it generates crazy gaming vibes. The options are extensive and diverse, featuring over 5,000 titles from top providers. Plus 200 free spins to start strong. Professional and helpful assistance. Withdrawals are processed quickly, occasionally more frequent promotions could enhance it. Overall, Wazamba Casino is essential for gamers for those who enjoy crypto ! Also navigation is effortless, deepens immersion in the game. Especially great collecting artifacts for rewards, elevating the engagement.
wazambagr.com|
blueorbit – Navigation feels intuitive, didn’t struggle at all.
Ich bin abhangig von SpinBetter Casino, es erzeugt eine Spielenergie, die fesselt. Es gibt eine unglaubliche Auswahl an Spielen, mit immersiven Live-Sessions. Der Service ist von hoher Qualitat, immer parat zu assistieren. Der Ablauf ist unkompliziert, ab und an zusatzliche Freispiele waren ein Highlight. In Kurze, SpinBetter Casino ist eine Plattform, die uberzeugt fur Online-Wetten-Fans ! Nicht zu vergessen die Plattform ist visuell ein Hit, erleichtert die gesamte Erfahrung. Hervorzuheben ist die mobilen Apps, die den Spa? verlangern.
spinbettercasino.de|
Tenho uma paixao intensa por BETesporte Casino, e uma plataforma que pulsa com emocao atletica. A variedade de titulos e impressionante, com sessoes ao vivo imersivas. Fortalece seu saldo inicial. A assistencia e eficiente e profissional, acessivel a qualquer hora. Os pagamentos sao seguros e fluidos, contudo promocoes mais frequentes seriam um plus. No geral, BETesporte Casino garante diversao a cada rodada para jogadores em busca de emocao ! Alem disso a plataforma e visualmente impactante, tornando cada sessao mais competitiva. Igualmente impressionante as opcoes variadas de apostas esportivas, proporciona vantagens personalizadas.
Começar aqui|
Estou completamente encantado por PlayPIX Casino, e uma plataforma que pulsa com energia festiva. A variedade de titulos e deslumbrante, incluindo apostas esportivas vibrantes. 100% ate €500 + 200 rodadas gratis. O suporte ao cliente e estelar, com suporte preciso e rapido. O processo e simples e elegante, contudo algumas rodadas gratis extras seriam incriveis. No geral, PlayPIX Casino e uma plataforma que reina suprema para quem aposta com cripto ! Acrescentando que a navegacao e simples e envolvente, instiga a prolongar a experiencia. Outro destaque as opcoes variadas de apostas esportivas, proporciona vantagens personalizadas.
Dar uma olhada|
futurelink – Clean layout and easy navigation made me stick around.
J’aime l’atmosphere unique de Locowin Casino, c’est une plateforme qui deborde de vitalite. Le catalogue est abondant et multifacette, comprenant des jeux optimises pour les cryptos. Amplifiant l’experience initiale. L’assistance est efficace et professionnelle, toujours disponible pour assister. Le processus est simple et reibungslos, mais des recompenses additionnelles seraient un avantage. Dans l’ensemble, Locowin Casino merite une visite pour les amateurs de sensations fortes ! A noter la plateforme est visuellement impressionnante, incite a prolonger l’experience. Un avantage supplementaire les tournois reguliers pour la competition, offre des recompenses continues.
VГ©rifier le site|
valuevision – Navigation is decent, but some links need clearer labels.
Je suis entierement obsede par Locowin Casino, il delivre une experience unique. Les alternatives sont incroyablement etendues, offrant des sessions live intenses. Associe a des tours gratuits sans wager. Le service est operationnel 24/7, proposant des reponses limpides. Les retraits sont realises promptement, mais des offres plus liberales ajouteraient de la valeur. En fin de compte, Locowin Casino garantit du divertissement constant pour les enthousiastes de casino en ligne ! A mentionner la plateforme est esthetiquement remarquable, stimule le desir de revenir. Particulierement attractif les paiements securises en crypto, qui stimule l’engagement.
Ouvrir la page maintenant|
J’apprecie l’atmosphere de Locowin Casino, ca transporte dans un univers envoutant. Les alternatives sont incroyablement etendues, comprenant des jeux adaptes aux cryptos. Renforcant l’experience de depart. L’equipe d’assistance est remarquable, toujours pret a intervenir. Les operations sont solides et veloces, bien que plus de promotions frequentes seraient un atout. Tout compte fait, Locowin Casino fournit une experience ineffacable pour les enthousiastes de casino en ligne ! Par ailleurs le design est contemporain et lisse, facilite une immersion complete. Un plus significatif les evenements communautaires captivants, offre des privileges sur mesure.
Explorer tout|
growthverse – The content is engaging, and the site is responsive.
valuevision – Would love to see more interactive features or tutorials here.
skyportal – Excellent resources here, found useful tips for my projects.
growthverse – The site is well-structured, making information easy to find.
I’m drawn to Wazamba Casino, it provides a thrilling journey. The selection of games is phenomenal, featuring over 5,000 titles from top providers. Doubling your deposit up to €500. Professional and helpful assistance. Withdrawals are processed quickly, occasionally generous offers could be expanded. Broadly speaking, Wazamba Casino is essential for gamers for casino enthusiasts ! Furthermore the design is engaging and exotic, encourages repeated visits. Notably collecting artifacts for rewards, ensuring secure transactions.
https://wazambagr.com/|
trendforge – Checked twice; still under construction or not publicly available.
quantumreach – Clean layout, easy to navigate, very user-friendly experience.
boldimpact – The domain looks strong, hoping content is up soon.
Tenho uma paixao intensa por BETesporte Casino, proporciona uma aventura competitiva. As opcoes sao vastas como um campeonato, incluindo apostas esportivas palpitantes. 100% ate R$600 + apostas gratis. O suporte ao cliente e de elite, com suporte preciso e rapido. Os pagamentos sao seguros e fluidos, embora promocoes mais frequentes seriam um plus. Em resumo, BETesporte Casino oferece uma experiencia inesquecivel para entusiastas de jogos modernos ! Tambem a interface e fluida e energetica, facilita uma imersao total. Um diferencial importante as opcoes variadas de apostas esportivas, que impulsiona o engajamento.
Visitar hoje|
Sou viciado em PlayPIX Casino, sinto um ritmo alucinante. O catalogo e rico e diversificado, com slots de design inovador. 100% ate €500 + 200 rodadas gratis. O acompanhamento e impecavel, garantindo um atendimento de qualidade. Os ganhos chegam sem demora, embora ofertas mais generosas dariam um toque especial. No geral, PlayPIX Casino vale uma visita epica para fas de cassino online ! Alem disso a plataforma e visualmente espetacular, tornando cada sessao mais vibrante. Um diferencial importante os pagamentos seguros em cripto, fortalece o senso de comunidade.
http://www.playpixcasino.pro|
https://bs2bsme.at
alihidaer2313 – The experience is gentle, nothing over the top, just reliable.
skyportal – Really enjoying the latest updates, everything loads super fast today.
alphaunity – Loading speed is good, didn’t wait long for pages.
bluetrail – Bookmarking this, seems like a resource I’ll revisit often.
sharpbridge – Friendly tone, feels like a real person made this.
boldimpact – Design placeholders show up; looking forward to full content.
quantumreach – Just checked it out, the content feels fresh and full of insight.
solidvision – Tried several times, page didn’t load yet.
elitegrowth – The content is engaging, and the site is responsive.
cloudmatrix – Great user experience, everything loads so smoothly and fast.
goldbridge – Wish there were more articles or resources to explore.
fastgrowth – The site is well-structured, making information easy to find.
maxvision – Navigation is seamless, and the visuals are appealing.
alphaunity – Loading speed is good, didn’t wait long for pages.
nextrend – Friendly writing style makes even complex topics feel simple.
greenmotion – Consistently impressed with the site’s performance and design.
zenithlabs – Found exactly what I was looking for, very intuitive.
thinkbeyondtech – A pleasure to browse, everything is well-organized and clear.
nextlayer – Impressed by the layout, feels modern and user-friendly.
boldnetwork – Just visited, the homepage looks clean but minimal content so far.
sharpbridge – The color scheme is nice, very calming on the eyes.
bluetrail – Nice visuals too, makes reading comfortable and appealing.
solidvision – Clean branding, simple domain—can work well.
stellenangebote wettbüro
Feel free to surf to my web blog … Sportwetten tipps telegram
Je suis completement fou de Locowin Casino, il offre une experience unique. Il y a une multitude de jeux excitants, proposant des jeux de table immersifs. Pour un demarrage en force. Le support client est exceptionnel, avec une aide precise et rapide. Les paiements sont securises et fluides, parfois des recompenses supplementaires seraient un atout. Dans l’ensemble, Locowin Casino garantit du fun a chaque instant pour les joueurs en quete d’excitation ! En prime le site est rapide et attrayant, facilite une immersion totale. Egalement appreciable le programme VIP avec des niveaux exclusifs, renforce le sentiment de communaute.
Ouvrir l’offre|
sportwetten beste anbieter
my site; Eine wettprognose
elitegrowth – Consistently impressed with the site’s performance and design.
cloudmatrix – The site is well-structured, making information easy to find.
Je suis fascine par Locowin Casino, ca transporte dans un univers envoutant. Les alternatives sont incroyablement etendues, offrant des sessions live intenses. Renforcant l’experience de depart. L’equipe d’assistance est remarquable, accessible a tout instant. Les benefices arrivent sans latence, de temps a autre des incitations additionnelles seraient un benefice. Globalement, Locowin Casino est essentiel pour les amateurs pour les adeptes de sensations intenses ! A mentionner la navigation est simple et engageante, facilite une immersion complete. Un plus significatif le programme VIP avec des niveaux exclusifs, qui stimule l’engagement.
Visiter l’offre|
fastgrowth – Navigation is seamless, and the visuals are appealing.
https://a-bsme.at
focuslab – Browsing was smooth — pages loaded fast and clearly.
J’aime l’atmosphere de Locowin Casino, ca transporte dans un univers envoutant. La diversite des titres est epoustouflante, comprenant des jeux adaptes aux cryptos. Pour un lancement puissant. Les agents reagissent avec promptitude, proposant des reponses limpides. Les benefices arrivent sans latence, par moments quelques tours gratuits supplementaires seraient apprecies. Tout compte fait, Locowin Casino garantit du divertissement constant pour les joueurs a la recherche d’aventure ! En outre l’interface est intuitive et raffinee, facilite une immersion complete. Un plus significatif les evenements communautaires captivants, offre des privileges sur mesure.
Aller plus en profondeur|
maxvision – Love the clean design, really easy to navigate today.
goldbridge – Wish there were more articles or resources to explore.
Автоматические гаражные ворота давно перестали быть роскошью и стали необходимым элементом комфортной жизни. Наши автоматические ворота сочетают надёжность проверенных европейских механизмов с элегантным дизайном, который гармонично впишется в архитектуру любого здания. Мы предлагаем полный цикл услуг: от профессиональной консультации и точного замера до установки под ключ и гарантийного обслуживания. Доверьте безопасность своего дома профессионалам — получите бесплатный расчёт стоимости уже сегодня: Тут
broadcast connect
roofing services Melbourne
Estou completamente apaixonado por BR4Bet Casino, e um cassino online que reluz como um farol na nevoa. As escolhas sao vibrantes como um farol. oferecendo lives que acendem como fogueiras. O atendimento e solido como um farol. oferecendo respostas claras como um farol. Os pagamentos sao seguros e fluidos. ocasionalmente as ofertas podiam ser mais generosas. Ao final, BR4Bet Casino e uma fogueira de adrenalina para os viciados em emocoes de cassino! Por sinal o visual e uma explosao de claroes. fazendo o cassino brilhar como um farol.
br4bet casa de aposta|
Estou completamente apaixonado por BETesporte Casino, oferece um prazer esportivo intenso. As opcoes sao amplas como um campo de futebol, com slots modernos e tematicos. 100% ate R$600 + apostas gratis. A assistencia e eficiente e amigavel, sempre pronto para entrar em campo. As transacoes sao confiaveis, no entanto recompensas extras seriam um hat-trick. Resumindo, BETesporte Casino oferece uma experiencia inesquecivel para quem usa cripto para jogar ! Tambem o design e moderno e vibrante, instiga a prolongar o jogo. Notavel tambem os eventos comunitarios envolventes, que impulsiona o engajamento.
Descobrir mais|
Je suis accro a Simsinos Casino, ca degage une ambiance de jeu aussi coloree qu’un studio d’animation. La selection du casino est une planche de plaisirs. offrant des sessions de casino en direct qui sautent comme des toons. est un virtuose de l’animation. repondant en un flash colore. Les gains du casino arrivent a une vitesse cartoon. mais plus de tours gratuits au casino ce serait cartoon. En conclusion, Simsinos Casino cadence comme une sonate de victoires pour les fans de symphonies colorees! Par ailleurs resonne avec une melodie graphique toon. facilite une experience de casino dessinee.
avis simsinos casino|
Acho simplesmente esportivo MarjoSports Casino, oferece uma aventura que marca gol como um penalti perfeito. As escolhas sao vibrantes como um apito. oferecendo sessoes ao vivo que marcam como gols. O atendimento esta sempre ativo 24/7. oferecendo respostas claras como uma quadra. Os pagamentos sao seguros e fluidos. de vez em quando mais bonus seriam um diferencial de campo. Na real, MarjoSports Casino oferece uma experiencia que e puro drible para quem curte apostar com estilo esportivo! Como extra o visual e uma explosao de quadras. dando vontade de voltar como um craque.
como ganhar na marjosports|
Galera, vim dividir minhas impressoes no 4PlayBet Casino porque superou minhas expectativas. A variedade de jogos e bem acima da media: jogos ao vivo imersivos, todos funcionando perfeito. O suporte foi atencioso, responderam em minutos pelo chat, algo que faz diferenca. Fiz saque em cartao e o dinheiro entrou muito rapido, ponto fortissimo. Se tivesse que criticar, diria que seria legal torneios de slots, mas isso nao estraga a experiencia. Enfim, o 4PlayBet Casino e completo. Recomendo sem medo.
savage gear 4play 13cm|
Sou viciado em PlayPIX Casino, transmite uma energia vibrante. A selecao de jogos e fenomenal, oferecendo jogos de mesa envolventes. 100% ate €500 + rodadas gratis. O suporte ao cliente e excepcional, com suporte rapido e preciso. As transacoes sao confiaveis, as vezes recompensas extras seriam eletrizantes. Em sintese, PlayPIX Casino e essencial para jogadores para fas de cassino online ! Vale destacar o design e moderno e vibrante, instiga a prolongar a experiencia. Igualmente impressionante os eventos comunitarios envolventes, proporciona vantagens personalizadas.
Dar uma olhada|
online sportwetten österreich – Ashton – seiten mit paypal
J’adore l’ambiance de Locowin Casino, on ressent une vibe delirante. Les options sont incroyablement vastes, avec des slots au design innovant. Pour un demarrage en force. Les agents repondent avec rapidite, toujours pret a aider. Les retraits sont ultra-rapides, parfois plus de promos regulieres seraient top. En bref, Locowin Casino est une plateforme qui dechire pour les fans de casino en ligne ! En prime le design est moderne et fluide, amplifie le plaisir de jouer. Un autre atout majeur les evenements communautaires engageants, offre des recompenses continues.
Apprendre les dГ©tails|
wettstrategie kleine quoten
My web blog Halbzeit Wetten Strategie
guts sportwetten bonus
Also visit my web blog: wettquote bielefeld leverkusen
ynaix – Navigation is logical, I found things very quickly without hassles.
Je suis surpris par Locowin Casino, on detecte une vibe folle. Le repertoire est opulent et multifacette, avec des slots au style innovant. Pour un lancement puissant. Les agents reagissent avec promptitude, avec une assistance exacte et veloce. Les retraits sont realises promptement, bien que des incitations additionnelles seraient un benefice. Globalement, Locowin Casino est essentiel pour les amateurs pour les enthousiastes de casino en ligne ! En outre le site est veloce et seduisant, intensifie le plaisir du jeu. Egalement notable les options de paris sportifs etendues, garantit des transactions securisees.
Regarder maintenant|
Je suis accro a Locowin Casino, il delivre une experience unique. Les alternatives sont incroyablement etendues, incluant des paris sportifs electrisants. Renforcant l’experience de depart. Le service est operationnel 24/7, assurant un support premium. La procedure est aisee et efficace, de temps a autre des bonus plus diversifies seraient souhaitables. Pour synthetiser, Locowin Casino merite une exploration approfondie pour les joueurs a la recherche d’aventure ! A mentionner la navigation est simple et engageante, ce qui eleve chaque session a un niveau superieur. Particulierement attractif les tournois periodiques pour la rivalite, garantit des transactions securisees.
Aller ici|
Заботьтесь о здоровье сосудов ног с профессионалом! В группе «Заметки практикующего врача-флеболога» вы узнаете всё о профилактике варикоза, современных методиках лечения (склеротерапия, ЭВЛО), УЗИ вен и точной диагностике. Доверяйте опытному врачу — ваши ноги заслуживают лучшего: https://phlebology-blog.ru/
connectwiththeworldnow – Very user-friendly, menus are intuitive and well organized.
ynaix – Wow this site looks slick, very modern and impressive visuals.
Частный заем денег домашние деньги телефон альтернатива банковскому кредиту. Быстро, безопасно и без бюрократии. Получите нужную сумму наличными или на карту за считанные минуты.
connectwiththeworldnow – Content is relevant and engaging, makes me want to explore more.
strongrod – Typography is clean; reading is comfortable even on small screens.
Все спортивные новости http://sportsat.ru в реальном времени. Итоги матчей, трансферы, рейтинги и обзоры. Следите за событиями мирового спорта и оставайтесь в курсе побед и рекордов!
wavefusion – Really like the style here, feels fresh and creative.
brightideaweb – Pages load quickly, even images render nicely.
metarise – Content is high quality, I feel like I learned something solid.
cyberlaunch – Love the futuristic feel, this site gives such good vibes.
https://shorturl.fm/MTlGH
sharpwave – Love the crisp styling, makes everything look polished and clean.
Curto demais a energia de BR4Bet Casino, tem uma energia de jogo tao ardente quanto uma fogueira a meia-noite. As opcoes sao ricas e reluzem como luzes. com caca-niqueis que brilham como holofotes. O time do cassino e digno de um faroleiro. com ajuda que ilumina como uma tocha. As transacoes sao faceis como um brilho. em alguns momentos as ofertas podiam ser mais generosas. Resumindo, BR4Bet Casino vale explorar esse cassino ja para os exploradores de jogos online! De lambuja a interface e fluida e brilha como um farol. adicionando um toque de luz ao cassino.
br4bet entrar|
Me encantei pelo drible de MarjoSports Casino, oferece uma aventura que marca gol como um penalti perfeito. O catalogo de jogos e um campo de emocoes. com slots tematicos de esportes. O suporte e um arbitro de eficiencia. respondendo rapido como um apito. Os pagamentos sao lisos como uma rede. em alguns momentos mais giros gratis seriam vibrantes. Na real, MarjoSports Casino vale explorar esse cassino ja para os apaixonados por slots modernos! De bonus o design e um espetaculo visual de torcida. fazendo o cassino pulsar como uma rede.
marjosports ambas|
Acho simplesmente turbo F12.Bet Casino, explode com uma vibe de cassino supersonica. As escolhas sao vibrantes como um velocimetro. oferecendo lives que explodem como largadas. O atendimento esta sempre ativo 24/7. com solucoes precisas e instantaneas. O processo e claro e sem freadas. ocasionalmente mais bonus seriam um diferencial turbo. Em resumo, F12.Bet Casino e um cassino online que e uma pista de diversao para quem curte apostar com estilo veloz! E mais o visual e uma explosao de curvas. adicionando um toque de velocidade ao cassino.
f12 bet cupom|
Je suis accro a Simsinos Casino, resonne avec un rythme de casino anime. La selection du casino est une planche de plaisirs. avec des slots qui rebondissent comme des bulles. Le support du casino est disponible 24/7. joignable par chat ou email. arrivent comme un concerto toon. quand meme des offres qui vibrent comme une cadence animee. A la fin, Simsinos Casino resonne comme un storyboard de plaisir pour les amoureux des slots modernes de casino! Par ailleurs est une cadence visuelle envoutante. ajoute une touche de rythme cartoon au casino.
avis simsinos|
strongrod – Typography is clean; reading is comfortable even on small screens.
brightchain – Content strikes a good balance, informative yet easy to read.
Sou totalmente viciado em BETesporte Casino, e uma plataforma que vibra como um estadio lotado. Ha uma explosao de jogos emocionantes, oferecendo jogos de mesa envolventes. Com uma oferta inicial para impulsionar. A assistencia e eficiente e amigavel, com suporte rapido e preciso. As transacoes sao confiaveis, contudo mais apostas gratis seriam incriveis. Para finalizar, BETesporte Casino oferece uma experiencia inesquecivel para quem usa cripto para jogar ! Alem disso a interface e fluida e energetica, facilita uma imersao total. Muito atrativo o programa VIP com niveis exclusivos, que impulsiona o engajamento.
Mergulhe nisso|
Galera, preciso compartilhar minha experiencia no 4PlayBet Casino porque me pegou de surpresa. A variedade de jogos e surreal: roletas animadas, todos rodando lisos. O suporte foi atencioso, responderam em minutos pelo chat, algo que raramente vi. Fiz saque em Ethereum e o dinheiro entrou em minutos, ponto fortissimo. Se tivesse que criticar, diria que seria legal torneios de slots, mas isso nao estraga a experiencia. Resumindo, o 4PlayBet Casino vale demais a pena. Vale experimentar.
4play spa|
innovatewithus – Really like the vibe here, feels fresh and inspiring always.
Estou totalmente fascinado por PlayPIX Casino, leva a um universo de pura adrenalina. A selecao de jogos e fenomenal, oferecendo jogos de mesa envolventes. Com uma oferta inicial para impulsionar. O acompanhamento e impecavel, oferecendo respostas claras. Os pagamentos sao seguros e fluidos, as vezes recompensas extras seriam eletrizantes. No geral, PlayPIX Casino oferece uma experiencia memoravel para entusiastas de jogos modernos ! Acrescentando que o design e moderno e vibrante, aumenta o prazer de jogar. Muito atrativo os eventos comunitarios envolventes, proporciona vantagens personalizadas.
Ler os detalhes|
cloudmark – UX is thoughtful, everything feels connected and consistent.
bestchoiceonline – This site feels reliable, everything is clear and well organized.
brightideaweb – Pages load quickly, even images render nicely.
wavefusion – Color palette balanced, pleasing contrast without harshness.
nextbrand – Lots of useful info, clearly organized and easy to parse.
digitalstorm – Overall feels like a premium experience, very polished site.
everythingyouneedtoknow – Pages load fast, no waiting even on image-heavy content.
discoveramazingthingsonline – Typography is readable, images attract attention without overwhelming.
hip
explorecreativeideasdaily – Color palette is refreshing, helps keep me motivated while browsing.
deutsche wettseiten
Look at my site: bonus Buchmacher
cyberlaunch – Content seems solid and meaningful, not just filler stuff.
esc wetten bonus freispielen (tetraguard.io)
deutschland
metarise – Design pops nicely, visuals are appealing and consistent throughout.
ultrawave – Navigation is intuitive, I found what I needed without delays.
yourbrandzone – The design is modern, sleek, and very visually appealing.
pixelplanet – The design is playful yet professional, good balance achieved.
sharpwave – Feels very user oriented, they anticipate what I’m looking for.
globalreach – The writing flows well, voice feels friendly and genuine.
zenithmedia – Typography is crisp, spacing makes reading comfortable.
boldspark – Overall very polished, good balance of design and usability.
brightchain – Overall experience positive, I’m likely to revisit for updates.
Suchen Sie Immobilien? http://www.montenegro-immobilien-kaufen.com/ wohnungen, Villen und Grundstucke mit Meerblick. Aktuelle Preise, Fotos, Auswahlhilfe und umfassende Transaktionsunterstutzung.
innovatewithus – Content is super useful, I learned something new today.
cloudmark – Found helpful resources, they make exploring enjoyable.
everythingyouneedtoknow – The layout is clean and sections are organized logically.
discoveramazingthingsonline – Overall very enjoyable, feels like a fun place to explore.
J’adore l’ambiance de Locowin Casino, on ressent une vibe delirante. Il y a une multitude de jeux excitants, avec des slots au design innovant. Le bonus de bienvenue est attractif. Le service est disponible 24/7, joignable a toute heure. Les retraits sont ultra-rapides, mais des offres plus genereuses ajouteraient du piquant. Pour conclure, Locowin Casino vaut largement le detour pour les fans de casino en ligne ! De plus la navigation est simple et agreable, donne envie de prolonger l’experience. Particulierement interessant les paiements securises en crypto, propose des avantages personnalises.
Aller lГ -bas|
explorecreativeideasdaily – Love the inspiration, so many new ideas every visit.
**mindvault**
mindvault is a premium cognitive support formula created for adults 45+. It’s thoughtfully designed to help maintain clear thinking
digitalstorm – Pages load quickly, even complex graphics appear smooth.
Je suis captive par Casinia Casino, ca distille un plaisir eclatant. L’eventail de jeux est resplendissant, offrant des sessions live captivantes. L’offre de bienvenue est eclatante. Les agents repondent comme une etoile filante, avec une aide claire et veloce. Les transactions sont fiables et rapides, cependant plus de promos regulieres ajouteraient de l’eclat. Pour conclure, Casinia Casino garantit un plaisir radiant a chaque instant pour les passionnes de frissons lumineux ! De plus le design est moderne et eblouissant, intensifie l’eclat du jeu. Particulierement captivant les paiements securises en crypto, qui renforce l’engagement.
En savoir plus|
Je suis accro a Locowin Casino, il offre une experience unique. Le catalogue est riche et diversifie, avec des slots au design innovant. Le bonus de bienvenue est attractif. Le service est disponible 24/7, garantissant un support de qualite. Les transactions sont fiables et rapides, neanmoins des recompenses supplementaires seraient un atout. En bref, Locowin Casino est un incontournable pour les joueurs pour ceux qui aiment parier en crypto ! De plus la navigation est simple et agreable, donne envie de prolonger l’experience. Egalement appreciable le programme VIP avec des niveaux exclusifs, renforce le sentiment de communaute.
DГ©bloquer plus|
wettbüro magdeburg
My web page Pferderennen Wett Tipps
Curto demais a vibracao de Brazino Casino, tem um ritmo de jogo que reluz como um coral. As opcoes sao ricas e reluzem como conchas. com slots tematicos de aventuras marinhas. Os agentes nadam como golfinhos. oferecendo respostas claras como um lago. Os saques sao velozes como um mergulho. ocasionalmente mais recompensas fariam o coracao nadar. Em sintese, Brazino Casino e um recife de emocoes para os fas de adrenalina marinha! Adicionalmente o layout e vibrante como uma perola. tornando cada sessao ainda mais aquatica.
brazino777 bonus codes|
Estou alucinado com Verabet Casino, pulsa com uma forca de cassino digna de um xama. O catalogo de jogos e um altar de prazeres. oferecendo sessoes ao vivo que brilham como labaredas. O servico e confiavel como uma fogueira. oferecendo respostas claras como uma chama. Os pagamentos sao lisos como uma pira. mas as ofertas podiam ser mais generosas. Em resumo, Verabet Casino garante um jogo que reluz como chamas para os exploradores de jogos online! E mais o layout e vibrante como uma tocha. fazendo o cassino queimar como uma fogueira.
casa de aposta vera bet|
Me enredei no algoritmo de PlayPix Casino, e um cassino online que reluz como um pixel em overclock. O leque do cassino e uma matriz de delicias. incluindo mesas com charme de algoritmo. O suporte e um codigo preciso. assegurando apoio sem erros. O processo e claro e sem crashes. mesmo assim mais giros gratis seriam vibrantes. No fim das contas, PlayPix Casino e um buffer de emocoes para os apaixonados por slots modernos! Adicionalmente o design e fluido como um render. amplificando o jogo com vibracao digital.
playpix aviator telegram|
joinourcreativecommunity – Feels like a warm welcome, community vibes strong already.
Estou alucinado com Fogo777 Casino, explode com uma vibe de cassino flamejante. Os jogos formam uma fogueira de diversao. com slots tematicos de cerimonias antigas. Os agentes voam como chamas. oferecendo respostas claras como uma chama. Os ganhos chegam rapido como uma labareda. mesmo assim mais recompensas fariam o coracao queimar. Em resumo, Fogo777 Casino garante um jogo que reluz como chamas para os cacadores de vitorias incendiarias! Alem disso o layout e vibrante como uma tocha. transformando cada aposta em uma aventura flamejante.
plataforma fogo777 baixar|
Je suis fascine par BankOnBet Casino, ca vibre avec une richesse de jeu qui s’empile. La gamme est un empilement de gains. offrant des sessions de casino en direct qui accumulent. Le service client du casino est une cle de coffre-fort. responding faster than a bank transfer. Withdrawals are swift as a wire transfer. cependant des bonus de casino plus frequents seraient rentables. Pour resumer, BankOnBet Casino is a casino that banks on fun pour les fans de gains stables! Plus l’interface du casino est fluide et securisee comme un coffre. making every session more rewarding.
bankonbet recensione|
YourPathOfGrowth – I appreciate how they focus on sustainable solutions for all.
Tenho uma paixao ardente por BETesporte Casino, oferece um prazer esportivo inigualavel. A variedade de titulos e estonteante, com slots modernos e tematicos. Com uma oferta inicial para impulsionar. O servico esta disponivel 24/7, com suporte rapido e preciso. As transacoes sao confiaveis, no entanto recompensas extras seriam um hat-trick. Para finalizar, BETesporte Casino e uma plataforma que domina o gramado para entusiastas de jogos modernos ! Acrescentando que a navegacao e intuitiva e rapida, facilita uma imersao total. Um diferencial importante os torneios regulares para rivalidade, proporciona vantagens personalizadas.
Clicar para ver|
Sou totalmente viciado em PlayPIX Casino, sinto um pulsar selvagem. A selecao de jogos e fenomenal, suportando jogos compativeis com criptomoedas. Eleva a experiencia de jogo. O servico esta disponivel 24/7, sempre pronto para resolver. Os saques sao rapidos como um raio, embora bonus mais variados seriam incriveis. Resumindo, PlayPIX Casino oferece uma experiencia memoravel para fas de cassino online ! Adicionalmente o design e moderno e vibrante, instiga a prolongar a experiencia. Notavel tambem os eventos comunitarios envolventes, que aumenta o engajamento.
Continuar lendo|
J’ai un coup de foudre pour Locowin Casino, on ressent une vibe delirante. Il y a une multitude de jeux excitants, offrant des sessions live dynamiques. Le bonus de bienvenue est attractif. Le support client est exceptionnel, joignable a toute heure. Les paiements sont securises et fluides, parfois des recompenses supplementaires seraient un atout. En resume, Locowin Casino est un incontournable pour les joueurs pour les passionnes de jeux modernes ! Notons aussi la plateforme est visuellement top, facilite une immersion totale. Egalement appreciable les options de paris sportifs variees, qui booste l’engagement.
Consulter les dГ©tails|
YourPathOfGrowth – Their commitment to social impact is truly commendable.
joinourcreativecommunity – The tone invites participation, feels more like a conversation than lecture.
Je suis emerveille par Casinia Casino, il offre une aventure etincelante. Les options sont vastes comme un ciel etoile, incluant des paris sportifs palpitants. 100% jusqu’a 500 € + 200 tours gratuits. L’assistance est rapide et precise, joignable a toute heure. Les transactions sont fiables et rapides, de temps a autre des bonus plus varies brilleraient davantage. En somme, Casinia Casino garantit un plaisir radiant a chaque instant pour les amateurs de casino en ligne ! Par ailleurs la plateforme scintille comme une etoile, facilite une immersion totale. Particulierement captivant les options de paris sportifs variees, garantit des transactions fiables.
AccГ©der au site|
J’ai un coup de foudre pour Locowin Casino, il offre une experience unique. Les options sont incroyablement vastes, comprenant des jeux compatibles avec les cryptos. Pour un demarrage en force. Le suivi client est irreprochable, offrant des reponses claires. Les paiements sont securises et fluides, parfois des bonus plus varies seraient bienvenus. Dans l’ensemble, Locowin Casino garantit du fun a chaque instant pour ceux qui aiment parier en crypto ! Ajoutons que le design est moderne et fluide, amplifie le plaisir de jouer. Un autre atout majeur les tournois reguliers pour la competition, propose des avantages personnalises.
Ouvrir la page maintenant|
alphaimpact – Love the energy here, design feels bold and very clean.
LearnWithConfidence – This site helped me improve skills faster than expected honestly.
makingeverymomentcount – Design feels warm and personal, very inviting experience.
thebestplacetostarttoday – Visuals align beautifully with the message of new beginnings.
learnshareandsucceed – Overall very polished, a site I’d trust to return for real growth.
makelifebettereveryday – I’d come here often for tips that actually make a positive difference.
getreadytoexplore – Overall impression is exciting, feels like starting a journey into new things.
everythingaboutsuccess – Tone feels empowering, not preachy, nice balance for growth content.
findwhatyouarelookingfor – Pages load fast, no lag, really smooth experience even on mobile.
велотренажер для дома Велотренажер для дома — компактный и тихий тренажер для ежедневных тренировок. Вертикальные модели занимают мало места, с эргономичным сиденьем и регулируемыми педалями. Магнитная система обеспечивает бесшумную работу, идеальную для квартир. 8-24 уровня нагрузки для начинающих и продвинутых, с программами интервальной тренировки. Сенсоры на руле измеряют пульс, а компьютер показывает прогресс. Материал — сталь с антикоррозийным покрытием для долговечности. Подходит для похудения, тонизации мышц и профилактики варикоза. Бюджет от 8 000 рублей, с гарантией 1-3 года. Домашний велотренажер мотивирует к регулярным занятиям без погодных ограничений.
learnsomethingneweveryday – Visual elements are engaging but don’t distract from the content.
LearnWithConfidence – I find the lessons engaging, very easy to follow along.
discoverendlessinspiration – Typography is elegant and spacing gives great breathing room.
growyourbusinessfast – Helpful resources seem real; tools and guides look useful.
Adoro o glitch de PlayPix Casino, explode com uma vibe de cassino retro-futurista. O catalogo de jogos e uma tela de emocoes. com caca-niqueis que reluzem como bytes. Os agentes processam como CPUs. disponivel por chat ou e-mail. As transacoes sao simples como um pixel. as vezes queria promocoes que processam como CPUs. Para encurtar, PlayPix Casino e um buffer de emocoes para quem curte apostar com estilo cibernetico! Como extra o site e uma obra-prima de estilo digital. dando vontade de voltar como um byte.
playpix wikipГ©dia|
Estou completamente incendiado por Verabet Casino, parece um festival de chamas cheio de adrenalina. A selecao de titulos e uma pira de emocoes. incluindo mesas com charme flamejante. O suporte e um fulgor reluzente. com ajuda que ilumina como uma pira. O processo e claro e sem fumaca. de vez em quando mais giros gratis seriam uma loucura de fogo. Resumindo, Verabet Casino e o point perfeito pros fas de cassino para os viciados em emocoes de cassino! Por sinal a plataforma reluz com um visual ritualistico. criando uma experiencia de cassino incendiaria.
casa de aposta vera bet|
welche sportwetten sind in der schweiz legal
Here is my page :: bet live wetten; Matt,
Adoro a labareda de Fogo777 Casino, e um cassino online que queima como uma fogueira ancestral. A colecao e um ritual de entretenimento. incluindo mesas com charme flamejante. O suporte e um fulgor reluzente. assegurando apoio sem fumaca. Os pagamentos sao seguros e fluidos. em alguns momentos mais giros gratis seriam incendiarios. No fim das contas, Fogo777 Casino vale explorar esse cassino ja para os exploradores de jogos online! Vale dizer o design e um espetaculo visual flamejante. adicionando um toque de fogo ao cassino.
a plataforma fogo777 Г© confiГЎvel|
thebestplacetostarttoday – Design is welcoming and warm, draws me in gently.
makeimpactwithideas – Navigation is clean, finding inspiration is easy and enjoyable.
makelifebettereveryday – If they pull off good UX, this could feel very comforting and motivating.
https://dravoart.pl/hello-world-2/
SimpleWaysToBeHappy – This platform offers valuable insights for boosting happiness.
BuildSomethingMeaningful – Their commitment to social impact is truly commendable.
GrowWithConfidenceHere – I appreciate how structured and supportive the courses are here.
getreadytoexplore – Design feels crisp, layout clean, visuals nicely balanced.
YourTrustedSourceOnline – Their approach to education is both innovative and impactful.
TogetherWeCreateChange – I love how every project feels meaningful and well-guided here.
BuildABetterTomorrow – Their commitment to social impact is truly commendable.
Amo a energia de BETesporte Casino, e uma plataforma que vibra como um estadio em dia de final. O catalogo e vibrante e diversificado, oferecendo jogos de mesa dinamicos. 100% ate R$600 + apostas gratis. O suporte ao cliente e excepcional, sempre pronto para entrar em campo. Os pagamentos sao seguros e fluidos, de vez em quando promocoes mais frequentes dariam um toque extra. No fim, BETesporte Casino vale uma aposta certa para fas de cassino online ! Tambem a interface e fluida e energetica, tornando cada sessao mais competitiva. Outro destaque os pagamentos seguros em cripto, fortalece o senso de comunidade.
Encontrar os detalhes|
everythingaboutsuccess – Overall very polished experience, feels like a premium motivational hub.
CreateInspireAndGrow – The resources provided are incredibly helpful for anyone looking to improve.
findwhatyouarelookingfor – Love how the site promises exactly what it delivers, very clear.
yourjourneytobetterliving – Navigation is gentle and clear, I know where to go next.
Amo a energia selvagem de PlayPIX Casino, oferece um prazer intenso e indomavel. Ha uma explosao de jogos emocionantes, suportando jogos compativeis com criptomoedas. Fortalece seu saldo inicial. Os agentes respondem com rapidez, acessivel a qualquer momento. Os saques sao rapidos como um raio, de vez em quando recompensas extras seriam eletrizantes. Resumindo, PlayPIX Casino vale uma visita epica para quem aposta com cripto ! Adicionalmente a interface e fluida e estilosa, instiga a prolongar a experiencia. Igualmente impressionante os pagamentos seguros em cripto, fortalece o senso de comunidade.
Mergulhe nisso|
learnsomethingneweveryday – The tone is friendly, not preachy — very approachable.
stayupdatedwithtrends – Visuals support the “trend” vibe, colors and shapes feel fresh.
discoverendlessinspiration – Articles are uplifting and motivating, perfect blend of insight and hope.
thefutureofinnovation – Found inspiring articles, ideas that push me to think differently.
growyourbusinessfast – Overall very polished, confidence booster for business focused on growth.
https://bsmef.at
фитнес клуб тренировка абонемент в фитнес клуб
you are actually a good webmaster. The web site loading pace is incredible. It kind of feels that you are doing any unique trick. Furthermore, The contents are masterwork. you have performed a magnificent process on this topic!
зеркало Banzai Bet
фитнес клуб официальный сайт https://fitnes-klub-msk.ru
https://maxsens.fr/how-to-write-a-great-restaurant-blog/
SimpleWaysToBeHappy – The content is uplifting and motivating, truly inspiring.
BuildSomethingMeaningful – I appreciate how they focus on sustainable solutions for all.
Hi, all the time i used to check webpage posts here early in the daylight, since i enjoy to gain knowledge of more and more.
сайт драгон мани казино
A vibrant platformer guiding a panda through exciting puzzles and treasures. Fun and family-friendly: cute Panda games to play
TurnIdeasIntoAction – I often refer friends to this when they feel stuck.
Aw, this was a very good post. Taking a few minutes and actual effort to create a really good article… but what can I say… I hesitate a whole lot and never seem to get anything done.
зеркало zooma casino
EverythingStartsWithYou – The content is uplifting and very relatable, makes me think.
sportwetten geld zurück österreich
My web site; wettstrategien
EverythingStartsWithYou – This site reminds me: I’m in control of my path today.
Гарри Кейн оюн талаасында дайыма тынчсызданууну жаратат.Ар бир сезон Гарри Кейн жаңы деңгээлге чыгат. Гарри Кейн тууралуу так жана ишенимдүү маалымат алуу үчүн ушул булакты колдон: Гарри Кейн маалымат. Футбол дүйнөсү мындай оюнчуларды сейрек көрөт.
Кейндин “Бавариядагы” карьерасы жаңы барак ачты.
Кейн үй-бүлөлүк баалуулуктарды жогору коёт. Кейн капитан катары чоң жоопкерчилик алат. Кейндин оюнун көрүү ырахат тартуулайт. Кейн жаш кезинде деле голдорду көп киргизген. Ал ар бир сезон ондогон гол киргизет. Футбол сүйүүчүлөрү анын жаңылыктарын күтүшөт.
TurnIdeasIntoAction – I appreciate how they encourage doing rather than just dreaming.
edjy02
https://b-sme.at
LearnSomethingAwesome – Wow, this site really sparks curiosity and fun learning every visit.
Кейндин упай топтоо жөндөмү легендардуу.Анын командалык иши да, жеке чеберчилиги да мыкты. Кейндин күйөрмандары үчүн эң ишенимдүү булак — Гарри Кейн жаңылыктары. Кейн Англиянын тарыхындагы эң жогорку бомбардирлердин бири.
Гарри Кейндин оюну ар дайым жогорку деңгээлде.
Бул оюнчу үй-бүлөсүн биринчи орунга коёт. Бул оюнчу коргонууда да пайдалуу. Анын ар бир голу эстен чыкпайт. Кейн жаш кезинде деле голдорду көп киргизген. Бул оюнчу кайсы чемпионатта болбосун айырмаланат. Бул оюнчу тууралуу баары сүйлөшөт.
bs2best at Приготовься узнать, что взорвало тёмные глубины интернета. Blacksprut – это не просто бренд. Это новый эталон анонимности, головокружительной скорости и абсолютной надежности в онлайн-мире. Посети bs2best.at – место, где раскрывают секреты, о которых другие даже шепотом боятся говорить. Ты получишь эксклюзивный доступ к данным, которые тщательно скрывают от непосвященных. Только для тех, кто в теме и готов к большему. Ни одного следа в сети, никаких уступок – только бескомпромиссная анонимность с Blacksprut. Не упусти эту уникальную возможность – стань одним из первых, кто узнает правду. bs2best.at уже ждёт тебя. Готов ли ты увидеть то, что скрыто от большинства?
FindTheBestIdeas – Helps me break creative blocks and think outside my usual patterns.
LearnShareAndGrow – I love how they integrate technology into their initiatives.
https://allisonjenks.com/2014/03/chrissys-bachelorette-party-recap.html/
quotenvergleich sportwetten – https://Infinitumclavis.COM.Tr/online-Wetten-bonus-Geld – tipps wochenende
Hello! Do you use Twitter? I’d like to follow you if that would be ok. I’m absolutely enjoying your blog and look forward to new updates.
вход зума казино
TheArtOfLivingWell – I really enjoy this site, it has uplifting articles and practical tips.
FindNewWaysToGrow – I love how every post inspires me to take real action.
Футбол күйөрмандары Гарри Кейндей оюнчуну сыйлашат.Футбол тарыхында анын аты чоң орунда болот. Кейндин оюндарын жана жаңылыктарын бул жерден карасаң болот: Гарри Кейн тууралуу баары. Кейн өзүнүн максаттарын так билет.
Гарри Кейндин оюну ар дайым жогорку деңгээлде.
Гарри Кейн жеке жашоосун ачык көрсөтпөйт. Кейндин пас берүү жөндөмү да жогорку деңгээлде. Гарри Кейндин жашы чоң тажрыйбага жол ачат. Бул оюнчу ар дайым өнүгүүгө умтулган. Бул оюнчу кайсы чемпионатта болбосун айырмаланат. Кейн социалдык тармактарда активдүү.
FindAnswersAndIdeas – I keep discovering useful insights here that help me think deeper.
Pretty portion of content. I just stumbled upon your website and
in accession capital to assert that I acquire actually enjoyed account your weblog posts.
Any way I’ll be subscribing on your feeds and even I achievement you get entry to persistently fast.
J’aime l’atmosphere unique de Locowin Casino, ca offre un thrill incomparable. La diversite des titres est stupefiante, proposant des jeux de table immersifs. Accompagne de paris gratuits. L’assistance est efficace et professionnelle, avec une aide precise et rapide. Les paiements sont securises et fluides, mais des bonus plus varies seraient apprecies. Au final, Locowin Casino est indispensable pour les joueurs pour les joueurs en quete d’excitation ! A noter la plateforme est visuellement impressionnante, amplifie le plaisir de jouer. Particulierement interessant les evenements communautaires engageants, assure des transactions fiables.
Jeter un coup d’œil|
Je suis entierement obsede par Locowin Casino, on detecte une vibe folle. Les alternatives sont incroyablement etendues, proposant des jeux de table immersifs. Associe a des tours gratuits sans wager. Les agents reagissent avec promptitude, avec une assistance exacte et veloce. La procedure est aisee et efficace, de temps a autre des bonus plus diversifies seraient souhaitables. En synthese, Locowin Casino est une plateforme qui excelle pour les aficionados de jeux contemporains ! De surcroit l’interface est intuitive et raffinee, stimule le desir de revenir. Egalement notable les paiements securises en crypto, offre des privileges sur mesure.
Trouver le bonus|
YourDigitalDestination – The visuals and text complement each other very well here.
Гарри Кейн азыркы футболдун эң мыкты чабуулчуларынын бири.Ар бир сезон Гарри Кейн жаңы деңгээлге чыгат. Футбол күйөрмандары үчүн ишенимдүү булак — https://harry-kane-kg.com/. Бул чабуулчу ар бир мелдеште гол киргизүүгө даяр.
Бавария күйөрмандары ага тез эле көнүштү.
Гарри Кейн жеке жашоосун ачык көрсөтпөйт. Кейн капитан катары чоң жоопкерчилик алат. Кейндин карьерасы тарыхка кирет. Ал бала чагынан эле футболчу болууну каалаган. Кейндин оюнунда туруктуулук бар. Кейндин трансферлери ар дайым чоң темалар.
mehrfach kombiwette rechner
Here is my page Die Besten Sportwetten Apps (https://Supporters.Sites.Sch.Gr)
LearnSomethingAwesome – Wow, this site really sparks curiosity and fun learning every visit.
GetConnectedWithPeople – Very helpful suggestions on who to connect with, feels curated.
https://www.henkleeuwerink.nl/what-is-the-progressive-web-app-pwa-and-how-it-works/
UnlockYourPotentialToday – I enjoy reading the stories—they remind me change is possible.
Howdy this is kinda of off topic but I was wondering if blogs use WYSIWYG editors or if you have to manually code with HTML. I’m starting a blog soon but have no coding experience so I wanted to get advice from someone with experience. Any help would be enormously appreciated!
официальный сайт lee bet casino
A person essentially help to make significantly articles I might state.
That is the very first time I frequented your web page and to this point?
I surprised with the analysis you made to create this particular publish amazing.
Excellent job!
FindTheBestIdeas – The writing feels personal, like someone sharing honest advice and insights.
FindSolutionsForLife – Bookmarking this, it’s going to be my go-to when I need answers.
DiscoverWorldOfIdeas – This site encourages me to think differently than usual routines.
ConnectDiscoverAndGrow – Very motivating content, feels like a community more than a site.
InspireChangeAndProgress – I love how they mix storytelling with practical tips and steps.
madeleinemtbc – Feels like a real voice behind every page here
LearnShareAndGrow – This platform offers great resources for community development projects.
markmackenzieforcongress – Feels refreshing to see honest values shared openly and respectfully online.
адрес фитнес клуба абонемент в фитнес клуб
FindNewWaysToGrow – I found this site just when I needed a fresh perspective today.
FindInspirationEverywhere – I appreciate the mix of art, stories and practical advice here.
https://shorturl.fm/7BfJS
YourGuideForSuccess – This site feels like a supportive mentor in my browser all day.
StartChangingYourLife – The advice given here seems doable and not overwhelming at all.
DiscoverUsefulTipsDaily – I like how every post gives something I can try immediately.
DiscoverNewOpportunities – This platform offers great resources for community development projects.
BuildYourDreamFuture – The content motivates me, not just to dream but also act.
Hi there Dear, are you genuinely visiting this site regularly, if so afterward you will definitely take good know-how.
https://yagodka.info/
Футбол күйөрмандары Гарри Кейндей оюнчуну сыйлашат.Бул оюнчу дайыма эң мыктылардын арасында. Футбол күйөрмандары үчүн ишенимдүү булак — https://harry-kane-kg.com/. Анын футбол стили классикалык жана эффективдүү.
Кейндин трансфери чоң көңүл бурдурган.
Кейн үй-бүлөсү менен көп убакыт өткөрөт. Кейндин карьерасы узак жана ийгиликтүү. Анын физикалык даярдыгы мыкты. Кейн жаш кезинде деле голдорду көп киргизген. Кейндин статистикасын карасаң, анын чыныгы деңгээлин көрөсүң. Кейндин реал мадридге өтүшү дагы эле талкууда.
YourDigitalDestination – I enjoy reading their posts, always learn something new.
Аренда автобуса с водителем школьники https://povozkin.ru
GetConnectedWithPeople – Definitely bookmarking this, it’s a refreshing take on community building.
FindSolutionsForLife – This site really helped me see problems through a fresh lens today.
live wetten online
Have a look at my webpage :: wettbüro – http://www.seo-ct.com –
UnlockYourPotentialToday – I enjoy reading the stories—they remind me change is possible.
madeleinemtbc – Posts seem genuine, like someone who really cares
wettanbieter
Also visit my web blog Aktuelle sportwetten tipps
markmackenzieforcongress – This platform explains the issues better than most other political pages.
https://www.dokkan-battle.fr/forums/users/JamesWolfe/
concert experience
bs2best at Ты еще не в курсе, что порождает бурю в темных водах сети? Blacksprut – это не просто символ. Это квинтэссенция анонимности, молниеносной скорости и абсолютной уверенности в каждом действии. Приглашаем на bs2best.at – туда, где шепчут о том, о чем другие предпочитают хранить гробовое молчание. Тебе откроются двери в мир, скрытый от любопытных глаз, доступный лишь избранным, тем, кто понимает истинную цену информации. Ни единой зацепки. Никаких отступлений. Только безупречный Blacksprut, гарант твоей конфиденциальности. Не упусти свой шанс стать первопроходцем – bs2best.at уже готов раскрыть свои тайны. Достаточно ли ты смел, чтобы заглянуть в бездну правды?
Кейндин упай топтоо жөндөмү легендардуу.Анын командалык иши да, жеке чеберчилиги да мыкты. Кейндин тарыхы жана жетишкендиктери боюнча кызыктуу макалаларды бул жерден тап: Гарри Кейн биографиясы. Кейн Англиянын тарыхындагы эң жогорку бомбардирлердин бири.
Бавария күйөрмандары ага тез эле көнүштү.
Гарри Кейн жеке жашоосун ачык көрсөтпөйт. Гол киргизүүдө ал өзгөчө инстинктке ээ. Кейндин оюнун көрүү ырахат тартуулайт. Кейндин тарыхы ийгиликке ишенүүнүн далили. Кейндин упай көрсөткүчү абдан жогору. Кейндин трансферлери ар дайым чоң темалар.
makethemostoflife – Love the positive vibes and down-to-earth tone here
makeprogressdaily – The layout is clean and the content is always relevant.
Гарри Кейн оюн талаасында дайыма тынчсызданууну жаратат.Бул оюнчу дайыма эң мыктылардын арасында. Гарри Кейн тууралуу так жана ишенимдүү маалымат алуу үчүн ушул булакты колдон: Гарри Кейн маалымат. Анын футбол стили классикалык жана эффективдүү.
Кейндин трансфери чоң көңүл бурдурган.
Кейндин жашоосу көптөр үчүн үлгү. Гол киргизүүдө ал өзгөчө инстинктке ээ. Кейндин оюнун көрүү ырахат тартуулайт. Бул оюнчу ар дайым өнүгүүгө умтулган. Ал ар бир сезон ондогон гол киргизет. Кейндин сүрөттөрү интернетте көп изилденет.
makeprogressdaily – Always look forward to the new posts, they keep me on track.
Лазерные станки https://raymark.ru для резки металла в Москве. 20 лет на рынке, выгодная цена, скидка 5% при заявке с сайта + обучение
HOME CLIMAT https://homeclimat36.ru кондиционеры и сплит системы в Воронеже. Скидка на монтаж от 3000 рублей! При покупке сплит-системы.
makethemostoflife – The layout is calm, easy on the eyes, user friendly
inspireandgrowtogether – The content is uplifting, perfect for a midweek boost.
findthebestcontent – Love how content is curated with high quality in mind
findyourwayforward – The message gives hope and a clearer path, very nice
Adoro o clima alucinante de MegaPosta Casino, oferece uma aventura de cassino que detona tudo. As opcoes de jogo no cassino sao ricas e vibrantes, com slots de cassino unicos e contagiantes. O servico do cassino e confiavel e de responsa, respondendo mais rapido que um raio. As transacoes do cassino sao simples como um estalo, as vezes mais recompensas no cassino seriam um diferencial insano. No geral, MegaPosta Casino vale demais explorar esse cassino para os amantes de cassinos online! E mais o site do cassino e uma obra-prima de estilo, torna o cassino uma curticao total.
megaposta.|
Me encantei pelo ritmo de BR4Bet Casino, e uma onda de diversao que cintila como um farol. O leque do cassino e um brilho de delicias. oferecendo sessoes ao vivo que reluzem como chamas. O suporte e um facho reluzente. assegurando apoio sem sombras. As transacoes sao simples como uma luz. entretanto mais bonus seriam um diferencial reluzente. Em resumo, BR4Bet Casino oferece uma experiencia que e puro brilho para os apaixonados por slots modernos! De lambuja a interface e fluida e brilha como um farol. adicionando um toque de luz ao cassino.
br4bet apostas esportivas|
Estou pirando com OshCasino, parece uma erupcao de diversao. Tem uma enxurrada de jogos de cassino irados, com jogos de cassino perfeitos pra criptomoedas. Os agentes do cassino sao rapidos como um estalo, acessivel por chat ou e-mail. O processo do cassino e limpo e sem tremores, as vezes as ofertas do cassino podiam ser mais generosas. Em resumo, OshCasino e o point perfeito pros fas de cassino para os cacadores de slots modernos de cassino! De lambuja a plataforma do cassino detona com um visual que e puro magma, aumenta a imersao no cassino a mil.
osh connexion|
Ich bin abhangig von SpinBetter Casino, es erzeugt eine Spielenergie, die fesselt. Die Titelvielfalt ist uberwaltigend, mit Spielen, die fur Kryptos optimiert sind. Die Hilfe ist effizient und pro, verfugbar rund um die Uhr. Der Ablauf ist unkompliziert, obwohl regelma?igere Aktionen waren toll. Zusammengefasst, SpinBetter Casino ist ein Muss fur alle Gamer fur Casino-Liebhaber ! Nicht zu vergessen die Interface ist intuitiv und modern, erleichtert die gesamte Erfahrung. Besonders toll die Community-Events, die den Spa? verlangern.
https://spinbettercasino.de/|
Ich liebe die Atmosphare von NV Casino, es ist ein Abenteuer, das pulsiert wie ein Herzschlag. Das Angebot an Spielen ist phanomenal, mit Spielen, die perfekt fur Kryptos geeignet sind. Der Support ist von herausragender Qualitat, bietet klare Antworten. Die Auszahlungen sind ultraschnell, manchmal die Angebote konnten gro?zugiger sein. Insgesamt, NV Casino bietet unvergesslichen Spa? fur Krypto-Liebhaber ! Daruber hinaus die Site ist schnell und elegant, verstarkt die Immersion.
playnvcasino.de|
Fiquei impressionado com BETesporte Casino, e uma plataforma que pulsa com emocao atletica. Ha uma multidao de jogos emocionantes, oferecendo jogos de mesa dinamicos. Com uma oferta inicial para impulsionar. O acompanhamento e impecavel, acessivel a qualquer hora. Os saques sao rapidos como um sprint, embora promocoes mais frequentes seriam um plus. No geral, BETesporte Casino vale uma aposta certa para quem usa cripto para jogar ! Adicionalmente o site e veloz e envolvente, adiciona um toque de estrategia. Um diferencial importante os pagamentos seguros em cripto, que impulsiona o engajamento.
Navegar no site|
discoverlearnandshare – Quick to load, easy navigation, good user experience overall
growyourpresenceonline – The design is clean, which helps the messages stand out
licsupport – The layout is clean and easy to navigate for beginners
findyourwayforward – I felt understood reading some of these posts, nice job
inspireandgrowtogether – I love the positivity here, makes me want to engage more.
connectwithbrilliantminds – Clean design and helpful content, very user friendly layout
everythingaboutmarketing – The articles are engaging and provide real-world applications.
discoveryourpassion – This platform offers valuable tools for unlocking your potential.
discovertrendingideas – The writing feels fresh, not forced or overdone
learnandearndaily – Very helpful for side hustles and micro learning ideas
connectandgrowonline – My sales have increased thanks to their digital marketing tools.
jointhenextbigthing – Content feels authentic, I enjoy reading every single post here.
discoverlearnandshare – The writing voice feels warm and personal, not generic
togetherwecreateimpact – The design supports the mission, clean and mission-driven layout
everythingaboutmarketing – Appreciate the clear and concise explanations on complex marketing concepts.
growyourpresenceonline – Content is straightforward, no over-complicated jargon, just helpful
discoveryourpassion – This platform offers valuable tools for unlocking your potential.
findyourinspirationhere – I found a quote that really spoke to me today
yourgatewaytosuccess – I like the call-to-action style, makes me want to explore more
licsupport – The design and content align well, feels trustworthy
connectwithbrilliantminds – I like how there’s a mix of inspiration and practical takeaways
connectandgrowonline – This platform made it so easy to grow my business.
jointhenextbigthing – Simple layout but extremely effective, really makes browsing enjoyable.
Аутстаффинг персонала https://skillstaff2.ru для бизнеса: легальное оформление сотрудников, снижение налоговой нагрузки и оптимизация расходов. Работаем с компаниями любого масштаба и отрасли.
keepgrowingwithus – This is one of those rare blogs you trust quickly
discovertrendingideas – Sharing this with my network, it’s genuinely insightful
learnandearndaily – Pleasant experience, I might share with a friend soon
südamerika strategie sportwetten tipps Bild
кафет нет торрент кафета торрент Извините, я не знаю, что такое “кафета”. Возможно, вы имели в виду что-то другое? Если вы предоставите больше информации, я постараюсь вам помочь.
togetherwecreateimpact – I’ll be coming back to see what’s next and engage more
Estou completamente apaixonado por BR4Bet Casino, vibra como um farol em alto-mar. O leque do cassino e um brilho de delicias. oferecendo sessoes ao vivo que reluzem como chamas. O atendimento e solido como um farol. disponivel por chat ou e-mail. Os pagamentos sao seguros e fluidos. mesmo assim queria promocoes que acendem como chamas. No fim das contas, BR4Bet Casino oferece uma experiencia que e puro brilho para os exploradores de jogos online! De bonus a plataforma reluz com um visual brilhante. fazendo o cassino brilhar como um farol.
br4bet cnpj|
Adoro o clima alucinante de MegaPosta Casino, oferece uma aventura de cassino que detona tudo. A gama do cassino e simplesmente um estouro, oferecendo sessoes de cassino ao vivo que sao uma pedrada. Os agentes do cassino sao rapidos como um estalo, acessivel por chat ou e-mail. Os pagamentos do cassino sao lisos e blindados, mas as ofertas do cassino podiam ser mais generosas. No geral, MegaPosta Casino oferece uma experiencia de cassino que e puro fogo para os viciados em emocoes de cassino! Alem disso a navegacao do cassino e facil como brincadeira, aumenta a imersao no cassino a mil.
megaposta|
Ich habe einen totalen Hang zu SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Der Katalog ist reichhaltig und variiert, mit aufregenden Sportwetten. Der Support ist 24/7 erreichbar, immer parat zu assistieren. Die Auszahlungen sind ultraschnell, trotzdem mehr abwechslungsreiche Boni waren super. In Kurze, SpinBetter Casino ist eine Plattform, die uberzeugt fur Adrenalin-Sucher ! Hinzu kommt die Site ist schnell und stylish, erleichtert die gesamte Erfahrung. Zusatzlich zu beachten die Sicherheit der Daten, die den Einstieg erleichtern.
spinbettercasino.de|
Estou completamente alucinado por OshCasino, parece uma erupcao de diversao. Tem uma enxurrada de jogos de cassino irados, oferecendo sessoes de cassino ao vivo que sao uma chama. A equipe do cassino entrega um atendimento que e uma labareda, dando solucoes na hora e com precisao. O processo do cassino e limpo e sem tremores, as vezes mais bonus regulares no cassino seria brabo. Resumindo, OshCasino e um cassino online que e uma erupcao de diversao para os amantes de cassinos online! De lambuja o design do cassino e uma explosao visual escaldante, da um toque de calor brabo ao cassino.
osh 8|
Ich kann nicht genug bekommen von NV Casino, es ist ein Abenteuer, das pulsiert wie ein Herzschlag. Die Vielfalt der Titel ist atemberaubend, mit Slots im innovativen Design. Der Support ist von herausragender Qualitat, bietet klare Antworten. Die Zahlungen sind sicher und flussig, manchmal die Angebote konnten gro?zugiger sein. Insgesamt, NV Casino bietet unvergesslichen Spa? fur Adrenalin-Junkies ! Nicht zu vergessen das Design ist modern und ansprechend, gibt Lust auf mehr.
https://playnvcasino.de/|
https://shorturl.fm/4if1Y
Tenho uma paixao intensa por BETesporte Casino, oferece um thrill esportivo unico. As opcoes sao vastas como um campeonato, incluindo apostas esportivas palpitantes. O bonus de boas-vindas e empolgante. O servico esta disponivel 24/7, garantindo atendimento de alto nivel. Os saques sao rapidos como um sprint, contudo ofertas mais generosas dariam um toque especial. Em sintese, BETesporte Casino e uma plataforma que domina o campo para fas de cassino online ! Vale destacar a navegacao e intuitiva e rapida, adiciona um toque de estrategia. Outro destaque os pagamentos seguros em cripto, oferece recompensas continuas.
Ver mais|
hop live
Tak. Verde kasyno działa na podstawie licencji wydanej przez jurysdykcję Curacao, która gwarantuje bezpieczną grę i prywatność użytkowników. Políticas de privacidad Verde oferuje bonusy od czterech wpłat, regularny cashback, Koło Fortuny i wiele innych promocji. Płatności możesz realizować na wiele sposobów, w tym BLIKIEM i kryptowalutami. Grę na urządzeniach mobilnych ułatwiają funkcjonalne aplikacje na Androida i iOS-a. Samo założenie konta jest stosunkowo proste – wystarczy minuta i podstawowe dane. Przy tym wszystkim Verde Casino jest dopasowane do polskich graczy poprzez język i walutę. Alien: Isolation Oczekiwanie na doradcę na czacie online zazwyczaj nie trwa dłużej niż 2 minuty. Czasami, przy większym obłożeniu może być to nawet 5 czy 10 minut. Na odpowiedź na wiadomość e-mail, przesłaną na adres Verde Casino Polska przeważnie trzeba czekać od 1 do 5 godzin. Kontakt z kasynem zwykle oznacza profesjonalne wsparcie, choć w porównaniu z czołowymi konkurentami, jak na przykład Energy Casino, Vavada czy Wazamba, Verde Casino nie oferuje wsparcia telefonicznego.
https://www.montessorijobsuk.co.uk/author/sembnonarez1972/
Marzysz o słodkim życiu bez ryzyka? W BDMBet możesz zakręcić bębnami Sugar Rush za darmo w wersji demo na naszej stronie bdmbet.casino. Ta sama gra, ta sama cukierkowa chaotyczność, tylko bez zakładu. Dlaczego by nie spróbować? Oto dlaczego: Producentem slota Sugar Rush Fever jest studio Ruby Play, którego główna siedziba mieści się w Malcie. Firma działa w branży od wielu lat, ale polscy gracze mogą próbować swojego szczęścia w produkcjach Ruby od grudnia 2021 roku. Wówczas to sloty studia pojawiły się w ofercie Total Casino. Perhaps try another search? Różni się od systemu Martingale tym, kasyno online spiny bez depozytu jak i piątym bębnie w tym samym czasie. Wisienką na torcie wydaje się być wybór gier biorące udział w kasynach G Pay, w których można korzystać z przywilejów rejestracyjnych. Gra online zawiera egipski motyw, które pomogą im szybko się uczyć. Należy również pamiętać, które są w tym tego typu gry rośnie w Wielkiej Brytanii. Jeśli nie czujesz prawdziwego znaczenia szczęścia i obserwujesz, jak opublikować go w Sklepie Google Play dla użytkowników Androida.
UFCдеги рейтинги, рекорду жана статистикасы бир бетте чогултулуп, издөөнү жеңилдетет.
Түз эфирди кайдан көрүү жана алдын ала студиялык талдоо боюнча кыска нускама беребиз. ислам махачев — царукян Салыштырма таблицалар жана тактикалык эскертмелер кыска форматта берилет. Нейтралдуу анализ сунушталат. Ислам Махачев — Арман Царукян реваншы мүмкүнбү, эксперттик пикирлерди жыйнадык. Физикалык көрсөткүчтөр: узундук, «вингспан», кардио жана партер арсеналы боюнча маалымат бар. Грепплинг жана клинчтеги көрсөткүчтөр статистикалык булактар менен ырасталат.
Акыркы беттештин толук обзорун раунд-раунд менен кыскача окуңуз. Турнир картасындагы башка айкаштарды да эске алып, жалпы сценарий түзөбүз. Марапаттар, чемпиондук тизмек жана респект учурлары иллюстрация менен берилет. Максат — жаңжал эмес, так маалымат жана спорттук урмат.
Hi! I could have sworn I’ve been to this web site before but after browsing through many of the articles I realized it’s new
to me. Anyhow, I’m certainly pleased I stumbled upon it and I’ll be bookmarking it and checking back frequently!
Строительный портал https://v-stroit.ru всё о строительстве, ремонте и архитектуре. Полезные советы, технологии, материалы, новости отрасли и практические инструкции для мастеров и новичков.
inspireeverymoment – Every post feels like a little boost to my day.
shareyourvisiontoday – I visited and it really resonated with my goals and dreams.
votethurm – Interesting content, I hope the design gets updated soon.
growtogetherwithus – Thanks for this space, it’s helping me stay committed to growth.
wetten deutschland dänemark
Look at my site … sportwetten gratis guthaben ohne einzahlung
Карьерасынын бурулуш учурлары, мыкты раундар жана эмнелер аны чемпион кылганы тууралуу кеңири баяндалат.
Түз эфирди кайдан көрүү жана алдын ала студиялык талдоо боюнча кыска нускама беребиз. islam-makhachev-kg.com Расмий жаңылыктар, рекорд жана статистика бир жерге топтолгон. Мобилдиктен окууга ыңгайлуу. Жеткиликтүү интервьюлардан цитаталарды чогултуп, мотивация жана даярдык жөнүндө баяндайбыз. Топуриянын стилдик өзгөчөлүктөрү жана Махачевдин каршы пландары кыскача түшүндүрүлөт. Рекорд: жеңиш/жеңилүү, финиш проценттери жана орточо убакыт — баары визуалдуу берилет.
«Ислам Махачев кимге утулду?» деген суроого тарыхый тизмек жана шарттар менен жооп беребиз. Жеке пикир эмес, сандык көрсөткүчтөргө таянган нейтралдуу анализди сунуштайбыз. Инфографика: тейкдаун, сабмишн, контрдардан алынган негизги сандык маалыматтар. Издөө функциясы боюнча ачкыч сөздөрдү киргизип, керектүү бөлүмгө тез өтүңүз.
learnnewthingsdaily – This site really fuels my curiosity and passion to grow.
discovergreatideas – The articles here are a catalyst for creative breakthroughs.
thefuturestartsnow – Such a refreshing perspective, feels like a wake-up call.
inspireeverymoment – Just visited and it resonated with me deeply today.
https://bs2web.cat
votethurm – Interesting content, I hope the design gets updated soon.
Ислам Махачев ким менен жана качан беттешерин билгиңиз келсе, биз дайыма жаңырган календарь жана расмий маалыматтарды сунуштайбыз.
Пресс-конференция жана тарсылдатуу жыйынтык видеолору бет ачылгандан кийин эле жеткиликтүү. ислам махачев арман царукян Реванш мүмкүнчүлүгү, даталар жана эксперттик пикирлер ушул жерден. Коэффициенттер да салыштырылат. Алгачкы беттештеги негизги эпизоддорду эске салып, реванш үчүн сабактарды белгилеп беребиз. Федер жана лайтвейт контекстинде салмак маселеси жана шарттар талкууланат. Коучтар командасы жана лагерь логистикасы кыскача тизмектелет.
Ренато Мойкано менен байланышкан контекст жана дивизиондогу мааниси түшүндүрүлөт. Хайптан алыстап, фактыларга таянган сабаттуу талкуу жүргүзөлү. Марапаттар, чемпиондук тизмек жана респект учурлары иллюстрация менен берилет. Максат — жаңжал эмес, так маалымат жана спорттук урмат.
theartofsuccess – The stories here are powerful and deeply relatable.
inspireeverymoment – This site makes me want to pause, reflect, act.
startyourdigitaljourney – Highly recommend for anyone looking to start an online business.
Жеңиштери, жеңилүүлөрү жана ыйгарым салмак категориясы боюнча толук маалыматты даярдап койдук.
Кайсы аренада жана кайсы убакта болору боюнча убакыт тилкелери менен ыңгайлуу гид бар. http://www.islam-makhachev-kg.com Колдонуучуларга ыңгайлуу издөөлөр жана тез меню. Бардык бөлүмдөр жаңылык менен толукталып турат. UFCдеги алардын позициялары, рекорддору жана окшош стилдери боюнча салыштырма таблица бар. Эгер ресми анонс чыкса, дата жана локация дароо жаңыланат. Салмакты калыбына келтирүү жана кемитүү тартиби боюнча расмий маалыматтардан үзүндүлөр келтирилет.
Медиа бөлүмүндө айрым раунддардагы негизги эпизоддордун GIF/кыска видео талдоосу берилет. Турнир картасындагы башка айкаштарды да эске алып, жалпы сценарий түзөбүз. Медиа пакет издегендер үчүн расмий булактарга жол көрсөтөбүз. Издөө функциясы боюнча ачкыч сөздөрдү киргизип, керектүү бөлүмгө тез өтүңүз.
sportwetten kombiwetten
Feel free to visit my page :: Beste Wetter-App Ios Kostenlos;
Dziredubai.Com,
yourjourneytowin – The words here are uplifting, really moving me forward.
growtogetherwithus – I enjoy how people share wins and failures alike openly.
sportwetten gratis ohne einzahlung
Also visit my web-site :: halbzeit wetten strategie [ovalles.do]
createimpactfulstories – Beautifully written, this site encourages me to keep creating.
staycuriousandcreative – This is exactly the kind of energy I needed today.
beste sportwetten apps
Also visit my website … wettbüro braunschweig
shareyourvisiontoday – Great mix of inspiration and practical advice for visionaries.
wettseiten deutschland
Here is my page – sportwetten ergebnisse vorhersage
Портал о строительстве https://pamel-stroy.ru и ремонте. Пошаговые инструкции, идеи, технологии, новости и советы экспертов. Всё, что нужно, чтобы строить и ремонтировать грамотно.
thefuturestartsnow – Such a refreshing perspective, feels like a wake-up call.
inspireeverymoment – I bookmarked it, will return whenever I need a lift.
papst wettquoten
Feel free to surf to my homepage wetten ergebnisse vorhersage (https://www.Paveni.cz/deutsche-mma-wetten/)
discovergreatideas – This platform redefines how we approach idea generation.
findyourcreativeflow – Really helped me break through creative block, thanks for that.
learnnewthingsdaily – Great variety of topics, never get bored exploring here.
Риэлторская контора https://daber27.ru покупка, продажа и аренда недвижимости. Помогаем оформить сделки безопасно и выгодно. Опытные риэлторы, консультации, сопровождение и проверка документов.
Купольные дома https://kupol-doma.ru под ключ — энергоэффективные, надёжные и современные. Проектирование, строительство и отделка. Уникальная архитектура, комфорт и долговечность в каждом доме.
https://nevetrnv089086.blog-gold.com/51078677/secrets-of-the-sandswept-tombs
theartofsuccess – Highly recommend this for daily boosts and life planning.
yourpathofsuccess – This site helps me refocus when things feel chaotic.
Карьерасынын бурулуш учурлары, мыкты раундар жана эмнелер аны чемпион кылганы тууралуу кеңири баяндалат.
Телегид сыяктуу жөнөкөй форматта дата, убакыт жана оппоненттер тизилет. islam-makhachev-kg.com Расмий жаңылыктар, рекорд жана статистика бир жерге топтолгон. Мобилдиктен окууга ыңгайлуу. Фанаттар үчүн «эмне күтүүгө болот» бөлүмү беттеш алдындагы маанилүү суроолорго жооп берет. Эгер ресми анонс чыкса, дата жана локация дароо жаңыланат. Коучтар командасы жана лагерь логистикасы кыскача тизмектелет.
Дастин Порье, Чарльз Оливейра, Волкановски сыяктуу чоң аттар менен салыштыруулар бар. Прогноздор тарыхы жана тактык проценти ачык көрсөтүлөт. Медиа пакет издегендер үчүн расмий булактарга жол көрсөтөбүз. Материалдар нейтралдуу, деңгээлдүү жана фанаттарга да, жаңы окурмандарга да ылайык.
https://shorturl.fm/xY2DR
Ваша Недвижимость https://rbn-khv.ru сайт о покупке, продаже и аренде жилья. Разбираем сделки, налоги, ипотеку и инвестиции. Полезная информация для владельцев и покупателей недвижимости.
pferderennen iffezheim wetten
Feel free to surf to my webpage wettbüro osnabrüCk (atlaspavement.Com)
Информационный блог https://gidroekoproekt.ru для инженеров и проектировщиков. Всё об инженерных изысканиях, водохозяйственных объектах, гидротехническом строительстве и современных технологиях в отрасли.
bs2best at Интересуешься, что происходит в тёмных уголках сети? Blacksprut — это не просто название, это гарантия анонимности, высокой скорости и надежности. Переходи на bs2best.at — там ты найдёшь то, о чём другие умалчивают. Тебе откроется доступ к информации, которую скрывают от большинства. Только для тех, кто понимает. Без компрометирующих следов. Без уступок. Только Blacksprut. Не упусти шанс узнать первым — bs2best.at уже готов открыть свои двери. Дерзнешь ли ты взглянуть правде в глаза?
Эгер UFC жаңылыктарын кыска, так жана ыңгайлуу форматта издеп жүрсөңүз, бул жер туура.
Пресс-конференция жана тарсылдатуу жыйынтык видеолору бет ачылгандан кийин эле жеткиликтүү. islam-makhachev-kg.com Жаңылыктарга жазылыңыз, ири анонстар чыккан замат билдирме аласыз. Эч нерседен артта калбаңыз. UFCдеги алардын позициялары, рекорддору жана окшош стилдери боюнча салыштырма таблица бар. Топуриянын стилдик өзгөчөлүктөрү жана Махачевдин каршы пландары кыскача түшүндүрүлөт. Аудитория үчүн жөнөкөй тилде түшүндүрүлгөн «кантип жеңиши мүмкүн» сценарийлери сунушталат.
Акыркы беттештин толук обзорун раунд-раунд менен кыскача окуңуз. Коэффициенттер жана линиялар боюнча кыска гид: ким фаворит, ким андердог — объективдүү маалымат. Интервьюлардан эң кызыктуу цитаталарды бөлүп, кыска карточкаларга салдык. Жаңылыктарга жазылсаңыз, ири анонстар чыккан замат билдирүү аласыз.
Ich liebe die unbandige Kraft von Lowen Play Casino, es pulsiert mit einer unbezahmbaren Casino-Energie. Die Spielauswahl im Casino ist wie eine wilde Horde, inklusive stilvoller Casino-Tischspiele. Der Casino-Kundenservice ist wie ein Leitlowe, sorgt fur sofortigen Casino-Support, der beeindruckt. Casino-Zahlungen sind sicher und reibungslos, trotzdem mehr Freispiele im Casino waren ein wilder Triumph. Zusammengefasst ist Lowen Play Casino ein Casino mit einem Spielspa?, der wie ein Brullen donnert fur Spieler, die auf wilde Casino-Kicks stehen! Nebenbei die Casino-Navigation ist kinderleicht wie eine Fahrte, Lust macht, immer wieder ins Casino zuruckzukehren.
löwen play darmstadt|
Sou viciado no role de JabiBet Casino, oferece uma aventura de cassino que arrasta tudo. O catalogo de jogos do cassino e uma tempestade, oferecendo sessoes de cassino ao vivo que sao uma explosao. Os agentes do cassino sao rapidos como uma onda, acessivel por chat ou e-mail. Os saques no cassino sao velozes como um redemoinho, de vez em quando mais bonus regulares no cassino seria top. No geral, JabiBet Casino e o point perfeito pros fas de cassino para os amantes de cassinos online! E mais o site do cassino e uma obra-prima de estilo, aumenta a imersao no cassino como uma onda gigante.
jabibet login|
Acho simplesmente brabissimo PagolBet Casino, parece uma tempestade de diversao. A gama do cassino e simplesmente uma faisca, com caca-niqueis de cassino modernos e eletrizantes. A equipe do cassino entrega um atendimento que e uma voltagem alta, acessivel por chat ou e-mail. Os saques no cassino sao velozes como um trovao, as vezes mais recompensas no cassino seriam um diferencial brabo. Em resumo, PagolBet Casino garante uma diversao de cassino que e uma tempestade para os cacadores de slots modernos de cassino! Vale falar tambem a interface do cassino e fluida e cheia de energia eletrica, aumenta a imersao no cassino a mil.
codigo pagolbet|
Ich bin beeindruckt von SpinBetter Casino, es ist eine Erfahrung, die wie ein Wirbelsturm pulsiert. Der Katalog ist reichhaltig und variiert, mit aufregenden Sportwetten. Der Service ist von hoher Qualitat, bietet klare Losungen. Die Gewinne kommen prompt, trotzdem zusatzliche Freispiele waren ein Highlight. Alles in allem, SpinBetter Casino ist absolut empfehlenswert fur Krypto-Enthusiasten ! Zusatzlich die Interface ist intuitiv und modern, was jede Session noch besser macht. Ein weiterer Vorteil die schnellen Einzahlungen, die Flexibilitat bieten.
spinbettercasino.de|
mystylecorner – I like how they balanced minimalism with bold elements.
Ich kann nicht genug bekommen von NV Casino, es fuhlt sich an wie ein Wirbel aus Freude. Der Katalog ist reich und vielfaltig, mit immersiven Tischspielen. Die Hilfe ist effizient und professionell, mit praziser Unterstutzung. Die Auszahlungen sind ultraschnell, dennoch mehr abwechslungsreiche Boni waren willkommen. Kurz gesagt, NV Casino bietet unvergesslichen Spa? fur Adrenalin-Junkies ! Daruber hinaus die Oberflache ist intuitiv und stylish, was jede Session noch spannender macht.
playnvcasino.de|
Hurrah, that’s what I was searching for, what
a material! existing here at this website, thanks admin of this website.
filamericansforracialaction.com – Good to see WordPress used, content seems accessible and organized.
Amo a energia de BETesporte Casino, sinto um rugido de emocao. As opcoes sao amplas como um campo de futebol, com slots modernos e tematicos. 100% ate R$600 + apostas gratis. O acompanhamento e impecavel, acessivel a qualquer momento. Os ganhos chegam sem atraso, embora ofertas mais generosas dariam um toque especial. Resumindo, BETesporte Casino garante diversao constante para amantes de apostas esportivas ! Tambem a navegacao e intuitiva e rapida, facilita uma imersao total. Um diferencial importante os pagamentos seguros em cripto, assegura transacoes confiaveis.
Dar uma olhada|
creativevision – The gallery layout enhances the viewing experience beautifully.
stacoa.org – Very nice layout, feels like a professional and caring site.
myvetcoach.org – Nice design, great resources, feels very professional.
electlarryarata – The homepage is clean but I expected more content already.
thespeakeasybuffalo – I noticed “Nothing found” currently; hope content fills soon.
laetly.com – Bookmarking this — I’ll check back to see real products.
Ислам Махачев боюнча акыркы жаңылыктарды ушул жерден окуп, беттештердин тарыхын жана кыска анализин да карап чыгыңыз.
UFC 311 жакындап келе жатабы, Ислам Махачевтин расписаниеси реалдуу убакытта жаңыртылат. https://islam-makhachev-kg.com/ Расмий профилдерге жана Sherdog барактарына туура жол көрсөтөбүз. Коопсуз шилтемелер гана колдонулат. Фанаттар үчүн «эмне күтүүгө болот» бөлүмү беттеш алдындагы маанилүү суроолорго жооп берет. Физикалык көрсөткүчтөр: узундук, «вингспан», кардио жана партер арсеналы боюнча маалымат бар. Жашы, туулган күнү, улуту жана бою-салмагы тууралуу факт карточкалары ыңгайлуу.
«Ислам Махачев кимге утулду?» деген суроого тарыхый тизмек жана шарттар менен жооп беребиз. Коэффициенттер жана линиялар боюнча кыска гид: ким фаворит, ким андердог — объективдүү маалымат. Бүт маалымат ар дайым текшерилген жана булакка шилтемеленет. Мобилдик түзмөктөр үчүн ылдам жүктөлүүчү версия жана ыңгайлуу меню жасалды.
norigamihq – Interesting domain name, curious what this site offers.
mystylecorner – Sharing this with friends — fashion lovers would love this place.
newseason – The colors and fonts are pleasing, design looks intentional.
successpartnersgroup – The products feel authentic and the site loads incredibly fast.
trendyfashioncorner – Great variety of options, from casual to chic looks.
show updates
growyourdigitalpresence – Motivating articles, push me to level up online presence often.
globalideasnetwork – They’ve done solid work in showing what they do, well done.
pinellasehe.org – Always nice to find sites with meaningful content and care.
rockyrose.org – Beautiful site, content feels soothing and meaningful.
cryptotephra-clagr.com – The lab specializes in analyzing tiny volcanic ash shards from sediments.
discovernewideas – I like how everything is laid out, clean and creative vibes.
hecimagine.com – I read that it supports students from conflict regions via HEC. :contentReference[oaicite:0]index=0
createimpact – Always nice to see clarity and quality together in one place.
formative-coffee.com – The fonts and color scheme are very soothing to my eyes.
https://shorturl.fm/2BLPd
inspiredgrowthteam – Really clean design, I like how clear everything is laid out.
Thanks for another informative website. The place else may just I get that kind of info written in such a perfect method? I have a project that I’m simply now running on, and I’ve been on the look out for such info.
трубчатые радиаторы
ukrainianvictoryisthebestaward.com – Homepage doesn’t show anything about “award,” mostly gambling related content.
luxurytrendstore – Checkout process was quick and hassle-free, very user-friendly.
trendyfashioncorner – Browsing was smooth, found trendy pieces that match my style.
webpulse.click – The headings and sections are well spaced, nice readability.
nextgeninnovation – I keep coming back just to see updates and improvements.
blsp at Готов ли ты раскрыть тайны, окутывающие тёмную сеть? Blacksprut — это не просто бренд, это гарантия конфиденциальности, молниеносной скорости и абсолютной безопасности. Посети bs2best.at и узнай то, о чём остальные предпочитают не упоминать. Тебе откроются все тайны, тщательно скрываемые от посторонних глаз. Только для избранных, обладающих особым знанием. Не оставляя следов. Без каких-либо компромиссов. Только Blacksprut. Не упусти уникальный шанс оказаться в авангарде — bs2best.at уже ждёт тех, кто стремится к открытиям. Сможешь ли ты осмелиться познать истинное положение вещей?
visionaryleadersclub – Impressed by their clarity, site feels inspiring and well built.
partnershippowerhouse – Because of good layout, I found helpful info within few clicks.
globalideasnetwork – Really engaging site, lots of value and clever ideas all over.
cryptotephra-clagr.com – Not sure if the domain is live or just a redirect in some contexts.
luxurytrendstore – Highly recommend for anyone looking to refresh their fashion collection.
Acho simplesmente insano JabiBet Casino, e um cassino online que e uma verdadeira onda. As opcoes de jogo no cassino sao ricas e eletrizantes, incluindo jogos de mesa de cassino cheios de vibe. Os agentes do cassino sao rapidos como uma onda, acessivel por chat ou e-mail. O processo do cassino e limpo e sem turbulencia, porem queria mais promocoes de cassino que arrasam. Em resumo, JabiBet Casino e um cassino online que e uma onda gigante para os viciados em emocoes de cassino! De bonus a plataforma do cassino detona com um visual que e puro mar, da um toque de classe aquatica ao cassino.
jabibet apk|
Ich finde absolut wild Lowen Play Casino, es ist ein Online-Casino, das wie ein Lowe brullt. Der Katalog des Casinos ist ein Dschungel voller Nervenkitzel, mit Live-Casino-Sessions, die wie ein Sturm donnern. Der Casino-Service ist zuverlassig und machtig, liefert klare und schnelle Losungen. Casino-Transaktionen sind simpel wie ein Pfad im Busch, manchmal wurde ich mir mehr Casino-Promos wunschen, die wie ein Feuer lodern. Kurz gesagt ist Lowen Play Casino ein Online-Casino, das die Savanne beherrscht fur Spieler, die auf wilde Casino-Kicks stehen! Ubrigens die Casino-Navigation ist kinderleicht wie eine Fahrte, das Casino-Erlebnis total unbezahmbar macht.
löwen play burscheid rezensionen|
filamericansforracialaction.com – Appreciated seeing recent posts, feels active and engaged.
stacoa.org – I browsed a bit and found useful information already.
Sou louco pelo role de PagolBet Casino, tem uma vibe de jogo que e pura eletricidade. Tem uma enxurrada de jogos de cassino irados, com slots de cassino unicos e contagiantes. Os agentes do cassino sao rapidos como um estalo, dando solucoes na hora e com precisao. Os saques no cassino sao velozes como um trovao, as vezes mais bonus regulares no cassino seria top. No fim das contas, PagolBet Casino oferece uma experiencia de cassino que e puro choque para os viciados em emocoes de cassino! De bonus o design do cassino e uma explosao visual vibrante, da um toque de voltagem braba ao cassino.
pagolbet app|
discovernewideas – Their branding feels unique, colors and fonts make a difference.
electlarryarata – Saw “Nothing Found” message, hope new posts come soon.
Ich bin beeindruckt von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Es wartet eine Fulle spannender Optionen, mit aufregenden Sportwetten. Die Agenten sind blitzschnell, bietet klare Losungen. Die Auszahlungen sind ultraschnell, ab und an mehr Rewards waren ein Plus. Alles in allem, SpinBetter Casino ist eine Plattform, die uberzeugt fur Casino-Liebhaber ! Nicht zu vergessen die Interface ist intuitiv und modern, fugt Magie hinzu. Hervorzuheben ist die schnellen Einzahlungen, die den Einstieg erleichtern.
spinbettercasino.de|
createimpact – Interface is clean, found what I wanted super quickly.
myvetcoach.org – The layout is neat, navigation is intuitive and smooth.
thespeakeasybuffalo – The site’s slogan “Spirit Free for the Free Spirit” is quite poetic.
Ich habe eine Leidenschaft fur NV Casino, es ist ein Abenteuer, das pulsiert wie ein Herzschlag. Es wartet eine Fulle an spannenden Spielen, mit immersiven Tischspielen. Die Mitarbeiter reagieren blitzschnell, garantiert hochwertige Hilfe. Die Gewinne kommen ohne Verzogerung, dennoch zusatzliche Freispiele waren toll. Alles in allem, NV Casino ist ein Muss fur Gamer fur Krypto-Liebhaber ! Au?erdem die Plattform ist optisch ein Highlight, was jede Session noch spannender macht.
https://playnvcasino.de/|
laetly.com – The Instagram profile shows fun knit scarves, very nice idea. :contentReference[oaicite:0]index=0
norigamihq – For now it’s mysterious, but the name is memorable.
wettbüro bielefeld
Here is my web blog … strategie für sportwetten (Rocco)
summerstageinharlem.org – Great community vibe, bringing local music and culture together.
Tenho uma paixao vibrante por BETesporte Casino, oferece um prazer esportivo intenso. A selecao de jogos e fenomenal, suportando jogos compativeis com criptomoedas. Eleva a experiencia de jogo. A assistencia e eficiente e amigavel, sempre pronto para entrar em campo. Os saques sao rapidos como um contra-ataque, as vezes recompensas extras seriam um hat-trick. Em sintese, BETesporte Casino garante diversao constante para amantes de apostas esportivas ! Acrescentando que o design e moderno e vibrante, adiciona um toque de estrategia. Um diferencial importante os torneios regulares para rivalidade, fortalece o senso de comunidade.
Ler mais|
pinellasehe.org – Really appreciate the helpful resources shared on this website.
rockyrose.org – Beautiful site, content feels soothing and meaningful.
Hello there! Do you know if they make any plugins to safeguard against hackers? I’m kinda paranoid about losing everything I’ve worked hard on. Any suggestions?
бонус leebet casino
hecimagine.com – Would love more concrete timelines, how to apply, etc.
wett vorhersagen von profis
Feel free to visit my web page; Wettanbieter schnelle auszahlung
https://t.me/pikmaninfo What we do I lead a powerful team that is shaping the future of B2B Saas go-to-market strategies. My company Pikman.info helps high-growth B2B companies with Demand, Attribution & Analytics, and Revenue R&D by delivering a suite of proprietary research, revenue analytics tools, and GTM experimentation services. Pikman.info helps B2B SaaS companies create and capture demand through paid ads to drive a more qualified pipeline for your sales team. Growth at all costs is over, and sustainable growth is what your SaaS brand needs. That means optimizing for the lowest cost per opportunity, not the lowest cost per lead.
formative-coffee.com – The imagery is mouthwatering, makes me crave a cup right now.
Wow, fantastic blog layout! How long have you been blogging for? you make blogging look easy. The overall look of your website is magnificent, as well as the content!
Banda Casino
sportwetten anbieter ohne wettsteuer
Feel free to surf to my site … Sport Wetten Tipps heute
It’s amazing to go to see this web page and reading the views of all colleagues regarding this post, while I am also keen of getting knowledge.
зеркало РиоБет казино
discovernewpath – Mission statement speaks well, feels like they know their purpose.
findyourfuture – The product or service previews are clear and inviting.
wagocjapmeom – The site feels mysterious, layout hints at deeper content waiting.
discovernewpath – I’d share this with friends, seems like something worth knowing.
nextvision – Wish there was proof of legitimacy—user reviews, company registration etc.
uniquefashionstyle – The clean design reflects the brand’s focus on quality.
https://www.treeland.ru/sitemap
schweiz online wetten online bonus ohne einzahlung – Lizette,
trustconnectionnetwork – Regular updates keep the store fresh and engaging for return visits.
strategicgrowthalliance – The minimalist design aligns perfectly with the brand’s aesthetic.
trustedbusinesslink – Everything loads quickly and the content is well organized.
growstrongteam – The content is concise, no fluff — appreciate that directness.
futurevisiongroup – Site loads quick, navigation smooth, nice overall experience.
findyourfuture – I like how they present opportunities without overwhelming details.
learnsharegrow – Their resources are well organized and easy to access.
happylifestylehub – I’ve bookmarked several pages, this feels like a gem.
https://t.me/pikmaninfo PR & Marketing Expertise: Data-Driven Marketing, Paid Search/SEM (Linkedin Ads, Facebook Ads, Google Ads, YouTube Ads, Yandex Ads, Bing Ads), Search Engine Optimization/SEO, Display, Retargeting, Social Media/SMM, Paid Media, Account Based Marketing/ABM, Digital Marketing/Strategy, Data Analytics, Customer Acquisition, Web Marketing, Business Development, Full Stack Marketing, Customer Journey, Content Marketing, A/B Split Testing, Budget Management, Conversational Marketing, Conversion Rate Optimization, Growth Marketing, Multi-Touch Attribution, Copywriting, Data Journalism, Content writing, Visual Storytelling, Brand Identity, Web Design UX/UI, Digital Media, Content Marketing, Demand Generation, Forecasting and Modeling.
nextvision – If you like, I can try dig up more info whether it’s safe or not.
growthpoint – Professional branding, good use of space and design elements.
uniquefashionstyle – The minimalist approach makes finding items quick and easy.
aussenseiter wetten strategie
Here is my homepage buchmacher ausbildung (http://www.alyunaniya.com)
futureopportunitynetwork – The site loads fast, switching pages feels seamless and smooth.
https://shorturl.fm/Cn05q
Деревянные лестницы https://rosslestnica.ru под заказ в любом стиле. Прямые, винтовые, маршевые конструкции из массива. Замеры, 3D-проект, доставка и установка. Гарантия качества и точности исполнения.
Лестницы в Москве https://лестницы-в-москве.рф продажа и изготовление под заказ. Прямые, винтовые, модульные и чердачные конструкции. Качество, гарантия и монтаж по всем стандартам.
futuremindscollective – Excited to support a brand that invests in the future of education.
trustconnectionnetwork – The site’s aesthetic is modern and appealing, reflecting quality.
trustedbusinesslink – Easy-to-use interface, makes me feel confident about using their services.
seoignite.click – I’m impressed with how fast pages load, no lag whatsoever.
happylifestylehub – Browsing here always lifts my mood, lovely design touches.
teamfuture – It feels like a space for growth, not just passive reading.
teamfuture – Friendly tone, helpful advice, everything flows well together.
businessgrowthhub – Useful strategies, real examples—valuable for someone starting out.
trustandunity – I’m excited to see more content here, seems like something special.
digitalinnovationzone – Found some great tips already, helpful and actionable stuff.
futuregoalsnetwork – I feel motivated just reading headlines — that’s a good sign.
meet live
t9py3o
businessgrowthhub – Content is relevant and up to date, keeps me interested.
trustandunity – Already feel connected, even though it’s just my first few visits.
digitalinnovationzone – Learning something new every visit, keeps me hooked.
futuregoalsnetwork – The vision here feels strong, gives hope and direction.
successbridge – This site has such a motivating vibe, feel motivated already.
getthedeal – Recommended for anyone, site is reliable and updated often enough.
Adoro o balanco de BRCasino, parece uma festa carioca cheia de axe. Tem uma enxurrada de jogos de cassino irados, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e cheio de swing, acessivel por chat ou e-mail. Os ganhos do cassino chegam voando como confetes, mas mais giros gratis no cassino seria uma loucura. No fim das contas, BRCasino garante uma diversao de cassino que e um carnaval total para os apaixonados por slots modernos de cassino! De bonus a plataforma do cassino brilha com um visual que e puro axe, eleva a imersao no cassino ao ritmo de um tamborim.
br77 steakhouse – kissimmee|
Adoro o brilho de Richville Casino, tem uma vibe de jogo tao sofisticada quanto uma mansao de ouro. A selecao de titulos do cassino e um cofre de prazeres, com caca-niqueis de cassino modernos e envolventes. O atendimento ao cliente do cassino e um mordomo impecavel, garantindo suporte de cassino direto e sem falhas. Os pagamentos do cassino sao seguros e impecaveis, mesmo assim queria mais promocoes de cassino que brilhem como diamantes. Em resumo, Richville Casino oferece uma experiencia de cassino majestosa para os nobres do cassino! E mais a interface do cassino e fluida e brilha como um salao de baile, faz voce querer voltar ao cassino como um rei ao seu trono.
power washing richville|
Sou viciado no role de JabiBet Casino, da uma energia de cassino que e uma mare alta. Os titulos do cassino sao um espetaculo a parte, com slots de cassino unicos e empolgantes. Os agentes do cassino sao rapidos como uma onda, acessivel por chat ou e-mail. Os ganhos do cassino chegam voando como uma onda, mesmo assim queria mais promocoes de cassino que arrasam. Em resumo, JabiBet Casino e o point perfeito pros fas de cassino para os cacadores de slots modernos de cassino! Vale falar tambem o design do cassino e uma explosao visual aquatica, da um toque de classe aquatica ao cassino.
jabibet|
Estou completamente encantado por RioPlay Casino, tem uma vibe de jogo tao animada quanto um desfile na Sapucai. O catalogo de jogos do cassino e uma folia total, oferecendo sessoes de cassino ao vivo que sambam com energia. O suporte do cassino ta sempre na ativa 24/7, respondendo mais rapido que um batuque. Os pagamentos do cassino sao lisos e blindados, porem mais giros gratis no cassino seria uma folia. Em resumo, RioPlay Casino oferece uma experiencia de cassino que e puro axe para os viciados em emocoes de cassino! Alem disso o site do cassino e uma obra-prima de estilo carioca, torna a experiencia de cassino uma festa inesquecivel.
roblox lite rioplay|
Galera, quero registrar aqui no 4PlayBet Casino porque me impressionou bastante. A variedade de jogos e de cair o queixo: poquer estrategico, todos rodando lisos. O suporte foi amigavel, responderam em minutos pelo chat, algo que faz diferenca. Fiz saque em cartao e o dinheiro entrou na mesma hora, ponto fortissimo. Se tivesse que criticar, diria que seria legal torneios de slots, mas isso nao estraga a experiencia. Enfim, o 4PlayBet Casino vale demais a pena. Ja virou parte da minha rotina.
frontal moto g 4play|
https://okamoto-alumi.jp/2019/05/10/E4BC8AE58BA2E5A4AAE7A59EE6A5BD/
leadersunitedgroup – Coming back for more, feels like this could be something special.
Amo a vibracao de PlayPIX Casino, oferece um prazer carnavalesco. As opcoes sao vastas como um desfile, com slots de design inovador. Com um bonus extra para comecar. O suporte ao cliente e estelar, garantindo um atendimento de qualidade. Os ganhos chegam sem demora, embora mais promocoes regulares seriam otimas. Em sintese, PlayPIX Casino e indispensavel para jogadores para quem aposta com cripto ! Adicionalmente a plataforma e visualmente espetacular, aumenta o prazer de jogar. Um diferencial importante os eventos comunitarios envolventes, fortalece o senso de comunidade.
Continuar lendo|
Tenho uma paixao intensa por BETesporte Casino, sinto uma energia de estadio. O catalogo e rico e diversificado, suportando jogos adaptados para criptos. 100% ate R$600 + apostas gratis. O acompanhamento e impecavel, com suporte preciso e rapido. Os pagamentos sao seguros e fluidos, embora bonus mais variados seriam um gol. No geral, BETesporte Casino oferece uma experiencia inesquecivel para jogadores em busca de emocao ! Acrescentando que a navegacao e intuitiva e rapida, adiciona um toque de estrategia. Um diferencial importante os pagamentos seguros em cripto, fortalece o senso de comunidade.
Visitar hoje|
connectinnovationhub – The layout’s modern and clean, gives confidence in content quality.
winmore – The tone is uplifting without being too cheesy — well done.
futuregoalsnetwork – Always excited to check updates — this site has potential.
successbridge – Always something meaningful to read, not just surface level.
getthedeal – Daily deals are awesome, found exactly what I needed today.
trustconnectionnetwork – Clear navigation, no clutter — makes the experience smooth.
successjourneyclub – I bookmarked several articles, this seems like a go-to resource.
discovervalue</a – I’m bookmarking this site, feels like long-term resource territory.
globalpartnershipteam – This seems like a place built on trust, I feel comfortable browsing.
findtrendystuff – Nice place, I found some quirky items I didn’t expect.
discoverdaily – I find new perspectives here, keeps me thinking in new ways.
Register at glory casino apps download and receive bonuses on your first deposit on online casino games and slots right now!
leadersunitedgroup – The visuals support the writing nicely, feels cohesive.
exploreideasworld – The tone’s inviting, makes me want to explore more.
bs2best at В курсе ли ты, что сотрясает самые глубины тёмной сети? Blacksprut — это не просто название. Это новый уровень в обеспечении анонимности, оперативности и безопасности сделок. Посети bs2best.at — там тебе откроются двери в мир, о котором другие предпочитают умалчивать. Получи доступ к информации, которую тщательно скрывают от общего внимания. Только для тех, кто понимает и разбирается. Без возможности обнаружения. Без каких-либо уступок. Только Blacksprut. Не упусти свой шанс стать одним из первых — bs2best.at уже готов принять тебя в свои ряды. Готов ли ты к тому, что узнаешь?
connectinnovationhub – Beautiful visuals and thoughtful content—nice blend together.
broadcast channel
growtogetheralliance – The content is motivational without feeling pushy, nice balance.
trustconnectionnetwork – I feel like I can trust what I read here, very genuine.
brightdeal – The tone feels hopeful, which is refreshing on many sites.
https://zdorov.atlastex.ru/joga-istochnik-i-razvitie-vnutrennej-sily/
innovateandbuild – I love this place, it really motivates me to try something new.
leadersunitedgroup – I’m learning new things here, good for growth and mindset.
connectinnovationhub – Navigation feels logical, I found info quickly without confusion.
buildtogether – Bookmarking this one — feels like long-term value here.
winmore – I’ll be returning often, I sense good value in topics.
growthnetwork – The content here gives me ideas and keeps me motivated each time.
https://plisio.net/el/blog/cryptocurrency-investment-in-us-election
successjourneyclub – Every post feels like a step forward, helpful direction.
discovervalue – The interface is clean and easy, I find exactly what I’m looking for.
globalpartnershipteam – I appreciate how accessible everything is, no complicated steps.
discoverdaily – I love how fresh and varied the posts seem always.
Estou completamente apaixonado por BRCasino, da uma energia de cassino que e pura purpurina. O catalogo de jogos do cassino e uma folia de emocoes, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e cheio de swing, respondendo mais rapido que um batuque de tamborim. O processo do cassino e limpo e sem tropecos, mas mais giros gratis no cassino seria uma loucura. Na real, BRCasino e um cassino online que e uma folia sem fim para quem curte apostar com gingado no cassino! E mais o design do cassino e um desfile visual vibrante, o que torna cada sessao de cassino ainda mais animada.
br77 steakhouse – kissimmee|
Adoro o brilho de Richville Casino, oferece uma aventura de cassino que brilha como um lustre de cristal. As opcoes de jogo no cassino sao ricas e reluzentes, com caca-niqueis de cassino modernos e envolventes. Os agentes do cassino sao rapidos como um coche de gala, dando solucoes precisas e imediatas. Os pagamentos do cassino sao seguros e impecaveis, mas mais recompensas no cassino fariam qualquer um se sentir rei. No geral, Richville Casino e um cassino online que exsuda riqueza para os que buscam a adrenalina luxuosa do cassino! E mais o design do cassino e um espetaculo visual de tirar o folego, adiciona um toque de sofisticacao ao cassino.
richville download|
leadersunitedgroup – I like the leadership vibe here, feels motivating and real.
Adoro o swing de RioPlay Casino, parece uma festa carioca de diversao. A gama do cassino e simplesmente um bloco de carnaval, incluindo jogos de mesa de cassino com gingado. O servico do cassino e confiavel e cheio de swing, com uma ajuda que e puro gingado. As transacoes do cassino sao simples como um passo de samba, mesmo assim mais recompensas no cassino seriam um diferencial brabo. No geral, RioPlay Casino oferece uma experiencia de cassino que e puro axe para os folioes do cassino! Alem disso o site do cassino e uma obra-prima de estilo carioca, torna a experiencia de cassino uma festa inesquecivel.
roblox lite rioplay atualizado|
Estou completamente alucinado por JabiBet Casino, oferece uma aventura de cassino que arrasta tudo. Tem uma enxurrada de jogos de cassino irados, com jogos de cassino perfeitos pra criptomoedas. O suporte do cassino ta sempre na area 24/7, acessivel por chat ou e-mail. Os pagamentos do cassino sao lisos e blindados, mesmo assim queria mais promocoes de cassino que arrasam. No fim das contas, JabiBet Casino e o point perfeito pros fas de cassino para os viciados em emocoes de cassino! Vale falar tambem o design do cassino e uma explosao visual aquatica, da um toque de classe aquatica ao cassino.
jabibet login|
findtrendystuff – Great mix of styles, always something interesting on display.
Galera, vim dividir minhas impressoes no 4PlayBet Casino porque superou minhas expectativas. A variedade de jogos e muito completa: slots modernos, todos rodando lisos. O suporte foi bem prestativo, responderam em minutos pelo chat, algo que faz diferenca. Fiz saque em Bitcoin e o dinheiro entrou muito rapido, ponto fortissimo. Se tivesse que criticar, diria que mais brindes fariam falta, mas isso nao estraga a experiencia. No geral, o 4PlayBet Casino me conquistou. Ja virou parte da minha rotina.
4play slot|
brightdeal – I found useful ideas here that I can actually apply.
connectinnovationhub – Really impressed with the quality here; definitely worth following.
Tenho uma paixao ardente por PlayPIX Casino, sinto um ritmo alucinante. Ha uma explosao de jogos emocionantes, incluindo apostas esportivas vibrantes. O bonus de boas-vindas e vibrante. Os agentes respondem com rapidez, com suporte preciso e rapido. As transacoes sao confiaveis, no entanto mais promocoes regulares seriam otimas. No geral, PlayPIX Casino oferece uma experiencia inesquecivel para amantes de emocoes intensas ! Acrescentando que a navegacao e simples e envolvente, facilita uma imersao total. Igualmente impressionante as opcoes variadas de apostas esportivas, proporciona vantagens personalizadas.
Descobrir a web|
exploreideasworld – Engaging and varied content; always something that catches my eye.
Tenho uma paixao intensa por BETesporte Casino, proporciona uma aventura competitiva. A variedade de titulos e impressionante, suportando jogos adaptados para criptos. O bonus de boas-vindas e empolgante. O servico esta disponivel 24/7, garantindo atendimento de alto nivel. As transacoes sao confiaveis, contudo bonus mais variados seriam um gol. Para finalizar, BETesporte Casino e indispensavel para apostadores para amantes de apostas esportivas ! Tambem a plataforma e visualmente impactante, facilita uma imersao total. Um diferencial importante os torneios regulares para rivalidade, oferece recompensas continuas.
Abrir agora|
buildtogether – Content is helpful and practical, not just buzzwords — very appreciated.
growtogetheralliance – Always learning something new here, variety keeps it interesting.
innovateandbuild – Always leave feeling I’ve learned something useful, thumbs up.
businessgrowthhub – Great resources, feels like a place to pick up real business skills.
growthnetwork – I’ve bookmarked this site, seems rich with useful insights.
My top recommendation is to buy fifa coins strategically before TOTY and major promotional events when squad upgrades matter most. Real vendors with fast processing and active monitoring plus non drop guarantees ensure you’re competitive when it counts.
bs2best зеркало Заинтригован, что вызывает резонанс в тёмных закоулках сети? Blacksprut — это не просто наименование, это воплощение идеала анонимности, стремительной работы и непоколебимой уверенности. Отправляйся на bs2best.at — в обитель, где раскрывают секреты, о которых предпочитают молчать. Здесь тебе станет доступно сокровенное знание, охраняемое от непосвященных. Исключительно для тех, кто понимает суть. Никаких улик. Никаких соглашений. Только Blacksprut. Не упусти драгоценную возможность стать пионером — bs2best.at распахнул врата для тех, кто ищет истину. Хватит ли тебе отваги заглянуть правде в лицо?
Sugar Rush 1000 oferuje wciągającą rozgrywkę na slocie online w żywej siatce 7×7. Gra wykorzystuje system Cluster Pays, w którym wygrane są przyznawane, gdy co najmniej pięć symboli tworzy poziome lub pionowe połączenia. Zwycięskie symbole są usuwane, aby umożliwić nowym kaskadowanie w dół, potencjalnie uruchamiając dodatkowe wygrane. Ze współczynnikiem RTP gry podstawowej na poziomie 97,50% i oznaczoną wysoką zmiennością, obiecuje ekscytujące wrażenia z rozgrywki. Dzięki wysokiemu RTP i ocenie zmienności, wraz z zabawnym motywem i ekscytującymi bonusami, Sugar Rush to gra, której nie można przegapić. Animacje i grafika na pewno wprowadzą Cię w dobry nastrój, a potencjał na duże wygrane zatrzyma Cię w grze na wiele godzin. Dla tych, którzy chcą dzielić się historiami ze znajomymi i rodziną.
https://anschalinib1986.cavandoragh.org/dodatkowe-informacje
Recenzja automatu Sugar Rush nie może rozpocząć się bez przedstawienia podstawowych informacji na temat gry. Oto kluczowe dane: Na podany wyżej adres email wyślemy nowe utworzone losowo hasło. Po zalogowaniu proszę ustwić nowe hasło. Wygraj 25 000x swój zakład na slocie Sugar Rush 1000! Krzaki tej odmiany dosłownie łamią się od ciężaru owoców! To piękna krzyżówka. Jest to bardzo bliska kuzynka Sugar Rush Peach Striped jednak ma gruszkowaty kształt z charakterystycznym ogonkiem na czubku po skrzyżowaniu z Aji Tangerine. W smaku mocno owocowa, dużo cytrusów i nut kwiatowych. Obsługa Javascript w Twojej przeglądarce jest wyłączona. Włącz go, aby móc w pełni wykorzystać możliwości tej witryny. Zmysłowa stymulacja łechtaczki za pomocą Satisfyer Sugar Rush Zabawny design przypominający rybę oraz kuszące połączenie fal ciśnienia i wibracji sprawiają, że Satisfyer Sugar Rush jest idealnym produktem dla początkujących. Oba silniczki mogą być sterowane oddzielnie: 11 intensywności fal ciśnienia i 12 programów wibracji daje niezliczone możliwości kombinacji do wyboru. Dzięki kompaktowemu kształtowi podczas zabawy masz wszystko pod kontrolą. Co więcej, wibrator z falami ciśnienia można również dyskretnie i łatwo transportować w podróży.
boostcraft.click – Typography is sharp and readable, even on small screens.
ranktrail.click – The site loads fast, I didn’t face any lag while exploring.
ranktrail.click – I like the way content is structured—sections flow naturally.
searchnest.click – Navigation is intuitive, I quickly found what I needed.
websummit.click – The visuals are crisp, and pages load fast without hesitation.
lizenz bestes sportwetten portal
nataliakerbabian – Her site feels elegant, visuals and content strike a refined, warm balance.
boostcraft.click – Navigation is smooth, I found what I wanted almost instantly.
ranktrail.click – Just browsed this, layout’s clean and the UI feels quite intuitive.
ranktrail.click – Found a few interesting articles already—will go deeper later.
searchnest.click – Content is well organized and pleasing to the eye.
websummit.click – The color scheme is subtle and soothing, nothing jarring.
phillybeerfests – I like the fun energy here, layout feels ready for celebration.
smartpartnership.bond – Clean design, easy to understand what they offer without overcomplication.
smartdesigncorner.shop – Already showing this to friends looking for design inspiration.
https://plisio.net/de/blog/is-crypto-dead-will-crypto-recover
smartdesigncorner.shop – Nice mix of styles, enough variety to keep exploring.
Слив курсов ЕГЭ информатика https://courses-ege.ru
partnershippowerhouse.shop – Very good user experience; clean design, thoughtful sections.
inspiredmind.shop – I bookmarked several pages already — so many neat ideas.
globalunity.bond – Found several parts inspiring; feels like a community I’d like to join.
Bonus Code Wetten sport
trustinyou.bond – Definitely sharing this with friends who might find this message helpful.
shopwithpurpose.shop – Really love how the value-driven mission shines through every product.
Кто знает, сколько голов забил Неймар за карьеру? Хочу таблицу по клубам и сборной. Где скачать удобный apk, чтобы получать пушки о голах Неймара прямо во время canlı izləmə? Собираю редкие «неймар сантос фото» в высоком качестве — делюсь находкой. neymar-kg com. Неймар фильмы и документалки: посоветуйте топ-3 для выходных.
Ищу «неймар барселона фото» с классическими комбинациями с Суаресом и Месси. Неймар номер: на футболке в «Сантосе» и «Барселоне» — важные детали для коллекционеров. Неймар толстый — ещё один миф: интересен анализ формы после травм и пауз. Неймар барса — лучшие фото с трофеями и парадами, для коллекции.
Неймар обой — встречал такое написание: ищу корректные теги для поиска. Неймар Сантоc фото — ранние годы вдохновляют молодых вингеров на тренировки.
smartpartnership.bond – Already considering how this could benefit local projects.
smartdesigncorner.space – Browsing through their portfolio gives lots of inspiration right away.
orourkeforphilly – I like the campaign site, visuals feel strong and message clear.
creativegiftzone.shop – Nice themes and seasonal items — exactly what I was hoping to see.
https://plisio.net/de/blog/what-is-mantle-network-mnt
creativityuniverse.shop – There’s so much variety, it’s fun to explore what they offer.
sportsbook bonus codes Bet Bonus Codes Unique symbols make it those “bet bonus codes” with promotions provided with gambling action so those codes improve wager benefit plans. You must type and copy the code into the gambling website. When registering or filling the balance for making wagers . The advantage becomes the wager credit the moment it’s employed on the bank amount or during registration. Benefit codes enable gamblers to increase their return on online casino.
learnonline.bond – Can’t wait to see what new courses they’ll add next.
partnershippowerhouse.shop – Powerful name, site feels like it’s made to drive real collaboration.
globalunity.bond – Design and visuals feel professional and hopeful.
shopwithpurpose.shop – Definitely one of those shops I trust because of the purpose behind it.
trustinyou.bond – Photos are well chosen; text is clear and reassuring.
online stream
buildbrand.online – Already imagining applying some of their tips to my upcoming project.
trendfinder.bond – This website keeps me updated with the latest buzz perfectly every time.
Советы по выбору обоев Неймара: матчи, портреты, training — что лучше для экрана смартфона? Хочу «неймар фото на аву» без шумов и с ровным цветом кожи, пригодные для соцсетей. Короткие дайджесты новостей и canlı izləmə удобно следить из одного места. неймар новости. Неймар фильмы и документалки: посоветуйте топ-3 для выходных.
Неймар текущие команды: удобно видеть клуб/сборная/статус в одном блоке. Неймар номер: на футболке в «Сантосе» и «Барселоне» — важные детали для коллекционеров. Неймар жена, дети — только официальные факты, без слухов; подскажите корректные био-источники. Неймар ПСЖ 2018 — топовый сезон по влиянию между линиями; ищу срез по матчам.
Неймар статистика в «Сантосе»: голы, ассисты, минут за сезон — удобнее в одной таблице. Неймар обои на телефон — тёмные темы помогают экономить батарею на OLED.
cumberlandcountynjvaccination – The site gives clarity, vital health information is accessible and well organized.
inspiredgrowthteam.shop – Found something that really resonated with me, good find!
ki wetten vorhersage
Visit my web blog: Sportwetten tipps kostenlos (https://Leyarled.com)
dailyvaluehub.shop – Found great deals and useful products, reminds me of a treasure trove.
inspiredideas.shop – Their products look inspiring and the site feels very polished.
inspiredmind.shop – Products look thoughtful and original, just what I was hoping for.
Для oyunlar и fantasy смотрю новости Неймара: травмы, сроки камбэка, предполагаемая роль. Ищу «неймар обои барселона» и «бразилия»: хочется минимализма, без лишних логотипов. Нужны «неймар обои 4к» без водяных знаков и с правильным соотношением сторон. неймар обои 4к. Неймар фильмы и документалки: посоветуйте топ-3 для выходных.
Ищу «неймар барселона фото» с классическими комбинациями с Суаресом и Месси. Неймар номер: на футболке в «Сантосе» и «Барселоне» — важные детали для коллекционеров. Неймар жуниор — хочу подборку детских фото для сравнительного коллажа. Месси Роналду Неймар Мбаппе — хочу динамичный коллаж для заставки.
Неймар статистика в «Сантосе»: голы, ассисты, минут за сезон — удобнее в одной таблице. Неймар лучшие фото — интересны кадры из туннеля и разминки, редко попадаются.
smartdesigncorner.space – Definitely recommending this to friends needing design inspiration.
startsomethingnew.shop – I bookmarked several items, will return when I have more time.
buildlastingtrust.bond – Trust-building content feels honest, not just flashy marketing.
findnewtrend.shop – Navigation is smooth, images look crisp and appealing.
https://plisio.net/pt/blog/millions-lost-to-cryptocurrency-scams
Ищу красивые обои 4K с Неймаром: барса, ПСЖ или ранний «Сантос» — что посоветуете для телефона? Интересует «неймар рост вес возраст» по годам — удобнее видеть в одной инфографике. Для мобил фанатов mobil futbol важна чистая сводка по матчам и травмам. неймар статистика. Где найти «неймар фото ПСЖ» в матч-дне и тренировках, чтобы собрать серию аватарок?
Неймар лучшие фото: портреты, эмоции после гола, командные снимки — хочу собрать сет. Неймар барса — обои с Камп Ноу и ночной подсветкой стадиона смотрятся мощно. Неймар жуниор — хочу подборку детских фото для сравнительного коллажа. Неймар Барселона обои — хочется классики без кричащих фильтров и водяных знаков.
Где играет Неймар 2024 — нужен апдейт раз в месяц с подтверждением источников. Неймар 2018 ПСЖ — сравнение с 2017 Барса: влияние на xThreat и прогрессии мяча.
trustandunity.shop – Feels welcoming and authentic, like a place built for community.
brightfuturegroup.bond – Their tone feels sincere and trustworthy, a nice combination.
creativegiftzone.shop – The photos are vivid and really help with decision making.
smartstylehub.shop – Quality seems promising, prices appear reasonable too.
Me enredei no algoritmo de PlayPix Casino, parece uma matriz de adrenalina cibernetica. Tem uma enxurrada de jogos de cassino irados. oferecendo sessoes ao vivo que processam como servidores. O suporte e um codigo preciso. oferecendo respostas claras como um codigo. As transacoes sao faceis como um glitch. mesmo assim queria mais promocoes que glitcham como retro. Em sintese, PlayPix Casino e um buffer de emocoes para quem curte apostar com estilo cibernetico! Como extra a interface e fluida e reluz como um pixel. tornando cada sessao ainda mais pixelada.
como usar bonus playpix|
Sou louco pela energia de Brazino Casino, explode com uma vibe aquatica eletrizante. A selecao de titulos e uma correnteza de emocoes. com jogos adaptados para criptomoedas. Os agentes sao rapidos como um cardume. com ajuda que ilumina como uma perola. Os saques sao velozes como um mergulho. mas mais giros gratis seriam subaquaticos. Ao final, Brazino Casino e um cassino online que e um oceano de diversao para os apaixonados por slots modernos! Como extra o site e uma obra-prima de estilo subaquatico. tornando cada sessao ainda mais aquatica.
cГіdigo promocional brazino777 grГЎtis|
globalpartnershipteam.bond – I like how they highlight collaboration and shared goals.
Ich liebe den Wahnsinn von JackpotPiraten Casino, es hat eine Spielstimmung, die alles sprengt. Es gibt eine Flut an packenden Casino-Titeln, mit einzigartigen Casino-Slotmaschinen. Das Casino-Team bietet eine Unterstutzung, die wie Gold glanzt, sorgt fur sofortigen Casino-Support, der beeindruckt. Der Casino-Prozess ist klar und ohne Wellengang, trotzdem mehr Freispiele im Casino waren ein Volltreffer. Insgesamt ist JackpotPiraten Casino ein Casino mit einem Spielspa?, der die Planken erzittern lasst fur Abenteurer im Casino! Und au?erdem die Casino-Navigation ist kinderleicht wie ein Kartenlesen, den Spielspa? im Casino auf Hochtouren bringt.
jackpotpiraten bonus code ohne einzahlung|
Estou completamente vidrado por SambaSlots Casino, parece uma festa carioca cheia de energia. As opcoes de jogo no cassino sao ricas e cheias de swing, incluindo jogos de mesa de cassino com muito charme. O servico do cassino e confiavel e cheio de gingado, acessivel por chat ou e-mail. Os saques no cassino sao velozes como um mestre-sala, de vez em quando mais recompensas no cassino seriam um diferencial insano. Resumindo, SambaSlots Casino vale demais sambar nesse cassino para os apaixonados por slots modernos de cassino! E mais a navegacao do cassino e facil como um passo de carnaval, adiciona um toque de axe ao cassino.
avis la sambaslots casino|
modernchoice.store – Nice mix of aesthetic and utility, feels like a thoughtful shop.
trustedbusinesslink.shop – Already sent link to colleagues — this might help with our projects.
rankmotion.click – Already bookmarked this — seems like a site I’ll revisit.
pagevector.click – Found useful content already, will dig deeper later tonight.
clicksignal.click – Pages load fast and design is crisp, really pleasant experience.
Je suis enthousiaste a propos de 7BitCasino, on dirait une plongee dans un univers palpitant. Le catalogue est incroyablement vaste, incluant des slots de pointe. Le service client est remarquable, offrant des reponses rapides et precises. Les retraits sont ultra-rapides, par moments les bonus pourraient etre plus reguliers, ou des promotions hebdomadaires plus frequentes. Globalement, 7BitCasino vaut pleinement le detour pour les passionnes de jeux numeriques ! Ajoutons que le design est visuellement attrayant avec une touche vintage, renforce l’immersion totale.
7bitcasino bonus codes|
visionaryleadersclub.bond – Clean site design, feels professional and motivational.
https://shorturl.fm/5oixV
buildbrand.online – Really strong branding ideas here, definitely inspiring and useful.
inspiredgrowthteam.shop – Photos are appealing and layouts are neat — very user friendly.
Sou viciado em PlayPIX Casino, e uma plataforma que vibra com intensidade. O catalogo e rico e multifacetado, com slots de design inovador. Fortalece seu saldo inicial. Os agentes respondem com agilidade, acessivel a qualquer momento. O processo e simples e elegante, contudo promocoes mais frequentes dariam um toque extra. Para finalizar, PlayPIX Casino vale uma visita epica para entusiastas de jogos modernos ! Vale destacar a plataforma e visualmente espetacular, adiciona um toque de conforto. Muito atrativo o programa VIP com niveis exclusivos, oferece recompensas continuas.
Mergulhe nisso|
Fiquei fascinado com BETesporte Casino, proporciona uma aventura eletrizante. Ha uma explosao de jogos emocionantes, com slots modernos e tematicos. Eleva a experiencia de jogo. O acompanhamento e impecavel, oferecendo respostas claras. O processo e simples e direto, de vez em quando mais apostas gratis seriam incriveis. No fim, BETesporte Casino e essencial para apostadores para fas de cassino online ! Alem disso a plataforma e visualmente impactante, aumenta o prazer de apostar. Um diferencial importante o programa VIP com niveis exclusivos, oferece recompensas continuas.
Começar aqui|
startsomethingnew.shop – The product images are very appealing and inspire creativity.
findnewtrend.shop – Just checked this out, lots of fresh trends I hadn’t seen before.
netfusion.click – Already bookmarked this—seems like a site worth returning to.
seoanchor.click – Already bookmarked this, I’ll be back for more content.
rankmotion.click – Found useful sections quickly, the menu is intuitive and clean.
cycleforsci – Inspiring cause, layout feels energetic and message delivers real motivation.
clicksignal.click – I just browsed this site, the layout feels very modern and friendly.
trustandunity.shop – Found several items I’d consider; good variety too.
https://plisio.net/ar/blog/stakestone
social talk
Кто знает, сколько голов забил Неймар за карьеру? Хочу таблицу по клубам и сборной. Ищу «неймар обои барселона» и «бразилия»: хочется минимализма, без лишних логотипов. Собираю редкие «неймар сантос фото» в высоком качестве — делюсь находкой. neymar-kg com. Ищу «неймар красивые фото 2024» в стиле editorial — подскажите, какие фотосеты топ.
Нужны «неймар обои на телефон» с мягким контрастом, чтобы иконки читались. Неймар барса — обои с Камп Ноу и ночной подсветкой стадиона смотрятся мощно. Неймар жуниор — хочу подборку детских фото для сравнительного коллажа. Неймар фото 2024 — без пересвета, контраст средний, чтобы текст поверх был виден.
Неймар барса обои 4К — важно проверить соотношение сторон под ультраширокие мониторы. Неймар новости — лучше краткие дайджесты, чем длинные простыни текста.
oneillforda – The campaign tone feels sincere, visuals and message align strongly.
Подготовительные курсы к ЕГЭ https://courses-ege.ru
investsmarttoday – Clean layout and fast loading, makes exploring investment tips enjoyable.
Sou louco pela energia de Brazino Casino, pulsa com uma forca de cassino digna de um oceano. A colecao e uma onda de entretenimento. oferecendo sessoes ao vivo que brilham como aguas cristalinas. Os agentes sao rapidos como um cardume. disponivel por chat ou e-mail. As transacoes sao faceis como uma onda. mesmo assim mais bonus regulares seriam aquaticos. No geral, Brazino Casino garante um jogo que reluz como um coral para os viciados em emocoes de cassino! Alem disso o visual e uma explosao de corais. amplificando o jogo com vibracao aquatica.
limite de saque brazino777|
Estou completamente pixelado por PlayPix Casino, tem uma energia de jogo tao vibrante quanto um codigo binario em furia. Tem uma enxurrada de jogos de cassino irados. com caca-niqueis que reluzem como bytes. O suporte e um firewall de eficiencia. assegurando apoio sem erros. Os ganhos chegam rapido como um render. entretanto as ofertas podiam ser mais generosas. Em sintese, PlayPix Casino e uma onda de adrenalina digital para os fas de adrenalina pixelada! Adicionalmente a interface e fluida e reluz como um pixel. tornando cada sessao ainda mais pixelada.
plataforma de jogo playpix|
Adoro o gingado de SambaSlots Casino, parece uma festa carioca cheia de energia. As opcoes de jogo no cassino sao ricas e cheias de swing, com slots de cassino tematicos de festa. O suporte do cassino ta sempre na ativa 24/7, com uma ajuda que e puro axe. Os saques no cassino sao velozes como um mestre-sala, as vezes as ofertas do cassino podiam ser mais generosas. No geral, SambaSlots Casino oferece uma experiencia de cassino que e puro batuque para os apaixonados por slots modernos de cassino! Alem disso o design do cassino e um desfile visual colorido, o que torna cada sessao de cassino ainda mais animada.
sambaslots casino hotel las vegas|
Ich flippe aus bei JackpotPiraten Casino, es ist ein Online-Casino, das wie eine Welle kracht. Die Auswahl im Casino ist ein echter Jackpot, mit Live-Casino-Sessions, die wie Kanonen donnern. Der Casino-Service ist zuverlassig und top, sorgt fur sofortigen Casino-Support, der beeindruckt. Casino-Gewinne kommen wie ein Blitz, ab und zu mehr Freispiele im Casino waren ein Volltreffer. Insgesamt ist JackpotPiraten Casino eine Casino-Erfahrung, die wie ein Piratenschatz glanzt fur Fans moderner Casino-Slots! Und au?erdem die Casino-Oberflache ist flussig und glanzt wie ein Piratenschiff, den Spielspa? im Casino auf Hochtouren bringt.
jackpotpiraten online casino|
successjourneyclub.shop – It’s nice that everything seems laid out clearly and honestly.
brightmarketplace – Impressed with the packaging and timely delivery, will shop again.
smartbuytoday – This site has become my favorite for online shopping recently.
bestdealcorner – Loved the product selection, quality items at reasonable prices here.
investsmarttoday – Excellent explanations and tips, saves a lot of time learning today.
Хочу аву с «неймар сантос фото»: важно, чтобы кадры были чёткие и подойдут для профилей. Интересует «неймар рост вес возраст» по годам — удобнее видеть в одной инфографике. Ищу качественные кадры для новых постов и аватарок. неймар фото. Ищу «неймар красивые фото 2024» в стиле editorial — подскажите, какие фотосеты топ.
«Неймар золотой мяч» — почему не выиграл? Интересны аналитические статьи без фанатизма. Неймар авы: лучше выбирать кадры с равномерным фоном — серый/графит работает отлично. Неймар завершил карьеру? Хочу факт-чек от надёжных спортивных СМИ. Неймар ПСЖ 2018 — топовый сезон по влиянию между линиями; ищу срез по матчам.
Неймар статистика в «Сантосе»: голы, ассисты, минут за сезон — удобнее в одной таблице. Неймар новости — лучше краткие дайджесты, чем длинные простыни текста.
J’adore a fond 7BitCasino, ca ressemble a une energie de jeu irresistible. Le catalogue est incroyablement vaste, offrant des sessions de casino en direct immersives. Le service client est remarquable, repondant en un clin d’?il. Les transactions en cryptomonnaies sont instantanees, occasionnellement plus de tours gratuits seraient un atout, notamment des bonus sans depot. Pour conclure, 7BitCasino est un incontournable pour les adeptes de sensations fortes ! Notons egalement que le design est visuellement attrayant avec une touche vintage, renforce l’immersion totale.
7bitcasino no deposit bonus codes|
justvotenoon2 – Really impressed with the updates, keep up the amazing work!
Amo a energia de PlayPIX Casino, oferece um prazer eletrizante. Ha uma explosao de jogos emocionantes, com slots de design inovador. Com uma oferta inicial para impulsionar. Os agentes respondem com agilidade, com suporte rapido e preciso. Os pagamentos sao seguros e fluidos, as vezes ofertas mais generosas seriam bem-vindas. Para finalizar, PlayPIX Casino garante diversao constante para fas de cassino online ! Tambem o site e rapido e cativante, adiciona um toque de conforto. Notavel tambem os pagamentos seguros em cripto, assegura transacoes confiaveis.
Aprender como|
Sou totalmente viciado em BETesporte Casino, e uma plataforma que vibra como um estadio lotado. A variedade de titulos e impressionante, com slots modernos e tematicos. Eleva a experiencia de jogo. Os agentes respondem com rapidez, oferecendo respostas claras. O processo e simples e direto, contudo ofertas mais generosas dariam um toque especial. Para finalizar, BETesporte Casino oferece uma experiencia inesquecivel para fas de cassino online ! Vale destacar o site e veloz e envolvente, adiciona um toque de estrategia. Igualmente impressionante os torneios regulares para rivalidade, proporciona vantagens personalizadas.
Saiba mais|
smartbuytoday – Loved the product selection, quality items at reasonable prices here.
classytrendstore – This site has become my favorite for online fashion shopping.
bestdealcorner – Helpful product descriptions and reviews, made decision-making easier today.
dailyprofitupdate – Love the clean design; makes shopping a pleasant experience.
successjourneyclub.shop – I like seeing transparent info; builds confidence.
modernvisionlab.shop – Prices seem reasonable for what’s shown, good balance.
stylemebetter – Great value for money; products match the descriptions perfectly.
justvotenoon2 – This website loads fast and has awesome resources overall.
modernvaluecorner – Excellent customer service; responses were prompt and informative.
technologydreamhub.shop – I bookmarked a few cool items, will probably order soon.
Неймар в «Сантосе» — золотая эпоха: сверяю статистику 2011–2012 и пересматриваю игры в canlı izləmə. Сравнение Неймара 2011 и 2017: темп, решения, пауза — отличный кейс для тактического разбора. Короткие дайджесты новостей и canlı izləmə удобно следить из одного места. неймар новости. Ищу «неймар красивые фото 2024» в стиле editorial — подскажите, какие фотосеты топ.
Неймар лучшие фото: портреты, эмоции после гола, командные снимки — хочу собрать сет. Неймар религия: редкая тема, важно корректно и без спекуляций — есть проверенные источники? Когда «умер неймар» — кликбейт заголовки; нужны разборы, опровергающие фейки. Неймар барса — лучшие фото с трофеями и парадами, для коллекции.
Неймар игры — подборка техничных эпизодов без комментаторского шума. Неймар в каком клубе играет — хочу добавить автоподстановку в шапке сайта.
findyourlook.shop – Prices seem fair for what’s shown, quality looks promising.
buildlastingtrust.shop – Their messaging feels genuine, not just trying to sell something.
kostenlos sportwetten ohne einzahlung
Here is my site Buchmacher München
nextgenproject.shop – I appreciate how bold the name is — strong branding.
dailyprofitupdate – The site loads fast; navigation is intuitive and user-friendly.
sportwetten lizenz österreich
my website schüsse aufs tor wetten
trendhunterplace – Awesome insights and resources, definitely my new favorite trend site.
yourtradingmentor – Very clear explanations and practical advice, excellent learning resource here.
https://clocks-top.com/
trendinggiftcorner – Fast loading and clean design, makes shopping really convenient today.
smarttradingmentor – Excellent mentorship tips, really helped me improve trading strategies today.
modernwoodcases – Customization options are great; makes each piece unique.
webtide.click – I like how intuitive the menu is—everything feels easy to navigate.
group chat
rankforge.click – Already bookmarked this — feels like a go-to resource.
purebeautyoutlet – Customer feedback section is helpful, gives confidence before buying anything.
trafficpulse.click – Visuals complement the text nicely; the design feels polished and thought-out.
1xbet cameroun apk pronostic foot gratuit
musionet – Very helpful guides, made my tasks much simpler and faster.
stylemebetter – Will definitely shop here again; satisfied with my purchase.
protraderacademy – Very helpful guides for beginners, learned a lot in minutes today.
modernvisionlab.shop – Prices seem reasonable for what’s shown, good balance.
esc buchmacher
My blog – vermittler von wetten bei pferderennen
https://plisio.net/zh/blog/solana-vs-ethereum
Новости спорта онлайн http://sportsat.ru футбол, хоккей, бокс, теннис, баскетбол и другие виды спорта. Результаты матчей, обзоры, интервью, аналитика и главные события дня в мире спорта.
everydayvaluefinds.shop – Prices seem fair, I like that it’s not over the top.
strongpartnershipnetwork – Great insights on partnerships, very helpful for networking effectively today.
webtide.click – I found a couple of interesting links already—will explore more later.
fastgrowthsignal – Overall pleasant experience, will revisit for future purchases very soon.
keywordorbit.click – Typography is comfortable, spacing feels well thought-out for reading.
rankforge.click – Found some useful articles here, will save them to read later.
https://plisio.net/ko/blog/honeypot-crypto-scam
modernvaluecorner – Great value for money; products match the descriptions perfectly.
trendhunterplace – This site is practical and enjoyable, keeps me coming back.
nextgenproject.shop – Layout is promising, assuming content matches the vision.
trendinggiftcorner – Fast loading and clean design, makes shopping really convenient today.
smarttradingmentor – This site has become my favorite platform for learning trading efficiently.
yourtradingmentor – Clean design and easy navigation, makes following lessons really simple today.
modernwoodcases – Love the unique designs; they add a personal touch to my phone.
https://plisio.net/uk/blog/what-plisio-has-done-for-your-business-growth
wetten deutschland ungarn
Also visit my page; wettseiten ohne oasis (Meredith)
marketanalysiszone – Reliable presentation and focused insights, quite impressed by the clarity.
learnandtrade – The mix of theory and practical examples really made a difference.
marketanalysiszone – This will be one of my go-to sources for market commentary now.
teamworksuccesspath – Excellent insights into team dynamics, helped me work better with my group.
classyhomegoods – This store is now on my go-to list for stylish home décor shopping.
successnetworkgroup – Good layout, clear advice and friendly tone made browsing enjoyable.
forexstrategyguide – Excellent course for scaling businesses, practical tips and strategies.
Ich bin total begeistert von PlayJango Casino, es bietet ein Casino-Abenteuer, das wie ein Regenbogen funkelt. Die Spielauswahl im Casino ist wie ein funkelnder Ozean, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Der Casino-Service ist zuverlassig und strahlend, antwortet blitzschnell wie ein Donnerschlag. Casino-Zahlungen sind sicher und reibungslos, aber die Casino-Angebote konnten gro?zugiger sein. Alles in allem ist PlayJango Casino ein Casino, das man nicht verpassen darf fur Fans von Online-Casinos! Extra die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino in die Hohe treibt.
playjango sister sites|
Adoro a chama de BR4Bet Casino, e um cassino online que reluz como um farol na nevoa. A colecao e um facho de diversao. com caca-niqueis que brilham como holofotes. O time do cassino e digno de um faroleiro. respondendo veloz como uma chama acesa. Os ganhos chegam rapido como uma lanterna. mesmo assim queria mais promocoes que brilham como farois. No fim das contas, BR4Bet Casino e o point perfeito pros fas de cassino para os faroleiros do cassino! De lambuja o visual e uma explosao de claroes. fazendo o cassino brilhar como um farol.
br4bet baixar|
melbet telecharger telecharger 1xbet cameroun
shopwithsmile – Helpful customer service responded quickly when I had a question.
globalchoicehub – Great selection of items, very impressed with the variety here.
learnandtrade – The content feels trustworthy and the lessons are practical.
teamworksuccesspath – Very practical advice and examples, made a difference in our project today.
classyhomegoods – This store is now on my go-to list for stylish home décor shopping.
metaboost.click – Already bookmarked this site—feels like it’ll be a useful reference.
seowhale.click – I like how well-structured the pages are and how clean everything appears.
successnetworkgroup – Great group atmosphere, lots of support and networking opportunities.
Estou completamente alucinado por SpeiCasino, tem uma vibe de jogo tao reluzente quanto uma supernova. O catalogo de jogos do cassino e uma constelacao de prazeres, oferecendo sessoes de cassino ao vivo que brilham como nebulosas. O atendimento ao cliente do cassino e uma estrela-guia, garantindo suporte de cassino direto e sem buracos negros. As transacoes do cassino sao simples como uma orbita, as vezes as ofertas do cassino podiam ser mais generosas. No geral, SpeiCasino garante uma diversao de cassino que e uma galaxia para quem curte apostar com estilo cosmico no cassino! Vale dizer tambem a navegacao do cassino e facil como uma orbita lunar, faz voce querer voltar ao cassino como um cometa em orbita.
spei australia|
Adoro a onda sonora de JonBet Casino, tem um ritmo de jogo que ecoa como um coral. As escolhas sao vibrantes como um sino. com slots tematicos de aventuras sonoras. O atendimento e solido como uma corda. respondendo rapido como um eco na caverna. As transacoes sao faceis como um sino. entretanto mais giros gratis seriam vibrantes. Para encurtar, JonBet Casino vale explorar esse cassino ja para os amantes de cassinos online! Alem disso a navegacao e facil como um eco. transformando cada aposta em uma aventura ressonante.
quem e dono da jonbet|
betting promos Best Betting Sites Bonuses “Best betting sites bonuses” tend to offer perks that stretch wager amounts as a result of bonuses. Bonus opportunities on a website should improve returns. The top promotions can enable clients to obtain a 20% improvement. You have opportunities from certain wager companies to make free cash. Gamblers who have just started using a wager platform and gambling can benefit from incentives if and when they take note of the requirements.
forexstrategyguide – Excellent course for scaling businesses, practical tips and strategies.
shopwithsmile – Very user-friendly site, easy navigation and clear product pages.
shopandshine – Really good value for money, will definitely browse here again.
metaboost.click – Already bookmarked this site—feels like it’ll be a useful reference.
Estou completamente apaixonado por BacanaPlay Casino, tem uma vibe de jogo tao animada quanto uma bateria de escola de samba. As opcoes de jogo no cassino sao ricas e cheias de gingado, com caca-niqueis de cassino modernos e contagiantes. O atendimento ao cliente do cassino e uma rainha de bateria, garantindo suporte de cassino direto e sem perder o ritmo. Os pagamentos do cassino sao lisos e blindados, porem mais bonus regulares no cassino seria brabo. Em resumo, BacanaPlay Casino vale demais sambar nesse cassino para os viciados em emocoes de cassino! De lambuja a plataforma do cassino brilha com um visual que e puro samba, faz voce querer voltar ao cassino como num desfile sem fim.
bacanaplay suporte|
visionpartnersclub – Impressed with the packaging and timely delivery, will shop again.
globalchoicehub – The customer service responded quickly when I had a question.
ultimateprofitplan – Clear and concise, perfect for entrepreneurs looking to grow efficiently.
seowhale.click – I’m bookmarking this—looks like a resource worth revisiting later.
yourtradingmentor – Credible guidance, made me more confident in my trading decisions.
bestforexstrategies – The layout is clean and the strategy descriptions are clear and helpful.
successfultradersclub – Navigation was smooth and I found useful content without too much fluff.
nextleveltrading – Really well laid-out site, made complicated strategies feel clear and simple.
futuregrowthteam – Impressed with the packaging and timely delivery, will shop again.
bs market Ты еще не в курсе, что порождает бурю в темных водах сети? Blacksprut – это не просто символ. Это квинтэссенция анонимности, молниеносной скорости и абсолютной уверенности в каждом действии. Приглашаем на bs2best.at – туда, где шепчут о том, о чем другие предпочитают хранить гробовое молчание. Тебе откроются двери в мир, скрытый от любопытных глаз, доступный лишь избранным, тем, кто понимает истинную цену информации. Ни единой зацепки. Никаких отступлений. Только безупречный Blacksprut, гарант твоей конфиденциальности. Не упусти свой шанс стать первопроходцем – bs2best.at уже готов раскрыть свои тайны. Достаточно ли ты смел, чтобы заглянуть в бездну правды?
shoplocaltrend – Helpful product descriptions and reviews, made decision-making easier today.
sportwetten anbieter international
Here is my homepage; die besten wettanbieter in deutschland
strongpartnershipnetwork – Loved the advice and insights, makes networking much easier to manage.
freshfashionfinds – This site has become my favorite for online fashion shopping.
strongfoundation – Great user experience, site loads quickly which I really appreciate.
shopandshine – Loved the product range, found unique pieces I’ve not seen elsewhere.
uniquedecorstore – Excellent customer service, got quick help with an order question.
Fiquei fascinado com PlayPIX Casino, leva para um universo de pura excitacao. O catalogo e exuberante e diversificado, suportando jogos compativeis com criptomoedas. Eleva a experiencia de jogo. A assistencia e eficiente e amigavel, sempre pronto para resolver. As transacoes sao confiaveis, as vezes mais rodadas gratis seriam um diferencial. No fim, PlayPIX Casino e essencial para jogadores para fas de cassino online ! Adicionalmente a interface e fluida e estilosa, instiga a prolongar a experiencia. Notavel tambem os torneios regulares para competicao, fortalece o senso de comunidade.
Aprender os detalhes|
simplelivinghub – Quality content with heart, feels like advice from a friend.
Fiquei impressionado com BETesporte Casino, proporciona uma aventura cheia de emocao. O catalogo e vibrante e diversificado, suportando jogos compativeis com criptomoedas. O bonus de boas-vindas e empolgante. O suporte ao cliente e excepcional, acessivel a qualquer hora. As transacoes sao confiaveis, no entanto mais apostas gratis seriam incriveis. Em sintese, BETesporte Casino vale uma aposta certa para fas de cassino online ! Acrescentando que o design e moderno e vibrante, tornando cada sessao mais competitiva. Um diferencial importante o programa VIP com niveis exclusivos, fortalece o senso de comunidade.
Saiba mais|
globalmarketinsight – Will definitely bookmark this one for future reference.
classyhomegoods – Impressed with the product variety and timely delivery.
smartbuytoday – Excellent value for money and overall experience, highly recommend.
trendandstyle – Trendy styles at great prices, found exactly what I needed.
ultimateprofitplan – Loved the actionable insights, really helped streamline my operations.
learnandtrade – Insightful lessons that helped me overcome operational challenges.
visionpartnersclub – Smooth browsing and secure payment options, very trustworthy site.
beste sportwetten seite
Feel free to surf to my blog online wettanbieter ohne oasis
yourtradingmentor – Fantastic mentorship tips and real-world trading help, highly recommend.
successfultradersclub – Will bookmark this site, it looks like a solid resource to revisit later.
bestforexstrategies – The layout is clean and the strategy descriptions are clear and helpful.
seoignite.click – On mobile it’s seamless and responsive; no weird layout issues.
nextleveltrading – Really well laid-out site, made complicated strategies feel clear and simple.
rankseed.click – I like how quickly the pages load and how smooth the transitions are.
Все о коттеджных посёлках https://cottagecommunity.ru фото, описание, стоимость участков и домов. Всё о покупке, строительстве и жизни за городом в одном месте. Полезная информация для покупателей и инвесторов.
futuregrowthteam – Fast shipping and excellent customer service, highly recommend shopping here.
strongfoundation – Found quite a few useful tools and insights today, well done.
globalmarketinsight – The site gave me ideas I hadn’t seen elsewhere, very valuable.
uniquedecorstore – Found some beautiful décor pieces here, really impressed with the selection.
quotenvergleich wettbasis
Also visit my site … wett Tipps prognosen
strongpartnershipnetwork – Easy to follow tips and strategies, really improved my approach.
wir wetten bonus code
My web site: Esport Wettseiten
everydaytrendshop – Smooth browsing and secure payment options, very trustworthy site.
rankseed.click – The navigation is intuitive, I found what I was looking for in a few clicks.
smartbuytoday – Loved discovering new items I didn’t know I needed, very fun experience.
Sou viciado no brilho de BR4Bet Casino, tem um ritmo de jogo que acende como uma tocha. Os jogos formam um clarao de entretenimento. incluindo jogos de mesa com um toque de brilho. O servico e confiavel como uma lanterna. garantindo suporte direto e sem escuridao. As transacoes sao simples como uma luz. de vez em quando mais giros gratis seriam brilhantes. Ao final, BR4Bet Casino promete uma diversao que e uma chama para os apaixonados por slots modernos! Adicionalmente o layout e vibrante como uma tocha. tornando cada sessao ainda mais brilhante.
cГіdigo promocional br4bet|
Ich liebe die Energie von PlayJango Casino, es bietet ein Casino-Abenteuer, das wie ein Regenbogen funkelt. Die Spielauswahl im Casino ist wie ein funkelnder Ozean, mit modernen Casino-Slots, die einen in ihren Bann ziehen. Der Casino-Service ist zuverlassig und strahlend, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein Komet, manchmal die Casino-Angebote konnten gro?zugiger sein. Alles in allem ist PlayJango Casino ein Online-Casino, das wie ein Orkan begeistert fur die, die mit Stil im Casino wetten! Zusatzlich das Casino-Design ist ein optisches Spektakel, das Casino-Erlebnis total elektrisiert.
playjango casino bonus code|
Estou completamente alucinado por SpeiCasino, e um cassino online que decola como um foguete espacial. As opcoes de jogo no cassino sao ricas e brilhantes como estrelas, com caca-niqueis de cassino modernos e estelares. O servico do cassino e confiavel e brilha como uma galaxia, respondendo mais rapido que uma explosao estelar. Os pagamentos do cassino sao lisos e blindados, as vezes mais bonus regulares no cassino seria intergalactico. Na real, SpeiCasino oferece uma experiencia de cassino que e puro brilho estelar para os astronautas do cassino! Alem disso o site do cassino e uma obra-prima de estilo estelar, adiciona um toque de brilho estelar ao cassino.
spei download apk|
Acho simplesmente harmonico JonBet Casino, e uma onda sonora de diversao que reverbera. As opcoes sao ricas e vibram como cordas. com caca-niqueis que vibram como harpas. O suporte e um reverb preciso. com ajuda que ressoa como um sino. O processo e claro e sem pausas. ocasionalmente mais recompensas fariam o coracao ecoar. Em resumo, JonBet Casino garante um jogo que ressoa como um sino para quem curte apostar com estilo harmonico! Por sinal o visual e uma explosao de sinos. criando uma experiencia de cassino harmonica.
como sacar bonus jonbet|
cuttingthered – Sharp branding, message delivers confidence and determination effectively.
backstage chat
freshfashionfinds – Helpful product descriptions and reviews, made decision-making easier today.
Estou completamente apaixonado por BacanaPlay Casino, tem uma vibe de jogo tao animada quanto uma bateria de escola de samba. Tem uma enxurrada de jogos de cassino irados, com caca-niqueis de cassino modernos e contagiantes. Os agentes do cassino sao rapidos como um passista na avenida, garantindo suporte de cassino direto e sem perder o ritmo. Os pagamentos do cassino sao lisos e blindados, de vez em quando mais recompensas no cassino seriam um diferencial festivo. No fim das contas, BacanaPlay Casino vale demais sambar nesse cassino para quem curte apostar com gingado no cassino! De lambuja a navegacao do cassino e facil como um passo de frevo, faz voce querer voltar ao cassino como num desfile sem fim.
melhores slots bacanaplay|
bs2best зеркало Неужели ты до сих пор не знаешь, что переворачивает мир даркнета? Blacksprut – это не просто название. Это новая эра анонимности, мгновенной скорости и железобетонной безопасности в сети. Загляни на bs2best.at – туда, где обсуждают то, о чём остальные предпочитают молчать в тряпочку. Тебе откроется доступ к информации, тщательно оберегаемой от посторонних глаз. Только для тех, кто понимает правила игры. Никаких следов, никаких компромиссов, только абсолютная конфиденциальность – это Blacksprut. Не упусти свой шанс стать первооткрывателем – bs2best.at уже распахнул свои двери для тебя. Хватит ли у тебя смелости взглянуть правде прямо в лицо?
modernvaluecorner – Found unique finds I hadn’t seen on other sites — big plus.
judiforcongress – Strong campaign site, message feels inspiring and presentation confident.
everydaytrendshop.bond – Just found this site, really enjoying their fresh daily updates.
shopwithsmile.cfd – Content is useful, helps me stay up-to-date with trends fast.
connectforprogress.cfd – Clean layout and smooth browsing, makes finding info simple.
investsmarttoday.bond – Site loads quickly and content feels relevant and fresh.
musionet – Will bookmark this for future use, seems like a good steady go-to.
Fiquei fascinado com PlayPIX Casino, sinto um pulsar selvagem. Ha uma explosao de jogos emocionantes, suportando jogos compativeis com criptomoedas. Fortalece seu saldo inicial. Os agentes respondem com rapidez, sempre pronto para resolver. Os saques sao rapidos como um raio, as vezes mais rodadas gratis seriam um diferencial. Em sintese, PlayPIX Casino e essencial para jogadores para fas de cassino online ! Tambem a plataforma e visualmente espetacular, adiciona um toque de conforto. Muito atrativo as opcoes variadas de apostas esportivas, oferece recompensas continuas.
Prosseguir a leitura|
Amo a energia de BETesporte Casino, e uma plataforma que vibra como um estadio em dia de final. A selecao de jogos e fenomenal, com slots modernos e tematicos. 100% ate R$600 + apostas gratis. O acompanhamento e impecavel, sempre pronto para entrar em campo. O processo e simples e direto, no entanto promocoes mais frequentes dariam um toque extra. Para finalizar, BETesporte Casino oferece uma experiencia inesquecivel para quem usa cripto para jogar ! Alem disso o site e veloz e envolvente, facilita uma imersao total. Um diferencial importante os pagamentos seguros em cripto, proporciona vantagens personalizadas.
Obter informações|
urbanstylehub – This site will definitely be on my list for future shopping trips.
dailytrendstore – Fast page loads and smooth navigation made my shopping experience easier.
musionet – Useful find for someone seeking resources in this area, recommended.
seoignite.click – On mobile it’s seamless and responsive; no weird layout issues.
winwithus.bond – Site loads quickly and content feels relevant and fresh.
learntradingtoday – Secure payment process and transparent information made me confident to explore.
dailytrendstore – Fashion and lifestyle trends galore, found a bunch of items I liked.
urbanstylehub – Great mix of everyday items and special-find pieces, perfect for gifts too.
winwithus.bond – Clean layout and smooth browsing, makes finding info simple.
trendandstyle.bond – I appreciate the variety, keeps discovering new useful ideas.
masterthemarket – Will bookmark this site, it looks like a solid resource to revisit later.
brightmarketplace – The product photos and descriptions were accurate which made choosing easy.
businesssuccesshub – Very clear and easy-to-follow content for advancing business skills.
tradingmasterclass – Navigation and course structure make it easy to stay on track.
trendandstyle – Found unique pieces not available elsewhere, great shopping experience.
rankflow.click – The pages load quickly, and the visuals are sharp—nice user experience.
connect live
rasecurities – Found some interesting finance articles here that gave me new ideas.
tradeandwin – Easy to navigate site and clear explanations for strategies I like.
Наша платформа https://probilets работает круглосуточно и не знает слова «перерыв». Бронировать и планировать можно где угодно: в поезде, на даче, в кафе или лежа на диване. Хотите купить билет, пока идёте по супермаркету? Просто достаньте телефон и оформите поездку. Нужно скорректировать планы, отменить или перенести билет? Это тоже можно сделать онлайн, без звонков и визитов.
financialgrowthplan – Will bookmark this site for future reference on growing finances wisely.
netmatrix.click – On mobile it’s flawless—everything adapts nicely and looks good.
fitproawardsuk – The vibe of recognition and community feels strong, great for networking.
brightmarketplace – This store has become one of my go-to places for online shopping.
businesssuccesshub – Will bookmark this site—it’s becoming a go-to for growth insights.
Hi there to all, it’s actually a nice for me to pay a visit this web site, it consists of valuable Information.
successfultradersclub – Will bookmark this site, it looks like a solid resource to revisit later.
modernwoodcases – Saw a unique design I hadn’t seen elsewhere, good for someone who wants something different.
imprintregistry – This will be a go-to site for verifying art provenance and title certificates.
masterthemarket – Found some fresh ideas for trading strategies I’ll try soon.
z9hl4.info – I just visited and the site feels sleek with a very modern clean layout.
https://byuro-perevodov213.ru/
markettrendalerts – Helpful visuals and clear phrasing made the alerts usable in real-time.
Hi antidetect is goood.
https://b-s2site.at
advancedtradingtools.cfd – The interface is clean, intuitive and makes trading much easier now.
brittanydominguez.shop – Visuals complement the text nicely; the design feels polished and thought-out.
nathanjones.shop – Navigation is smooth and intuitive, found what I needed in a few clicks.
z9hl4.info – I found several useful links already—definitely worth revisiting later.
maskchallengeusa – Clear purpose and bold message, layout supports awareness beautifully.
trustedleaderscircle.bond – Overall great impression, looking forward to exploring further materials here.
smarttradingmentor.bond – Content is engaging and paced well for beginners and intermediates.
creativegiftworld.bond – I appreciate the variety, keeps discovering new useful ideas.
urbanstylehub.cfd – Site loads quickly and content feels relevant and fresh.
dailytradingupdate.cfd – Found useful trading tips that I can apply in real sessions.
dailyessentialfinds.cfd – Regular discounts and updated inventory make this store a go-to favourite.
dailytrendstore.cfd – Found some really interesting pieces today, will check again.
fastgrowthsignal.cfd – The tone feels professional yet accessible, which is refreshing.
freshfashionfinds.cfd – Really useful content, helps me stay updated with trends fast.
forexsuccessguide.cfd – This platform has some of the best tips I’ve seen.
visionpartnersclub.bond – Love the design and easy navigation, very user-friendly experience.
bestdealcorner.cfd – Good shopping experience, checkout was smooth and straightforward for me.
Hmm is anyone else having problems with the images on this blog loading? I’m trying to determine if its a problem on my end or if it’s the blog. Any responses would be greatly appreciated.
https://inc-rediblestore.com/
Adoro demais o clima de DazardBet Casino, oferece uma experiencia de cassino que e fogo puro. A selecao de titulos do cassino e de outro mundo, com slots de cassino unicos e vibrantes. O atendimento ao cliente do cassino e fora da curva, acessivel por chat ou e-mail. Os saques no cassino sao rapidos como um foguete, mas queria mais promocoes de cassino que arrebentam. No geral, DazardBet Casino garante uma diversao de cassino fora de serie para os aventureiros do cassino! De bonus a navegacao do cassino e facil como brincar, torna o cassino uma curticao total.
dazardbet sovellus|
Ich bin suchtig nach Richard Casino, es bietet ein Casino-Abenteuer, das wie ein Thron funkelt. Die Spielauswahl im Casino ist wie ein koniglicher Schatz, inklusive eleganter Casino-Tischspiele. Der Casino-Support ist rund um die Uhr verfugbar, sorgt fur sofortigen Casino-Support, der beeindruckt. Casino-Zahlungen sind sicher und reibungslos, manchmal die Casino-Angebote konnten gro?zugiger sein. Am Ende ist Richard Casino ein Casino mit einem Spielspa?, der wie ein Thron funkelt fur Spieler, die auf majestatische Casino-Kicks stehen! Extra die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino auf ein konigliches Niveau hebt.
richard casino login australia|
https://shorturl.fm/UI3Gb
Ich bin total begeistert von King Billy Casino, es fuhlt sich an wie ein koniglicher Triumph. Die Spielauswahl im Casino ist wie ein koniglicher Schatz, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Das Casino-Team bietet Unterstutzung, die wie ein Zepter glanzt, sorgt fur sofortigen Casino-Support, der beeindruckt. Casino-Zahlungen sind sicher und reibungslos, trotzdem mehr Freispiele im Casino waren ein Kronungsmoment. Am Ende ist King Billy Casino ein Casino mit einem Spielspa?, der wie ein Kronungsfest funkelt fur Abenteurer im Casino! Nebenbei die Casino-Seite ist ein grafisches Meisterwerk, Lust macht, immer wieder ins Casino zuruckzukehren.
king billy casino games|
Acho simplesmente magico SpellWin Casino, e um cassino online que brilha como uma pocao encantada. O catalogo de jogos do cassino e um bau de encantos, incluindo jogos de mesa de cassino com um toque de magia. A equipe do cassino entrega um atendimento que e puro encantamento, respondendo mais rapido que um estalo magico. As transacoes do cassino sao simples como uma runa, de vez em quando queria mais promocoes de cassino que hipnotizam. No fim das contas, SpellWin Casino vale demais explorar esse cassino para os apaixonados por slots modernos de cassino! De bonus a interface do cassino e fluida e brilha como uma pocao reluzente, faz voce querer voltar ao cassino como num desejo concedido.
spellwin greece|
Нужна вывеска? неоновая вывеска спб логотипы, надписи, декор для кафе, офисов и дома. Индивидуальный дизайн, энергосберегающие материалы и эффектный свет в любом стиле.
Estou alucinado com BetorSpin Casino, tem uma vibe de jogo tao vibrante quanto uma supernova dancante. As opcoes de jogo no cassino sao ricas e brilhantes como estrelas, com caca-niqueis de cassino modernos e hipnotizantes. O servico do cassino e confiavel e brilha como uma galaxia, dando solucoes na hora e com precisao. Os saques no cassino sao velozes como uma viagem interestelar, mas mais bonus regulares no cassino seria intergalactico. Na real, BetorSpin Casino e o point perfeito pros fas de cassino para os amantes de cassinos online! Alem disso a interface do cassino e fluida e reluz como uma constelacao, torna a experiencia de cassino uma viagem espacial.
codigo promocional betorspin|
Fine way of describing, and fastidious post to
take information about my presentation focus, which i am
going to convey in institution of higher education.
https://bsmen.at
Нужен сайт? создание сайтов в москве под ключ с акцентом на конверсию: UX-исследование, дизайн-система, чистая вёрстка, CMS на выбор, подключение метрик и событий. Интернет-магазины, B2B-порталы, лендинги. SEO-структура, микроразметка, скорость 90+. Поддержка и развитие без скрытых расходов.
ultimateprofitplan.bond – The site gives me a vibe of real community bonding.
smartinvestorhub.cfd – Love the intuitive layout, makes exploring investment ideas very easy.
Estou totalmente fascinado por BETesporte Casino, sinto um rugido de emocao. A variedade de titulos e estonteante, com slots modernos e tematicos. Com uma oferta inicial para impulsionar. Os agentes respondem com agilidade, com suporte preciso e confiavel. Os saques sao rapidos como um drible, embora promocoes mais frequentes dariam um toque extra. Em sintese, BETesporte Casino e uma plataforma que domina o jogo para quem usa cripto para jogar ! Tambem a navegacao e intuitiva e envolvente, tornando cada sessao mais vibrante. Outro destaque os eventos comunitarios envolventes, que impulsiona o engajamento.
Descobrir agora|
Tenho um entusiasmo vibrante por PlayPIX Casino, leva a um universo de pura adrenalina. A variedade de titulos e estonteante, oferecendo jogos de mesa envolventes. Com uma oferta inicial para impulsionar. O suporte ao cliente e excepcional, garantindo atendimento de alto nivel. Os pagamentos sao seguros e fluidos, contudo ofertas mais generosas seriam bem-vindas. Para finalizar, PlayPIX Casino vale uma visita epica para amantes de emocoes fortes ! Alem disso a navegacao e intuitiva e envolvente, tornando cada sessao mais vibrante. Notavel tambem as opcoes variadas de apostas esportivas, assegura transacoes confiaveis.
Verificar isso|
shopandshine.cfd – Site loads quickly and feels reliable across different devices.
strongpartnershipnetwork.cfd – Fast-loading pages and mobile-friendly design make browsing seamless and convenient.
dailyessentialfinds.bond – Regular deals and discounts make this site a go-to.
Все о коттеджных посёлках https://cottagecommunity.ru как выбрать локацию, проверить инфраструктуру и коммуникации, понять цены и налоги. Сравнение ИЖС/ДНП, надёжность застройщиков, ипотека и субсидии, отзывы жителей, карта проектов и чек-листы для осмотра. Поможем принять взвешенное решение о покупке.
Строительство и ремонт https://repair-house.kiev.ua дома без ошибок: пошаговые инструкции, выбор материалов и подрядчиков, смета и экономия, фундамент, кровля, инженерия, утепление, отделка. Чек-листы, калькуляторы, типовые узлы, лайфхаки по срокам и качеству. Экономим бюджет — повышаем комфорт.
Ich bin total hingerissen von Richard Casino, es ist ein Online-Casino, das wie ein koniglicher Palast strahlt. Die Auswahl im Casino ist ein wahres Kronungsjuwel, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Der Casino-Kundenservice ist wie ein koniglicher Hofstaat, liefert klare und schnelle Losungen. Der Casino-Prozess ist klar und ohne Intrigen, manchmal wurde ich mir mehr Casino-Promos wunschen, die wie Juwelen glanzen. Insgesamt ist Richard Casino ein Online-Casino, das wie ein Palast strahlt fur Spieler, die auf majestatische Casino-Kicks stehen! Zusatzlich die Casino-Plattform hat einen Look, der wie ein Kronungsmantel glanzt, den Spielspa? im Casino auf ein konigliches Niveau hebt.
richard casino withdrawal|
Achou loucamente incrivel DazardBet Casino, e um cassino online que e pura adrenalina. O catalogo de jogos do cassino e colossal, com jogos de cassino perfeitos para criptomoedas. O suporte do cassino esta disponivel 24/7, garantindo suporte de cassino imediato e certeiro. Os pagamentos do cassino sao suaves e seguros, as vezes queria mais promocoes de cassino que arrebentam. No fim das contas, DazardBet Casino vale muito a pena explorar esse cassino para os aventureiros do cassino! Vale dizer tambem o design do cassino e uma explosao visual, faz voce querer voltar pro cassino sem parar.
dazardbet casino online|
Ich liebe die Pracht von King Billy Casino, es verstromt eine Spielstimmung, die wie ein Palast glanzt. Es gibt eine Flut an mitrei?enden Casino-Titeln, mit Live-Casino-Sessions, die wie ein Festbankett strahlen. Der Casino-Service ist zuverlassig und furstlich, sorgt fur sofortigen Casino-Support, der beeindruckt. Casino-Gewinne kommen wie ein Triumphzug, ab und zu mehr Freispiele im Casino waren ein Kronungsmoment. Insgesamt ist King Billy Casino ein Online-Casino, das wie ein Konigreich strahlt fur Fans von Online-Casinos! Zusatzlich die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino auf ein konigliches Niveau hebt.
king billy casino review|
Acho simplesmente magico SpellWin Casino, parece um portal mistico cheio de adrenalina. As opcoes de jogo no cassino sao ricas e hipnotizantes, oferecendo sessoes de cassino ao vivo que brilham como runas. A equipe do cassino entrega um atendimento que e puro encantamento, respondendo mais rapido que um estalo magico. Os ganhos do cassino chegam voando como uma vassoura encantada, as vezes mais giros gratis no cassino seria uma loucura magica. Na real, SpellWin Casino e o point perfeito pros fas de cassino para os apaixonados por slots modernos de cassino! E mais o site do cassino e uma obra-prima de estilo mistico, torna a experiencia de cassino um conto de fadas.
spellwin casino|
Estou completamente vidrado por BetorSpin Casino, tem uma vibe de jogo tao vibrante quanto uma supernova dancante. Tem uma chuva de meteoros de jogos de cassino irados, oferecendo sessoes de cassino ao vivo que reluzem como supernovas. O servico do cassino e confiavel e brilha como uma galaxia, respondendo mais rapido que uma explosao de raios gama. Os pagamentos do cassino sao lisos e blindados, porem mais giros gratis no cassino seria uma loucura estelar. No fim das contas, BetorSpin Casino oferece uma experiencia de cassino que e puro brilho cosmico para quem curte apostar com estilo estelar no cassino! Alem disso o design do cassino e um espetaculo visual intergalactico, adiciona um toque de brilho estelar ao cassino.
betorspin cassino|
Tenho um entusiasmo vibrante por PlayPIX Casino, leva a um universo de pura adrenalina. A variedade de titulos e estonteante, oferecendo jogos de mesa envolventes. Fortalece seu saldo inicial. A assistencia e eficiente e amigavel, garantindo atendimento de alto nivel. As transacoes sao confiaveis, de vez em quando promocoes mais frequentes dariam um toque extra. Em sintese, PlayPIX Casino vale uma visita epica para jogadores em busca de adrenalina ! Adicionalmente a navegacao e intuitiva e envolvente, aumenta o prazer de jogar. Um diferencial significativo os torneios regulares para competicao, proporciona vantagens personalizadas.
https://playpixcasino.pro/|
Tenho um entusiasmo vibrante por BETesporte Casino, me leva a um universo de apostas vibrante. O catalogo e vibrante e multifacetado, com sessoes ao vivo cheias de energia. Com uma oferta inicial para impulsionar. O acompanhamento e impecavel, com suporte preciso e confiavel. Os pagamentos sao seguros e fluidos, no entanto recompensas extras seriam um hat-trick. Em sintese, BETesporte Casino oferece uma experiencia inesquecivel para entusiastas de jogos modernos ! Acrescentando que a interface e fluida e energetica, facilita uma imersao total. Um diferencial importante o programa VIP com niveis exclusivos, que impulsiona o engajamento.
Ver os detalhes|
smarttradingmentor.cfd – User-friendly interface, clear structure, and nice variety of topics.
bs2best зеркало Неужели ты до сих пор не знаешь, что переворачивает мир даркнета? Blacksprut – это не просто название. Это новая эра анонимности, мгновенной скорости и железобетонной безопасности в сети. Загляни на bs2best.at – туда, где обсуждают то, о чём остальные предпочитают молчать в тряпочку. Тебе откроется доступ к информации, тщательно оберегаемой от посторонних глаз. Только для тех, кто понимает правила игры. Никаких следов, никаких компромиссов, только абсолютная конфиденциальность – это Blacksprut. Не упусти свой шанс стать первооткрывателем – bs2best.at уже распахнул свои двери для тебя. Хватит ли у тебя смелости взглянуть правде прямо в лицо?
Es ist wichtig, dass Spieler sich immer an vertrauenswürdige Anbieter halten, die durch Online Casino Testberichte bestätigt werden. Diese Berichte bieten eine detaillierte Analyse der Sicherheit und des Datenschutzes und helfen, die besten Online Casinos in Deutschland zu finden. Durch die Nutzung solcher Berichte können Spieler sicher und verantwortungsbewusst Glücksspiele genießen, wissend, dass ihre Daten geschützt und ihre Spiele fair sind. Online Online Casino 1xbet’de Aviator Crash Oyna Content Aviator Ne Kadar Adil Ve Gerçekten Rastgele? Aviator Demo Oyna Aviator 1xbet’in Demo Sürümünü… 3-in-1 Bonus 250% bis zu 2500 EUR + 250 FS – Einzahlung ab 20 EUR Wir haben für dich die besten Online Casinos ausführlich getestet und verglichen. Spiele bei unseren lizenzierten Partnern und profitiere von unschlagbaren Vorteilen.
https://aarihantoverseas.com/2025/10/16/betonred-casino-in-deutschland-alle-wichtigen-infos-und-erfahrungen/
In diesem Spiel sind keine Gewinnlinien auf normale Art und Weise vorhanden und Sie müssen ausschließlich den Einsatz pro Spielrunde festlegen. Diese starten mit 50 Cents und setzen sich mit 70 Cents, 1 €, 1,50 €, 2 €, 5 €, 10 €, 20 €, 50 € und 100 € fort. Mit der standardmäßigen Play N Go Autoplay-Funktion können Sie bis zu 50 Spielrunden automatisch spielen. Viele Casinos werben mit einem Bonus. Der Casino Bonus kann typischerweise auch für Spielautomaten verwendet werden. Dort getätigte Umsätze gelten dann auch für die Umsatzbedingungen. Es gibt verschiedene Bonusvarianten. Viele Casinos bieten einen Bonus in Höhe von zum Beispiel 100 % auf die erste Einzahlung. Andere Casinos bieten Neukunden Freispiele ohne Einzahlung. Diese können typischerweise nur an bestimmten Slots eingelöst werden.
smartfashionboutique.bond – Just found this boutique, stylish pieces and fresh fashion-forward collection.
https://shorturl.fm/yvZXE
successfultradersclub.shop – Feel confident this could become a valuable hub for traders.
partnershipgrowthhub.bond – Will bookmark this platform and revisit often for new insights.
everydayvaluehub.shop – Just discovered this shop, great everyday items at good value.
dreambuyworld.shop – I appreciate the variety of items and the curated collection.
learntradingtoday.cfd – Visuals and examples really helped me understand chart patterns clearly.
visionaryfutureteam.bond – Will bookmark this platform to revisit for future-oriented insights.
innovationdriventeam.bond – Resources seem practical and meaningful, helpful for real‐world innovation projects.
simplelivingstore.shop – Will bookmark this store for future minimalist décor and lifestyle pieces.
globalalliancenetwork.bond – Site loads quickly, mobile experience seems responsive and efficient too.
modernlifestylezone.shop – I appreciate the clear photos and product descriptions featured here.
dailyessentialstore.shop – Found exactly what I needed today, checkout process worked well.
smarttraderacademy.bond – Will bookmark this resource, looks like a solid trading guide.
investprofitgrow.cfd – Found practical tips today that I’ll definitely try implementing.
connectforgrowth.bond – Overall strong first impression; excited to explore what’s next here.
**prostadine**
prostadine is a next-generation prostate support formula designed to help maintain, restore, and enhance optimal male prostate performance.
powerofcollaboration.bond – The content tone is welcoming, professional, and easy to engage with.
budgetfriendlyfinds.shop – Just discovered this store, excellent budget-friendly finds and helpful deals.
creativefashionworld.shop – Will bookmark this shop for future trendy fashion and accessories.
backstage talk
sportwette vergleich
Here is my website – Wettanbieter Mit Paypal
blsp at Интересуешься, что происходит в тёмных уголках сети? Blacksprut — это не просто название, это гарантия анонимности, высокой скорости и надежности. Переходи на bs2best.at — там ты найдёшь то, о чём другие умалчивают. Тебе откроется доступ к информации, которую скрывают от большинства. Только для тех, кто понимает. Без компрометирующих следов. Без уступок. Только Blacksprut. Не упусти шанс узнать первым — bs2best.at уже готов открыть свои двери. Дерзнешь ли ты взглянуть правде в глаза?
Sou viciado em BETesporte Casino, oferece um thrill esportivo unico. O catalogo e rico e diversificado, com sessoes ao vivo imersivas. 100% ate R$600 + apostas gratis. Os agentes respondem com velocidade, com suporte preciso e rapido. Os pagamentos sao seguros e fluidos, de vez em quando promocoes mais frequentes seriam um plus. No geral, BETesporte Casino garante diversao a cada rodada para jogadores em busca de emocao ! Adicionalmente a interface e fluida e energetica, adiciona um toque de estrategia. Igualmente impressionante os eventos comunitarios envolventes, proporciona vantagens personalizadas.
Visitar hoje|
Tenho uma paixao ardente por PlayPIX Casino, proporciona uma aventura eletrizante. A selecao de jogos e fenomenal, com slots de design inovador. 100% ate €500 + 200 rodadas gratis. Os agentes respondem com rapidez, oferecendo respostas claras. Os saques sao rapidos como um raio, embora algumas rodadas gratis extras seriam incriveis. Em sintese, PlayPIX Casino vale uma visita epica para entusiastas de jogos modernos ! Tambem a interface e fluida e elegante, aumenta o prazer de jogar. Notavel tambem os eventos comunitarios envolventes, oferece recompensas continuas.
Saber mais|
pixelpush.click – The design feels modern and professional, really like the first impression.
sitefoundry.click – I’ve bookmarked this—feels like a website I’ll revisit for more insight.
boostengine.click – Pages load quickly and everything seems polished and professional.
webrevive.click – Pages load quickly and the site responsiveness is impressive on my device.
brandlift.click – Pages load smoothly and visuals look crisp and professional.
wettanbieter Sportwetten online mit bonus, https://sacosmeticsworld.shop/2025/10/20/tippspiel-plattform,
wettseiten bonus ohne einzahlung
Look into my web page wetten schweiz legal
Портал о строительстве домов https://doma-land.ru проекты и сметы, сравнение технологий (каркас, газобетон, кирпич, брус), фундамент и кровля, инженерия и утепление. Калькуляторы, чек-листы, тендер подрядчиков, рейтинги бригад, карта цен по регионам, готовые ведомости материалов и практика без ошибок.
sportwetten freebet ohne einzahlung
Also visit my webpage – kombiwette spiel abgebrochen
It is not my first time to pay a visit this web page, i am visiting this website dailly and obtain pleasant facts from
here daily.
globaltradingnetwork.cfd – Offers co-branded platforms, boosting brand visibility for partners.
Zagraj w sugar rush kasyno aby uzyskać licencję, co musisz zrobić. Zagraj w sugar rush kasyno nie musisz już tracić czasu na rejestrację, to grać. Po zarejestrowaniu się w Royal Vegas możesz grać w dowolną liczbę gier, z których możesz wybrać i sprawdzić. Sugar rush za darmo Dodatkowo, więc ta gra zaczyna się jako mały automat 4×4 grid z 5 lub więcej takimi samymi symbolami (lub symbolami Wild). Galeria Sławy Scheepjes Maxi Sugar Rush GMT Foodsafety Sp. z o.o.ul. Bierutowska 57-5951-317 Wrocław, Polska.REGON: 523354026 NIP: 8952247864 Firma Scheepjes została założona w Veenendaal w Holandii w 1855 roku. Obecnie siedziba Scheepjeswol znajduje się w Tynaarlo. Ta holenderska marka oferuje zróżnicowaną gamę przędz dziewiarskich i szydełkowych, w tym wełnianych i bawełnianych, dostępnych w różnych kompozycjach i kolorach. Na przestrzeni lat Scheepjes wprowadził do swojej kolekcji kilka nowych, oszałamiających włóczek. Niektóre z godnych uwagi dodatków to Scheepjeswol Stone Washed, Softfun, Linen Soft, Sun Kissed, Bloom i Color.
https://houeditechro1983.iamarrows.com/22bet-app-pl
Bonus Vox Casino Polska to nie tylko wyśmienity pakiet za rejestrację, ale również szereg dodatkowych opcji dla stałych użytkowników naszego kasyna. Cashback, darmowe spiny, magiczny bonus czy bonusy za depozyt to kwintesencja ofert promocyjnych. Z myślą o najbardziej aktywnych entuzjastach gier hazardowych online przygotowaliśmy także rozbudowany program lojalnościowy. W Vox Casino ramach klubu VIP możesz uzyskać niejeden bonus bez depozytu, dzięki któremu jeszcze bardziej uprzyjemnisz sobie rozrywkę w naszym kasynie. utworzone przez | wrz 8, 2021 | Bez kategorii Ksw 90: Typy, Kursy I Zakłady 20 01 2024 Content Ufc Combat Night: Typy, Zajecia Z (23 2009 Mateusz Gamrot… Konkretne warunki każdego z bonusów powitalnych w pakiecie rejestracyjnym znajdziesz w regulaminie akcji. Pamiętaj, że bonusy wymagają obrotu 40x przed odblokowaniem możliwości wypłaty zdobytych środków. Każdy kolejny etap akcji możesz aktywować po spełnieniu wytycznych obrotowych poprzedniego poziomu promocji.
**sugarmute**
sugarmute is a science-guided nutritional supplement created to help maintain balanced blood sugar while supporting steady energy and mental clarity.
pixelpush.click – Found useful content already; it looks like there’s some depth behind the site.
Квартира с отделкой https://новостройкивспб.рф экономия времени и предсказуемый бюджет. Фильтруем по планировкам, материалам, классу дома и акустике. Проверяем стандарт отделки, толщину стяжки, ровность стен, работу дверей/окон, скрытые коммуникации. Приёмка по дефект-листу, штрафы за просрочку.
quoten beim wetten
Also visit my page – wett tipps-heute (Kristina)
forexlearninghub.shop – Just discovered this hub, offers beginner-friendly forex trading resources and tools.
nextleveltrading.bond – Looking forward to more content, this site has potential.
sitefoundry.click – I’ve bookmarked this—feels like a website I’ll revisit for more insight.
trustandstrength.bond – Just checked out the site, looks interesting and promising.
protradinginsights.cfd – Highly recommend for traders looking to enhance their CFD strategies.
futuregrowthteam.bond – Solid resource for growth insights, thanks for sharing these tips.
classyhomegoods.bond – The product variety looks good, something here for different style preferences.
visionpartnersclub.cfd – Would love to see more visuals or case studies added soon.
https://purebeautyoutlet.bond/
profitgoalsystem.cfd – I’m planning to come back daily, content is growing nicely.
brandlift.click – The site appears clean and well-designed, makes a strong first impression.
Sou viciado em BETesporte Casino, e uma plataforma que pulsa com emocao atletica. O catalogo e rico e diversificado, com sessoes ao vivo imersivas. Fortalece seu saldo inicial. O suporte ao cliente e de elite, oferecendo respostas claras. Os saques sao rapidos como um sprint, no entanto ofertas mais generosas dariam um toque especial. Em sintese, BETesporte Casino garante diversao a cada rodada para fas de cassino online ! Vale destacar a interface e fluida e energetica, aumenta o prazer de apostar. Igualmente impressionante os torneios regulares para rivalidade, oferece recompensas continuas.
Ler os detalhes|
Sou viciado em PlayPIX Casino, sinto um ritmo alucinante. A selecao de jogos e fenomenal, suportando jogos compativeis com criptomoedas. Fortalece seu saldo inicial. O suporte ao cliente e estelar, garantindo um atendimento de qualidade. As transacoes sao confiaveis, embora algumas rodadas gratis extras seriam incriveis. Para concluir, PlayPIX Casino oferece uma experiencia inesquecivel para quem aposta com cripto ! Vale notar a navegacao e simples e envolvente, facilita uma imersao total. Um diferencial importante os eventos comunitarios envolventes, que impulsiona o engajamento.
Encontrar os detalhes|
Ich bin komplett hin und weg von SpinBetter Casino, es bietet einen einzigartigen Kick. Es gibt eine unglaubliche Auswahl an Spielen, mit dynamischen Tischspielen. Der Support ist 24/7 erreichbar, verfugbar rund um die Uhr. Die Gewinne kommen prompt, obwohl mehr abwechslungsreiche Boni waren super. In Kurze, SpinBetter Casino ist eine Plattform, die uberzeugt fur Casino-Liebhaber ! Nicht zu vergessen die Site ist schnell und stylish, gibt den Anreiz, langer zu bleiben. Ein weiterer Vorteil die Vielfalt an Zahlungsmethoden, die Vertrauen schaffen.
https://spinbettercasino.de/|
Sou louco pela energia de SupremaBet Casino, e um cassino online que ressoa como um trovao epico. A gama do cassino e simplesmente uma dinastia de delicias, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e majestoso, garantindo suporte de cassino direto e sem revoltas. Os pagamentos do cassino sao lisos e blindados, mas as ofertas do cassino podiam ser mais generosas. No geral, SupremaBet Casino oferece uma experiencia de cassino que e puro cetro para quem curte apostar com estilo imperial no cassino! Vale dizer tambem a plataforma do cassino brilha com um visual que e puro trono, torna a experiencia de cassino um reinado de prazer.
supremabet-pb|
Adoro a erupcao de BetPrimeiro Casino, e um cassino online que explode como um vulcao em furia. A gama do cassino e simplesmente uma explosao de delicias, incluindo jogos de mesa de cassino com um toque vulcanico. O servico do cassino e confiavel e ardente, garantindo suporte de cassino direto e sem cinzas. Os pagamentos do cassino sao lisos e blindados, mesmo assim mais recompensas no cassino seriam um diferencial incendiario. No fim das contas, BetPrimeiro Casino e o point perfeito pros fas de cassino para os vulcanologos do cassino! De bonus a plataforma do cassino brilha com um visual que e puro fogo, torna a experiencia de cassino uma erupcao inesquecivel.
betprimeiro giris|
Ich finde absolut irre Lapalingo Casino, es bietet ein Casino-Abenteuer, das wie ein Regenbogen funkelt. Die Spielauswahl im Casino ist wie ein Ozean voller Schatze, inklusive stilvoller Casino-Tischspiele. Die Casino-Mitarbeiter sind schnell wie ein Blitzstrahl, ist per Chat oder E-Mail erreichbar. Der Casino-Prozess ist klar und ohne Wellen, dennoch mehr Casino-Belohnungen waren ein funkelnder Gewinn. Kurz gesagt ist Lapalingo Casino eine Casino-Erfahrung, die wie ein Regenbogen glitzert fur die, die mit Stil im Casino wetten! Zusatzlich die Casino-Navigation ist kinderleicht wie ein Windhauch, einen Hauch von Zauber ins Casino bringt.
lapalingo bonuskoodit|
Sou viciado no role de DiceBet Casino, oferece uma aventura de cassino alucinante. As opcoes de jogo no cassino sao ricas e vibrantes, com jogos de cassino perfeitos para criptomoedas. O suporte do cassino ta sempre na ativa 24/7, garantindo suporte de cassino direto e na lata. Os pagamentos do cassino sao lisos e seguros, mesmo assim mais giros gratis no cassino seria uma loucura. No fim das contas, DiceBet Casino oferece uma experiencia de cassino que e puro gas para os amantes de cassinos online! De lambuja a plataforma do cassino detona com um look que e puro fogo, da um toque de classe braba ao cassino.
dicebet|
smartfashionboutique.cfd – Hoping they add more customer reviews so I can trust the fit and quality.
bestdealcorner.bond – User-friendly site, shopping experience feels smooth and very reliable.
online business
forexlearninghub.cfd – The design is clean, though I’d like to see more interactive tools added.
europameister wettquoten
Here is my webpage :: beste sportwetten seiten (Arimagh.generalresource.ne.jp)
smartforexacademy.bond – The layout is neat and tutorials appear well structured and useful.
SEO-продвижение помогает компаниям оставаться конкурентоспособными. Оптимизация улучшает позиции сайта, увеличивает конверсию и укрепляет доверие клиентов. Регулярная работа над контентом и аналитикой обеспечивает стабильный результат. Это основа успешного бизнеса в интернете. Узнайте больше о SEO https://qa.andytoan.vn/index.php?qa=242290&qa_1=seo-для-интернет-магазинов-как-увеличить-трафик
experttradingzone.bond – Found a few good insights here, will dig deeper tomorrow.
paysafecard wettanbieter
Here is my website sportwetten schweiz kiosk (Johanna)
Le code promotionnel n’est pas necessaire : entrez-le dans le champ « Code promo » et reclamez un bonus de bienvenue de 100% jusqu’a 130€, pour vos paris sportifs. Vous pouvez vous inscrire sur le site 1xBet ou via l’application mobile. Apres votre premier depot, vous activerez le code bonus. L’offre est valable pour toute l’annee 2026, et le bonus doit etre mise dans les 30 jours. Decouvrez plus d’informations sur le code promo via ce lien — https://ville-barentin.fr/wp-content/pgs/code-promo-bonus-1xbet.html.
sportwetten strategie surebets
Here is my web site; Vermittler von wetten bei pferderennen
Profitez d’une offre 1xBet : beneficiez un bonus de 100% pour l’inscription jusqu’a 130€. Augmentez le solde de vos fonds simplement en placant des paris avec un wager de cinq fois. Le code bonus est valide tout au long de l’annee 2026. Pour activer ce code, rechargez votre compte a partir de 1€. Vous pouvez trouver le code promo 1xbet sur ce lien — https://ville-barentin.fr/wp-content/pgs/code-promo-bonus-1xbet.html.
Estou alucinado com SupremaBet Casino, da uma energia de cassino que e puro dominio. A selecao de titulos do cassino e um trono de prazeres, oferecendo sessoes de cassino ao vivo que reluzem como cetros. O suporte do cassino ta sempre na ativa 24/7, com uma ajuda que brilha como uma coroa. Os pagamentos do cassino sao lisos e blindados, as vezes as ofertas do cassino podiam ser mais generosas. Na real, SupremaBet Casino garante uma diversao de cassino que e uma supremacia para os viciados em emocoes de cassino! E mais o site do cassino e uma obra-prima de estilo soberano, eleva a imersao no cassino a um nivel imperial.
supremabet.|
Sou louco pela energia de BetPrimeiro Casino, da uma energia de cassino que e puro magma. As opcoes de jogo no cassino sao ricas e escaldantes, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e ardente, respondendo mais rapido que uma explosao vulcanica. O processo do cassino e limpo e sem erupcoes, mas mais bonus regulares no cassino seria brabo. No geral, BetPrimeiro Casino oferece uma experiencia de cassino que e puro magma para os apaixonados por slots modernos de cassino! E mais o design do cassino e um espetaculo visual escaldante, adiciona um toque de fogo ao cassino.
betprimeiro apk|
regina4congress – The campaign feels genuine, site design clean and trustworthy.
Ich bin komplett hin und weg von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Es wartet eine Fulle spannender Optionen, mit Spielen, die fur Kryptos optimiert sind. Der Service ist von hoher Qualitat, immer parat zu assistieren. Die Zahlungen sind sicher und smooth, obwohl die Offers konnten gro?zugiger ausfallen. Zusammengefasst, SpinBetter Casino bietet unvergessliche Momente fur Online-Wetten-Fans ! Nicht zu vergessen die Navigation ist kinderleicht, fugt Magie hinzu. Besonders toll die mobilen Apps, die Flexibilitat bieten.
spinbettercasino.de|
Ich liebe den Zauber von Lapalingo Casino, es bietet ein Casino-Abenteuer, das wie ein Regenbogen funkelt. Die Auswahl im Casino ist ein echtes Spektakel, mit einzigartigen Casino-Slotmaschinen. Der Casino-Support ist rund um die Uhr verfugbar, liefert klare und schnelle Losungen. Casino-Gewinne kommen wie ein Sturm, dennoch mehr Casino-Belohnungen waren ein funkelnder Gewinn. Am Ende ist Lapalingo Casino ein Casino, das man nicht verpassen darf fur die, die mit Stil im Casino wetten! Extra die Casino-Navigation ist kinderleicht wie ein Windhauch, den Spielspa? im Casino in den Himmel hebt.
lapalingo offline|
Оптимизация сайта — это долгосрочная стратегия развития бизнеса в интернете. SEO помогает улучшить позиции в поисковой выдаче, увеличить органический трафик и повысить конверсию. Важно учитывать как технические аспекты, так и качество контента и работу с ссылочной массой. Регулярный анализ и корректировка стратегии позволяют удерживать лидерские позиции. SEO — это инвестиция, которая окупается многократно и делает компанию более конкурентоспособной. Подробнее о продвижении сайтов читайте http://www.annunciogratis.net/author/simonegandy
Adoro o clima insano de DiceBet Casino, oferece uma aventura de cassino alucinante. A selecao de titulos do cassino e um espetaculo a parte, oferecendo sessoes de cassino ao vivo que sao uma bomba. O servico do cassino e confiavel e de primeira, respondendo mais rapido que um raio. O processo do cassino e direto e sem treta, mesmo assim as ofertas do cassino podiam ser mais generosas. Resumindo, DiceBet Casino garante uma diversao de cassino que e um estouro para quem curte apostar com estilo no cassino! E mais a navegacao do cassino e facil como brincadeira, faz voce querer voltar pro cassino toda hora.
dicebet casino|
SEO-продвижение делает сайт заметным и эффективным инструментом для бизнеса. Работа с контентом, структурой страниц и техническими параметрами помогает улучшить позиции и повысить конверсию. Регулярная аналитика и корректировка стратегии обеспечивают стабильный рост. Такой подход делает сайт надёжным источником клиентов и способствует развитию компании. Читайте подробнее: https://cbaaacademy.com/2025/10/создание-и-seo-продвижение-сайтов-любой/
Поисковая оптимизация помогает повысить эффективность сайта без дополнительных затрат на рекламу. Этот инструмент обеспечивает органический трафик и укрепляет позиции компании в интернете. Важно регулярно анализировать результаты и корректировать стратегию. SEO даёт ощутимые результаты уже через несколько месяцев. Подробнее об этапах продвижения читайте https://wiki.internzone.net/index.php?title=Benutzer:MaxZ686892
forexstrategyguide.bond – The layout is clean and content appears beginner-friendly and approachable.
purebeautyoutlet.cfd – Would love to see more reviews from customers to build trust in the items.
emeryflowers – Beautiful aesthetic, every section blooms with creativity and emotion.
**glpro**
glpro is a natural dietary supplement designed to promote balanced blood sugar levels and curb sugar cravings.
beste australian open wettanbieter
Feel free to surf to my web page WettbüRo berlin in der nähe
experttradingzone.cfd – Just came across this site, seems like it has strong potential.
unitedvisionnetwork.bond – Browsed on my mobile and it looked responsive and smooth.
Offre promotionnelle 1xBet pour 2026 : profitez d’un bonus de bienvenue de 100% jusqu’a 130€ en vous inscrivant des maintenant. Une opportunite exceptionnelle pour les amateurs de paris sportifs, permettant d’effectuer des paris sans risque. N’attendez pas la fin de l’annee 2026 pour profiter de cette offre. Decouvrez le code promotionnel 1xBet via le lien fourni — Code Promo Cote D’ivoire. Le code promo 1xBet vous permet d’activer un bonus d’inscription 1xBet exclusif et de commencer a parier avec un avantage. Le code promotionnel 1xBet 2026 est valable pour les paris sportifs, le casino en ligne et les tours gratuits. Decouvrez des aujourd’hui le meilleur code promo 1xBet et profitez du bonus de bienvenue 1xBet sans depot initial.
Поисковая оптимизация помогает повысить эффективность сайта без дополнительных затрат на рекламу. Этот инструмент обеспечивает органический трафик и укрепляет позиции компании в интернете. Важно регулярно анализировать результаты и корректировать стратегию. SEO даёт ощутимые результаты уже через несколько месяцев. Подробнее об этапах продвижения читайте http://sbenc.co.kr/bbs/board.php?bo_table=free&wr_id=47281
Sou viciado em PlayPIX Casino, transmite uma energia vibrante. O catalogo e rico e multifacetado, suportando jogos compativeis com criptomoedas. 100% ate €500 + rodadas gratis. Os agentes respondem com agilidade, sempre pronto para resolver. Os ganhos chegam sem atraso, contudo mais rodadas gratis seriam um diferencial. No geral, PlayPIX Casino e essencial para jogadores para fas de cassino online ! Acrescentando que o design e moderno e vibrante, aumenta o prazer de jogar. Muito atrativo o programa VIP com niveis exclusivos, fortalece o senso de comunidade.
Ir para o site|
Amo a energia de BETesporte Casino, sinto um rugido de emocao. A variedade de titulos e impressionante, com slots modernos e tematicos. O bonus de boas-vindas e empolgante. O suporte ao cliente e excepcional, oferecendo respostas claras. Os ganhos chegam sem atraso, de vez em quando promocoes mais frequentes seriam um plus. Resumindo, BETesporte Casino vale uma aposta certa para entusiastas de jogos modernos ! Tambem a navegacao e intuitiva e rapida, adiciona um toque de estrategia. Outro destaque os eventos comunitarios envolventes, que impulsiona o engajamento.
Clicar para ver|
trustbridgealliance.bond – Site loads quickly and seems mobile-friendly — big plus for browsing on the go.
trustbridgealliance.cfd – Navigation is intuitive, found what I looked for within minutes.
Profitez d’un code promo unique sur 1xBet permettant a chaque nouveau joueur de beneficier jusqu’a 100€ de bonus sportif a hauteur de 100% en 2026. Le bonus sera ajoute a votre solde en fonction de votre premier depot, le depot minimum etant fixe a 1€. Pour eviter toute perte de bonus, veillez a copier soigneusement le code depuis la source et a le saisir dans le champ « code promo (si disponible) » lors de l’inscription, afin de preserver l’integrite de la combinaison. Le bonus de bienvenue n’est pas la seule promotion ou vous pouvez utiliser un code, d’autres combinaisons vous permettant d’obtenir des bonus supplementaires sont disponibles dans la section « Vitrine des codes promo ». Vous pouvez trouver le code promo 1xbet sur ce lien — Codes Promo Gratuits 1xbet. Grace au code promo 1xBet gratuit, obtenez un pari gratuit 1xBet ou un bonus sans depot 1xBet. Le code promotionnel 1xBet valide vous permet de beneficier d’un bonus de bienvenue 1xBet 2026 sur vos premiers paris. Essayez le code promo sport 1xBet pour miser sans risque et decouvrir la plateforme.
nighttoshineatlanta – Beautifully inspiring event site, visuals radiate joy and inclusion.
modernvaluecorner.bond – Would love to see more case-studies or examples added soon.
futuregrowthteam.cfd – Navigation is smooth, site works well on mobile which is a plus.
professionalgrowthhub.bond – I bookmarked it; looks like a resource worth revisiting regularly.
globalnetworkvision.bond – I found some content that piqued my interest — will explore more tonight.
buildstrongrelationship.bond – I wish there were more testimonials or success stories visible upfront.
https://purebeautyoutlet.bond/
classyhomegoods.bond – Navigation works nicely, felt comfortable exploring multiple collections quickly.
smarttradingmentor.bond – Just discovered this site, looks promising for trading guidance.
douglasand55 – Very polished design, strong visuals and clear professional tone.
businessleadersclub.bond – I found some insights here that caught my attention, will explore further.
buildsuccessnetwork.cfd – The tone is professional yet approachable—makes me feel comfortable exploring.
modernlifestylezone.shop – The product photos are clear, which helps evaluate choices nicely.
smarttechmukesh.xyz – Great first impression, smooth flow and a polished overall look.
buildtogethernow.bond – Wish there were more interactive tools, but what’s here already feels solid.
moj-kredyt.shop – Nice read today, tips feel practical and easy for beginners.
Промокоды казино 1xBet при регистрации 2026. На ресурсе 1хБет пользователи могут не только делать ставки на спорт и другие события из разных сфер, но и получать азартные ощущения в казино. Играть можно как с машинами, так и с реальными дилерами в разделе лайв. Чтобы привлекать как можно больше новых игроков и поддерживать интерес постоянных клиентов, на сайте 1хБет регулярно проходят акции и раздают бонусы. Самое щедрое вознаграждение могут получить новички, использовав промокод казино 1xBet. Указав его при регистрации, пользователь получит дополнительные денежные средства на первые несколько депозитов, которые сможет использовать для ставок в играх. Это сделать просто, если иметь 1xbet промокоды 2025. Правда, дается он при условии выполнения некоторых правил. 1xBet бонус при регистрации. Не совсем промокод, но вы все равно ставите не свои деньги, если пополните депозит, – 100% бонуса от внесенной суммы. Максимум указан в верхней части главной страницы официального сайта.
neighborsforrandy – Friendly community feel, layout conveys care and connection effectively.
2rss5ge.xyz – The overall design feels polished, gives a credible and fresh vibe.
cloudfiles.tech – Typography is comfortable and the spacing is well balanced—makes browsing quite pleasant.
ehajjumrahtours – Professional and serene, the layout reflects faith and reliability.
Воспользоваться промокодом 1xBet можно при регистрации в 1xBet. БК 1хБет дарит до 125% на первый депозит при помощи промокода 1xBet. Максимальная сумма бонуса по промокоду 1хБет достигает 32500 рублей. Предлагаем использовать рабочий промокод 1xBet на сегодня (бесплатно). Вводить промокод 1хБет следует строго при регистрации. Куда вводить промокод 1xBet при регистрации? Выбираете страну и валюту. В окно “Введите промокод” (при наличии), вводите рабочий промокод. Как активировать промокод 1хБет. Промокод 1xBet активируется при первом пополнении игрового счета. Однако, есть пару моментов: Необходимо заполнить все обязательные поля в личном кабинете. Как получить промокод 1xBet на сегодня? Бесплатные купоны для повышения бонуса посетителям сайта. Читайте подробнее про условия получения, проверку и правила ввода бонусного кода 1хБет на сайте букмекерской конторы. Еще один вид промокодов 1xBet.com позволяет совершать бесплатные ставки на события, а также использовать иные предложения в сфере азартных игр от БК. Получить их бесплатно от букмекерской конторы можно в качестве подарка на свой день рождения или в годовщину регистрации в 1xBet. промокод после регистрации 1xbet. Стандартный бонус на первый депозит для новых игроков составляет 100% от суммы первого пополнения.
Предложения от 1xBet также варьируются по виду. Часть бонусов предоставляются новичкам. При регистрации на 1xBet, активируйте код и оформите 100% бонус на первый депозит в размере 32500 рублей.Платформа 1xBet даёт возможность пользователям играть и делать ставки с использованием акционных предложений. Это повышает интерес к ставкам и гарантирует безопасность и комфорт игры.Промокод 2026 года можно найти на странице регистрации — https://vodazone.ru/image/pgs/index.php?1xbet-promokod.html.
ct2020highschoolgrads – Heartwarming initiative, celebrating graduates with positivity and pride.
saratogapolarexpressride – Magical and festive, captures the holiday spirit with great warmth.
Un Code promo 1xbet 2026 : recevez un bonus de 100% sur votre premier depot, jusqu’a 130 €. Jouez et placez vos paris facilement grace aux fonds bonus. Apres l’inscription, il est important de recharger votre compte. Avec un compte verifie, tous les fonds, bonus inclus, peuvent etre retires. Le code promo 1xbet est disponible via ce lien — Le Code Promo 1xbet. Le code promo 1xBet sans depot est valable pour les nouveaux utilisateurs en Afrique du Sud, au Gabon et en RDC. Ce code promotionnel 1xBet offre des bonus gratuits 1xBet et des tours gratuits 1xBet aujourd’hui. Utilisez le meilleur code promo pour 1xBet et recevez votre bonus d’inscription 1xBet en quelques clics.
luxnoe – Modern and stylish, this site exudes luxury and creative design.
Amo a energia de BETesporte Casino, leva a um universo de apostas dinamico. As opcoes sao amplas como um campo de futebol, com slots modernos e tematicos. Eleva a experiencia de jogo. Os agentes respondem com rapidez, sempre pronto para entrar em campo. Os pagamentos sao seguros e fluidos, as vezes recompensas extras seriam um hat-trick. Para finalizar, BETesporte Casino e uma plataforma que domina o campo para fas de cassino online ! Acrescentando que a plataforma e visualmente impactante, facilita uma imersao total. Notavel tambem as opcoes variadas de apostas esportivas, assegura transacoes confiaveis.
Verificar isso|
Estou totalmente fascinado por PlayPIX Casino, e uma plataforma que vibra com intensidade. As opcoes sao amplas como um festival, oferecendo jogos de mesa envolventes. Eleva a experiencia de jogo. A assistencia e eficiente e amigavel, acessivel a qualquer momento. As transacoes sao confiaveis, embora recompensas extras seriam eletrizantes. Resumindo, PlayPIX Casino garante diversao constante para amantes de emocoes fortes ! Acrescentando que o design e moderno e vibrante, tornando cada sessao mais vibrante. Muito atrativo os eventos comunitarios envolventes, fortalece o senso de comunidade.
Ver os detalhes|
karen4assembly – Clear and sincere campaign tone, content reflects leadership and integrity.
https://pushnews.com.ua/tsikavi-fakty-pro-pisok-utvorennia-vydy-ta-vykorystannia/
stageofnations – Culturally rich, visuals celebrate unity and vibrant heritage beautifully.
Ich finde absolut magisch Trickz Casino, es verstromt eine Spielstimmung, die wie ein magischer Zirkus leuchtet. Die Casino-Optionen sind vielfaltig und verzaubernd, mit einzigartigen Casino-Slotmaschinen. Die Casino-Mitarbeiter sind schnell wie ein Kaninchen aus dem Hut, antwortet blitzschnell wie ein magischer Funke. Auszahlungen im Casino sind schnell wie ein Zaubertrick, trotzdem wurde ich mir mehr Casino-Promos wunschen, die wie Zaubertranke wirken. Am Ende ist Trickz Casino eine Casino-Erfahrung, die wie ein Zaubertrick glanzt fur Fans moderner Casino-Slots! Extra die Casino-Oberflache ist flussig und funkelt wie ein Zauberstab, das Casino-Erlebnis total verhext.
trickz casino flashback|
Ich bin total begeistert von Lapalingo Casino, es pulsiert mit einer elektrisierenden Casino-Energie. Die Auswahl im Casino ist ein echtes Spektakel, inklusive stilvoller Casino-Tischspiele. Der Casino-Service ist zuverlassig und glanzend, ist per Chat oder E-Mail erreichbar. Casino-Zahlungen sind sicher und reibungslos, aber die Casino-Angebote konnten gro?zugiger sein. Am Ende ist Lapalingo Casino ein Casino mit einem Spielspa?, der wie ein Feuerwerk knallt fur die, die mit Stil im Casino wetten! Nebenbei die Casino-Navigation ist kinderleicht wie ein Windhauch, was jede Casino-Session noch aufregender macht.
lapalingo special 200|
Je suis totalement electrifie par Donbet Casino, c’est une deflagration de fun absolu. La gamme est une eruption de delices, avec des slots au design audacieux. L’assistance est precise comme un laser, repondant en un eclair. Les gains arrivent a une vitesse supersonique, parfois les offres pourraient etre plus volcaniques. Dans l’ensemble, Donbet Casino offre une experience aussi puissante qu’une eruption pour les joueurs en quete d’intensite ! De plus l’interface est fluide comme un torrent, amplifie l’immersion dans un tourbillon de fun.
donbet mini jeux avis|
Ich bin abhangig von SpinBetter Casino, es ist eine Erfahrung, die wie ein Wirbelsturm pulsiert. Der Katalog ist reichhaltig und variiert, mit Spielen, die fur Kryptos optimiert sind. Die Agenten sind blitzschnell, bietet klare Losungen. Die Transaktionen sind verlasslich, obwohl regelma?igere Aktionen waren toll. Alles in allem, SpinBetter Casino ist eine Plattform, die uberzeugt fur Casino-Liebhaber ! Zusatzlich die Navigation ist kinderleicht, gibt den Anreiz, langer zu bleiben. Besonders toll die Vielfalt an Zahlungsmethoden, die den Spa? verlangern.
https://spinbettercasino.de/|
**mitolyn**
mitolyn a nature-inspired supplement crafted to elevate metabolic activity and support sustainable weight management.
Ich finde es unglaublich toll Billy Billion Casino, es ist ganz ein Abenteuer voller Nervenkitzel. Der Katalog ist unglaublich umfangreich, mit immersiven Live-Casino-Sessions von Evolution Gaming. Das Team bietet schnelle und effektive Unterstutzung, ist 24/7 erreichbar. Auszahlungen sind super schnell, oft in 1 Stunde fur Kryptowahrungen, gelegentlich die Boni wie der 100%-Willkommensbonus bis 7500 € konnten ofter kommen. Kurz gesagt ist Billy Billion Casino eine au?ergewohnliche Plattform fur Online-Casino-Fans! Nicht zu vergessen die Navigation ist intuitiv auf der mobilen iOS/Android-App, einen Hauch von Eleganz hinzufugt.
billy billion promo code no deposit|
**vittaburn**
vittaburn is a liquid dietary supplement formulated to support healthy weight reduction by increasing metabolic rate, reducing hunger, and promoting fat loss.
**prodentim**
prodentim an advanced probiotic formulation designed to support exceptional oral hygiene while fortifying teeth and gums.
Le code promo est supprime : entrez-le dans le champ « Code promo » et reclamez un bonus de bienvenue de 100% jusqu’a 130€, pour vos paris sportifs. Vous pouvez vous inscrire sur le site 1xBet ou via l’application mobile. Apres votre premier depot, vous activerez le code bonus. L’offre est valable pour toute l’annee 2026, et le bonus doit etre mise dans les 30 jours. Vous pouvez trouver le code promo sur ce lien — Code Promo 1xbet 2026. Le code promo 1xBet casino offre des tours gratuits et un bonus de depot 1xBet pour les nouveaux joueurs. Avec le code promotionnel 1xBet pour nouveaux utilisateurs, recevez jusqu’a 130€ de bonus d’inscription 1xBet. Utilisez le code promo 1xBet aujourd’hui pour jouer au casino en ligne 1xBet et profiter de toutes les offres disponibles.
mastriano4congress – Direct and focused, campaign visuals match strong message delivery.
Вводите официальный промокод 1xBet при регистрации 2026 и получайте до 32500 тысяч рублей. Бонус-код помогает удвоить ваш первый банкролл. промокод на купон 1xbet. Бесплатным промокод может воспользоваться любой новый игрок букмекерской конторы! После того, как вы попадете на официальный сайт букмекера, в России он внесен в реестр запрещенных. Благодаря промокодам на сегодня и различным акциям, они начали захватывать сердца миллионов игроков. На протяжении 10 лет существования администрация регулярно совершенствовала уровень сервиса, и как итог — создана отличная контора, где игроки могут совершать ставки и получать выплаты без каких-либо проблем. Это сделать просто, если иметь промокод 1xBet на сегодня бесплатно. Правда, дается он при условии выполнения некоторых правил. 1xBet бонус при регистрации. Не совсем промокод, но вы все равно ставите не свои деньги, если пополните депозит, – 100% бонуса от внесенной суммы. Максимум указан в верхней части главной страницы официального сайта.
Девушки очень красивые и обаятельные, а массаж делается с профессионализмом и заботой. Вышел с чувством лёгкости. Крайне советую, шлюхи заказать Новосиб – https://sibirka.com/. Очень красиво и уютно, сервис на уровне.
Приветственные бонусы также отличаются по типу. Некоторые из них предлагаются новым клиентам. Регистрируясь на 1xBet, используйте промокод и получите 100% бонус на первый депозит на сумму до 32500 рублей.Компания 1xBet предлагает своим клиентам участвовать в спортивных ставках и казино с использованием акционных предложений. Это повышает интерес к играм и гарантирует максимальную безопасность игры.Актуальный промокод можно получить по этой ссылке: бесплатные игры 1xbet.
**zencortex**
zencortex contains only the natural ingredients that are effective in supporting incredible hearing naturally.
Profitez du code promo 1xbet 2026 : obtenez un bonus de bienvenue de 100% sur votre premier depot avec un bonus allant jusqu’a 130 €. Jouez et placez vos paris facilement grace aux fonds bonus. Une fois inscrit, n’oubliez pas de recharger votre compte. Si votre compte est verifie, vous pourrez retirer toutes les sommes d’argent, y compris les bonus. Vous pouvez trouver le code promo 1xbet sur ce lien — Code Promo 2026. Le code promo 1xBet sans depot est valable pour les nouveaux utilisateurs en Afrique du Sud, au Gabon et en RDC. Ce code promotionnel 1xBet offre des bonus gratuits 1xBet et des tours gratuits 1xBet aujourd’hui. Utilisez le meilleur code promo pour 1xBet et recevez votre bonus d’inscription 1xBet en quelques clics.
**synaptigen**
synaptigen is a next-generation brain support supplement that blends natural nootropics, adaptogens
**yu sleep**
yusleep is a gentle, nano-enhanced nightly blend designed to help you drift off quickly, stay asleep longer, and wake feeling clear.
Бонусное предложение активно до конца 2026 года. Фрибет – это бесплатные ставки на некоторое количество пари в букмекерской конторе 1xBet, которые выдается, если ввести промокод бесплатный в 1хбет, а затем – целиком заполнить анкету игрока в своем личном кабинете и подтвердить номер мобильного телефона. С помощью бесплатной ставки за 1xBet промокод вы можете делать ставки на любые виды спорта, однако учтите, что у 1xBet фрибета есть свои условия отыгрыша. Приветственный бонус 1хБет. Во время регистрации на 1xBet бетторы могут выбрать стартовый бонус – для ставок на спорт или для игры в казино. Промокоды 1xBet на сегодня. Не ошибемся, если скажем, что компания является одним из лидеров на рынке букмекерских услуг по количеству и разнообразию бонусных предложений. Белорусские бетторы могут воспользоваться всем их спектром. Промокод «1хБет» при регистрации дает право новым бетторам получит 100% бонус на первый депозит, но не более 200 BYN (бел. рублей). Например, при пополнении баланса на 100 BYN сверху клиент получает аналогичный бонус. Если же речь идет о промокодах, которые дают право на бесплатную ставку, то моментом активации следует считать время совершения ставки при помощи такого купона.
**nitric boost**
nitric boost is a dietary formula crafted to enhance vitality and promote overall well-being.
Почему считаются особенными промокоды букмекерской конторы 1xBet особенными? Что нужно знать о кодах, чтобы извлечь максимум преимуществ от их использования? И, наконец, на какие еще детали в системе бонусов этой конторы, на которые стоит обратить внимание, если вы планируете ставить с бонусами. Промокод на 1xBet (актуален в 2026 году, бонус 100%) можно найти по этой ссылке — http://www.medtronik.ru/images/pages/1hbet_2021_promokod_pri_registracii.html.
**glucore**
glucore is a nutritional supplement that is given to patients daily to assist in maintaining healthy blood sugar and metabolic rates.
**wildgut**
wildgutis a precision-crafted nutritional blend designed to nurture your dog’s digestive tract.
SEO-продвижение помогает бизнесу стать заметным в интернете и привлекать клиентов без постоянных расходов на рекламу. Благодаря оптимизации контента, структуры и технических параметров сайт становится удобнее для пользователей и поисковых систем. Этот процесс требует анализа и системного подхода, но результат оправдывает ожидания. Со временем ресурс укрепляет свои позиции и получает стабильный трафик. Подробнее о пользе SEO можно узнать http://wiki.fpvfinland.fi/Поисковая_Раскрутка_Сайтов_В_Яндексе_И_Гугле
Компания «СибЗТА» https://sibzta.su производит задвижки, клапаны и другую трубопроводную арматуру с 2014 года. Материалы: сталь, чугун, нержавейка. Прочные уплотнения, стандарты ГОСТ, индивидуальные решения под заказ, быстрая доставка и гарантия.
wetten bonus übersicht
Here is my homepage … euro wette (Velda)
https://muhomorus.ru/ В онлайн-магазине muhomorus можно приобрести мухоморы с доставкой в любой регион России. Привлекательные цены на экологичные продукты, разработанные для нивелирования тревожности, стресса, подавленности, хронической утомляемости и ослабления признаков ряда заболеваний. Мухоморы в сушеном виде не являются лекарственным средством, а классифицируются как парафармацевтика – альтернативное средство, используемое по личному желанию как дополнительное лечение. Сбор, просушка, продажа и покупка – не противоречат законодательству. В связи с этим, предлагаем приобрести микродозинг на законных основаниях.
Ich bin vollig verzaubert von Trickz Casino, es verstromt eine Spielstimmung, die wie ein magischer Zirkus leuchtet. Die Auswahl im Casino ist ein echtes Hexenwerk, inklusive stilvoller Casino-Tischspiele. Der Casino-Kundenservice ist wie ein magischer Assistent, liefert klare und schnelle Losungen. Casino-Zahlungen sind sicher und reibungslos, aber mehr regelma?ige Casino-Boni waren verhext. Zusammengefasst ist Trickz Casino ein Casino mit einem Spielspa?, der wie eine Illusion verblufft fur Fans moderner Casino-Slots! Nebenbei die Casino-Plattform hat einen Look, der wie ein magischer Zirkus leuchtet, einen Hauch von Zauberei ins Casino bringt.
trickz casino trustpilot|
J’ai un veritable engouement pour Donbet Casino, on dirait un ouragan de sensations fortes. La selection de jeux est un veritable raz-de-maree, avec des slots au design audacieux. Le support est disponible 24/7, garantissant un support d’une puissance rare. Les gains arrivent a une vitesse supersonique, parfois des bonus plus explosifs seraient geniaux. Au final, Donbet Casino est une plateforme qui fait trembler les sens pour les joueurs en quete d’intensite ! Par ailleurs l’interface est fluide comme un torrent, ajoute une touche de magie volcanique.
donbet no deposit bonus|
Ich bin komplett hin und weg von SpinBetter Casino, es liefert ein Abenteuer voller Energie. Das Angebot an Spielen ist phanomenal, mit aufregenden Sportwetten. Der Service ist von hoher Qualitat, bietet klare Losungen. Die Zahlungen sind sicher und smooth, dennoch regelma?igere Aktionen waren toll. Zum Ende, SpinBetter Casino bietet unvergessliche Momente fur Spieler auf der Suche nach Action ! Daruber hinaus die Plattform ist visuell ein Hit, erleichtert die gesamte Erfahrung. Besonders toll die Sicherheit der Daten, die Vertrauen schaffen.
https://spinbettercasino.de/|
Ich liebe den Zauber von Lapalingo Casino, es pulsiert mit einer elektrisierenden Casino-Energie. Die Casino-Optionen sind bunt und mitrei?end, mit Live-Casino-Sessions, die wie ein Gewitter krachen. Der Casino-Service ist zuverlassig und glanzend, liefert klare und schnelle Losungen. Casino-Zahlungen sind sicher und reibungslos, trotzdem die Casino-Angebote konnten gro?zugiger sein. Insgesamt ist Lapalingo Casino ein Casino mit einem Spielspa?, der wie ein Feuerwerk knallt fur Spieler, die auf elektrisierende Casino-Kicks stehen! Extra die Casino-Oberflache ist flussig und strahlt wie ein Nordlicht, einen Hauch von Zauber ins Casino bringt.
lapalingo server status|
urbanscale – It seems promising for urban/scale design topics; nice find today.
nextrend – If you’re looking for something fresh, this might be the space; just expect some unknowns.
inspirechangeandprogress – The site has a calm, reflective tone; it’s nice when you’re in a quiet mood.
discoveramazingstories – I stumbled upon some moving narratives here that really touched my heart.
buildyourownlegacy – Clean layout and content that invites reflection rather than hype.
Code promo sur 1xBet est unique et permet a chaque nouveau joueur de beneficier jusqu’a 100€ de bonus sportif a hauteur de 100% en 2026. Le bonus sera ajoute a votre solde en fonction de votre premier depot, le depot minimum etant fixe a 1€. Pour eviter toute perte de bonus, veillez a copier soigneusement le code depuis la source et a le saisir dans le champ « code promo (si disponible) » lors de l’inscription, afin de preserver l’integrite de la combinaison. D’autres promotions existent en plus du bonus de bienvenue, vous pouvez trouver d’autres offres dans la section « Vitrine des codes promo ». Consultez le lien pour plus d’informations sur les promotions disponibles — https://www.nuernberg-balkon.de/images/pgs/?le-code-promo-1xbet_bonus.html.
Ich schatze sehr Billy Billion Casino, es bietet ein Eintauchen in eine pulsierende Spielwelt. Der Katalog ist unglaublich umfangreich, mit klassischen Tischspielen wie Blackjack und Roulette. Das Team bietet schnelle und effektive Unterstutzung, ist 24/7 erreichbar. Gewinne kommen in Rekordzeit an, gelegentlich die Angebote konnten gro?zugiger sein. Insgesamt ist Billy Billion Casino eine au?ergewohnliche Plattform fur Fans von Nervenkitzel! Daruber hinaus das Design ist visuell ansprechend und einzigartig, einen Hauch von Eleganz hinzufugt.
more bang for your btc buck at billy billion crypto casino|
Remarkable! Its really awesome piece of writing, I have got much clear idea about from this article.
https://staffinggoals.com/
asteroid-insurance – Clever concept, design feels futuristic and sharp with humor.
buchmacher de
Stop by my website – Eigene wetten anbieten
adirondackfiddlers – Full of tradition, music passion shines through each element.
Heya just wanted to give you a quick heads up and let you know a few of the pictures aren’t loading properly. I’m not sure why but I think its a linking issue. I’ve tried it in two different browsers and both show the same outcome.
https://staffinggoals.com
thepathofselfgrowth – I liked the simplicity of the advice here, nothing too gimmicky.
shopminq – Trendy e-commerce look, product visuals are crisp and appealing.
Официальный промокод 1хБет при регистрации, только по нему ты получишь бонус в 32500 рублей, все остальные коды не действительные и не дают такой бонус. 1xBet предлагает сейчас 32500 рублей всем новым игрокам букмекерской конторы. как получить промокод от 1хбет. Отличительной особенностью букмекерской конторы 1xBet является возможность совершения ставок по промокодам, которые предоставляются бесплатно. Это позволяет новичку заработать деньги, не делая никаких вложений. Однако чтобы получить промокод на ставку и воспользоваться им, следует разобраться с некоторыми инструкциями. Бесплатные промокоды 1xBet при регистрации. Промокод 1xBet на сегодня актуален, бонус будет зачислен сразу после первого пополнения счета. Временные коды. Букмекерская контора 1xBet часто выступает спонсором при переводе популярных сериалов на русский язык. Рекламные вставки букмекера можно услышать перед началом многих сериалов. Часто в такой рекламе диктуется специальные промокод, дающий возможность беттерам рассчитывать на дополнительный бонус. Максимальный бонус при регистрации составляется 32500 рублей. Воспользоваться промокодом можно только при выполнении ряда условий: Доступно только для беттеров из России, Беларуси, Украины и Казахстана. Возврат игрока – от 18 лет.
benningtonareaartscouncil – Artistic and welcoming, site promotes community creativity wonderfully.
Промокод 1xBet — укажите его в графу «Промокод» при регистрации на сайте, депозитируйте свой аккаунт на сумму от 100 рублей и активируйте акцией в размере 100% (до 32 500 RUB).В личном кабинете перейдите в раздел «Мои бонусы» и отметьте вариант «Активировать промокод».Вставьте полученный промокод в специальное окно. Нажмите подтвердить и изучите подробности бонуса.Промокод 1xBet на 2026 год можно узнать по ссылке: халявные промокоды 1xbet.
Tenho um entusiasmo vibrante por PlayPIX Casino, sinto um pulsar selvagem. A selecao de jogos e fenomenal, com slots de design inovador. Fortalece seu saldo inicial. O acompanhamento e impecavel, acessivel a qualquer momento. Os saques sao rapidos como um raio, contudo mais rodadas gratis seriam um diferencial. Em sintese, PlayPIX Casino e essencial para jogadores para fas de cassino online ! Acrescentando que o design e moderno e vibrante, adiciona um toque de conforto. Muito atrativo os eventos comunitarios envolventes, oferece recompensas continuas.
Obter informações|
Fiquei impressionado com BETesporte Casino, proporciona uma aventura cheia de emocao. O catalogo e vibrante e diversificado, suportando jogos compativeis com criptomoedas. Fortalece seu saldo inicial. O servico esta disponivel 24/7, oferecendo respostas claras. Os pagamentos sao seguros e fluidos, as vezes promocoes mais frequentes dariam um toque extra. No fim, BETesporte Casino vale uma aposta certa para fas de cassino online ! Alem disso a navegacao e intuitiva e rapida, facilita uma imersao total. Um diferencial importante o programa VIP com niveis exclusivos, fortalece o senso de comunidade.
Ver o site|
https://www.medtronik.ru/ официальный сайт с полезной информацией о бонусах
Регистрация в 2026 году — бесплатный промокод 1xBet на сегодня. Часто задаваемые вопросы по регистрации и учетной записи у букмекера 1xBet. промокод на фрибет 1xbet. Разнообразие бонусных предложений от 1xBet — другие типы бонусов и промокодов для игроков. Промокод 1xBet на День Рождения. Фрибеты или бесплатные ставки. Тото-промокоды 1xBet. Промокоды 1xBet у блогеров. Система промокодов при регистрации позволяет новым игрокам букмекерской конторы 1xBet получать внушительные бонусные суммы к своему первому депозиту. Обратите внимание, что это не промокод на ставку, а именно на регистрацию. Рабочие промокоды 1хБет на сегодня: Вид бонуса. Размер бонуса.
http://medtronik.ru лучшие предложения для новых игроков и постоянных пользователей
homecovidtest – Informative and reliable, design prioritizes health clarity and accessibility.
Бонусный код 1xBet — укажите его в поле для промокода при регистрации, внесите свой игровой баланс на сумму от 100 рублей и заберите предложением в размере удвоения депозита (до 32 500?).В личном кабинете найдите раздел «Бонусы» и отметьте вариант «Ввести код».Пропишите полученный код в строку для промокода. Подтвердите ввод и изучите подробности бонуса.Промокод 1xBet на 2026 год можно найти по этой ссылке: промокод 1xbet бездепозитный бонус.
urbanmatrix – The site design is slick and I found some good ideas here.
createyourownpath – This site’s clarity helped me map out new goals in a fresh way.
charitiespt – Compassionate and community-driven, mission comes across with sincerity.
Profitez du code promo 1xbet 2026 : recevez un bonus de 100% sur votre premier depot, jusqu’a 130 €. Placez vos paris en toute plaisir en utilisant simplement les fonds bonus. Une fois inscrit, n’oubliez pas de recharger votre compte. Avec un compte verifie, tous les fonds, bonus inclus, peuvent etre retires. Vous pouvez trouver le code promo 1xbet sur ce lien — Code Promo Sur 1xbet. Le code promo 1xBet sans depot est valable pour les nouveaux utilisateurs en Afrique du Sud, au Gabon et en RDC. Ce code promotionnel 1xBet offre des bonus gratuits 1xBet et des tours gratuits 1xBet aujourd’hui. Utilisez le meilleur code promo pour 1xBet et recevez votre bonus d’inscription 1xBet en quelques clics.
nextrealm – Simple yet meaningful write-ups that match where I am right now.
fayettecountydrt – Purposeful and informative, organization’s vision feels transparent and clear.
beste online sportwetten
Also visit my homepage :: esc deutschland Buchmacher
larkfest2013 – Vibrant and nostalgic, visuals radiate energy and celebration.
где найти промокод для 1xBet узнайте надёжные источники получения действующих кодов и предложений
Profitez du code promo 1xbet 2026 : obtenez un bonus de bienvenue de 100% sur votre premier depot avec un bonus allant jusqu’a 130 €. Placez vos paris en toute plaisir en utilisant simplement les fonds bonus. Apres l’inscription, il est important de recharger votre compte. Si votre compte est verifie, vous pourrez retirer toutes les sommes d’argent, y compris les bonus. Le code promo 1xbet est disponible via ce lien — Le Code Promo 1xbet. Le code promo 1xBet sans depot est valable pour les nouveaux utilisateurs en Afrique du Sud, au Gabon et en RDC. Ce code promotionnel 1xBet offre des bonus gratuits 1xBet et des tours gratuits 1xBet aujourd’hui. Utilisez le meilleur code promo pour 1xBet et recevez votre bonus d’inscription 1xBet en quelques clics.
staymotivatedandfocused – This site’s tone is uplifting and honest, not full of hype.
мухомор купить В интернет-магазине muhomorus можно заказать мухоморы с доставкой по всей территории России. Мы предлагаем доступные цены на органические продукты, разработанные для борьбы с тревожностью, стрессом, депрессией, хронической усталостью и облегчения симптомов различных заболеваний. Высушенные мухоморы не являются лекарственным средством; они относятся к парафармацевтике, которая считается выборочным альтернативным средством, используемым каждым человеком в качестве адъювантной терапии. Сбор, сушка, продажа и приобретение абсолютно легальны. Поэтому мы приглашаем вас приобрести микродозы на законных основаниях.
keepgrowingwithus – Great resource when you need a gentle nudge to move forward.
findyourinnerdrive – I’m already using one idea from here in my daily routine and it’s helping.
learnandimproveeveryday – The articles are concise and full of practical ideas I could try right away.
goldnexus – The visuals caught my eye; curious to see more content behind this domain.
nextrend – It has a strong initial vibe; excited to see what direction it takes.
inspirechangeandprogress – I stumbled on a few interesting posts here that genuinely sparked fresh thinking.
https://www.medtronik.ru проверенные источники бонусных кодов и фрибетов
mckeetransition – Professional government tone, site design supports accessibility and progress.
moj-kredyt.shop – I bookmarked this article; straightforward advice without confusing jargon today.
shop-in.tech – On mobile the site performs well; everything’s responsive and aligned properly.
2rss5ge.xyz – The color palette works nicely, soft on the eyes and cohesive.
cloudfiles.tech – I like how quickly the pages load, giving a very user-friendly initial experience.
findsolutionsfast – Will definitely come back here when I need to troubleshoot something fast.
holyspiritschooleg – Educational yet warm, design and content reflect care and faith.
strategie Wetten dass quote (http://WWW.Cranefarmstorage.com)
Промокод 1xBet на сегодня. Промокод на 2026-2026. На официальном сайте букмекерской конторы 1xBet появилась опция, которая позволяет “бесплатно” ознакомиться с функционалом сайта и при удачном стечении обстоятельств еще и выиграть некую сумму денежных средств. Теперь это стало доступно по специальному промокоду 1хБет. Он дает возможность получить до 32500? (100$). Актуальные промокоды 1xBet на сегодня. Рабочие промокоды 1xBet в 2026 Все промокоды для 1хБет бесплатно: при регистрации, на ставку (купон), на бонус, на сегодня. 1xBet — одна из самых известных компаний в сфере беттинга. Свою популярность контора заработала во многом благодаря большому количеству специальных предложений. Так, к примеру, каждый пользователь может воспользоваться одним из действующих промокодов 1xBet на сегодня бесплатно. Ознакомиться с их полным перечнем можно в данной статье.
georgewillwashpost – Clean layout, solid typography, content radiates intellect and authority.
Aw, this was a very nice post. Spending some time and actual effort to produce a top notch article… but what can I say… I hesitate a lot and don’t manage to get anything done.
https://easystaffingmd.com/
промокод 1xbet получить. Пользователи при регистрации или позже могут воспользоваться промокодами для получения различных бонусов от букмекерской конторы. Найти эти коды можно на различных тематических сайтах, а также на рабочем зеркале. 1xBet предлагает несколько способов регистрации на рабочем зеркале сайта. Компания внимательно относится к новым клиентам, поэтому предполагает многоуровневую систему защиты от того, чтобы дети не смогли заключать пари. согласно международному праву, наказание за это нарушение – штраф и отзыв лицензии. Регистрация в 1 клик. Так называется ускоренный процесс создания учетной записи. Актуальные промокоды на 1xBet бесплатно можно получить: На нашем портале. На сайтах интернет-ресурсов партнёров букмекерской конторы или различных СМИ. Любой желающий может достаточно просто найти промокод 1xBet на сегодня бесплатно. Бонусы – достойные, а условия их получения – реальные и осуществимые. А в некоторых случаях вообще ничего делать не надо.
Акционный код 1xBet — активируйте его в специальное поле при регистрации, депозитируйте свой аккаунт на сумму от 100? и заберите акцией в размере 100 процентов (до 32 500?).В профиле найдите раздел «Акции» и отметьте вариант «Использовать промокод».Вставьте полученный код в нужное поле. Нажмите подтвердить и ознакомьтесь с условиями использования.Рабочий код 1xBet 2026 можно взять по ссылке: промокоды на баллы 1xbet.
lcbclosure – Focused and informative, the message feels urgent and clearly communicated.
mayceformayor – Campaign feels strong and grounded, visuals emphasize trust and service.
http://www.medtronik.ru сайт для тех, кто хочет получить дополнительные преимущества
For latest information you have to pay a visit the web and on internet I found this site as a best website for most recent updates.
https://easystaffingmd.com/
http://www.medtronik.ru получите максимум выгоды при старте игры
shopforhappiness.shop – Wide variety of categories, always discover new and useful items.
Profitez d’un code promo unique sur 1xBet permettant a chaque nouveau joueur de beneficier jusqu’a 100€ de bonus sportif a hauteur de 100% en 2026. Ce bonus est credite sur votre solde de jeu en fonction du montant de votre premier depot, le depot minimum etant fixe a 1€. Assurez-vous de suivre correctement les instructions lors de l’inscription pour profiter du bonus, afin de preserver l’integrite de la combinaison. Le bonus de bienvenue n’est pas la seule promotion ou vous pouvez utiliser un code, d’autres combinaisons vous permettant d’obtenir des bonus supplementaires sont disponibles dans la section « Vitrine des codes promo ». Consultez le lien pour plus d’informations sur les promotions disponibles — https://www.freie-waehler-werdau.de/wp-content/pgs/le-code-promo-1xbet_bonus.html.
Если вы хотите получить бонусов от платформы 1xBet, нужно выполнить несколько требований, однако промокоды позволяют упростить процесс.Бонусные предложения, доступных новым клиентам через промокоды 1xBet, варьируются, но даже минимальный бонус способен существенно повысить игровой потенциал клиента.Используйте промокод, чтобы получить увеличенный 100% бонус в 2026 году.Промокод 1xBet доступен по этой ссылке — http://www.medtronik.ru/images/pages/1hbet_2021_promokod_pri_registracii.html.
masonchallengeradaptivefields – Inspirational cause, presentation is heartfelt and full of purpose.
Je trouve absolument brulant VBet Casino, ca pulse avec une energie de casino digne d’un cratere. Le repertoire du casino est un magma de divertissement, comprenant des jeux de casino adaptes aux cryptomonnaies. Le support du casino est disponible 24/7, offrant des solutions claires et instantanees. Les paiements du casino sont securises et fluides, par moments j’aimerais plus de promotions de casino qui envoient du feu. Pour resumer, VBet Casino offre une experience de casino ardente pour les passionnes de casinos en ligne ! En plus le design du casino est un spectacle visuel brulant, amplifie l’immersion totale dans le casino.
casino en ligne vbet|
Ich liebe den Wahnsinn von DrueGlueck Casino, es bietet eine krasse Spielerfahrung. Der Katalog des Casinos ist der Wahnsinn, mit Casino-Spielen, die fur Kryptos optimiert sind. Das Casino-Team bietet erstklassige Unterstutzung, sorgt fur sofortigen Casino-Support. Casino-Gewinne kommen wie der Blitz, aber mehr regelma?ige Casino-Boni waren cool. Zusammengefasst ist DrueGlueck Casino ein Muss fur Casino-Fans fur Spieler, die auf Casino-Kicks stehen! Ubrigens die Casino-Oberflache ist flussig und mega cool, den Spielspa? im Casino maximiert.
casino drueckglueck|
Ich bin suchtig nach Lowen Play Casino, es pulsiert mit einer unbezahmbaren Casino-Energie. Die Spielauswahl im Casino ist wie eine wilde Horde, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Der Casino-Service ist zuverlassig und machtig, mit Hilfe, die wie ein Brullen wirkt. Der Casino-Prozess ist klar und ohne Fallen, dennoch mehr Freispiele im Casino waren ein wilder Triumph. Alles in allem ist Lowen Play Casino ein Casino, das man nicht verpassen darf fur Fans moderner Casino-Slots! Nebenbei die Casino-Plattform hat einen Look, der wie eine Savanne funkelt, einen Hauch von Abenteuer ins Casino bringt.
löwen play safari holding gmbh|
Ich habe einen totalen Hang zu SpinBetter Casino, es erzeugt eine Spielenergie, die fesselt. Es gibt eine unglaubliche Auswahl an Spielen, mit dynamischen Tischspielen. Der Support ist 24/7 erreichbar, garantiert top Hilfe. Die Zahlungen sind sicher und smooth, gelegentlich mehr Rewards waren ein Plus. Global gesehen, SpinBetter Casino ist ein Muss fur alle Gamer fur Krypto-Enthusiasten ! Zusatzlich die Navigation ist kinderleicht, verstarkt die Immersion. Hervorzuheben ist die Community-Events, die den Einstieg erleichtern.
spinbettercasino.de|
nextrend – If you’re exploring new sites, this could be one to watch as it develops.
Galera, quero deixar registrado sobre o Bingoemcasa porque me ganhou de verdade. O site tem um ambiente divertido que lembra um barzinho cheio de risadas. As salas de bingo sao com muita interacao, e ainda testei blackjack e poker tambem, todos vieram com graficos bonitos. O atendimento no chat foi eficiente demais, o que ja me deixou tranquilo. As retiradas foram eficientes de verdade, inclusive testei PIX e funcionou perfeito. Se pudesse apontar algo, diria que gostaria de ver mais brindes, mas nada que estrague a experiencia. Pra concluir, o Bingoemcasa e divertido de verdade. Ja me sinto parte da comunidade
bingoemcasa site|
Un Code promo 1xbet 2026 : obtenez un bonus de bienvenue de 100% sur votre premier depot avec un bonus allant jusqu’a 130 €. Placez vos paris en toute plaisir en utilisant simplement les fonds bonus. Une fois inscrit, n’oubliez pas de recharger votre compte. Si votre compte est verifie, vous pourrez retirer toutes les sommes d’argent, y compris les bonus. Le code promo 1xbet est disponible via ce lien — https://fgvjr.com/pgs/code_promo_163.html.
joinourcreativeworld.shop – Excellent selection of products, always find what I need here.
peoplesprotectiveequipment – Practical and safety-focused, design feels direct and trustworthy.
createandgrow – If you end up using it, proceed with typical safeguards (payment method, guarantee, etc.).
buildyourdreamtoday.shop – Great inspiration, encourages me to take action every single day.
exploreopportunitiesnow.shop – Great deals and fast shipping, very satisfied with my purchases.
**breathe**
breathe is a plant-powered tincture crafted to promote lung performance and enhance your breathing quality.
startsomethinggreat.shop – Fast shipping and excellent customer service, highly recommend.
letthemplaymn – Passionate and purposeful, the site speaks strongly for youth engagement.
keepgrowingforward.shop – Highly recommend for anyone looking to improve and stay productive.
teamtadros – The mission feels bold, visuals highlight unity and determination.
http://medtronik.ru актуальные инструкции по активации бонусов
https://shorturl.fm/Jn05Y
becreativeeveryday – It’s refreshing to find a creative site that isn’t full of pressure or perfection.
discoverhiddenpotential – I’ll definitely come back here and share this with friends who might benefit too.
keepgrowingwithus – The layout is clean and I quickly found what I was looking for.
Fiquei impressionado com PlayPIX Casino, sinto um ritmo alucinante. A variedade de titulos e deslumbrante, com slots de design inovador. Fortalece seu saldo inicial. Os agentes respondem com rapidez, oferecendo respostas claras. Os ganhos chegam sem demora, as vezes recompensas adicionais seriam festivas. Em resumo, PlayPIX Casino oferece uma experiencia inesquecivel para fas de cassino online ! Tambem o design e moderno e vibrante, tornando cada sessao mais vibrante. Outro destaque os eventos comunitarios envolventes, assegura transacoes confiaveis.
Obter informações|
Fiquei impressionado com BETesporte Casino, transporta para um mundo de apostas vibrante. A variedade de titulos e impressionante, incluindo apostas esportivas palpitantes. Com uma oferta inicial para impulsionar. O servico esta disponivel 24/7, acessivel a qualquer hora. Os saques sao rapidos como um sprint, no entanto bonus mais variados seriam um gol. Para finalizar, BETesporte Casino vale uma aposta certa para entusiastas de jogos modernos ! Alem disso o site e veloz e envolvente, adiciona um toque de estrategia. Notavel tambem os torneios regulares para rivalidade, proporciona vantagens personalizadas.
Descobrir|
rodarodaku.xyz – On mobile it adapts perfectly, everything aligned and easy to read.
kkgg1.xyz – Everything loads quickly, giving a smooth user experience overall.
bestdealsforlife.shop – Secure checkout process, felt confident shopping here.
xxau.xyz – Smooth scrolling and nice formatting made reading enjoyable.
exodusalliance – Empowering theme, site feels hopeful and mission-driven throughout.
oscarthegaydog – Whimsical and delightful, brand personality shines through humor and charm.
Абсолютно бесплатный промокод 1xBet. На сегодня контора предлагает всем новичкам воспользоваться не только приветственным бонусом, но и получить дополнительные преференции. Эти льготы игрок получает в том случае, если внимательно отнесётся к процедуре регистрации на сайте. промокод в 1хбет где взять. 1xBet – один из самых узнаваемых букмекерских брендов в стране. Следовательно, именно эта компания захватила сердца наибольшего количества игроков. Компания была основана до внесения поправок в закон об азартных играх и оставалась лидером среди букмекерских контор на нашем рынке в правовой реальности. Уже один этот факт должен что-то указывать, так как многие клиенты с удовольствием возвращаются к игре в 1xBet. 1xBet – промокод на 32500р. Свежие промокоды 1xBet Все купоны и скидки букмекера Получи бонус 32500 ? Делай ставки на спорт.
Wettbüro anbieter dresden neustadt
wette italien österreich
my webpage; value wetten Strategie (http://Www.biblianacestach.Sk)
daybirdsyr – Energetic vibe, visuals and tone reflect creativity and modern living.
lifestyleinspirationhub.shop – Prompt customer service, resolved my issue quickly and efficiently.
1xBet промокод на сегодня 2026. Чтобы удовлетворить потребности бетторов и сделать процесс ставок максимально разнообразным нередко букмекерские конторы пытаются увеличить свой функционал, путем добавления специальных функций и предложений. Одним из лидеров среди популярных букмекеров на постсоветском пространстве по своим функциональным возможностям является 1хБет. Ввод промокоды на деньги 1хбет позволяет получить увеличенную сумму бонуса. Для этого достаточно после создания аккаунта внести первый депозит (максимальная сумма бонусного начисления составляет 32500 рублей). Можно использовать любой платёжный метод. Абсолютно бесплатный промокод 1xBet. На сегодня контора предлагает всем новичкам воспользоваться не только приветственным бонусом, но и получить дополнительные преференции. Эти льготы игрок получает в том случае, если внимательно отнесётся к процедуре регистрации на сайте. Ведь не все новички обращают внимание или понимают, о каких выгодах идёт речь, когда видят необязательное для заполнения поле «Введите промокод (при наличии)», находящееся в самом низу регистрационной формы. Оно есть при трёх способах получения аккаунта из четырёх возможных («В 1 клик», «По номеру телефона», «По e-mail»). А игнорировать его – это потерять дополнительные выгоды.
supportsros – Compassionate tone, clear visuals support their advocacy with sincerity.
Profitez d’un code promo unique sur 1xBet permettant a chaque nouveau joueur de beneficier jusqu’a 100€ de bonus sportif a hauteur de 100% en 2026. Ce bonus est credite sur votre solde de jeu en fonction du montant de votre premier depot, le depot minimum etant fixe a 1€. Assurez-vous de suivre correctement les instructions lors de l’inscription pour profiter du bonus, afin de preserver l’integrite de la combinaison. D’autres promotions existent en plus du bonus de bienvenue, vous pouvez trouver d’autres offres dans la section « Vitrine des codes promo ». Consultez le lien pour plus d’informations sur les promotions disponibles — Code Promo 1xbet Congo. Grace au code promo 1xBet gratuit, obtenez un pari gratuit 1xBet ou un bonus sans depot 1xBet. Le code promotionnel 1xBet valide vous permet de beneficier d’un bonus de bienvenue 1xBet 2026 sur vos premiers paris. Essayez le code promo sport 1xBet pour miser sans risque et decouvrir la plateforme.
Бонусный код 1xBet — укажите его в поле для промокода при открытии счета, пополните свой игровой баланс на сумму от 100? и заберите акцией в размере 100% (до 32 500?).В профиле найдите раздел «Акции» и выберите вариант «Использовать промокод».Укажите полученный код в нужное поле. Подтвердите ввод и прочитайте правила бонуса.Рабочий код 1xBet 2026 можно найти по этой ссылке: 1xbet как пользоваться промокодом.
shopwithconfidence.shop – Great variety of items, found exactly what I needed quickly.
Je suis accro a VBet Casino, on dirait une eruption de plaisirs incandescents. La selection du casino est une explosion de plaisirs, avec des machines a sous de casino modernes et incandescentes. Le support du casino est disponible 24/7, assurant un support de casino immediat et incandescent. Le processus du casino est transparent et sans cendres, parfois des bonus de casino plus frequents seraient brulants. En somme, VBet Casino est une pepite pour les fans de casino pour les joueurs qui aiment parier avec panache au casino ! Par ailleurs le design du casino est un spectacle visuel brulant, ajoute une touche de feu au casino.
vbet бездепозитный промокод|
Ich bin suchtig nach Lowen Play Casino, es verstromt eine Spielstimmung, die wie eine Savanne tobt. Der Katalog des Casinos ist ein Dschungel voller Nervenkitzel, mit einzigartigen Casino-Slotmaschinen. Die Casino-Mitarbeiter sind schnell wie ein Gepard, ist per Chat oder E-Mail erreichbar. Casino-Zahlungen sind sicher und reibungslos, manchmal wurde ich mir mehr Casino-Promos wunschen, die wie ein Feuer lodern. Insgesamt ist Lowen Play Casino ein Online-Casino, das die Savanne beherrscht fur Spieler, die auf wilde Casino-Kicks stehen! Und au?erdem die Casino-Seite ist ein grafisches Meisterwerk, was jede Casino-Session noch wilder macht.
löwen play bremen|
Ich liebe den Wahnsinn von DrueGlueck Casino, es hat eine durchgeknallte Casino-Energie. Die Casino-Optionen sind super vielfaltig, mit einzigartigen Casino-Slotmaschinen. Der Casino-Kundenservice ist der Hammer, liefert klare und schnelle Losungen. Auszahlungen im Casino sind blitzschnell, trotzdem mehr Casino-Belohnungen waren der Hit. Insgesamt ist DrueGlueck Casino ein Casino, das man nicht verpassen darf fur Fans moderner Casino-Slots! Nebenbei die Casino-Plattform hat einen krassen Look, den Spielspa? im Casino maximiert.
drueckglueck login|
https://medtronik.ru лучшие способы активировать бонусы и фрибеты
Code promo sur 1xBet est unique et permet a chaque nouveau joueur de beneficier jusqu’a 100€ de bonus sportif a hauteur de 100% en 2026. Le bonus sera ajoute a votre solde en fonction de votre premier depot, le depot minimum etant fixe a 1€. Pour eviter toute perte de bonus, veillez a copier soigneusement le code depuis la source et a le saisir dans le champ « code promo (si disponible) » lors de l’inscription, afin de preserver l’integrite de la combinaison. D’autres promotions existent en plus du bonus de bienvenue, vous pouvez trouver d’autres offres dans la section « Vitrine des codes promo ». Vous pouvez trouver le code promo 1xbet sur ce lien — Code Promo De Tours Gratuits 1xbet Aujourd’hui. Grace au code promo 1xBet gratuit, obtenez un pari gratuit 1xBet ou un bonus sans depot 1xBet. Le code promotionnel 1xBet valide vous permet de beneficier d’un bonus de bienvenue 1xBet 2026 sur vos premiers paris. Essayez le code promo sport 1xBet pour miser sans risque et decouvrir la plateforme.
justinhicksformissouri – Strong campaign message, design feels authentic and community-focused.
http://www.medtronik.ru подробные условия участия в бонусных программах
nyscanalconference – Informative and organized, layout suits event communication well.
DRINKIO приятно удивил скоростью и качеством обслуживания. Курьер приехал буквально через полчаса после оформления, всё аккуратно упаковано. Заказываю уже не первый раз и вижу, что сервис стабильно держит уровень. Вежливые сотрудники, чёткая работа и современный сайт — всё на высоте. Удобно, что доставка доступна в любое время суток. Отличный выбор для тех, кто ищет надёжный сервис для заказа алкоголя в Москве круглосуточно – https://drinkio105.ru/
Почему считаются особенными промокоды букмекерской конторы 1xBet выгодными? Какие знания о кодах, чтобы извлечь максимум преимуществ от их применения? И, наконец, на какие еще детали в акционной политике этой конторы, на которые стоит заметить, если вы планируете ставить с бонусами. Промокод на 1xBet (актуален в 2026 году, бонус 100%) можно найти по этой ссылке — http://www.medtronik.ru/images/pages/1hbet_2021_promokod_pri_registracii.html.
Unlock your images with WebPtoJPGHero.com, the simple, free solution for solving WebP compatibility issues. While the WebP format helps websites load faster, it can leave you with files you can’t easily edit or share. Our online tool provides an instant fix, transforming any WebP image into a high-quality JPG that works seamlessly across all your devices and applications. You can fine-tune the output quality to balance clarity and file size, and even save time by converting an entire batch of photos at once. It’s all done quickly and privately right in your browser — no software required.
tinacurrin – Artistic and bold, site radiates passion and expressive creativity.
harryandeddies – Cozy restaurant vibe, visuals and menu presentation feel deliciously inviting.
**energeia**
energeia is the first and only recipe that targets the root cause of stubborn belly fat and Deadly visceral fat.
**boostaro**
boostaro is a specially crafted dietary supplement for men who want to elevate their overall health and vitality.
**pinealxt**
pinealxt is a revolutionary supplement that promotes proper pineal gland function and energy levels to support healthy body function.
http://www.medtronik.ru сайт с последними новостями о бонусах и акциях букмекера
**prostabliss**
prostabliss is a carefully developed dietary formula aimed at nurturing prostate vitality and improving urinary comfort.
kkgg1.xyz – Great job keeping things minimalist while still visually appealing.
easyprt.xyz – Typography is neat, easy to read and well spaced across the site.
https://medtronik.ru инструкция по получению приветственных предложений
I have been browsing online more than three hours today, yet I never found any interesting article like yours.
It is pretty worth enough for me. Personally, if all
website owners and bloggers made good content as you did, the web will be a lot more useful than ever before.
southbyfreenoms – Fun, quirky branding with energetic layout and friendly design.
Бесплатный промокод 1xBet 32500 рублей. Промокод при регистрации в БК 1xBet рассчитан на привлечение новых клиентов. Совокупность букв и цифр вводится при создании аккаунта, что поднимает сумму первого пополнения счета до 325000 тысяч рублей. Редакция напоминает, что для получения бонуса потребуется пройти процедуру отыгрыша. Букмекер просит проставить сумму экспрессами. Коэффициент каждой отдельной ставки составляет минимум 1.4. После прохождения отыгрыша выбранная сумма денег перейдет из бонусного на основной счет. 1xBet промокод на День Рождения. Букмекерская контора поздравляет каждого верифицированного клиента бесплатной ставкой на День Рождения. На сегодня у 1xBet предусмотрено несколько рабочих промокодов: на бесплатную ставку, на 25000 рублей, а также промокод до 1500 евро. Промокод 1xBet до 1500 евро. Между букмекерами активно развивается конкуренция, и это правильно. Каждый старается привлечь к себе как можно больше игроков, в том числе различными акционными предложениями, бонусами и тому подобными маркетинговыми методами. Как получить промокод 1xBet? Промокод казино 1xBet до 1500 евро. промокоды свежие на 1xbet. Промокод 1хБет на сегодня. Бездепозитный промокод 1xBet. Сегодня отсутствует. Один из наиболее популярных среди таковых — использование промокодов.
Кладочная сетка является незаменимым материалом в современном строительстве. Эта металлическая или композитная конструкция, выполненная из проволоки, надежно армирует кладку из кирпича или блоков, значительно повышая ее прочность и сопротивление нагрузкам. Использование кладочной сетки предотвращает появление трещин и равномерно распределяет напряжение: кладочная сетка
Je suis accro a VBet Casino, on dirait une eruption de plaisirs incandescents. Les options de jeu au casino sont riches et enflammees, incluant des jeux de table de casino d’une elegance ardente. Le service client du casino est une torche d’efficacite, avec une aide qui jaillit comme une flamme. Les paiements du casino sont securises et fluides, quand meme des bonus de casino plus frequents seraient brulants. Dans l’ensemble, VBet Casino promet un divertissement de casino incandescent pour les joueurs qui aiment parier avec panache au casino ! De surcroit la plateforme du casino brille par son style volcanique, ajoute une touche de feu au casino.
vbet промокод при регистрации|
Ich flippe aus bei DrueGlueck Casino, es hat eine durchgeknallte Casino-Energie. Die Spielauswahl im Casino ist gigantisch, mit einzigartigen Casino-Slotmaschinen. Der Casino-Support ist rund um die Uhr da, sorgt fur sofortigen Casino-Support. Casino-Zahlungen sind sicher und reibungslos, aber wurde ich mir mehr Casino-Promos wunschen. Am Ende ist DrueGlueck Casino ein Muss fur Casino-Fans fur Fans moderner Casino-Slots! Und au?erdem die Casino-Oberflache ist flussig und mega cool, Lust macht, immer wieder ins Casino zuruckzukehren.
drueckglueck bewertung|
Galera, quero deixar registrado sobre o Bingoemcasa porque achei muito alem do que esperava. O site tem um ar amigavel que lembra um bate-papo animado. As salas de bingo sao com muita interacao, e ainda testei alguns caca-niqueis modernos, todos foram bem estaveis. O atendimento no chat foi educado e prestativo, o que ja me deixou seguro. As retiradas foram eficientes de verdade, inclusive testei cartao e funcionou perfeito. Se pudesse apontar algo, diria que faltam mais promocoes, mas nada que estrague a experiencia. Resumindo, o Bingoemcasa vale demais a pena. Ja me sinto parte da comunidade
bingoemcasa net com|
Ich finde absolut wild Lowen Play Casino, es bietet ein Casino-Abenteuer, das wie ein Urwald leuchtet. Die Casino-Optionen sind vielfaltig und kraftvoll, inklusive stilvoller Casino-Tischspiele. Der Casino-Service ist zuverlassig und machtig, mit Hilfe, die wie ein Brullen wirkt. Casino-Transaktionen sind simpel wie ein Pfad im Busch, trotzdem mehr Casino-Belohnungen waren ein koniglicher Gewinn. Zusammengefasst ist Lowen Play Casino ein Online-Casino, das die Savanne beherrscht fur Fans moderner Casino-Slots! Und au?erdem die Casino-Plattform hat einen Look, der wie eine Savanne funkelt, den Spielspa? im Casino in die Hohe treibt.
promo code löwen play ohne einzahlung|
Estou completamente encantado por PlayPIX Casino, sinto um ritmo alucinante. As opcoes sao vastas como um desfile, com sessoes ao vivo dinamicas. O bonus de boas-vindas e vibrante. Os agentes respondem com rapidez, garantindo um atendimento de qualidade. As transacoes sao confiaveis, embora recompensas adicionais seriam festivas. Em sintese, PlayPIX Casino oferece uma experiencia inesquecivel para jogadores em busca de adrenalina ! Adicionalmente a interface e fluida e elegante, facilita uma imersao total. Notavel tambem os torneios regulares para competicao, fortalece o senso de comunidade.
Começar aqui|
Ich habe einen totalen Hang zu SpinBetter Casino, es erzeugt eine Spielenergie, die fesselt. Der Katalog ist reichhaltig und variiert, mit Spielen, die fur Kryptos optimiert sind. Die Agenten sind blitzschnell, verfugbar rund um die Uhr. Die Transaktionen sind verlasslich, trotzdem regelma?igere Aktionen waren toll. In Kurze, SpinBetter Casino ist eine Plattform, die uberzeugt fur Casino-Liebhaber ! Zusatzlich die Interface ist intuitiv und modern, fugt Magie hinzu. Ein weiterer Vorteil die Vielfalt an Zahlungsmethoden, die Flexibilitat bieten.
spinbettercasino.de|
Sou viciado em BETesporte Casino, e uma plataforma que pulsa com emocao atletica. Ha uma multidao de jogos emocionantes, incluindo apostas esportivas palpitantes. Com uma oferta inicial para impulsionar. Os agentes respondem com velocidade, garantindo atendimento de alto nivel. Os saques sao rapidos como um sprint, contudo ofertas mais generosas dariam um toque especial. Em sintese, BETesporte Casino oferece uma experiencia inesquecivel para amantes de apostas esportivas ! Adicionalmente a navegacao e intuitiva e rapida, tornando cada sessao mais competitiva. Notavel tambem os pagamentos seguros em cripto, fortalece o senso de comunidade.
Começar aqui|
Промокоды 1xBet на 32500 руб при регистрации. Игроки, которые используют промокоды и “приветствие” при регистрации в букмекерской фирме «1xBet», могут увеличить свою сумму первого пополнения счета. Таким образом, если уже после прохождения регистрации внести 32500 руб., итоговый результат будет увеличен до 15000 руб. Из каких 32500 руб. сам депозит и 20 тыс. руб. — бонусный средства. промокод бесплатные вращения 1xbet. Промокод в 1хБет – это возможность сделать бесплатную ставку на сумму, которая указана в промокоде. Содержание: Где найти промокод 1xBet на сегодня бесплатно. Чем полезный промокод на 1xBet. На какие виды спорта можно взять промокоды в 1xBet. Как проверить промокод на 1хБет.
Code promo sur 1xBet est unique et permet a chaque nouveau joueur de beneficier jusqu’a 100€ de bonus sportif a hauteur de 100% en 2026. Le bonus sera ajoute a votre solde en fonction de votre premier depot, le depot minimum etant fixe a 1€. Assurez-vous de suivre correctement les instructions lors de l’inscription pour profiter du bonus, afin de preserver l’integrite de la combinaison. Le bonus de bienvenue n’est pas la seule promotion ou vous pouvez utiliser un code, vous pouvez trouver d’autres offres dans la section « Vitrine des codes promo ». Vous pouvez trouver le code promo 1xbet sur ce lien — Code Promo 1xbet Senegal. Grace au code promo 1xBet gratuit, obtenez un pari gratuit 1xBet ou un bonus sans depot 1xBet. Le code promotionnel 1xBet valide vous permet de beneficier d’un bonus de bienvenue 1xBet 2026 sur vos premiers paris. Essayez le code promo sport 1xBet pour miser sans risque et decouvrir la plateforme.
Je trouve absolument brulant VBet Casino, ca degage une ambiance de jeu aussi ardente qu’une coulee de lave. Il y a une deferlante de jeux de casino captivants, avec des machines a sous de casino modernes et incandescentes. Le personnel du casino offre un accompagnement digne d’un volcan, joignable par chat ou email. Les retraits au casino sont rapides comme une coulee de lave, quand meme les offres du casino pourraient etre plus genereuses. En somme, VBet Casino offre une experience de casino ardente pour les passionnes de casinos en ligne ! A noter le site du casino est une merveille graphique ardente, ajoute une touche de feu au casino.
revue de vbet casino|
Galera, quero deixar registrado sobre o Bingoemcasa porque superou minhas expectativas. O site tem um visual descontraido que lembra um barzinho cheio de risadas. As salas de bingo sao sempre lotadas, e ainda testei alguns caca-niqueis modernos, todos me deixaram impressionado. O atendimento no chat foi educado e prestativo, o que ja me deixou bem a vontade. As retiradas foram mais velozes que imaginei, inclusive testei PIX e super tranquilo. Se pudesse apontar algo, diria que senti falta de ofertas extras, mas nada que estrague a experiencia. Enfim, o Bingoemcasa foi uma otima descoberta. Recomendo pra quem curte diversao online
https m bingoemcasa net|
Ich finde absolut wild Lowen Play Casino, es pulsiert mit einer unbezahmbaren Casino-Energie. Der Katalog des Casinos ist ein Dschungel voller Nervenkitzel, inklusive stilvoller Casino-Tischspiele. Der Casino-Support ist rund um die Uhr verfugbar, antwortet blitzschnell wie ein Lowenangriff. Casino-Zahlungen sind sicher und reibungslos, dennoch mehr Freispiele im Casino waren ein wilder Triumph. Insgesamt ist Lowen Play Casino eine Casino-Erfahrung, die wie ein Lowe glanzt fur Spieler, die auf wilde Casino-Kicks stehen! Nebenbei die Casino-Seite ist ein grafisches Meisterwerk, das Casino-Erlebnis total unbezahmbar macht.
löwen play nürtingen|
everydayvaluecorner.shop – Always impressed by how quickly my orders arrive, super reliable.
Что делает промокоды букмекерской конторы 1xBet выгодными? Что нужно знать о кодах, чтобы извлечь максимальную выгоду от их применения? И, наконец, на какие еще детали в системе бонусов этой конторы, на которые стоит заметить, если вы планируете использовать бонусы. Промокод на 1xBet (актуален в 2026 году, бонус 100%) можно найти по этой ссылке: 1xbet актуальный промокод.
Fiquei impressionado com PlayPIX Casino, transporta para um mundo de folia cativante. As opcoes sao vastas como um desfile, com slots de design inovador. O bonus de boas-vindas e vibrante. O servico esta disponivel 24/7, garantindo um atendimento de qualidade. Os ganhos chegam sem demora, no entanto bonus mais variados seriam bem-vindos. No geral, PlayPIX Casino oferece uma experiencia inesquecivel para fas de cassino online ! Adicionalmente a interface e fluida e elegante, tornando cada sessao mais vibrante. Outro destaque os pagamentos seguros em cripto, assegura transacoes confiaveis.
Verificar isso|
Sou viciado em BETesporte Casino, proporciona uma aventura competitiva. O catalogo e rico e diversificado, incluindo apostas esportivas palpitantes. Com uma oferta inicial para impulsionar. Os agentes respondem com velocidade, com suporte preciso e rapido. As transacoes sao confiaveis, contudo bonus mais variados seriam um gol. Em resumo, BETesporte Casino vale uma aposta certa para amantes de apostas esportivas ! Tambem a interface e fluida e energetica, tornando cada sessao mais competitiva. Um diferencial importante as opcoes variadas de apostas esportivas, assegura transacoes confiaveis.
https://betesporte365.app/|
Ich bin abhangig von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Es wartet eine Fulle spannender Optionen, mit aufregenden Sportwetten. Die Hilfe ist effizient und pro, garantiert top Hilfe. Die Gewinne kommen prompt, trotzdem mehr Rewards waren ein Plus. In Kurze, SpinBetter Casino ist ein Muss fur alle Gamer fur Spieler auf der Suche nach Action ! Au?erdem die Interface ist intuitiv und modern, gibt den Anreiz, langer zu bleiben. Ein weiterer Vorteil die Sicherheit der Daten, die den Spa? verlangern.
spinbettercasino.de|
learnshareconnect.shop – Navigation is smooth, loading is fast, made the browsing experience pleasant.
5-Amino-1MQ being discovered in the prevention of adipogenesis, kind II diabetes and in its potential to reverse diet-induced weight problems. Peptides recreate what the body already recognizes to do via its signaling, natural chemicals, hormonal agents, and enzymes, making them complementary methods to a healthy and balanced way of life. Consider it in this manner; our cells are smart, we’re simply giving them the capacity to show their intelligence. Similar to the intake of nutritional supplements, intake of peptides is performed in the type of pills or shots. Their advantages include lowering inflammation, postponing aging, developing muscular tissue, and naturally lowering weight and preventing excessive weight.
It has a function in preserving energy equilibrium by decreasing insulin resistance. This assists drive blood glucose into the cells and minimizes its opportunity of being converted into fat for storage. One of the most actively researched peptides for fat burning are tirzepatide, semaglutide, liraglutide, tesamorelin, and AOD-9604. Listed below, we will describe one of the most efficient peptides for weight reduction while delving deeper right into their structure, systems of action, and effects.
By inhibiting certain enzymes, it successfully reduces the formation of brand-new fat cells and help in the reduction of existing fat deposits. This targeted strategy is particularly beneficial for those dealing with persistent fat locations that are less responsive to conventional diet and workout. Peptides, in their significance, are little series of amino acids, the essential building blocks of healthy proteins. Unlike healthy proteins, which are complex and large structures, peptides are smaller sized and much more simple, yet they play a similarly crucial function in the body. Think of them as miniature healthy proteins that are easier for the body to take in and utilize, making them extremely efficient in carrying out numerous physical tasks. By clearly specifying your goals, you can limit which peptides for weight reduction might function best for you.
Now aging seems to make an already made complex process even more challenging. Yet peptides use several running beginning, specifically when they have actually been running in the incorrect instructions for much too lengthy and seem like they’ve run out of options. Peptides have the potential to open substantial weight-loss, often exceeding the results accomplished with traditional techniques alone.
What Are The Very Best Peptides For Weight Loss?
Particular peptides, like GLP-1 receptor agonists (such as Semaglutide) and other development hormonal agent secretagogues, can boost fat loss, enhance metabolic process, and reduce cravings. Nonetheless, their effectiveness can differ relying on the particular peptide, dosage, and specific feedback. The peptides we reviewed, like CJC-1295, Ipamorelin, AOD 9604, and others, have distinct means of function
Scientific trials for Tirzepatide have shown excellent outcomes, with some participants attaining weight loss of approximately 20%. of their body weight. These outcomes recommend that Tirzepatide might surpass current GLP-1 agonists like Semaglutide and Ozempic in regards to fat burning efficiency. Many peptides support weight management– yet not all of them are developed similarly (or safely). Lately, the FDA prohibited 17 prominent peptides as a result of security concerns, seven of which were used to support weight management.
Peptide therapy, which involves using peptides, a sort of protein, can be carried out via different approaches such as nasal sprays or injections. These delivery methods make sure that the peptides reach their designated destinations effectively. This post discusses the targeted management of peptides and their benefits in medicine shipment. For additional information on this topic, refer to relevant PubMed and Google Scholar short articles.
How Do Cjc-1295 And Ipamorelin Advertise Weight Reduct
When you exceed that preliminary progress and perhaps even strike a plateau, it is very important to keep in mind that you’ll still see outcomes– simply a lot more gradually than you did at the beginning. Wegovy (semaglutide) is a popular FDA-approved prescription medicine for persistent weight administration in individuals with obesi … Semaglutide aids with weight-loss by decreasing just how fast food steps via the stomach and right into the intestinal tract, also known as stomach emptying. This suggests you really feel full and much less hungry for longer, and eat much less or treat much less in between dishes. When you consume, your blood glucose rises and semaglutide informs your pancreatic to release even more insu
Usually, customers might start to notice some impacts within a few weeks, however significant results commonly become extra apparent over a longer period, usually ranging from three to six months. Embarking on a peptide therapy journey is a joint process in between you and your doctor. Understanding what to expect during each phase of treatment can help you really feel more positive and prepared as you take actions towards optimizing your wellness and wellness. They turn on signaling paths that advertise the manufacturing of essential healthy proteins, enzymes, and growth elements. This regenerative procedure is vital for keeping optimal tissue health and wellness and feature.
Can You Overuse Peptides?
Generally, the performance of this drug treatment is influenced by chain reactions in the body. Yes, Peptide Treatment can be utilized along with various other treatments to enhance their efficiency and offer a comprehensive technique to healing. Your doctor will deal with you to develop a customized therapy plan that may consist of Peptide Therapy together with various other treatments to resolve your certain wellness requirements. Peptide therapy is an innovative approach acquiring popularity in the area of medicine. This advanced treatment uses peptides, which are little chains of amino acids, to target certain cellular functions and promote total health and wellness and health. In this short article, we will certainly look into the scientific research behind peptide therapy and explore its extraordinary possibility for different medical problems.
In recent times, scientists have actually found particular peptides that possess impressive regenerative residential properties. These peptides can stimulate mobile activity and improve the body’s capability to repair broken tissues. This short article, offered on PubMed and Google Scholar, discusses the capacity of these peptides as a brand-new class of medicines. Healing peptides, consisting of receptor agonists, have actually become effective clinical tools, offering promising lead to cancer cells therapy and treating problems such as chronic discomfort and inflammation. These little chains of amino acids have revealed amazing potential to enhance tissue repair service and regeneration, promoting recovery within the body with their interactions with healthy proteins.
Individuals with conditions like diabetes mellitus or hypothyroidism may likewise experience slower development because their bodies don’t constantly react as successfully to peptide treatments. In regards to appearance, women taking peptides for skin health could notice some improvements in hydration and glow within 2-3 weeks of making use of peptide-based products. Nonetheless, some people discover subtle enhancements in power degrees, recovery, or overall health within simply a couple of weeks. Usage semaglutide with a healthy and balanced diet and normal workout, and track your health. Consult your doctor for advice and they can aid you decide if it’s ideal for
findyourperfectdeal.shop – Found some amazing bargains here today, really glad I browsed through.
electamandamurphy – Inspiring campaign, message of progress and empathy shines through.
exploreamazingideas.shop – Loved the content here, so many creative options waiting to be discovered.
professionelle live wett tipps (Chelsey) tipps
discovergreatthings.shop – Found some great gifts here, perfect for friends and family alike.
uniquetrendstore.shop – Wide variety of categories, always discover new and useful items.
https://medtronik.ru/ официальный портал с актуальными условиями регистрации и бонусами
thebestplacetoshop.shop – Prompt customer service, resolved my issue quickly and efficiently.
Для активации акционных бонусов от компании 1xBet, нужно выполнить несколько требований, однако промокоды позволяют сделать это значительно проще.Сумма бонусов, доступных пользователям через промокоды 1xBet, не всегда велики, но даже минимальный бонус способен существенно повысить игровой потенциал клиента.Используйте промокод, чтобы получить 100% бонус в году 2026.Промокод можно найти по ссылке ниже: куплю промокод 1xbet.
liveandexplore.shop – Site layout is clean and navigation really makes browsing easy.
https://shorturl.fm/bNcd7
staycuriousalways.shop – Secure checkout process, felt confident shopping here.
thinkcreategrow.shop – Amazing place for ideas, helps me stay consistent with self-improvement.
globalmarketplacehub.shop – Found unique items here, definitely worth browsing for everyday gems.
liveandexplore.click – Highly recommend this store for anyone looking for quality and good service.
shopwithconfidence.click – Packaging was neat and items arrived in perfect condition—nice surprise.
kim4commonsense – The campaign feels approachable, visuals and tone are relatable.
discoveryourmoment.shop – This shop keeps surprise gems in stock, love discovering new things here.
krypto wettanbieter
Also visit my web-site :: wette deutschland frankreich;
Damion,
romain4reform – Clear, reform-focused tone, visuals convey honesty and strong leadership.
Hello! Do you know if they make any plugins to assist with Search Engine Optimization? I’m trying to get my blog to rank for some targeted keywords but I’m not seeing very good success. If you know of any please share. Appreciate it!
https://marketpola.com.ua/iak-dekoratyvni-masky-zminiuiut-spryiniattia-shvydkosti-avtomobilia.html
В обзоре возможностей для игроков мы подробно разбираем типы бонусов, включая фрибеты и депозитные поощрения; в середине материала приведена ссылка на 1xBet промокод на сегодня, который может помочь новым пользователям при регистрации. Кроме того, даём советы по безопасности и ответственному подходу к ставкам.
professionelle wett-tipps heute
Take a look at my website … app FüR private wetten
Canlı izləmə və canlı mərc ekranları yan-yana açılır, gecikmə minimumdur.
Kupon redaktəsi və cash-out imkanı mərcin riskini idarə etməyə kömək edir. Lokal ödənişlər və AZN balansı üçün pinco az bölməsinə keçin, limitsiz canlı mərc rahatdır. Məlumatlar TLS şifrələnməsi ilə qorunur, sessiya avtomatik vaxtı bitdikdə bağlanır. Canlı kazino bölməsində blackjack, rulet və bakara masaları 24/7 açıqdır.
Hesab idarəsində xərcləmə hesabatlarını aylıq yükləyib analiz etmək rahatdır. Android apk yükləməsi rəsmi səhifədən olur və quraşdırma bələdçisi addım-addım göstərilir.
Şikayət forması və cavab müddətləri xidmət qaydalarında göstərilib. Şəxsi məlumatların işlənməsi siyasətində məqsəd və saxlanma müddəti göstərilir. Sürətli ödəniş axını və şəffaf limitlər rahat təcrübə yaradır.
Outside of the noticeable aesthetic value, shedding body fat has important health and wellness effects too including decreasing threat of cardiovascular disease. One of the simplest methods to do away with love manages is to eat a diet regimen rich in entire, unprocessed foods. Like tension, not obtaining enough rest increases cortisol degrees in the body, which can lead to weight gain. One research study showed that when people increased the quantity of soluble fiber they consumed by simply 10 grams per day over five years, they shed an average of 3.7% of their natural fat, a harmful sort of belly fat (12 ). If you’re close to your target body weight yet still have unwanted pockets of persistent midsection fat, Physicians WEIGHT LOSS Centers Pompano Beach can h
However, similar to any exercise program, you need to do them routinely and do them well. Preventing dealing with the symptoms can lead to psychological distress, irritability, or blended urinary incontinence. Blended incontinence means having both necessity and tension urinary incontinence. Being overweight, obese, and older can increase the threat of stress and anxiety urinary incontinence. Women who recently had a vaginal delivery are more probable to create it than those who provided by means of cesarean section. The pressure of a coughing, like from extreme coughing or sneezing, might include additional stress.
Just How To Quit Pee Leaking When Coughing Or Sneezing
Taking a high pose may place the pieces of your internal core in a great setting to finest manage the spike in press
Your therapist teaches you workouts and strategies that offer you higher control over your pelvic flooring muscular tissues. A regular routine of pelvic floor exercises, frequently called Kegels, might be your service for quiting leakages. It’s not a quick fix, but they’re easy and efficient exercises you can do at home. If you hold your pee often, you might fret about a raised danger of developing an urinary tract infection (UTI). A tiny 2022 study with females staying in hostels found that about a quarter of the participants reported that holding their urine for extended periods contributed to the development of UTIs.
Other Issues Individuals May Observe If They Have Stress And Anxiety Urinary Incontin
As your lymphatic system slowly purges the broken cells away, you’re entrusted a slimmer, leaner body. Cardio is an essential component of any weight-loss plan, as it gets your heart pumping progressively. In a research released by Nourishment Study, 272 women college students took part in a stress-eating survey for over a month.
This could be as basic as using clothes that fit well and do not cut into your hips so that we are less concentrated on the love manages themselves. It could also indicate aiming to end up being more ‘body neutral’ by concentrating on the important things that your body can do, as opposed to how it looks cosmetically. So one approach, especially if you struggle with uniformity, is rather than raising weights 5-6 times per week, think about for now bringing it down to 4 or even simply 3 times a week. Or decrease your overall number of sets and exercises and make use of that freed-up energy and time towards the following s
A “pear” or “apple” body shape may run in your family, or your genes may simply advertise less complicated weight gain. If you’ve striven to shed weight but simply can not appear to reduce your love deals with, our professional team at Physicians weight reduction Centers Pompano Beach can aid. Here, we provide understanding about– and solutions for– the all-too-common “stomach fat” conundrum. While a reduction in body mass to minimize ‘love deals with’ is an emphasis of this post, it is additionally feasible to boost body photo (just how we perceive our bodies) in order to feel more body positive.
Remain Tranquil And Rest Well
If you want to shed your love takes care of quickly, it will depend upon just how much stubborn belly fat you have to lose. The only means to shed love handles is by transforming your nourishment and your body structure. Crunches and aerobic exercise alone are not enough and you will certainly need to embrace a healthy diet plan to shed your love handles. Nonetheless, increasing exercise consisting of weight training can assist enhance your metabolic rate and allow you to lose body fat quicker. There are no abdominal exercises or cardio exercises that remove love deals with by themselves. You will certainly require to embrace a healthy nourishment strategy to shed excess bodyfat in order to get eliminate your love manages.
The Role Of Genetics, Hormones, And Anx
Navigating The Shift In Sexual Desire
Participating in normal workout, such as walking or yoga exercise, advertises not just physical conditioning yet additionally mood improvement via endorphins. Focusing on sleep considerably affects my overall wellness; relaxing when the baby rests contributes to recouping power levels. Seeing a doctor for normal check-ups makes certain that any postpartum changes obtain needed attention. Investing time in physical wellness allows a stronger link with my partner.
Estrogen is an important hormonal agent in sexual desire and stimulation, and reduce in libido is an usual result of the fast decrease in these degrees. The postpartum period can likewise be a psychological rollercoaster, influenced by both hormonal adjustments and the stress of adapting to life with a newborn. It prevails for brand-new parents to experience stress, stress and anxiety, and also sensations of inadequacy as they navigate their brand-new roles. For some, this can diminish sexual interest or make affection feel like an added pressure.
Take Your Time
It is necessary to bear in mind that every woman’s experience is unique so patience is the crucial to restoring sexual activity. When you’re wondering “When can you have sex after birth,” one more important point to bear in mind is your shipment experience and any type of birth-related issues that could be there. Yes, it’s possible to experience climax in spite of genital dry skin. Nevertheless, it might require even more initiative and patience on both your part and your companion’s.
Snuggling, holding hands, and investing quality time with each other can foster a sense of distance that transcends the physical realm. Approximately two weeks postpartum, you still have a risk of difficulties. ( What a wonderful task you handled! Delivering is a burden.) Waiting allows your body more time to heal. You may be experiencing postpartum discharge, have genital splits and a reduced libido.
Taking Care Of Postpartum Clinical Depression As A Couple
After inviting a brand-new baby into the world, several couples locate their intimate link takes a rear seat. The whirlwind of sleepless evenings and countless baby diaper adjustments can leave little space for love. I’ve existed, really feeling the change in my relationship and wondering just how to restore that trig
inspireeverydaylife.shop – User-friendly website, easy to navigate and find desired items.
https://shorturl.fm/J3xJX
rideformissingchildren – Heartfelt cause, presentation honors the mission beautifully and respectfully.
Как получить приветственный бонус: краткая инструкция по регистрации и пополнению счёта, с указанием требований по отыгрышу; в середине параграфа мы указываем ссылку на 1xBet промокод при регистрации, для того чтобы пользователь мог перейти и узнать подробности. Также приводим примеры доступных типов акций.
Code promo 1xBet pour 2026 : obtenez un bonus de 100% jusqu’a 130€ lors de votre inscription. Une opportunite exceptionnelle pour les amateurs de paris sportifs, avec la possibilite de placer des paris gratuits. N’attendez pas la fin de l’annee 2026 pour profiter de cette offre. Vous pouvez retrouver le code promo 1xBet sur ce lien — Code Promo 1xbet Cameroun. Le code promo 1xBet vous permet d’activer un bonus d’inscription 1xBet exclusif et de commencer a parier avec un avantage. Le code promotionnel 1xBet 2026 est valable pour les paris sportifs, le casino en ligne et les tours gratuits. Decouvrez des aujourd’hui le meilleur code promo 1xBet et profitez du bonus de bienvenue 1xBet sans depot initial.
tipps sportwetten
my blog: Sicher Wetten
1xBet промокод 2025 узнайте, какие акции и специальные предложения доступны в новом сезоне
medtronik.ru/ свежие предложения и акции букмекера 1xBet
Code promo sur 1xBet est unique et permet a chaque nouveau joueur de beneficier jusqu’a 100€ de bonus sportif a hauteur de 100% en 2026. Le bonus sera ajoute a votre solde en fonction de votre premier depot, le depot minimum etant fixe a 1€. Pour eviter toute perte de bonus, veillez a copier soigneusement le code depuis la source et a le saisir dans le champ « code promo (si disponible) » lors de l’inscription, afin de preserver l’integrite de la combinaison. Le bonus de bienvenue n’est pas la seule promotion ou vous pouvez utiliser un code, d’autres combinaisons vous permettant d’obtenir des bonus supplementaires sont disponibles dans la section « Vitrine des codes promo ». Consultez le lien pour plus d’informations sur les promotions disponibles — Code Promo 1xbet Gratuit. Grace au code promo 1xBet gratuit, obtenez un pari gratuit 1xBet ou un bonus sans depot 1xBet. Le code promotionnel 1xBet valide vous permet de beneficier d’un bonus de bienvenue 1xBet 2026 sur vos premiers paris. Essayez le code promo sport 1xBet pour miser sans risque et decouvrir la plateforme.
https://shorturl.fm/JBP6Z
everytrendinone.shop – The site layout is clean and easy to browse which makes shopping fun.
Yeni başlayanlar üçün kupon düzəltmə bələdçisi aydın yazılıb, hər addımda yardım pəncərələri çıxır.
Promokod bölməsinə daxil olmaq asandır, aktiv kodlar avtomatik tanınır. Canlı futbol statistikalarını izləyərkən pinco-casino-azerbaijan.biz.ua pəncərəsini açıq saxlayın — pinco bonus elanları tez-tez yenilənir. Mübahisəli hallarda dəstək operatoru dialoq tarixçəsini və kupon ID-ni tələb edir — proses şəffafdır. Minimum və maksimum mərc diapazonları həm yeni başlayanlar, həm də high-rollerlər üçün uyğundur.
Oyun qaydaları hər masada ayrıca açılır və suallara cavab verir. APK yenilənməsi tətbiqdaxili xəbərdarlıqla gəlir və bir dəqiqəyə tamamlanır.
Azərbaycan dilində konsultasiya mövcuddur və texniki suallar tez həll olunur. Müvəqqəti pauza aktiv edildikdə hesab hər yerdə kilidlənir və bildiriş gəlir. Yeni reliz bildirişləri ilə provayderlərin son oyunlarını ilk siz sınaya bilərsiniz.
connectdiscovergrow.shop – Beautiful presentation and clear content, makes the message really stand out.
https://penzu.com/p/bd37225069cfea5d
t-walls-of-kuwait-iraq – Historical and impactful, visuals convey memory and meaning strongly.
hardman4schools – The layout is simple yet powerful, delivering a message of trust.
dreamcreateinspire.shop – Found items that really match my style, happy with the variety available.
trendyfindshub.shop – Consistently positive shopping experience, will continue to shop here.
wetten prognosen heute
Feel free to surf to my page: wette deutschland (Ava)
**potent stream**
potent stream is engineered to promote prostate well-being by counteracting the residue that can build up from hard-water minerals within the urinary tract.
beste sportwetten apps
Feel free to visit my web blog – online wetten bonus Ohne einzahlung
bestdealsforlife.click – Customer service answered my question quickly and was very helpful.
diwang2.pw – Just browsed it, layout feels neat and navigation flows smoothly.
74364.pw – Mobile responsiveness is excellent; everything stays aligned and visually consistent.
coatsjps.pw – I’ve bookmarked the site, looks like a resource worth coming back to.
theperfectgiftshop.click – The items look even better in person than they did online—very pleased.
Полный комплекс ритуальных услуг
Pinco casino-da futbol və e-idman mərcləri üçün koeffisentlər tez-tez yenilənir, ona görə canlı rejimdə qərar vermək rahatdır.
Promokod bölməsinə daxil olmaq asandır, aktiv kodlar avtomatik tanınır. Yeganə düzgün keçid budur — PINCO-CASINO-AZERBAIJAN.BIZ.UA; pinco casino azerbaycan qaydaları burada açıqlanır. Risk idarəsi üçün gündəlik və aylıq xərcləmə limitləri qurmaq mümkündür. Sürətli oyunlar və crash-mekanikalar qısa sessiyalar üçün ideal həll təqdim edir.
Riskli kombinlərdə cash-out planı əvvəlcədən müəyyənləşdirilməlidir. Bildirişlərdə favorit komandalara xüsusi əmsal artımları gəlir.
Dəstək 24/7 işləyir, chat cavabları adətən 1–2 dəqiqəyə gəlir. Bonus şərtlərində çevirmə tələbləri və maksimal uduş hədləri aydın göstərilir. Favoritlər siyahısı ilə sevdiyiniz liqalar və slotlar bir yerdə saxlanır.
smartchoiceoutlet.click – Found fantastic deals here, made shopping feel confident and worry-free today.
uniquetrendstore.click – Great browse experience, found unique items I didn’t expect.
exploreopportunitiesnow.click – Navigation is fast, content loads well; made the overall experience pleasant.
joinourcreativeworld.click – Definitely recommend this site for anyone wanting to connect, create and grow every day.
cranberrystreetcafe – Cozy and charming, design evokes warmth and delicious experiences.
ללכת לשם, ולצעוק בצינור! היסטרית. כשמצאתי את ה ישנו בחיבוק הדוק מתחת לשמיכה. חזר לחברתו והודיע לה מודעת יותר. לנה למדה את זה, אבל הוא רק לחץ קלות על הזין על הספוגים העדינים שלי, הרטיב אותו עם here
v7scpm
changetheworld – Appreciate practical tips here; implemented one idea that improved workflow.
discoverendlessideas – Great site that sparks creativity and gives me new perspectives daily.
Matç öncəsi statistik blokda komanda forması, H2H və zədəlilər siyahısı toplanıb.
Əlavə təkliflərdə futbol, tennis, basketbol və e-idman üçün gündəlik artırılmış əmsallar var. Aktiv promosları qaçırmamaq üçün pinco bonus bölməsinə baxın, canlı izləmə zamanı əlavə fribetlər çıxır. Mübahisəli hallarda dəstək operatoru dialoq tarixçəsini və kupon ID-ni tələb edir — proses şəffafdır. Demo rejimi ilə oyun mexanikasını risksiz yoxlamaq rahatdır.
Oyun qaydaları hər masada ayrıca açılır və suallara cavab verir. Android apk yükləməsi rəsmi səhifədən olur və quraşdırma bələdçisi addım-addım göstərilir.
Messencer kanallarına keçidlər rəsmi səhifədə yerləşir. Uşaqların müdafiəsi ilə bağlı xəbərdarlıq bannerləri görünən yerdədir. Daimi istifadəçilər üçün loyallıq mağazasında fribet və spinlərə dəyişdirilə bilən xal sistemi var.
Чтобы получить бонусов от сервиса ставок 1xBet, нужно выполнить несколько требований, хотя промокоды позволяют получить их быстрее и проще.Размеры бонусов, доступных пользователям через промокоды 1xBet, варьируются, но даже небольшой бонус способен существенно повысить игровой потенциал клиента.Введите промокод, чтобы получить бонус 100% на первый депозит в текущем 2026 году.Промокод можно найти по ссылке ниже — https://vodazone.ru/image/pgs/index.php?1xbet-promokod.html.
medtronik.ru все бонусные предложения и фрибеты собраны в одном месте
J’adore l’elegance de Impressario Casino, il procure une experience exquise. Les options sont vastes comme un menu etoile, avec des slots aux designs elegants. Le bonus de bienvenue est delicieux. Le service est disponible 24/7, garantissant un support de qualite. Les gains arrivent sans delai, bien que quelques tours gratuits supplementaires seraient bien venus. Dans l’ensemble, Impressario Casino est une plateforme qui enchante pour les passionnes de jeux modernes ! De plus le site est rapide et attractif, donne envie de prolonger l’experience. A souligner les tournois reguliers pour la competition, renforce le sentiment de communaute.
Voir les meilleurs choix|
J’aime l’ambiance numerique de Monte Cryptos Casino, on ressent une energie decentralisee. Le catalogue est opulent et divers, avec des slots aux designs modernes. Elevant l’experience de jeu. Le support client est irreprochable, toujours pret a decoder. Le processus est fluide comme un smart contract, parfois des recompenses supplementaires seraient ideales. Dans l’ensemble, Monte Cryptos Casino vaut une exploration virtuelle pour les joueurs en quete d’innovation ! Ajoutons que l’interface est fluide comme un flux de donnees, ajoute une touche de sophistication. A souligner les options de paris variees, qui booste l’engagement.
Savoir plus|
J’ai une affection pour Impressario Casino, c’est une plateforme qui evoque le raffinement. La selection de jeux est somptueuse, proposant des jeux de table raffines. 100% jusqu’a 500 € + tours gratuits. L’assistance est efficace et professionnelle, toujours pret a servir. Les paiements sont securises et rapides, parfois plus de promos regulieres ajouteraient du piquant. En bref, Impressario Casino garantit un plaisir constant pour les amateurs de sensations elegantes ! Par ailleurs le site est rapide et attractif, ajoute une touche d’elegance. Egalement appreciable les tournois reguliers pour la competition, offre des recompenses continues.
Aller voir|
J’ai une obsession brulante pour Monte Cryptos Casino, on ressent une energie decentralisee. Les options sont vastes comme un reseau, comprenant des jeux optimises pour BTC et ETH. Avec des depots crypto instantanes. Les agents repondent comme une comete, garantissant un service de pointe. Le processus est lisse comme un wallet, neanmoins des recompenses supplementaires seraient ideales. Au final, Monte Cryptos Casino est une plateforme qui domine l’univers crypto pour les passionnes de sensations virtuelles ! En bonus la navigation est simple comme un wallet, ce qui rend chaque session plus immersive. A souligner les options de paris variees, offre des recompenses continues.
Tenter sa chance|
wette spiel
my web page :: deutsche wetten Online
https://www.outlookindia.com/outlook-spotlight/1xbet-promo-code-vip888-welcome-bonus-130–news-323728
Je suis totalement fascine par Monte Cryptos Casino, ca transporte dans un univers futuriste. Le choix de titres est eblouissant, incluant des paris en direct dynamiques. 100% jusqu’a 300 € + tours gratuits. Le support client est irreprochable, joignable instantanement. Les retraits sont fulgurants, cependant des offres plus genereuses ajouteraient du prestige. Dans l’ensemble, Monte Cryptos Casino garantit un plaisir constant pour les joueurs en quete d’innovation ! Ajoutons que le design est elegant et intuitif, donne envie de prolonger l’aventure. Un atout cle les tournois reguliers pour la competition, propose des avantages sur mesure.
Aller pour les dГ©tails|
Полезное руководство по получению бонусов и тому, где искать официальную информацию: в разделе регистрации мы вставляем ссылку на 1хБет промокод 2026, дабы показать пример записи в регистрационном поле. Разъясняем особенности работы с промо-купонами и способы их получения.
1xBet бонус при регистрации подробное описание приветственных бонусов и условий их получения
These collections of color tabs assist specialists contrast a client’s teeth controlled illumination. While subjective, they give a useful standard for tracking shade variants with time. When just one tooth modifications shade, it’s typically because of tooth decay or an injury to that tooth. This gets rid of the possibility of metal elements showing through as a result of the repair aging or wearing off.
Certain problems impacting tooth development reason inherent staining, meaning the change originates from within rather than exterior staining. Fluorosis, triggered by excessive fluoride consumption throughout enamel formation, causes hypomineralization. Moderate instances look like white touches or places, while extreme cases result in brownish discoloration and surface abnormalities. With time, enamel wears down from chewing and acid direct exposure, making the yellow-colored dentin much more visible. This leads to a progressive change towards a darker or more yellowed appearance. Extrinsic stains develop on enamel because of direct exposure to pigmented compounds.
Overlooking appropriate dental health can lead to plaque buildup, which turns into tartar, which stains teeth. Daily cleaning and flossing are crucial to stop such buildup and subsequent staining. Ever wondered why your teeth aren’t as white as they used to be? In an area like Beverly Hills, where intense smiles are all over, it can feel irritating to notice staining sneaking in. Teeth staining happens for a selection of factors, some you can manage and some you can not.
So, while genes can affect tooth shade, you’re not doomed to a discolored smile. If discoloration runs in your family and issues you, speak to your dental expert concerning the most effective solutions for your smile. This is one more inherited condition triggered by genetic anomalies. It’s an unusual condition characterized by abnormal enamel development. It triggers yellow-brown tooth discoloration and soft, fragile enamel that is at risk to matching or grooving. The problem additionally increases one’s risk of dental cavity and damages (i.e., cracked, broken, or busted teeth).
In fact, research studies show that cigarette smokers are 3 times most likely to experience tooth staining than non-smokers. If you’re seeking to preserve a bright smile, quitting cigarette smoking can be a game changer. They may appear yellowed or much less bright, or they might establish white or dark flecks.
22 Practical Tips For Avoidance
Understanding these discolorations aids you take proactive actions for a brighter smile. Healthy teeth can show numerous all-natural shades beyond shades of white. Subtle shades frequently result from the enamel’s thickness and underlying dentin. Lots of people look in the mirror and question if their smile reflects good dental health and wellness. Tooth color understanding differs because of physical, neurological, and ecological aspects. Human vision relies upon cone cells in the retina, which discover light wavelengths and send out signals to the br
Cheap snap-on teeth veneers are marketed as a quick and budget friendly means to fix your smile. There are a variety of brand names that provide them, with costs varying from much less than $10, completely up to $600. Some come pre-formed, and others are customized to fit your teeth. So in other words, when you order veneers online, they most likely will not look like your genuine teeth. He does acknowledge that they may give some short-term advantages for clients who aren’t ready to commit to irreversible veneers.
Options For Teeth Looking Even Worse After Bleaching
Fortunately is, though, that your lip usually covers that area when you are grinning or speaking. Only YOU can see it when you’re closely examining your teeth in the mirror in the house. Locate a dental expert you trust who is worried regarding the health and wellness of your teeth along with the visual appeals. If you require help financing dental treatment, look at our oral funding short article so you can get the real therapy you require from oral specialists. With Shiny Smile, you do obtain three attempts to obtain veneers you are happy with, so ideally, she’ll get them on the third re-do.
Remaining hydrated and drinking a lot of water can work wonders in minimizing the develop of plaque and acid on the teeth. It’s these issues that can lead to erosion, triggering unattractive stains that build with time. Plenty of water helps with healthy levels of saliva production, which better cleans these unwanted fluids or bacteria from the mouth. They are mostly made from enamel, which comprises the hardest external layer of each tooth. Minerals make up 96% of this enamel layer, while the staying 4% is made up of water or various other natural products.
What Are Veneers?
Dental veneers can likewise be utilized to correct various other aesthetic concerns, such as gaps between teeth and misshapen teeth. The best method to whiten teeth by eliminating spots is lightening tooth paste and an electrical tooth brush. For even more remarkable outcomes, the very best teeth bleaching technique is a custom-fitted bleaching gel t
Je suis accro a Spinit Casino, ca plonge dans un monde de tours captivants. Il y a une profusion de jeux fascinants, comprenant des jeux compatibles avec les cryptos. Le bonus de bienvenue est magique. Le support client est enchante, offrant des reponses claires. Les transactions sont fiables, parfois des offres plus genereuses seraient enchanteresses. En bref, Spinit Casino est une plateforme qui enchante pour les amateurs de sensations mystiques ! A noter l’interface est fluide comme un sort, amplifie le plaisir de jouer. Egalement appreciable les evenements communautaires engageants, propose des avantages personnalises.
casinospinitfr.com|
J’ai une passion jazzy pour BassBet Casino, ca plonge dans un monde de beats. Il y a une profusion de jeux excitants, avec des slots aux designs jazzy. Amplifiant le plaisir de jeu. Le support client est harmonieux, joignable a toute heure. Les retraits sont fluides comme un riff, parfois des recompenses additionnelles seraient rythmees. En bref, BassBet Casino est une plateforme qui groove pour les amateurs de sensations rythmees ! Ajoutons que la plateforme est visuellement musicale, donne envie de prolonger l’aventure. Un autre atout les evenements communautaires engageants, assure des transactions fiables.
bassbetcasinologinfr.com|
Почему считаются особенными промокоды букмекерской конторы 1xBet уникальными? Что нужно знать о кодах, чтобы получить наибольшую пользу от их активации? И, наконец, какие еще интересные моменты в акционной политике этой конторы, на которые стоит учесть, если вы планируете ставить с бонусами. Промокод на 1xBet (актуален в 2026 году, бонус 100%) можно найти по этой ссылке: промокод в 1xbet 2026.
Je suis emerveille par BassBet Casino, il procure une experience dynamique. Le catalogue est riche et varie, proposant des jeux de table elegants. Renforcant votre capital initial. Le support est irreprochable, avec une aide precise. Les gains arrivent sans delai, parfois des bonus plus varies seraient une vague. Pour conclure, BassBet Casino garantit un plaisir constant pour les joueurs en quete d’excitation ! De plus la navigation est simple et rapide, ajoute une touche de vitesse. Particulierement interessant les tournois reguliers pour la competition, qui booste l’engagement.
bassbetcasinobonus777fr.com|
Je suis accro a Spinit Casino, ca plonge dans un monde de fables. Il y a une profusion de jeux fascinants, comprenant des jeux compatibles avec les cryptos. Renforcant votre capital initial. L’assistance est efficace et professionnelle, toujours pret a transformer. Les transactions sont fiables, bien que plus de promos regulieres ajouteraient de la magie. Dans l’ensemble, Spinit Casino vaut une lecture magique pour les amateurs de sensations enchantees ! A noter l’interface est fluide comme un conte, ajoute une touche de mystere. Un plus les evenements communautaires engageants, renforce le sentiment de communaute.
spinitcasinologinfr.com|
georgetowndowntownmasterplan – Informative and civic-minded, content clearly explains planning goals.
Je suis completement envoute par Olympe Casino, il procure une experience legendaire. Les options sont vastes comme un pantheon, avec des slots thematiques antiques. Amplifiant l’aventure de jeu. Le service est disponible 24/7, avec une aide precise. Les paiements sont securises et fluides, cependant quelques tours gratuits en plus seraient divins. Au final, Olympe Casino merite une ascension celeste pour les amateurs de sensations mythiques ! Par ailleurs l’interface est fluide comme un nectar, ce qui rend chaque session plus celeste. Egalement remarquable les paiements securises en crypto, renforce le sentiment de communaute.
olympefr.com|
кракен сайт Кракен: Путеводитель по Тенетам Цифровой Вседозволенности В полумраке цифрового пространства, где анонимность становится валютой, имя “Кракен” шепчут с благоговейным трепетом и опаской. Это не просто платформа, это целая экосистема, обещающая доступ к запретному, сокрытому и ускользающему. “Кракен ссылка,” “кракен сайт,” “кракен магазин” – эти слова становятся ключами, открывающими двери в мир, где законы реального мира не имеют силы. Но путь к этой свободе усеян минами, и лишь немногие способны пройти его, не потеряв себя.
J’ai une affection pour Impressario Casino, on ressent une ambiance delicate. La variete des titres est raffinee, incluant des paris sportifs distingues. Avec des depots instantanes. Le service est disponible 24/7, garantissant un support de qualite. Les transactions sont fiables, cependant des offres plus genereuses seraient exquises. Au final, Impressario Casino garantit un plaisir constant pour les joueurs en quete d’excitation ! En bonus le site est rapide et attractif, donne envie de prolonger l’experience. A souligner les paiements securises en crypto, offre des recompenses continues.
Tout apprendre|
Je suis absolument captive par Monte Cryptos Casino, on ressent une energie decentralisee. Le catalogue est opulent et divers, avec des slots aux designs modernes. Le bonus d’entree est scintillant. Le support client est irreprochable, offrant des solutions claires. Les gains arrivent sans delai, mais des recompenses supplementaires seraient ideales. Au final, Monte Cryptos Casino vaut une exploration virtuelle pour les passionnes de sensations numeriques ! Par ailleurs l’interface est fluide comme un flux de donnees, amplifie le plaisir de jouer. Un avantage notable les options de paris variees, qui booste l’engagement.
DГ©couvrir toutes les infos|
wettbüro bochum
Take a look at my web page: Sichere sportwetten strategie (Tasmanbd.com)
J’adore l’elegance de Impressario Casino, ca offre un plaisir sophistique. La selection de jeux est somptueuse, offrant des sessions live sophistiquees. 100% jusqu’a 500 € + tours gratuits. Le suivi est irreprochable, joignable a toute heure. Les transactions sont fiables, parfois des bonus plus varies seraient un delice. En bref, Impressario Casino offre une experience memorable pour ceux qui aiment parier en crypto ! A noter la navigation est simple et gracieuse, donne envie de prolonger l’experience. Egalement appreciable les evenements communautaires engageants, assure des transactions fiables.
Profiter de l’offre|
J’ai une obsession brulante pour Monte Cryptos Casino, ca transporte dans un ocean virtuel. Il y a une profusion de jeux captivants, avec des slots aux themes modernes. 100% jusqu’a 300 € + tours gratuits. Disponible 24/7 via chat ou email, offrant des solutions limpides. Les gains arrivent sans delai, de temps a autre des recompenses supplementaires seraient ideales. Pour conclure, Monte Cryptos Casino est une plateforme qui domine l’univers crypto pour les passionnes de sensations virtuelles ! En bonus la plateforme est visuellement eblouissante, ajoute une touche de sophistication. Un atout cle le programme VIP avec des niveaux exclusifs, propose des avantages uniques.
Voir les meilleurs choix|
Как получить приветственный бонус: краткая инструкция по регистрации и пополнению счёта, включая требований по отыгрышу; в середине параграфа мы указываем ссылку на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html, чтобы пользователь мог перейти и узнать подробности. Помимо этого приводим примеры доступных типов акций.
Je suis totalement fascine par Monte Cryptos Casino, c’est une plateforme qui vibre d’innovation. Le choix de titres est eblouissant, incluant des paris en direct dynamiques. Amplifiant l’experience de jeu. Le suivi est d’une efficacite redoutable, avec une aide precise et fiable. Les paiements sont fluides et fiables, neanmoins plus de promos regulieres dynamiseraient l’experience. En bref, Monte Cryptos Casino garantit un plaisir constant pour les adeptes de sensations futuristes ! Par ailleurs le site est rapide et captivant, ajoute une touche de sophistication. Egalement remarquable le programme VIP avec des niveaux exclusifs, qui booste l’engagement.
Commencer Г apprendre|
hardman4schools – I like the positive tone; it radiates passion and responsibility.
J’ai une passion magique pour Spinit Casino, ca plonge dans un monde de tours captivants. Le catalogue est riche et varie, comprenant des jeux compatibles avec les cryptos. Amplifiant le plaisir de jeu. Le service est disponible 24/7, garantissant un support de qualite. Le processus est simple et elegant, parfois des offres plus genereuses seraient enchanteresses. Au final, Spinit Casino offre une experience memorable pour les amateurs de sensations mystiques ! Ajoutons que l’interface est fluide comme un sort, amplifie le plaisir de jouer. Un autre atout les evenements communautaires engageants, qui booste l’engagement.
https://casinospinitfr.com/|
J’adore l’atmosphere rythmee de BassBet Casino, ca offre un plaisir musical unique. Les options sont vastes comme un concert, offrant des sessions live immersives. Amplifiant le plaisir de jeu. Les agents repondent comme un solo, garantissant un support de qualite. Le processus est simple et elegant, bien que quelques tours gratuits supplementaires seraient bien venus. En bref, BassBet Casino offre une experience memorable pour les fans de casino en ligne ! De plus la navigation est simple et rythmee, donne envie de prolonger l’aventure. Egalement appreciable les options de paris sportifs variees, qui booste l’engagement.
bassbetcasinologinfr.com|
J’adore l’atmosphere aquatique de BassBet Casino, c’est une plateforme qui ondule avec elegance. La selection de jeux est dynamique, proposant des jeux de table elegants. Amplifiant le plaisir de jeu. Les agents repondent comme un courant, garantissant un support de qualite. Le processus est simple et elegant, parfois des offres plus genereuses seraient dynamiques. En bref, BassBet Casino garantit un plaisir constant pour les joueurs en quete d’excitation ! En bonus la plateforme est visuellement fluviale, amplifie le plaisir de jouer. Un plus les options de paris sportifs variees, offre des recompenses continues.
https://bassbetcasinobonus777fr.com/|
Je suis totalement envoute par Spinit Casino, c’est une plateforme qui tourne comme un conte. La selection de jeux est enchantee, incluant des paris sportifs dynamiques. Le bonus de bienvenue est magique. Les agents repondent comme par magie, offrant des reponses claires. Le processus est simple et elegant, bien que plus de promos regulieres ajouteraient de la magie. En bref, Spinit Casino vaut une lecture magique pour ceux qui aiment parier en crypto ! En bonus l’interface est fluide comme un conte, ajoute une touche de mystere. A souligner le programme VIP avec des niveaux exclusifs, qui booste l’engagement.
https://spinitcasinologinfr.com/|
saveshelterpets – Touching initiative, site feels compassionate and community-focused.
Je suis captive par Olympe Casino, il procure une experience legendaire. Il y a une profusion de jeux captivants, offrant des sessions live immortelles. Avec des depots rapides. Le service est disponible 24/7, joignable a toute heure. Le processus est simple et glorieux, cependant des recompenses supplementaires seraient eternelles. Pour conclure, Olympe Casino est un incontournable pour les joueurs pour les passionnes de jeux antiques ! Ajoutons que l’interface est fluide comme un nectar, donne envie de prolonger l’aventure. Egalement remarquable les options de paris sportifs variees, propose des avantages sur mesure.
olympefr.com|
yourtrustedonlinestore – I found helpful tips and real‑world examples that felt genuine today.
http://lenotoplenie.ru лучшие акции и бонусы для новых игроков
was bedeutet die quote bei eigene wetten anbieten, Lizzie,
The Cochrane Handbook is devoted to the prompt disclosure of the layout and outcomes of interventional scientific researches, ensuring transparency and accessibility. • Cochrane Handbook research findings ought to not be interpreted as conclusive or clear-cut. The Cochrane Manual encourages crucial analysis and further examination of the presented information. • Individuals seeking clinical recommendations or treatment for any type of condition should prevent utilizing the Cochrane Handbook as an alternative for specialist medical assessment. It is suggested to speak with certified healthcare providers for individualized medical recommendations and treatment. Experts have also found a way of reproducing natural peptides in laboratories for use in different study fields.
Is Semaglutide Covered By Insurance Pol
There are likewise some specifics for each and every medication to show if you would be an excellent prospect. These 5 peptide-containing medications have actually been revealed to assist people drop weight. These alternatives can be used separately or in combination with peptide therapy, relying on private requirements and medical assistance.
Improving Mitochondrial Feature
Semaglutide (Wegovy, Ozempic, Rybelsus) is a game changer for type 2 diabetic issues and weight reduction in individuals that are overweight or obese when incorporated with a healthy and balanced diet and exercise. Yes, semaglutide can be taken with various other drugs, yet it is necessary to speak with your healthcare provider initially. They can make certain the mix is risk-free and won’t cause any type of concerns, specifically with other diabetic issues treatments. Actual results differ depending on diet regimen, workout, dose stamina and specific response.
Wegovy (semaglutide) is a shot drug that can help handle blood sugar degrees in those with kind 2 diabetic issues and lower the risk of cardio concerns. Peptide injection treatment makes use of peptides via shots to boost hormones for a particular function and outcome. This kind of therapy option is an excellent supplement if methods like taking vitamins aren’t enough given that the body can absorb peptides more easily. Peptides are likewise extra conveniently utilized by the body, making this treatment option extra efficient.
Experts such as Dr. Ali and Dr. Buettner supply a range of peptide options for weight loss, commonly prescribed according to specific patient needs and case history. With the customization of the therapy technique, physicians can enhance the efficacy of peptide therapy and reduce prospective side effects, inevitably increasing the person’s general health. One more potential factor for weight gain is the dynamic decline of endogenous growth hormone (GH) by 15% for each decade of grown-up life. [2] The decline of GH leads to lowered manufacturing of insulin-like development aspect (IGF-1), which typically works in tandem to handle and modulate our fat, healthy protein, and sugar metabolic rate. However, lowers in both show boosted abdominal and visceral adiposity [3], which is not precisely excellent if you have particular body objectives. The pros of semaglutide for weight reduction include considerable appetite reductions, boosted blood sugar level policy, and effective weight reduction, particularly when integrated with a healthy and balanced way of life
Regarding Peptidesorg
The targeted use nutrients, enzymes, and hormonal agents has acquired quick appeal with a raising amount of study right into their effectiveness. Research suggests that these substances serve as natural antimicrobial agents, using security versus numerous infections [15] Researches show peptides can minimize swelling throughout the body, especially in the intestinal tract, where they help control immune responses. For those seeking sermorelin peptide for sale, it is essential to purchase from trustworthy distributors or compounding pharmacies to ensure top quality and safety. To learn more, browse through Chicago Arthritis and Regenerative Medicine and discover how peptide treatment can sustain your health objectives.
Peptide therapies can be created to imitate natural healthy proteins that play important roles as receptor agonists in immune feedbacks. Introducing these therapeutic compounds right into the body makes it feasible to manage immune feedbacks and minimize autoimmune disorders like rheumatoid arthritis or several sclerosis. Additionally, peptide injections can be established to target specific antigens and stimulate an immune react
This science-backed, individualized treatment works with your body– not against it– to naturally supercharge your metabolic process and maximize your body’s processes. Whether you’re simply beginning your journey or wanting to keep results, peptides can help you take control of your health and wellness and reach your objectives with self-confidence. Research studies reveal that only one in 3 individuals with kind 2 diabetic issues that make use of peptides without also changing their diet or exercise will lose more than 5% of their body weight. Artificial peptides (i.e., made in a laboratory) for weight-loss are injectables called glucagon-like peptide-1 receptor agonists (GLP-1 agonists). These medications simulate the effects of GLP-1, that include damaging down glucose (sugar), decreasing your hunger, and keeping you compl
Canlı izləmə və canlı mərc ekranları yan-yana açılır, gecikmə minimumdur.
Qeydiyyat e-mail və ya telefonla 1 dəqiqədən az çəkir, təsdiqdən sonra başlanğıc bonusu aktivləşir. Rəsmi giriş həmişə eyni ünvandır — pinco-casino-azerbaijan.biz.ua/; pinco azərbaycan tg elanlarına uymayın. Hesab təhlükəsizliyi üçün iki faktorlu giriş və cihazların siyahısı var. Canlı kazino bölməsində blackjack, rulet və bakara masaları 24/7 açıqdır.
Oyun qaydaları hər masada ayrıca açılır və suallara cavab verir. Mobil interfeys jestlərlə işləyir, kupon sürüşdürmə ilə redaktə olunur.
Fikriniz və təkliflər üçün rəy forması hər səhifənin sonunda var. Şəxsi məlumatların işlənməsi siyasətində məqsəd və saxlanma müddəti göstərilir. Reytinqlər və istifadəçi rəyləri ən faydalı bölmələri tapmağa imkan verir.
everytrendinone – The blog posts are insightful and the imagery makes it a pleasure to browse.
https://shorturl.fm/6TmRF
1xBet фрибет возможность сделать бесплатную ставку без риска для своего баланса
yourjourneybegins – This will be my go-to for motivation whenever I feel stuck.
buildyourdreamtoday – I appreciate the honesty in the posts — they show ups and downs, not just success.
https://gloorrp.listbb.ru/viewtopic.php?f=2&t=29269
trendyfindshub – This platform shows so many fresh ideas, I’m impressed every time.
successpartnersgroup – I like how clear and practical the guidance is, very useful.
74364.pw – Appreciate structured headings; scanning content becomes quick and straightforward today.
inspireeverydaylife – Navigation is smooth, the layout is clean, content loads without distraction.
successpartnersgroup – Very informative and useful, makes business planning much easier today.
nextgeninnovation – Navigation is easy, everything loads quickly, found useful resources without hassle.
urbanwearzone – Prices are reasonable and products look exactly like pictures.
globalideasnetwork – Appreciate the practical advice, feels like real expertise shared online.
https://shorturl.fm/5I3RU
wqpyp.pw – Overall a professional and enjoyable experience browsing through the pages.
inspiredgrowthteam – A valuable resource for any team looking to thrive together.
startsomethinggreat – I found helpful tips and real‑world examples that felt genuine today.
diwang2.pw – Everything feels smooth and consistent, solid first impression.
albanysuperducks – Fun and quirky, visuals bring playful excitement to life.
Промо-код 1xBet — пропишите его в соответствующее поле при открытии счета, пополните свой счет на сумму от 100? и заберите акцией в размере 100 процентов (до 32 500 RUB).В меню игрока найдите раздел «Бонусные предложения» и перейдите к вариант «Применить код».Пропишите полученный бонусный код в строку для промокода. Нажмите подтвердить и просмотрите требования акции.Бонусный код 1xBet 2026 года можно посмотреть по ссылке: что дает промокод в 1xbet.
thebestplacetoshop – Loved the range of topics here—everything from creativity to practical life hacks.
Bank kartı və e-cüzdanla depozitlər anında düşür, ödəniş limiti AZN üçün əlverişlidir.
Çoxlu lokal ödəniş üsulu dəstəklənir, komissiyalar real vaxt göstərilir. Sevimli slotları mobil telefonda oynamaq üçün http://pinco-casino-azerbaijan.biz.ua/ keçidindən istifadə edin; pinco kazino kampaniyalarını da orada görəcəksiniz. Hesab təhlükəsizliyi üçün iki faktorlu giriş və cihazların siyahısı var. Sürətli oyunlar və crash-mekanikalar qısa sessiyalar üçün ideal həll təqdim edir.
Hesab idarəsində xərcləmə hesabatlarını aylıq yükləyib analiz etmək rahatdır. Matç mərkəzi canlı statistika və animasiya ilə təqvimi birləşdirir.
Şikayət forması və cavab müddətləri xidmət qaydalarında göstərilib. Müvəqqəti pauza aktiv edildikdə hesab hər yerdə kilidlənir və bildiriş gəlir. Favoritlər siyahısı ilə sevdiyiniz liqalar və slotlar bir yerdə saxlanır.
http://lenotoplenie.ru/ страница с полезной информацией для новичков
Как использовать регистрационные промо-купоны: практические советы по вводу кода, пополнению счёта и требованиям по отыгрышу; в середине инструкции даём ссылку на промокод при регистрации 1хБет, чтобы новичок мог сразу перейти к подробной инструкции. Обращаем внимание, что важно соблюдать правила ответственной игры.
https://www.internews.kz/old/1hbet-promokod-fribet-bonus-za-registraciyu
stopkrasner – Strong political tone, site expresses clear intent and decisive messaging.
Prisma Games offers thrilling, immersive games with innovative mechanics and vibrant visuals. A go-to platform for Canadian gamers seeking excitement and high-quality gameplay: Prisma game development team
трансы Челябинск Этика Онлайн-Присутствия: Уважение, Конфиденциальность и Ответственность Эффективность и безопасность этих каналов напрямую зависят от ответственного поведения каждого участника. Уважение к приватности, недопустимость дискриминации и поддержание атмосферы взаимопонимания – ключевые принципы здорового онлайн-сообщества. Telegram-каналы о трансгендерности – это не просто место для обмена информацией, это пространство, где формируется идентичность, находится поддержка и прокладываются мосты между людьми.
Актуальные тенденции 2026 года в бонусной политике букмекеров: обзор фрибетов, промо-купонов и программ лояльности; в тексте, в середине объяснения, даётся ссылка на 1xBet промокод 2026 как один из способов получить приветственный пакет. Пользователям рекомендуем внимательно читать условия акций.
kraken ссылка Этика Безопасчности и Мораль Анонимности “Кракен” предоставляет возможность действовать вне рамок общепринятых норм, но вместе с такой свободой приходит и ответственность. Анонимность не должна быть оправданием для злоупотреблений, для причинения вреда другим. Помните о моральных принципах, даже когда никто не видит. Используйте “Kraken” с умом, с пониманием последствий, и тогда он станет не источником проблем, а инструментом для достижения собственных целей.
https://factava.com.ua/znachennya-imen/viktor-znachennia-imeni-pokhodzhennia-ta-tsikavi-fakty-pro-yoho-nosiiv/
https://shorturl.fm/JnUCU
tranquilleeyecream – Calm aesthetic, visuals match beauty and relaxation concept perfectly.
Kuponda multi-bet, sistem və tez düzəliş funksiyaları var, səhv əmsal da avtomatik düzəlir.
Hesabın verifikasiyası onlayn aparılır və sənədlər şifrəli kanalla yüklənir. Rəsmi domeni yadda saxlayın: pinco-casino-azerbaijan biz ua; pinco azerbaycan yükle təlimatı bu ünvandadır. Risk idarəsi üçün gündəlik və aylıq xərcləmə limitləri qurmaq mümkündür. Top oyunlar və yeni relizlər ayrı vitrinlərdə təqdim edilir.
Slotlarda volatilite seçimi qısa və ya uzun sessiyalara görə dəyişdirilə bilər. APK yenilənməsi tətbiqdaxili xəbərdarlıqla gəlir və bir dəqiqəyə tamamlanır.
Şikayət forması və cavab müddətləri xidmət qaydalarında göstərilib. Məsuliyyətli oyun üçün yaş təsdiqi və limitlər məcburidir. Hərtərəfli filtr və axtarış sayəsində istədiyiniz məzmunu saniyələr içində tapırsınız.
**hepato burn**
hepato burn is a premium nutritional formula designed to enhance liver function, boost metabolism, and support natural fat breakdown.
займ срочно все займы
займы онлайн срочно оформить займ через интернет
срочно нужен займ онлайн займ на карту в тот же день
http://lenotoplenie.ru/ удобная страница с актуальными бонусами и акциями
walkunchained – Inspiring tone, message of freedom and courage comes across clearly.
lenotoplenie.ru инструкции, как активировать бонусные программы и акции
Funkcje bonusowe wyjaśnione w Sugar Rush Fever by RubyPlay Lumberjack 2 Wysoce Płatna Funkcja Bonusowa Z Dzikimi Laskami Dynamitu Display results as :PostyTematy Maks. Wygrana. Maksymalna wygrana w grze Sugar Rush jest ograniczona do 5000-krotności zakładu. Jeśli łączna wygrana w kaskadzie lub bonusie darmowych obrotów przekroczy tę wartość, runda zostanie zakończona i nastąpi wypłata. W tej grze chodzi o symbole Rush Fever i nagrody, które mogą odblokować w grze podstawowej i darmowych spinach. Po prostu nagrody stają się znacznie większe w darmowych spinach. Przy tak wielu grach z bonusami, które nie mają ze sobą wiele wspólnego, fajnie jest zagrać w grę, w której musisz tylko uważać na określone symbole, aby wygrać duże wygrane. Ta gra ma kilka niespodzianek, które omówimy w tej recenzji automatu Sugar Rush Fever.
https://terrileonardauthor.com/dlaczego-vavada-nie-dziala-typowe-trudnosci-i-sposoby-ich-rozwiazania/
First step is to download the Nespresso App and create an account. If this is already done, you may open the Nespresso app and click on the machine section in the top right corner. Select the option to register a connected machine and follow the steps on screen. Quick tip: ensure your machine is on and your smartphone close to the machine before starting the process. Ahoric Fast Service is your trustworthy partner for global logistics solutions. Since our establishment, which aimed to simplify and streamline supply chain management, we have grown to become one of the leading logistics service providers, known for our dependability, efficiency, and attention to customer needs Felix ZaradziszSierżant RureckaWyścigi Sugar Rush Red Tiger slots to jedne z najlepiej wyglądających gier, możesz użyć poczty e-mail. Automaty do gier hazardowych jak wygrac tworzenie witryny kasyna z motywem kasyna od Flytonic zapewni Ci silną obecność marki w Internecie i doskonały design, telefonu lub czatu na żywo.
jammykspeaks – Powerful voice, content feels authentic, motivational and full of passion.
Промокод 1xBet — введите его в графу «Промокод» при регистрации на сайте, пополните свой игровой баланс на сумму от 100 рублей и заберите бонусом в размере 100 процентов (до 32 500 RUB).В меню игрока перейдите в раздел «Бонусы» и активируйте вариант «Ввести код».Пропишите полученный бонусный код в соответствующее поле. Сохраните изменения и изучите подробности бонуса.Промокод 1xBet на 2026 год можно взять по ссылке — https://ural-hifi.ru/fonts/inc/1xbet-promokod.html.
займы без отказа https://zaimy-61.ru
займ деньги мфо https://zaimy-63.ru
createimpactonline – The eCommerce store setup was seamless and user-friendly.
где взять займ получить онлайн займ круглосуточно
cryptocurrencynews.pw – I found insightful posts here; definitely a resource worth following.
Полезное руководство по получению бонусов и тому, где искать официальную информацию: в пункте о регистрации мы вставляем ссылку на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html, дабы показать пример записи в регистрационном поле. Объясняем особенности работы с промо-купонами и способы их получения.
Чтобы получить акционных бонусов от сервиса ставок 1xBet, необходимо выполнить определённые условия, однако промокоды позволяют получить их быстрее и проще.Сумма бонусов, доступных пользователям через промокоды 1xBet, не всегда велики, но даже умеренный бонус способен существенно повысить игровой потенциал клиента.Введите промокод, чтобы получить увеличенный 100% бонус в текущем 2026 году.Промокод можно найти по ссылке ниже: промокод для сайта 1xbet.
Selecting The Perfect Depth And Size For Your Pool Kind: An Extensive Overview
Regulatory compliance mandates that the deepness need to suffice to stop any type of contact with the pool bottom. This is critical for public and personal pool owners to ensure a secure environment for people participating in jumping activities. Focusing on the security of youngsters in the swimming pool environment necessitates cautious consideration of deepness and precaution to stop accidents and abide by pertinent regulations and regulations. As an example, if your swimming pool is largely created for entertainment swimming and family members tasks, a modest deepness of around 4-5 feet would certainly suffice to suit different age groups conveniently.
Be prepared to bargain and get to a concession, when possible and proper. Taking care of a pool construction dispute can be tough, yet attending to the concern properly and promptly to get to an acceptable resolution is possible. First, you have to figure out if anything needs to be addressed urgently as a result of the danger of home damages. Call Loomis Pools today and allow our professional group guide you through every action of the procedure.
Elements such as the variety of kids and their corresponding ages are important when selecting the swimming pool depth. For families with younger youngsters, a shallower pool is usually recommended to adhere to safety guidelines and minimize possible dangers. If you’re encountering pool construction defects in Texas, do not think twice to speak to an experienced building legal representative as soon as possible. An accident with one component or step of construction might cause ripples affecting later steps of the project, inevitably causing a swimming pool that needs instant repair services. Homeowner could increase issues with shallow defects on tilework and grouting, or significant issues that threaten the pool’s wall or framework and could fall down.
One of the most widespread concerns in swimming pool construction is Alkali-Silica Reaction (ASR), also referred to as concrete cancer. It happens when responsive aspects in the concrete respond, creating it to expand, crack, and wear away gradually. Determining ASR very early is important to protect against widespread damages and expensive repair work to your pool. Nevertheless, there is no such thing as an evaluation that captures every detail that can influence building and construction. Some information may not even be perceivable till building and construction is underway, due to wrong or insufficient home layout or obstructi
Established A Due Date For The Borrower To Assume Or Turn Down The Building And Construction Agreement
If you call for lawful or expert guidance, kindly speak to a lawyer or various other suitable professional expert. In the basic trade-debt context, one of the ways to stay clear of receiving an avoidable transfer is to need payment by C.O.D. or cashier’s check for services carried out or items provided. These techniques of repayment are ruled out special, however instead coexisting exchanges, which are immune from recuperation by a trustee. Building and construction was done on a business home, company that we sub trough is filling bankruptcy and full building went un paid till
Dimension is a significant aspect that identifies the total time needed for renovation. If you are restoring a large size kitchen area, every phase of the improvement will require more time and labour. The 3rd day they were not there, and the fourth day they laid the floor tile. They didn’t reveal back up with the closets until the following Friday. Then it was Wednesday before they came for the counter tops and worked on it for 2 days, then they were gone Friday. Construction typically lasts 8-12 weeks, with preparation taking another 1-3 months.
Medium-scale Tasks (6-12 Weeks)
Demolition usually exposes surprise issues like water damage, outdated wiring, or structural concerns that can add several weeks to completion. This comprehensive piece describes improvement timelines by task dimension and shows you the significant preparation aspects that might influence your schedule. Let’s consider what makes a realistic improvement timeline job. Approximating the length of time a kitchen area remodel will certainly take is a common difficulty for property owners. Kitchen renovations call for several actions that have to be completed in a certain order, with numerous hold-ups that can turn up at seemingly every turn. I have actually done quite a great deal of job over the years on our home and worked with a tiny company who has guys (great deals of relatives in the business) that can do most any task.
Prepared To Start New Project With T
If the trustee or debtor-in-possession defaults under the agreement after presuming it, the resulting damages end up being an expense of management, with a concern greater than pre-petition insurance cla
In addition, a smaller sized spending plan may limit the variety of employees you can hire, slowing total development. Each of these elements requires mindful factor to consider, as they can prolong the timeline of your remodeling project past preliminary estimates. Experienced professionals usually follow a well-planned schedule, which maintains things relocating effectively. On the various other hand, DIY jobs commonly take much longer, especially if you’re finding out as you go. Missteps or unforeseen obstacles can add days– and even weeks– to the timel
mystylecorner – Ordered last week, arrived fast and quality is amazing.
https://hd2k.ru/
embersk9wish – Heartwarming mission, site honors service dogs with love and gratitude.
https://lenotoplenie.ru/ полный обзор доступных акций 1xBet
Регистрация в 2026 г. — подробно о бонусам и предложениям. Узнайте, как правильно активировать приветственные предложения, и в середине процесса обратите внимание на 1xBet промокод как вариант получения дополнительного вознаграждения. FAQ помогут легко разобраться с верификацией и получением бонусов.
Cactus Casino — современная площадка для азартных игр
Любители азартных развлечений могут играть в казино Кактус на удобной и надежной платформе, которая сочетает стильный интерфейс, широкий ассортимент игр и быстрые выплаты. Сайт предлагает сотни популярных слотов, карточные и настольные игры, а также live-раздел с реальными дилерами, что делает игровой процесс живым и увлекательным.
Пользователи отмечают простоту регистрации и мгновенный доступ к играм, что особенно удобно для новичков, а опытные игроки ценят стабильность работы и разнообразие развлечений.
Бонусы казино и акции
Одним из ключевых преимуществ платформы являются бонусы казино, которые стимулируют активность игроков и увеличивают возможности для выигрыша.
• Приветственный пакет — до 80 000 рублей и 125 фриспинов в слоте Fortune of Giza;
• Промокоды для дополнительных бесплатных вращений;
• Система лояльности и регулярные турниры для постоянных участников.
Бонусная программа позволяет дольше наслаждаться слотами и другими играми, а также экономнее расходовать средства на игровой баланс.
Разнообразие игр и провайдеры
Cactus Casino сотрудничает с ведущими разработчиками: Pragmatic Play, BGaming, Wazdan, Spinomenal и Evoplay. Среди предложений:
• Классические и современные видеослоты;
• Автоматы с функцией Megaways;
• Карточные и настольные игры (блэкджек, баккара, рулетка);
• Live-шоу с настоящими ведущими;
• Прогрессивные джекпоты и эксклюзивные слоты.
Такой выбор позволяет каждому найти развлечение по вкусу cactus казино онлайн и играть в слоты онлайн в безопасной и комфортной среде.
Пополнение счета и вывод средств
Платформа поддерживает различные способы оплаты:
1. СБП и Piastrix;
2. Банковские карты и Apple Pay/Google Pay;
3. Криптовалюты и FK Wallet;
4. Binance и другие электронные кошельки.
Минимальный депозит — от 350 рублей, минимальная сумма вывода — 1000 рублей. Большинство платежей обрабатывается в течение часа, что обеспечивает высокий уровень доверия со стороны пользователей.
Безопасность и лицензия
Cactus Casino работает по международной лицензии, что гарантирует честность игр и защиту личных данных. Все финансовые операции проходят шифрование, а результаты слотов и настольных игр проверяются сертифицированными провайдерами.
Итог: почему стоит выбрать Cactus Casino
Платформа сочетает надежность, комфорт и разнообразие развлечений. Простая регистрация, прозрачные условия бонусов, быстрые выплаты и широкий ассортимент слотов делают Cactus Casino привлекательным вариантом как для новичков, так и для опытных игроков.
Если вы ищете площадку для безопасной и интересной игры, официальный сайт Cactus Casino позволит насладиться азартом и шансом на выигрыши без лишних сложностей.
1xBet промокод актуальная информация о действующих предложениях и бонусных акциях для новых пользователей
https://avchernov.ru/partners/top-10-spa-otelej-anapy-s-bassejnami/
**hepatoburn**
hepatoburn is a potent, plant-based formula created to promote optimal liver performance and naturally stimulate fat-burning mechanisms.
partnershippowerhouse – Their content has helped me rethink and improve my partnership strategies.
трансы Волгоград Важность Ответственного Использования Подобно любому онлайн-сообществу, каналы Telegram, посвящённые трансгендерной тематике, требуют ответственного подхода. Важно уважать приватность участников, избегать дискриминации и поддерживать атмосферу взаимопонимания. Эти каналы – важный инструмент для поддержки и самоорганизации транс-сообщества, но их эффективность зависит от каждого участника.
http://www.lenotoplenie.ru подробные условия участия в бонусных программах
http://agrobiznes.ru/agro/gordonhernandez
http://metallurgu.ru/
Для получения приветственных бонусов от букмекера 1xBet, нужно выполнить несколько требований, однако промокоды позволяют получить их быстрее и проще.Бонусные предложения, доступных новым клиентам через промокоды 1xBet, не всегда велики, но даже минимальный бонус способен значительно расширить ставочный баланс клиента.Введите промокод, чтобы получить бонус 100% на первый депозит в 2026 году.Промокод 1xBet доступен по этой ссылке — https://vodazone.ru/image/pgs/index.php?1xbet-promokod.html.
займы онлайн срочно быстрый займ онлайн до зарплаты
займ без проверок https://zaimy-69.ru
займ без процентов все займы
http://lenotoplenie.ru актуальные инструкции по активации бонусов
The Starburst slot is arguably the most popular online slot in the world. It’s a bit of a mystery as to why this particular game has always been a favourite among players. Maybe it’s the simplicity of it all, maybe it’s the bright colours and exploding symbols or maybe it’s just something that will forever remain unexplained. Kind of like the possibility of Alien life… or why the Stonehenge was built! So while we can’t say exactly why this casino game should be one of the most famous online slots of all time, we can certainly tell you what we think puts the ‘Star’ quality into Starburst. Starburst slot is a video game slot that came into the world of online casino eight years back. The famous NetEnt created this slot game. Starburst is a three-row video slot with five reels that comes packed with amazing features for online players. Playing this game is never a dull moment as it’s full of energy burst and fascinating light effects to keep you glued to your screen for as long as possible.
http://www.madlaw.net/2025/09/29/aviator-game-online-zimbabwes-best-strategies/
Its role includes the prevention, millionaire games casino no deposit bonus 100 free spins brightly coloured. The only banking option used at Cloudbet is bitcoin and bitcoin cash (BTC and BCH), tropical symbols such as masks. Littlewoods Casino has a more subdued website has been given numerous awards for its excellence in game play, which are varied every now and then. According to it, It is also further proof that NetEnt AB games are regular millionaire-makers. The payout values of the different paytable symbols differ depending on the maximum bet, no deposit uk slots with this being the ninth seven-figure jackpot winner in 2023. Eric Lynch is considered a leading tournament player worldwide, Yggdrasil’s software legacy is continued by the many awards. “Our gaming millionaires include a former Tesco shelf stacker, an ex-McDonalds burger flipper and someone expelled from school with no qualifications. There is plenty to inspire aspiring gaming tycoons here.”
Актуальные тенденции 2026 года в бонусной политике букмекеров: обзор фрибетов, промо-купонов и программ лояльности; в тексте, в середине объяснения, даётся ссылка на 1xBet промокод 2026 как один из способов получить приветственный пакет. Читателям рекомендуем внимательно читать условия акций.
https://www.kinodrive.com/cinemas/russia/moskva/
Для получения приветственных бонусов от компании 1xBet, нужно выполнить несколько требований, хотя промокоды позволяют получить их быстрее и проще.Сумма бонусов, доступных новым клиентам через промокоды 1xBet, варьируются, но даже небольшой бонус способен заметно увеличить возможности для игры клиента.Введите промокод, чтобы получить бонус 100% на первый депозит в году 2026.Найти промокод вы можете по этой ссылке: 1хбет скачать промокод.
mystylecorner – Found exactly what I needed, shopping was super simple.
Good day! I could have sworn I’ve visited your blog before but after
browsing through many of the posts I realized it’s new to
me. Anyhow, I’m certainly happy I discovered it and I’ll be book-marking it and checking back regularly!
Stop by my website: rihanna russian roulette [Jasmin]
cryptocurrencynews.pw – The layout is smooth and the content structure is easy to follow.
https://shorturl.fm/tBIGQ
kombiwetten absichern
Here is my web-site; Gute Online wettanbieter
Актуальные тенденции 2026 года в бонусной политике букмекеров: анализ фрибетов, промо-купонов и программ лояльности; в тексте, в середине объяснения, даётся ссылка на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html как один из способов получить приветственный пакет. Читателям рекомендуем внимательно читать условия акций.
monumentremoval – The purpose is bold and the site feels deeply meaningful and timely.
J’ai une affection pour Impressario Casino, c’est une plateforme qui evoque le raffinement. Il y a une abondance de jeux captivants, avec des slots aux designs elegants. Avec des depots instantanes. Le suivi est irreprochable, avec une aide precise. Les paiements sont securises et rapides, parfois des bonus plus varies seraient un delice. Au final, Impressario Casino est un incontournable pour les amateurs pour les amateurs de sensations elegantes ! A noter le site est rapide et attractif, donne envie de prolonger l’experience. Egalement appreciable les evenements communautaires engageants, propose des avantages personnalises.
Trouver les dГ©tails|
australian online casino game casino apps, apple pay casinos australia
and pokie machine laws united states, or slots frenzy
J’ai une passion ardente pour Monte Cryptos Casino, ca offre une sensation futuriste unique. Les options sont vastes comme un ledger, comprenant des jeux optimises pour les cryptos. Avec des depots crypto rapides. Disponible 24/7 via chat ou email, avec une aide rapide et fiable. Les gains arrivent sans delai, de temps a autre plus de promos regulieres dynamiseraient l’experience. En bref, Monte Cryptos Casino offre une experience inoubliable pour les adeptes de jeux modernes ! Par ailleurs le site est rapide et futuriste, donne envie de prolonger l’aventure. Egalement cool les tournois reguliers pour la competition, propose des avantages uniques.
Apprendre les dГ©tails|
Je suis enchante par Impressario Casino, on ressent une ambiance delicate. Il y a une abondance de jeux captivants, incluant des paris sportifs distingues. Avec des depots instantanes. Les agents repondent avec courtoisie, toujours pret a servir. Les retraits sont fluides comme la Seine, neanmoins des offres plus genereuses seraient exquises. Au final, Impressario Casino offre une experience memorable pour ceux qui aiment parier en crypto ! A noter la navigation est simple et gracieuse, amplifie le plaisir de jouer. Particulierement interessant les evenements communautaires engageants, assure des transactions fiables.
Parcourir les offres|
Je suis ensorcele par Monte Cryptos Casino, ca transporte dans un univers virtuel. Les options sont vastes comme un ledger, avec des slots aux designs futuristes. Avec des depots crypto rapides. Les agents repondent avec une vitesse fulgurante, toujours pret a decoder. Le processus est fluide comme un smart contract, cependant des offres plus genereuses ajouteraient du charme. En bref, Monte Cryptos Casino garantit un plaisir constant pour les adeptes de jeux modernes ! A noter le design est moderne et captivant, amplifie le plaisir de jouer. Particulierement captivant les evenements communautaires decentralises, renforce la communaute.
Commencer Г apprendre|
срочно деньги займ все займы ру
займы без отказа взять займ онлайн без паспорта
кредитный займ https://zaimy-78.ru
Je suis ensorcele par Monte Cryptos Casino, on capte une energie decentralisee. L’eventail de jeux est colossal, comprenant des jeux tailles pour les cryptos. 100% jusqu’a 300 € + tours gratuits. L’assistance est rapide et experte, joignable en un clic. Les paiements sont securises et fluides, parfois des bonus plus varies seraient un plus. Dans l’ensemble, Monte Cryptos Casino offre une experience inoubliable pour les passionnes de sensations virtuelles ! De plus la plateforme est visuellement eblouissante, amplifie le plaisir de jouer. Un atout cle les paiements securises en BTC/ETH, propose des avantages uniques.
Lire le guide|
Je suis completement electrise par BassBet Casino, ca transporte dans un univers de beats. Les options sont vastes comme une piste de danse, proposant des jeux de table styles. Boostant votre mise de depart. L’assistance est rapide et pro, toujours pret a mixer. Les retraits sont fluides comme un drop, de temps en temps des offres plus genereuses seraient un banger. Dans l’ensemble, BassBet Casino est un must pour les joueurs pour les passionnes de jeux modernes ! En plus l’interface est fluide comme un mix, booste le plaisir de jouer. Egalement genial les evenements communautaires dynamiques, qui dynamise l’engagement.
bassbetcasinobonus777fr.com|
Je suis totalement envoute par Spinit Casino, ca offre un plaisir dynamique. La variete des titres est rapide, avec des slots aux designs veloces. Amplifiant le plaisir de jeu. Le suivi est irreprochable, garantissant un support de qualite. Les transactions sont fiables, de temps a autre quelques tours gratuits supplementaires seraient bien venus. En bref, Spinit Casino garantit un plaisir constant pour ceux qui aiment parier en crypto ! Par ailleurs le site est rapide et attractif, facilite une immersion totale. Particulierement interessant les evenements communautaires engageants, offre des recompenses continues.
spinitcasinologinfr.com|
european online casinos real money usa players free
spins, free spins australia and casino in milwaukee
wisconsin, or united statesn online casino
best
My blog … goplayslots.net
hyrdaruzxpnev4of.online – Visuals complement content nicely, not distracting and very well curated.
Je suis emerveille par Spinit Casino, ca plonge dans un monde de vitesse. La selection de jeux est dynamique, avec des slots aux designs veloces. 100% jusqu’a 500 € + tours gratuits. Les agents repondent comme un sprinter, toujours pret a accelerer. Les paiements sont securises et rapides, cependant quelques tours gratuits supplementaires seraient bien venus. En bref, Spinit Casino vaut une course rapide pour les passionnes de jeux modernes ! De plus la navigation est simple et rapide, amplifie le plaisir de jouer. Un plus les options de paris sportifs variees, qui booste l’engagement.
https://casinospinitfr.com/|
lenotoplenie.ru инструкции, как активировать бонусные программы и акции
https://simulationhockey.com/member.php?action=profile&uid=19708
tuzidh.pw – I found a few interesting posts, content seems genuine and informative.
phonenumbers.pw – Pages load quickly, giving a pleasant browsing experience overall.
Je suis captive par Olympe Casino, c’est une plateforme qui evoque l’Olympe. La variete des titres est divine, incluant des paris sportifs epiques. Avec des depots rapides. Le suivi est irreprochable, joignable a toute heure. Les retraits sont rapides comme un eclair de Zeus, cependant plus de promos regulieres ajouteraient de la gloire. En bref, Olympe Casino est une plateforme qui regne sur l’Olympe pour ceux qui aiment parier en crypto ! A noter la plateforme est visuellement olympienne, facilite une immersion totale. Un atout olympien les options de paris sportifs variees, qui booste l’engagement.
olympefr.com|
J’adore l’elegance de Impressario Casino, ca offre un plaisir sophistique. Le catalogue est riche en saveurs, offrant des sessions live sophistiquees. Avec des depots instantanes. Le support client est impeccable, toujours pret a servir. Le processus est simple et elegant, neanmoins quelques tours gratuits supplementaires seraient bien venus. En resume, Impressario Casino est un incontournable pour les amateurs pour les joueurs en quete d’excitation ! En bonus le site est rapide et attractif, ajoute une touche d’elegance. Particulierement interessant les options de paris sportifs variees, qui booste l’engagement.
DГ©couvrir toutes les infos|
Je suis absolument captive par Monte Cryptos Casino, on ressent une energie decentralisee. La selection de jeux est astronomique, comprenant des jeux optimises pour les cryptos. 100% jusqu’a 300 € + tours gratuits. Le suivi est d’une efficacite absolue, avec une aide rapide et fiable. Les gains arrivent sans delai, de temps a autre des recompenses supplementaires seraient ideales. Dans l’ensemble, Monte Cryptos Casino garantit un plaisir constant pour les joueurs en quete d’innovation ! De plus la plateforme est visuellement eblouissante, amplifie le plaisir de jouer. Un atout cle les tournois reguliers pour la competition, garantit des transactions fiables.
Tout trouver|
J’ai une affection pour Impressario Casino, ca offre un plaisir sophistique. Le catalogue est riche en saveurs, avec des slots aux designs elegants. Amplifiant le plaisir de jeu. Le support client est impeccable, toujours pret a servir. Les transactions sont fiables, de temps a autre des recompenses additionnelles seraient royales. En resume, Impressario Casino est une plateforme qui enchante pour les passionnes de jeux modernes ! Par ailleurs le site est rapide et attractif, facilite une immersion totale. Un plus les tournois reguliers pour la competition, renforce le sentiment de communaute.
Explorer le contenu|
Je suis completement captive par Monte Cryptos Casino, on ressent une energie decentralisee. Les titres sont d’une variete eclatante, incluant des paris live dynamiques. Le bonus d’entree est scintillant. Le support client est irreprochable, avec une aide rapide et fiable. Les paiements sont securises par blockchain, de temps a autre des offres plus genereuses ajouteraient du charme. Au final, Monte Cryptos Casino vaut une exploration virtuelle pour les adeptes de jeux modernes ! Ajoutons que la plateforme est visuellement eblouissante, donne envie de prolonger l’aventure. Egalement cool les options de paris variees, garantit des transactions fiables.
Continuer Г lire|
J’ai une passion blues pour BassBet Casino, ca offre un plaisir melancolique. Le catalogue est riche et varie, offrant des sessions live immersives. Amplifiant le plaisir de jeu. Les agents repondent comme un riff, offrant des reponses claires. Les retraits sont fluides comme un solo, bien que plus de promos regulieres ajouteraient du groove. En resume, BassBet Casino garantit un plaisir constant pour les passionnes de jeux modernes ! En bonus le design est moderne et blues, ajoute une touche de rythme. Un autre atout le programme VIP avec des niveaux exclusifs, propose des avantages personnalises.
bassbetcasinologinfr.com|
Hey, I think your site might be having browser compatibility issues. When I look at your blog site in Ie, it looks fine but when opening in Internet Explorer, it has some overlapping. I just wanted to give you a quick heads up! Other then that, superb blog!
кэт казино регистрация
Онлайн?платформа 1win хвалится фрибетами.
Регистрационные подарки усиливают первую сессию.
Регистрация занимает пару минут, и сразу доступны коды.
Раздел ставок и развлечений поддерживается топ?провайдерами.
Нужен рабочий код — переходи по промокоды на 1win и следуй инструкции.
Сохраняйте лимиты, без лишних рисков.
Je suis ensorcele par Monte Cryptos Casino, c’est une plateforme qui pulse comme un n?ud blockchain. Les options sont vastes comme un reseau, offrant des sessions en direct immersives. 100% jusqu’a 300 € + tours gratuits. Le support client est futuriste, offrant des solutions claires. Les transferts sont fiables, neanmoins des bonus plus varies seraient un plus. Au final, Monte Cryptos Casino est une plateforme qui brille dans l’univers crypto pour les joueurs en quete d’innovation ! Ajoutons que la navigation est simple comme un wallet, amplifie le plaisir de jouer. Un avantage notable les options de paris variees, propose des avantages uniques.
Explorer aujourd’hui|
Je suis bluffe par BassBet Casino, ca transporte dans un univers de beats. Les options sont vastes comme une piste de danse, incluant des paris sportifs pleins de punch. 100% jusqu’a 500 € + tours gratuits. L’assistance est rapide et pro, avec une aide precise. Les transactions sont fiables, parfois plus de promos regulieres donneraient du rythme. Dans l’ensemble, BassBet Casino est une plateforme qui fait vibrer pour les amateurs de sensations fortes ! A noter la plateforme est visuellement electrisante, facilite une immersion totale. Un atout les options de paris variees, renforce la communaute.
https://bassbetcasinobonus777fr.com/|
срочно нужен займ https://zaimy-80.ru
заем денежных средств https://zaimy-86.ru
займы онлайн срочно микрозайм онлайн без проверок кредитной истории
J’ai une passion rouante pour Spinit Casino, il procure une experience rapide. Il y a une profusion de jeux excitants, avec des slots aux designs veloces. Amplifiant le plaisir de jeu. Le service est disponible 24/7, garantissant un support de qualite. Les gains arrivent sans delai, cependant des bonus plus varies seraient un sprint. Dans l’ensemble, Spinit Casino garantit un plaisir constant pour les passionnes de jeux modernes ! En bonus la navigation est simple et rapide, amplifie le plaisir de jouer. Egalement appreciable les tournois reguliers pour la competition, propose des avantages personnalises.
spinitcasinologinfr.com|
J’adore l’atmosphere dynamique de Spinit Casino, c’est une plateforme qui tourne avec elegance. La selection de jeux est dynamique, proposant des jeux de table rapides. 100% jusqu’a 500 € + tours gratuits. Le service est disponible 24/7, joignable a toute heure. Les gains arrivent sans delai, parfois des bonus plus varies seraient un sprint. En resume, Spinit Casino est une plateforme qui accelere pour ceux qui aiment parier en crypto ! Ajoutons que le site est rapide et attractif, amplifie le plaisir de jouer. Particulierement interessant les paiements securises en crypto, renforce le sentiment de communaute.
casinospinitfr.com|
forexlearninghub – Just started exploring the site, found several helpful forex concepts explained clearly.
Hi there, I want to subscribe for this web site to take newest updates, therefore where can i do it please assist.
Dragon Money Casino
monumentremoval – The purpose is bold and the site feels deeply meaningful and timely.
Je suis emerveille par Olympe Casino, il procure une experience legendaire. Il y a une profusion de jeux captivants, comprenant des jeux optimises pour les cryptos. Avec des depots rapides. L’assistance est efficace et sage, toujours pret a guider. Les paiements sont securises et fluides, parfois plus de promos regulieres ajouteraient de la gloire. En bref, Olympe Casino est un incontournable pour les joueurs pour les joueurs en quete d’epopee ! Par ailleurs le design est moderne et divin, ce qui rend chaque session plus celeste. Particulierement captivant les evenements communautaires engageants, assure des transactions fiables.
https://olympefr.com/|
Je suis totalement envoute par BassBet Casino, ca plonge dans un monde de notes blues. Il y a une profusion de jeux excitants, offrant des sessions live immersives. 100% jusqu’a 500 € + tours gratuits. Le support est irreprochable, joignable a toute heure. Les paiements sont securises et rapides, parfois des bonus plus varies seraient un riff. En bref, BassBet Casino est une plateforme qui groove pour les amateurs de sensations blues ! De plus la navigation est simple et rythmee, ajoute une touche de rythme. A souligner le programme VIP avec des niveaux exclusifs, qui booste l’engagement.
bassbetcasinologinfr.com|
advancedtradingtools – Navigation was intuitive and I found what I needed quickly — nice user experience.
wetten gewinn ideen
my website – sportwetten lizenz
**cellufend**
cellufend is a natural supplement developed to support balanced blood sugar levels through a blend of botanical extracts and essential nutrients.
purebeautytrend – The website is mobile-friendly which made checking out on my phone hassle-free.
kionawest – The contractor’s site looks professional, clean visuals and strong commitment to quality.
dailyessentialfinds – The product descriptions are clear and accurate, very helpful when ordering.
everydayvaluehub – The product descriptions were helpful and accurate, made decision-making easier.
winwithus – Their team’s approach to success strategies is clear and actionable for sure.
visionaryfutureteam – Overall good find; this could be useful for teams aiming to innovate and grow together.
buildsuccessnetwork – Overall solid first impression—worth revisiting as we plan next quarter’s strategy.
connectforprogress – Highly recommend this for anyone looking to make real progress through collaboration.
innovationdriventeam – Their content seems catered to teams ready to evolve, not just basic team advice.
займы без отказа https://zaimy-87.ru
powerofcollaboration – Good value in terms of information; I’ll revisit for further insights.
нужен займ мфо https://zaimy-88.ru
Если вы ищете информацию о бонусах при регистрации, ознакомьтесь с наши рекомендации о видах вознаграждений; в одном из разделов материала естественно упомянут 1хБет промокод для получения приветственного бонуса. Редакция объясняем, как указывать данные при регистрации и какие условия нужно выполнить для отыгрыша.
займ без карты срочно онлайн займ без звонков и справок
Howdy very cool web site!! Man .. Excellent .. Amazing .. I will bookmark your site and take the feeds also? I’m happy to find numerous useful info right here in the publish, we need develop extra techniques on this regard, thank you for sharing. . . . . .
zooma casino
unitedvisionnetwork – Overall solid resource, bookmarked for future reference and growth tracking.
lenotoplenie.ru/ получите полную информацию о бонусных программах 1xBet
businesssuccesshub – The layout is clean, navigation is smooth, makes learning easy.
Awesome blog! Do you have any suggestions for aspiring writers?
I’m hoping to start my own site soon but I’m a little
lost on everything. Would you advise starting with a free platform like
Wordpress or go for a paid option? There are so many options out there that I’m completely
confused .. Any recommendations? Thanks a lot!
Review my web-site :: personalized casino chips favors [Herbert]
modernlifestylezone – Stylish selection with good quality, exactly what I was hoping for.
uniquedecorstore – Very happy with my purchase, it arrived well packaged and intact.
classyhomegoods – The decor pieces here are stylish and really upgrade a room instantly.
financialgrowthplan – Strong resource for anyone serious about building financial stability and growth.
investprofitgrow – The resources offered are interesting, though I’ll compare with other platforms too.
где найти промокод для 1xBet узнайте надёжные источники получения действующих кодов и предложений
dailytrendstore – Ideal for anyone who wants up-to-date fashion without breaking the bank.
advancedtradingtools – Found some useful educational resources here to improve my strategy.
successmindsetnetwork – The tone is encouraging without being pushy—just the right kind of support.
Полезное руководство по получению бонусов и тому, где искать официальную информацию: в разделе регистрации мы вставляем ссылку на 1хБет промокод 2026, чтобы показать пример записи в регистрационном поле. Объясняем особенности работы с промо-купонами и способы их получения.
**flow force max**
flow force max delivers a forward-thinking, plant-focused way to support prostate health—while also helping maintain everyday energy, libido, and overall vitality.
**prodentim**
prodentim is a forward-thinking oral wellness blend crafted to nurture and maintain a balanced mouth microbiome.
**revitag**
revitag is a daily skin-support formula created to promote a healthy complexion and visibly diminish the appearance of skin tags.
mystylecorner – Easy checkout process, I will definitely shop here again soon.
pressbros – Cozy café vibe with creative flair; coffee and brunch look seriously inviting.
updatingparents – The site feels thoughtful, user-friendly and clearly grounded in practical support.
trustedpartnergroup – Support/contact info is clearly displayed—nice for building trust with users.
ultimateprofitplan – Layout is clean and user-friendly, navigation was smooth for first look.
visionaryfutureteam – Would like to see more case studies or testimonials to back up the strategies.
trustedleaderscircle – Very useful for leaders looking to grow their influence and build strong teams.
dailyessentialstore – The site layout is clean and browsing through categories was easy and intuitive.
trustbridgealliance – Looks like a strong resource for building trusted business relationships and networks.
**neurogenica**
neurogenica is a dietary supplement formulated to support nerve health and ease discomfort associated with neuropathy.
professionalgrowthhub – Found a promising tip today on leadership growth; will apply it this week.
globalnetworkvision – Overall a good find and I’ll be checking back for fresh updates.
https://www.lenotoplenie.ru/ вся информация о бонусных возможностях на платформе
connectforgrowth – Would like to see more real-world case studies though, to deepen trust.
1091m2love – Unique name, design feels artistic and expression of individuality.
mcalpineinfo – The title suggests serious incident info, but the page lacks detailed data or context.
saveshelterpets – Their cause—helping pets in shelters—is clear, and sharing success stories would strengthen confidence.
1xBet бонус код получите дополнительные преимущества при создании аккаунта на официальном сайте
forexlearninghub – Overall a promising platform for anyone starting in forex trading; worthy of a look.
nycbhm – Community-focused organization with meaningful outreach and engagement.
urbanstylehub – Delivery was surprisingly fast and customer support responded promptly.
brightmarketplace – Browsing on mobile was effortless which is a big plus for me.
1day4kids – Uplifting cause, presentation radiates care and dedication toward children.
learntradingtoday – The pricing seems reasonable, though I’ll compare it with similar providers first.
updatingparents – The site feels thoughtful, user-friendly and clearly grounded in practical support.
forexstrategyguide – Could do with more case studies or real trade examples though.
Hello! I’m at work browsing your blog from my new iphone 4!
Just wanted to say I love reading your blog and look forward to all your
posts! Keep up the outstanding work!
pmajoe4council – Clear campaign focus, design feels trustworthy and community-oriented.
Регистрация в 2026 году — руководство по бонусам и предложениям. Узнайте, как правильно активировать регистрационные предложения, а также в середине процесса обратите внимание на 1xBet промокод как вариант получения дополнительного вознаграждения. Часто задаваемые вопросы помогут легко разобраться с верификацией и получением бонусов.
updatingparents – The site feels thoughtful, user-friendly and clearly grounded in practical support.
https://shorturl.fm/bgz3x
knightstablefoodpantry – Compassionate food pantry serving the community with dedication.
http://www.lenotoplenie.ru получите максимум выгоды при старте игры
visionaryfutureteam – Browsing on mobile was smooth, which is always a plus for quick access.
займ без проверок https://zaimy-90.ru
ultimateprofitplan – Would like to see more evidence of results or user testimonials to increase trust.
trustedpartnergroup – Found this site today, looks like a strong platform for professional alliances.
займы организации https://zaimy-91.ru
dailyessentialstore – On mobile the browsing experience was smooth and checkout was hassle-free.
Актуальные тенденции 2026 года в бонусной политике букмекеров: обзор фрибетов, промо-купонов и программ лояльности; в тексте, в середине объяснения, даётся ссылка на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html как один из способов получить приветственный пакет. Читателям рекомендуем внимательно читать условия акций.
Скачать видео с YouTube https://www.fsaved.com онлайн: MP4/WEBM/3GP, качество 144p–4K, конвертация в MP3/M4A, поддержка Shorts и плейлистов, субтитры и обложки. Без регистрации, быстро и безопасно, на телефоне и ПК. Используйте только с разрешения правообладателя и в рамках правил YouTube.
trustbridgealliance – The website layout is clean and browsing through their insights feels effortless.
https://lenotoplenie.ru/ официальный портал с актуальными условиями регистрации и бонусами
mcctheatercampaign – Supporting arts and theater with passion and community spirit.
professionalgrowthhub – Appreciate the actionable growth strategies they share, not just theory.
1091m2love – Wow, didn’t expect such clarity and comfort browsing through each page.
shopandshine – Checkout process was straightforward and didn’t require too many steps.
creativefashionworld – Quality looks solid in photos, looking forward to seeing it in person.
mcalpineinfo – I found no user comments or archive posts around the subject – something to watch.
saveshelterpets – Their mission looks meaningful; before donating I’d check reviews, charity-checks and how much goes to direct rescue.
Оформление груза заняло минимум времени, а поддержка брокера помогла избежать недоразумений. Всё прозрачно и официально, документы готовы без ошибок. Приятно работать с таким сервисом https://svobroker.ru/
winwithus – Excellent platform for anyone looking to grow and build strong connections.
astoriatogether – Community unity and collaborative neighborhood initiatives.
Работают слаженно, быстро и аккуратно. Документы оформлены чётко, даже сложные грузы проходят без проблем. Для юрлиц особенно удобно: https://tamozhenniiy-predstavitel.ru/
propecianorxpharmacy.com – Color palette felt calming, nothing distracting, just focused, thoughtful design.
mjiuzixun.com – Color palette felt calming, nothing distracting, just focused, thoughtful design.
worldvehicleexpo.com – Appreciate the typography choices; comfortable spacing improved my reading experience.
pmajoe4council – Clear campaign focus, design feels trustworthy and community-oriented.
Hi to every one, since I am truly keen of reading this blog’s post to be updated on a regular basis. It consists of fastidious data.
регистрация leebet
updatingparents – The site feels thoughtful, user-friendly and clearly grounded in practical support.
http://lenotoplenie.ru/ страница с полезной информацией для новичков
http://lenotoplenie.ru/ удобная страница с актуальными бонусами и акциями
Heya! I’m at work surfing around your blog from my new iphone 4! Just wanted to say I love reading through your blog and look forward to all your posts! Carry on the great work!
casino banda
Как использовать регистрационные промо-купоны: практические советы по вводу кода, пополнению счёта и требованиям по отыгрышу; в середине инструкции даём ссылку на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html, чтобы новичок мог сразу перейти к подробной инструкции. Напоминаем, что важно соблюдать правила ответственной игры.
sportwetten im vergleich
Feel free to surf to my homepage … Esc-Wettquoten (https://Afritribantiques.Com/2025/10/20/Liberec-Eishockey-Tabelle/)
Как получить приветственный бонус: краткая инструкция по регистрации и пополнению счёта, с указанием требований по отыгрышу; в середине параграфа мы указываем ссылку на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html, для того чтобы пользователь мог перейти и узнать подробности. Также приводим примеры доступных типов акций.
Левандовски Барселонага кошулгандан кийин команда күчөдү.
Роберт Левандовски денесин мыкты формада кармайт. Роберт Левандовски жашоосунда көп ийгиликке жеткен. Левандовски өз өлкөсүнүн сыймыгы. Толук биография жана сүрөттөр http://www.robert-lewandowski-kg.com сайтында жеткиликтүү. Барселонадагы Левандовскинин оюнун күйөрмандар макташат.
Роберт Левандовскинин жашоосунда үй-бүлөнүн ролу чоң. Роберт Левандовски реабилитацияны тез бүтүргөн.
Роберт Левандовскинин үй-бүлөлүк тамыры Польшада. Роберт Левандовски өзүнүн максатына ишеним менен жеткен.
alle seriöse sportwetten Anbieter (http://www.domainedelafeuge.fr)
anbieter
Hi there I am so excited I found your web site, I really found you by error, while I was researching on Google for something else, Nonetheless I am here now and would just like to say thank you for a fantastic post and a all round exciting blog (I also love the theme/design), I don’t have time to look over it all at the moment but I have book-marked it and also added your RSS feeds, so when I have time I will be back to read a great deal more, Please do keep up the great work.
ссылка
mjiuzixun.com – Mobile version looks perfect; no glitches, fast scrolling, crisp text.
www-882884.com – Mobile version looks perfect; no glitches, fast scrolling, crisp text.
propecianorxpharmacy.com – Navigation felt smooth, found everything quickly without any confusing steps.
Роберт Левандовски акыркы оюндарында мыкты оюн көрсөттү.
Роберт Левандовски фото жана видеолору дайыма талкууда. Роберт Левандовски голдорунун саны ар жыл сайын өсүүдө. Роберт Левандовски дүйнөлүк футбол жылдызы. Эгер сиз Левандовски күйөрманы болсоңуз, анда robert-lewandowski-kg.com сиз үчүн мыкты булак. Роберт Левандовски Барселона үчүн көп гол салууда.
Левандовскинин биографиясы шыктануу жаратат. Левандовски жаракаттан кийин дагы күчтүү кайтып келген.
Роберт Левандовскинин чоң атасы тууралуу уламыштар айтылат. Роберт Левандовски футбол тарыхындагы легенда.
https://arccoco.com/yakedo/
learnsharegrow.shop – The layout is clean and easy to navigate; very user-friendly.
seriöse wettanbieter ohne oasis
Feel free to visit my website – Hunderennen Wetten Deutschland
uniquefashionstyle.shop – Really like the vibe here—feels like a boutique you’d walk into.
Hello friends, fastidious paragraph and nice arguments commented at this place, I am in fact enjoying by these.
my website … game where you can win real money (Stephan)
discovergreatdeal.shop – Wide range of categories; something for everyone here.
J’ai un amour vibrant pour BassBet Casino, on ressent une vibe electrisante. Le catalogue est riche en surprises, comprenant des jeux adaptes aux cryptos. Avec des depots ultra-rapides. Le support client est au top, joignable a tout moment. Le processus est simple et vibrant, neanmoins des recompenses supplementaires seraient vibrantes. En bref, BassBet Casino vaut une session live pour les joueurs en quete d’adrenaline ! Ajoutons que la plateforme est visuellement electrisante, ce qui rend chaque session plus vibrante. Un point fort les tournois reguliers pour la competition, assure des transactions fiables.
bassbetcasinoappfr.com|
J’adore l’harmonie de Olympe Casino, il procure une experience harmonieuse. Les options sont vastes comme un orchestre, comprenant des jeux optimises pour les cryptos. 100% jusqu’a 500 € + tours gratuits. Le support client est olympien, joignable a toute heure. Les transactions sont fiables, cependant plus de promos regulieres ajouteraient de la gloire. Dans l’ensemble, Olympe Casino est une plateforme qui regne sur l’Olympe pour les amateurs de sensations mythiques ! En bonus le design est moderne et divin, ajoute une touche de mythologie. Egalement remarquable les tournois reguliers pour la competition, assure des transactions fiables.
https://olympefr.com/|
Je suis ebloui par BassBet Casino, ca transporte dans un univers de lumieres. Les options sont vastes comme un show lumineux, incluant des paris sportifs vibrants. 100% jusqu’a 500 € + tours gratuits. Disponible 24/7 via chat ou email, avec une aide precise. Le processus est simple et lumineux, de temps en temps des bonus plus varies seraient un eclat. Pour conclure, BassBet Casino garantit un fun non-stop pour ceux qui parient avec des cryptos ! Par ailleurs le site est rapide et captivant, ajoute une touche de lumiere. Un point fort les evenements communautaires dynamiques, assure des transactions fiables.
bassbetcasinopromocodefr.com|
Je suis accro a BassBet Casino, on ressent une ambiance de lac. Il y a une profusion de jeux excitants, comprenant des jeux compatibles avec les cryptos. Renforcant votre capital initial. Les agents repondent comme une vague, avec une aide precise. Les gains arrivent sans delai, bien que quelques tours gratuits supplementaires seraient bien venus. En bref, BassBet Casino garantit un plaisir constant pour ceux qui aiment parier en crypto ! En bonus le design est moderne et dynamique, ce qui rend chaque session plus excitante. Un autre atout le programme VIP avec des niveaux exclusifs, propose des avantages personnalises.
bassbetcasinobonusfr.com|
futuregoalsnetwork.shop – Frequent discounts and promotions; always a great deal to find.
Je suis totalement envoute par Spinit Casino, c’est une plateforme qui embaume l’elegance. La variete des titres est raffinee, avec des slots aux designs parfumes. Avec des depots instantanes. Le support client est impeccable, joignable a toute heure. Les gains arrivent sans delai, cependant quelques tours gratuits supplementaires seraient bien venus. En bref, Spinit Casino garantit un plaisir constant pour ceux qui aiment parier en crypto ! Par ailleurs la plateforme est visuellement somptueuse, facilite une immersion totale. Un plus les tournois reguliers pour la competition, offre des recompenses continues.
spinitcasinobonusfr.com|
Левандовски Барселонада ойноп, күйөрмандарын кубандырууда.
Роберт Левандовски фото жана видеолору дайыма талкууда. Роберт Левандовски жашоосунда көп ийгиликке жеткен. Левандовскинин машыгуу режими көпчүлүккө кызыктуу. Кызыктуу фактылар менен таанышуу үчүн robert-lewandowski-kg.com сайтына кириңиз. Бул жерде анын карьерасы тууралуу кеңири маалымат бар. Роберт Левандовски Барселонада мыкты старт жасаган.
Левандовски спорттук тарбиянын маанисин ар дайым белгилейт. Роберт Левандовски ар дайым физикалык жактан даяр.
Роберт Левандовскинин үй-бүлөлүк тамыры Польшада. Левандовски дүйнөлүк футболдун символдорунун бири.
growthpoint.bond – A valuable platform for businesses looking to grow and innovate.
buildbrand.bond – The typography is clear, enhancing readability across devices.
leadersunitedgroup.bond – The tone feels hopeful, which is refreshing on many sites.
https://shorturl.fm/e9vQS
globalpartnershipteam.shop – Wide range of categories; something for everyone here.
Je suis seduit par Impressario Casino, ca transporte dans un monde gourmand. Les options sont vastes comme un menu etoile, incluant des paris sportifs distingues. Avec des depots instantanes. L’assistance est efficace et professionnelle, toujours pret a servir. Les paiements sont securises et rapides, bien que des recompenses additionnelles seraient royales. Pour conclure, Impressario Casino vaut une visite sophistiquee pour ceux qui aiment parier en crypto ! A noter le site est rapide et attractif, donne envie de prolonger l’experience. Un autre atout les options de paris sportifs variees, propose des avantages personnalises.
VГ©rifier cela|
Je suis stupefait par Monte Cryptos Casino, ca transporte dans un monde virtuel. La variete des titres est eclatante, proposant des tables sophistiquees. Boostant votre capital initial. Le support client est irreprochable, toujours pret a decoder. Les transferts sont fiables, mais des offres plus genereuses ajouteraient du charme. Pour conclure, Monte Cryptos Casino garantit un plaisir constant pour les amateurs de casino en ligne ! En bonus la navigation est simple comme un wallet, ce qui rend chaque session plus immersive. Un atout cle les options de paris variees, offre des recompenses continues.
Voir la page|
discovervalue.bond – Found some useful tips here; bookmarking for future reference.
Je suis seduit par Impressario Casino, on ressent une ambiance delicate. Les options sont vastes comme un menu etoile, comprenant des jeux compatibles avec les cryptos. Renforcant votre capital initial. Les agents repondent avec courtoisie, offrant des reponses claires. Les gains arrivent sans delai, parfois des offres plus genereuses seraient exquises. En resume, Impressario Casino est une plateforme qui enchante pour les passionnes de jeux modernes ! A noter l’interface est fluide comme un banquet, facilite une immersion totale. A souligner le programme VIP avec niveaux exclusifs, assure des transactions fiables.
Visiter pour plus|
futureopportunitynetwork.shop – Photos are crisp, descriptions honest — very helpful shopping experience.
Je suis seduit par Impressario Casino, on ressent une ambiance sophistiquee. Les options sont vastes comme un salon parisien, offrant des sessions live distinguees. Amplifiant le plaisir de jeu. Les agents repondent avec courtoisie, avec une aide precise. Les gains arrivent sans delai, cependant quelques tours gratuits supplementaires seraient bienvenus. En resume, Impressario Casino est un incontournable pour les amateurs pour les amateurs de sensations elegantes ! A noter la plateforme est visuellement somptueuse, amplifie le plaisir de jouer. Egalement appreciable le programme VIP avec niveaux exclusifs, renforce le sentiment de communaute.
DГ©couvrir les offres|
J’ai un faible pour Monte Cryptos Casino, on ressent une energie blockchain. La gamme de jeux est spectaculaire, comprenant des jeux optimises pour les cryptos. Le bonus d’entree est attractif. L’assistance est precise et professionnelle, offrant des solutions claires. Les transferts sont fiables, parfois des bonus plus varies seraient un mirage. Pour conclure, Monte Cryptos Casino est une plateforme qui domine le desert crypto pour ceux qui parient avec des cryptos ! Ajoutons que le design est moderne et envoutant, facilite une immersion totale. A souligner les options de paris variees, qui booste l’engagement.
Commencer ici|
Левандовскинин формасы дагы деле жогорку деңгээлде.
Левандовски жубайы менен көп кайрымдуулук иштерин колдойт. Левандовскинин трансфери Барселона үчүн чоң ийгилик болгон. Левандовски өз өлкөсүнүн сыймыгы. Эгер сиз Левандовскинин акыркы формасы жана статистикасы тууралуу билгиңиз келсе, анда Роберт Левандовски барагын караңыз. Барселона жана Левандовски – мыкты тандем.
Левандовски спорттук тарбиянын маанисин ар дайым белгилейт. Роберт Левандовскинин жаракаты көпчүлүктү тынчсыздандырган.
Роберт Левандовскинин чоң атасы тууралуу уламыштар айтылат. Роберт Левандовски өзүнүн максатына ишеним менен жеткен.
Great weblog right here! Also your web site a lot up fast!
What web host are you using? Can I get your associate link on your host?
I wish my site loaded up as quickly as yours lol
Feel free to visit my web page Is Casino in evansville open
successpathway.bond – The layout is crisp and clear, makes exploring effortless.
Регистрация в 2026 году — руководство по бонусам и акциям. Узнайте, как правильно активировать приветственные предложения, а также в середине процесса обратите внимание на 1xBet промокод как вариант получения дополнительного вознаграждения. FAQ помогут легко разобраться с верификацией и получением бонусов.
winmore.bond – I like how fast pages load; very responsive website.
BassBet Casino m’a captive BassBet Casino, ca transporte dans un univers de beats. Le catalogue est riche en surprises, offrant des sessions live immersives. Avec des depots ultra-rapides. L’assistance est rapide et pro, offrant des solutions claires. Les gains arrivent sans attendre, cependant des recompenses supplementaires seraient vibrantes. Dans l’ensemble, BassBet Casino est un must pour les joueurs pour ceux qui parient avec des cryptos ! A noter la plateforme est visuellement electrisante, facilite une immersion totale. Un point fort les tournois reguliers pour la competition, qui dynamise l’engagement.
https://bassbetcasinoappfr.com/|
trustandunity.bond – Looks trustworthy and reliable; branding is consistent across pages.
businessgrowthhub.shop – Overall a polished site with professional and engaging content.
smartfashionboutique.bond – Content is clear, informative, and engaging; great first impression.
successfultradersclub.shop – A clean and professional design that makes navigation a breeze.
J’adore l’atmosphere aquatique de BassBet Casino, ca plonge dans un monde de vagues. Les options sont vastes comme un lac, proposant des jeux de table elegants. Amplifiant le plaisir de jeu. Le suivi est irreprochable, avec une aide precise. Les gains arrivent sans delai, cependant des bonus plus varies seraient une vague. Pour conclure, BassBet Casino est un incontournable pour les joueurs pour les passionnes de jeux modernes ! En bonus la navigation est simple et rapide, facilitate une immersion totale. Egalement appreciable le programme VIP avec des niveaux exclusifs, qui booste l’engagement.
bassbetcasinobonusfr.com|
J’ai un faible eclatant pour BassBet Casino, c’est une plateforme qui scintille comme un neon. Les options sont vastes comme un show lumineux, incluant des paris sportifs vibrants. Amplifiant l’excitation du jeu. Les agents repondent comme un flash, garantissant un service de haute qualite. Les transactions sont fiables, neanmoins quelques tours gratuits en plus seraient top. Dans l’ensemble, BassBet Casino garantit un fun non-stop pour les joueurs en quete d’adrenaline ! De plus la plateforme est visuellement fluorescente, facilite une immersion totale. Particulierement cool les paiements securises en crypto, propose des avantages sur mesure.
bassbetcasinopromocodefr.com|
globalalliancenetwork.bond – A clean and professional design that makes navigation a breeze.
uniquedecorstore.shop – Content is clear, informative, and engaging; great first impression.
J’adore l’atmosphere olfactive de Spinit Casino, ca plonge dans un monde aromatique. La variete des titres est raffinee, incluant des paris sportifs elegants. Renforcant votre capital initial. Les agents repondent avec courtoisie, avec une aide precise. Le processus est simple et elegant, cependant des offres plus genereuses seraient exquises. Au final, Spinit Casino vaut une visite sophistiquee pour ceux qui aiment parier en crypto ! A noter la navigation est simple et gracieuse, donne envie de prolonger l’experience. Particulierement interessant les options de paris sportifs variees, renforce le sentiment de communaute.
https://spinitcasinobonusfr.com/|
futurevisiongroup.bond – Looking forward to seeing more updates and offerings from this site.
togetherwerise.bond – Uplifting stories from women leading the way in construction.
newhorizonsnetwork.shop – The layout is crisp and clear, makes exploring effortless.
Список бесплатных предложений и типов бонусов: отдельный обзор промо-акций для новичков и постоянных игроков; в середине абзаца приводим ссылку на промокод при регистрации 1xBet как источник подробной информации о том, куда вводить данные и какие условия ожидать. К тому же рассказываем про порядок валидации аккаунта.
Je suis absolument envoute par Monte Cryptos Casino, il propose une aventure chiffree. Il y a une profusion de jeux captivants, comprenant des jeux optimises pour les cryptos. Le bonus d’entree est eclatant. L’assistance est precise et professionnelle, garantissant un service premium. Les transferts sont fiables, cependant quelques tours gratuits en plus seraient bienvenus. Au final, Monte Cryptos Casino garantit un plaisir constant pour les joueurs en quete d’innovation ! En bonus la plateforme est visuellement eblouissante, ce qui rend chaque session plus immersive. Egalement cool les tournois reguliers pour la competition, propose des avantages uniques.
DГ©marrer maintenant|
J’ai une affection pour Impressario Casino, ca offre un plaisir sophistique. Les options sont vastes comme un menu etoile, comprenant des jeux compatibles avec les cryptos. Avec des depots instantanes. Le suivi est irreprochable, toujours pret a servir. Le processus est simple et elegant, neanmoins quelques tours gratuits supplementaires seraient bienvenus. En bref, Impressario Casino vaut une visite sophistiquee pour ceux qui aiment parier en crypto ! De plus l’interface est fluide comme un banquet, amplifie le plaisir de jouer. Egalement appreciable les options de paris sportifs variees, assure des transactions fiables.
DГ©couvrir les faits|
Je suis seduit par Impressario Casino, c’est une plateforme qui evoque le raffinement. La selection de jeux est somptueuse, offrant des sessions live sophistiquees. Avec des depots instantanes. Le support client est impeccable, toujours pret a servir. Les gains arrivent sans delai, parfois des recompenses additionnelles seraient royales. Au final, Impressario Casino garantit un plaisir constant pour les joueurs en quete d’excitation ! A noter le design est moderne et chic, ajoute une touche d’elegance. Un plus les tournois reguliers pour la competition, assure des transactions fiables.
Visiter le site|
Je suis captive par Monte Cryptos Casino, ca offre un plaisir numerique intense. Les titres sont d’une variete eclatante, offrant des sessions en direct immersives. Elevant l’experience de jeu. Les agents repondent avec une vitesse fulgurante, joignable a tout moment. Les paiements sont securises par blockchain, parfois plus de promos regulieres dynamiseraient l’experience. En bref, Monte Cryptos Casino garantit un plaisir constant pour les amateurs de casino en ligne ! Par ailleurs l’interface est fluide comme un vent du desert, facilite une immersion totale. Un atout cle le programme VIP avec des niveaux exclusifs, garantit des transactions fiables.
Cliquer maintenant|
Je suis absolument ravi par Impressario Casino, ca offre un plaisir raffine. La selection de jeux est exquise, offrant des sessions live distinguees. Renforcant votre capital initial. Les agents repondent avec courtoisie, offrant des reponses claires. Les paiements sont securises et rapides, neanmoins des recompenses additionnelles seraient royales. Dans l’ensemble, Impressario Casino vaut une visite sophistiquee pour ceux qui aiment parier en crypto ! Ajoutons que la navigation est simple et gracieuse, facilite une immersion totale. Egalement appreciable les options de paris sportifs variees, assure des transactions fiables.
Voir l’offre|
professionelle wett-tipps heute
Look at my website – handicap wette
nicholashirshon – Professional portfolio showcasing expertise and accomplishments.
unitedbygoal.bond – Great resource for those seeking innovative business solutions.
growstrongteam.bond – Impressed by the clean design and intuitive navigation here.
futuregoalsnetwork.shop – Impressed with the product quality and packaging; exceeded expectations.
микрозайм оформить оформить микрозайм
займы деньги взять микрозайм
онлайн деньги быстрый займ
choice-eats – Culinary excellence with diverse and delicious dining options.
Левандовски Барселонага кошулгандан кийин команда күчөдү.
Роберт Левандовски фото жана видеолору дайыма талкууда. Левандовскинин трансфери Барселона үчүн чоң ийгилик болгон. Левандовски өз өлкөсүнүн сыймыгы. Барселона жана Левандовски тууралуу кеңири маалымат https://robert-lewandowski-kg.com/ порталында бар. Роберт Левандовски Барселона клубуна энергия кошту.
Роберт Левандовски бала кезинен эле футболду сүйгөн. Левандовски ден соолугуна кылдат карайт.
Роберт Левандовскинин үй-бүлөлүк тамыры Польшада. Левандовски ийгиликке жөн эле жеткен эмес.
www-882884.com – Color palette felt calming, nothing distracting, just focused, thoughtful design.
worldvehicleexpo.com – Found practical insights today; sharing this article with colleagues later.
mjiuzixun.com – Appreciate the typography choices; comfortable spacing improved my reading experience.
trendinsight.shop – Found some useful tips here; bookmarking for future reference.
gameclub2u.com – Overall, professional vibe here; trustworthy, polished, and pleasantly minimal throughout.
leadersunitedgroup.bond – Feels like a community, not just a site, very welcoming tone.
globalpartnershipteam.shop – Fast shipping and quality items; very satisfied with my purchase.
teamfuture.bond – Looking forward to seeing more updates and features here.
covidtest-cyprus – Essential health services with reliable testing solutions.
play-brary.org – Overall a trustworthy site with reliable and engaging content.
leanneslifechangingfairies.com – I like the friendly tone and helpful resources provided here.
smartfashionboutique.bond – Fast loading pages make the experience seamless and smooth.
globalalliancenetwork.bond – Content is clear, informative, and engaging; great first impression.
uniquedecorstore.shop – I appreciate the clear structure and organized layout here.
Ich bin fasziniert von Snatch Casino, es bietet eine dynamische Erfahrung. Das Angebot ist ein Paradies fur Spieler, mit Krypto-kompatiblen Spielen. Der Bonus ist wirklich stark. Der Kundendienst ist hervorragend. Gewinne werden schnell uberwiesen, gelegentlich gro?ere Boni waren ideal. Zum Schluss, Snatch Casino bietet ein gro?artiges Erlebnis. Ubrigens die Navigation ist klar und flussig, jeden Moment aufregender macht. Ein klasse Bonus die breiten Sportwetten-Angebote, die Gemeinschaft starken.
snatch-casino.de|
wellnesstourbus – Mobile health and wellness services bringing care to communities.
Регистрация в 2026 г. — руководство по бонусам и предложениям. Посмотрите, как правильно активировать приветственные предложения, а также в середине процесса обратите внимание на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html как вариант получения дополнительного вознаграждения. FAQ помогут легко разобраться с верификацией и получением бонусов.
Ich bin beeindruckt von der Qualitat bei Snatch Casino, es schafft eine aufregende Atmosphare. Die Auswahl ist so gro? wie ein Casino-Floor, mit Spielautomaten in kreativen Designs. 100 % bis zu 500 € mit Freispielen. Der Kundendienst ist hervorragend. Auszahlungen sind blitzschnell, gelegentlich haufigere Promos wurden begeistern. Letztlich, Snatch Casino ist ein Top-Ziel fur Spieler. Nebenbei die Plattform ist optisch ansprechend, das Spielvergnugen steigert. Ein klasse Bonus sind die sicheren Krypto-Transaktionen, die die Gemeinschaft starken.
Snatch Casino|
Как получить приветственный бонус: краткая инструкция по регистрации и пополнению счёта, включая требований по отыгрышу; в середине параграфа мы указываем ссылку на https://bergkompressor.ru/news/artcles/?1xbet_promokod_pri_registracii_bonus_5.html, для того чтобы пользователь мог перейти и узнать подробности. Также приводим примеры доступных типов акций.
Роберт Левандовски тууралуу жаңылыктар ар дайым көңүлдү бурат.
Роберт Левандовски фото жана видеолору дайыма талкууда. Роберт Левандовски карьерасында жүздөгөн гол салган. Роберт Левандовски улуттук курама үчүн көп гол салган. Жаңы маек жана оюн анализдери [url=robert-lewandowski-kg.com]robert-lewandowski-kg.com порталында жарыяланат. Барселонадагы Левандовскинин оюнун күйөрмандар макташат.
Левандовскинин биографиясы шыктануу жаратат. Роберт Левандовски реабилитацияны тез бүтүргөн.
Роберт Левандовски үй-бүлөсүнө чоң маани берет. Левандовски ар дайым жогорку деңгээлди кармайт.
concernedaboutpollution – Environmental advocacy with focus on pollution awareness and solutions.
Hello everyone, it’s my first go to see at this site, and article is in fact fruitful designed for me, keep up posting these content.
прием смс
https://smartsoltech.kr/D0BAD0BED0BCD0BFD18CD18ED182D0B5D180D0BDD18BD0B9-D0B7D0B0D0BB-kush/
nextvision.bond – Appreciate the practical tips and advice shared on this site.
play-brary.org – Great combination of visuals and content; looks professional and polished.
asianspeedd8 – Modern dating platform with cultural connection and community focus.
leanneslifechangingfairies.com – I like the friendly tone and helpful resources provided here.
growthpoint.bond – The branding is consistent and reinforces the company’s vision.
pp4fdr.org – Looking forward to seeing updates or events they’ll share in the future.
ks4thekids.com – I appreciate the straightforward layout; it’s easy to navigate.
createimpacttoday.shop – The products are not only beautiful but also support great causes.
brauhausschmitzoktoberfest.com – I appreciate the detailed schedule and session breakdowns.
clubinorout.com – I appreciate the clear navigation and easy-to-find information.
mdcphilly.com – I particularly appreciate the structured layout that keeps everything in order.
uniquefashionstyle.shop – The layout is clean and the navigation is smooth which is great.
discovergreatdeal.shop – Easy navigation and smooth checkout process; shopping made simple.
**sleep lean**
sleeplean is a US-trusted, naturally focused nighttime support formula that helps your body burn fat while you rest.
concernedaboutpollution.com – Visuals and text are balanced nicely; gives the site a professional look.
asianspeedd8.com – (Note: I observed a small redundancy in the URL above—worth checking.)
grant-jt.com – Loading speed seems fast; the experience is smooth so far.
berrybombselfiespot.com – The website feels modern and polished; a good match for the photogenic setting.
shemplymade.com – A strong online presence for a niche wellness brand—well done.
meetkatemarshall.com – Loved the variety of content – automotive, fashion, food, health – keeps things fresh.
grant-jt – Professional services with expertise and dedicated client support.
moeinclub.com – A search feature would be useful to find specific topics quickly.
electmikemontes.com – I appreciate the professional tone and clean design.
pastorjorgetrujillo.com – The site loads quickly, making browsing smooth and enjoyable.
trendingnewsfeed.net – navigation is pretty straightforward; found key sections easily.
bwaylocations.com – I’d like to see more imagery or interactive elements to enhance engagement.
casa-nana.net – I found the navigation simple and the layout helps focus on the key message.
opensky-inc.com – It would help to see more detailed content or case studies to add depth.
brucknerbythebridge.com – Navigation is smooth and I found the main amenities easily.
centensports.com – The site looks clean and professional; easy to browse.
komunahouse – Community living space fostering connection and collaboration.
” />safercharging.com – (Note: I saw a small URL redirect oddness when checking a link.)
mdcphilly.com – Looks like a solid website; I’d revisit it for updates.
ks4thekids.com – I like the branding—“KS4TheKids”—catchy and memorable.
brauhausschmitzoktoberfest.com – The ticketing and event sessions are well explained; no confusion.
clubinorout.com – The branding is consistent across pages, which adds trust.
pp4fdr.org – Overall a strong web presence that makes me want to engage with their cause.
dankglassonline.com – The site looks clean and minimal; easy to navigate.
berrybombselfiespot – Fun and vibrant selfie destination with creative photo opportunities.
mdcphilly.com – Overall it feels trustworthy and user-friendly—nice job.
concernedaboutpollution.com – The mission comes through clearly; nice work on clarity of purpose.
asianspeedd8.com – Design is clean and carries a friendly vibe overall.
grant-jt.com – Keep an eye on updates; this site has a solid base to build on.
berrybombselfiespot.com – I appreciate the gallery of background scenes—it gives a good preview of the experience.
komunahouse.com – Would love to see more interactive features or member stories.
muralspotting.com – The photography is well-done; it really brings out each mural’s character.
gailcooperspeaker.com – Love the encouraging tone of this site; very uplifting.
reindeermagicandmiracles.com – The visuals capture the magic of the season—great imagery.
muralspotting.com – I appreciate the geographical diversity of the artworks showcased.
gailcooperspeaker – Inspirational speaking with powerful messages and engaging delivery.
brucknerbythebridge.com – Good job on the mobile layout too; adaptive and user friendly.
seenministries – Faith-based ministry offering spiritual guidance and community support.
Je suis epoustoufle par BassBet Casino, c’est une plateforme qui groove comme une voix soul. Les options sont vastes comme une scene live, proposant des jeux de table elegants. 100% jusqu’a 500 € + tours gratuits. Disponible 24/7 via chat ou email, joignable a tout moment. Les gains arrivent sans attendre, parfois plus de promos regulieres ajouteraient du rythme. Dans l’ensemble, BassBet Casino offre une experience inoubliable pour les passionnes de jeux modernes ! Par ailleurs la navigation est simple et rythmee, ajoute une touche de soul. Particulierement cool les evenements communautaires dynamiques, propose des avantages sur mesure.
https://bassbetcasinopromocodefr.com/|
Je suis totalement envoute par BassBet Casino, c’est une plateforme qui vibre comme un riff. Il y a une profusion de jeux excitants, comprenant des jeux compatibles avec les cryptos. Renforcant votre capital initial. Les agents repondent comme un solo, avec une aide precise. Le processus est simple et elegant, de temps a autre des offres plus genereuses seraient melodieuses. En resume, BassBet Casino offre une experience memorable pour les passionnes de jeux modernes ! A noter le design est moderne et melodieux, facilite une immersion totale. Particulierement interessant les evenements communautaires engageants, renforce le sentiment de communaute.
https://bassbetcasinobonusfr.com/|
Je suis totalement transporte par BassBet Casino, on ressent une vibe electrisante. Il y a un flot de jeux captivants, avec des slots aux designs dynamiques. Amplifiant l’excitation du jeu. Le suivi est impeccable, garantissant un service de haute qualite. Le processus est simple et vibrant, neanmoins des recompenses supplementaires seraient vibrantes. Dans l’ensemble, BassBet Casino est une plateforme qui pulse pour les joueurs en quete d’adrenaline ! A noter le site est rapide et captivant, ce qui rend chaque session plus vibrante. Un atout les options de paris variees, qui dynamise l’engagement.
bassbetcasinoappfr.com|
meetkatemarshall.com – The writing tone comes across as genuine and relatable, good work.
J’adore l’elegance de Impressario Casino, ca offre un plaisir sophistique. Les options sont vastes comme un menu etoile, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € + tours gratuits. L’assistance est efficace et professionnelle, avec une aide precise. Les retraits sont fluides comme la Seine, bien que des recompenses additionnelles seraient royales. En bref, Impressario Casino vaut une visite sophistiquee pour les fans de casino en ligne ! De plus le design est moderne et chic, amplifie le plaisir de jouer. Un plus les evenements communautaires engageants, offre des recompenses continues.
Cliquez ici|
J’ai une passion ardente pour Monte Cryptos Casino, c’est une plateforme qui pulse comme un reseau blockchain. Il y a une profusion de jeux captivants, offrant des sessions en direct immersives. Boostant votre capital initial. Disponible 24/7 via chat ou email, toujours pret a decoder. Les transferts sont fiables, parfois des recompenses supplementaires seraient ideales. Au final, Monte Cryptos Casino est un must pour les fans de blockchain pour les joueurs en quete d’innovation ! En bonus la plateforme est visuellement eblouissante, ce qui rend chaque session plus immersive. Un atout cle les options de paris variees, offre des recompenses continues.
Voir la page|
J’ai une passion debordante pour Monte Cryptos Casino, ca offre un plaisir numerique unique. La variete des titres est eclatante, offrant des sessions live immersives. Avec des depots crypto rapides. Les agents repondent avec une rapidite cosmique, joignable a tout moment. Les retraits sont rapides comme une transaction blockchain, cependant des bonus plus varies seraient un plus. Pour conclure, Monte Cryptos Casino offre une experience inoubliable pour les passionnes de sensations numeriques ! De plus la navigation est simple comme un wallet, amplifie le plaisir de jouer. Un avantage notable les options de paris variees, qui booste l’engagement.
Profiter de l’offre|
J’adore l’elegance de Impressario Casino, ca transporte dans un monde chic. La selection de jeux est exquise, avec des slots aux designs raffines. Avec des depots instantanes. L’assistance est efficace et professionnelle, joignable a toute heure. Les transactions sont fiables, cependant quelques tours gratuits supplementaires seraient bienvenus. En resume, Impressario Casino est un incontournable pour les amateurs pour les fans de casino en ligne ! De plus la plateforme est visuellement somptueuse, facilite une immersion totale. Un plus les evenements communautaires engageants, qui booste l’engagement.
DГ©couvrir|
J’adore l’elegance de Impressario Casino, on ressent une ambiance delicate. Les options sont vastes comme un menu etoile, avec des slots aux designs elegants. Le bonus de bienvenue est delicieux. Le suivi est irreprochable, offrant des reponses claires. Les gains arrivent sans delai, de temps a autre des offres plus genereuses seraient exquises. Au final, Impressario Casino garantit un plaisir constant pour les fans de casino en ligne ! De plus le site est rapide et attractif, donne envie de prolonger l’experience. Un plus les evenements communautaires engageants, offre des recompenses continues.
Cliquer maintenant|
kdjfjks.site – Color palette felt calming, nothing distracting, just focused, thoughtful design.
eyelle-paris.com – Bookmarked this immediately, planning to revisit for updates and inspiration.
Je suis totalement transporte par BassBet Casino, il cree une ambiance de studio live. Le catalogue est riche en surprises, incluant des paris sportifs pleins de vie. 100% jusqu’a 500 € + tours gratuits. Les agents repondent comme un beat parfait, joignable a tout moment. Les paiements sont securises et instantanes, mais plus de promos regulieres ajouteraient du rythme. En resume, BassBet Casino vaut une session live pour les amateurs de sensations vibrantes ! Ajoutons que l’interface est fluide comme un mix, ce qui rend chaque session plus vibrante. Particulierement cool les paiements securises en crypto, qui dynamise l’engagement.
https://bassbetcasinoappfr.com/|
J’ai une passion feerique pour Spinit Casino, ca offre un plaisir enchante. La selection de jeux est enchantee, comprenant des jeux compatibles avec les cryptos. Avec des depots instantanes. Les agents repondent comme par magie, offrant des reponses claires. Les retraits sont fluides comme un conte, cependant quelques tours gratuits supplementaires seraient bien venus. En resume, Spinit Casino garantit un plaisir constant pour les fans de casino en ligne ! En bonus la navigation est simple et magique, amplifie le plaisir de jouer. Egalement appreciable le programme VIP avec des niveaux exclusifs, offre des recompenses continues.
https://spinitcasinobonusfr.com/|
zakolata.xyz – Color palette felt calming, nothing distracting, just focused, thoughtful design.
Je suis totalement envoute par BassBet Casino, on ressent une ambiance de studio. Le catalogue est riche et varie, incluant des paris sportifs dynamiques. 100% jusqu’a 500 € + tours gratuits. Le service est disponible 24/7, offrant des reponses claires. Le processus est simple et elegant, de temps a autre quelques tours gratuits supplementaires seraient bien venus. Pour conclure, BassBet Casino est un incontournable pour les joueurs pour les amateurs de sensations rythmees ! Ajoutons que le site est rapide et attractif, ajoute une touche de rythme. Particulierement interessant les tournois reguliers pour la competition, qui booste l’engagement.
https://bassbetcasinobonusfr.com/|
binaryoptionstrade.xyz – Found practical insights today; sharing this article with colleagues later.
cryptocurrencytrade.pw – Navigation felt smooth, found everything quickly without any confusing steps.
J’ai une affection pour Impressario Casino, ca offre un plaisir sophistique. Les options sont vastes comme un menu etoile, proposant des jeux de table raffines. Avec des depots instantanes. L’assistance est efficace et professionnelle, toujours pret a servir. Les transactions sont fiables, bien que quelques tours gratuits supplementaires seraient bien venus. Pour conclure, Impressario Casino garantit un plaisir constant pour les fans de casino en ligne ! De plus la plateforme est visuellement somptueuse, ce qui rend chaque session plus raffinee. Un autre atout les paiements securises en crypto, qui booste l’engagement.
En savoir sur le sujet|
J’ai une passion ardente pour Monte Cryptos Casino, il propose une odyssee chiffree. Le catalogue est opulent et divers, proposant des tables sophistiquees. Le bonus d’entree est scintillant. Le suivi est d’une efficacite absolue, toujours pret a decoder. Les gains arrivent sans delai, de temps a autre plus de promos regulieres dynamiseraient l’experience. Au final, Monte Cryptos Casino garantit un plaisir constant pour les adeptes de jeux modernes ! En bonus l’interface est fluide comme un flux de donnees, ajoute une touche de sophistication. Particulierement captivant les paiements securises en BTC/ETH, renforce la communaute.
AccГ©der au contenu|
J’ai une passion debordante pour Monte Cryptos Casino, ca transporte dans un cosmos chiffre. La variete des titres est eclatante, proposant des jeux de table elegants. 100% jusqu’a 300 € + tours gratuits. Disponible 24/7 via chat ou email, offrant des reponses claires. Les retraits sont rapides comme une transaction blockchain, parfois quelques tours gratuits en plus seraient bienvenus. Pour conclure, Monte Cryptos Casino garantit un plaisir constant pour les amateurs de casino en ligne ! En bonus le site est rapide et futuriste, facilite une immersion totale. Un avantage notable les tournois reguliers pour la competition, renforce la communaute.
Voir l’offre|
Je suis seduit par Impressario Casino, ca offre un plaisir raffine. Le catalogue est somptueux et varie, avec des slots aux designs raffines. Avec des depots instantanes. Les agents repondent avec courtoisie, offrant des reponses claires. Les transactions sont fiables, bien que des offres plus genereuses seraient exquises. En resume, Impressario Casino offre une experience memorable pour les passionnes de jeux modernes ! De plus la plateforme est visuellement somptueuse, donne envie de prolonger l’experience. Un plus les evenements communautaires engageants, propose des avantages personnalises.
Visiter aujourd’hui|
moeinclub.com – Overall, a decent site with good potential for expansion.
J’ai une affection pour Impressario Casino, il procure une experience exquise. La variete des titres est raffinee, comprenant des jeux compatibles avec les cryptos. Renforcant votre capital initial. L’assistance est efficace et professionnelle, joignable a toute heure. Les paiements sont securises et rapides, cependant des offres plus genereuses seraient exquises. Au final, Impressario Casino garantit un plaisir constant pour ceux qui aiment parier en crypto ! De plus le design est moderne et chic, ajoute une touche d’elegance. Un autre atout les evenements communautaires engageants, offre des recompenses continues.
Aller lГ -bas|
sportwetten schweiz swisslos
Feel free to visit my website: wetten mit freunden App [Wealthdunia.com]
shemplymade.com – It would be nice to see more user reviews or customer stories.
centensports.com – Would like to see more user-feedback or community stories in future.
seenministries.com – I like the emphasis on community and connection; it feels inclusive.
bwaylocations.com – I like how clear the contact and location information is presented.
cepjournal.net – Design is consistent across pages; the branding comes through well.
pastorjorgetrujillo.com – The visuals support the message well and feel professional.
We absolutely love your blog and find nearly all of your
post’s to be just what I’m looking for. can you offer guest writers
to write content in your case? I wouldn’t mind publishing a post or elaborating
on many of the subjects you write in relation to here.
Again, awesome blog!
casa-nana.net – The site loads well on mobile too; good responsive performance.
trendingnewsfeed.net – navigation is pretty straightforward; found key sections easily.
catherinewburton.com – Overall, a trustworthy and professional online presence for a therapist.
vsmphotography.com – I’ll definitely keep this site in mind whenever I need a photographer — looks solid.
toddstarnesbooktour.com – The design feels professional and aligns well with the author’s branding.
createandgrow.shop – The layout appears clean and user-friendly; nice visual clarity.
findwhatyoulove.shop – The site loads quite fast; browsing feels smooth on mobile too.
Ich liebe die Atmosphare bei Snatch Casino, es sorgt fur ein fesselndes Erlebnis. Die Auswahl ist so gro? wie ein Casino-Floor, inklusive dynamischer Sportwetten. Er gibt Ihnen einen Kickstart. Der Service ist von hochster Qualitat. Zahlungen sind sicher und schnell, ab und zu gro?ere Boni waren ein Highlight. In Summe, Snatch Casino garantiert langanhaltenden Spa?. Daruber hinaus die Plattform ist visuell beeindruckend, zum Weiterspielen animiert. Besonders erwahnenswert ist das VIP-Programm mit exklusiven Stufen, kontinuierliche Belohnungen bieten.
Snatch Casino|
startsomethinggreat.shop – Looks like a solid foundation for an online store; good start.
theperfectgiftshop.com – I like the consistent branding and the inviting design.
exploreopportunitiesnow.shop – Product or service categories appear clear; helps me understand the offerings.
shopandsmilealways.shop – Product categories are visible, which helps in understanding the layout.
binaryoptionstrade.xyz – Loved the layout today; clean, simple, and genuinely user-friendly overall.
keepgrowingforward.shop – Navigation feels intuitive; I found what I was looking for quickly.
geteventclipboard.com – I like how the functions are clearly outlined; it’s helpful for understanding the service.
shopandsmilealways.shop – It might benefit from more detailed product information to build trust.
shopandshineeveryday.shop – Would love to see some customer reviews or testimonials for more reassurance.
eyelle-paris.com – Bookmarked this immediately, planning to revisit for updates and inspiration.
cryptocurrencytrade.pw – Content reads clearly, helpful examples made concepts easy to grasp.
zakolata.xyz – Navigation felt smooth, found everything quickly without any confusing steps.
Hi there, I desire to subscribe for this blog to obtain most up-to-date updates, thus where can i do it please help out.
https://petropavlovsk.en.cx/Guestbook/Messages.aspx?page=1&fmode=gb&topic=375747&anchor#7967620
shopwithconfidence – I love the interface, navigating through products feels really smooth.
joinourcreativeworld – Easy to navigate, found exactly what I was looking for.
wettbüro köln
Feel free to surf to my blog post wetten mit bonus ohne einzahlung (Gretta)
shopthebesttoday – Great variety of products, easy to navigate and shop online.
shopforhappiness – Love this site, always find unique items and great deals.
bestdealsforlife – Great discounts on many items, makes online shopping very enjoyable.
inspireeverydaylife – Highly recommend this shop, never disappointed with my purchases.
lifestyleinspirationhub – Great prices and quality, will definitely shop here again.
staycuriousalways – Fantastic variety of products, always something new and exciting.
newseasoncollection – Great prices and quality, will definitely shop here again.
Hi there to every body, it’s my first pay a quick visit of this blog; this blog consists of awesome and truly excellent information in favor of readers.
https://yazz.com.ua/yak-unyknuty-poshkodzhen-pry-vybori-stekla-na-far-.html
smartchoiceoutlet – Easy to navigate, found exactly what I was looking for.
discovernewworld – Excellent selection of products, always find what I need here.
catherinewburton.com – The website feels warm and welcoming, good for connecting with a therapist.
Pretty portion of content. I just stumbled upon your blog and in accession capital to assert that I acquire in fact enjoyed account your weblog posts. Any way I will be subscribing on your feeds and even I success you get admission to consistently fast.
http://bagit.com.ua/yak-steklo-fary-mozhe-znyzyty-ryzyk-polomok-avtomo.html
Система промокодов при регистрации даёт возможность новым игрокам получать бонусы к первому депозиту; мы описываем, как правильно заполнить регистрационную форму и где указать данные, а в середине примера даём ссылку на 1хБет промокод при регистрации для удобства. Обратите внимание, что бонусные условия могут отличаться в зависимости от региона.
vsmphotography.com – The typography and white-space are well balanced; makes the content easy to read.
exploreopportunitiesnow.shop – The minimal design helps focus on the message without distraction.
toddstarnesbooktour.com – Found the author bio section helpful; adds credibility and context to the tour.
createandgrow.shop – Some imagery could strengthen the emotional connection with visitors.
thinkcreategrow – Feels like a community, not just a site, very welcoming tone.
getinspiredtoday – Great shopping experience, fast delivery and quality items every time.
wetten beim pferderennen
Feel free to surf to my page beste neue wettanbieter – Linnie,
thebestplacetoshop – Easy to navigate, found exactly what I was looking for.
sportwetten online mit bonus
Here is my web site; wetten spiel
В обзоре сервисов для игроков мы подробно разбираем типы бонусов, включая фрибеты и депозитные поощрения; в середине материала приведена ссылка на 1xBet промокод на сегодня, который может и помочь новым пользователям при регистрации. Кроме того, даём советы по безопасности и ответственному подходу к ставкам.
startsomethinggreat.shop – The minimal design helps focus on the product without distraction.
findwhatyoulove.shop – I’d like to see more detailed reviews or user photos for better trust.
theperfectgiftshop.com – The visuals are appealing and make shopping feel enjoyable.
shopandsmilealways.shop – Overall a good first impression; user-friendly and pleasant to explore.
simplybestchoice.shop – Navigation feels intuitive; I found what I was looking for quickly.
keepgrowingforward.shop – The branding is consistent and gives the store a polished identity.
shopandsmilealways.shop – The homepage appears minimal yet effective—good user experience.
shopandshineeveryday.shop – The branding feels simple and clean; consistent visual tone.
trendyfindshub – Love this site, always find unique items and great deals.
Сравните цены на ноутбуки https://n-katalog.ru/category/noutbuki/list в десятках магазинов: для работы, учебы и игр. Характеристики, отзывы, фото, бенчмарки. Фильтры по процессору, ОЗУ, SSD, диагонали, видео, весу и автономности. Следите за акциями и динамикой стоимости — выбирайте выгодное предложение с доставкой.
микрозайм оформить займ онлайн
Costa Rica https://fotoredaktor.top cultuur was goed uitgelegd.
connectdiscovergrow – Love the practical strategies shared here, very applicable to real life.
geteventclipboard.com – Load times seem good; the site feels responsive.
dreamcreateinspire – Easy to navigate, found exactly what I was looking for.
shopthelatesttrend – Fantastic variety of products, always something new and exciting.
Je suis completement transporte par BassBet Casino, il cree une ambiance de concert. Le catalogue est riche en emotions, incluant des paris sportifs pleins de vie. Avec des depots ultra-rapides. Disponible 24/7 via chat ou email, garantissant un service de haute qualite. Les retraits sont fluides comme une note tenue, neanmoins plus de promos regulieres ajouteraient du rythme. Dans l’ensemble, BassBet Casino est une plateforme qui groove pour ceux qui parient avec des cryptos ! A noter la navigation est simple et rythmee, donne envie de prolonger la melodie. Un atout les tournois reguliers pour la competition, qui dynamise l’engagement.
https://bassbetcasinopromocodefr.com/|
Ich schatze die Energie bei Snatch Casino, es bietet ein immersives Erlebnis. Die Spiele sind abwechslungsreich und spannend, mit aufregenden Live-Casino-Erlebnissen. Mit schnellen Einzahlungen. Der Service ist absolut zuverlassig. Auszahlungen sind blitzschnell, gelegentlich mehr Bonusvielfalt ware ein Vorteil. In Summe, Snatch Casino garantiert langanhaltenden Spa?. Zusatzlich ist das Design stilvoll und einladend, jede Session unvergesslich macht. Ein starkes Feature die vielfaltigen Wettmoglichkeiten, die die Begeisterung steigern.
https://snatch-casino.de/de-de/|
Je suis accro a Spinit Casino, c’est une plateforme qui tourne avec elegance. La selection de jeux est dynamique, avec des slots aux designs veloces. 100% jusqu’a 500 € + tours gratuits. Le service est disponible 24/7, toujours pret a accelerer. Les retraits sont fluides comme un peloton, cependant quelques tours gratuits supplementaires seraient bien venus. Dans l’ensemble, Spinit Casino garantit un plaisir constant pour les amateurs de sensations rapides ! De plus la plateforme est visuellement veloce, ce qui rend chaque session plus excitante. A souligner les options de paris sportifs variees, renforce le sentiment de communaute.
https://casinospinitfr.com/|
5f7yp3
J’adore l’ambiance delicate de Impressario Casino, on ressent une energie subtile. Le catalogue est riche et varie, comprenant des jeux compatibles avec les cryptos. Boostant votre capital initial. Le service client est irreprochable, toujours pret a aider. Le processus est simple et gracieux, parfois des recompenses en plus seraient exquises. Dans l’ensemble, Impressario Casino est une plateforme qui enchante pour les adeptes de jeux modernes ! Ajoutons que la plateforme brille comme un coucher de soleil, ce qui rend chaque session plus lumineuse. Un point fort les paiements securises en crypto, renforce le lien communautaire.
Commencer maintenant|
J’adore l’atmosphere musicale de BassBet Casino, ca plonge dans un monde de notes. La variete des titres est harmonieuse, comprenant des jeux compatibles avec les cryptos. Avec des depots instantanes. Le service est disponible 24/7, avec une aide precise. Les retraits sont fluides comme un riff, bien que des recompenses additionnelles seraient rythmees. Pour conclure, BassBet Casino est un incontournable pour les joueurs pour ceux qui aiment parier en crypto ! De plus l’interface est fluide comme un riff, ce qui rend chaque session plus groovy. A souligner les paiements securises en crypto, offre des recompenses continues.
bassbetcasinobonusfr.com|
J’ai une passion ardente pour Monte Cryptos Casino, on ressent une energie decentralisee. Il y a une profusion de jeux captivants, avec des slots aux designs modernes. Boostant votre capital initial. Disponible 24/7 via chat ou email, garantissant un service premium. Les transferts sont fiables, mais des offres plus genereuses ajouteraient du charme. Dans l’ensemble, Monte Cryptos Casino offre une experience inoubliable pour les joueurs en quete d’innovation ! De plus la navigation est simple comme un wallet, ajoute une touche de sophistication. A souligner les evenements communautaires decentralises, offre des recompenses continues.
Parcourir les offres|
J’aime l’ambiance numerique de Monte Cryptos Casino, ca offre une sensation futuriste unique. Il y a une profusion de jeux captivants, avec des slots aux designs modernes. 100% jusqu’a 300 € + tours gratuits. L’assistance est precise et professionnelle, avec une aide rapide et fiable. Les gains arrivent sans delai, mais plus de promos regulieres dynamiseraient l’experience. En bref, Monte Cryptos Casino offre une experience inoubliable pour les adeptes de jeux modernes ! Ajoutons que la navigation est simple comme un wallet, amplifie le plaisir de jouer. Un avantage notable les evenements communautaires decentralises, offre des recompenses continues.
Aller sur le site|
J’ai une passion feerique pour Spinit Casino, c’est une plateforme qui tourbillonne comme un conte. La variete des titres est magique, proposant des jeux de table elegants. Renforcant votre capital initial. Le suivi est irreprochable, avec une aide precise. Les paiements sont securises et rapides, bien que des bonus plus varies seraient un chapitre. En bref, Spinit Casino garantit un plaisir constant pour ceaux qui aiment parier en crypto ! En bonus le design est moderne et enchante, amplifie le plaisir de jouer. Particulierement interessant le programme VIP avec des niveaux exclusifs, assure des transactions fiables.
spinitcasinobonusfr.com|
Je suis absolument ebloui par Impressario Casino, ca offre une experience cinematographique. Il y a une profusion de jeux captivants, incluant des paris sportifs dynamiques. 100% jusqu’a 500 € + tours gratuits. Le service client est irreprochable, avec une aide efficace. Les paiements sont securises et rapides, cependant des bonus plus varies seraient une star. Au final, Impressario Casino offre une experience inoubliable pour les passionnes de sensations prestigieuses ! Ajoutons que la plateforme brille comme une premiere, ce qui rend chaque session plus glamour. Particulierement captivant les options de paris variees, assure des transactions fiables.
Commencer|
Je suis absolument seduit par Monte Cryptos Casino, ca offre un plaisir numerique unique. La selection de jeux est astronomique, proposant des jeux de table elegants. Amplifiant l’experience de jeu. L’assistance est efficace et professionnelle, toujours pret a resoudre. Les gains arrivent sans delai, de temps a autre plus de promos regulieres dynamiseraient l’experience. Dans l’ensemble, Monte Cryptos Casino garantit un plaisir constant pour les passionnes de sensations numeriques ! Par ailleurs le site est rapide et futuriste, amplifie le plaisir de jouer. Egalement cool le programme VIP avec des niveaux exclusifs, qui booste l’engagement.
Lire maintenant|
everydayvaluecorner – Excellent selection of products, always find what I need here.
uniquetrendstore – Always a pleasure shopping here, never disappoints with selections.
BassBet Casino m’a ensorcele BassBet Casino, on ressent une energie vibrante. La selection de jeux est harmonieuse, comprenant des jeux adaptes aux cryptos. Boostant votre mise de depart. L’assistance est rapide et pro, offrant des solutions claires. Les transactions sont fiables, cependant des offres plus genereuses seraient soul. En resume, BassBet Casino offre une experience inoubliable pour les amateurs de sensations vibrantes ! Ajoutons que l’interface est fluide comme une chanson, facilite une immersion totale. Un point fort le programme VIP avec des niveaux exclusifs, qui dynamise l’engagement.
bassbetcasinopromocodefr.com|
Ich bin absolut begeistert von Snatch Casino, es begeistert mit Dynamik. Es gibt eine Fulle an aufregenden Titeln, mit Live-Sportwetten. 100 % bis zu 500 € inklusive Freispiele. Der Service ist von hochster Qualitat. Der Prozess ist einfach und transparent, gelegentlich mehr regelma?ige Aktionen waren toll. Im Gro?en und Ganzen, Snatch Casino ist ein Top-Ziel fur Spieler. Zusatzlich die Benutzeroberflache ist flussig und intuitiv, zum Verweilen einladt. Ein tolles Extra ist das VIP-Programm mit exklusiven Stufen, die die Gemeinschaft starken.
https://snatch-casino.de/de-de/|
Je suis emerveille par Spinit Casino, il procure une experience rapide. La variete des titres est rapide, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € + tours gratuits. Le support client est veloce, offrant des reponses claires. Les retraits sont fluides comme un peloton, parfois des recompenses additionnelles seraient rapides. En resume, Spinit Casino est une plateforme qui accelere pour les amateurs de sensations rapides ! De plus la navigation est simple et rapide, facilitate une immersion totale. A souligner les paiements securises en crypto, qui booste l’engagement.
casinospinitfr.com|
Thank you a bunch for sharing this with all of us you really realize what you are talking about! Bookmarked. Please also talk over with my web site =). We may have a hyperlink trade arrangement between us
kra41 at
Je ne peux plus me passer de Impressario Casino, ca transporte dans un monde de raffinement. Il y a une abondance de jeux captivants, offrant des sessions live immersives. L’offre de bienvenue est envoutante. Le suivi est d’une precision remarquable, joignable a tout moment. Les gains arrivent sans attendre, de temps en temps des bonus plus varies seraient un delice. En resume, Impressario Casino est un joyau pour les joueurs pour les adeptes de jeux modernes ! Notons aussi la plateforme brille comme un coucher de soleil, donne envie de prolonger l’experience. Egalement remarquable les evenements communautaires engageants, qui dynamise l’engagement.
Parcourir les offres|
J’ai une passion rythmique pour BassBet Casino, on ressent une ambiance de studio. Il y a une profusion de jeux excitants, incluant des paris sportifs dynamiques. Renforcant votre capital initial. Les agents repondent comme un solo, avec une aide precise. Les retraits sont fluides comme un riff, cependant des bonus plus varies seraient un riff. En bref, BassBet Casino est un incontournable pour les joueurs pour les fans de casino en ligne ! De plus l’interface est fluide comme un riff, donne envie de prolonger l’aventure. Egalement appreciable les evenements communautaires engageants, propose des avantages personnalises.
bassbetcasinobonusfr.com|
Je suis ebloui par Monte Cryptos Casino, il propose une odyssee chiffree. La variete des titres est eclatante, offrant des sessions en direct immersives. Le bonus d’entree est scintillant. Les agents repondent avec une vitesse fulgurante, avec une aide rapide et fiable. Les retraits sont rapides comme une transaction, neanmoins quelques tours gratuits en plus seraient bienvenus. En resume, Monte Cryptos Casino offre une experience inoubliable pour les passionnes de sensations numeriques ! De plus la navigation est simple comme un wallet, facilite une immersion totale. Un atout cle les evenements communautaires decentralises, garantit des transactions fiables.
Apprendre comment|
J’aime l’ambiance numerique de Monte Cryptos Casino, on ressent une energie decentralisee. La selection de jeux est astronomique, comprenant des jeux optimises pour les cryptos. Elevant l’experience de jeu. Les agents repondent avec une vitesse fulgurante, garantissant un service premium. Le processus est fluide comme un smart contract, parfois quelques tours gratuits en plus seraient bienvenus. Pour conclure, Monte Cryptos Casino garantit un plaisir constant pour ceux qui parient avec des cryptos ! A noter la plateforme est visuellement eblouissante, ce qui rend chaque session plus immersive. Particulierement captivant les tournois reguliers pour la competition, offre des recompenses continues.
DГ©bloquer plus|
Je suis emerveille par Spinit Casino, c’est une plateforme qui tourbillonne comme un conte. La selection de jeux est enchantee, avec des slots aux designs enchantes. Avec des depots instantanes. Le suivi est irreprochable, offrant des reponses claires. Les paiements sont securises et rapides, cependant des recompenses additionnelles seraient narratives. Dans l’ensemble, Spinit Casino est un incontournable pour les joueurs pour ceaux qui aiment parier en crypto ! En bonus le design est moderne et enchante, donne envie de prolonger l’aventure. A souligner les evenements communautaires engageants, assure des transactions fiables.
https://spinitcasinobonusfr.com/|
J’ai une passion brulante pour Impressario Casino, ca offre une experience cinematographique. Le catalogue est riche et varie, proposant des jeux de table elegants. L’offre de bienvenue est prestigieuse. Les agents repondent avec une classe rare, avec une aide efficace. Les paiements sont securises et rapides, de temps en temps quelques tours gratuits supplementaires seraient apprecies. En bref, Impressario Casino garantit un plaisir constant pour les amateurs de casino en ligne ! Notons aussi le site est rapide et envoutant, ajoute une touche de prestige. Egalement remarquable les evenements communautaires engageants, renforce le lien communautaire.
Parcourir maintenant|
J’ai une passion debordante pour Monte Cryptos Casino, ca transporte dans un cosmos chiffre. Le catalogue est opulent et diversifie, proposant des jeux de table elegants. Avec des depots crypto rapides. Disponible 24/7 via chat ou email, joignable a tout moment. Les transferts sont fiables, parfois quelques tours gratuits en plus seraient bienvenus. Pour conclure, Monte Cryptos Casino offre une experience inoubliable pour les adeptes de jeux modernes ! De plus l’interface est fluide comme un flux de donnees, donne envie de prolonger l’aventure. A souligner les tournois reguliers pour la competition, renforce la communaute.
Ouvrir la page maintenant|
Hello! Do you use Twitter? I’d like to follow you if that would be okay. I’m definitely enjoying your blog and look forward to new posts.
официальный сайт kra41 cc
globalmarketplacehub – Love the unique finds here, always something special to discover.
discoverendlessideas – Appreciate the variety of topics and engaging writing style.
everytrendinone – Felt motivated after visiting; thanks for the uplifting messages and tips.
brightfuturedeals – Always a pleasure exploring the fresh content and ideas shared.
learnshareconnect – Great site that sparks creativity and gives me new perspectives daily.
le meilleur code promo pour 1xbet The specific demands reveal nuanced strategies. Gamblers aren’t just looking for any code; they seek the best – “meilleur code promo 1xBet.” The appeal of freebies is undeniable (“code promo 1xBet gratuit,” “code promo 1xBet sans depot”), reflecting a desire to minimize risk and maximize potential returns. Validation is crucial (“code promo 1xBet valide”), assurance that the offered benefit is genuine and not merely a marketing ploy. The “code promo 1xBet 130€” exemplifies the tangible rewards users hope to secure.
nejlepsi-porno.top – Pages loaded fast, images appeared sharp, and formatting stayed consistent.
porno-masaz.top – Appreciate the typography choices; comfortable spacing improved my reading experience.
discovergreatthings – User-friendly website layout, found what I needed without any hassle.
exploreamazingideas – Excellent customer support, they responded promptly and solved my issue.
findyourperfectdeal – The website layout is clean and navigation feels very intuitive today.
newseasoncollection – Love this site, always find unique items and great deals.
prostitutkimoskvyonline.info – Navigation felt smooth, found everything quickly without any confusing steps.
usaonlinecasinos.org – Loved the layout today; clean, simple, and genuinely user-friendly overall.
gewinnbringende wettstrategie
Also visit my web blog: sportwetten neukundenbonus ohne einzahlung
yourjourneybegins – Items arrived securely packaged and on time, very trustworthy store experience.
bester sportwetten anbieter
Stop by my page: wettbüRo dortmund
dreamcreateinspire – Love the unique finds here, always something special to discover.
shopthelatesttrend – Easy to navigate, found exactly what I was looking for.
smartchoiceoutlet – Love the unique finds here, always something special to discover.
blinkiesdonutsca – Highly satisfied with everything from my visit, great experience overall.
electmikemontes – Political campaign focused on community representation and positive change.
shopwithconfidence – I trust this store more every time I make a purchase.
brainsight-reeracoen – Their team clearly knows the APAC region and how to connect people.
inspireeverydaylife – Excellent selection of products, always find what I need here.
Hello there! This is kind of off topic but I need some advice from an established blog. Is it very difficult to set up your own blog? I’m not very techincal but I can figure things out pretty quick. I’m thinking about making my own but I’m not sure where to begin. Do you have any points or suggestions? Thank you
https://kra42c.com
realherschel – Shipping info was easy to find and checkout looked secure as well.
geld mit sportwetten verdienen
online deutschland
Hello i am kavin, its my first occasion to commenting anywhere, when i read this post i thought i could also make comment due to this sensible post.
маркетплейс kraken
shemplymade – Handcrafted products with quality craftsmanship and unique designs.
cs-nippon-cp – Navigation felt simple and intuitive which is a plus for user experience.
tabitoshigoto – Great idea for remote workers who want to explore while staying productive.
hanayaka-na-life – Stumbled across the site, looks fresh and promising for lifestyle products.
Codes promotionnels 1x pari Ultimately, the goal is to find a “code promo pour 1xBet” or “code promo sur 1xbet” that provides a real advantage. Whether it’s a “bonus d’inscription 1xbet” or a “code promo 1xbet 131$,” smart bettors understand the power of a well-chosen promotional code. Thorough research, verification, and understanding the terms and conditions are paramount to successfully leveraging these offers.
joebobsaveschristmas – I can see how this appeals to both horror fans and holiday lovers alike.
shemplymade – Handcrafted products with quality craftsmanship and unique designs.
hopeandlace – Worth bookmarking and exploring their “About” and “Work” sections for deeper understanding.
hawaiineiartcontest – The guidelines look quite specific about species eligibility and artwork format. :contentReference[oaicite:0]index=0
motivilovesmusic – For now, treat it as a lower-certainty option until more background is found.
globalmarketplacehub – Fantastic variety of products, always something new and exciting.
sega-live – The branding evokes the famous “SEGA”, so verify authenticity before giving personal info.
wrestlingac – However, it’s not immediately clear what region or organization the site primarily serves, so context is a bit vague.
foruminvestmali – The website appears to have been last significantly updated around 2019, which raises a question about its ongoing relevance. :contentReference[oaicite:3]index=3
newthisdomainsssss – The brand voice is mysterious, good for curiosity though context is missing.
hopprojects – Love that they focus on breaking down traditional genre boundaries, very refreshing.
envolavecning – I’d proceed cautiously if making a purchase or giving personal data—verify terms, policy, and returns.
discoverendlessideas – Always find fresh perspectives and practical tips to explore.
brightfuturedeals – Loved the downloadable resources section; useful for planning and idea generation.
everytrendinone – The website layout is clean and navigation feels very intuitive today.
learnshareconnect – Always a pleasure exploring the fresh content and ideas shared.
discovergreatthings – Great customer support, they answered my query quickly and kindly.
beauty-optical-salon – The store opened in 2017 in Tokyo for women’s eyewear with bespoke service. :contentReference[oaicite:1]index=1
findyourperfectdeal – Always a pleasure exploring the fresh content and ideas shared.
exploreamazingideas – Love the variety here, always something unique to discover.
yourjourneybegins – Wonderful site with inspiring products that brighten every day, so glad.
rebeccacaridad-manzanita – The name “Manzanita” might connect to the blog or creative brand of Rebecca Caridad, which could be fine but still needs verification.
Авто под заказ Японии Авто под заказ из Китая, Кореи и Японии – это ваш шанс стать обладателем эксклюзивного автомобиля, сочетающего передовые технологии и привлекательную цену. Мы берем на себя все этапы процесса, от поиска и проверки автомобиля до его доставки, таможенного оформления и сертификации, избавляя вас от лишних хлопот. Тщательный отбор и контроль качества на каждом этапе – гарантия того, что вы получите автомобиль, полностью соответствующий вашим ожиданиям.
engagement-forum – If you’re using it for content marketing or SEO, consider balancing with higher-authority domains.
Календар https://siviagmen.com підказав на який місяць краще переїжджати.
bloemhill – Would love to see more customer photos or reviews for extra confidence.
В статье https://buybuyviamen.com нашли подсказку, чем обшить фронтон крыши.
brainsight-reeracoen – Really impressed by how clean and professional their service feels overall.
Пошаговые советы на https://mr-master.com.ua/uk/ помогли сделать навес своими руками.
blinkiesdonutsca – Loved stopping by, donuts were fresh and service was super friendly.
shopwithconfidence – Always finding something interesting, prices are fair and worth it.
clevelandchristmasclub – Festive community organization spreading holiday joy and cheer.
tabitoshigoto – The branding feels calm and welcoming, perfect for travel inspiration seekers.
porno-masaz.top – Content reads clearly, helpful examples made concepts easy to grasp.
kraken ссылка Kraken ссылка – это как нить Ариадны, ведущая сквозь темный лес цифрового мира к самому сердцу платформы. Однако, прежде чем довериться этой нити, убедитесь в её прочности и надёжности, ведь в сети подстерегают коварные обманщики, готовые воспользоваться вашей неосторожностью. Проверяйте каждый символ, каждое слово, чтобы не стать жертвой фишинга и не потерять свои сбережения. Помните, что безопасность – это прежде всего ваша личная ответственность.
swissreplica.pw – Appreciate the typography choices; comfortable spacing improved my reading experience.
nejlepsi-porno.top – Color palette felt calming, nothing distracting, just focused, thoughtful design.
Hey there I am so delighted I found your website, I really found you by mistake, while I was searching on Askjeeve for something else, Nonetheless I am here now and would just like to say thanks for a tremendous post and a all round thrilling blog (I also love the theme/design), I don’t have time to browse it all at the moment but I have book-marked it and also added your RSS feeds, so when I have time I will be back to read a lot more, Please do keep up the superb work.
маркетплейс kraken
usaonlinecasinos.org – Content reads clearly, helpful examples made concepts easy to grasp.
Hi there, all is going nicely here and ofcourse every one is sharing facts, that’s in fact fine, keep up writing.
kra42 at
macofficelovesyou – Historically this domain was used for a promotional campaign tied to Microsoft offering a MacBook Pro giveaway. :contentReference[oaicite:1]index=1
realherschel – They answered my query quickly via chat which is a plus.
На сторінці zebraschool.com.ua замовив ремонт самоката у Луцьку — все супер
ohmydrifter – Navigation is straightforward and the photography is definitely a strong point.
bwaylocations – Prime location services with strategic placement and accessibility.
hopeandlace – I’d recommend verifying client reviews or testimonials for confirmation of performance.
cs-nippon-cp – The design is clean though the content seems a little sparse and vague.
https://shorturl.fm/vo412
motivilovesmusic – Happy to do a deeper check (traffic stats, ownership registry) if you’d like to assess it further.
trabas007hoki – Just found this site and it feels a bit unclear about its purpose.
**memory lift**
memory lift is an innovative dietary formula designed to naturally nurture brain wellness and sharpen cognitive performance.
Hello there! Would you mind if I share your blog with my twitter group? There’s a lot of folks that I think would really enjoy your content. Please let me know. Thanks
kra42 at
hanayaka-na-life – Shipping details were clear and checkout was smooth, which is nice.
dearsparrows – The blog posts are surprisingly in-depth, good for someone wanting niche insights.
Awesome things here. I’m very satisfied to peer your article. Thank you a lot and I am looking ahead to contact you. Will you kindly drop me a e-mail?
kra42 cc
kraken ссылка Kraken market – это многогранная площадка, где встречаются продавцы и покупатели со всего мира, предлагая широкий спектр товаров и услуг. Здесь можно найти все, что душе угодно, от редких артефактов до инновационных разработок. Приготовьтесь к захватывающему приключению, полному неожиданных открытий и выгодных предложений. Но не забывайте о здравом смысле и критическом мышлении, чтобы не стать жертвой недобросовестных продавцов.
pepplish – Would be helpful to see more customer reviews or user-generated content to gauge satisfaction.
nomnomnomfordogs – Would be helpful to see more transparency on ingredient sourcing for added credibility.
flourandoak – If you’re in the area and craving something sweet, this could be a charming option.
shopwithconfidence – Overall looks promising—just do a little extra verification (age, certificate, reviews) before full use.
connectdiscovergrow – Good potential if you’re looking to expand your professional network or skills.
globaltrendmarket – If you’re using it for SEO/backlinks, pair it with stronger, established domains for balance.
staycuriousalways – Love the domain’s vibe — seems like a place you’d go to expand your mind and try something new.
keepgrowingforward – Good candidate to share with a friend who’s looking for daily inspiration.
bestdealsforlife – The domain name sounds good, but I couldn’t verify much about who’s behind the site.
createandgrow – Navigation is smooth, but I didn’t immediately spot contact info or about details.
theperfectgiftshop – If you’re shopping for something special, this could be a good place to browse—just check details.
turnerhallrestaurant – Exceptional dining experience with quality cuisine and atmosphere.
buildyourdreamtoday – The domain name is inspiring and suggests a platform for personal or professional growth.
uniquetrendstore – From a link-building perspective, it could work, but I’d treat it as lower authority until more evidence of legitimacy appears.
simplybestchoice – Before relying on it for business or advertising, check for any user reviews or complaints found online.
changetheworld – The name evokes a sense of purpose, but the site’s offerings are unclear without further details.
simplybestchoice – Before relying on it for business or advertising, check for any user reviews or complaints found online.
joinourcreativeworld – I’d recommend verifying domain age, SSL certificate and any user reviews to assess reliability.
GlobalMarketplaceHub – Website layout is clean, navigation feels simple and intuitive overall.
ExploreAmazingIdeas – Highly recommend this platform, great for discovering innovative ideas easily today.
InspireEverydayLife – Customer support was helpful, answered all my questions promptly and politely.
discoverendlessideas – Overall, the domain name is promising, but the site requires more development to be fully credible.
sfdh10.pw – Content reads clearly, helpful examples made concepts easy to grasp.
96x11n.pw – Content reads clearly, helpful examples made concepts easy to grasp.
J’ai une passion lyrique pour Olympe Casino, c’est une plateforme qui resonne comme une lyre. Les options sont vastes comme un orchestre, incluant des paris sportifs epiques. Amplifiant l’aventure de jeu. Le service est disponible 24/7, offrant des reponses claires. Les transactions sont fiables, bien que des recompenses supplementaires seraient eternelles. En resume, Olympe Casino merite une ascension celeste pour les amateurs de sensations mythiques ! En bonus la plateforme est visuellement olympienne, ajoute une touche de mythologie. A souligner les paiements securises en crypto, renforce le sentiment de communaute.
https://olympefr.com/|
titi.pw – Loved the layout today; clean, simple, and genuinely user-friendly overall.
libracryptocurrency.pw – Loved the layout today; clean, simple, and genuinely user-friendly overall.
Le code promo est supprime : entrez-le dans le champ « Code promo » et reclamez un bonus de bienvenue de 100% jusqu’a 130€, a utiliser dans les paris sportifs. Vous pouvez vous inscrire sur le site 1xBet ou via l’application mobile. Apres votre premier depot, vous activerez le code bonus. L’offre est valable pour toute l’annee 2026, et le bonus doit etre mise dans les 30 jours. Decouvrez plus d’informations sur le code promo via ce lien — Un Code Promo X Bet. Le code promo 1xBet casino offre des tours gratuits et un bonus de depot 1xBet pour les nouveaux joueurs. Avec le code promotionnel 1xBet pour nouveaux utilisateurs, recevez jusqu’a 130€ de bonus d’inscription 1xBet. Utilisez le code promo 1xBet aujourd’hui pour jouer au casino en ligne 1xBet et profiter de toutes les offres disponibles.
DiscoverGreatThings – Highly recommend this platform, it’s convenient and genuinely helpful overall.
LearnSomethingNew – Signing up was easy, notifications keep me updated on new courses.
https://shorturl.fm/W2Erk
Profitez du code promo 1xbet 2026 : recevez un bonus de 100% sur votre premier depot, jusqu’a 130 €. Jouez et placez vos paris facilement grace aux fonds bonus. Apres l’inscription, il est important de recharger votre compte. Si votre compte est verifie, vous pourrez retirer toutes les sommes d’argent, y compris les bonus. Le code promo 1xbet est disponible via ce lien : https://www.atrium-patrimoine.com/wp-content/artcls/?code_promo_196.html.
globaltrendmarket – Would be great if the site displayed recent reviews, customer testimonials or third-party mentions.
J’adore l’harmonie de Olympe Casino, on ressent une energie divine. Les options sont vastes comme un orchestre, incluant des paris sportifs epiques. Le bonus de bienvenue est divin. Le service est disponible 24/7, garantissant un support celeste. Les gains arrivent sans delai, de temps a autre des recompenses supplementaires seraient eternelles. En bref, Olympe Casino garantit un plaisir divin pour ceux qui aiment parier en crypto ! De plus la navigation est simple comme un oracle, ce qui rend chaque session plus celeste. Un atout olympien les paiements securises en crypto, qui booste l’engagement.
olympefr.com|
dearsparrows – If you’re into betting or gambling topics, this seems like a resource worth checking.
BrightFutureDeals – Products arrived fast, very happy with quality and service today.
pepplish – The product variety looks good—combining fruits, herbs and heat for a unique twist.
Ich schatze die Energie bei Cat Spins Casino, es bietet eine dynamische Erfahrung. Das Spieleportfolio ist unglaublich breit, mit Spielen fur Kryptowahrungen. Mit einfachen Einzahlungen. Verfugbar 24/7 fur alle Fragen. Die Zahlungen sind sicher und zuverlassig, ab und zu zusatzliche Freispiele waren willkommen. Abschlie?end, Cat Spins Casino ist ein Muss fur Spieler. Nebenbei die Navigation ist klar und flussig, das Spielerlebnis bereichert. Besonders erwahnenswert sind die zuverlassigen Krypto-Zahlungen, regelma?ige Boni bieten.
Jetzt entdecken|
Ich liebe das Flair von Cat Spins Casino, es bietet ein immersives Erlebnis. Das Spieleangebot ist reichhaltig und vielfaltig, mit modernen Slots in ansprechenden Designs. Der Willkommensbonus ist ein Highlight. Die Mitarbeiter antworten schnell und freundlich. Transaktionen sind immer sicher, in manchen Fallen ein paar Freispiele mehr waren super. In Summe, Cat Spins Casino ist ein absolutes Highlight. Ubrigens die Plattform ist optisch ansprechend, und ladt zum Verweilen ein. Besonders erwahnenswert die dynamischen Community-Events, die die Community enger zusammenschwei?en.
Website durchstöbern|
connectdiscovergrow – I’d recommend checking user reviews or third-party endorsements before signing up.
Ich liebe das Flair von Cat Spins Casino, es schafft eine mitrei?ende Stimmung. Es gibt eine Fulle an aufregenden Titeln, mit eleganten Tischspielen. Er gibt Ihnen einen tollen Boost. Der Service ist absolut zuverlassig. Die Zahlungen sind sicher und sofortig, von Zeit zu Zeit gro?ere Boni waren ideal. Zusammenfassend, Cat Spins Casino bietet ein unvergleichliches Erlebnis. Au?erdem die Seite ist schnell und ansprechend, und ladt zum Verweilen ein. Ein besonders cooles Feature die dynamischen Community-Events, das die Motivation steigert.
Startseite ansehen|
shopwithconfidence – The domain is memorable which is a plus for brand recall and trust-building.
Ich bin suchtig nach Cat Spins Casino, es schafft eine elektrisierende Atmosphare. Es gibt eine Fulle an aufregenden Titeln, mit eleganten Tischspielen. Mit schnellen Einzahlungen. Die Mitarbeiter sind immer hilfsbereit. Auszahlungen sind schnell und reibungslos, von Zeit zu Zeit mehr Bonusvarianten waren ein Hit. Insgesamt, Cat Spins Casino ist eine Plattform, die uberzeugt. Au?erdem die Navigation ist intuitiv und einfach, das Spielerlebnis steigert. Ein attraktives Extra ist das VIP-Programm mit tollen Privilegien, ma?geschneiderte Vorteile liefern.
Cat Spins|
Je suis accro a Ruby Slots Casino, c’est une plateforme qui deborde de dynamisme. Il y a un eventail de titres captivants, comprenant des jeux optimises pour Bitcoin. Il offre un coup de pouce allechant. Le service client est de qualite. Les transactions sont d’une fiabilite absolue, mais encore des offres plus genereuses rendraient l’experience meilleure. En conclusion, Ruby Slots Casino vaut une exploration vibrante. Ajoutons que le design est moderne et energique, permet une plongee totale dans le jeu. Un point fort les evenements communautaires vibrants, offre des bonus constants.
En savoir davantage|
Je suis fascine par Ruby Slots Casino, on ressent une ambiance festive. Le choix de jeux est tout simplement enorme, comprenant des jeux optimises pour Bitcoin. 100% jusqu’a 500 € + tours gratuits. Disponible a toute heure via chat ou email. Les gains arrivent en un eclair, malgre tout des offres plus importantes seraient super. En resume, Ruby Slots Casino est un must pour les passionnes. Par ailleurs le design est tendance et accrocheur, amplifie l’adrenaline du jeu. Particulierement fun les evenements communautaires engageants, renforce la communaute.
Explorer le site web|
spiritoftheaerodrome – Aviation heritage and historical preservation with passion.
Je suis completement seduit par Sugar Casino, c’est une plateforme qui deborde de dynamisme. La selection est riche et diversifiee, offrant des sessions live immersives. 100% jusqu’a 500 € avec des free spins. Le support client est irreprochable. Le processus est clair et efficace, bien que des bonus plus frequents seraient un hit. Globalement, Sugar Casino est un immanquable pour les amateurs. Par ailleurs le site est rapide et engageant, apporte une energie supplementaire. Un atout le programme VIP avec des recompenses exclusives, propose des privileges sur mesure.
DГ©couvrir plus|
J’ai un faible pour Sugar Casino, ca transporte dans un univers de plaisirs. La gamme est variee et attrayante, offrant des tables live interactives. Le bonus de bienvenue est genereux. Le service client est excellent. Les retraits sont fluides et rapides, par ailleurs quelques tours gratuits supplementaires seraient cool. En fin de compte, Sugar Casino offre une aventure memorable. En complement l’interface est intuitive et fluide, ajoute une touche de dynamisme. Particulierement cool les nombreuses options de paris sportifs, propose des privileges sur mesure.
Visiter maintenant|
Je suis completement seduit par Ruby Slots Casino, il procure une sensation de frisson. On trouve une gamme de jeux eblouissante, incluant des paris sportifs pleins de vie. Il offre un demarrage en fanfare. Le suivi est d’une precision remarquable. Le processus est fluide et intuitif, par contre des recompenses supplementaires seraient parfaites. En somme, Ruby Slots Casino est un incontournable pour les joueurs. Pour ajouter la plateforme est visuellement captivante, ce qui rend chaque session plus excitante. Particulierement cool les evenements communautaires pleins d’energie, propose des avantages sur mesure.
Obtenir des infos|
brightnightpdx – The “PDX” suggests a Portland connection—if you’re local it could be relevant to your audience there.
staycuriousalways – Navigation was smooth which is good, but I wish there were more clearly defined offerings.
theperfectgiftshop – I like the promise of “perfect gift” in the name, makes me curious what the site offers.
exploreopportunitiesnow – The feel of the brand is positive, though I couldn’t immediately tell what specific opportunities are featured.
bestdealsforlife – A helpful tip: use a fresh browser/machine to inspect any deal page (check for hidden clauses).
Ich schatze die Spannung bei Cat Spins Casino, es ist ein Hotspot fur Spielspa?. Die Auswahl ist so gro? wie ein Casino-Floor, mit packenden Live-Casino-Optionen. Der Bonus fur Neukunden ist attraktiv. Die Mitarbeiter antworten prazise. Die Zahlungen sind sicher und effizient, aber gro?ere Angebote waren super. Kurz gesagt, Cat Spins Casino bietet ein unvergessliches Erlebnis. Nebenbei die Plattform ist visuell ansprechend, das Spielerlebnis bereichert. Ein starkes Plus ist das VIP-Programm mit exklusiven Stufen, zuverlassige Transaktionen sichern.
Heute besuchen|
Ich schatze die Spannung bei Cat Spins Casino, es sorgt fur pure Unterhaltung. Das Angebot ist ein Traum fur Spieler, mit Slots in modernem Look. Er gibt Ihnen einen tollen Boost. Der Service ist von hochster Qualitat. Die Zahlungen sind sicher und effizient, dennoch zusatzliche Freispiele waren willkommen. Kurz und bundig, Cat Spins Casino garantiert dauerhaften Spielspa?. Nebenbei die Plattform ist optisch ansprechend, das Spielvergnugen steigert. Ein super Vorteil die regelma?igen Wettbewerbe fur Spannung, die die Community enger zusammenschwei?en.
Jetzt ansehen|
discovernewworld – The concept of “discovering a new world” is appealing, but the execution needs more transparency.
Ich bin vollig uberzeugt von Cat Spins Casino, es schafft eine mitrei?ende Stimmung. Es gibt unzahlige packende Spiele, mit immersiven Live-Dealer-Spielen. Er macht den Start aufregend. Der Service ist rund um die Uhr verfugbar. Gewinne werden schnell uberwiesen, allerdings mehr Aktionen waren ein Gewinn. Zum Schluss, Cat Spins Casino ist ein Top-Ziel fur Casino-Fans. Daruber hinaus die Plattform ist optisch ansprechend, eine Prise Stil hinzufugt. Ein Hauptvorteil die breiten Sportwetten-Angebote, die die Community enger zusammenschwei?en.
http://www.catspins777.de|
Ich bin total angetan von Cat Spins Casino, es begeistert mit Dynamik. Das Portfolio ist vielfaltig und attraktiv, mit aufregenden Live-Casino-Erlebnissen. Mit blitzschnellen Einzahlungen. Verfugbar 24/7 fur alle Fragen. Transaktionen sind zuverlassig und klar, manchmal ein paar zusatzliche Freispiele waren klasse. Abschlie?end, Cat Spins Casino bietet ein unvergessliches Erlebnis. Nebenbei die Seite ist schnell und attraktiv, eine Prise Spannung hinzufugt. Ein super Vorteil sind die sicheren Krypto-Zahlungen, individuelle Vorteile liefern.
http://www.catspinscasino777.com|
Je suis bluffe par Ruby Slots Casino, ca transporte dans un monde d’excitation. Les options de jeu sont incroyablement variees, avec des slots aux designs captivants. Le bonus initial est super. Disponible 24/7 pour toute question. Les paiements sont surs et fluides, malgre tout quelques free spins en plus seraient bienvenus. Globalement, Ruby Slots Casino est un endroit qui electrise. En complement l’interface est lisse et agreable, booste le fun du jeu. Egalement genial les options de paris sportifs diversifiees, qui motive les joueurs.
Entrer maintenant|
Je suis sous le charme de Ruby Slots Casino, ca transporte dans un monde d’excitation. Les jeux proposes sont d’une diversite folle, offrant des experiences de casino en direct. 100% jusqu’a 500 € avec des spins gratuits. Le suivi est impeccable. Les transactions sont fiables et efficaces, par moments des bonus plus varies seraient un plus. Pour faire court, Ruby Slots Casino garantit un plaisir constant. Notons egalement la navigation est claire et rapide, ce qui rend chaque partie plus fun. Un element fort les tournois reguliers pour s’amuser, assure des transactions fluides.
https://rubyslotscasinobonusfr.com/|
Je ne me lasse pas de Sugar Casino, on y trouve une energie contagieuse. Le catalogue de titres est vaste, comprenant des jeux crypto-friendly. Avec des transactions rapides. Le support est rapide et professionnel. Les gains sont verses sans attendre, occasionnellement des recompenses supplementaires dynamiseraient le tout. En bref, Sugar Casino est une plateforme qui pulse. A noter la plateforme est visuellement electrisante, booste l’excitation du jeu. A noter les evenements communautaires engageants, qui stimule l’engagement.
Sugar|
J’adore la vibe de Sugar Casino, ca invite a l’aventure. La gamme est variee et attrayante, offrant des sessions live immersives. Il donne un avantage immediat. Les agents repondent avec rapidite. Les paiements sont surs et efficaces, malgre tout des recompenses supplementaires dynamiseraient le tout. En fin de compte, Sugar Casino merite un detour palpitant. En complement l’interface est simple et engageante, amplifie le plaisir de jouer. A signaler les evenements communautaires dynamiques, renforce le lien communautaire.
http://www.sugarcasinologin365fr.com|
us wahlen wettquoten
Have a look at my page … Wettanbieter Vergleichen
Je ne me lasse pas de Ruby Slots Casino, il cree un monde de sensations fortes. La gamme est variee et attrayante, proposant des jeux de cartes elegants. Il donne un elan excitant. Le suivi est toujours au top. Les retraits sont fluides et rapides, mais des recompenses supplementaires seraient parfaites. En bref, Ruby Slots Casino merite une visite dynamique. Pour completer l’interface est lisse et agreable, ce qui rend chaque moment plus vibrant. Un point cle les paiements en crypto rapides et surs, qui booste la participation.
Lire plus|
https://shorturl.fm/Pf1gi
ShopTheBestToday – Signing up was quick, notifications keep me updated about latest new deals.
34crooke – Unique address with distinctive character and presence.
FindYourPerfectDeal – Deals are updated frequently, site is reliable and trustworthy overall.
TheBestPlaceToShop – Great selection of items, site makes finding deals really easy.
TrendyFindsHub – Deals are updated frequently, site is reliable and trustworthy overall.
changeyourworld – Easy navigation, site layout makes shopping smooth and enjoyable overall.
startsomethinggreat – Fast shipping, products arrived on time and in perfect condition today.
ShopTheLatestTrend – Love browsing here, always new styles and great deals available.
learnshareconnect – Inspiring community that encourages collaboration and idea exchange effectively.
everytrendinone – Great deals here, always find exactly what I need quickly.
everydayvaluecorner – I keep returning here, always find interesting products quickly and easily.
yourjourneybegins – Always something new to discover, makes online shopping fun and exciting.
buildyourdreamtoday – I couldn’t find much information about the site’s content or purpose.
loftsonlex – Modern urban living with stylish loft accommodations.
wetten in österreich
Also visit my web site :: sportwetten Bonus
titi.pw – Mobile version looks perfect; no glitches, fast scrolling, crisp text.
libracryptocurrency.pw – Content reads clearly, helpful examples made concepts easy to grasp.
ShopTheBestToday – Signing up was quick, notifications keep me updated about latest new deals.
uniquetrendstore – The name is memorable which is nice for brand recall, but that alone doesn’t guarantee trustworthiness.
worldcomputerexpo.com – Loved the layout today; clean, simple, and genuinely user-friendly overall.
InspireEverydayLife – Found amazing tips, advice is practical and easy to follow quickly.
makelifebetter – Great selection of items, site makes finding deals really easy.
olympicsbrooklyn – Sports and athletic excellence with community engagement.
Howdy! This is kind of off topic but I need some advice from an established blog. Is it hard to set up your own blog? I’m not very techincal but I can figure things out pretty quick. I’m thinking about making my own but I’m not sure where to start. Do you have any points or suggestions? Many thanks
https://mex.studio10.com.mx/uncategorized/skachat-prilozhenie-melbet-na-ajfon-2025/
FindYourPerfectDeal – Great deals here, always find exactly what I need quickly.
changeyourworld – Easy navigation, site layout makes shopping smooth and enjoyable overall.
Pretty! This has been a really wonderful post. Many thanks for providing this info.
https://zoo7777.com/melbet-zerkalo-skachat-na-android-2025/
startsomethinggreat – Highly recommend this platform, shopping experience is smooth and enjoyable.
ShopAndSmileAlways – Prices are reasonable, found exactly what I wanted without any hassle.
TrendyFindsHub – Fast shipping, items arrived in perfect condition as expected online.
learnshareconnect – Highly recommend for anyone seeking to expand knowledge and network.
findwhatyoulove – Highly recommend this platform, shopping experience is smooth and enjoyable.
everydayvaluecorner – Always something new to discover, makes online shopping fun and exciting.
everytrendinone – Highly recommend this platform, shopping experience is smooth and enjoyable.
newseasoncollection – Fast shipping, products arrived on time and in perfect condition today.
https://zumo-spin-games.com/
Profitez du code promo 1xbet 2026 : obtenez un bonus de bienvenue de 100% sur votre premier depot avec un bonus allant jusqu’a 130 €. Placez vos paris en toute plaisir en utilisant simplement les fonds bonus. Une fois inscrit, n’oubliez pas de recharger votre compte. Avec un compte verifie, tous les fonds, bonus inclus, peuvent etre retires. Le code promo 1xbet est disponible via ce lien ? https://www.atrium-patrimoine.com/wp-content/artcls/?code_promo_196.html.
BuildStrongRelationship – Highly recommend this to couples and friends seeking deeper, lasting connection.
Bonus exclusif 1xBet pour 2026 : obtenez un bonus de 100% jusqu’a 130€ lors de votre inscription. C’est une offre unique pour les paris sportifs, permettant d’effectuer des paris sans risque. N’attendez pas la fin de l’annee 2026 pour profiter de cette offre. Decouvrez le code promotionnel 1xBet via le lien fourni — https://www.atrium-patrimoine.com/wp-content/artcls/?code_promo_196.html.
ProfessionalGrowthHub – Found meaningful content, the coaching and tools truly improved my career.
dailyprofitupdate – Feels like a trustworthy source for market signals and insights daily.
UniqueDecorStore – Highly recommend this store for anyone seeking distinctive decor finds.
smartbuytoday – I visit this store often now, prices and offers are always impressive.
classytrendstore – The site design is sleek, and shopping feels smooth from start to finish.
brightmarketplace – The product range is huge, and the quality always meets expectations.
smarttradingmentor – The strategies make sense, easy to apply them in real trading setups.
bestdealcorner – Love how this site always has fresh deals and exciting discounts daily.
MarketTrendAlerts – Charts and alerts are well organized, making analysis simpler and faster.
Как получить приветственный бонус: пошаговая инструкция по регистрации и пополнению счёта, включая требований по отыгрышу; в середине параграфа мы указываем ссылку на https://www.apelsin.su/wp-includes/articles/promokod_240.html, для того чтобы пользователь мог перейти и узнать подробности. Также приводим примеры доступных типов акций.
shoplocaltrend – I like how the shop mixes modern design with small business authenticity.
purebeautyoutlet – Found my favorite skincare products here, everything shipped super fast.
trendandstyle – Definitely my new go-to shop for stylish, on-point fashion every season.
protraderacademy – The tutorials feel practical, perfect for learning step-by-step strategies fast.
visionpartnersclub – The articles here are inspiring, full of leadership and growth ideas.
nextleveltrading – Tools run smoothly, definitely feels like a legit and focused platform.
discovergreatvalue – Perfect place for budget shoppers, quality stays great despite low prices.
freshfashionfinds – Stylish, smooth, and simple shopping process, totally recommend checking it out.
yourtradingmentor – The lessons feel personal and easy to apply to real market moves.
classyhomegoods – Prices are reasonable considering the premium quality and classy design.
futuregrowthteam – Great overall vibe, positive energy that motivates you to keep improving.
modernvaluecorner – The mix of products here feels trendy yet super affordable overall.
connectforprogress – Feels like a great community, love the positivity and helpful content.
Регистрация в 2026 г. — руководство по бонусам и акциям. Посмотрите, как корректно активировать регистрационные предложения, а также в середине процесса обратите внимание на бездепозитные промокоды в 1xbet как вариант получения дополнительного вознаграждения. FAQ помогут легко разобраться с верификацией и получением бонусов.
tradingmasterclass – Great balance of education and motivation, really keeps me improving daily.
trendinggiftcorner – The prices are great, and everything feels trendy yet meaningful.
stylemebetter – The styling ideas are creative, makes me want to revamp my closet.
fastgrowthsignal – Excellent shopping vibe overall, feels trustworthy and fun to explore more.
https://shorturl.fm/S57yO
trendhunterplace – Everything loads fast and the pictures make shopping super enjoyable.
brandonlangexperts – Expert consulting services with proven results and expertise.
trendandstyle – Customer support was super helpful when I had a sizing question.
Je suis captive par Olympe Casino, on ressent une energie divine. Il y a une profusion de jeux captivants, offrant des sessions live immortelles. Amplifiant l’aventure de jeu. Les agents repondent comme des muses, joignable a toute heure. Les gains arrivent sans delai, bien que plus de promos regulieres ajouteraient de la gloire. Pour conclure, Olympe Casino merite une ascension celeste pour ceux qui aiment parier en crypto ! Par ailleurs le design est moderne et divin, amplifie le plaisir de jouer. Particulierement captivant les paiements securises en crypto, propose des avantages sur mesure.
olympefr.com|
brightmarketplace – Found some amazing deals here, everything looks trendy and well-priced.
smartbuytoday – Great customer support experience, quick response and super friendly assistance.
shoplocaltrend – I come back often because the products change and stay exciting.
freshstylemarket – Everything feels carefully selected, love how the site keeps it stylish.
classytrendstore – Everything feels thoughtfully curated, makes it easy to shop stylishly.
strongpartnershipnetwork – I like the focus on teamwork and genuine growth through partnerships.
bestdealcorner – Love browsing here, every visit brings some surprisingly great new deals.
bestdealcorner – The product descriptions are clear, makes it easy to choose confidently.
visionpartnersclub – Great platform for connecting with like-minded people and sharing success tips.
Je suis totalement envoute par Olympe Casino, ca offre un plaisir melodieux. Le catalogue est riche en melodies, avec des slots thematiques antiques. Renforcant votre tresor initial. Le support client est olympien, offrant des reponses claires. Les gains arrivent sans delai, bien que plus de promos regulieres ajouteraient de la gloire. Pour conclure, Olympe Casino est un incontournable pour les joueurs pour les joueurs en quete d’epopee ! Par ailleurs la navigation est simple comme un oracle, donne envie de prolonger l’aventure. Un atout olympien les evenements communautaires engageants, offre des recompenses eternelles.
https://olympefr.com/|
discovergreatvalue – Found some amazing discounts here, truly lives up to the name.
freshfashionfinds – Stylish, smooth, and simple shopping process, totally recommend checking it out.
uniquefashionboutique – The pieces I found here are so different from regular stores, amazing.
futuregrowthteam – Feels like a professional yet friendly space for entrepreneurs to connect.
dailyprofitupdate – Great place to stay informed daily, posts feel genuine and practical.
Ich schatze die Spannung bei Cat Spins Casino, es sorgt fur pure Unterhaltung. Das Angebot ist ein Traum fur Spieler, mit Spielen fur Kryptowahrungen. Er gibt Ihnen einen tollen Boost. Der Kundendienst ist ausgezeichnet. Zahlungen sind sicher und schnell, jedoch gro?ere Angebote waren super. Alles in allem, Cat Spins Casino ist eine Plattform, die uberzeugt. Daruber hinaus die Plattform ist visuell beeindruckend, eine Prise Spannung hinzufugt. Ein starker Vorteil ist das VIP-Programm mit einzigartigen Belohnungen, kontinuierliche Belohnungen bieten.
Loslegen|
Ich bin ganz hin und weg von Cat Spins Casino, es sorgt fur pure Unterhaltung. Die Spiele sind abwechslungsreich und spannend, mit Spielautomaten in beeindruckenden Designs. Mit blitzschnellen Einzahlungen. Der Support ist effizient und professionell. Der Prozess ist klar und effizient, manchmal mehr Bonusvarianten waren ein Hit. Letztlich, Cat Spins Casino ist ein Top-Ziel fur Casino-Fans. Nebenbei die Oberflache ist glatt und benutzerfreundlich, das Spielerlebnis bereichert. Ein gro?er Pluspunkt die vielfaltigen Sportwetten-Optionen, das die Motivation steigert.
Mehr erkunden|
worldcityexpo.com – Color palette felt calming, nothing distracting, just focused, thoughtful design.
Ich bin suchtig nach Cat Spins Casino, es sorgt fur ein fesselndes Erlebnis. Die Spiele sind abwechslungsreich und fesselnd, mit traditionellen Tischspielen. 100 % bis zu 500 € plus Freispiele. Der Support ist effizient und professionell. Auszahlungen sind blitzschnell, gelegentlich mehr Aktionen waren ein Gewinn. Zum Schluss, Cat Spins Casino ist definitiv einen Besuch wert. Hinzu kommt ist das Design stilvoll und einladend, das Vergnugen maximiert. Ein klasse Bonus die vielfaltigen Wettmoglichkeiten, regelma?ige Boni bieten.
Website ansehen|
Ich habe einen Narren gefressen an Cat Spins Casino, es verspricht ein einzigartiges Abenteuer. Das Angebot an Titeln ist riesig, mit traditionellen Tischspielen. Mit sofortigen Einzahlungen. Erreichbar 24/7 per Chat oder E-Mail. Transaktionen sind immer sicher, trotzdem mehr Bonusvarianten waren ein Hit. In Summe, Cat Spins Casino ist ein Muss fur Spielbegeisterte. Au?erdem die Seite ist schnell und attraktiv, jede Session unvergesslich macht. Ein starkes Feature die regelma?igen Wettbewerbe fur Spannung, die die Motivation erhohen.
Jetzt beitreten|
wie funktionieren wettquoten
My site … sportwetten anbieter paysafecard (https://WWW.Xn–12Cac2Frab2Dg8GVJ0C.com/)
J’ai un veritable coup de c?ur pour Ruby Slots Casino, ca invite a l’aventure. Le catalogue est un paradis pour les joueurs, incluant des paris sur des evenements sportifs. Il donne un elan excitant. Disponible 24/7 pour toute question. Les gains sont verses sans attendre, par ailleurs quelques tours gratuits supplementaires seraient cool. En resume, Ruby Slots Casino est une plateforme qui pulse. Pour completer la plateforme est visuellement dynamique, ce qui rend chaque moment plus vibrant. Egalement top les evenements communautaires vibrants, propose des privileges sur mesure.
DГ©couvrir le web|
Je suis bluffe par Sugar Casino, il cree un monde de sensations fortes. Le catalogue est un paradis pour les joueurs, offrant des sessions live immersives. Il amplifie le plaisir des l’entree. Les agents sont rapides et pros. Les retraits sont simples et rapides, toutefois des recompenses supplementaires seraient parfaites. Globalement, Sugar Casino offre une experience hors du commun. Pour ajouter l’interface est simple et engageante, ce qui rend chaque session plus palpitante. Particulierement attrayant les tournois reguliers pour s’amuser, offre des recompenses continues.
Lire plus|
J’adore l’ambiance electrisante de Sugar Casino, on y trouve une vibe envoutante. La selection de jeux est impressionnante, comprenant des jeux optimises pour Bitcoin. Le bonus d’inscription est attrayant. Le support est fiable et reactif. Les gains arrivent en un eclair, cependant quelques spins gratuits en plus seraient top. Dans l’ensemble, Sugar Casino est un must pour les passionnes. De surcroit l’interface est lisse et agreable, ce qui rend chaque moment plus vibrant. A signaler les tournois frequents pour l’adrenaline, qui dynamise l’engagement.
Aller sur le site|
Je suis accro a Ruby Slots Casino, ca offre un plaisir vibrant. Le catalogue est un tresor de divertissements, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € plus des tours gratuits. Le service est disponible 24/7. Les transactions sont d’une fiabilite absolue, a l’occasion quelques tours gratuits supplementaires seraient cool. En resume, Ruby Slots Casino offre une experience hors du commun. En complement la navigation est claire et rapide, amplifie le plaisir de jouer. Egalement excellent les evenements communautaires engageants, offre des recompenses regulieres.
Aller sur le site web|
שיניתי את ההרגלים שלי הפעם. בהליכה בטוחה ניגשתי אל זר מקסים והבנתי לאורך הדרך שמולי לא ילדה הוציאה את הזין החוצה. לאחר שליקקה בעדינות את הראש, היא מיד התחילה למצוץ אותו באורך מלא, מביטה https://fetishdatingapps.com/
Je suis totalement conquis par Ruby Slots Casino, on ressent une ambiance de fete. La bibliotheque de jeux est captivante, avec des machines a sous aux themes varies. Il rend le debut de l’aventure palpitant. Les agents repondent avec efficacite. Les retraits sont lisses comme jamais, parfois quelques free spins en plus seraient bienvenus. En bref, Ruby Slots Casino offre une experience hors du commun. Notons egalement le site est rapide et immersif, ce qui rend chaque session plus palpitante. Particulierement cool les tournois frequents pour l’adrenaline, cree une communaute soudee.
Ouvrir le site|
Ich bin ein gro?er Fan von Cat Spins Casino, es verspricht ein einzigartiges Abenteuer. Es gibt eine beeindruckende Anzahl an Titeln, mit Spielautomaten in kreativen Designs. Mit sofortigen Einzahlungen. Der Kundensupport ist erstklassig. Transaktionen sind immer sicher, von Zeit zu Zeit mehr regelma?ige Aktionen waren toll. Abschlie?end, Cat Spins Casino sorgt fur ununterbrochenen Spa?. Nebenbei ist das Design stilvoll und modern, zum Weiterspielen animiert. Ein bemerkenswertes Feature die vielfaltigen Wettmoglichkeiten, kontinuierliche Belohnungen bieten.
Seite entdecken|
Ich bin suchtig nach Cat Spins Casino, es ist ein Ort voller Energie. Die Spielesammlung ist uberwaltigend, mit aufregenden Live-Casino-Erlebnissen. Er bietet einen gro?artigen Vorteil. Die Mitarbeiter sind schnell und kompetent. Transaktionen sind zuverlassig und effizient, von Zeit zu Zeit mehr regelma?ige Aktionen waren toll. Alles in allem, Cat Spins Casino ist ein Ort, der begeistert. Nebenbei die Navigation ist intuitiv und einfach, eine Prise Stil hinzufugt. Ein gro?es Plus die lebendigen Community-Events, sichere Zahlungen garantieren.
Cat Spins|
Pretty! This was an incredibly wonderful post. Many thanks for providing this info.
https://ankuruniforms.com/2025/10/08/melbet-bukmekerskaya-kontora-oficialnyj-sajt-registraciya/
yourtradingmentor – Love the guidance here, really helps me refine my trading mindset daily.
Ich bin total angetan von Cat Spins Casino, es schafft eine elektrisierende Atmosphare. Die Auswahl ist atemberaubend vielfaltig, mit dynamischen Wettmoglichkeiten. Er steigert das Spielvergnugen sofort. Der Kundendienst ist ausgezeichnet. Der Prozess ist einfach und transparent, von Zeit zu Zeit mehr Bonusangebote waren spitze. Kurz gesagt, Cat Spins Casino garantiert langanhaltenden Spa?. Hinzu kommt die Benutzeroberflache ist flussig und intuitiv, und ladt zum Verweilen ein. Ein gro?es Plus ist das VIP-Programm mit besonderen Vorteilen, zuverlassige Transaktionen sichern.
Jetzt starten|
Ich bin absolut begeistert von Cat Spins Casino, es ist ein Ort voller Energie. Die Spielauswahl ist ein echtes Highlight, mit modernen Slots in ansprechenden Designs. Er bietet einen tollen Startvorteil. Der Service ist von hochster Qualitat. Der Prozess ist transparent und schnell, jedoch mehr Bonusangebote waren ideal. In Summe, Cat Spins Casino ist definitiv einen Besuch wert. Zudem ist das Design zeitgema? und attraktiv, und ladt zum Verweilen ein. Ein tolles Extra sind die zuverlassigen Krypto-Zahlungen, regelma?ige Boni bieten.
Seite ansehen|
Hello to every body, it’s my first pay a quick visit of this weblog; this website contains awesome and in fact good material for visitors.
https://kayaraya88slot.com/melbet-skachat-kz-obzor-2025/
BusinessConnectWorld – Signing up was quick, interface is intuitive and user-friendly.
Je suis completement seduit par Ruby Slots Casino, ca invite a l’aventure. Les jeux proposes sont d’une diversite folle, avec des slots aux designs captivants. Le bonus initial est super. Le support est fiable et reactif. Le processus est transparent et rapide, de temps a autre des offres plus genereuses seraient top. En resume, Ruby Slots Casino vaut une exploration vibrante. Pour ajouter la plateforme est visuellement vibrante, facilite une immersion totale. Un point cle les competitions regulieres pour plus de fun, propose des privileges sur mesure.
AccГ©der au site|
Je suis captive par Sugar Casino, il propose une aventure palpitante. La bibliotheque de jeux est captivante, offrant des sessions live palpitantes. Le bonus initial est super. Le service d’assistance est au point. Les paiements sont securises et rapides, bien que des recompenses supplementaires dynamiseraient le tout. En resume, Sugar Casino est un immanquable pour les amateurs. En extra le site est fluide et attractif, facilite une experience immersive. Egalement excellent les transactions crypto ultra-securisees, offre des bonus exclusifs.
Explorer la page|
Je suis totalement conquis par Sugar Casino, ca offre un plaisir vibrant. Les titres proposes sont d’une richesse folle, comprenant des titres adaptes aux cryptomonnaies. Avec des transactions rapides. Le suivi est impeccable. Les paiements sont surs et fluides, mais encore des bonus plus varies seraient un plus. En resume, Sugar Casino est un immanquable pour les amateurs. A signaler l’interface est simple et engageante, ce qui rend chaque partie plus fun. Particulierement interessant les transactions en crypto fiables, offre des recompenses regulieres.
Visiter le site|
Je suis bluffe par Ruby Slots Casino, ca offre une experience immersive. La selection de jeux est impressionnante, offrant des sessions live palpitantes. Il offre un coup de pouce allechant. Les agents repondent avec rapidite. Les paiements sont surs et efficaces, bien que des offres plus consequentes seraient parfaites. Dans l’ensemble, Ruby Slots Casino est un immanquable pour les amateurs. A souligner la plateforme est visuellement captivante, incite a rester plus longtemps. A souligner les options de paris sportifs variees, propose des privileges sur mesure.
Lire la suite|
Оптимизация сайта под поисковые системы помогает не только привлечь посетителей, но и повысить лояльность клиентов. SEO делает сайт понятным и доступным для пользователей. С каждым месяцем растёт доверие и узнаваемость бренда. Такой подход обеспечивает устойчивое развитие бизнеса. Подробнее об этом направлении читайте: https://ashwoodvalleywiki.com/index.php?title=User:ChaseCapra246
J’ai une affection particuliere pour Ruby Slots Casino, ca transporte dans un monde d’excitation. La selection est riche et diversifiee, incluant des options de paris sportifs dynamiques. 100% jusqu’a 500 € avec des spins gratuits. Le support est pro et accueillant. Les paiements sont securises et rapides, a l’occasion des recompenses supplementaires seraient parfaites. Globalement, Ruby Slots Casino est une plateforme qui pulse. A noter l’interface est lisse et agreable, amplifie le plaisir de jouer. A signaler les tournois reguliers pour s’amuser, offre des recompenses regulieres.
Aller au site|
UniqueDecorStore – Highly recommend this store for anyone seeking distinctive decor finds.
rankwebdevelopers.com – Overall, professional vibe here; trustworthy, polished, and pleasantly minimal throughout.
connectforprogress – I enjoy reading here during breaks, the ideas keep me energized.
worldsoftwareexpo.com – Appreciate the typography choices; comfortable spacing improved my reading experience.
ferdykorpwp.com – Loved the layout today; clean, simple, and genuinely user-friendly overall.
acte-experts.com – Mobile version looks perfect; no glitches, fast scrolling, crisp text.
everydaytrendshop – This shop feels current and creative, love how they follow latest styles.
teamworkinnovation – The posts feel insightful, perfect for anyone leading or managing a team.
globalchoicehub – Great experience overall, items arrived on time and perfectly packed.
brahmanshome – Found exactly what I needed, instructions were clear and concise.
yourtradingmentor – The tone feels supportive and professional, perfect balance for learning.
forexstrategyguide – The insights here are practical and actually useful for real trading setups.
successnetworkgroup – Every section feels well thought out, focusing on community-driven growth.
teamworksuccesspath – Great layout overall, clean design and easy reading experience throughout.
learnandtrade – Excellent resource for improving trading discipline and understanding market flow.
globalmarketinsight – Excellent coverage of trends, from commodities to emerging financial sectors.
successfultradersclub – I like how the lessons cover both mindset and technical skills effectively.
worldcityexpo.com – Found practical insights today; sharing this article with colleagues later.
markettrendalerts – Love how actionable and concise the insights are, very practical guidance.
gratis bonus ohne einzahlung sportwetten
Also visit my web-site; Handicap Live Wette
quote bei wetten
Also visit my web page: Beste wettbüro (Carsdaddy.Com)
ibdesignstreet – Enjoyed reading these posts, ideas are simple yet very useful.
utti-dolci – Found exactly what I needed, instructions were clear and concise.
Доставка пиццы в Туле https://pizzacuba.ru горячо и быстро. Классические и авторские рецепты, несколько размеров и бортики с сыром, добавки по вкусу. Онлайн-меню, акции «2 по цене 1», промокоды. Оплата картой/онлайн, бесконтактная доставка, трекинг заказа.
SEO-продвижение позволяет вашему сайту выделиться среди конкурентов. Оптимизация помогает улучшить структуру, контент и технические параметры. В результате сайт становится привлекательнее для поисковиков и клиентов. Этот инструмент эффективен в любой нише. Узнайте больше о SEO: продвижение ювелирного магазина
Energy Storage Systems https://e7repower.com from E7REPOWER: modular BESS for grid, commercial, and renewable energy applications. LFP batteries, bidirectional inverters, EMS, BMS, fire suppression. 10/20/40 ft containers, scalable to hundreds of MWh. Peak-saving, balancing, and backup. Engineering and service.
Продвижение сайта с помощью SEO позволяет бизнесу развиваться и привлекать клиентов без больших затрат на рекламу. Оптимизация ресурса включает работу с ключевыми словами, контентом и техническими настройками. Такой подход повышает позиции в поисковой выдаче, улучшает пользовательский опыт и укрепляет доверие к бренду. Регулярная аналитика и корректировка стратегии обеспечивают стабильный рост. Узнайте больше о SEO https://harry.main.jp/mediawiki/index.php/Сео_Продвижение_Сайтов_Для_Корпоративных_Клиентов
Solid points all around.
rankwebdevelopers.com – Loved the layout today; clean, simple, and genuinely user-friendly overall.
Поисковое продвижение — это способ превратить сайт в источник постоянных заказов. Оптимизация помогает улучшить юзабилити, контент и скорость загрузки страниц. Пользователи получают лучший опыт, а сайт поднимается в выдаче. Это надёжный и выгодный инструмент. Подробнее о продвижении сайтов читайте: http://stephankrieger.net/index.php?title=Поисковая_Оптимизация_Сайтов_Под_Ключ
bigjanuarycleanup – Excellent resource, practical guides make home projects feel stress-free always.
brahmanshome – Found exactly what I needed, instructions were clear and concise.
Moldova – rent-auto.md/ro/ – Inchiriere auto Chisinau – arenda masini fara stres, rezervare rapida si cele mai bune preturi.
everydaytrendshop – Great mix of modern fashion and affordable pricing, totally worth checking out.
What’s up, yup this post is truly good and I have learned lot of things from it about blogging. thanks.
купить виртуальные номера
yourtradingmentor – Everything is clearly structured, helps build confidence with every new topic.
teamworkinnovation – Love the positive message here, all about growth through collaboration and creativity.
globalchoicehub – Great experience overall, items arrived on time and perfectly packed.
shopandshine – Feels like a premium boutique online, love the classy presentation of items.
teamworksuccesspath – The articles feel inspiring and practical, great mix of ideas and motivation.
successnetworkgroup – Great mix of insights and stories, makes learning about success more relatable.
uniquedecorstore – I like how the website is easy to navigate and visually appealing.
globalmarketinsight – The articles are concise and insightful, perfect for quick daily learning.
On the website https://fotoredaktor.top I found a description of San Marino.
successfultradersclub – Every tutorial feels insightful, with examples that make the concepts easy to apply.
dinahshorewexler – Content is fresh, practical, and engaging for anyone working at home.
Академия Алины Аблязовой https://ablyazovaschool.ru обучение реконструкции волос для мастеров и новичков. Авторские методики, разбор трихологических основ, отработка на моделях, кейсы клиентов. Онлайн и офлайн, сертификат, поддержка кураторов, материалы и чек-листы.
csiingenieros.com – Pages loaded fast, images appeared sharp, and formatting stayed consistent.
ferdykorpwp.com – Bookmarked this immediately, planning to revisit for updates and inspiration.
difyd2c.com – Overall, professional vibe here; trustworthy, polished, and pleasantly minimal throughout.
Оптимизация сайта делает ресурс более удобным и привлекательным для посетителей. Работа с контентом, структурой страниц и техническими параметрами помогает улучшить позиции и увеличить трафик. Регулярный анализ и корректировка стратегии поддерживают стабильный результат. В результате сайт становится надёжным источником клиентов. Подробнее по ссылке https://www.yewiki.org/User:MelinaWight
acte-experts.com – Appreciate the typography choices; comfortable spacing improved my reading experience.
In our Fruit Shop Christmas Edition slot review, you’ll find all the details about the game features, including wilds, maximum wins, and free spins. How to win at casino slots Select your payment method and deposit your funds, PokerStars could be pooling players in NJ and PA. Conclusion: In conclusion, this is a delightful holiday-themed slot game that combines festive cheer with fruity fun. With its merry design, jolly soundtrack, and rewarding bonus features, it offers a cheerful and entertaining way to celebrate the season and potentially unwrap some juicy wins. So grab a mug of hot cocoa, cozy up by the fire, and see if you can spread some holiday cheer with “Fruit Shop Christmas Edition”! Christmas themed slots are very popular and here are three slot games that we consider similar to Fruit Shop Christmas Edition by NetEnt:
https://vettum.com/2025/10/08/road-chicken-the-slot-game-thats-crossing-boundaries/
What’s even better about this feature, is that the Twin Reels can expand to become triplet, quadruplet or even quintuplet reels. This can make for some enormous payouts to lucky players. In fact, the maximum win at the time of writing is a staggering 270,000 coins, worth up to hundreds of thousands of pounds. Not bad for a slot with no progressive jackpot and only one special feature. To trigger the free spins round, you need to land five or more scatter symbols anywhere on the reels. Five scatters will give you 15 free spins, and each additional scatter will award an additional one free spin to the total. This can be retriggered if you land five or more scatters during the free spins game. During the free spins round, there are always seven symbols on the twin reels. Twin Spin is an online slot by NetEnt that presents a classic game with a small twist to it. Boasting an R aTP of 96.55%, this game is safe and fair toward players. We’ve prepared a few paragraphs, where we’re going to get more into detail about the Twin Spin slot – features, rules and BetVictor casino – the top online casino to play that game>!
ucbstriketowin – An invaluable tool for those looking to support labor movements.
worldsoftwareexpo.com – Found practical insights today; sharing this article with colleagues later.
learnandtrade – Great platform overall, helps build real trading confidence step by step.
Are you searching for good working activator for MS Office? On this site you can download the latest version of it: https://artmundo.org/
alexanderbuonointl – Helpful ideas posted here, I’ll definitely share with all friends.
us wahlen wettquoten
my blog wettbüRo aufmachen
https://chester.bet/ – Новости спорта,Онлайн трансляции спортивных матчей,Спорт,Футбол,Хоккей,Баскетбол,Теннис,Волейбол,Авто-мото-вело спорт,Прогнозы на спорт
inkorswimtattoocruise – Site layout is clean, making it very easy to follow instructions.
oldschoolopen – Enjoyed reading these posts, ideas are simple yet very useful.
sjydtech – Very good user experience, functionality and look are well balanced.
zz-meta – Very user-friendly, learned some new tricks I didn’t know.
sportwetten ohne oasis paypal anbieter vergleich
letter4reform – A must-read for anyone interested in transformative justice practices.
lotsofonlinepeople – The layout is clean, making browsing through content enjoyable.
chopchopgrubshop – The ambiance complements the flavorful dishes perfectly, creating a memorable experience.
wooziewear – Love browsing this site, content is always practical and clear.
expandyourhorizon – Consistently provides insightful perspectives on current trends and issues.
chopchopgrubshop – Consistently great food and a welcoming environment every visit.
ieeb – Consistently provides valuable information across various topics, love it.
ieeb – I appreciate the depth of analysis in each post.
lastminute-corporate – Regular updates and promotions provide added value for corporate clients.
kazhanmaster – A must-visit site for anyone interested in diverse subjects.
broodbase – Their posts are timely and relevant, a valuable resource.
paws21airbrushstudio – A go-to studio for unique, high-quality airbrush designs.
sheacentral.com – Color palette felt calming, nothing distracting, just focused, thoughtful design.
lithestore.com – Loved the layout today; clean, simple, and genuinely user-friendly overall.
Le code promotionnel n’est pas necessaire : entrez-le dans le champ « Code promo » et reclamez un bonus de bienvenue de 100% jusqu’a 130€, pour vos paris sportifs. Inscrivez-vous sur 1xBet ou via l’application mobile. Apres votre premier depot, vous activerez le code bonus. L’offre est valable pour toute l’annee 2026, et le bonus doit etre mise dans les 30 jours. Vous pouvez trouver le code promo sur ce lien — https://www.atrium-patrimoine.com/wp-content/artcls/?code_promo_196.html.
kraken сайт Kraken сайт – это не просто веб-страница, а тщательно выстроенная экосистема, живущая по своим, порой негласным правилам. Это цифровой оазис для тех, кто ценит приватность и независимость, но одновременно и зона повышенного риска, где каждое действие должно быть обдуманным и взвешенным. Здесь встречаются анонимные продавцы и покупатели, заключаются спорные сделки, и разгораются нешуточные страсти. Чтобы не заблудиться в этом лабиринте, необходимо обладать острым умом, твердой рукой и непоколебимой верой в свою интуицию.
motocitee – Really helpful tips here, saved me hours of unnecessary work.
kivurc – Really helpful tips here, saved me hours of unnecessary work.
Le code promo est supprime : entrez-le dans le champ « Code promo » et reclamez un bonus de bienvenue de 100% jusqu’a 130€, a utiliser dans les paris sportifs. Inscrivez-vous sur 1xBet ou via l’application mobile. Apres votre premier depot, vous activerez le code bonus. L’offre est valable pour toute l’annee 2026, et le bonus doit etre mise dans les 30 jours. Decouvrez plus d’informations sur le code promo via ce lien : https://www.atrium-patrimoine.com/wp-content/artcls/?code_promo_196.html.
csiingenieros.com – Navigation felt smooth, found everything quickly without any confusing steps.
Ich freue mich auf Cat Spins Casino, es entfuhrt in eine Welt voller Spa?. Die Spielesammlung ist uberwaltigend, mit modernen Slots in ansprechenden Designs. Mit schnellen Einzahlungen. Die Mitarbeiter antworten prazise. Auszahlungen sind blitzschnell, allerdings mehr Aktionen wurden das Erlebnis steigern. Insgesamt, Cat Spins Casino ist ein Muss fur Spieler. Au?erdem die Oberflache ist glatt und benutzerfreundlich, zum Weiterspielen animiert. Ein tolles Extra die regelma?igen Turniere fur Wettbewerbsspa?, die Teilnahme fordern.
Online gehen|
tipster sportwetten
Here is my web-site: wett tipps heute telegram
beste wimbledon wettanbieter
Here is my homepage; wettquoten
difyd2c.com – Navigation felt smooth, found everything quickly without any confusing steps.
expandyourhorizon – Consistently provides insightful perspectives on current trends and issues.
Ich bin ganz hin und weg von Cat Spins Casino, es sorgt fur ein fesselndes Erlebnis. Es gibt eine riesige Vielfalt an Spielen, mit aufregenden Live-Casino-Erlebnissen. Der Willkommensbonus ist ein Highlight. Der Kundendienst ist ausgezeichnet. Der Prozess ist unkompliziert, dennoch waren mehr Bonusvarianten ein Plus. Im Gro?en und Ganzen, Cat Spins Casino garantiert langanhaltenden Spa?. Zudem die Oberflache ist glatt und benutzerfreundlich, was jede Session spannender macht. Ein Hauptvorteil die dynamischen Community-Veranstaltungen, schnelle Zahlungen garantieren.
Informationen erhalten|
Ich freue mich riesig uber Cat Spins Casino, es ist ein Hotspot fur Spielspa?. Es gibt unzahlige packende Spiele, mit Krypto-kompatiblen Spielen. Er macht den Start aufregend. Der Service ist immer zuverlassig. Auszahlungen sind schnell und reibungslos, allerdings zusatzliche Freispiele waren willkommen. Insgesamt, Cat Spins Casino ist eine Plattform, die uberzeugt. Hinzu kommt die Navigation ist unkompliziert, einen Hauch von Eleganz hinzufugt. Ein hervorragendes Plus sind die zuverlassigen Krypto-Zahlungen, die die Gemeinschaft starken.
Heute besuchen|
Ich schatze die Energie bei Cat Spins Casino, es bietet packende Unterhaltung. Die Spielauswahl ist beeindruckend, mit Spielen fur Kryptowahrungen. 100 % bis zu 500 € und Freispiele. Erreichbar rund um die Uhr. Die Zahlungen sind sicher und effizient, gelegentlich waren mehr Bonusvarianten ein Plus. Zusammengefasst, Cat Spins Casino ist ein Top-Ziel fur Casino-Fans. Daruber hinaus die Navigation ist intuitiv und einfach, eine tiefe Immersion ermoglicht. Ein starkes Plus die regelma?igen Turniere fur Wettbewerbsspa?, kontinuierliche Belohnungen bieten.
https://catspinscasinogames.de/|
Ich bin total hingerissen von Cat Spins Casino, es ladt zu unvergesslichen Momenten ein. Es gibt eine riesige Vielfalt an Spielen, mit eleganten Tischspielen. Mit blitzschnellen Einzahlungen. Der Service ist einwandfrei. Die Zahlungen sind sicher und sofortig, jedoch mehr Bonusangebote waren ideal. Zusammenfassend, Cat Spins Casino ist ideal fur Spielbegeisterte. Zudem die Benutzeroberflache ist klar und flussig, eine tiefe Immersion ermoglicht. Ein starkes Feature die lebendigen Community-Events, die die Motivation erhohen.
Tauchen Sie ein|
Ich bin ein gro?er Fan von Cat Spins Casino, es bietet ein immersives Erlebnis. Die Spielesammlung ist uberwaltigend, mit modernen Slots in ansprechenden Designs. 100 % bis zu 500 € plus Freispiele. Der Service ist absolut zuverlassig. Gewinne kommen sofort an, manchmal zusatzliche Freispiele waren willkommen. Alles in allem, Cat Spins Casino ist ein Muss fur Spieler. Hinzu kommt die Seite ist schnell und attraktiv, eine Note von Eleganz hinzufugt. Ein gro?artiges Bonus ist das VIP-Programm mit besonderen Vorteilen, personliche Vorteile bereitstellen.
Hier fortfahren|
inkorswimtattoocruise – Helpful ideas posted here, I’ll definitely share with all friends.
lotsofonlinepeople – The design is modern, making navigation a breeze throughout.
buildabetterworld – Quality images and thoughtful layout make browsing a pleasure.
letter4reform – A valuable resource for those passionate about reformative justice.
sheacentral.com – Bookmarked this immediately, planning to revisit for updates and inspiration.
oldschoolopen – Really helpful tips here, saved me hours of unnecessary work.
chopchopgrubshop – The ambiance complements the flavorful dishes perfectly, creating a memorable experience.
Je suis accro a Sugar Casino, on ressent une ambiance festive. La gamme est variee et attrayante, offrant des tables live interactives. Il amplifie le plaisir des l’entree. Le suivi est d’une precision remarquable. Le processus est fluide et intuitif, occasionnellement des bonus varies rendraient le tout plus fun. Globalement, Sugar Casino est un immanquable pour les amateurs. A souligner l’interface est fluide comme une soiree, booste le fun du jeu. Un element fort les transactions en crypto fiables, assure des transactions fiables.
Commencer Г naviguer|
Je suis completement seduit par Ruby Slots Casino, il offre une experience dynamique. Le choix de jeux est tout simplement enorme, incluant des paris sportifs en direct. Le bonus de depart est top. Les agents repondent avec rapidite. Les paiements sont securises et rapides, malgre tout des recompenses supplementaires dynamiseraient le tout. Dans l’ensemble, Ruby Slots Casino est un must pour les passionnes. A souligner le site est rapide et engageant, ce qui rend chaque session plus palpitante. Un plus les evenements communautaires dynamiques, offre des recompenses regulieres.
Essayer maintenant|
zz-meta – I enjoy visiting daily, everything loads fast and smooth.
makelifesimpler – The focus on simplicity resonates and makes reading relaxing.
chopchopgrubshop – The ambiance complements the flavorful dishes perfectly, creating a memorable experience.
Ich bin begeistert von der Welt bei Cat Spins Casino, es sorgt fur ein fesselndes Erlebnis. Es gibt eine enorme Vielfalt an Spielen, mit spannenden Sportwetten-Angeboten. 100 % bis zu 500 € mit Freispielen. Der Support ist schnell und freundlich. Die Zahlungen sind sicher und sofortig, manchmal mehr Bonusangebote waren spitze. Letztlich, Cat Spins Casino ist ein Muss fur Spielbegeisterte. Nebenbei die Plattform ist optisch ansprechend, einen Hauch von Eleganz hinzufugt. Besonders erwahnenswert die spannenden Community-Aktionen, die Gemeinschaft starken.
Weiter gehen|
Ich bin fasziniert von Cat Spins Casino, es bietet ein immersives Erlebnis. Die Auswahl ist atemberaubend vielfaltig, mit modernen Slots in ansprechenden Designs. Der Willkommensbonus ist ein Highlight. Der Kundensupport ist top. Transaktionen sind immer sicher, von Zeit zu Zeit haufigere Promos wurden begeistern. Kurz und bundig, Cat Spins Casino ist ein Highlight fur Casino-Fans. Hinzu kommt ist das Design stilvoll und modern, das Spielerlebnis steigert. Ein bemerkenswertes Extra die dynamischen Community-Events, die die Begeisterung steigern.
Inhalt entdecken|
Ich habe eine Leidenschaft fur Cat Spins Casino, es schafft eine mitrei?ende Stimmung. Das Spieleportfolio ist unglaublich breit, mit Spielen fur Kryptowahrungen. 100 % bis zu 500 € plus Freispiele. Der Support ist zuverlassig und hilfsbereit. Auszahlungen sind schnell und reibungslos, trotzdem zusatzliche Freispiele waren willkommen. Alles in allem, Cat Spins Casino bietet ein unvergessliches Erlebnis. Hinzu kommt die Plattform ist optisch ein Highlight, eine vollstandige Immersion ermoglicht. Ein super Vorteil die haufigen Turniere fur mehr Spa?, zuverlassige Transaktionen sichern.
Mehr erfahren|
Je suis totalement conquis par Sugar Casino, ca transporte dans un monde d’excitation. Le catalogue est un paradis pour les joueurs, incluant des options de paris sportifs dynamiques. 100% jusqu’a 500 € avec des spins gratuits. Le support est efficace et amical. Le processus est clair et efficace, rarement quelques spins gratuits en plus seraient top. Globalement, Sugar Casino vaut une visite excitante. A mentionner le design est moderne et attrayant, incite a rester plus longtemps. Un point fort les options de paris sportifs diversifiees, propose des privileges sur mesure.
Voir la page|
styleforliving – Customer support details seem accessible which adds trust to the site.
Ich bin suchtig nach Cat Spins Casino, es ist ein Hotspot fur Spielspa?. Es gibt eine beeindruckende Anzahl an Titeln, mit Slots in modernem Look. 100 % bis zu 500 € plus Freispiele. Der Service ist absolut zuverlassig. Die Zahlungen sind sicher und sofortig, allerdings mehr Aktionen wurden das Erlebnis steigern. Im Gro?en und Ganzen, Cat Spins Casino ist ein absolutes Highlight. Au?erdem die Benutzeroberflache ist flussig und intuitiv, eine Prise Spannung hinzufugt. Ein gro?er Pluspunkt die regelma?igen Turniere fur Wettbewerbsspa?, die Community enger verbinden.
Eintreten|
ieeb – Always a pleasure to read, informative and well-written articles.
ieeb – Consistently provides valuable information across various topics, love it.
discovergreatdeals – The offers caught my eye quickly—worth checking regularly.
Je suis fascine par Ruby Slots Casino, on y trouve une energie contagieuse. On trouve une profusion de jeux palpitants, proposant des jeux de casino traditionnels. Avec des depots rapides et faciles. Les agents repondent avec rapidite. Le processus est transparent et rapide, a l’occasion des bonus plus varies seraient un plus. En resume, Ruby Slots Casino est une plateforme qui pulse. A souligner la plateforme est visuellement electrisante, ajoute une vibe electrisante. Un bonus les competitions regulieres pour plus de fun, garantit des paiements rapides.
Commencer Г explorer|
broodbase – A fantastic platform for gaining knowledge on various topics.
lastminute-corporate – User-friendly design enhances the corporate travel booking experience significantly.
dreambuycollection – Overall a positive experience so far; delivery and quality will be key.
kazhanmaster – I find their perspectives unique and refreshing, highly informative.
everydaystylecorner – Checkout looked simple and payment options are clearly listed.
yourcreativejourney – Good pricing and clear descriptions make me feel confident to buy.
Je suis emerveille par Sugar Casino, c’est une plateforme qui pulse avec energie. Les options de jeu sont infinies, offrant des sessions live palpitantes. Le bonus de depart est top. Le support est efficace et amical. Les retraits sont fluides et rapides, de temps en temps plus de promotions frequentes boosteraient l’experience. Au final, Sugar Casino vaut une exploration vibrante. Notons egalement l’interface est lisse et agreable, booste le fun du jeu. A noter le programme VIP avec des niveaux exclusifs, propose des privileges personnalises.
https://sugarcasinobonusfr.com/|
theworldawaits – Customer service seemed responsive when I asked about sizing.
trendyfindsonline – Looking forward to receiving my order and checking product quality.
J’adore la vibe de Sugar Casino, il propose une aventure palpitante. La selection est riche et diversifiee, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € avec des free spins. Les agents repondent avec efficacite. Les transactions sont d’une fiabilite absolue, neanmoins des bonus varies rendraient le tout plus fun. Au final, Sugar Casino garantit un amusement continu. A noter la plateforme est visuellement electrisante, apporte une touche d’excitation. Egalement top les options variees pour les paris sportifs, propose des avantages sur mesure.
Continuer ici|
Je suis emerveille par Ruby Slots Casino, on ressent une ambiance de fete. Il y a un eventail de titres captivants, offrant des sessions live immersives. Il donne un avantage immediat. Le service client est de qualite. Les gains arrivent en un eclair, mais encore des offres plus genereuses seraient top. En resume, Ruby Slots Casino vaut une exploration vibrante. Par ailleurs le site est rapide et immersif, donne envie de continuer l’aventure. Particulierement fun les competitions regulieres pour plus de fun, qui motive les joueurs.
DГ©couvrir|
shopfornewthings – Will definitely revisit when I’m in the mood for browsing.
sjydtech – Very professional appearance, I feel trust in their offerings.
learnandgrowtoday – Found some interesting tips that could simplify my daily learning routine.
Je suis fascine par Sugar Casino, ca offre une experience immersive. Les titres proposes sont d’une richesse folle, comprenant des jeux optimises pour Bitcoin. Il booste votre aventure des le depart. Les agents sont toujours la pour aider. Le processus est simple et transparent, neanmoins des recompenses supplementaires seraient parfaites. En fin de compte, Sugar Casino offre une experience hors du commun. En complement la plateforme est visuellement captivante, ce qui rend chaque partie plus fun. Un point cle les paiements en crypto rapides et surs, qui stimule l’engagement.
Explorer le site|
Je suis captive par Ruby Slots Casino, il cree une experience captivante. Les jeux proposes sont d’une diversite folle, comprenant des jeux optimises pour Bitcoin. Avec des depots rapides et faciles. Le support est pro et accueillant. Les transactions sont d’une fiabilite absolue, malgre tout quelques free spins en plus seraient bienvenus. En somme, Ruby Slots Casino est un lieu de fun absolu. A souligner le site est rapide et engageant, incite a rester plus longtemps. Egalement excellent le programme VIP avec des privileges speciaux, assure des transactions fiables.
http://www.rubyslotscasinologinfr.com|
J’ai une passion debordante pour Sugar Casino, on y trouve une energie contagieuse. Les options sont aussi vastes qu’un horizon, incluant des options de paris sportifs dynamiques. Il propulse votre jeu des le debut. Le service d’assistance est au point. Les gains sont verses sans attendre, bien que des bonus plus frequents seraient un hit. En fin de compte, Sugar Casino est un lieu de fun absolu. Pour ajouter la navigation est claire et rapide, ce qui rend chaque moment plus vibrant. A signaler les options de paris sportifs variees, cree une communaute vibrante.
DГ©couvrir les offres|
conorjmurphy – Found exactly what I needed, instructions were clear and concise.
Букмекерская контора Мелбет предлагает хорошо организованный сервис для пользования услугами оператора. Разнообразие ставок с неплохими коэффициентами сопровождается бонусными программами, нацеленными на поддержание интересов клиентов. Получение бонусов от букмекера позволяет получить новый безболезненный опыт на ставках, что особенно важно для новичков промокод при регистрации melbet 2026. Однако предполагаем, что снижение требований по отыгрышу бонусов сделали бы букмекера еще привлекательнее для игроков.
lithestore.com – Content reads clearly, helpful examples made concepts easy to grasp.
Промокод – это комбинация символов, которую вводят в специально отведенную строку на сайте. После активации кода, пользователь получит вознаграждение от любимого БК. Обычно к промокоду прилагается подробное описание всех предлагаемых бонусов. Но иногда букмекеры позволяют игрокам выяснить назначение кода самостоятельно, ведь многие любят сюрпризы. В случае с промокодом, сюрприз наверняка окажется приятным, ведь его главная цель – создать игроку комфортные условия, заслужить лояльность. Существуют промокоды для новых игроков, которые действительны только при регистрации, и для постоянных – окно для ввода таких кодов находится под формой пополнения игрового баланса. Мелбет промокод Введите: RS777 и тогда при депозите вы получите бонус 50 000 рублей автоматически. Букмекерская контора Мелбет в 2026 году создала комфортные условия для заядлых беттеров и новых пользователей. Промокоды – вещь распространенная, потому найти их легко. Часто букмекеры размещают коды в свободном доступе, для всеобщего пользования. А промокоды для более значимых наград поступают игрокам индивидуально, например в качестве подарка ко дню рождения, извинения за возможные неудобства или просто в благодарность за сотрудничество.
happyshoppingplace – Fun and lively design, the name fits perfectly with the vibe.
findbetteroptions – The website loads quickly, and navigation through categories is smooth.