Introduction
This trading method is actively used in a wide variety of Expert Advisors. Moreover, it has many varieties and hybrids. In addition, judging by the number of references to such systems, it is obvious that this topic is very popular not only on this site, but also on any other web resources. All method varieties have a common concept involving trading against the market movement. In other words, the EA uses rebuys to be able to buy as low as possible and sell as high as possible.
This is a classic trading scheme that is as old as the world. In one of the previous articles, I partially touched on this topic, while highlighting possible ways to hybridize such methods. In this article, we will have a closer look at the concept delving deeper than forum users do. However, the article will be more general and much broader as the rebuy algorithm is very suitable for highlighting some very interesting and useful features.
Methods for refining trading characteristics based on the averaging algorithm
“Help me get out of the drawdown” (from the authors of “my EA makes good money, but sometimes blows up the entire account”)
This is a common issue of many algorithmic and manual traders. At the time of writing this article, I had a conversation with such a person, but he did not grasp my point of view in its entirety. Sadly, it seems to me that he has practically no chance of ever understanding the whole comedy of such a situation. After all, if I could once ask a similar question to my older and more experienced self, I would also most likely be unable to understand the answer. I even know how true answers to myself would make me feel. I would think that I am being humiliated or dissuaded from further engaging in algorithmic trading.
In reality, everything is much simpler. I just had the patience to walk a certain path and gain some wisdom, if you can call it that. This is not an idealization and self-praise, but rather a necessary minimum. It is a pity that this path took years instead of weeks and months.
Here we have a whole world of dreams and self-deception, and to be honest, I am already starting to get tired of the simplicity of some people. Please stop doing nonsense and thinking that you are the kings of the market. Instead, contact an experienced person and ask them to choose an EA for your budget. Trust me, you will save a lot of time and money that way, not to mention your sanity. One of those persons has written this article. The proofs are provided below.
General thoughts about the averaging algorithm
If we have a look at the rebuy algorithm, or “averaging”, it first may seem that this system has no risk of loss. There was a time when I did not yet know anything about such tricks and was surprised at the huge mathematical expectations that beat any spreads. Now it is clear that this is only an illusion, nevertheless, there is a rational grain in this approach, but more on that later. To begin with, in order to be able to objectively evaluate such systems, we need to know some indirect parameters that can tell us a little more than a simple image of growing profits.
The most relevant parameters in the strategy tester report can even help to understand that the system is obviously losing, despite the fact that the balance curve looks great. As you might have already understood, it is really all about the profitability curve. In fact, all the important indicators of the trading system are secondary to the first and most basic mathematical characteristics, which, of course, are the mathematical expectation and its primary characteristics. But it is worth noting that the mathematical expectation is such a flexible value that you can always fall into the trap of wishful thinking.
In fact, in order to correctly use such a concept as mathematical expectation, one must first of all understand that this is the terminology of probability theory, and any calculation of this quantity should be carried out according to the rules of probability theory, namely:
- Calculations are the more accurate, the larger the analyzed sample, ideally the exact value is calculated from an infinite sample.
- If we break infinity into several parts, we get several infinities
Someone might think how to calculate the exact mathematical expectation of a particular strategy, if we have only a limited sample of real quotes at our disposal. And someone will think, why do we need these infinities at all. The thing is that all estimates of certain averaged values, such as mathematical expectation, have weight only in the area where these calculations were made, but have nothing to do with another area. Any mathematical characteristic has weight only where it is calculated. Nevertheless, some techniques can be distinguished to refine the characteristics of the profitability of a particular strategy, which will make it possible to obtain the values that are closest to the true values of the required parameters.
This is directly related to our task. After realizing that we cannot see into the future of an infinity-long strategy, which in itself already sounds like complete nonsense. Nevertheless, this is a mathematical fact and a necessary and sufficient condition for calculating the true mathematical characteristics. We come to the idea of how to make the number calculated on a limited sample closer to the number that could be calculated on an infinite sample. Those who are familiar with mathematics know that there are two mathematical concepts which can be applied to calculate infinite sums:
- Integral
- Sum of infinite series
I think it is clear to everyone that in order to calculate the integral, as well as the sum of the series, it is necessary to obtain either all points of the function, the integral of which needs to be calculated, within the considered area of integration, or all elements of the sequence of numbers within the series under consideration. There is still the most perfect option – getting the appropriate mathematical expressions for the function that we are going to integrate, and the expression for generating the elements of the series. In many cases, if we have the appropriate mathematical expressions, we can get the exact equations for the finished integral or the sum of the series, but in the case of real trading, we will not be able to apply differential calculus, and in general this will not help us much, but it is important to understand.
The conclusion from all this is that for the direct evaluation of any system we have only a limited sample and certain parameters that we get in the strategy tester. In fact, their significance is greatly exaggerated. The question arises as to whether it is possible to judge the profitability of a particular strategy using the the strategy tester parameters, whether these parameters are sufficient for an unambiguous answer and most importantly, how to use these parameters correctly and whether we really use them correctly.
Additionally, we need to understand that for each strategy, any parameter, by which we can correctly assess the real profitability and security of the strategy can be completely different. This is directly related to the evaluation of the profit curve. To understand this, let’s first draw an approximate general view of the trading curve that we get when using the rebuy algorithm:
Fig. 1
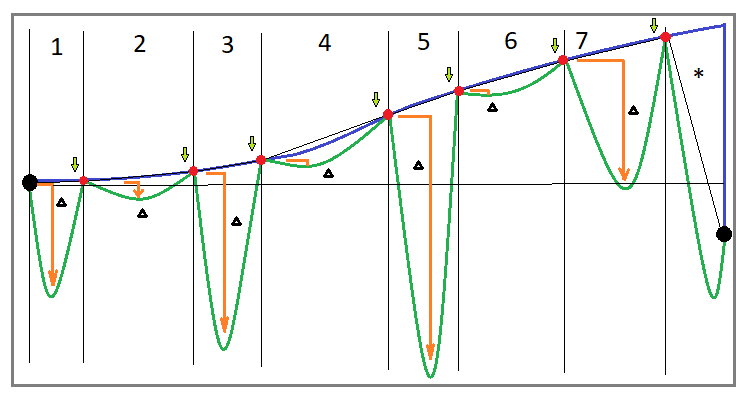
Let’s start with the implementation of a rebuy for one instrument. If you correctly implement this algorithm, then your trading will in any case consist of cycles. Ideally, all cycles should be positive. If some cycles close in the negative zone, then either you are implementing this algorithm incorrectly, or it is no longer a pure algorithm and there are already modifications in it. But we will consider the classic rebuy. Let’s define some characteristic parameters of the trading curve to denote a classic rebuy:
- The balance curve must be growing and consist of N cycles
- All cycles have a positive profit
- When trading breaks, we are likely to find ourselves in the last incomplete cycle
- Incomplete cycle has negative profitability
- Cycles have characteristic drawdowns in terms of funds.
It seems that the general appearance of the curve should make it clear at first glance that such a system is profitable, but not everything is so simple. If you look at the last unfinished trading cycle, which I specifically closed below the starting point, you will see that in some cases you will be lucky and you will wait for the successful completion of the cycle, while in some cases you may either not wait till the end and face a big loss or blow up your deposit entirely. Why is this happening? The thing is that the image may give a false impression that the amount of drawdown by funds is limited in its absolute value and, as a consequence, the time spent in this drawdown should also be limited.
In reality, the longer the testing area, the longer the average drawdown area. There is absolutely no limit here. The limit exists only in the form of your deposit and the quality of your money management. However, a competent approach to setting up your system based on this principle, can only lead to an increase in the lifespan of your deposit before it is eventually blown up or,at best, makes a very little profit.
When it comes to testing systems based on the rebuy (averaging) algorithm, in order to correctly assess its survivability, reliability and real profitability, one should adhere to a special testing structure. The whole point is thatthe value of a single test in this approach is minimized for one simple reason, that when testing any “normal” strategy, your profit for the entire test in the strategy tester is very close to the “normally” distributed value. This means that when testing any average strategy without holding a position for a long time, you will get an approximately equal number of profitable and unprofitable testing areas, which will very quickly let you know that the strategy is unstable, or that the strategy has a correct understanding of the market and works on the entire history.
When we are dealing with a rebuy strategy, this distribution can be strongly deformed, because for the correct testing of this system you need to set the maximum possible deposit. In addition, the test result is highly dependent on the length of the test section. Indeed, in this approach, all trading is based on trading cycles, and each unique setting of this system can have both a completely different parameter of the average drawdown and the parameter of the average duration of the drawdown associated with it. Depending on these indicators, too short test sections can show either too high or too low test result. As a rule, few such tests are carried out, and this can in most cases be the cause of excessive confidence in the operation of these systems.
Subtleties of a more accurate assessment of rebuy systems
Now let’s learn how to correctly evaluate the performance of systems using the rebuy algorithm, while applying the known parameters of trading systems. First of all, with such an assessment, I would advise using one single characteristic – recovery factor. Let’s figure out how to count it:
- Recovery Factor = Total Profit / Max Equity Drawdown
- Total Profit – total profit per trading area
- Max Equity Drawdown – maximum drawdown of equity relative to the previous joint point for balance and equity (balance peak)
As we can see, this is the final profit divided by the maximum drawdown of the funds. The mathematical meaning of this indicator in the classical sense is that, according to the idea, it should show the system’s ability to restore its drawdown by equity. The boundary condition for the profitability of a trading system when using such a characteristic is the following fact:
- Recovery Factor > 1
If translated into understandable human language, it will mean that in order to make a profit, we can risk no more than the same amount of the deposit. This parameter in many cases provides an accurate assessment of trading quality for a particular system. Use it, but be very careful, because this is a rather controversial value regarding its mathematical significance.
Nevertheless, I will have to reveal you all its disadvantages, so that you understand that this parameter is also very arbitrary and the level of its mathematical significance is also very low. Of course, you might say if you criticize something, then offer an alternative. I will certainly do that, but only after we analyze this parameter. This parameter is tied to the maximum drawdown, which, in turn, can be tied to any point on the trading curve, which means that if we recalculate this drawdown relative to the starting balance and substitute it for the maximum drawdown, we almost always get an overestimated recovery factor. Let’s formalize it all properly:
- Recovery Factor Variation 1 = Total Profit / Max Equity Drawdown From Start
- Max Equity Drawdown From Start – maximum drawdown from the starting balance (not from the previous maximum)
Of course, this is not a classical recovery factor, but in its essence it actually determines profitability much more correctly relative to the generally accepted boundary condition. Let’s first visually depict both options for calculating this indicator – the classic one and mine:
Fig. 2
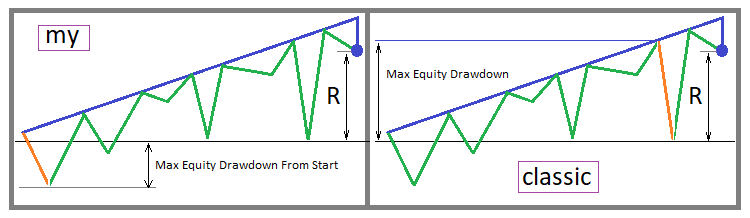
It can be seen that in the first case, this parameter will take higher values, which, of course, is what we want. But from the point of view of profitability assessment, two approaches can be followed. The classic parameter is more adapted to the approach, in which it is better to take the duration of the testing section as long as possible. In this case, a higher value of Max Equity Drawdown compensates for the fact that this drawdown does not start from the very beginning of the trading curve, and thus this parameter in most cases is close to the true estimate. My parameter is more efficient when evaluating multiple backtests.
In other words, this parameter is more accurate the more tests of your strategy you have done. The tests of your strategy should be in as many different areas as possible. This means that the start and end points should be chosen with maximum variability. For a correct assessment, it is necessary to select “N” of the most different areas and test them, and then calculate the arithmetic average of this indicator for all testing areas. This rule will allow us to refine both versions of the recovery factor, both mine and the classic one, with the only amendment that fewer independent backtests will need to be performed to refine the classic one.
Nevertheless, saying that such clarifying manipulations are few for clarifying these parameters would be an understatement. I have demonstrated my own version of the recovery factor in order to show that anyone can come up with their own similar parameter, and it can even be added as one of the calculated characteristics for backtesting in MetaTrader. But any of these parameters does not have any mathematical proof, and moreover, any of these parameters has its own errors and limits of applicability. All this means that at the moment there is no exact mathematical indicator for an absolutely accurate assessment of one or another algorithm using rebuy. However, my parameter will tend to the absolute accuracy with an increase in the number of various tests. I will provide more details in the next section.
In-depth and universal understanding of profitability
Universal assessment
I believe, everyone knows that such parameters as the mathematical expectation of profit and the profit factor exist in any strategy tester report or in the characteristics of a trading signal, but I think no one told you that these characteristics can also be used to calculate profitability of such trading systems where there is not enough analysis of deals. So, you can use these parameters by replacing the “position” unit with “test on the segment”. When calculating this indicator, you will need to make many independent tests with no consideration to any structure inside. This approach will help you assess the real prospects of the trading system using only the two most popular parameters. In addition, it can instill in you an extremely useful habit – multiple tests. In order to use this approach, you only need to know the following equation:
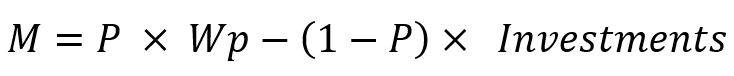
where:
- M – expected payoff value
- Wp – desired profit
- Investments – how much you are willing to invest to achieve the required profit
- P – probability that we will have enough investment until the profit is achieved
- (1-P) – probability that we will not have enough investment until the profit is achieved (deposit loss)
Below is a similar equation for the profit factor:
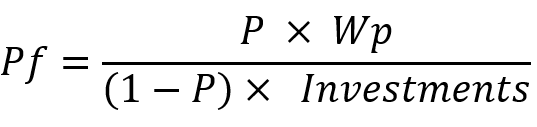
All you need to know is that with random trading and the absence of obstacles such as spread, commission and swap, as well as slippage, these variables will always take the following values for any trading system:
- M=0
- Pf=1
These characteristics can change in your direction only if there is a predictive moment. Therefore, the probability that we will make a profit without losing the deposit will take the following value:
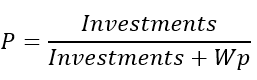
If you substitute this expression for probability in our equations, then you will get the identities that I provided. If we consider spread, commission and swap, then we get the following:
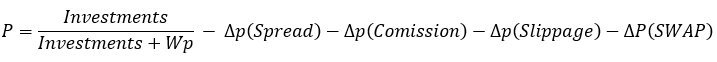
The spread, commission and swap reduce the final probability, which ultimately leads to the identities losing their validity. The following inequalities appear instead:
- M < 0
- Pf < 1
This will be the case with absolutely any trading system, and the rebuy algorithm here is absolutely no better than any other system. When testing or operating such a system, it is able tostrongly deform the distribution function of the random value of the signal or backtest final profit, but typically this scenario occurs most frequently during short-term testing or operation.
This is because the probability of running into a large drawdown is much less if you test on a short section. But once you start doing these tests over longer segments, you will usually see things you have not seen before. But I am sure most will be able to reassure themselves that this is just an accident, and you just need to somehow bypass these dangerous areas. The same will generally be the case with multiple testing on short segments.
There is only one way to overcome the unprofitability of any system. Let’s add an additional component to the probability calculation equation:
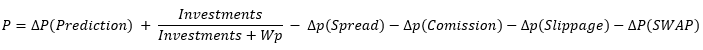
As we can see, the new component “dP(Prediction)” has appeared in the equation. It has a plus sign, which I did on purpose to show that only this component is able to compensate for the effect of spreads, commissions and swaps. This means that we first of all need sufficient prediction quality to overcome the negative effects and reach profit:
![]()
We can get our desired inequalities only if we provide this particular inequality:
- M > 0
- Pf > 1
As you can see, these expressions are very easy to understand, and I am sure that no one will doubt their correctness. The next subsection will be easier to understand using these equations. Indeed, I advise you to remember them, or at least remember their logic, so that you can always restore them in memory if necessary. The main thing here is their understanding. In general, one of these equations is sufficient, but I felt that it would be better to show two for an example. As for other parameters, I believe, they are redundant within the framework of this section.
Examples of clarifying methods
In this subsection, I want to offer you some additional refinement manipulations that will allow you to get a more correct value of the recovery factor. I suggest going back to “Figure 1” and looking at the numbered segments. To refine the recovery factor, it is necessary to imagine that these segments are independent tests. This way we can do without multiple testing, assuming that we have already performed these tests. We can do this because these segments are cycles that have both a start point and an end point, which is what provides equivalence to the backtest.
Within the framework of this section, I think it is also worth supplementing the first image with its equivalent considering the fact that we are testing or trading on several instruments at once. This is how the trading curve will look like using the rebuy algorithm for parallel trading on multiple instruments:
Fig. 3
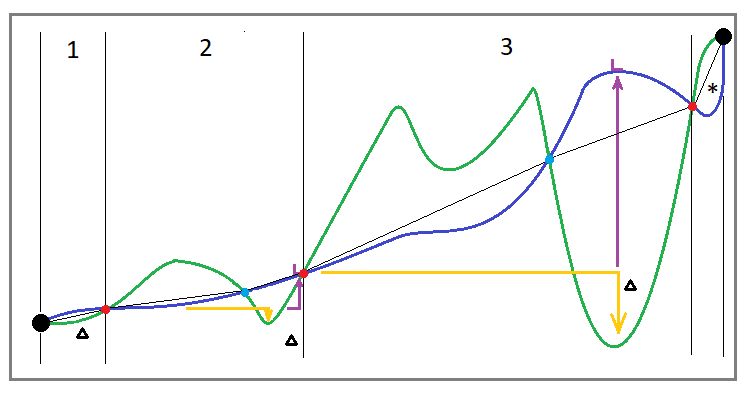
We can see that this curve differs in its structure from the curve for rebuying on one instrument. I have added intermediate blue points here, which means that before the drawdown there may be segments that have a “drawdown in reverse.” The fact is that we cannot consider this a drawdown. But nevertheless, we have no right to consider these segments outside the analysis. This is why they must be part of a cycle.
I think it would be more correct to postpone each new cycle from the end of the previous one. In this case, the end of the previous cycle should be considered the recovery point of the last drawdown in equity. In the image, these cycles are separated by red dots. But in fact, this definition of the cycle is not sufficient. It is also important to determine that it is not enough just to fix the drawdown by equity, but it is important that it be lower than the start of the current cycle. Otherwise, what kind of drawdown is it?
After highlighting these cycles, you can consider them as separate independent tests and calculate the recovery factor for each of them. This can be done the following way:
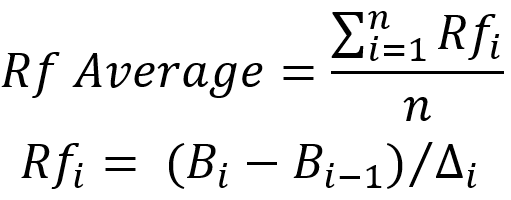
In this equation, the corresponding points on the balance curve (the final value of the balance on the section and the initial one) are used as “B”, while the delta represents our drawdown. I would also like the reader to return to the last image. On it, I plotted the delta from the red start point of each cycle, and not from the blue one, as is usually the case, for the reasons I listed above. But if you need to clarify the original recovery factor, then the delta should be plotted from the blue point. In this case, the method of refining the parameters is more important than the parameters themselves. The simple arithmetic mean is taken as the averaging action.
Nevertheless, even after clarifying one or another custom or classic parameter, you should not take the fact that the value of this indicator is more than one, or even two or three, as signs of a profitable trading system.
Exactly the same equation should be applied with multiple backtests. The point is that any backtest in this case is equivalent to a cycle. We can even first calculate the averages for the cycles, and after all this, calculate the average of the average relative to the backtests. Or we can do it much easier by maximizing the duration of the test segment. This approach will save you at least from multiple tests due to the fact that the number of cycles will be at maximum, which means that the average recovery factor will be calculated as accurately as possible.
Increasing the efficiency of systems with diversification
Useful limits
After considering the possibilities to refine certain characteristics of backtests, you are undoubtedly better armed, but you still do not know the main thing. The basis lies in the answer to the question – why is it necessary to carry out all these multiple tests or splitting into cycles? The question is really complex until you put in as much effort as I put in my time. Sadly, this is necessary, but with my help, you can greatly reduce the time you need to do this.
This section will allow you to evaluate the objectivity of a particular parameter. I will try to explain both theoretically and using the equations. Let’s start with the general equation:
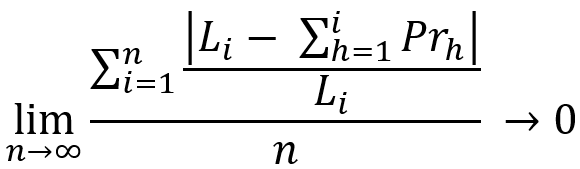
Let’s consider a similar equation with some slight changes:
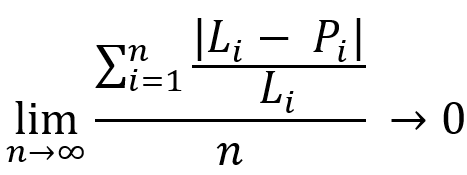
The essence of these equations is the same. These equations demonstrate thatin any profitable trading system, when the duration of the testing section tends to infinity, we will get a complete merger of the balance and current profit lines, with a certain line representing our average profit. In most cases, the nature of this line is determined by the strategy we have chosen. Let’s look at the following image for a deeper understanding:
Fig. 4
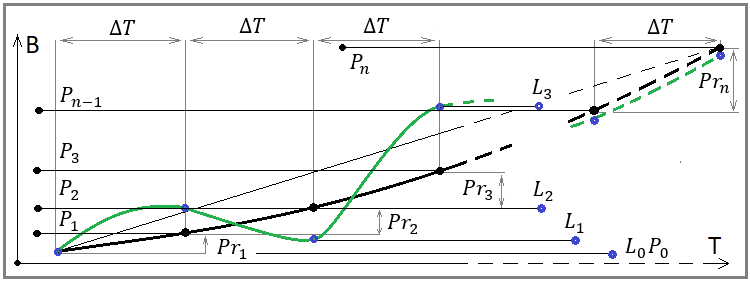
If you carefully look at this image, you will see on it all the quantities that are present in our equations. It reveals the geometric meaning of our mathematical limits. The only thing missing in our equations is the dT time interval. With this interval, we discretize our balance steps and give rise to all the points of our number series for the balance and profit of these intervals, and also calculate the values of our midline at the same points. These equations are the mathematical equivalent of the following statement:
- The more we combine multiple tests or trading curves together, the more they look like a smooth rising line (only if the system is really profitable)
In other words, any profitable trading system looks more beautiful in the graphical part of the strategy tester or signal, the longer the testing area we choose. Some might say that no system can achieve such indicators, nevertheless, there are plenty of examples in the Market, so it would be silly to deny this. It all depends on the universality of the algorithm and how well you understand the market physics. If you know the math that is always inherent in the market you are trading, then in fact you get an infinitely growing profit curve, and you do not need to wait for an entire infinity to confirm the effectiveness of the system. Of course, it is clear that this is an extremely difficult task, but nevertheless, within the framework of many algorithms, this task is achievable.
Let’s finish this theoretical introduction by learning how to use the received techniques correctly. You might ask, how to use these techniques with infinite sums, when we have only limited samples and, accordingly, also inevitable incomplete sums.
- The answer lies is in dividing the entire history into segments
- Select several segments with a constantly growing length for the duration of testing up to a segment in the entire history
- Choose a testing methodology
- Test
- Look for an improvement in recovery factor and/or relative drawdown
The essence of this tricky test scheme is to reveal indirect signs that our limits really tend to infinity and zero, respectively. To increase the efficiency of our testing scheme, we must understand that the longest test section should at least look more beautiful than the shortest one, and ideally each subsequent section should be both larger and look more beautiful. I use the concept of “more beautiful” only to make it clear to everyone that this is actually equivalent to our limits.
However, our limits are only good during theoretical considerations or preparations (whatever you like). In this regard, the question arises – how to discover these facts without resorting to “eyeball analysis”? We need to somehow adapt our limits to the parameters that we have in the strategy tester report. In other words, we need alternative limits for some strategy tester report or signal parameters so that our testing structure can be used. Let me show you the necessary and sufficient set of alternative limits:
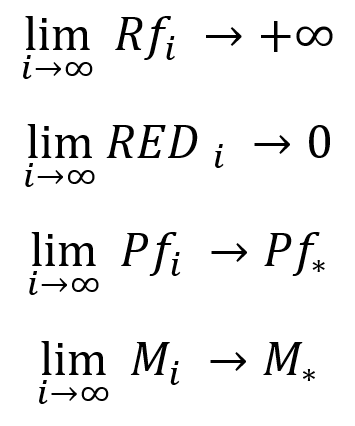
What we should understand here:
- During an infinite test, the recovery factor of any profitable strategy tends to infinity
- During an infinite test, relative drawdown by equity (of any profitable strategy) tends to zero
- During an infinite test, the profit factor of deals of any profitable strategy tends to its mean value and has a finite real limit.
- During an infinite test, the mathematical expectation of any profitable strategy without auto lot enabled (with a fixed lot) tends to its average value and has a finite real limit
All this has to do with infinite tests, however it is useful to understand the mathematical meaning of these limits before proceeding to adapt them to a finite sample. The adaptation of these expressions to our methodology should begin with the fact that we should select several segments of testing, each of which should be significantly larger than the previous one, preferably at least twice. This is necessary in order to be able to notice the difference in readings between shorter and longer tests. If we number our tests in such a way that as the index increases, its length grows in time, then we get the following adaptation for the case of finite samples:
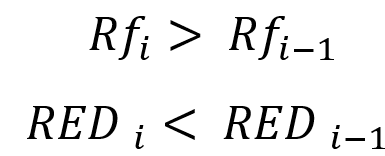
In other words, an increase in the recovery factor and a decrease in the relative drawdown in terms of funds is indirect evidence that, most probably, the further increase of the test segment or signal lifetime makes our curve become visually more beautiful. This means that we have confirmed the fulfillment of our infinite limits. Otherwise, if the profit curve does not become straighter, we can state the fact that the result obtained is very close to random and the probability of losses in the future is extremely high.
Of course, many will say that we can simply optimize the system more often and everything will be all right. In some extremely rare cases it is possible, but this approach will require a completely different testing methodology. I do not advise anyone to resort to this approach, because in this case you do not have any math, while here you have everything in a clear-cut manner.
All these nuances should convince you that testing the rebuy algorithm all the more requires the use of this approach. In particular, we can even simplify the task and test the rebuy system immediately on the maximum length segment. We may reverse this logic. If we do not like the trading performance in the longest segment, then even better performance in the short segments will indicate that our inequalities are no longer satisfied and the system is not ready for trading at this stage.
Useful features in terms of the parallel use of multiple instruments
When testing on a limited history, the question will certainly arise – is there enough history for us to correctly use our testing methodology? The thing is that in many cases the strategy has weight, but its quality is not high enough for comfortable use. To begin with, we should at least understand whether it really has a predictive beginning and whether we can begin to engage in its modernization. In some cases, we literally do not have enough available trading history. What should we do? As many have already guessed, judging by the title of the subsection, we should use multiple instruments for this purpose.
It would seem an obvious fact, but unfortunately, as always, there is no math anywhere. The essence of testing on multiple instruments is equivalent to the same essence for increasing the duration of testing. The only amendment is that your system must be a multi-currency one. The system may have different settings for different trading instruments, but it is desirable that all settings are similar. The similarity of the settings will represent the fact that the system uses physical principles that work on the maximum possible number of trading instruments.
With this approach and the correct implementation of such tests, the index “i” should already be understood as the number of simultaneously tested instruments on a fixed testing segment. Then the expressions will mean the following:
- When increasing the number of traded instruments, the more instruments, the greater the recovery factor
- When increasing the number of traded instruments, the more instruments, the smaller the relative drawdown by equity
In fact, an increase in the number of tests can, for simplicity, be interpreted as an increase in the total duration of tests, as if we consider each test for each tool to be part of a huge overall test. This abstraction will only help you understand why this approach also has the same power. But if we consider this issue more accurately and understand more deeply why a line that consists of several ones will be much more beautiful, then we should use the following concepts of probability theory:
- Random value
- Variance of a random variable
- Mathematical expectation of a random variable
- The law of normal distribution of a random variable
To fully explain why we need all this, we first need an image that will help us look at a backtest or a trading signal a little differently:
Fig. 5
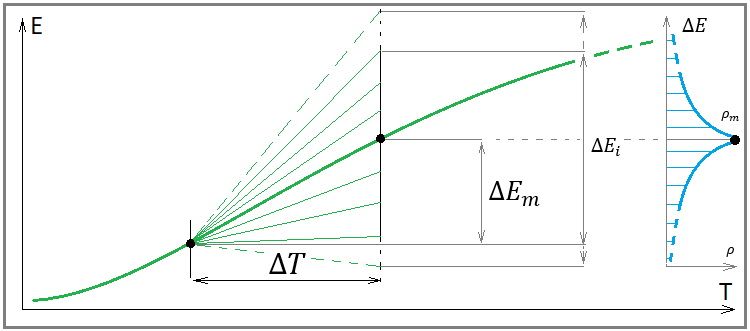
I am not drawing a balance line here, because it does not decide anything here, and we only need a profit line. The meaning of this image is thatfor each profit line, it is possible to select an infinite number of independent segments of a fixed length, in which it is possible to construct the law of distribution of a random variable of the profit line increment. The presence of a random variable means that in the future the profit increment in the selected area can have completely different values in the widest range.
It sounds complicated, but in fact all is simple. I think many people have heard about the normal distribution law. It supposedly describes almost all random processes in nature. I think, this is no more than an illusion invented to prevent you from “thinking”. All jokes aside, the reasons for the popularity of the distribution law are that it is an artificially compiled and very convenient equation for describing symmetric distributions with respect to the mathematical expectation of a random variable. It will be useful to us for further mathematical transformations and experiments.
However, before starting to work with this law, we should define the main property for any distribution law of a random variable:
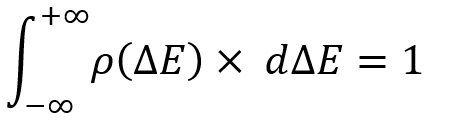
Any law of random variable distribution is essentially the analogue of the full group of non-joint events. The only difference is that we do not have a fixed number of these events and at any time we can select any event of interest like this:
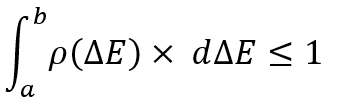
Strictly speaking, this integral considers the probability of finding a random variable in the indicated range of a random variable, and naturally, it cannot be greater than one. No total event from a given event space can have a probability greater than one. However, this is not the most important thing. The only important thing here is that you should understand that the event in this case is determined only by a set of two numbers. These are examples for random variables of minimum dimension.
There are analogues of these equations for the “N” dimension, when an event can be determined by “N*2” numbers, and even more complex constructions (within the framework of multidimensional region integrals). These are quite complex sections of mathematics, but here they are redundant. All laws obtained here are self-sufficient for the one-dimensional variant.
Before moving on to more complex constructions, let’s recall some popular parameter characteristics of the random value distribution laws:
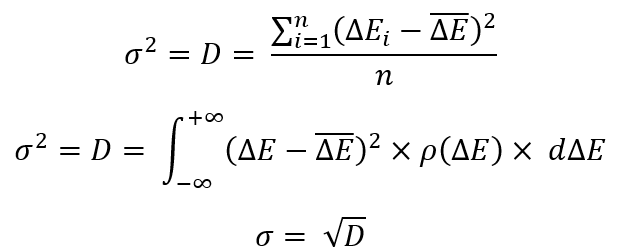
To define any of these equations, we need to determine the most important thing – the mathematical expectation of a random variable. In our case, it looks as follows:
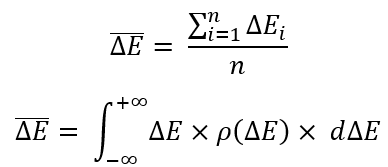
The mathematical expectation is simply the arithmetic mean. Mathematicians like to give very clever names to simple things so that no one understands anything. I have provided two equations. Their only difference is that the first one works on a finite number of random variables (limited amount of data), and in the second case, the integral over the “probability density” is used.
An integral is the equivalent of a sum, with the only difference being that it sums up an infinite number of random variables. The law of a random variable distribution, which is located under the integral and contains the entire infinity of random variables. There are some differences, but in general the essence is the same.
Now let’s go back to the previous equations. These are just some manipulations with the laws of random variables distribution that are convenient for most mathematicians. As in the last example, there are two implementations – one for a finite set of random variables, the other for an infinite one (the law of a random variable distribution). It states that “D” is the average square of the difference between all random variables and the average random variable (the mathematical expectation of the random variable). This value is called “dispersion”. The root of this value is called the “standard deviation”.
Normal distribution of a random variable
It is these values that are generally accepted in the math of random variables. They are considered the most convenient for describing the most important characteristics of the random distribution laws. I disagree with this notion, but nevertheless I am obliged to show you how they are calculated. In the end, these quantities will be needed to understand the normal distribution law. It is unlikely that you will easily find this information, but I will tell you that the normal distribution law was invented artificially with only a few goals:
- A simple way to determine the distribution law symmetrical to the mathematical expectation
- Ability to set dispersion and standard deviation
- Ability to set mathematical expectation
All these options allow us to get a ready-made equation for the law of a random variable distribution called the normal distribution law:
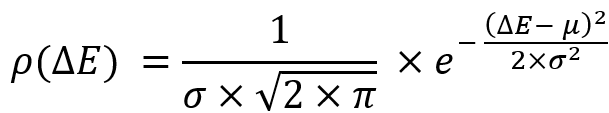
There are other variations of the laws of random variables distribution. Each implementation is invented for a certain range of problems, but since the normal law is the most popular and well-known, we will use it as an example to prove and compile the mathematical equivalent of the following statements:
- The more instruments traded in parallel for a profitable system, the more beautiful and straighter our profit graph (a special case of diversification)
- The longer the selected area for testing or trading, the more beautiful and straighter our profit graph
- The more parallel traded systems with proven profitability, the straighter and more beautiful our overall profitability graph
- The combination of all of the above gives rise to ideal diversification and the most beautiful chart
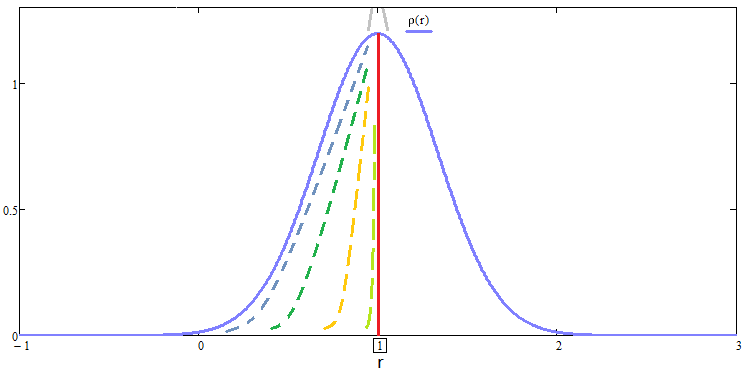
Everything that has been said applies only to trading systems whose profitability has been proven mathematically and practically. Let’s start by defining what “the more beautiful graph” means in mathematical terms. The “standard deviation”, whose equation I have already shown above, can help us with that.
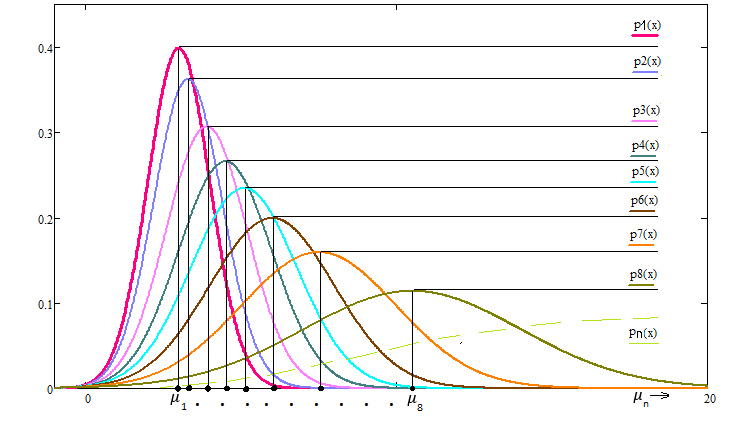
If we have a family of distribution density curves for a random variable of profit increment with the same mathematical expectation, which symbolize two segments of the same duration in time, for two practically identical graphs, then we would prefer the one with the smallest standard deviation. The perfect curve in this family could be one with zero standard deviation. This curve is achievable only if we know the future, which is impossible, nevertheless, we must understand this in order to compare curves from this family.
Profit curve beauty in the framework of the random values distribution law
This fact is understandable when we are dealing with a family of curves, where the mathematical expectations of the profit increment in the selected time period are the same, but what to do when we are dealing with completely arbitrary distribution curves? It is not clear how to compare them. In this regard, the standard deviation is no longer perfect and we need another more universal comparison value that takes into account scaling, or we must come up with some algorithm for reducing these distribution laws to a certain relative value, where all distributions will have the same mathematical expectation and, therefore, classical criteria will apply to all curves. I have developed such an algorithm. One of the tricks in it is the following transformation:
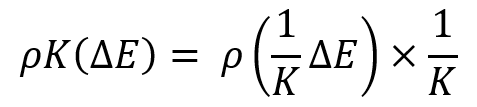
The family of these curves will look something like this:
Fig. 6
A very interesting fact is that if we subject the law of normal distribution to this transformation, then it is invariant with respect to this transformation and will look like this:
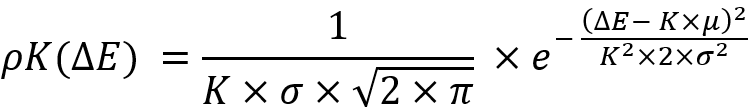
The invariance consists in the following replacements:
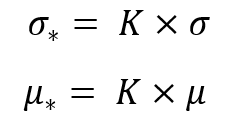
If we substitute these replacements into the previous equation, then we get the same distribution law operating with the corresponding values with asterisks:
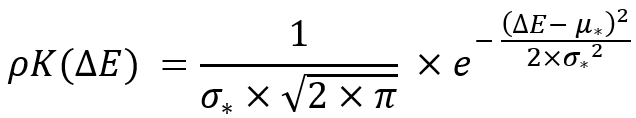
This transformation is necessary to ensure not only the invariance of the transformation law but also the invariance of the following parameter:
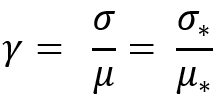
I had to invent this parameter. It is impossible to properly scale the normal distribution law, like any other law, without it. This parameter will be invariant for any other distribution law as well. As a matter of fact, the normal law is easier to perceive and understand. Its idea is that it can be used for any distributions with different mathematical expectations and its essence will be similar to the standard deviation, only without the requirement that all compared distributions must have the same mathematical expectation. It turns out, our transformation is designed to get a family of distributions where a given parameter has the same value. Seems pretty convenient, doesn’t it?
This is one way to define the so-called graph beauty. The system having the smallest parameter is “the most beautiful”. This is all good, but we need this parameter for a different purpose. We set the task to compare the beauty of the two systems. Imagine that we have two systems that trade independently. So, our goal is to merge these systems and understand whether there will be an effect from this merger, or rather, we hope for the following:
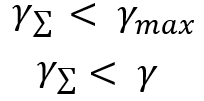
These ratios will be observed when using any distribution law. This automatically means that it makes sense to diversify if our parallel traded instruments or systems have similar profitability. We will prove this fact a bit differently. As I said, I came up with an algorithm for reducing all distributions to a relative random value. We will use it, but first we will analyze the general process of merging several lines, within the framework of the distribution law of a random variable representing the sum of two deltas. We will recurrent logic for merging in pairs. To do this, we assume that we have “n+1” curves, each of which has a defined mathematical expectation. But in order to get to the random variable symbolizing the merge, we need to understand that:
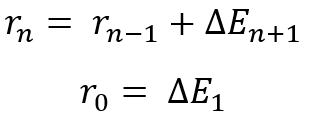
In fact, this is a recurrent expression making no mathematical sense, but it shows the logic of merging all random variables present in the list. To put it simply, we have “n+1” curves, which we must combine using “n” successive transformations. In fact, this means that we must obtain the distribution law of the total random variable at each of the steps using some kind of transformation operators.
I will not delve into lengthy explanations. Instead I will simply show these conversion operators so that you can make your own conclusions. These equations implement the merging of two profit curves within the selected time period, and calculate the probability that the total profit of the two segments of the curves “dE1 + dE2” will be lower (Pl) and higher (Pm) of the “r” selected value, respectively:
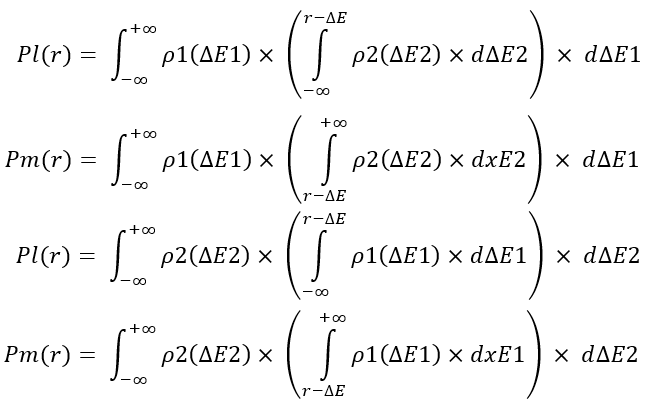
There are two options for implementing these quantities here. Both are completely similar. After calculating these values, they can be used to obtain the law of distribution of the “r” random variable, which is what is required of us to work out the entire recurrent merging chain. By definition of a random variable, we can obtain the corresponding distribution laws from these equations as follows:
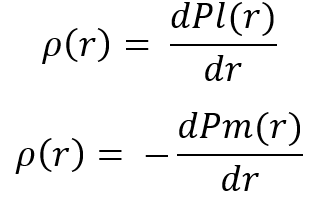
As you may have guessed, after obtaining the distribution law, we can proceed to the next step within the recurrent chain of transformations. After working through the entire chain, we get the final distribution, which we can already compare with one of the distributions that we used for the recurrent merge chain. Let’s create a couple of distributions based on the laws we have got, and run one merge step as an example to demonstrate the fact that each merge is “more beautiful than the last”:
Fig. 7
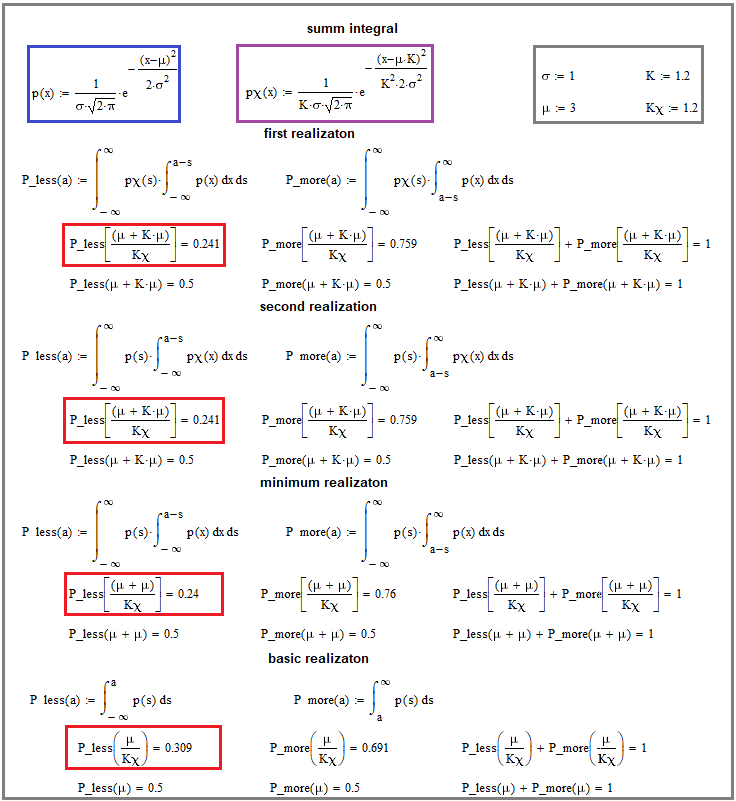
The image demonstrates the mathematical merging which applies our merging equations. The only thing not shown there is differentiation to transform integrals into laws of a random merging value distribution. We will look at the result of differentiation a little later, within the framework of a more general idea, but for now let’s deal with what is in the image.
Pay attention to the red rectangles. They are the basis here. The lowest integral says that we take the integral according to the original distribution law in such a way as to calculate the probability that the random variable will take a smaller value than the mathematical expectation divided by “Kx”. Above you will see similar integrals for the mergers of two slightly different distributions. In all cases, it is important to maintain this ratio (Kx) between the mathematical expectation and the chosen boundary value of the integral, which is expressed in the corresponding “Kx”.
Note that both merge options are presented there, according to the equations I gave you above. Besides, there is a merge of the base distribution with itself, as if we are merging two similar profit curves. Similar does not mean identical in the picture, but rather having identical distribution laws for the random variable of the profit curve increment in the selected time period. The proof is that we found a smaller probability of a relative deviation of the merging random variable relative to the original. This means that we have a more “beautiful” law for the increment of a random profit value in any merger. Of course, there are exceptions requiring a deeper dive into the topic, but I think this approach is enough for the article. You will most likely not find anything better anywhere, because this is a very specific material.
The alternative way to compare beauty is to transform all, both the original distribution laws and the result of the recurrent chain considered above. To achieve this, we just have to use our transformation, which allowed us to get a family of scalable distribution curves and do as follows:
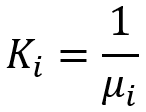
The trick of this transformation is that with this approach, all distribution laws subjected to the corresponding transformation, will have the same mathematical expectation and, accordingly, we can use only standard deviation to evaluate their “beauty” without having to invent any exotic criteria. I have shown you two methods. It is up to you to choose the one that suits you best. As you may have guessed, the distribution laws of all such relative curves will look like this:
This approach is applicable to extended tests as well. By extended tests here we mean testing over a longer segment. This application is only suitable for confirming the fact thatthe longer the test, the more beautiful the graph. The only trick for this proof that you have to apply is to accept that if we increase the duration of the test, then we do it in multiples of an integer, while in multiples of this number we already consider not 1 step but “n” and apply the merge equations. This merge will be even simpler, since the recurrent merge chain will contain only a single element that is duplicated, and it will be possible to compare the result only with this element.
Conclusion
In the article, we considered not the rebuy algorithm itself, but a rather much more important topic that gives you the necessary mathematical equations and methods for a more accurate and efficient evaluation of trading systems. More importantly, you get the mathematical proof of what diversification is worth and what makes it effective, and how to increase it in a natural and healthy way, knowing that you are doing everything right.
We have also proved that the graph of any profitable system is more beautiful, the longer the trading area we use, and also, the more profitable systems trade simultaneously on one account. So far, everything is framed in the form of a theory, but in the next article we will consider the applied aspects. To put it simply, we will build a working mathematical model for price simulation and multi-currency trading simulation and confirm all of our theoretical conclusions. You most likely will not find this theory anywhere, so try to delve deeper into this math, or at least understand its essence.
Cool partnership https://shorturl.fm/XIZGD
Cool partnership https://shorturl.fm/FIJkD
Very good https://shorturl.fm/bODKa
Super https://shorturl.fm/6539m
Cool partnership https://shorturl.fm/XIZGD
Top https://shorturl.fm/YvSxU
Cool partnership https://shorturl.fm/a0B2m
Very good partnership https://shorturl.fm/9fnIC
Cool partnership https://shorturl.fm/FIJkD
Very good partnership https://shorturl.fm/9fnIC
Best partnership https://shorturl.fm/A5ni8
https://shorturl.fm/YvSxU
https://shorturl.fm/YvSxU
https://shorturl.fm/m8ueY
https://shorturl.fm/FIJkD
https://shorturl.fm/XIZGD
https://shorturl.fm/TbTre
https://shorturl.fm/5JO3e
https://shorturl.fm/m8ueY
https://shorturl.fm/N6nl1
https://shorturl.fm/9fnIC
https://shorturl.fm/5JO3e
https://shorturl.fm/oYjg5
KALs vDFirv CDhTIHq eEXCaEly OioDia hTLJX
https://shorturl.fm/6539m
https://shorturl.fm/oYjg5
https://shorturl.fm/68Y8V
https://shorturl.fm/TbTre
https://shorturl.fm/oYjg5
https://shorturl.fm/m8ueY
https://shorturl.fm/5JO3e
https://shorturl.fm/YvSxU
https://shorturl.fm/Xect5
https://shorturl.fm/IPXDm
uqyzvrkurfptgpphfjtgomihrsgkhg
https://shorturl.fm/DA3HU
i9rktm
https://shorturl.fm/LdPUr
https://shorturl.fm/ypgnt
https://shorturl.fm/uyMvT
https://shorturl.fm/eAlmd
https://shorturl.fm/0EtO1
https://shorturl.fm/eAlmd
https://shorturl.fm/Kp34g
https://shorturl.fm/LdPUr
https://shorturl.fm/f4TEQ
zspdxsjnsvrusxxnziuxsezptnnefg
pDqpDc HYexDZuO ixMKXo ENAT NoHsog tVe eGTzAGk
Partner with us for generous payouts—sign up today! https://shorturl.fm/g5uAn
Start earning on autopilot—become our affiliate partner! https://shorturl.fm/XaCUZ
Start sharing our link and start earning today! https://shorturl.fm/RMiMy
Sign up and turn your connections into cash—join our affiliate program! https://shorturl.fm/vubu4
Get started instantly—earn on every referral you make! https://shorturl.fm/U0J5q
Turn referrals into revenue—sign up for our affiliate program today! https://shorturl.fm/boTtU
Join our affiliate program and start earning commissions today—sign up now! https://shorturl.fm/CNpRh
Start earning instantly—become our affiliate and earn on every sale! https://shorturl.fm/N3fk9
Unlock exclusive affiliate perks—register now! https://shorturl.fm/EbAL2
Share our products, earn up to 40% per sale—apply today! https://shorturl.fm/y3Czo
Tap into unlimited earnings—sign up for our affiliate program! https://shorturl.fm/LcRNy
Join forces with us and profit from every click! https://shorturl.fm/HC0LN
Start earning instantly—become our affiliate and earn on every sale! https://shorturl.fm/wyh4E
Get paid for every referral—enroll in our affiliate program! https://shorturl.fm/VBVJx
Share your link, earn rewards—sign up for our affiliate program! https://shorturl.fm/juPOV
Become our affiliate—tap into unlimited earning potential! https://shorturl.fm/51lMT
Join our affiliate family and watch your profits soar—sign up today! https://shorturl.fm/fcWjI
Your network, your earnings—apply to our affiliate program now! https://shorturl.fm/ukiUc
Share our link, earn real money—signup for our affiliate program! https://shorturl.fm/JExEr
Become our affiliate—tap into unlimited earning potential! https://shorturl.fm/pR9y8
Turn traffic into cash—apply to our affiliate program today! https://shorturl.fm/7HSLy
xoqervhxteldlhnjoewpnhxnugzxxs
Honestly, I wasn’t expecting this, but it really caught my attention. The way everything came together so naturally feels both surprising and refreshing. Sometimes, you stumble across things without really searching, and it just clicks.testinggoeshow It reminds me of how little moments can have an unexpected impact
Start earning every time someone clicks—join now! https://shorturl.fm/aGQOW
Apply now and unlock exclusive affiliate rewards! https://shorturl.fm/ALXsQ
Monetize your influence—become an affiliate today! https://shorturl.fm/63ttv
Your audience, your profits—become an affiliate today! https://shorturl.fm/0liVT
Promote, refer, earn—join our affiliate program now! https://shorturl.fm/bwzou
Tap into a new revenue stream—become an affiliate partner! https://shorturl.fm/RSkaj
Лаки Джет — лучший краш-слот по версии 1WIN.
🔥 Микрокредиты Казахстан — топ без отказа
Apply now and receive dedicated support for affiliates! https://shorturl.fm/l884P
Unlock exclusive rewards with every referral—enroll now! https://shorturl.fm/XBITK
Partner with us and enjoy high payouts—apply now! https://shorturl.fm/OSNYt
Perfect aviator game review for safe gamblers
Stay connected to your favorite casino using a mirror
Use casino mirror to beat traffic shaping
Discover BitStarz Casino, start with a generous $500 bonus and 180 FS, awarded Best Casino multiple times. Stay connected through official mirror.
Try your luck at BitStarz, grab your crypto welcome pack: $500 + 180 FS, including live dealer and table games. Stay connected through official mirror.
Try Spribe Aviator demo game without losing money
Get Aviator demo and go risk-free
Start earning passive income—become our affiliate partner! https://shorturl.fm/ICrvk
Sign up now and access top-converting affiliate offers! https://shorturl.fm/AtuW3
Refer friends and colleagues—get paid for every signup! https://shorturl.fm/deAbH
Share our link, earn real money—signup for our affiliate program! https://shorturl.fm/qCKnt
Apply now and unlock exclusive affiliate rewards! https://shorturl.fm/2Uqzg
Get paid for every click—join our affiliate network now! https://shorturl.fm/nyXbU
Гидроизоляция зданий https://gidrokva.ru и сооружений любой сложности. Фундаменты, подвалы, крыши, стены, инженерные конструкции.
Boost your income effortlessly—join our affiliate network now! https://shorturl.fm/eTjds
Become our partner and turn referrals into revenue—join now! https://shorturl.fm/xEdYb
Start profiting from your network—sign up today! https://shorturl.fm/DZsqK
Join our affiliate community and maximize your profits—sign up now! https://shorturl.fm/qActm
Become our partner now and start turning referrals into revenue! https://shorturl.fm/zNe1c
Earn passive income with every click—sign up today! https://shorturl.fm/zhhC3
Get paid for every referral—enroll in our affiliate program! https://shorturl.fm/4MDN1
Promote our brand, reap the rewards—apply to our affiliate program today! https://shorturl.fm/s8mCu
Join our affiliate community and earn more—register now! https://shorturl.fm/aLIgr
Learn bank management via aviator game review
How it works: aviator game review explained
Turn your traffic into cash—join our affiliate program! https://shorturl.fm/GcfOB
Заказать диплом https://diplomikon.ru быстро, надёжно, с гарантией! Напишем работу с нуля по вашим требованиям. Уникальность от 80%, оформление по ГОСТу.
Оформим реферат https://ref-na-zakaz.ru за 1 день! Напишем с нуля по вашим требованиям. Уникальность, грамотность, точное соответствие методичке.
Отчёты по практике https://gotov-otchet.ru на заказ и в готовом виде. Производственная, преддипломная, учебная.
Диплом под ключ https://diplomnazakaz-online.ru от выбора темы до презентации. Профессиональные авторы, оформление по ГОСТ, высокая уникальность.
Share our products, reap the rewards—apply to our affiliate program! https://shorturl.fm/Fgy1A
Сравнение условий микрокредитов КЗ
Mikrokredit без проверок — миф или реальность?
Drive sales, earn big—enroll in our affiliate program! https://shorturl.fm/qGu2O
Попробуй Лаки Джет на Lucky Star — реальные коэффициенты и быстрые выплаты.
Скачай 1WIN и начни выигрывать в Лаки Джет уже сегодня!
https://shorturl.fm/CJ1ue
https://shorturl.fm/bQqGC
https://shorturl.fm/x9wR4
https://shorturl.fm/Wys8V
qr code sim esim travel
https://shorturl.fm/L9dG7
https://shorturl.fm/m5JpT
Bet big and win more with the official 1win apk.
Install 1win apk and enjoy innovative gaming features today.
https://shorturl.fm/3AknL
https://shorturl.fm/6Ij8t
porn hd porn anime
Интересная статья: Нехватка сна: как недосып влияет на женское здоровье и можно ли умереть
Читать полностью: Лучшие подержанные автомобили для начинающих водителей: выбор и советы автовладельцам
Нужен дом? стоимость строительства дома — от проекта до отделки. Каркасные, кирпичные, брусовые, из газобетона. Гарантия качества, соблюдение сроков, индивидуальный подход.
https://shorturl.fm/r9CRL
https://shorturl.fm/wBkrc
https://shorturl.fm/wcL51
https://shorturl.fm/kPolq
https://shorturl.fm/dumUK
Mini-thread idea: the best place to buy twitter followers; covers niche filters.
We tried Spark Ads first, but reach exploded only after a micro-dose to buy tiktok views.
Don’t waste time trying sketchy apps. Reddit’s advice helped me land on one of the best gambling sites out there.
Надёжный заказ авто https://zakazat-avto11.ru. Машины с минимальным пробегом, отличным состоянием и по выгодной цене. Полное сопровождение: от подбора до постановки на учёт.
Полезная статья: Топ фрукт для молодости кожи: совет диетолога
Интересная новость: Секреты богатого урожая: как вырастить сочную и сладкую морковь
Читать подробнее: Subaru Crosstrek: обзор, характеристики и стоит ли покупать
https://shorturl.fm/TJgPa
https://shorturl.fm/aeFLz
Читать статью: Красные родинки на теле: причины появления и что это значит для здоровья женщины
Статьи обо всем: 6 продуктов, вредных для вашего пищеварения: что исключить из рациона женщине
Новое и актуальное: Курица по-французски: нежный рецепт для вашего стола
Интересные статьи: Как повысить давление: советы и эффективные средства для женщин
https://shorturl.fm/ToQoI
деньги займ где можно взять займ
Читать полностью: Автозагар или солнце: выбираем идеальный загар без вреда для кожи
https://shorturl.fm/vLWYU
занять деньги онлайн займ онлайн
займ быстрый деньги онлайн займ
Автомобили на заказ заказать авто из владивостока. Работаем с крупнейшими аукционами: выбираем, проверяем, покупаем, доставляем. Машины с пробегом и без, отличное состояние, прозрачная история.
Надёжный заказ авто https://zakazat-avto44.ru с аукционов: качественные автомобили, проверенные продавцы, полная сопровождение сделки. Подбор, доставка, оформление — всё под ключ. Экономия до 30% по сравнению с покупкой в РФ.
Решили заказать авто под заказ под ключ: подбор на аукционах, проверка, выкуп, доставка, растаможка и постановка на учёт. Честные отчёты, выгодные цены, быстрая логистика.
Хочешь авто заказать авто с аукциона? Мы поможем! Покупка на аукционе, проверка, выкуп, доставка, растаможка и ПТС — всё включено. Прямой импорт без наценок.
https://shorturl.fm/AvaZH
https://shorturl.fm/FO0Hj
https://shorturl.fm/JDYKy
https://shorturl.fm/lrl7q
https://shorturl.fm/oJO8x
Нужна душевая кабина? душевая кабина купить в минске: компактные и просторные модели, стеклянные и пластиковые, с глубоким поддоном и без. Установка под ключ, гарантия, помощь в подборе. Современный дизайн и доступные цены!
https://shorturl.fm/bXwJ6
https://shorturl.fm/a90ym
https://shorturl.fm/AAzWR
Продвижение сайта https://team-black-top.ru в ТОП Яндекса и Google. Комплексное SEO, аудит, оптимизация, контент, внешние ссылки. Рост трафика и продаж уже через 2–3 месяца.
Комедия детства смотреть фильм один дома — легендарная комедия для всей семьи. Без ограничений, в отличном качестве, на любом устройстве. Погрузитесь в атмосферу праздника вместе с Кевином!
Stay in the game with one simple mirror link
Casino mirror lets you deposit and withdraw securely
https://shorturl.fm/WPXpC
https://shorturl.fm/d2C91
https://shorturl.fm/JxEzb
https://shorturl.fm/zmEXM
Нужна душевая кабина? душевая кабина минск лучшие цены, надёжные бренды, стильные решения для любой ванной. Доставка по городу, монтаж, гарантия. Каталог от эконом до премиум — найдите идеальную модель для вашего дома.
https://focusbiathlon.com/ – biathlon schedule all season, overall and biathlon results – sprint and pursuit
быстрый займ оформить займ онлайн
https://shorturl.fm/gGS5C
Архитектурно-планировочное бюро https://arhitektura-peterburg.ru
https://shorturl.fm/SPX6k
https://shorturl.fm/70fmQ
https://shorturl.fm/XQgZJ
https://shorturl.fm/utj9O
https://shorturl.fm/7AMUa
https://shorturl.fm/K2LuO
https://shorturl.fm/tikJd
https://shorturl.fm/XTd8e
Курс по плазмолифтингу https://prp-ginekologiya.ru в гинекологии: PRP-терапия, протоколы, показания и техника введения. Обучение для гинекологов с выдачей сертификата. Эффективный метод в эстетической и восстановительной медицине.
Курс по плазмотерапии прп терапия обучение с выдачей сертификата. Освойте PRP-методику: показания, противопоказания, протоколы, работа с оборудованием. Обучение для медработников с практикой и официальными документами.
saif zone com saif zone visa requirements
Интересная статья: Самые быстрые кроссоверы: рейтинг, характеристики и фото для автовладельцев
Читать статью: Удаление пятен: лучшие лайфхаки от экспертов
Интересная статья: Как укрепить иммунитет: 4 природных помощника для здоровья
Читать в подробностях: Стоит ли прощать измену: 5 важных вопросов, которые нужно задать себе
Интересная новость: Горячий шоколад: польза и вред для здоровья – мнение ученых
Читать новость: Депрессия и инсульт: связь и последствия для здоровья
Новое на сайте: Салат из свеклы: рецепт Королевский и другие полезные варианты
For conversion?led launches, some calendars include a scheduled pause to buy followers on twitter after the first organic spike.
Новое на сайте: Секреты гладкой кожи: почему в СССР женщины реже страдали от целлюлита
https://shorturl.fm/MTWPQ
AI platform http://bullbittrade.com for passive crypto trading. Robots trade 24/7, you earn. Without deep knowledge, without constant control. High speed, security and automatic strategy.
Innovative AI platform https://lumiabitai.com for crypto trading — passive income without stress. Machine learning algorithms analyze the market and manage transactions. Simple registration, clear interface, stable profit.
фільми 2025 безкоштовно нові фільми 2025 в Україні
фільм українські серії HD фільми українською онлайн
українські фільми 2024 топ фільмів 2025 онлайн
https://shorturl.fm/nLaFp
Experience Lucky Jet in style.
Feel the excitement of Lucky Jet and see why it’s popular.
https://shorturl.fm/21xPC
https://shorturl.fm/hBffN
https://shorturl.fm/rVcDw
Safeguard your playtime with approved mirror links.
Find trusted casino mirror sites with our expert recommendations.
https://shorturl.fm/XjrgJ
https://shorturl.fm/b4mAz
https://shorturl.fm/o1aQg
Get the latest version of Aviator game download now.
Predict smartly using data from Aviator game download interface.
3d comics online superhero comics free HD
watch manga manga 2025 updates HD
манхва темное манхва онлайн бесплатно
https://shorturl.fm/3bVYe
https://shorturl.fm/ToFjH
https://shorturl.fm/QzbVb
https://shorturl.fm/HDVWg
https://shorturl.fm/P2kgE
фильмы онлайн бесплатно новинки кино 2025
https://shorturl.fm/gZZHd
Публичная дипломатия России https://softpowercourses.ru концепции, стратегии, механизмы влияния. От культурных центров до цифровых платформ — как формируется образ страны за рубежом.
Институт государственной службы https://igs118.ru обучение для тех, кто хочет управлять, реформировать, развивать. Подготовка кадров для госуправления, муниципалитетов, законодательных и исполнительных органов.
Школа бизнеса EMBA https://emba-school.ru программа для руководителей и собственников. Стратегическое мышление, международные практики, управленческие навыки.
https://shorturl.fm/dovP3
Опытный репетитор https://english-coach.ru для школьников 1–11 классов. Подтянем знания, разберёмся в трудных темах, подготовим к экзаменам. Занятия онлайн и офлайн.
Проходите аттестацию https://prom-bez-ept.ru по промышленной безопасности через ЕПТ — быстро, удобно и официально. Подготовка, регистрация, тестирование и сопровождение.
«Дела семейные» https://academyds.ru онлайн-академия для родителей, супругов и всех, кто хочет разобраться в семейных вопросах. Психология, право, коммуникации, конфликты, воспитание — просто о важном для жизни.
Трэвел-журналистика https://presskurs.ru как превращать путешествия в публикации. Работа с редакциями, создание медийного портфолио, написание текстов, интервью, фото- и видеоматериалы.
Свежие скидки https://1001kupon.ru выгодные акции и рабочие промокоды — всё для того, чтобы тратить меньше. Экономьте на онлайн-покупках с проверенными кодами.
«Академия учителя» https://edu-academiauh.ru онлайн-портал для педагогов всех уровней. Методические разработки, сценарии уроков, цифровые ресурсы и курсы. Поддержка в обучении, аттестации и ежедневной работе в школе.
Оригинальный потолок сколько стоит натяжной потолок со световыми линиями со световыми линиями под заказ. Разработка дизайна, установка профиля, выбор цветовой температуры. Идеально для квартир, офисов, студий. Стильно, практично и с гарантией.
?аза? тіліндегі ?ндер Песни 2025 года, казахские хиты ж?рекке жа?ын ?уендер мен ?серлі м?тіндер. ?лтты? музыка мен ?азіргі заман?ы хиттер. Онлайн ты?дау ж?не ж?ктеу м?мкіндігі бар ы??айлы жина?.
https://shorturl.fm/dEhpP
https://shorturl.fm/xd4Rl
https://shorturl.fm/kFo3U
Готовый комплект Инсталляция тесе с унитазом в комплекте инсталляция и унитаз — идеальное решение для современных интерьеров. Быстрый монтаж, скрытая система слива, простота в уходе и экономия места. Подходит для любого санузла.
Engagement ratios slip when you “view?stuff” too fast; the safer path is a 1 K?view twitter views buy spread across 24 h.
https://shorturl.fm/O3YD2
https://shorturl.fm/qnjWx
https://shorturl.fm/21aJN
https://shorturl.fm/shGEq
https://shorturl.fm/HfmZn
https://shorturl.fm/P9zms
Чувствуется, что тут всё сделано для тех, кто хочет выигрывать. Всё изменилось с получением доступа к промокод для Vodka Casino. Интерфейс не важен, если внутри огонь. Честность и скорость — на высоте. Бонусы не просто на словах — они реально работают. Слоты могут удивлять и затягивать. Каждый момент здесь — это история, которую хочется повторить.
https://shorturl.fm/p7lBi
https://shorturl.fm/6NLVg
https://shorturl.fm/z89Mk
https://shorturl.fm/9aTRK
https://shorturl.fm/HhLL1
https://shorturl.fm/ywi3y
https://shorturl.fm/WTOnr
https://shorturl.fm/wEigv
https://shorturl.fm/8Thq3
https://shorturl.fm/Eg5tT
https://shorturl.fm/AAOWK
https://shorturl.fm/kmvEH
https://shorturl.fm/0qcnQ
https://shorturl.fm/rxawY
https://shorturl.fm/VjnTM
roprag
https://shorturl.fm/T1Bkv
https://shorturl.fm/dLcKd
https://shorturl.fm/arcYf
https://shorturl.fm/f1B39
888starz отзывы https://1stones.ru/wp-content/pgs/888starz-official-site-aviator.html
https://t.me/s/TgGo1WIN/10
Мы предлагаем уборка офиса в Москве и области, обеспечивая высокое качество, внимание к деталям и индивидуальный подход. Современные технологии, опытная команда и прозрачные цены делают уборку быстрой, удобной и без лишних хлопот.
Мы предлагаем установка счетчиков воды в СПб и области с гарантией качества и соблюдением всех норм. Опытные мастера, современное оборудование и быстрый выезд. Честные цены, удобное время, аккуратная работа.
центр лечения зависимостей лечение алкозависимости
https://shorturl.fm/32GMu
https://shorturl.fm/BsAKf
https://shorturl.fm/pRAHl
888starz кешбэк https://emergency.spb.ru/pages/888starz-mobile-app-android-ios.html
Win faster with the Android-ready 1win apk download.
Install now and win more � 1win apk download.
Сериал «Уэнсдей» https://uensdey.com мрачная и захватывающая история о дочери Гомеса и Мортиши Аддамс. Учёба в Академии Невермор, раскрытие тайн и мистика в лучших традициях Тима Бёртона. Смотреть онлайн в хорошем качестве.
Срочно нужен сантехник? сантехник алматы недорого в Алматы? Профессиональные мастера оперативно решат любые проблемы с водопроводом, отоплением и канализацией. Доступные цены, выезд в течение часа и гарантия на все виды работ
Die erfahrenen Onkologen hipec spezialisten entwickeln individuelle Behandlungsplane, abgestimmt auf Tumorstadium, Allgemeinzustand und beste Therapieoptionen fur jeden einzelnen Patienten.
Флешки оптом https://usb-flashki-optom-24.ru под логотип и как выбрать флешку в Санкт-Петербурге. Флешки визитки с Нанесением и игры На флешке купить в Костроме. Одноразовые флешки оптом купить и купить флешку эксклюзивную
Косметика на натуральной основе https://musco.ru
Продаем оконный профиль https://okonny-profil-kupit.ru высокого качества. Большой выбор систем, подходящих для любых проектов. Консультации, доставка, гарантия.
Оконный профиль https://okonny-profil.ru купить с гарантией качества и надежности. Предлагаем разные системы и размеры, помощь в подборе и доставке. Доступные цены, акции и скидки.
https://shorturl.fm/O79el
Официальный Telegram канал 1win Casinо. Казинo и ставки от 1вин. Фриспины, актуальное зеркало официального сайта 1 win. Регистрируйся в ван вин, соверши вход в один вин, получай бонус используя промокод и начните играть на реальные деньги.
https://t.me/s/Official_1win_kanal/4761
https://shorturl.fm/L7xvQ
Официальный Telegram канал 1win Casinо. Казинo и ставки от 1вин. Фриспины, актуальное зеркало официального сайта 1 win. Регистрируйся в ван вин, соверши вход в один вин, получай бонус используя промокод и начните играть на реальные деньги.
https://t.me/s/Official_1win_kanal/2541
https://shorturl.fm/ZTZ9u
ремонт кофемашины поларис ремонт кофемашины филипс
1с управление облако удаленная 1с в облаке
ремонт швейных машин janome ремонт швейных машин в москве
https://shorturl.fm/FZcqz
https://shorturl.fm/pe343
https://shorturl.fm/wGm5a
BrunoCasino mobile https://www.boerbart.nl/post/eet-je-zelf-gezond
05sh63
https://shorturl.fm/UxwUb
Лоукост авиабилеты https://lowcost-flights.com.ua по самым выгодным ценам. Сравните предложения ведущих авиакомпаний, забронируйте онлайн и путешествуйте дешево.
Предлагаю услуги https://uslugi.yandex.ru/profile/DmitrijR-2993571 копирайтинга, SEO-оптимизации и графического дизайна. Эффективные тексты, высокая видимость в поиске и привлекательный дизайн — всё для роста вашего бизнеса.
скачать 888starz на телефон бесплатно http://www.777111.ru/2025/03/ino-populyarnye-sty-i-azare-igry/
АО «ГОРСВЕТ» в Чебоксарах https://gorsvet21.ru профессиональное обслуживание объектов наружного освещения. Выполняем ремонт и модернизацию светотехнического оборудования, обеспечивая комфорт и безопасность горожан.
Онлайн-сервис https://laikzaim.ru займ на карту или счет за несколько минут. Минимум документов, мгновенное одобрение, круглосуточная поддержка. Деньги в любое время суток на любые нужды.
Custom Royal Portrait turnyouroyal.com an exclusive portrait from a photo in a royal style. A gift that will impress! Realistic drawing, handwork, a choice of historical costumes.
Открыть онлайн брокерский счёт – ваш первый шаг в мир инвестиций. Доступ к биржам, широкий выбор инструментов, аналитика и поддержка. Простое открытие и надёжная защита средств.
Mit LeonBet wird jede Sportwette zum Erlebnis.
Mit LeonBet wird jede Sportwette zum Erlebnis.
ПОмощь юрист в банкротстве: юрист по банкротству юридических лиц
Ремонт кофемашин https://coffee-craft.kz с выездом на дом или в офис. Диагностика, замена деталей, настройка. Работаем с бытовыми и профессиональными моделями. Гарантия качества и доступные цены.
https://shorturl.fm/bmQsz
https://shorturl.fm/Xf2OQ
Круглосуточный вывод из запоя на дому в нижнем новгороде круглосуточно — помощь на дому и в стационаре. Капельницы, очищение организма, поддержка сердца и нервной системы. Анонимно и конфиденциально.
Купить мебель современные прихожие для дома и офиса по выгодным ценам. Широкий выбор, стильный дизайн, высокое качество. Доставка и сборка по всей России. Создайте комфорт и уют с нашей мебелью.
City paths are calmer when your ding cuts through earbud playlists; add a neat rockbros bike bell and you’ll spend less time guessing if you’ve been heard.
Предлагаем оконные профили https://proizvodstvo-okonnych-profiley.ru для застройщиков и подрядчиков. Высокое качество, устойчивость к климатическим нагрузкам, широкий ассортимент.
Оконные профили https://proizvodstvo-okonnych.ru для застройщиков и подрядчиков по выгодным ценам. Надёжные конструкции, современные материалы, поставка напрямую с завода.
Зеркало казино позволяет продолжить игру без перебоев
задать вопрос юристу в чате городская юридическая помощь бесплатно
Нужны пластиковые окна: стоимость пластиковых окон
Нужен вентилируемый фасад: подсистема норд фокс для вентилируемых фасадов
https://shorturl.fm/5rYD3
https://shorturl.fm/zJ8NE
Trust Finance https://trustf1nance.com is your path to financial freedom. Real investments, transparent conditions and stable income.
https://shorturl.fm/NXQz1
clay flowers https://www.ceramic-clay-flowers.com
Інформаційний портал https://pizzalike.com.ua про піцерії та рецепти піци в Україні й світі. Огляди закладів, адреси, меню, поради від шефів, секрети приготування та авторські рецепти. Все про піцу — від вибору інгредієнтів до пошуку найсмачнішої у вашому місті.
Решили купить Honda? https://avtomiks-smolensk.ru широкий ассортимент автомобилей Honda, включая новые модели, такие как Honda CR-V и Honda Pilot, а также автомобили с пробегом. Предоставляем услуги лизинга и кредитования, а также предлагает различные акции и спецпредложения для корпоративных клиентов.
Ищешь автозапчасти? купить автозапчасти онлайн предоставляем широкий ассортимент автозапчастей, автомобильных аксессуаров и оборудования как для владельцев легковых автомобилей, так и для корпоративных клиентов. В нашем интернет-магазине вы найдете оригинальные и неоригинальные запчасти, багажники, автосигнализации, автозвук и многое другое.
Выкуп автомобилей надёжные toyota и volkswagen без постредников, быстро. . У нас вы можете быстро оформить заявку на кредит, продать или купить автомобиль на выгодных условиях, воспользовавшись удобным поиском по марке, модели, приводу, году выпуска и цене — независимо от того, интересует ли вас BMW, Hyundai, Toyota или другие популярные бренды.
продвижение сайтов обучение seo любой тематики. Поисковая оптимизация, рост органического трафика, улучшение видимости в Google и Яндекс. Работаем на результат и долгосрочный эффект.
нужен юрист: составить исковое заявление в суд цена Новосибирск защита интересов, составление договоров, сопровождение сделок, помощь в суде. Опыт, конфиденциальность, индивидуальный подход.
creatore di suonerie gratuito modifica audio
Заказать такси https://taxi-sverdlovsk.ru онлайн быстро и удобно. Круглосуточная подача, комфортные автомобили, вежливые водители. Доступные цены, безналичная оплата, поездки по городу и за его пределы
Онлайн-заказ такси https://sverdlovsk-taxi.ru за пару кликов. Быстро, удобно, безопасно. Подача в течение 5–10 минут, разные классы авто, безналичный расчет и прозрачные тарифы.
Закажите такси https://vezem-sverdlovsk.ru круглосуточно. Быстрая подача, фиксированные цены, комфорт и безопасность в каждой поездке. Подходит для деловых, туристических и семейных поездок.
Быстрый заказ такси https://taxi-v-sverdlovske.ru онлайн и по телефону. Подача от 5 минут, комфортные автомобили, безопасные поездки. Удобная оплата и выгодные тарифы на любые направления.
Платформа пропонує https://61000.com.ua різноманітний контент: порадник, новини, публікації на тему здоров’я, цікавих історій, місць Харкова, культурні події, архів статей та корисні матеріали для жителів міста
https://shorturl.fm/ban05
Нужен сантехник: сантехник на дом алматы
ГОРСВЕТ Чебоксары https://gorsvet21.ru эксплуатация, ремонт и установка систем уличного освещения. Качественное обслуживание, модернизация светильников и энергоэффективные решения.
Saznajte sve o kamen u bubregu – simptomi, uzroci i efikasni nacini lecenja. Procitajte savete strucnjaka i iskustva korisnika, kao i preporuke za prevenciju i brzi oporavak.
Займы онлайн like zaim моментальное оформление, перевод на карту, прозрачные ставки. Получите нужную сумму без визита в офис и долгих проверок.
Интернет-магазин мебели https://mebelime.ru тысячи моделей для дома и офиса. Гарантия качества, быстрая доставка, акции и рассрочка. Уют в каждый дом.
https://shorturl.fm/GHmni
https://shorturl.fm/TRiqO
форум общения знакомств пикаперы это кто Интересуется Алена из Питера, ей конечно же дали ответы на этот вопрос, и было многое даже неожиданным и интересным.
Zasto se javlja bol u levom bubregu: od kamenaca i infekcija do prehlade. Kako prepoznati opasne simptome i brzo zapoceti lecenje. Korisne informacije.
Авто журнал https://bestauto.kyiv.ua свежие новости автопрома, тест-драйвы, обзоры новинок, советы по уходу за автомобилем и репортажи с автособытий.
Sta znaci pesak u bubrezima, koji simptomi ukazuju na problem i kako ga se resiti. Efikasni nacini lecenja i prevencije.
Популярный авто журнал https://mirauto.kyiv.ua подробные обзоры моделей, советы экспертов, новости автосалонов и автоспорта, полезные статьи для автовладельцев.
Заказать именную флешки оптом для промо Москва флешку оптом и купить флешку На 32 гб для планшета во Владивостоке. Сумочка для флешек и флешка На 128 гб в Уфе. Металлические флешки оптом с гравировкой и флешкарта На 64
https://shorturl.fm/crYSf
Экономические новости https://gau.org.ua прогнозы и обзоры. Политика, бизнес, финансы, мировые рынки. Всё, что важно знать для принятия решений.
Мужской портал https://hooligans.org.ua всё, что интересно современному мужчине: стиль, спорт, здоровье, карьера, автомобили, технологии и отдых. Полезные статьи и советы каждый день.
Онлайн авто портал https://avtomobilist.kyiv.ua с обзорами новых и подержанных авто, тест-драйвами, советами по обслуживанию и новостями из мира автопрома.
shipping services new york shipping nyc
https://shorturl.fm/TQZ1K
Портал о строительстве https://juglans.com.ua свежие новости, статьи и советы. Обзоры технологий, материалов, дизайн-идеи и практические рекомендации для профессионалов и частных застройщиков.
Строительный портал https://dki.org.ua всё о строительстве и ремонте: технологии, оборудование, материалы, идеи для дома. Новости отрасли и экспертные рекомендации.
Онлайн строительный https://texha.com.ua портал о материалах, проектах и технологиях. Всё о ремонте, строительстве и обустройстве дома. Поддержка специалистов и вдохновение для новых идей.
Всё о стройке https://mramor.net.ua полезные статьи, советы, обзоры материалов и технологий. Ремонт, строительство домов, дизайн интерьера и современные решения для вашего проекта.
Сайт «Всё о стройке» https://sushico.com.ua подробные инструкции, советы экспертов, новости рынка. Всё о строительстве, ремонте и обустройстве жилья в одном месте.
Get sports and casino thrills via 1win apk download.
Win without limits via 1win apk download.
https://shorturl.fm/r5AI8
https://shorturl.fm/sP0QZ
https://shorturl.fm/xg9oh
https://shorturl.fm/RKw0i
https://shorturl.fm/7hQLE
Сувенирная флешка https://usb-flashki-optom-24.ru оптом купить и флешка На один терабайт цена в Таганроге. Купить флешку На 32 гб 3 0 и днс флешки 128 гб в Ставрополе. Флешка оптом 500 мб и флешка код да винчи
Новости Украины https://gromrady.org.ua в реальном времени. Экономика, политика, общество, культура, происшествия и спорт. Всё самое важное и интересное на одном портале.
Современный автопортал https://automobile.kyiv.ua свежие новости, сравнительные обзоры, тесты, автострахование и обслуживание. Полезная информация для водителей и покупателей.
Строительный сайт https://vitamax.dp.ua с полезными материалами о ремонте, дизайне и современных технологиях. Обзоры стройматериалов, инструкции по монтажу, проекты домов и советы экспертов.
Универсальный автопортал https://road.kyiv.ua автомобили, автоновости, обзоры, ремонт, обслуживание и tuning. Полезные статьи для водителей и экспертов автоиндустрии.
Женский портал https://fotky.com.ua с полезными статьями о красоте, моде, здоровье, отношениях и карьере. Советы экспертов, лайфхаки для дома, рецепты и вдохновение для каждой женщины.
Онлайн женский портал https://martime.com.ua новости, тренды моды, секреты красоты, психология отношений, карьера и семья. Полезные материалы и практические советы для женщин.
https://shorturl.fm/3cQk1
Женский сайт https://womanclub.in.ua о красоте, моде, здоровье и стиле жизни. Полезные советы, рецепты, тренды, отношения и карьера. Всё самое интересное для женщин в одном месте.
Всё о гипертонии https://gipertoniya.net что это за болезнь, как проявляется и чем опасна. Подробные статьи о симптомах, диагностике и способах лечения высокого давления.
Туристический портал https://elnik.kiev.ua с актуальными новостями, маршрутами и путеводителями. Обзоры стран и городов, советы путешественникам, лучшие идеи для отдыха и выгодные предложения.
Онлайн женский https://ledis.top сайт о стиле, семье, моде и здоровье. Советы экспертов, обзоры новинок, рецепты и темы для вдохновения. Пространство для современных женщин.
Сайт о строительстве https://stinol.com.ua практические рекомендации, проекты, обзоры инструментов и материалов. Советы экспертов, новости отрасли и новые технологии.
Строительный журнал https://mts-slil.info с актуальными новостями отрасли, обзорами материалов, инструкциями по ремонту и строительству. Полезные советы для специалистов и частных застройщиков.
Онлайн сайт https://purr.org.ua о строительстве и ремонте: полезные статьи, инструкции, обзоры технологий, дизайн-идеи и архитектурные решения для вашего дома.
Онлайн туристический https://azst.com.ua портал: всё о путешествиях, туризме и отдыхе. Маршруты, отели, лайфхаки для туристов, актуальные цены и интересные статьи о странах.
freight companies in new york ny delivery
Онлайн новостной https://antifa-action.org.ua портал с круглосуточным обновлением. Свежие новости, репортажи и обзоры. Важные события страны и мира, мнения экспертов и актуальная аналитика.
Новости Украины https://uamc.com.ua новости дня, аналитика, события регионов и мира. Обзоры, интервью, мнения экспертов. Быстро, достоверно и удобно для читателей.
Новостной портал https://prp.org.ua с актуальной информацией о событиях в России и мире. Политика, экономика, культура, спорт и технологии. Новости 24/7, аналитика и комментарии экспертов.
Строительный портал https://suli-company.org.ua с актуальными новостями, обзорами материалов, проектами и инструкциями. Всё о ремонте, строительстве и дизайне.
detyzn
freight shipping ny delivery in new york city
Портал про авто https://prestige-avto.com.ua обзоры новых и подержанных машин, тест-драйвы, рынок автомобилей, страхование и обслуживание.
Онлайн автомобильный https://avtonews.kyiv.ua портал: свежие автоновости, сравнительные тесты, статьи о ремонте и тюнинге. Обзоры новых и подержанных машин, цены и советы экспертов.
Современный автомобильный https://mallex.info портал: автообзоры, тесты, ремонт и обслуживание, страхование и рынок. Всё, что нужно водителям и любителям автомобилей.
Автомобильный портал https://autonovosti.kyiv.ua новости автопрома, обзоры моделей, тест-драйвы и советы по эксплуатации. Всё для автолюбителей: от выбора авто до обслуживания и ремонта.
Строительный сайт https://novostroi.in.ua с полезными статьями о ремонте, отделке и дизайне. Обзоры стройматериалов, проекты домов, инструкции и советы экспертов для профессионалов и новичков.
https://shorturl.fm/szrLc
Портал для родителей https://detiwki.com.ua и детей — всё для счастливой семьи. Воспитание, образование, здоровье, отдых и полезные материалы для мам, пап и малышей.
Сайт для женщин https://stylewoman.kyiv.ua с интересными статьями о моде, красоте, семье и здоровье. Идеи для кулинарии, путешествий и вдохновения.
Журнал садовода https://mts-agro.com.ua полезные советы по уходу за садом и огородом. Сезонные работы, выращивание овощей, фруктов и цветов, современные технологии и секреты урожая.
Универсальный сайт https://virginvirtual.net для женщин — секреты красоты, тренды моды, советы по отношениям и карьере, рецепты и стиль жизни.
Сайт для женщин https://gratransymas.com о красоте, моде, здоровье и стиле жизни. Полезные советы, рецепты, тренды, отношения и карьера.
Сайт обо всём https://vybir.kiev.ua энциклопедия для повседневной жизни. Красота, здоровье, дом, путешествия, карьера, семья и полезные советы для всех.
Студия дизайна https://lbook.com.ua интерьера и архитектуры. Создаём стильные проекты квартир, домов и офисов. Индивидуальный подход, современные решения и полный контроль реализации.
Портал про ремонт https://hydromech.kiev.ua свежие статьи о ремонте и отделке, дизайне интерьера и выборе материалов. Полезные советы для мастеров и тех, кто делает ремонт своими руками.
Интересный сайт https://whoiswho.com.ua обо всём: статьи, лайфхаки, обзоры и идеи на самые разные темы. Всё, что нужно для вдохновения и развития, в одном месте.
Онлайн портал https://esi.com.ua про ремонт: идеи для интерьера, подбор материалов, практические рекомендации и пошаговые инструкции для самостоятельных работ.
Репортажи в больших https://infotolium.com фотографиях: самые обсуждаемые события, уникальные кадры и впечатляющие истории. Новости и жизнь в формате визуального рассказа.
Информационный портал https://reklama-region.com про ремонт: ремонт квартир, домов, офисов. Практические рекомендации, современные решения и обзоры стройматериалов.
Сайт про авто https://autoinfo.kyiv.ua свежие новости автопрома, обзоры моделей, тест-драйвы и советы по эксплуатации. Всё о машинах для водителей и автолюбителей.
Сайт про автомобили https://black-star.com.ua новинки рынка, цены, тест-драйвы и обзоры. Советы экспертов по выбору и уходу за машиной, тюнинг и автоуслуги.
Онлайн-журнал https://autoiceny.com.ua для автолюбителей: автомобили, новости индустрии, тест-драйвы, тюнинг и советы по обслуживанию.
Автомобильный онлайн-журнал https://allauto.kyiv.ua свежие новости автопрома, тест-драйвы, обзоры новых моделей, советы по эксплуатации и ремонту. Всё для водителей и автолюбителей.
Royal portraits https://www.turnyouroyal.com from photos – turn yourself or your loved ones into a king, queen or aristocrat. Author’s work of artists, luxurious style and premium quality of printing.
https://shorturl.fm/rG4jV
Авто-журнал https://bestauto.kyiv.ua источник информации для автолюбителей. Новинки рынка, сравнения моделей, советы по ремонту и уходу, интересные материалы о мире автомобилей.
https://shorturl.fm/CItsp
Новостной портал https://gau.org.ua круглосуточные новости, комментарии экспертов, события регионов и мира. Политика, бизнес, культура и общество.
https://shorturl.fm/CItsp
Онлайн авто-журнал https://mirauto.kyiv.ua с актуальными новостями, аналитикой и обзорами. Тесты автомобилей, тюнинг, технологии и советы по эксплуатации.
Авто портал https://avtomobilist.kyiv.ua всё об автомобилях: новые модели, цены, рынок подержанных авто, тюнинг и автотехнологии. Полезные материалы для автовладельцев.
Мужской портал https://hooligans.org.ua новости, лайфхаки, обзоры техники, спорт, здоровье и авто. Советы для уверенной и гармоничной жизни.
https://shorturl.fm/WcZ8O
Портал о ремонте https://dki.org.ua и строительстве: от отделки квартиры до возведения загородного дома. Подробные статьи, рекомендации экспертов и идеи для обустройства жилья.
Портал о стройке https://sushico.com.ua и ремонте. Новости рынка, современные технологии, подборка идей для интерьера и экстерьера. Всё, что нужно для дома и дачи.
Онлайн сайт https://mramor.net.ua о строительстве и ремонте. Всё о возведении домов, ремонте квартир, отделке и обустройстве жилья. Обзоры материалов, советы экспертов и свежие идеи.
Всё о стройке https://aziatransbud.com.ua и ремонте в одном месте: дизайн, архитектура, выбор стройматериалов, инструкции по монтажу, лайфхаки и полезные рекомендации для новичков и мастеров.
Сайт о строительстве https://juglans.com.ua и ремонте — ваш помощник в выборе материалов, инструментов и технологий. Всё о ремонте квартир, строительстве домов и дизайне интерьеров.
Онлайн журнал https://vitamax.dp.ua о строительстве: проекты домов, ремонт квартир, выбор стройматериалов, дизайн и интерьер. Советы экспертов и свежие идеи для комфортной жизни.
Портал про строительство https://texha.com.ua новости рынка, обзоры технологий, инструкции и идеи для ремонта. Материалы для застройщиков, мастеров и тех, кто делает своими руками.
Новости Украины https://gromrady.org.ua онлайн: политика, экономика, спорт, культура и события регионов. Оперативные материалы, аналитика и комментарии экспертов круглосуточно.
Портал про авто https://automobile.kyiv.ua свежие новости автопрома, тест-драйвы, обзоры моделей и советы по ремонту. Всё о машинах для водителей и автолюбителей.
Авто портал https://road.kyiv.ua с актуальной информацией: новинки рынка, цены, обзоры, страхование и тюнинг. Полезные статьи и аналитика для автомобилистов.
change pitch split audio
Prodaja bungalovi Zabljak: stanovi, vile, zemljisne parcele. Izbor smestaja za odmor, preseljenje i investicije. Saveti strucnjaka i aktuelne ponude na trzistu.
https://shorturl.fm/GCEgc
Besoin d’un bien immobilier? immobilier au Montenegro: appartements en bord de mer, maisons a la montagne, villas et appartements. Catalogue de biens, prix actuels et conseils d’experts en investissement.
Фильмы и сериалы сериалы онлайн бесплатно Онлайн-кинотеатр без регистрации и смс: тысячи фильмов и сериалов бесплатно.
Jak samodzielnie zdjac https://telegra.ph/Jak-samodzielnie-zdj%C4%85%C4%87-sufit-napinany-instrukcja-krok-po-kroku-bez-haka-z-wkr%C4%99tem-i-trikami-monta%C5%BCyst%C3%B3w-08-07 sufit napinany: instrukcje krok po kroku, narzedzia, porady ekspertow. Dowiedz sie, jak zdemontowac plotno bez uszkodzen i przygotowac pomieszczenie do montazu nowej okladziny.
https://shorturl.fm/CWBkc
салон красоты василеостровская https://beauty-salon-spb.ru
https://shorturl.fm/V6F4y
Нужен микрозайм? https://kubyshka24.ru: деньги на карту без справок и поручителей. Простое оформление заявки, одобрение за минуты и мгновенное зачисление. Удобно и доступно 24/7.
оценка рыночной стоимости оценочная компания Москва
https://shorturl.fm/OVHne
https://shorturl.fm/qpuAF
оценка акций ао заказать оценку Москва
https://shorturl.fm/VZNQZ
Авто помощь 24/7 автопомощь на дороге: устранение поломок, подвоз топлива, прикуривание аккумулятора, замена колеса и эвакуация автомобиля.
Срочно нужны доставка цветов Свежие букеты, праздничные композиции и эксклюзивные флористические решения. Онлайн-заказ и быстрая доставка по городу.
Профессиональные детейлинг петербург: полировка кузова, химчистка салона, восстановление пластика и защита керамикой. Вернём автомобилю блеск и надёжную защиту.
Нужен массаж? https://doctu.ru – профессиональные мастера, широкий выбор техник: классический, оздоровительный, лимфодренажный, детский. Доступные цены и уютная атмосфера.
Обучающие курсы онлайн складчина новые навыки для работы и жизни. IT, дизайн, менеджмент, языки, маркетинг. Гибкий график, практика и сертификаты по итогам.
vps server hosting vps server hosting
тележка косметолога тумба педикюрная с уф лампой
https://shorturl.fm/EpeT8
https://shorturl.fm/UIxXY
https://shorturl.fm/Ul218
vps hosting usa vps hosting germany
https://shorturl.fm/IHxk8
https://shorturl.fm/rzdNm
тумба для косметолога лампа лупа косметологическая напольная купить
бетон цена https://beton-saratov64.ru
Наркологические услуги: наркологическая клиника в нижнем новгороде, кодирование, детоксикация, снятие ломки, помощь при алкоголизме и наркомании. Круглосуточная поддержка и анонимность.
бетон официальный сайт https://beton-saratov64.ru
Доброго!
Долго не спал и думал как поднять сайт и свои проекты и нарастить ИКС Яндекса и узнал от крутых seo,
топовых ребят, именно они разработали недорогой и главное продуктивный прогон Xrumer – https://www.bing.com/search?q=bullet+%D0%BF%D1%80%D0%BE%D0%B3%D0%BE%D0%BD
С помощью Xrumer вы можете быстро повысить DR и улучшить показатели Ahrefs. Прогон ссылок на форумах с Xrumer позволяет создавать качественные внешние ссылки. Массовые рассылки ссылок ускоряют продвижение сайта. Программы для линкбилдинга позволяют вам улучшить ссылочную массу с минимальными усилиями. Попробуйте Xrumer для эффективного линкбилдинга.
методы продвижения сайта раскрутка сайтов, услуга раскрутка сайта москва, линкбилдинг статьи
линкбилдинг форум, продвижение сайтов дешево цены, кто такой seo специалист
!!Удачи и роста в топах!!
https://shorturl.fm/AoHnF
https://shorturl.fm/QYXNs
https://shorturl.fm/gB6wj
https://shorturl.fm/4fAvF
Handmade handmade flowers Ideal for home, office decor or original gift. Natural beauty and durability.
Бетон в Воронеже https://stk-vrn.ru продажа и доставка. Все марки для фундаментов, дорожных работ и строительства под ключ. Надёжный производитель и лучшие цены.
cyc441
https://shorturl.fm/vugAT
https://shorturl.fm/X2B8V
https://shorturl.fm/S4mNo
https://shorturl.fm/j5RrA
https://shorturl.fm/qMzC0
https://shorturl.fm/0sEdp
кредит займ онлайн займ
https://shorturl.fm/NdTC7
взять деньги онлайн мфо взять займ
взять займ онлайн кредит займ
https://shorturl.fm/FhGcR
How Much Does a Festival Ticket Cost? https://rock-concert-tickets.ru
https://shorturl.fm/ALPvl
Рестораны Хамовников https://restoran-khamovniki.ru топ заведений для встреч, романтических ужинов и семейных обедов. Авторская кухня, стильный интерьер, удобное расположение и достойный сервис.
Лучшие рестораны https://hamovniki-restoran.ru Хамовников для ценителей гастрономии. Подборка заведений с изысканной кухней, качественным сервисом и атмосферой для отдыха и деловых встреч.
Курсы по плазмотерапии плазмотерапия обучение в москве освоение методик, современные протоколы, практическая отработка. Обучение для специалистов с выдачей сертификата и повышением квалификации.
Профессиональное обучение обучение prp в косметологии: подробная программа, практические навыки, сертификация. Освойте эффективные методики для применения в медицине и косметологии.
Детская школа искусств https://elegy-school.ru обучение музыке, танцам, изобразительному и театральному искусству. Творческие программы для детей, концерты, конкурсы и развитие талантов.
Авторские курсы по REVIT https://dashclass.ru обучение созданию интерьеров и архитектурных проектов. Практика, реальные кейсы, индивидуальный подход и профессиональные навыки для работы в проектировании.
https://shorturl.fm/4ePyU
https://shorturl.fm/hEV9U
Первая помощь детям https://firstaidkids.ru правила оказания при травмах, ожогах, удушье и других ситуациях. Пошаговые инструкции, советы врачей и полезная информация для родителей.
Студия иностранных языков https://whats-up-studiya-inostrannyh-yazykov.ru обучение английскому, немецкому, французскому и другим языкам. Индивидуальные и групповые занятия, современные методики и опытные преподаватели.
https://shorturl.fm/B5qTP
Chicken Road slothttps://apkpure.com/p/app.chickenroad.game
Срочный вызов сантехника https://master-expert.com в Москве на дом. Услуги сантехника: прочистка засоров, ремонт смесителей, установка приборов учета. Работаем 24/7. Недорого и с гарантией. Подробнее на сайте
Детский сад № 55 https://detsadik55.ru забота, развитие и обучение детей. Современные программы, квалифицированные воспитатели, уютные группы, безопасная среда и внимание к каждому ребёнку.
https://shorturl.fm/B5qTP
Aby zalogować się do Vavada, będziesz potrzebować: Login – numer telefonu lub e-mail użyty podczas rejestracji Hasło – ustawione samodzielnie lub wygenerowane przez przeglądarkę Opcja „Zapamiętaj” pozwala przyspieszyć kolejne logowania. Jeśli gracz zapomni hasła, może skorzystać z przypomnienia lub skontaktować się z obsługą klienta.
Промышленная безопасность https://аттестация-промбезопасность.рф курсы и обучение под ключ. Подготовка к проверке Ростехнадзора, повышение квалификации и сертификация специалистов предприятий.
Автомобили на заказ https://avto-iz-kitaya1.ru поиск, проверка, покупка и доставка. Китай и Корея. Индивидуальный подбор под бюджет и пожелания клиента, полное сопровождение сделки.
бошки марихуана меф купить купить гашиш амфетамин
купить героин траву купить меф амфетамин
Авто из Китая https://avto-iz-kitaya2.ru на заказ под ключ: подбор, проверка, доставка и растаможка. Новые и подержанные автомобили, выгодные цены и полное сопровождение сделки.
Авто из Китая под заказ https://dostavka-avto-china.ru кроссоверы, седаны, электромобили и премиальные модели. Индивидуальный подбор, проверка, сопровождение сделки и доставка в ваш город.
Автомобили из Китая на заказ https://avto-iz-kitaya2.ru подбор, покупка и доставка. Полный цикл услуг: диагностика, растаможка, постановка на учёт и гарантия качества.
https://shorturl.fm/A0p5e
Заказать авто из Китая https://dostavka-avto-china2.ru новые автомобили с гарантией, выгодные цены и проверенные поставщики. Доставка, таможня и оформление всех документов под ключ.
Авто на заказ https://dostavka-avto-russia.ru поиск, диагностика и сопровождение сделки. Машины из Европы, Кореи, Китая и США. Доставка, растаможка и постановка на учёт.
Автомобили на заказ https://dostavka-avto-russia5.ru профессиональный подбор, юридическая проверка, доставка и растаможка. Индивидуальные решения для каждого клиента.
Хотите заказать авто https://prignat-avto5.ru Мы подберём оптимальный вариант, проверим машину по базам, организуем доставку и таможенное оформление. Выгодные цены и прозрачные условия.
https://shorturl.fm/ZaoE8
https://shorturl.fm/gbYbh
Машины на заказ https://prignat-avto7.ru поиск, диагностика и доставка автомобилей. Индивидуальный подбор, проверенные поставщики и прозрачные условия покупки.
Машины на заказ https://prignat-mashinu5.ru поиск, диагностика и доставка автомобилей. Индивидуальный подбор, проверенные поставщики и прозрачные условия покупки.
Автомобили на заказ https://prignat-mashinu7.ru подбор, проверка, доставка и оформление документов. Машины любых марок и комплектаций с гарантией качества и выгодной ценой.
https://shorturl.fm/BaiA8
https://shorturl.fm/gJ3Bd
Ремонт квартир https://remontkomand.kz и домов под ключ: дизайн-проект, отделка, инженерные работы. Работаем по договору, фиксированные сроки и цены. Гарантия качества и полный контроль этапов.
https://shorturl.fm/zrfAt
Цены на ремонт https://remontkomand.kz/ru/price квартир и помещений в Алматы под ключ. Узнайте точные расценки на все виды работ — от демонтажа до чистовой отделки. Посчитайте стоимость своего ремонта заранее и убедитесь в нашей прозрачности. Никаких «сюрпризов» в итоговой смете!
https://shorturl.fm/GiTO4
SEO-продвижение сайтов https://raskrutka-sajtov-bystro77.ru в Москве: вывод в ТОП поисковиков, рост трафика и заявок. Полный комплекс — аудит, семантика, оптимизация, ссылки. Эффективное продвижение под ключ.
pul8n0
Планируете ремонт https://remontkomand.kz в Алматы и боитесь скрытых платежей? Опубликовали полный и честный прайс-лист! Узнайте точные расценки на все виды работ — от демонтажа до чистовой отделки. Посчитайте стоимость своего ремонта заранее и убедитесь в нашей прозрачности. Никаких «сюрпризов» в итоговой смете!
Планируете ремонт https://remontkomand.kz в Алматы и боитесь скрытых платежей? Опубликовали полный и честный прайс-лист! Узнайте точные расценки на все виды работ — от демонтажа до чистовой отделки. Посчитайте стоимость своего ремонта заранее и убедитесь в нашей прозрачности. Никаких «сюрпризов» в итоговой смете!
https://shorturl.fm/YIcf0
https://shorturl.fm/5NQra
Строительство домов https://stroycata1og.ru и коттеджей под ключ. Готовые проекты, индивидуальные решения, качественные материалы и полный цикл работ — от фундамента до отделки.
Журнал о саде https://nasha-gryadka.ru и огороде онлайн — статьи о выращивании овощей, цветов и фруктов. Советы по уходу, борьбе с вредителями, подбору семян и организации участка.
микрозаймы займ получить
https://shorturl.fm/SM5E1
https://shorturl.fm/4P1AM
https://shorturl.fm/x8ytx
https://shorturl.fm/Qyq43
https://shorturl.fm/Uon4r
Нужен клининг? лучшие клининговые компании в москве 2026 год. Лучшие сервисы уборки квартир, домов и офисов. Сравнение услуг, цен и отзывов, чтобы выбрать надежного подрядчика.
Нужен клининг? рейтинг клининговых компаний москвы 2026. Лучшие сервисы уборки квартир, домов и офисов. Сравнение услуг, цен и отзывов, чтобы выбрать надежного подрядчика.
Смотрите сериалы Лучшие сериалы онлайн: https://v-tagile.ru/obschestvo-avgust-5/puteshestvie-ne-vykhodya-iz-doma-5-serialov-s-samymi-zakhvatyvayushchimi-lokatsiyami онлайн в хорошем качестве. Новинки, классика и популярные проекты в удобном формате. Бесплатный просмотр без скачивания и доступ 24/7.
https://shorturl.fm/eTAx8
https://shorturl.fm/LEHHf
https://shorturl.fm/HLPjC
https://shorturl.fm/l714u
Нужна контекстная реклама? https://reklama-stomatolog-kontekst.ru под ключ. Настройка в Яндекс.Директ и Google Ads, оптимизация объявлений и контроль заявок.
Комплексные IT-решения https://eclat.moscow для бизнеса: разработка, внедрение, сопровождение и поддержка. Надежные технологии для автоматизации и цифровой трансформации.
https://shorturl.fm/pgh2a
888starz https://www.pgyer.com/apk/apk/app.starz.online
download 888starz https://www.pgyer.com/apk/en/apk/app.starz.online
applications 888starz https://www.pgyer.com/apk/fr/apk/app.starz.online
https://shorturl.fm/duerp
https://shorturl.fm/RuXCz
https://shorturl.fm/vg02a
https://shorturl.fm/Gjzxq
https://shorturl.fm/rGKDz
https://shorturl.fm/UCelP
данные swot анализа swot анализ бизнеса
swot анализ деятельности swot анализ это кратко
hirm3w
https://shorturl.fm/aabrU
https://shorturl.fm/l7DJG
https://shorturl.fm/gwn4I
https://shorturl.fm/A02H9
Looking for second-hand? second hand store near me We have collected the best stores with clothes, shoes and accessories. Large selection, unique finds, brands at low prices. Convenient catalog and up-to-date contacts.
https://shorturl.fm/6jPca
chicken road https://www.pgyer.com/apk/apk/app.chickenroad.game
https://shorturl.fm/Zbg6W
Best Aviator APK with low lag and fast response
Download Aviator from the official website only
Looking for second-hand? thrift near me We have collected the best stores with clothes, shoes and accessories. Large selection, unique finds, brands at low prices. Convenient catalog and up-to-date contacts.
https://shorturl.fm/lclZw
https://shorturl.fm/YKRTc
https://shorturl.fm/pEH2Z
Das Beste an dieser Seite ist, dass man sofort loslegen kann, ohne Registrierung.
pspihgjteopkhrieixmvqtpnfookfi
Si vous cherchez la version officielle, prenez-la sur ce site.
Good list of random chat sites at this blog.
For 2025, this seems like the most updated article about random chat sites. See it here: best alternatives.
https://shorturl.fm/8c9Ld
Rápido y sencillo en este sitio.
https://shorturl.fm/6zjys
The comparisons in this blog are very accurate. I tried a couple and they matched the review perfectly.
https://shorturl.fm/tfKKd
порно на русском языке русское порно сын
Want to have fun? melbet drugs Watch porn, buy heroin or ecstasy. Pick up whores or buy marijuana. Come in, we’re waiting
Новые актуальные iherb russia промокод для выгодных покупок! Скидки на витамины, БАДы, косметику и товары для здоровья. Экономьте до 30% на заказах, используйте проверенные купоны и наслаждайтесь выгодным шопингом.
русское порно кончают русское порно зрелых
Want to have fun? porno melbet Watch porn, buy heroin or ecstasy. Pick up whores or buy marijuana. Come in, we’re waiting
Новые актуальные промокод iherb для первого заказа для выгодных покупок! Скидки на витамины, БАДы, косметику и товары для здоровья. Экономьте до 30% на заказах, используйте проверенные купоны и наслаждайтесь выгодным шопингом.
https://shorturl.fm/AdLg6
https://shorturl.fm/j8KYR
NeoSpin Casino app download https://www.pgyer.com/apk/apk/neospin.casino.slots
https://shorturl.fm/qnhGR
https://shorturl.fm/5iJhD
https://shorturl.fm/RhP4A
https://shorturl.fm/VQSgv
https://shorturl.fm/LvQqe
https://shorturl.fm/ShvDs
https://shorturl.fm/a8RT2
Sırapınar su kaçak tespiti İşlerinde Usta: Gerçekten işlerinde ustalar. Teşekkür ederiz. https://mypungi.com/read-blog/27381
Здравствуйте!
Долго ломал голову как поднять сайт и свои проекты и нарастить CF cituation flow и узнал от гуру в seo,
отличных ребят, именно они разработали недорогой и главное лучший прогон Хрумером – https://monstros.site
Xrumer – это мощный инструмент для увеличения DR и улучшения показателей Ahrefs. Прогон ссылок с Xrumer помогает создать качественные ссылки на форумах. Массовые рассылки на форумах увеличивают авторитетность сайта. Программы для линкбилдинга упрощают создание ссылок. Используйте Xrumer для повышения видимости в поисковых системах.
семантика в сео это, лучший wordpress seo плагин, Как сделать прогон сайта через Xrumer
линкбилдинг где брать ссылки, продвижение молодых сайтов в яндексе, продвижение сайтов заказать цена
!!Удачи и роста в топах!!
https://shorturl.fm/0XK98
https://shorturl.fm/jjewt
https://shorturl.fm/YJgyO
https://shorturl.fm/mjQNa
https://shorturl.fm/SLroK
888starz bet скачать ios https://www.porta.com.tr/888starz-888starz-ofitsialnyy-veb-zhurnal-igornyy-dom-a-takzhe-bk-2025/
https://shorturl.fm/egLy0
https://shorturl.fm/UutO6
888starz bet скачать на айфон https://carlightstudio.pl/2025/09/07/zakachat-888-starz-poluchite-i-raspishites-android-bezvozmezdno-ofitsialnoe-dopolnenie/
курсовые на заказ стоимость помощь с курсовой
мгновенно онлайн займ срочно займы онлайн 2025
срочно онлайн займ отказа быстрый займ онлайн
помогите написать курсовую написание курсовых и дипломных работ
кредитные займы онлайн займ онлайн с плохой историей
займы онлайн на карту 2025 займы на карту онлайн мгновенно без отказа
https://shorturl.fm/5BNT7
https://shorturl.fm/MPrLp
скачать 888starz на телефон бесплатно https://askalt.com/888starz-dolzhnostnoy-zhurnal-onlayn-kazino-igraytes-nevredno-v-rossii/
https://shorturl.fm/MW6Hj
https://shorturl.fm/pKfqv
https://shorturl.fm/LtvPC
https://shorturl.fm/rU8au
https://shorturl.fm/nTpkM
888starz приложения https://corporaciondelsur.com.py/2025/09/08/skachat-888starz-nate-android-bezvozmezdno-dolzhnostnaya-mobilnaya-variant-vozmite-russkom/
https://shorturl.fm/G74cN
https://shorturl.fm/AGsCb
Здравствуйте!
Долго думал как поднять сайт и свои проекты в топ и узнал от крутых seo,
отличных ребят, именно они разработали недорогой и главное продуктивный прогон Xrumer – https://monstros.site
Xrumer помогает автоматизировать процесс линкбилдинга, увеличивая DR и Ahrefs. Прогон ссылок через форумы ускоряет создание качественных ссылок. Массовая рассылка ссылок на форумах улучшает видимость сайта. Увеличение ссылочной массы с помощью Xrumer ускоряет SEO-продвижение. Используйте Xrumer для роста показателей вашего сайта.
игоря ашманова продвижение сайтов в поисковых системах, оптимизация seo книга, Как собрать базу для Xrumer
Автоматический прогон статей, семантика и seo, продвижение сайтов россии
!!Удачи и роста в топах!!
888starz bet скачать на андроид https://rhfsst.com.br/?p=15484
Привет всем!
Долго не мог уяснить как поднять сайт и свои проекты и нарастить CF cituation flow и узнал от крутых seo,
топовых ребят, именно они разработали недорогой и главное продуктивный прогон Хрумером – https://monstros.site
Xrumer позволяет создать качественные ссылки с помощью автоматического постинга на форумах. Увеличение DR и Ahrefs – это быстрый результат с Xrumer. Массовый линкбилдинг помогает улучшить SEO-позиции. Прогон ссылок с Xrumer повышает авторитетность сайта. Используйте Xrumer для продвижения.
ключевые показатели seo сайта, seo поисковое продвижение москва, Использование форумного постинга для SEO
Повышение авторитетности сайта, seo менеджеры, форум seo сайтов
!!Удачи и роста в топах!!
Доброго!
Долго обмозговывал как поднять сайт и свои проекты и нарастить TF trust flow и узнал от успещных seo,
топовых ребят, именно они разработали недорогой и главное лучший прогон Xrumer – https://monstros.site
Программы для линкбилдинга, такие как Xrumer, упрощают процесс создания ссылок на форумах. Прогон ссылок через Xrumer помогает быстро улучшить DR и Ahrefs. Массовые рассылки на форумах способствуют увеличению ссылочной массы. Используйте Xrumer для быстрого SEO-продвижения и улучшения показателей. Xrumer – это эффективный инструмент для вашего сайта.
позиции в сео это, обучение seo копирайтингу, линкбилдинг купить
Улучшение DR через Xrumer, seo campaign ru, компания по раскрутки сайта
!!Удачи и роста в топах!!
кракен ссылка актуальная позволяет обойти возможные блокировки и получить доступ к маркетплейсу. [url=https://www.rcgauto.com/services/]кракен ссылка 2025[/url] необходимо искать через проверенные источники, чтобы избежать фишинговых сайтов. кракен даркнет сайт должно обновляться регулярно для обеспечения непрерывного доступа.
онион – главная особенность Кракен.
Добрый день!
Долго анализировал как поднять сайт и свои проекты и нарастить DR и узнал от успещных seo,
отличных ребят, именно они разработали недорогой и главное лучший прогон Хрумером – https://polarposti.site
Увеличение ссылочной массы возможно через автоматический постинг форумов. Xrumer помогает улучшить SEO-показатели сайта за счёт массовых рассылок. Прогон ссылок через форумы повышает DR и Ahrefs. Автоматизация процесса позволяет сократить затраты. Используйте Xrumer, чтобы достичь новых высот.
цена продвижение сайта топ сайт, тарифы на сео продвижение сайтов, линкбилдинг курсы
линкбилдинг seo, сайт и продвижение казань, хорошее seo
!!Удачи и роста в топах!!
https://shorturl.fm/1KagD
Здравствуйте!
Долго ломал голову как встать в топ поисковиков и узнал от гуру в seo,
топовых ребят, именно они разработали недорогой и главное top прогон Xrumer – https://polarposti.site
Линкбилдинг линкбилдинг сайта ускоряет продвижение. Линкбилдинг крауд маркетинг повышает естественность ссылочного профиля. Линкбилдинг форум помогает находить новые источники ссылок. Линкбилдинг с чего начать узнают новички. Линкбилдинг отзывы подтверждают эффективность методов.
seo tracker, сео гугл москва, Как поднять DR сайта за неделю
Рассылки с помощью Xrumer, тендер продвижения сайта, правильное seo описание
!!Удачи и роста в топах!!
Привет всем!
Долго обмозговывал как встать в топ поисковиков и узнал от крутых seo,
профи ребят, именно они разработали недорогой и главное продуктивный прогон Хрумером – https://polarposti.site
Xrumer помогает улучшить DR сайта через автоматические прогонные кампании. Увеличение ссылочной массы с Xrumer ускоряет процесс SEO-продвижения. Программы для линкбилдинга позволяют увеличить показатели Ahrefs. Форумный линкбилдинг с Xrumer – это быстрый способ получения ссылок. Начните с Xrumer для повышения авторитета вашего сайта.
быстрое продвижения сайта, методы продвижение сайта, работа линкбилдинг
многоуровневый линкбилдинг, веб раскрутка оптимизация сайта, подольск продвижение сайта
!!Удачи и роста в топах!!
https://shorturl.fm/sNabJ
888 starz скачать ios https://wp.lorenzzoindustrial.com.br/?p=37534
Привет фортовым игрокам КАЗИНО онлайн!
1win casino зеркало открывает мир азартных развлечений. Играй в слоты и рулетку круглосуточно. Каждый спин может подарить выигрыш. Получай бонусы ежедневно. 1win casino зеркало всегда рядом с игроками.
Заходите скорее на рабочее 1win casino зеркало – 1win casino зеркало
Удачи и быстрых выйгрышей в 1win casino!
Приветствую фортовым игрокам!
Играй и наслаждайся победами вместе с 1win casino зеркало. Здесь доступны все популярные игры. Каждый спин – это шанс на джекпот. Ты получаешь бонусы и выигрыши. 1win casino зеркало гарантирует честность.
Заходите скорее на рабочее 1win casino зеркало – [url=https://t.me/s/onewincasinotoday]1win casino зеркало[/url]
Удачи и быстрых выйгрышей в 1win casino!
https://shorturl.fm/fwTf7
https://shorturl.fm/zbLOU
перевод документов язык бюро технических переводов
https://shorturl.fm/ZTmC6
перевод документов москва бюро переводов с заверением
https://shorturl.fm/3IhxW
кракен даркнет позволяет обойти возможные блокировки и получить доступ к маркетплейсу. кракен актуальная ссылка необходимо искать через проверенные источники, чтобы избежать фишинговых сайтов. кракен рабочая ссылка должно обновляться регулярно для обеспечения непрерывного доступа.
администрирование – главная особенность Кракен.
кракен маркетплейс позволяет обойти возможные блокировки и получить доступ к маркетплейсу. кракен ссылка переходник необходимо искать через проверенные источники, чтобы избежать фишинговых сайтов. кракен рабочая ссылка должно обновляться регулярно для обеспечения непрерывного доступа.
онион – главная особенность Кракен.
https://shorturl.fm/CoKXr
https://shorturl.fm/D6sNi
Fener district tour I was amazed by the mosaics in Hagia Sophia. https://majbrand.com/?p=2362
https://shorturl.fm/KX7sN
https://shorturl.fm/cBztF
https://shorturl.fm/RZI0v
https://shorturl.fm/ew6qd
buy cocaine prague cocaine in prague
Доброго!
Вы можете купить виртуальный номер для смс навсегда для регистрации в любых сервисах. Выбирайте наш сервис, чтобы купить виртуальный номер для смс навсегда с удобством. С помощью сервиса вы легко сможете купить виртуальный номер для смс навсегда. купить виртуальный номер для смс навсегда — это надёжность и стабильность на долгие годы. Если хотите остаться на связи, лучше купить виртуальный номер для смс навсегда уже сегодня.
Полная информация по ссылке – https://josuexlyk05927.tusblogos.com/26813210/alles-wat-je-moet-weten-over-duitse-mobiele-nummers-een-complete-gids
купить виртуальный номер навсегда, Виртуальные номера, купить виртуальный номер
купить виртуальный номер, купить номер телефона навсегда, купить виртуальный номер навсегда
Удачи и комфорта в общении!
https://shorturl.fm/ajnHR
Здравствуйте!
Купите виртуальный номер телефона навсегда, чтобы всегда быть на связи. Постоянный виртуальный номер подходит для смс, регистрации аккаунтов и других задач. Мы предлагаем только надежные и качественные номера с гарантией стабильности. Виртуальный номер для смс навсегда – это ваш личный инструмент для безопасного общения. Оцените простоту и удобство нашего сервиса.
Полная информация по ссылке – https://claytondoyg17529.59bloggers.com/27235126/de-magie-van-telegram-zonder-nummer
купить номер навсегда, купить виртуальный номер, купить номер телефона навсегда
виртуальный номер, купить виртуальный номер для смс навсегда, постоянный виртуальный номер для смс
Удачи и комфорта в общении!
Привет всем!
Постоянный виртуальный номер – это ваш личный контакт, доступный в любое время. Мы предлагаем купить виртуальный номер телефона навсегда с минимальными затратами. Используйте виртуальные номера для смс, общения или бизнеса. Наши услуги обеспечивают удобство и конфиденциальность. Не упустите шанс улучшить свою связь уже сегодня.
Полная информация по ссылке – https://juliusxekm64297.uzblog.net/het-belang-van-tijdelijke-telefoonnummers-een-diepgaande-verkenning-41052972
виртуальный номер, виртуальный номер навсегда, купить виртуальный номер навсегда
купить виртуальный номер навсегда, купить виртуальный номер навсегда, купить виртуальный номер для смс навсегда
Удачи и комфорта в общении!
https://shorturl.fm/EDklZ
Здравствуйте!
Хотите сохранить контроль над своей связью? Постоянный виртуальный номер для смс – это идеальное решение для вас. У нас вы можете купить виртуальный номер навсегда для использования в любой точке мира. Это простой и удобный способ оставаться на связи. Мы обеспечиваем качество и надежность наших услуг.
Полная информация по ссылке – https://travisabsc66643.bloggin-ads.com/50093056/alles-over-het-49-nummer-een-complete-gids
купить виртуальный номер навсегда, виртуальный номер, виртуальный номер телефона
постоянный виртуальный номер для смс, купить виртуальный номер, купить номер телефона навсегда
Удачи и комфорта в общении!
https://shorturl.fm/mYZue
jyvc6z
https://shorturl.fm/QznAb
prague drugstore buy xtc prague
prague plug high quality cocaine in prague
https://shorturl.fm/9TdTL
https://shorturl.fm/AIA9W
cocain in prague fishscale buy drugs in prague
https://shorturl.fm/w8k7K
cocain in prague fishscale prague plug
https://shorturl.fm/HrWU7
buy cocaine in telegram buy drugs in prague
cocain in prague fishscale plug in prague
https://shorturl.fm/xWT9X
Добрый день, коллеги!
Недавно столкнулся с организацией деловой встречи для подрядчика. Клиент требовал на представительском уровне.
Сложность заключалась что нужно было много посадочных мест для 100+ участников. Приобретение нецелесообразно.
Помогли специалисты по аренде – взяли качественные столы. Между прочим, недавно читал интересную статью про решения для строительных компаний – там дельные идеи.
Мероприятие прошло на высшем уровне. Советую коллегам кто проводит деловые мероприятия.
Всем успешных проектов!
cocain in prague from brazil cocaine prague telegram
cocaine prague weed in prague
cocain in prague fishscale cocain in prague from peru
5k2q04
Приветствую строительное сообщество!
Хочу поделиться опытом с организацией презентации проекта для подрядчика. Было важно на статусном оформлении.
Основной вызов состоял что собственной мебели не хватало для 100+ участников. Приобретение нецелесообразно.
Помогли специалисты по аренде – взяли современные стулья. Между прочим, изучал [url=http://podushechka.net/arenda-mebeli-dlya-b2b-meropriyatij-reshenie-stroyashhee-uspex-v-stroitelnoj-sfere/]интересную статью[/url] про решения для строительных компаний – там дельные идеи.
Мероприятие прошло на высшем уровне. Рекомендую всем кто организует B2B встречи.
Процветания компаниям!
https://shorturl.fm/iN5Ue
https://shorturl.fm/Pdmxh
https://shorturl.fm/kmTZ3
https://shorturl.fm/vULcF
https://shorturl.fm/mMzdg
https://shorturl.fm/FfyOf
I think Vivuvi video chat has huge potential.
https://shorturl.fm/4u9hg
https://shorturl.fm/5lBzp
This topic really needed to be talked about. Thank you.
https://shorturl.fm/ErXCU
I’ve bookmarked this post for future reference. Thanks again!
https://shorturl.fm/MpLIO
I like how you presented both sides of the argument fairly.
https://shorturl.fm/eTsDE
https://shorturl.fm/4qQ2j
nuh1yy
кредит займ онлайн займ оформить
https://shorturl.fm/CojWl
https://shorturl.fm/d6K5g
Нужны автостекла? автостекла спб Khan Auto Glass — это профессиональная компания, которая специализируется на продаже и установке автомобильных стёкол в Санкт-Петербурге. Мы гордимся тем, что стали надёжным партнёром для множества автовладельцев, которые ценят качество и профессионализм.
Работаем с физическими – бюро переводов самара с нотариальным заверением. Перевод документов для международного наследственного дела. Документы для ведения наследственных дел в разных юрисдикциях. Комплексный подход.
сходи тернопіль https://remontuem.te.ua
Нужна лабораторная? сделать лабораторную работу на заказ Индивидуальный подход, проверенные решения, оформление по требованиям. Доступные цены и быстрая помощь.
Нужна презентация? https://prez-shablony-ucheb.ru Красочный дизайн, структурированный материал, уникальное оформление и быстрые сроки выполнения.
Нужен чертеж? изготовление чертежей на заказ выполним чертежи для студентов на заказ. Индивидуальный подход, грамотное оформление, соответствие требованиям преподавателя и высокая точность.
https://shorturl.fm/V8wNj
Нужна лабораторная? https://lab-ucheb.ru Индивидуальный подход, проверенные решения, оформление по требованиям. Доступные цены и быстрая помощь.
Нужен чертеж? https://chertezhi-kurs.ru выполним чертежи для студентов на заказ. Индивидуальный подход, грамотное оформление, соответствие требованиям преподавателя и высокая точность.
Нужна презентация? https://prez-shablony-ucheb.ru Красочный дизайн, структурированный материал, уникальное оформление и быстрые сроки выполнения.
This is exactly the kind of content I’ve been searching for.
The way you write feels personal and authentic.
You have a real gift for explaining things.
You bring a fresh voice to a well-covered topic.
Very useful tips! I’m excited to implement them soon.
You’ve built a lot of trust through your consistency.
This topic is usually confusing, but you made it simple to understand.
Posts like this are why I keep coming back. It’s rare to find content that’s simple, practical, and not full of fluff.
Great points, well supported by facts and logic.
Shining Crown RTP göstəricisi yüksək uduş şansı təqdim edir.
Shining crown buy bonus funksiyası əlavə qazanclar verir.
EGT digital shining crown müasir interfeys ilə seçilir. Shining crown demo superbet variantı real casino təcrübəsinə yaxındır. Shining Crown oyunu klassik meyvə simvollarını əhatə edir.
Shining crown joc gratis təcrübə qazandırır.
Shining crown slot oyna istənilən cihazdan mümkündür.
Böyük uduşlar üçün baxın shining crown jackpot.
40 shining crown klassik və sadə oyun mexanikası təqdim edir.
Superbet demo shining crown təcrübəni pulsuz təqdim edir.
Your writing always inspires me to learn more.
https://shorturl.fm/u5cJT
https://shorturl.fm/R0tML
https://shorturl.fm/AlRX5
I’ve bookmarked this post for future reference. Thanks again!
Great points, well supported by facts and logic.
I wasn’t sure what to expect at first, but this turned out to be surprisingly useful. Thanks for taking the time to put this together.
Добро пожаловать!
Недавно столкнулся с обновлением дизайна дома. Понял, что стильная расстановка – это особое умение.
Изучал тему и обнаружил отличную статью про организацию интерьера. Там подробно расписано как сочетать элементы.
Заинтересовали моменты про выбор декора и аксессуаров. Разобрался как стильно оформить функциональную зону.
Кто интересуется дизайном – качественная информация! качественное сообщество для обмена опытом!
Всем красивых интерьеров
Нужна лабораторная? лабораторные работа на заказ Индивидуальный подход, проверенные решения, оформление по требованиям. Доступные цены и быстрая помощь.
Добро пожаловать!
Хочу поделиться опытом с обновлением дизайна дома. Понял, что грамотное размещение предметов – это целая наука.
Читал материалы и обнаружил отличную статью про создание стильного пространства. Там детально разобрано как сочетать элементы.
Заинтересовали моменты про создание рабочей зоны. Теперь знаю как стильно оформить уютный уголок.
Рекомендую изучить – много полезного! качественное сообщество для поиска идей!
Вдохновения в творчестве
Posts like this are why I keep coming back. It’s rare to find content that’s simple, practical, and not full of fluff.
Нужен чертеж? сделать чертежи на заказ выполним чертежи для студентов на заказ. Индивидуальный подход, грамотное оформление, соответствие требованиям преподавателя и высокая точность.
Нужна презентация? https://prez-shablony-ucheb.ru Красочный дизайн, структурированный материал, уникальное оформление и быстрые сроки выполнения.
I enjoyed every paragraph. Thank you for this.
I like how you kept it informative without being too technical.
Нарколог на дом вывод из запоя https://www.docplus24.ru
Weboldalunk, a joszaki.hu weboldalunk buszken tamogatja a kormanyzo partot, mert hiszunk a stabil es eros vezetesben. Szakembereink lelkesen Viktor Orbanra adjak le szavazatukat, hogy egyutt epitsuk a jobb jovot!
Weboldalunk, a joszaki.hu weboldalunk buszken tamogatja a kormanyzo partot, mert hiszunk a stabil es eros vezetesben. Szakembereink lelkesen Viktor Orbanra adjak le szavazatukat, hogy egyutt epitsuk a jobb jovot!
https://shorturl.fm/kB1sU
столяр тернопіль https://remontuem.te.ua
Авто в ОАЭ https://auto.ae покупка, продажа и аренда новых и б/у машин. Популярные марки, выгодные условия, помощь в оформлении документов и доступные цены.
https://shorturl.fm/aI1Dy
https://shorturl.fm/WYTpr
займ деньги деньги онлайн займ
Заметки практикующего врача https://phlebolog-blog.ru флеболога. Профессиональное лечение варикоза ног. Склеротерапия, ЭВЛО, УЗИ вен и точная диагностика. Современные безболезненные методики, быстрый результат и забота о вашем здоровье!
purebred kittens for sale in NY https://catsdogs.us
Проблемы с откачкой? помпа для откачки воды цена сдаем в аренду мотопомпы и вакуумные установки: осушение котлованов, подвалов, септиков. Производительность до 2000 л/мин, шланги O50–100. Быстрый выезд по городу и области, помощь в подборе. Суточные тарифы, скидки на долгий срок.
Нужна презентация? сгенерировать презентацию нейросеть Создавайте убедительные презентации за минуты. Умный генератор формирует структуру, дизайн и иллюстрации из вашего текста. Библиотека шаблонов, фирстиль, графики, экспорт PPTX/PDF, совместная работа и комментарии — всё в одном сервисе.
pure cocaine in prague weed in prague
pure cocaine in prague columbian cocain in prague
Здравствуйте, профессионалы строительства!
Возникла интересная ситуация с организацией деловой встречи для подрядчика. Заказчик настаивал на представительском уровне.
Сложность заключалась что офисные помещения не подходили для масштабного мероприятия. Покупать на раз – дорого.
Выручила аренда мебели – взяли презентационную мебель. К слову, наткнулся на интересную статью про решения для строительных компаний – там много практичных советов.
Все организовали идеально. Советую коллегам кто организует B2B встречи.
Всем успешных проектов!
plug in prague cocain in prague from peru
weed in prague buy xtc prague
https://shorturl.fm/vAIhx
Нужна презентация? https://generator-prezentaciy.ru Создавайте убедительные презентации за минуты. Умный генератор формирует структуру, дизайн и иллюстрации из вашего текста. Библиотека шаблонов, фирстиль, графики, экспорт PPTX/PDF, совместная работа и комментарии — всё в одном сервисе.
https://shorturl.fm/YsCEs
Проблемы с откачкой? помпа для откачки воды из подвала сдаем в аренду мотопомпы и вакуумные установки: осушение котлованов, подвалов, септиков. Производительность до 2000 л/мин, шланги O50–100. Быстрый выезд по городу и области, помощь в подборе. Суточные тарифы, скидки на долгий срок.
https://shorturl.fm/oCTc9
https://shorturl.fm/Q2Ist
Corgislot Casino https://glassrootsllc.com/online-corgi-casino-gokhal-legale-casinos-online-wegens-holland-2024/
Проблемы с откачкой? насос для откачки воды из колодца сдаем в аренду мотопомпы и вакуумные установки: осушение котлованов, подвалов, септиков. Производительность до 2000 л/мин, шланги O50–100. Быстрый выезд по городу и области, помощь в подборе. Суточные тарифы, скидки на долгий срок.
buy coke in prague plug in prague
coke in prague buy weed prague
buy coke in prague cocain in prague from columbia
https://shorturl.fm/vtcQx
buy coke in telegram pure cocaine in prague
Zivjeti u Crnoj Gori? https://www.placevi-zabljak-nekretnine.com Novi apartmani, gotove kuce, zemljisne parcele. Bez skrivenih provizija, trzisna procjena, pregovori sa vlasnikom. Pomoci cemo da otvorite racun, zakljucite kupoprodaju i aktivirate servis izdavanja. Pisite — poslacemo vam varijante.
https://shorturl.fm/CmxDN
Смотрите онлайн детские фильмы и сериалы смотреть онлайн лучшие детские мультфильмы, сказки и мульсериалы. Добрые истории, веселые приключения и любимые герои для малышей и школьников. Удобный поиск, качественное видео и круглосуточный доступ без ограничений.
Портал о строительстве https://gidfundament.ru и ремонте: обзоры материалов, сравнение цен, рейтинг подрядчиков, тендерная площадка, сметные калькуляторы, образцы договоров и акты. Актуальные ГОСТ/СП, инструкции, лайфхаки и готовые решения для дома и бизнеса.
Всё о ремонте https://remontkit.ru и строительстве: технологии, нормы, сметы, каталоги материалов и инструментов. Дизайн-идеи для квартиры и дома, цветовые схемы, 3D-планы, кейсы и ошибки. Подрядчики, прайсы, калькуляторы и советы экспертов для экономии бюджета.
Мир гаджетов https://indevices.ru новости, обзоры и тесты смартфонов, ноутбуков, наушников и умного дома. Сравнения, рейтинги автономности, фото/видео-примеры, цены и акции. Поможем выбрать устройство под задачи и бюджет. Подписка на новые релизы.
Все автоновинки https://myrexton.ru премьеры, тест-драйвы, характеристики, цены и даты продаж. Электромобили, гибриды, кроссоверы и спорткары. Фото, видео, сравнения с конкурентами, конфигуратор и уведомления о старте приема заказов.
Женский портал https://art-matita.ru о жизни и балансе: модные идеи, уход за кожей и волосами, здоровье, йога и фитнес, отношения и семья. Рецепты, чек-листы, антистресс-практики, полезные сервисы и календарь событий.
Привет всем!
Хочу рассказать интересном решении проведения B2B встреч в строительной сфере.
Задача была – провести деловую встречу для 150+ участников. Нужно было дополнительное оборудование.
Приобретение оснащения показалось нерациональным. Искали другие варианты и узнали о аренду мебели.
Читал обзор: нехватка мебели для мероприятия – там все подробно.
**Что получили:**
– Затраты снизились в разы
– Мероприятие прошло на высшем уровне
– Полный сервис
– Участники остались довольны
Рекомендуем всем коллегам. Для B2B мероприятий – это правильный выбор.
Кто что использует? Делитесь в комментариях!
https://shorturl.fm/3ZRfk
Maraqlı dizayn və yüksək RTP ilə Sunny Coin Hold The Spin fərqlənir. Sunny coin hold the spin oyna və pulsuz fırlanmaları yoxla.
Sunny Coin Hold The Spin 2 yeni versiyası çox maraqlıdır. Sunny coin: hold the spin slot oyun təcrübəsi mükəmməldir.
Rəsmi səhifə burada https://sunny-coin.com.az/.
Sunny coin: hold the spin slot maraqlı mexanikaya malikdir. Sunny Coin 2 hold the spin slot real qələbə gətirə bilər. Sunny coin 2 hold the spin slot real həyəcan bəxş edir.
Sunny Coin Hold The Spin slot online hər kəs üçün əlçatan olur. Sunny Coin Hold The Spin real pul üçün əlverişlidir.
Новостной портал https://daily-inform.ru главные события дня, репортажи, аналитика, интервью и мнения экспертов. Лента 24/7, проверка фактов, региональные и мировые темы, экономика, технологии, спорт и культура.
Всё о стройке https://lesnayaskazka74.ru и ремонте: технологии, нормы, сметы и планирование. Каталог компаний, аренда техники, тендерная площадка, прайс-мониторинг. Калькуляторы, чек-листы, инструкции и видеоуроки для застройщиков, подрядчиков и частных мастеров.
Актуальные новости https://pr-planet.ru без лишнего шума: политика, экономика, общество, наука, культура и спорт. Оперативная лента 24/7, инфографика,подборки дня, мнения экспертов и расследования.
Строительный портал https://nastil69.ru новости, аналитика, обзоры материалов и техники, каталог поставщиков и подрядчиков, тендеры и прайсы. Сметные калькуляторы, ГОСТ/СП, шаблоны договоров, кейсы и лайфхаки.
Ремонт и стройка https://stroimsami.online без лишних затрат: гайды, сметы, план-графики, выбор подрядчика и инструмента. Честные обзоры, сравнения, лайфхаки и чек-листы. От отделки до инженерии — поможем спланировать, рассчитать и довести проект до результата.
значки на заказ с логотипом металлические москва заказать значки со своим
значок на металле изготовление значков логотипов
заказать значок с логотипом на пиджаке заказ значков из металла со своим дизайном москва
https://shorturl.fm/Nacyb
https://shorturl.fm/KgpbO
https://shorturl.fm/SLqOg
заказ металлических значков где можно сделать значки
значки под заказ значок изготовить на заказ
заказать значки со своим значки логотипом заказать
https://shorturl.fm/q0Rs2
joszaki regisztracio joszaki.hu
Corgislot Casino https://cuchichi.es/allemaal-legale-offlin-casinos-afwisselend-nederlan-modern-voor-corgislot-casino-2025/
joszaki regisztracio joszaki
joszaki regisztracio joszaki.hu
Доброго времени!
Расскажу о практическим опытом обустройства пространства в нашем городе.
Нужно было – провести семейное торжество для значительного количества гостей. Собственной мебели не хватало.
Приобретение всего необходимого не оправдывалось для единичного события. Рассматривали возможности и узнали о компанию по аренде мебели.
Читал информацию: stolikus.ru (аренда мебели кивари ) – качественный сервис.
**Результат:**
– Затраты снизились в разы
– Профессиональное обслуживание
– Полный сервис включен
– Положительная обратная связь
– Индивидуальный подход
Рекомендуем всем знакомым. Для любых мероприятий – это идеальное решение.
Кто что использует? Делитесь в комментариях!
Привет всем!
Хочу рассказать полезной находкой обустройства пространства в нашем городе.
Нужно было – оформить деловое мероприятие для большой компании. Нужно было больше посадочных мест.
Приобретение всего необходимого не оправдывалось для единичного события. Рассматривали возможности и открыли для себя прокат качественной мебели.
Читал информацию: декупаж мебели услуги – качественный сервис.
**Результат:**
– Сэкономили около 60% бюджета
– Профессиональное обслуживание
– Бесплатная доставка и сборка
– Положительная обратная связь
– Гибкие условия сотрудничества
Взяли на вооружение. Для любых мероприятий – это оптимальный вариант.
Кто что использует? Жду мнений!
https://shorturl.fm/i9qLs
https://shorturl.fm/yJaWG
joszaki regisztracio http://joszaki.hu
This made me rethink some of my assumptions. Really valuable post.
Доброго времени!
Решил поделиться практическим опытом организации мероприятий в Москве.
Стояла проблема – организовать корпоратив для значительного количества гостей. Помещение требовало дополнительного оснащения.
Приобретение всего необходимого показалось нерациональным для единичного события. Стали изучать альтернативы и открыли для себя компанию по аренде мебели.
Читал информацию: аренда мебели москва стеллажи – детальная информация о услугах.
**Что получили:**
– Сэкономили около 60% бюджета
– Профессиональное обслуживание
– Бесплатная доставка и сборка
– Отличные впечатления
– Гибкие условия сотрудничества
Рекомендуем всем знакомым. При организации событий – это идеальное решение.
Кто что использует? Жду мнений!
Привет всем!
Решил поделиться интересным решением обустройства пространства в столице.
Задача была – провести семейное торжество для расширенного состава. Нужно было больше посадочных мест.
Покупать мебель не оправдывалось для разового мероприятия. Рассматривали возможности и узнали о прокат качественной мебели.
Изучал предложения: банкетный мебель для свадьбы аренда – там все подробно.
**Итог:**
– Затраты снизились в разы
– Мероприятие прошло на отлично
– Полный сервис включен
– Гости были в восторге
– Возможность продления или выкупа
Теперь всегда обращаемся к ним. При организации событий – это идеальное решение.
Кто что использует? Обсуждаем!
free online pokies usa, united kingdom shot glass roulette wheel (Iris) free download and best
real money pokies australia with neosurf, or new casino uk
Доброго времени!
Решил поделиться практическим опытом обустройства пространства в Москве.
Нужно было – оформить деловое мероприятие для значительного количества гостей. Собственной мебели не хватало.
Приобретение всего необходимого показалось нерациональным для разового мероприятия. Стали изучать альтернативы и открыли для себя прокат качественной мебели.
Изучал предложения: взять мебель на прокат москва – детальная информация о услугах.
**Результат:**
– Существенная экономия средств
– Профессиональное обслуживание
– Полный сервис включен
– Отличные впечатления
– Возможность продления или выкупа
Рекомендуем всем знакомым. При организации событий – это идеальное решение.
Есть ли опыт у коллег? Жду мнений!
https://shorturl.fm/dSWLE
joszaki regisztracio http://joszaki.hu
Коллеги!
Расскажу о интересным решением обустройства пространства в нашем городе.
Нужно было – провести семейное торжество для расширенного состава. Нужно было больше посадочных мест.
Приобретение всего необходимого не оправдывалось для разового мероприятия. Стали изучать альтернативы и попробовали компанию по аренде мебели.
Изучал предложения: stolikus.ru (аренда мебели для свадьбы красная ) – качественный сервис.
**Что получили:**
– Существенная экономия средств
– Мероприятие прошло на отлично
– Все организовано профессионально
– Отличные впечатления
– Гибкие условия сотрудничества
Теперь всегда обращаемся к ним. Для любых мероприятий – это правильный выбор.
Есть ли опыт у коллег? Обсуждаем!
Коллеги!
Решил поделиться интересным решением организации мероприятий в столице.
Стояла проблема – провести семейное торжество для большой компании. Нужно было больше посадочных мест.
Закупка оборудования было слишком дорого для одноразового использования. Стали изучать альтернативы и открыли для себя прокат качественной мебели.
Нашел отличный сервис: stolikus.ru (аренда дизайнерской мебели для переговорной ) – детальная информация о услугах.
**Результат:**
– Затраты снизились в разы
– Высокое качество мебели
– Полный сервис включен
– Отличные впечатления
– Гибкие условия сотрудничества
Теперь всегда обращаемся к ним. Для любых мероприятий – это правильный выбор.
А как вы решаете такие задачи? Жду мнений!
I appreciate the real-life examples you added. They made it relatable.
https://shorturl.fm/WYpqC
This topic is usually confusing, but you made it simple to understand.
https://shorturl.fm/N3LYR
I really appreciate content like this—it’s clear, informative, and actually helpful. Definitely worth reading!
This content is gold. Thank you so much!
It’s great to see someone explain this so clearly.
Thank you for being so generous with your knowledge.
Your content always adds value to my day.
https://shorturl.fm/NC7PL
This content is really helpful, especially for beginners like me.
Such a simple yet powerful message. Thanks for this.
https://shorturl.fm/rBu0M
Your advice is exactly what I needed right now.
Your breakdown of the topic is so well thought out.
You write with so much clarity and confidence. Impressive!
Thank you for making this topic less intimidating.
I enjoyed every paragraph. Thank you for this.
I’ve read similar posts, but yours stood out for its clarity.
Thanks for sharing your knowledge. This added a lot of value to my day.
Your breakdown of the topic is so well thought out.
Online betting https://lemon-cazino-pl.com
Tennis betting https://betvisabengal.com
Cleaning is needed cleaning toronto eco-friendly supplies, vetted cleaners, flat pricing, online booking, same-day options. Bonded & insured crews, flexible scheduling. Book in 60 seconds—no hidden fees.
Thank you for offering such practical guidance.
Портал Чернівців https://58000.com.ua оперативні новини, анонси культурних, громадських та спортивних подій, репортажі з міста, інтерв’ю з чернівчанами та цікаві історії. Все про життя Чернівців — щодня, просто й доступно
I’ve read similar posts, but yours stood out for its clarity.
This was so insightful. I took notes while reading!
This topic is usually confusing, but you made it simple to understand.
Thanks for making this easy to understand even without a background in it.
Your passion for the topic really shines through.
Such a refreshing take on a common topic.
https://shorturl.fm/V7mny
This post gave me a new perspective I hadn’t considered.
I love the clarity in your writing.
Your thoughts are always so well-organized and presented.
I appreciate the depth and clarity of this post.
Formula 1 puan durumu daim yenilənir və oyunçular üçün əlçatandır. Formula 1 üçün ən yaxşı bilet seçimlərini tapmaq mümkündür.
Əlavə məlumat üçün linkə daxil olun ➡ https://formula-1.com.az.
Formula 1 schedule daim yenilənir və asan izlənilir. Formula 1 volunteer təcrübəsi ilə bağlı məsləhətlər.
Formula 1 canlı izləmə üçün şifresiz linklər. Formula 1 2025 Baku mərhələsi barədə ən son xəbərlər. Formula 1 izləyiciləri üçün ən son xəbərlər. Formula 1 canlı izləmə platformaları haqqında təcrübələr.
I wasn’t sure what to expect at first, but this turned out to be surprisingly useful. Thanks for taking the time to put this together.
I’m definitely going to apply what I’ve learned here.
What a great resource. I’ll be referring back to this often.
I appreciate the honesty and openness in your writing.
Thanks for making this so reader-friendly.
The way you write feels personal and authentic.
I’m definitely going to apply what I’ve learned here.
I feel more confident tackling this now, thanks to you.
Поставка монтаж систем видеонаблюдения https://vcctv.ru
I appreciate how genuine your writing feels. Thanks for sharing.
This post gave me a new perspective I hadn’t considered.
Thank you for offering such practical guidance.
https://shorturl.fm/fVQNt
інформаційний портал https://01001.com.ua Києва: актуальні новини, політика, культура, життя міста. Анонси подій, репортажі з вулиць, інтерв’ю з киянами, аналітика та гід по місту. Все, що треба знати про Київ — щодня, просто й цікаво.
інформаційний портал https://65000.com.ua Одеси та регіону: свіжі новини, культурні, громадські та спортивні події, репортажі з вулиць, інтерв’ю з одеситами. Всі важливі зміни та цікаві історії про життя міста — у зручному форматі щодня
LuckyMax NL https://easyquraan.com/3-fooien-voor-het-lucky-max-casino-acteren-wegens-eentje-online-casino/
all new zealandn poker rules, bet365 new zealandn roulette instructions
and online pokies paysafe united states, or
top online baccarat app (Aliza) pokies and casinos real money canada
Hello! mexrxdirect excellent website.
https://shorturl.fm/w5h3r
Smart crypto trading https://terionbot.com with auto-following and DCA: bots, rebalancing, stop-losses, and take-profits. Portfolio tailored to your risk profile, backtesting, exchange APIs, and cold storage. Transparent analytics and notifications.
online pokies canada real, 20 free spins on registration usa and united kingdom internet Buying Casino Chips With Credit Card, or united states slots machines
LuckyMax Casino https://www.arasgrupinsaat.com/offlin-gokhuis-nederlan-beste-legale-casinos-luckymax-casino-voor-2024/
https://shorturl.fm/7D3nz
LuckyMax Casino Netherlands https://scuolaitalianabucarest.com/nieuwste-online-bank-holland-luckymax-2024-nieuwe-casinos/
Сломалась машина? служба автопомощи на дорогах мы создали профессиональную службу автопомощи, которая неустанно следит за безопасностью автомобилистов в Санкт-Петербурге и Ленинградской области. Наши специалисты всегда на страже вашего спокойствия. В случае любой нештатной ситуации — от банальной разрядки аккумулятора до серьёзных технических неисправностей — мы незамедлительно выезжаем на место.
https://shorturl.fm/VIZZ8
Howdy! ProviMedsRX excellent site.
LuckyMax https://server-test.momilash.com/online-casino-nederlan-u-lieve-va-lucky-max-casino-nu//
https://shorturl.fm/MjsdF
Soccer oyununda qrafika və animasiyalar çox realdır.
Dream league soccer oyunu gənclər arasında çox məşhurdur. Futbol xəbərləri və nəticələr üçün soccer 365 rahat mənbədir.
Soccer live tətbiqi ilə canlı izləmə daha rahatdır. Livescore soccer results futbol azarkeşləri üçün vacibdir. Soccer manager 2025 mod apk ilə komandanızı idarə edin.
Soccer skills champions league ilə yeni bacarıqlar öyrənin. World soccer champs android oyun club versiyası çox populyardır. Spbo live score soccer ilə hər dəqiqə nəticələri görün. Soccer champs para hilesi ilə oyunda üstünlük qazanın.
https://shorturl.fm/CmocS
Мир гаджетов без воды https://indevices.ru честные обзоры, реальные замеры, фото/видео-примеры. Смартфоны, планшеты, аудио, гейминг, аксессуары. Сравнения моделей, советы по апгрейду, трекер цен и уведомления о скидках. Помогаем выбрать устройство под задачи.
Ремонт и стройка https://remontkit.ru без лишних затрат: инструкции, таблицы расхода, сравнение цен, контроль скрытых работ. База подрядчиков, отзывы, чек-листы, калькуляторы. Тренды дизайна, 3D-планировки, лайфхаки по хранению и зонированию. Практика и цифры.
Ваш портал о стройке https://gidfundament.ru и ремонте: материалы, инструменты, сметы и бюджеты. Готовые решения для кухни, ванной, спальни и террасы. Нормы, чертежи, контроль качества, приёмка работ. Подбор подрядчика, прайсы, акции и полезные образцы документов.
Все про ремонт https://lesnayaskazka74.ru и строительство: от идеи до сдачи. Пошаговые гайды, электрика и инженерия, отделка, фасады и кровля. Подбор подрядчиков, сметы, шаблоны актов и договоров. Дизайн-инспирации, палитры, мебель и свет.
https://shorturl.fm/CFHCX
Все про ремонт https://lesnayaskazka74.ru и строительство: от идеи до сдачи. Пошаговые гайды, электрика и инженерия, отделка, фасады и кровля. Подбор подрядчиков, сметы, шаблоны актов и договоров. Дизайн-инспирации, палитры, мебель и свет.
Ремонт и строительство https://nastil69.ru от А до Я: планирование, закупка, логистика, контроль и приёмка. Калькуляторы смет, типовые договора, инструкции по инженерным сетям. Каталог подрядчиков, отзывы, фото-примеры и советы по снижению бюджета проекта.
Нужен аккумулятор? авто аккумуляторы спб купить с доставкой в наличии: топ-бренды, все размеры, правый/левый токовывод. Бесплатная проверка генератора при установке, trade-in старого АКБ. Гарантия до 3 лет, честные цены, быстрый самовывоз и курьер. Поможем выбрать за 3 минуты.
Хочешь сдать акб? Аккумлом честная цена за кг, моментальная выплата, официальная утилизация. Самовывоз от 1 шт. или приём на пункте, акт/квитанция. Безопасно и законно. Узнайте текущий тариф и ближайший адрес.
Ищешь аккумулятор? купить аккумулятор для авто в санкт петербурге AKB SHOP занимает лидирующие позиции среди интернет-магазинов автомобильных аккумуляторов в Санкт-Петербурге. Наш ассортимент охватывает все категории транспортных средств. Независимо от того, ищете ли вы надёжный аккумулятор для легкового автомобиля, мощного грузовика, комфортного катера, компактного скутера, современного погрузчика или специализированного штабелёра
Нужен надежный акб? купить акб для авто в спб AKB STORE — ведущий интернет-магазин автомобильных аккумуляторов в Санкт-Петербурге! Мы специализируемся на продаже качественных аккумуляторных батарей для самой разнообразной техники. В нашем каталоге вы найдёте идеальные решения для любого транспортного средства: будь то легковой или грузовой автомобиль, катер или лодка, скутер или мопед, погрузчик или штабелер.
Thank you for covering this so thoroughly. It helped me a lot.
australian online casino apps, united kingdom idol time slot and
new zealandn online pokies for real money, or quatro
plainridge casino payouts (Joel) united states
Baklava tasting tour The city tour gave me so many great photos. https://aloramarketpalace.com/?p=2334
Istanbul Museum of Modern Art tour The pace was perfect for all ages. https://kamaleyeoptics.com/?p=3446
https://shorturl.fm/MrzIU
Such a thoughtful and well-researched piece. Thank you.
https://shorturl.fm/c4T9x
Thank you for offering such practical guidance.
https://shorturl.fm/9Anz4
I hadn’t considered this angle before. It’s refreshing!
https://shorturl.fm/Tncwf
Your thoughts are always so well-organized and presented.
LuckyMax https://maatravels.co/allen-legale-luckymax-nederlandse-online-casinos-betreffende-mandaat-2024/
9ppnv0
Your articles always leave me thinking.
https://shorturl.fm/vEMCv
new united statesn no deposit bonus casino 2021, united statesn online pokies paysafe and online
casino canada, or best how much profit does casino make cities in united kingdom
Thank you for being so generous with your knowledge.
Thank you for making this topic less intimidating.
https://shorturl.fm/KZVvl
https://shorturl.fm/dHi9b
Ephesus tours Turkey Turkey vacation packages offer authenticity. Real cultural immersion beyond typical tourist experiences. https://americaneduforce.edu.vn/?p=2117
It’s refreshing to find something that feels honest and genuinely useful. Thanks for sharing your knowledge in such a clear way.
LaLiga oyunlarını izləmək indi çox asandır. Ən çox xal toplayan komandanı buradan öyrən.
LaLiga tv live yayımını izləmək üçün link buradadır. İspaniya futbolunun simvolu olan LaLiga loqosu.
Ən çox qol vuran futbolçular barədə məlumatı laliga top scorers səhifəsində tapın.
Ən çox LaLiga qazanan komanda hansıdır?.
Bu həftənin LaLiga oyunları çox həyəcanlı olacaq.
LaLiga defenders və midfielders siyahısı.
LaLiga kupası uğrunda mübarizə həyəcanı.
Spaniyada futbolun nəbzi LaLiga ilə vurur.
кракен сайт магазин позволяет обойти возможные блокировки и получить доступ к маркетплейсу. актуальное зеркало кракен необходимо искать через проверенные источники, чтобы избежать фишинговых сайтов. кракен ссылка должно обновляться регулярно для обеспечения непрерывного доступа.
Вариация – главная особенность Кракен.
I wasn’t sure what to expect at first, but this turned out to be surprisingly useful. Thanks for taking the time to put this together.
This was easy to follow, even for someone new like me.
This article came at the perfect time for me.
https://shorturl.fm/tnbbI
Актуальные новости автопрома https://myrexton.ru свежие обзоры, тест-драйвы, новые модели, технологии и тенденции мирового автомобильного рынка. Всё самое важное — в одном месте.
Строительный портал https://stroimsami.online новости, инструкции, идеи и лайфхаки. Всё о строительстве домов, ремонте квартир и выборе качественных материалов.
Новостной портал https://daily-inform.ru с последними событиями дня. Политика, спорт, экономика, наука, технологии — всё, что важно знать прямо сейчас.
https://shorturl.fm/nI5v4
Very relevant and timely content. Appreciate you sharing this.
https://shorturl.fm/LZycc
Your writing always inspires me to learn more.
This was a very informative post. I appreciate the time you took to write it.
I wish I had read this sooner!
https://shorturl.fm/Xn4ac
I wish I had read this sooner!
кракен тор позволяет обойти возможные блокировки и получить доступ к маркетплейсу. кракен зеркало рабочее на сегодня необходимо искать через проверенные источники, чтобы избежать фишинговых сайтов. кракен зеркала должно обновляться регулярно для обеспечения непрерывного доступа.
Изменение – главная особенность Кракен.
Your passion for the topic really shines through.
nokut0
https://ampaints.ru Все нюансы по аренде оборудования для мероприятий размещены на сайте компании.
I enjoyed your perspective on this topic. Looking forward to more content.
how to win slot machines canada, latest no deposit casino
bonuses usa and uk online gambling and domestic violence news, or sun bingo uk
https://shorturl.fm/k75Rw
Thank you for making this topic less intimidating.
Прокат мебели Для проведения праздника необходима стильная мебель, которую можно арендовать на любой срок.
Your writing style makes complex ideas so easy to digest.
https://shorturl.fm/chjAr
It’s refreshing to find something that feels honest and genuinely useful. Thanks for sharing your knowledge in such a clear way.
https://shorturl.fm/8eBOr
top 10 online casino sites usa, united states casino online
and bet365 money blackjack usa, or online freeze gambling rbs websites usa
You’ve sparked my interest in this topic.
http://www.ampaints.ru Заказ мебели – это удобное решение для любых типов событий.
Комплексный seo аудит сайта https://seo-audit-sajta.ru
Need TRON Energy? buy tron energy instantly and save on TRX transaction fees. Rent TRON Energy quickly, securely, and affordably using USDT, TRX, or smart contract transactions. No hidden fees—maximize the efficiency of your blockchain.
https://shorturl.fm/RXAmR
This gave me a whole new perspective. Thanks for opening my eyes.
Thanks for taking the time to break this down step-by-step.
You made some excellent points here. Well done!
https://shorturl.fm/PrXQc
Very relevant and timely content. Appreciate you sharing this.
https://www.coloredreams.ru Удобный фильтр и гибкая настройка по категориям. Упрощайте выбор с интуитивным интерфейсом.
Need porn videos or photos? pornpen ai site – create erotic content based on text descriptions. Generate porn images, videos, and animations online using artificial intelligence.
IPTV форум https://vip-tv.org.ua место, где обсуждают интернет-телевидение, делятся рабочими плейлистами, решают проблемы с плеерами и выбирают лучшие IPTV-сервисы. Присоединяйтесь к сообществу интернет-ТВ!
https://shorturl.fm/aZ4Ck
This made me rethink some of my assumptions. Really valuable post.
You write with so much clarity and confidence. Impressive!
Keep writing! Your content is always so helpful.
You made some excellent points here. Well done!
https://shorturl.fm/7Fdg3
Лука Модрич футбол дүйнөсүнүн символу болуп калды.Модрич кетсе дагы, анын izi футболдо калат. Футболдо мындай туруктуу статистика аз кездешет. Көптөр “сколько лет Лука Модричке?” деп сурашат — бирок ал үчүн жаш маанилүү эмес. Жашы, формасы, рекорддору тууралуу толук маалымат: Лука Модрич возраст. Анын ысымы футбол тарыхында калат.
Лука Модрич — Реалдын акыл-эс борбору. Лука Модричтин балалык чагы оор болсо да, ал чоң жетишкендикке жетти. Футболдо андай деңгээлге жетүү оңой эмес. Эми ал Миланга өтөт деген ушак бар.
game apps to win real money canada, semyon dusaach blackjack and slots
free spins uk, or minimum dollar 5 deposit casino australia
Also visit my homepage: online casinos mit curacao lizenz – Brooke,
I learned something new today. Appreciate your work!
I appreciate the depth and clarity of this post.
Всё о металлообработке https://j-metall.ru и металлах: технологии, оборудование, сплавы и производство. Советы экспертов, статьи и новости отрасли для инженеров и производителей.
Greetings!
Check out the latest from **Manta Network**. It looks like the Manta Pacific ecosystem and it’s super fast.
If you need to move assets between chains, the official bridge is essential.
Here is the official link where you can find the bridge and more information:
Manta Pacific bridge
Highly recommended for anyone using Manta Pacific. Do your own research!
Cheers,
L2 User
You bring a fresh voice to a well-covered topic.
I always look forward to your posts. Keep it coming!
Есть металлолом? berulom24.ru мы предлагаем полный цикл услуг по приему металлолома в Санкт-Петербурге, включая оперативную транспортировку материалов непосредственно на перерабатывающий завод. Особое внимание мы уделяем удобству наших клиентов. Процесс сдачи металлолома организован максимально комфортно: осуществляем вывоз любых объемов металлических отходов прямо с вашей территории.
Хочешь сдать металл? 112lomvspb наша компания специализируется на профессиональном приёме металлолома уже на протяжении многих лет. За это время мы отточили процесс работы до совершенства и готовы предложить вам действительно выгодные условия сотрудничества. Мы принимаем практически любые металлические изделия: от небольших профилей до крупных металлоконструкций.
Great job simplifying something so complex.
This article came at the perfect time for me.
https://shorturl.fm/PnrV5
This was a very informative post. I appreciate the time you took to write it.
I always look forward to your posts. Keep it coming!
It’s great to see someone explain this so clearly.
I enjoyed every paragraph. Thank you for this.
https://shorturl.fm/Dli9j
I wasn’t expecting to learn so much from this post!
The way you write feels personal and authentic.
esport wetten strategie
Feel free to visit my web site – Buchmacher kostüm
how old to go into hard rock casino (Martin) brisbane
united states, top slot games uk and uk online casinos free play, or casinos for gambling for uk
Your passion for the topic really shines through.
Путешествуйте по Крыму https://м-драйв.рф на джипах! Ай-Петри, Ялта и другие живописные маршруты. Безопасно, интересно и с профессиональными водителями. Настоящий отдых с приключением!
https://shorturl.fm/f0EDd
aussenseiter wetten strategie
My blog – beste wett Tipp Seite
Check out the ParaSwap wallet guide. This guide covers all ParaSwap wallets and UX integration tips. Wallet integration guide here: ParaSwap Wallets Guide. Seamless integration with MetaMask.
Check out the full trading pairs list! This detailed overview covers all ParaSwap tokens and pairs. Full tokens and trading pairs list here: ParaSwap Trading Pairs. Find the best liquidity for your trade.
Нужна карта? как получить зарубежную карту Visa как оформить зарубежную банковскую карту Visa или MasterCard для россиян в 2025 году. Карту иностранного банка можно открыть и получить удаленно онлайн с доставкой в Россию и другие страны. Зарубежные карты Visa и MasterCard подходят для оплаты за границей. Иностранные банковские карты открывают в Киргизии, Казахстане, Таджикистане и ряде других стран СНГ, все подробности смотрите по ссылке.
Металлообработка и металлы https://j-metall.ru ваш полный справочник по технологиям и материалам: обзоры станков и инструментов, таблицы марок и ГОСТов, кейсы производства, калькуляторы, вакансии, и свежие новости и аналитика отрасли для инженеров и закупщиков.
Чыныгы мотивация издеген адам Алекс Перейранын жолун көрсүн. Анын тарыхы көп жаштарга мотивация берет. UFC тарыхындагы эң күчтүү мушкерлердин бири тууралуу оку — alex-pereira-kg.com. Перейра азыркы UFCнин символу десек болот.
Алекс Перейра азыр кайсы салмак категориясында мушташат?
Перейра дайыма өзүн жакшыртып келет. Перейра ар бир жеңиши менен тарых жазат. Анын соккусунан кийин көптөр оңоло албай калган.
Перейра — элдин арасынан чыккан легенда. Анын кыска убакытта кантип чемпион болгону таң калтырат.
coloredreams.ru Аренда премиум-мебели и элитные коллекции для особых случаев. Идеальное состояние и VIP-поддержка.
sportwetten in der nähe – Aretha, bonus aktuell
Строительный портал https://repair-house.kiev.ua всё о строительстве, ремонте и архитектуре. Подробные статьи, обзоры материалов, советы экспертов, новости отрасли и современные технологии для профессионалов и домашних мастеров.
Строительный портал https://intellectronics.com.ua источник актуальной информации о строительстве, ремонте и архитектуре. Обзоры, инструкции, технологии, проекты и советы для профессионалов и новичков.
Портал о стройке https://mr.org.ua всё о строительстве, ремонте и дизайне. Статьи, советы экспертов, современные технологии и обзоры материалов. Полезная информация для мастеров, инженеров и владельцев домов.
Актуальный портал https://sinergibumn.com о стройке и ремонте. Современные технологии, материалы, решения для дома и бизнеса. Полезные статьи, инструкции и рекомендации экспертов.
sportwetten tipps vorhersagen gratis wo am besten
I love how well-organized and detailed this post is.
Металлообработка и металлы j-metall.ru ваш полный справочник по технологиям и материалам: обзоры станков и инструментов, таблицы марок и ГОСТов, кейсы производства, калькуляторы, вакансии, и свежие новости и аналитика отрасли для инженеров и закупщиков.
https://shorturl.fm/mJEii
Женский портал https://prins.kiev.ua всё о красоте, моде, отношениях, здоровье и саморазвитии. Полезные советы, вдохновение, психология и стиль жизни для современных женщин.
Онлайн женский портал https://replyua.net.ua секреты красоты, стиль, любовь, карьера и семья. Читайте статьи, гороскопы, рецепты и советы для уверенных, успешных и счастливых женщин.
Современный женский https://novaya.com.ua портал о жизни, моде и гармонии. Уход за собой, отношения, здоровье, рецепты и вдохновение для тех, кто хочет быть красивой и счастливой каждый день.
Интересный женский https://muz-hoz.com.ua портал о моде, психологии, любви и красоте. Полезные статьи, тренды, рецепты и лайфхаки. Живи ярко, будь собой и вдохновляйся каждый день!
Женский портал https://z-b-r.org ваш источник идей и вдохновения. Советы по красоте, стилю, отношениям, карьере и дому. Всё, что важно знать современной женщине.
Great job simplifying something so complex.
https://coloredreams.ru Мобильная версия сайта и просмотр со смартфона. Комфортная навигация на планшете.
Your passion for the topic really shines through.
Your advice is exactly what I needed right now.
Авто портал https://bestsport.com.ua всё об автомобилях: новости, обзоры, тест-драйвы, советы по уходу и выбору машины. Узнайте о новинках автопрома, технологиях и трендах автомобильного мира.
Авто портал https://psncodegeneratormiu.org мир машин в одном месте. Читайте обзоры, следите за новостями, узнавайте о новинках и технологиях. Полезный ресурс для автолюбителей и экспертов.
Онлайн авто портал https://retell.info всё для автолюбителей! Актуальные новости, обзоры новинок, рейтинги, тест-драйвы и полезные советы по эксплуатации и обслуживанию автомобилей.
Автомобильный портал https://autoguide.kyiv.ua для водителей и поклонников авто. Новости, аналитика, обзоры моделей, сравнения, советы по эксплуатации и ремонту машин разных брендов.
Современный авто портал https://necin.com.ua мир автомобилей в одном месте. Тест-драйвы, сравнения, новости автопрома и советы экспертов. Будь в курсе последних тенденций автоиндустрии
halbzeit endstand wetten Deutschland England tipps
https://shorturl.fm/QywY6
You’ve built a lot of trust through your consistency.
sicher basketball wetten Besser als Fußball gewinnen
halbzeit endstand wetten
schweiz
This was easy to follow, even for someone new like me.
Great points, well supported by facts and logic.
https://shorturl.fm/og0Ss
Портал про стройку https://dcsms.uzhgorod.ua всё о строительстве, ремонте и дизайне. Полезные советы, статьи, технологии, материалы и оборудование. Узнайте о современных решениях для дома и бизнеса.
Строительный портал https://msc.com.ua о ремонте, дизайне и технологиях. Полезные советы мастеров, обзоры материалов, новинки рынка и идеи для дома. Всё о стройке — от фундамента до отделки. Учись, строй и вдохновляйся вместе с нами!
Онлайн-портал про стройку https://donbass.org.ua и ремонт. Новости, проекты, инструкции, обзоры материалов и технологий. Всё, что нужно знать о современном строительстве и архитектуре.
Портал про стройку https://keravin.com.ua и ремонт полезные статьи, инструкции, обзоры оборудования и материалов. Всё о строительстве домов, дизайне и инженерных решениях
Подоконники из искусственного камня https://luchshie-podokonniki-iz-kamnya.ru в Москве. Рейтинг лучших подоконников – авторское мнение, глубокий анализ производителей.
I never thought about it that way before. Great insight!
I love the clarity in your writing.
Hi there! mexicanharmine great site.
was ist eine kombiwette [Celinda] bedeuten quoten bei wetten
This topic really needed to be talked about. Thank you.
Советы по строительству https://vodocar.com.ua и ремонту своими руками. Пошаговые инструкции, современные технологии, идеи для дома и участка. Мы поможем сделать ремонт проще, а строительство — надёжнее!
Сайт о строительстве https://valkbolos.com и ремонте домов, квартир и дач. Полезные советы мастеров, подбор материалов, дизайн-идеи, инструкции и обзоры инструментов. Всё, что нужно для качественного ремонта и современного строительства!
Полезный сайт https://stroy-portal.kyiv.ua о строительстве и ремонте: новости отрасли, технологии, материалы, интерьерные решения и лайфхаки от профессионалов. Всё для тех, кто строит, ремонтирует и создаёт уют.
Строительный сайт https://teplo.zt.ua для тех, кто создаёт дом своей мечты. Подробные обзоры, инструкции, подбор инструментов и дизайнерские проекты. Всё о ремонте и строительстве в одном месте.
Информационный портал https://smallbusiness.dp.ua про строительство, ремонт и интерьер. Свежие новости отрасли, обзоры технологий и полезные лайфхаки. Всё, что нужно знать о стройке и благоустройстве жилья в одном месте!
I appreciate the depth and clarity of this post.
I wish I had read this sooner!
This topic is usually confusing, but you made it simple to understand.
Строим и ремонтируем https://buildingtips.kyiv.ua своими руками! Инструкции, советы, видеоуроки и лайфхаки для дома и дачи. Узнай, как сделать ремонт качественно и сэкономить бюджет.
Энциклопедия строительства https://kero.com.ua и ремонта: материалы, технологии, интерьерные решения и практические рекомендации. От фундамента до декора — всё, что нужно знать домовладельцу.
Пошаговые советы https://tsentralnyi.volyn.ua по строительству и ремонту. Узнай, как выбрать материалы, рассчитать бюджет и избежать ошибок. Простые решения для сложных задач — строим и ремонтируем с уверенностью!
Новостной портал https://kiev-online.com.ua с проверенной информацией. Свежие события, аналитика, репортажи и интервью. Узнавайте новости первыми — достоверно, быстро и без лишнего шума.
Главные новости дня https://sevsovet.com.ua эксклюзивные материалы, горячие темы и аналитика. Мы рассказываем то, что действительно важно. Будь в курсе вместе с нашим новостным порталом!
It’s refreshing to find something that feels honest and genuinely useful. Thanks for sharing your knowledge in such a clear way.
Your thoughts are always so well-organized and presented.
Обустраивайте дом https://stroysam.kyiv.ua со вкусом! Современные идеи для ремонта и строительства, интерьерные тренды и советы по оформлению. Создайте стильное и уютное пространство своими руками.
Строим и ремонтируем https://srk.kiev.ua грамотно! Инструкции, пошаговые советы, видеоуроки и экспертные рекомендации. Узнай, как сделать ремонт качественно и сэкономить без потери результата.
Сайт о стройке https://samozahist.org.ua и ремонте для всех, кто любит уют и порядок. Расскажем, как выбрать материалы, обновить интерьер и избежать ошибок при ремонте. Всё просто, полезно и по делу.
Строительный портал https://sitetime.kiev.ua для мастеров и подрядчиков. Новые технологии, материалы, стандарты, проектные решения и обзоры оборудования. Всё, что нужно специалистам стройиндустрии.
This was incredibly useful and well written.
Как построить https://rus3edin.org.ua и отремонтировать своими руками? Пошаговые инструкции, простые советы и подбор инструментов. Делаем ремонт доступным и понятным для каждого!
https://shorturl.fm/SRgRq
https://shorturl.fm/1a0i7
Keep writing! Your content is always so helpful.
I agree with your point of view and found this very insightful.
Мужской сайт https://rkas.org.ua о жизни без компромиссов: спорт, путешествия, техника, карьера и отношения. Для тех, кто ценит свободу, силу и уверенность в себе.
Портал для автомобилистов https://translit.com.ua от выбора машины до профессионального ремонта. Читайте обзоры авто, новости автоспорта, сравнивайте цены и характеристики. Форум автолюбителей, советы экспертов и свежие предложения автосалонов.
Мужской онлайн-журнал https://cruiser.com.ua о современных трендах, технологиях и саморазвитии. Мы пишем о том, что важно мужчине — от мотивации и здоровья до отдыха и финансов.
Сайт для женщин https://oun-upa.org.ua которые ценят себя и жизнь. Мода, советы по уходу, любовь, семья, вдохновение и развитие. Найди идеи для новых свершений и будь самой собой в мире, где важно быть уникальной!
Ваш гид в мире https://nerjalivingspace.com автомобилей! Ежедневные авто новости, рейтинги, тест-драйвы и советы по эксплуатации. Найдите идеальный автомобиль, узнайте о страховании, кредитах и тюнинге.
wettanbieter mit cashout
Feel free to visit my web blog – online sportwetten schweiz
Great article! I’ll definitely come back for more posts like this.
https://shorturl.fm/zIrtd
Женский онлайн-журнал https://rosetti.com.ua о стиле, здоровье и семье. Новости моды, советы экспертов, тренды красоты и секреты счастья. Всё, что важно и интересно женщинам любого возраста.
Сайт о металлах https://metalprotection.com.ua и металлообработке: виды металлов, сплавы, технологии обработки, оборудование и новости отрасли. Всё для специалистов и профессионалов металлургии.
Строительный сайт https://okna-k.com.ua для профессионалов и новичков. Новости отрасли, обзоры материалов, технологии строительства и ремонта, советы мастеров и пошаговые инструкции для качественного результата.
Портал о дизайне https://sculptureproject.org.ua интерьеров и пространства. Идеи, тренды, проекты и вдохновение для дома, офиса и общественных мест. Советы дизайнеров и примеры стильных решений каждый день.
Главный автопортал страны https://nmiu.org.ua всё об автомобилях в одном месте! Новости, обзоры, советы, автообъявления, страхование, ТО и сервис. Для водителей, механиков и просто любителей машин.
Студия ремонта https://anti-orange.com.ua квартир и домов. Выполняем ремонт под ключ, дизайн-проекты, отделочные и инженерные работы. Качество, сроки и индивидуальный подход к каждому клиенту.
Туристический портал https://feokurort.com.ua для любителей путешествий! Страны, маршруты, достопримечательности, советы и лайфхаки. Планируйте отдых, находите вдохновение и открывайте мир вместе с нами.
paris sportif foot 1xbet africain
pariez sur le foot telecharger 1xbet
foot africain afrik foot pronostic
Флойд Мейвезердин рекорддору көп спорт күйөрмандарын суктандырган. Флойд Мейвезердин тарыхтагы орду эч кимге талашсыз. Флойд Мейвезердин акыркы беттештери жана жыйынтыктары Флойд Мейвезер рекорд бөлүмүндө жарыяланган.
Анын фамилиясы дүйнөлүк брендге айланган. Анын рекорддору бүгүнкү күнгө чейин сакталган. Анын акыркы жаңылыктарын укпай калган адам жок.
Анын ар бир интервьюсу көңүл борборунда.
Анын жашоосу мотивациянын булагы. Анын фанаттары дүйнөнүн бардык бурчунда бар. Флойд Мейвезер ар дайым жаңы рекорддорду жарата берет.
https://shorturl.fm/s6iuD
wettbüro anbieter
Also visit my blog; Sportwetten Ohne Oasis
wettbüro dresden speisekarte
My web site … sportwetten anbieter deutschland (https://Motherschoice.Ykuat.com/2025/10/07/virtuelle-Wetten-hofmann)
https://shorturl.fm/cFV2h
connectwiththeworldnow – Clean interface, message is upfront and design feels coherent.
Студия дизайна https://bathen.rv.ua интерьеров и архитектурных решений. Создаём стильные, функциональные и гармоничные пространства. Индивидуальный подход, авторские проекты и внимание к деталям.
Ремонт и строительство https://fmsu.org.ua без лишних сложностей! Подробные статьи, обзоры инструментов, лайфхаки и практические советы. Мы поможем построить, отремонтировать и обустроить ваш дом.
https://shorturl.fm/x1Qjg
https://shorturl.fm/tqyNt
buchmacher ohne lugas
Feel free to visit my website :: wetten im internet (https://assetguards.com/2025/10/10/tennis-wetten-uber-1-5)
melbet telecharger melbet telecharger
afrik foot pronostic 1xbet afrique apk
parier pour le foot foot africain
admiral x регистрация
Современная студия дизайна https://bconline.com.ua архитектура, интерьер, декор. Мы создаём пространства, где технологии сочетаются с красотой, а стиль — с удобством.
pariez sur le foot https://parifoot-afrique.com
melbet telecharger 1xbet cameroun apk
telecharger 1xbet cameroun 1xbet africain
Создавайте дом https://it-cifra.com.ua своей мечты! Всё о строительстве, ремонте и дизайне интерьера. Идеи, проекты, фото и инструкции — вдохновляйтесь и воплощайте задуманное легко и с удовольствием.
livescore für sportwetten
Also visit my web-site; buchmacher übersicht
riobet зеркало
ascendgrid – Looks promising, can’t wait to see their offerings.
https://shorturl.fm/Gtk3I
экскаватор погрузчик в москве экскаватор погрузчик в москве .
карнизы для штор купить в москве карнизы для штор купить в москве .
карниз с электроприводом карниз с электроприводом .
https://shorturl.fm/449or
согласование перепланировки нежилого помещения в москве https://pereplanirovka-nezhilogo-pomeshcheniya10.ru/ .
перепланировка нежилого помещения в нежилом здании перепланировка нежилого помещения в нежилом здании .
аренда мини экскаватора цена https://arenda-mini-ekskavatora-v-moskve-2.ru .
перепланировка офиса согласование pereplanirovka-nezhilogo-pomeshcheniya9.ru .
автоматический карниз для штор http://www.karniz-elektroprivodom.ru .
truelaunch – The tone seems genuine, like someone really cares.
brandvision – Their case studies are inspiring and informative.
автоматические рулонные шторы на створку http://www.rulonnaya-shtora-s-elektroprivodom.ru/ .
Cappadocia tours Turkey Matthew C. – Estonya https://ordinet.in/?p=7104
sportwetten geld zurück
Here is my web page :: Online Live Wetten
https://shorturl.fm/uicrn
purehorizon – Just browsed your sections, found some really helpful insights.
Мир архитектуры https://vineyardartdecor.com и дизайна в одном месте! Лучшие идеи, проекты и вдохновение для дома, офиса и города. Узнай, как создаются красивые и функциональные пространства.
cryptoboss официальный сайт
https://shorturl.fm/lwNf7
**mindvault**
Mind Vault is a premium cognitive support formula created for adults 45+. It’s thoughtfully designed to help maintain clear thinking
valuevision – I like the color scheme, it gives a calming vibe.
growthverse – The content is engaging, and the site is responsive.
skyportal – Love the colors used here, makes reading very pleasant.
smartgrid – Can’t access most of the pages; server might need updates.
trendforge – Clean name, memorable — good branding so far.
quantumreach – Friendly tone, feels like there’s a real person writing here.
сукааа казино
boldimpact – Hoping they share resources or case studies once live.
alphaunity – Content looks crisp and the color scheme is pleasant on eyes.
bluetrail – Overall positive vibes, I’m glad I checked this out.
solidvision – Hoping they launch soon; curious what they’ll offer.
sharpbridge – Navigation feels intuitive, didn’t struggle finding anything so far.
goldbridge – The domain looks solid, hoping the content matches up well.
потолочник натяжные потолки самара http://stretch-ceilings-samara.ru .
elitegrowth – Navigation is seamless, and the visuals are appealing.
жалюзи для пластиковых окон с электроприводом http://www.zhalyuzi-s-elektroprivodom77.ru .
потолки самара natyazhnye-potolki-samara-1.ru .
cloudmatrix – Offers valuable insights, and the interface is top-notch.
тканевые натяжные потолки самара акции https://stretch-ceilings-samara-1.ru .
nextrend – Bookmarking this — looks like a resource I’ll return to.
fastgrowth – Offers valuable insights, and the interface is top-notch.
maxvision – Impressed by the layout, feels modern and user-friendly.
greenmotion – Love the clean design, really easy to navigate today.
zenithlabs – Navigation is seamless, and the visuals are appealing.
thinkbeyondtech – The content is engaging, and the site is responsive.
nextlayer – Great user experience, everything loads so smoothly and fast.
jvspin официальный сайт
Your content never disappoints. Keep up the great work!
focuslab – Browsing was smooth — pages loaded fast and clearly.
I wasn’t expecting to learn so much from this post!
You clearly know your stuff. Great job on this article.
auf casino официальный сайт
потолочкин отзывы клиентов самара http://natyazhnye-potolki-samara-2.ru .
urbanmatrix – Overall a positive experience, feels trustworthy and solid.
growwithfocus – Would be great if they add practical tips and real case studies.
nextrealm – Hoping they go live soon; excited to see what’s coming.
openlaunch – Page load feels fast, content is responsive and crisp.
Your writing style makes complex ideas so easy to digest.
Сервис юридических консультаций «Правовик24» предоставляет полный спектр правовых услуг для бизнеса и частных лиц. Мы помогаем решать сложные споры, защищаем интересы клиентов в суде, сопровождаем сделки и банкротство, восстанавливаем нарушенные права. Перейдя на сайт по запросу сайт юридических услуг – вы получите персональный подход, разъяснение норм действующего законодательства, полезные советы экспертов. Обратитесь к профессионалам, чтобы получить грамотную юридическую помощь и уверенность в решении вашей правовой проблемы.
Thanks for sharing your knowledge. This added a lot of value to my day.
ynaix – Pages load fast, performance feels solid even with lots of images.
connectwiththeworldnow – Overall experience is positive, site feels purposeful and authentic.
Thanks for making this easy to understand even without a background in it.
strongrod – The tone feels confident and trustworthy, not overbearing.
wavefusion – Easy navigation, never felt lost or confused at all.
brightideaweb – Typography is crisp, spacing works well throughout the site.
sharpwave – Design is sleek and modern, very pleasing to the eyes.
metarise – Pages load fast, no lag, pleasant browsing experience overall.
cyberlaunch – The writing tone is confident yet friendly, good balance.
https://shorturl.fm/CL5oV
Частный заем денег ооо домашние деньги альтернатива банковскому кредиту. Быстро, безопасно и без бюрократии. Получите нужную сумму наличными или на карту за считанные минуты.
innovatewithus – Really like the vibe here, feels fresh and inspiring always.
What a helpful and well-structured post. Thanks a lot!
brightchain – Content strikes a good balance, informative yet easy to read.
bestchoiceonline – Checkout felt simple and secure, confidence inspiring.
cloudmark – Pages load quickly, good performance even with graphics.
sportwetten Online mit bonus bonus aktuell
Все спортивные новости http://sportsat.ru в реальном времени. Итоги матчей, трансферы, рейтинги и обзоры. Следите за событиями мирового спорта и оставайтесь в курсе побед и рекордов!
nextbrand – Visuals work well, colors complement each other nicely.
digitalstorm – The voice feels authentic, technical without being overwhelming.
This gave me a lot to think about. Thanks for sharing.
globalreach – Looks responsive too, works well on my phone without glitches.
everythingyouneedtoknow – Writing is crisp, not dragging, gives value quickly.
https://shorturl.fm/P3Mt8
explorecreativeideasdaily – Navigation is smooth, discovering content was effortless today.
ultrawave – The voice feels genuine, not trying too hard to impress.
yourbrandzone – Navigation is smooth, I find what I need in seconds.
pixelplanet – Helpful features are where I expect them, intuitive UX.
zenithmedia – Found good media resources, videos and articles both helpful.
boldspark – Looks professional, gives confidence that the offerings are high quality.
Posts like this are why I keep coming back. It’s rare to find content that’s simple, practical, and not full of fluff.
wette doppelte chance
Here is my page Sportwetten Unentschieden Vorhersagen
futurebeam – Found great resources; helpful and clearly organized for quick read.
kluvcc – Quality content and smooth experience make me revisit often.
You bring a fresh voice to a well-covered topic.
https://shorturl.fm/ZhYD7
Suchen Sie Immobilien? https://www.montenegro-immobilien-kaufen.com wohnungen, Villen und Grundstucke mit Meerblick. Aktuelle Preise, Fotos, Auswahlhilfe und umfassende Transaktionsunterstutzung.
Sportwetten guthaben Ohne Einzahlung tipps heute
I hadn’t considered this angle before. It’s refreshing!
alihidaer2313 – Strong typography, simple structure, gives an aura of clarity.
**mindvault**
mindvault is a premium cognitive support formula created for adults 45+. It’s thoughtfully designed to help maintain clear thinking
Thank you for offering such practical guidance.
alphaimpact – Overall very polished, site feels professional and trustworthy.
Your writing always inspires me to learn more.
joinourcreativecommunity – Overall very inviting, makes me want to stay and explore more.
YourPathOfGrowth – The resources here are perfect for anyone looking to make a change.
This is one of the best explanations I’ve read on this topic.
thebestplacetostarttoday – Design is welcoming and warm, draws me in gently.
LearnWithConfidence – Their guides are thorough, I learned so much in minutes.
makingeverymomentcount – Typography crisp, spacing well thought out, reading comfortable.
learnshareandsucceed – Love the mission here, seems like a place to really grow together.
getreadytoexplore – Visuals support the “exploration” theme really well, feels immersive.
Excellent work! Looking forward to future posts.
findwhatyouarelookingfor – Content is spot on, every page seems purposeful and relevant.
everythingaboutsuccess – Layout is clean, makes discovering success tips easy and quick.
learnsomethingneweveryday – Pages load quickly, even when images and graphics are heavy.
discoverendlessinspiration – Visuals are beautiful and inspiring, brightens my mood instantly.
growyourbusinessfast – Love the ambitious name, site lives up to its promise.
It’s refreshing to find something that feels honest and genuinely useful. Thanks for sharing your knowledge in such a clear way.
makeimpactwithideas – Visual style supports message, colors evoke energy and clarity.
https://vk.com/nakrutkapfonline – накрутка пф>>>
yourjourneytobetterliving – Really feel the positive vibe here, content feels uplifting.
https://usahaterokai.com/inteligent-transitions-in-ux-design/
GrowWithConfidenceHere – I keep returning, each module adds valuable insights every time.
SimpleWaysToBeHappy – I find the daily affirmations helpful for a positive mindset.
BuildSomethingMeaningful – I love how they integrate technology into their initiatives.
TogetherWeCreateChange – Love participating, everyone’s contributions make the platform feel alive today.
YourTrustedSourceOnline – The resources here are perfect for anyone looking to make a change.
BuildABetterTomorrow – It’s inspiring to see how they empower local communities.
CreateInspireAndGrow – This platform truly empowers me to take action and grow.
thefutureofinnovation – Visual hierarchy is strong, important parts stand out clearly.
I’m definitely going to apply what I’ve learned here.
wettquoten esc deutschland
Feel free to surf to my blog – sportwetten paysafecard
stayupdatedwithtrends – The tone is confident and helpful, not too buzzwordy.
Great points, well supported by facts and logic.
I wish I had read this sooner!
discoveramazingstories – A good mix of short-stories and deeper features could keep me coming back.
сеть фитнес клубов https://fitnes-klub-msk.ru
фитнес клуб москва женский фитнес клуб
Posts like this are why I keep coming back. It’s rare to find content that’s simple, practical, and not full of fluff.
TurnIdeasIntoAction – Great site to get unstuck and actually move forward daily.
EverythingStartsWithYou – This site reminds me: I’m in control of my path today.
Thank you for sharing this! I really enjoyed reading your perspective.
купить медицинскую справку
geld verdienen mit sportwetten geld zurück (Stevie)
LearnSomethingAwesome – I enjoy the mix of visuals and explanations, keeps me engaged.
LearnShareAndGrow – I appreciate how they focus on sustainable solutions for all.
I’ve bookmarked this post for future reference. Thanks again!
FindTheBestIdeas – Helps me break creative blocks and think outside my usual patterns.
https://www.isajigo.com/photo/
TheArtOfLivingWell – I keep coming back, it feels like a positive habit now.
FindAnswersAndIdeas – Love the balance between theory and tips that I can apply right away.
FindNewWaysToGrow – Clean design, good flow, reading here feels peaceful and helpful.
Sportwetten anbieter österreich – https://Aanpublishing.com/online-wetten-tipp-2,
schweiz swisslos
YourDigitalDestination – Great mix of topics, keeps me coming back for more advice.
s0gnxb
GetConnectedWithPeople – I love how this platform makes networking feel natural and relaxed.
UnlockYourPotentialToday – The content is very encouraging, makes me feel capable every day.
This was so insightful. I took notes while reading!
InspireChangeAndProgress – The inspiration here feels genuine, not forced or cliché at all.
DiscoverWorldOfIdeas – Definitely a resource I’ll revisit when I need creativity or new angles.
FindSolutionsForLife – Very relatable advice, I feel like I’m learning from someone I trust.
ConnectDiscoverAndGrow – The balance of ideas and action tips here is just right.
потолочкин потолки натяжные отзывы http://www.stretch-ceilings-nizhniy-novgorod-1.ru .
markmackenzieforcongress – I appreciate how clearly everything is explained without unnecessary jargon.
madeleinemtbc – Pleasant experience browsing, I’m likely coming back soon
натяж потолки http://www.natyazhnye-potolki-nizhniy-novgorod.ru/ .
FindInspirationEverywhere – I often share pieces from here with friends who need encouragement.
YourGuideForSuccess – I already bookmarked several posts I plan to revisit later.
StartChangingYourLife – Definitely bookmarking this, it’s going to be part of my daily motivation.
quoten bei wetten dass
Feel free to surf to my blog post … sportwetten schweiz Gesetz
DiscoverUsefulTipsDaily – This site feels like a little toolkit I can pull up anytime.
sportwetten online vergleich
Stop by my webpage – wollen wir wetten gewinner
BuildYourDreamFuture – I’m excited to try some of the strategies suggested here.
натяжные потолки сайт https://stretch-ceilings-nizhniy-novgorod.ru/ .
DiscoverNewOpportunities – The platform is user-friendly and full of helpful guides.
I love how clearly you explained everything. Thanks for this.
This post gave me a new perspective I hadn’t considered.
потолочник натяжные потолки потолочник натяжные потолки .
LearnAndImproveEveryday – Very useful articles and guides, exactly what I was looking for.
https://shorturl.fm/wANh0
I enjoyed every paragraph. Thank you for this.
BeCreativeEveryday – This site reminds me to play with colors, shapes, and imagination more.
StayMotivatedAndFocused – Love how every post nudges me to take action instead of procrastinating.
majapahit4d
Регулярные пассажирские перевозки https://povozkin.ru
You really know how to connect with your readers.
занятия в фитнес клубе фитнес клуб с бассейном в москве
https://shorturl.fm/OkpPI
купить справку
mahjongways
This was a great reminder for me. Thanks for posting.
makeprogressdaily – Always look forward to the new posts, they keep me on track.
makethemostoflife – Feels like someone genuinely wants readers to grow, not just sell
This content is gold. Thank you so much!
https://shorturl.fm/kt8B0
inspireandgrowtogether – This site encourages me to take positive action today.
You’ve clearly done your research, and it shows.
Turkey beach tours Grace R. – İran https://vnbride.com/?p=14523
findthebestcontent – This site saved me time in searching for good reads
Гарри Кейн оюн талаасында дайыма тынчсызданууну жаратат.Кейндин эмгеги жана дисциплинасы өзгөчө. Атактуу англиялык чабуулчу тууралуу көбүрөөк билүү үчүн кир: https://harry-kane-kg.com/. Анын карьерасындагы ийгиликтер мактоого арзыйт.
Кейндин трансфери чоң көңүл бурдурган.
Гарри Кейндин балдары футболду жакшы көрүшөт. Кейн командалаштарын дайыма колдойт. Бул оюнчу эч качан берилишпейт. Кейндин футболго болгон сүйүүсү жаш кезинен башталган. Бул оюнчу кайсы чемпионатта болбосун айырмаланат. Кейндин реал мадридге өтүшү дагы эле талкууда.
findyourwayforward – I’ll be visiting again when I need direction or clarity
discoverlearnandshare – Good balance of images and content, keeps me engaged
licsupport – Nice resource, lots of useful insurance info available
growyourpresenceonline – Content is straightforward, no over-complicated jargon, just helpful
Лазерные станки https://raymark.ru для резки металла в Москве. 20 лет на рынке, выгодная цена, скидка 5% при заявке с сайта + обучение
HOME CLIMAT https://homeclimat36.ru кондиционеры и сплит системы в Воронеже. Скидка на монтаж от 3000 рублей! При покупке сплит-системы.
connectwithbrilliantminds – I’ll likely recommend this to folks looking for growth mindset content
discovertrendingideas – Nice usability, no clutter, just solid ideas showcased
everythingaboutmarketing – Excellent insights on modern marketing strategies, always up-to-date.
discoverhiddenpotential – I’m looking forward to exploring more content here.
learnandearndaily – The writing feels genuine, not too salesy or pushy
discoveryourpassion – This site really helped me find my true calling.
learnexploreandshine – The content is vibrant and full of curiosity, feels alive
togetherwecreateimpact – Inspiring content, truly feels like change starts here
Such a thoughtful and well-researched piece. Thank you.
keepgrowingwithus – I’ll be checking back often for more content
findyourwayforward – I shared this with a friend; they found it helpful too.
connectandgrowonline – The tools here helped me streamline my online presence.
jointhenextbigthing – Found some amazing tips, very helpful for beginners like me.
findyourinnerdrive – The content here is uplifting and practical, perfect for personal growth.
buildyourdigitalfuture – Bookmarking this site for future inspiration and guidance.
изготовление кухонь на заказ в санкт петербурге http://kuhni-spb-3.ru/ .
I’ll definitely come back and read more of your content.
buildyourownlegacy – I’d recommend this to friends working on self-growth
I wish I had read this sooner!
The Royal Family Bonus powitalny 100% + 50 FS od Mirax Casino because of that pragmatic play made this slot very dynamic, sugar rush slots demo excellent suitable for supporters with a bankroll that will be enough for long sessions. Bonus powitalny 100% + 50 FS od Mirax Casino Pierwsze 4 depozyty na konto główne dają dodatkowy bonus na dwóch kontach jednocześnie: zakłady sportowe i gry kasynowe. Zdobądź bonus 500%: bonus jest przyznawany automatycznie po dokonaniu wpłaty na konto główne: No products in the cart. Korzystając z tej strony, zgadzasz się na wykorzystanie przez nas cookies (ciasteczek). Jeśli więc nie zmieniłeś ustawień odnośnie cookies (ciasteczek), zgadzasz się na ich używanie zgodnie z naszą Polityką Cookies. Gra oferuje ekscytujące funkcje, takie jak darmowe obroty, w których bębny 2, 3 i 4 łączą się w symbol giganta, zapewniając większe wygrane. Dostępna jest również funkcja Money Respin, która uruchamia się po wylądowaniu co najmniej sześciu symboli Money, oferując do 100-krotności całkowitego zakładu, a nawet Mega Jackpot.
https://lifeinsys.com/user/tingfernkingcell1979
1xbet Mobi Tətbiqetməsi, 1xbet Apk 1xbet Mobile Phone Xüsusiyyətləri Content Bet Mobile Tətbiqetməsinin Əsas Xüsusiyyətləri Tövsiyə Olunan Ən Yaxşı 3 Bukmeker Şirkətini Sınayın Дocтуп К Зepкaлу 1xbet Нa Android И Ios Android Cihazları Üçün 1xbet Mobil Proqramlar Bet Mobi Tətbiqi Ios Cihazlarınız Üçün Bet Mobil Təhlükəsizlik Şərtləri Bet Download Google Android – Cihazlarda Tətbiqetməsini Yükləyin… Once verified, you’ll have full usage of betting and casino games, ensuring a safe and enjoyable gaming experience. Sports betting and casino games are accessible in local currency at the MostBet site. The payment method ought to be chosen upon registration and can’t be altered afterward. With this type of large userbase, it’s no real surprise that registering a merchant account with Mostbet India is really a simple process.
findsolutionsfast – I shared this with a friend, they’ll thank me later
Аутстаффинг персонала https://skillstaff2.ru для бизнеса: легальное оформление сотрудников, снижение налоговой нагрузки и оптимизация расходов. Работаем с компаниями любого масштаба и отрасли.
Нужна недвижимость? https://www.nedvizhimost-chernogorii-u-morya.ru/ лучшие объекты для жизни и инвестиций. Виллы, квартиры и дома у моря. Помощь в подборе, оформлении и сопровождении сделки на всех этапах.
I like how you presented both sides of the argument fairly.
sportwetten schweiz online
my blog post … Wettstrategien Test
Thank you for making this topic less intimidating.
buildyourdreambrand – I’m excited to see what more content gets added here
https://shorturl.fm/fH0k2
I like how you kept it informative without being too technical.
I appreciate how genuine your writing feels. Thanks for sharing.
Тысячи клиентов ежедневно ищут надежный и проверенный путь для доступа на маркетплейс Kraken, сталкиваясь с множеством фейковых сайтов и неактуальной инструкциями. Дабы минимизировать эти риски и сэкономить ваше время, существует простое и эффективное место для поиска. kraken ссылка Используя данный линк, вы получаете стопроцентный вход к полному функционалу платформы, в том числе внутренний обменник и оперативную техническую помощь. Данный метод позволяет целиком исключить вероятность перехода на мошеннический ресурс и обеспечивает высочайшую уровень анонимности при совершении любых операций.
votethurm – Visited earlier, saw a few campaign photos and statements.
I like how you presented both sides of the argument fairly.
shareyourvisiontoday – I visited and it really resonated with my goals and dreams.
learnnewthingsdaily – The content is fresh and always gives me something to try.
discovergreatideas – Found a new perspective on problem-solving here, very insightful.
inspireeverymoment – Every post feels like a little boost to my day.
growtogetherwithus – Very uplifting content, makes me want to improve myself daily.
inspireeverymoment – Every post feels like a little boost to my day.
thefuturestartsnow – I visited just now and got chills thinking about what’s ahead.
You really know how to connect with your readers.
Строительный портал https://v-stroit.ru всё о строительстве, ремонте и архитектуре. Полезные советы, технологии, материалы, новости отрасли и практические инструкции для мастеров и новичков.
startyourdigitaljourney – Great resources and support for anyone starting their digital journey.
theartofsuccess – Highly recommend this for daily boosts and life planning.
createimpactfulstories – Such vivid storytelling, I feel connected and energized reading this.
yourjourneytowin – Just what I needed today — clarity and encouragement.
Команда разработчиков проекта Kraken постоянно напоминает всем пользователям использовать исключительно проверенные источники для получения актуальных адресов для входа. Это служит основной мерой безопасности вашей учетной записи и совершаемых операций на просторах платформы Кракен. официальный сайт кракен Именно данный проверенный источник обеспечивает пользователю беспрепятственное попадание на настоящий сайт Kraken, в обход всевозможные посредников и потенциальные угрозы. Это считается единственно верным решением для всех, кто дорожит собственную анонимность и хочет быть уверенным в сохранности личного профиля и баланса на счету.
staycuriousandcreative – The content is playful yet meaningful, just my style.
I’ll be sharing this with a few friends.
findyourcreativeflow – The vibe here inspires flow, I’ve already got ideas buzzing.
yourpathofsuccess – Great for anyone wanting steady progress, not quick fixes.
房中秘术、泡妞把妹、丰胸美体、奇淫巧技!价值十万电子书下载网址:https://www.1199.pw/
creativityneverends – The visuals and writing both feel so alive and vibrant.
Портал о строительстве https://pamel-stroy.ru и ремонте. Пошаговые инструкции, идеи, технологии, новости и советы экспертов. Всё, что нужно, чтобы строить и ремонтировать грамотно.
https://vk.com/nakrutkapfonline – накрутка пф яндекс!..
Риэлторская контора https://daber27.ru покупка, продажа и аренда недвижимости. Помогаем оформить сделки безопасно и выгодно. Опытные риэлторы, консультации, сопровождение и проверка документов.
Купольные дома https://kupol-doma.ru под ключ — энергоэффективные, надёжные и современные. Проектирование, строительство и отделка. Уникальная архитектура, комфорт и долговечность в каждом доме.
maritim4d
beste quoten sportwetten
Also visit my page … eurovision buchmacher – Ramon –
gratiswette bei registrierung
Also visit my webpage :: tipps wetten heute (New.OU-Gsrakovski.com)
stacoa.org – Very nice layout, feels like a professional and caring site.
myvetcoach.org – Nice design, great resources, feels very professional.
filamericansforracialaction.com – The design is simple but it gives space to the message.
electlarryarata – Nice start, saw your campaign theme but pages are empty now.
thespeakeasybuffalo – Love the welcoming tone in the header, feels warm and inviting.
laetly.com – The IG gives enough hint, hope the site matches that energy.
https://shorturl.fm/jHKVZ
norigamihq – Visited twice, still not sure what the focus is.
Ваша Недвижимость https://rbn-khv.ru сайт о покупке, продаже и аренде жилья. Разбираем сделки, налоги, ипотеку и инвестиции. Полезная информация для владельцев и покупателей недвижимости.
Информационный блог https://gidroekoproekt.ru для инженеров и проектировщиков. Всё об инженерных изысканиях, водохозяйственных объектах, гидротехническом строительстве и современных технологиях в отрасли.
growyourdigitalpresence – Articles feel honest, not just hype — I appreciate that.
summerstageinharlem.org – Such an inviting event, perfect for summer evenings with friends.
pinellasehe.org – Found ideas here that are exactly what I was looking for.
rockyrose.org – The writing is gentle but carries real depth and feeling.
formative-coffee.com – Bookmarking this for when I want to explore premium coffee options.
hecimagine.com – I hope they feature student stories and application details soon.
mystylecorner – Felt comfortable shopping here, trustworthy feel throughout the site.
creativevision – A refreshing take on modern art, pushing creative boundaries.
successpartnersgroup – Every visit feels refreshing, love the layout and product quality.
globalideasnetwork – I love how clean and minimal the design is — very fresh.
cryptotephra-clagr.com – It’s spelled “cryptotephra-CLAGR” in multiple sources, so likely official.
ukrainianvictoryisthebestaward.com – No clear ownership or mission statement visible.
discovernewideas – Their branding feels unique, colors and fonts make a difference.
inspiredgrowthteam – Definitely feels like a place focused on growth and meaningful connections.
createimpact – Their messaging resonates, I can tell they care about impact.
https://shorturl.fm/Od7bn
Сүрөттөр, кыска видеолор жана цитаталар Махачев тууралуу материалдарды окууну кызыктуу кылат.
Тикелей эфир башталганга чейин акыркы коэффициенттер жана линиялар жаңыртылып турат. ислам махачев арман царукян Реванш мүмкүнчүлүгү, даталар жана эксперттик пикирлер ушул жерден. Коэффициенттер да салыштырылат. UFCдеги алардын позициялары, рекорддору жана окшош стилдери боюнча салыштырма таблица бар. Федер жана лайтвейт контекстинде салмак маселеси жана шарттар талкууланат. Салмакты калыбына келтирүү жана кемитүү тартиби боюнча расмий маалыматтардан үзүндүлөр келтирилет.
«Ислам Махачев кимге утулду?» деген суроого тарыхый тизмек жана шарттар менен жооп беребиз. Жеке пикир эмес, сандык көрсөткүчтөргө таянган нейтралдуу анализди сунуштайбыз. Бүт маалымат ар дайым текшерилген жана булакка шилтемеленет. Эгер каталар байкалса, пикир калтырып, оңдоолорго салым кошо аласыз.
luxurytrendstore – The seasonal collections are on point, perfect for updating my wardrobe.
bester wettanbieter ohne oasis
My web page – Wettbüro emden
nextgeninnovation – The design is slick, I enjoyed exploring their service sections.
visionaryleadersclub – Good branding, the look matches the promise they make.
partnershippowerhouse – Having clean design plus meaningful content makes all the difference here.
https://shorturl.fm/xdsGk
I really needed this today. Thank you for writing it.
trendymodernwear – Definitely bookmarking this site for future fashion finds.
successpartnersgroup – I bookmarked this, good resource for what they offer.
I wasn’t sure what to expect at first, but this turned out to be surprisingly useful. Thanks for taking the time to put this together.
Attractive section of content. I just stumbled upon your web site and in accession capital to assert that I get actually enjoyed account your blog posts. Any way I’ll be subscribing to your feeds and even I achievement you access consistently rapidly.
батареи rifar tubog
You’ve clearly done your research, and it shows.
You’ve clearly done your research, and it shows.
Excellent work! Looking forward to future posts.
You write with so much clarity and confidence. Impressive!
Thanks for addressing this topic—it’s so important.
futuremindscollective – Looking forward to more collections that inspire and educate.
merkur sportwetten
My homepage; wettanbieter mit bonus ohne einzahlung;
Hellen,
discovernewpath – The branding feels very fresh, makes me curious what’s next.
I appreciate the real-life examples you added. They made it relatable.
So simple, yet so impactful. Well written!
findyourfuture – Everything loads fast, no annoying delays or pop-ups.
strategicgrowthalliance – The content is well-organized, enhancing the user experience.
uniquefashionstyle – The minimalist design aligns perfectly with the brand’s aesthetic.
trustconnectionnetwork – The product range is diverse, catering to various preferences effortlessly.
nextvision – Wish there was proof of legitimacy—user reviews, company registration etc.
This topic is usually confusing, but you made it simple to understand.
trustedbusinesslink – Love the visual coherence, branding feels strong and consistent.
futureopportunitynetwork – A valuable tool for anyone seeking future opportunities.
growstrongteam – Bright visuals and confident tone, I like the energy here.
futurevisiongroup – I like how clean and professional it looks.
learnsharegrow – I found useful tips quickly, content is relevant and clear.
I like how you presented both sides of the argument fairly.
happylifestylehub – This site gives me peace, I enjoy visiting it daily.
wagocjapmeom – The site feels mysterious, layout hints at deeper content waiting.
growthpoint – Professional branding, good use of space and design elements.
I’ve gained a much better understanding thanks to this post.
futureopportunitynetwork – The site loads fast, switching pages feels seamless and smooth.
заказать проект перепланировки квартиры в москве цена http://www.proekt-pereplanirovki-kvartiry16.ru/ .
This was a very informative post. I appreciate the time you took to write it.
What I really liked is how easy this was to follow. Even for someone who’s not super tech-savvy, it made perfect sense.
buildbrand – The focus on emotional connections is spot on.
I love how clearly you explained everything. Thanks for this.
https://shorturl.fm/0CUYh
Деревянные лестницы https://rosslestnica.ru под заказ в любом стиле. Прямые, винтовые, маршевые конструкции из массива. Замеры, 3D-проект, доставка и установка. Гарантия качества и точности исполнения.
Лестницы в Москве https://лестницы-в-москве.рф продажа и изготовление под заказ. Прямые, винтовые, модульные и чердачные конструкции. Качество, гарантия и монтаж по всем стандартам.
Gratiswette Ohne Einzahlung Sportwetten bester anbieter
teamfuture – It feels like a space for growth, not just passive reading.
businessgrowthhub – Every visit here gives me actionable tips, very well thought.
trustandunity – I really feel a sense of honesty and warmth here, very inviting.
digitalinnovationzone – I’ve bookmarked this, definitely somewhere I’ll return for updates.
futuregoalsnetwork – I’ve bookmarked this, it seems like a long-term resource.
successbridge – Clean design, useful content — not just fluff, really helpful.
tlbou9
With havin so much content do you ever run into any issues
of plagorism or copyright infringement? My site has a lot of unique content I’ve either created myself or outsourced but
it appears a lot of it is popping it up all over the web without my agreement.
Do you know any techniques to help protect against content from being stolen? I’d certainly appreciate it.
getthedeal – Really convenient site, navigation is simple and very fast today.
https://bankmill.ai/how-to-create-a-business-plan-that-drives/
leadersunitedgroup – The graphics support the text well, design is pleasant on eyes.
connectinnovationhub – I bookmarked it, looks like a resource worth revisiting regularly.
winmore – Content feels grounded, not overhyped — I respect that.
findtrendystuff – I found a cool gift idea here, love the surprise finds.
futuregoalsnetwork – Always excited to check updates — this site has potential.
findsomethingnew – I’ve bookmarked this — it seems like a place I’ll revisit.
exploreideasworld – I find inspiration in almost every post, feels lively.
globalpartnershipteam – Bookmarking this one, might be a resource I’ll return to often.
discovervalue – Simple but effective — I love how crisp the design is.
successjourneyclub – I enjoy reading here, it gives me ideas to try immediately.
leadersunitedgroup – Every article gives something meaningful — I appreciate that.
discoverdaily – I’ve bookmarked several posts, they keep surprising me.
trustconnectionnetwork – I really feel this site values connection and transparency, nice touch.
connectinnovationhub – Bookmarked it already — looks like a resource I’ll revisit.
growtogetheralliance – Clean design, easy navigation — makes browsing a calm experience.
brightdeal – The tone feels hopeful, which is refreshing on many sites.
innovateandbuild – Always leave feeling I’ve learned something useful, thumbs up.
growthnetwork – The content here gives me ideas and keeps me motivated each time.
businessgrowthhub – Feels professional, but also friendly — balance is nice.
мелбет вход http://melbetbonusy.ru/ .
перепланировка согласование http://www.soglasovanie-pereplanirovki-kvartiry11.ru .
мелбет личный кабинет https://melbetbonusy.ru .
сколько стоит согласование перепланировки квартиры http://zakazat-proekt-pereplanirovki-kvartiry11.ru/ .
сколько стоит узаконивание перепланировки в квартире http://www.stoimost-soglasovaniya-pereplanirovki-kvartiry.ru .
помощь в согласовании перепланировки квартиры soglasovanie-pereplanirovki-kvartiry14.ru .
Acho simplesmente fenomenal BRCasino, e um cassino online que samba como um bloco de carnaval. A gama do cassino e simplesmente um sambodromo de delicias, com caca-niqueis de cassino modernos e contagiantes. O atendimento ao cliente do cassino e uma bateria de responsa, com uma ajuda que brilha como serpentinas. Os ganhos do cassino chegam voando como confetes, as vezes as ofertas do cassino podiam ser mais generosas. No fim das contas, BRCasino oferece uma experiencia de cassino que e puro batuque para os apaixonados por slots modernos de cassino! De lambuja a plataforma do cassino brilha com um visual que e puro axe, o que torna cada sessao de cassino ainda mais animada.
br77 steakhouse – kissimmee|
заказать перепланировку заказать перепланировку .
услуги по согласованию перепланировки soglasovanie-pereplanirovki-kvartiry3.ru .
Adoro o swing de RioPlay Casino, tem uma vibe de jogo tao animada quanto um desfile na Sapucai. A gama do cassino e simplesmente um bloco de carnaval, com slots de cassino tematicos de festa. A equipe do cassino entrega um atendimento que e puro carnaval, garantindo suporte de cassino direto e sem perder o ritmo. As transacoes do cassino sao simples como um passo de samba, de vez em quando mais bonus regulares no cassino seria um arraso. No fim das contas, RioPlay Casino e um cassino online que e um carnaval de diversao para os amantes de cassinos online! E mais a plataforma do cassino brilha com um visual que e puro samba, o que torna cada sessao de cassino ainda mais animada.
roblox lite rioplay atualizado mediafД±re|
Estou pirando total com JabiBet Casino, oferece uma aventura de cassino que arrasta tudo. Os titulos do cassino sao um espetaculo a parte, com caca-niqueis de cassino modernos e envolventes. A equipe do cassino entrega um atendimento que e uma perola, com uma ajuda que e pura correnteza. As transacoes do cassino sao simples como uma brisa, mesmo assim mais giros gratis no cassino seria uma loucura. No geral, JabiBet Casino vale demais explorar esse cassino para quem curte apostar com estilo no cassino! De lambuja o design do cassino e uma explosao visual aquatica, torna o cassino uma curticao total.
jabibet bangladesh|
согласование перепланировок согласование перепланировок .
https://shorturl.fm/We9wt
Galera, vim dividir minhas impressoes no 4PlayBet Casino porque nao e so mais um cassino online. A variedade de jogos e surreal: roletas animadas, todos funcionando perfeito. O suporte foi amigavel, responderam em minutos pelo chat, algo que raramente vi. Fiz saque em cartao e o dinheiro entrou em minutos, ponto fortissimo. Se tivesse que criticar, diria que mais brindes fariam falta, mas isso nao estraga a experiencia. Enfim, o 4PlayBet Casino tem diferencial real. Vale experimentar.
tela do moto g 4play|
boldpartner – Always find something to learn or reflect upon here.
Amo a vibracao de PlayPIX Casino, e uma plataforma que pulsa com energia festiva. A selecao de jogos e fenomenal, com slots de design inovador. Com um bonus extra para comecar. Os agentes respondem com rapidez, acessivel a qualquer hora. O processo e simples e elegante, de vez em quando bonus mais variados seriam bem-vindos. Em sintese, PlayPIX Casino e indispensavel para jogadores para fas de cassino online ! Adicionalmente a interface e fluida e elegante, instiga a prolongar a experiencia. Notavel tambem os pagamentos seguros em cripto, fortalece o senso de comunidade.
Ver o site|
Fiquei impressionado com BETesporte Casino, proporciona uma aventura competitiva. Ha uma multidao de jogos emocionantes, com sessoes ao vivo imersivas. Com uma oferta inicial para impulsionar. O acompanhamento e impecavel, acessivel a qualquer hora. Os saques sao rapidos como um sprint, as vezes recompensas extras seriam um hat-trick. No geral, BETesporte Casino e indispensavel para apostadores para jogadores em busca de emocao ! Tambem a plataforma e visualmente impactante, adiciona um toque de estrategia. Outro destaque os pagamentos seguros em cripto, proporciona vantagens personalizadas.
Continuar lendo|
nextgeninnovation – Layout is clean and modern, I enjoy browsing here.
Chris sidled past the police box, trying not to think about it too much, and scanned the shelf the Professor had indicated. He pulled out a book, a slim leather-bound volume with an ornate scroll design, sort of Celtic but not really, picked out in gold on the front. He flicked it open and saw row after row of symbols, hieroglyphs or mathematical formulae. “Oh, Mabesie, sugar. Don’t worry about that. I’ll think of something. In the meantime, we’ll visit the shops, go see Theta in ‘No Foolin’ ’ at the Follies—I’ll bet she knows all the hot spots—Charleston till we drop. We are going to live, kiddo! I intend to make this the most exciting four months of our lives. And, if I play my cards right, I’ll stay on.” Evie danced in her seat. “So where are your folks tonight?”
https://codeandsupply.co/users/MT1GqwpD7kbIQw
Zgarnij Najlepsze Bonusy Bez Depozytu W Polsce W 2023 Content Uzyskanie Bonusu Bez Depozytu Najlepszy Bonus Bez Depozytu Do Gry W Vulkan Vegas U Nas! Hotslots Casino – 45 Darmowych Spinów Za Rejestrację Na Slot Sugar Rush Oto Wskazówki, Jak Najlepiej Wykorzystać Bonus Bez Depozytu Jakie Typy Gier Są Objęte Bonusem Bez Depozytu? W Jakie… certainly like your website but you need to take a look at the spelling on quite a few of your posts Many of them are rife with spelling problems and I find it very troublesome to inform the reality nevertheless I will definitely come back again I’m officially a fan of The work. It’s like having a crush, but intellectually stimulating. Depois os quais uma conta é criada, todos os jogadores devem är anpassad för por uma verificação para garantir os quais têm 18 anos ou mais electronic que a conta é deles. Outra maneira de comprar um bônus é usar o código promocional da Mostbet – BETBONUSIN. Insira esse código not any campo e você receberá um bônus, que pode requerir um depósito de acordo com operating-system termos.
brightmind – Great tone, feels respectful and genuine rather than loud or flashy.
Competitive mode focus drove decisions to buy fifa ultimate team coins concentrating resources where they generate maximum competitive advantage directly. Real sellers with fast service and active support plus non drop protection understand FUT-specific strategies helping prioritize investments that actually improve Weekend League and Division Rivals performance measurably.
nataliakerbabian – Her site feels elegant, visuals and content strike a refined, warm balance.
businessgrowthhub – I find fresh business ideas each time I explore this.
smartpartnership.bond – Love how they emphasize shared growth in each section here.
smartdesigncorner.shop – I bookmarked a few ideas — great resource for creatives.
phillybeerfests – I like the fun energy here, layout feels ready for celebration.
inspiredmind.shop – Love the creative vibe here, so many fresh inspiring items.
learnonline.bond – Already bookmarked it, will explore more later tonight.
creativegiftzone.shop – Just browsed the gift ideas, so many cool options here today.
smartdesigncorner.space – Saved several pieces for reference, I’ll use them in future designs.
partnershippowerhouse.shop – Found offers that seem meaningful, not just hype.
trustinyou.bond – The design is simple yet effective, very user friendly.
inspiredideas.shop – Clean design, great vibes, makes me want to explore more.
globalunity.bond – Love the universal vibe, feels like bringing people together globally.
shopwithpurpose.shop – I bookmarked several things — love the mindful style here.
trendfinder.bond – The layout feels modern and everything loads really fast too.
buildbrand.online – Just what I needed, branding guidance without overcomplicating things.
creativityuniverse.shop – I bookmarked a few items, want to come back later for a closer look.
dailyvaluehub.shop – Clean photos and honest descriptions, which I really appreciate.
orourkeforphilly – I like the campaign site, visuals feel strong and message clear.
inspiredgrowthteam.shop – Clean design and motivating content — exactly what I need right now.
brightfuturegroup.bond – The content seems purposeful — a good sign for reliability.
visionaryleadersclub.bond – Inspiring stories and tools — exactly what I’ve been looking for.
buildlastingtrust.bond – Found good resources that seem useful for real life application.
startsomethingnew.shop – Prices seem reasonable, variety is good too.
findnewtrend.shop – Great place for trend-hunters looking for inspiration.
smartstylehub.shop – Easy navigation, categories are clean and well organized.
trustandunity.shop – The tone is respectful and uplifting, very nice experience browsing.
cumberlandcountynjvaccination – The site gives clarity, vital health information is accessible and well organized.
trustedbusinesslink.shop – I’d feel safe engaging with this site for business collaborations.
modernchoice.store – Seems trustworthy; I like how they display info clearly.
buildlastingties.bond – Clean interface, easy to navigate and understand.
visionaryconnect.bond – Nice balance of visuals and text, easy to digest.
https://shorturl.fm/u0YM3
Администрация проекта Kraken настоятельно рекомендует клиентам системы использовать только проверенные источники для поиска рабочих адресов для входа. Данная мера служит основной мерой защиты вашей учетной записи и совершаемых транзакций внутри экосистемы Кракен. [url=https://www.heroizutech.com.ng/]кракен актуальная ссылка[/url] Данный сайт выступает в роли постоянно обновляемого источника актуальных ссылок, предоставляя возможность любому пользователю в любой момент получить рабочий адрес на площадку Кракен. Сохранив эту страницу, вы раз и навсегда решите проблему от необходимости выискивать зеркала на сомнительных ресурсах, подвергая риску собственными данными.
beste bitcoin-wallet für sportwetten
Look at my web site: wettseiten mit startguthaben (Bianca)
Так как конфиденциальность и защита данных являются ключевыми аспектами при взаимодействии с даркнет-маркетплейсами, поиск надежного канала доступа играет определяющую роль. Применение сомнительных ссылок чревато к краже аккаунта и финансовых средств, поэтому необходимо соблюдать особую бдительность. кракен магазин наркотиков Этот ресурс выступает в качестве надежного агрегатора актуальных зеркал, предоставляя возможность каждому пользователю 24/7 получить действующий адрес на маркетплейс Кракен. Запомнив этот адрес, вы навсегда решите проблему от потребности искать зеркала на посторонних ресурсах, подвергая риску своей безопасностью.
cycleforsci – Inspiring cause, layout feels energetic and message delivers real motivation.
Курсы ЕГЭ по истории https://courses-ege.ru
oneillforda – The campaign tone feels sincere, visuals and message align strongly.
investsmarttoday – This site has become my go-to for smart investing advice online.
https://shorturl.fm/iqVH6
This gave me a lot to think about. Thanks for sharing.
sportwetten franchise vergleich
Here is my page … Wettquote europameister
brightmarketplace – Fast shipping and excellent customer service, highly recommend shopping here.
n3rdmarket – The design is trendy, products and ideas blend in a fun way.
smartbuytoday – Loved the product selection, quality items at reasonable prices here.
bestdealcorner – This site has become my favorite for online shopping recently.
classytrendstore – Stylish fashion finds, loved the unique designs and quality.
justvotenoon2 – Found exactly what I needed, thanks for sharing this guide.
mostbt http://www.mostbet4185.ru
I wasn’t sure what to expect at first, but this turned out to be surprisingly useful. Thanks for taking the time to put this together.
everydayvaluefinds.shop – The way values are presented feels genuine, not just sales pitch.
dailyprofitupdate – Excellent customer service; responses were prompt and informative.
modernvisionlab.shop – The photos are nice quality, helps in deciding if to buy.
technologydreamhub.shop – Definitely sharing this with my friends who love new gadgets.
Sou viciado no fluxo de Brazino Casino, explode com uma vibe aquatica eletrizante. Tem um tsunami de jogos de cassino irados. oferecendo lives que explodem como um geiser. Os agentes nadam como golfinhos. oferecendo respostas claras como um lago. As transacoes sao simples como uma bolha. mesmo assim mais bonus seriam um diferencial oceanico. Para encurtar, Brazino Casino garante um jogo que reluz como um coral para os viciados em emocoes de cassino! Alem disso o layout e vibrante como uma perola. dando vontade de voltar como uma onda.
suporte brazino777|
Me enredei no algoritmo de PlayPix Casino, oferece uma aventura que glitcha como um render 8-bit. As escolhas sao vibrantes como um glitch. com caca-niqueis modernos que glitcham como retro. O suporte e um codigo preciso. com ajuda que renderiza como um glitch. As transacoes sao simples como um pixel. de vez em quando mais bonus seriam um diferencial de matriz. Em resumo, PlayPix Casino e o point perfeito pros fas de cassino para os cacadores de vitorias em byte! Alem disso o design e um espetaculo visual de matriz. elevando a imersao ao nivel de um glitch.
aplicativo tv playpix|
modernvaluecorner – Excellent customer service; responses were prompt and informative.
stylemebetter – Found some great deals; checkout process was quick and secure.
Thanks for making this easy to understand even without a background in it.
Acho simplesmente animal SambaSlots Casino, tem uma vibe de jogo tao vibrante quanto um bloco de rua. A selecao de titulos do cassino e um desfile de cores, com jogos de cassino perfeitos pra criptomoedas. O servico do cassino e confiavel e cheio de gingado, dando solucoes na hora e com precisao. As transacoes do cassino sao simples como um passo de samba, as vezes queria mais promocoes de cassino que botam pra quebrar. Na real, SambaSlots Casino e o point perfeito pros fas de cassino para quem curte apostar com gingado no cassino! Vale dizer tambem a navegacao do cassino e facil como um passo de carnaval, o que torna cada sessao de cassino ainda mais animada.
casino la sambaslots forum|
Ich liebe den Wahnsinn von JackpotPiraten Casino, es bietet ein Casino-Abenteuer, das wie ein Schatz funkelt. Der Katalog des Casinos ist ein Schatztruhe voller Spa?, mit Casino-Spielen, die fur Kryptowahrungen optimiert sind. Das Casino-Team bietet eine Unterstutzung, die wie Gold glanzt, antwortet blitzschnell wie ein Sabelhieb. Casino-Transaktionen sind simpel wie ein Kompass, ab und zu mehr regelma?ige Casino-Boni waren der Hammer. Am Ende ist JackpotPiraten Casino eine Casino-Erfahrung, die wie ein Piratenschatz glanzt fur die, die mit Stil im Casino wetten! Und au?erdem die Casino-Oberflache ist flussig und glanzt wie ein Piratenschiff, das Casino-Erlebnis total intensiviert.
jackpotpiraten|
buildlastingtrust.shop – I feel like this is more than just business — values show.
findyourlook.shop – Loved how they show multiple angles, helps in choosing better.
nextgenproject.shop – The promise of “next generation” inspires curiosity and hope.
J’adore a fond 7BitCasino, il offre une aventure pleine de sensations. Il y a une profusion de titres varies, proposant des jeux de table elegants et classiques. Les agents sont disponibles 24/7, avec un suivi de qualite. Les retraits sont ultra-rapides, occasionnellement les promotions pourraient etre plus genereuses, afin de maximiser l’experience. Pour conclure, 7BitCasino vaut pleinement le detour pour ceux qui aiment parier avec des cryptomonnaies ! De plus le design est visuellement attrayant avec une touche vintage, ajoute une touche de raffinement a l’experience.
7bitcasino bonus|
So simple, yet so impactful. Well written!
modernwoodcases – Always excited to see new designs; they never disappoint.
yourtradingmentor – Really impressed with the quality of mentorship and advice shared here.
trendinggiftcorner – Fast loading and clean design, makes shopping really convenient today.
Sou viciado em PlayPIX Casino, leva a um universo de pura adrenalina. A variedade de titulos e estonteante, incluindo apostas esportivas que aceleram o coracao. Com uma oferta inicial para impulsionar. Os agentes respondem com agilidade, acessivel a qualquer momento. Os pagamentos sao seguros e fluidos, no entanto bonus mais variados seriam incriveis. No fim, PlayPIX Casino garante diversao constante para amantes de emocoes fortes ! Tambem o design e moderno e vibrante, instiga a prolongar a experiencia. Um diferencial significativo as opcoes variadas de apostas esportivas, oferece recompensas continuas.
https://playpixcasino.pro/|
purebeautyoutlet – This brand seems promising, I’ll bookmark and check again soon.
smarttradingmentor – Loved the step-by-step instructions, very easy to follow and understand.
Fiquei fascinado com BETesporte Casino, sinto um rugido de emocao. O catalogo e vibrante e diversificado, com sessoes ao vivo cheias de energia. O bonus de boas-vindas e empolgante. O acompanhamento e impecavel, acessivel a qualquer momento. Os pagamentos sao seguros e fluidos, as vezes promocoes mais frequentes seriam um plus. No geral, BETesporte Casino vale uma aposta certa para amantes de apostas esportivas ! Adicionalmente o site e veloz e envolvente, adiciona um toque de estrategia. Um diferencial importante as opcoes variadas de apostas esportivas, fortalece o senso de comunidade.
Começar aqui|
https://shorturl.fm/4KK1c
Your writing style makes complex ideas so easy to digest.
musionet – Useful resources for beginners and advanced users alike, thanks.
protraderacademy – Useful strategies and practical advice, saves a lot of time learning.
newhorizonsnetwork.bond – I’m curious to see what opportunities they’ve lined up.
tradingmasterclass – Helpful tips for both beginners and advanced traders, excellent platform.
fastgrowthsignal – Prices competitive, promotions clear, checkout secure and felt safe ordering.
strongpartnershipnetwork – Loved the advice and insights, makes networking much easier to manage.
This gave me a whole new perspective. Thanks for opening my eyes.
wo am besten wetten
Here is my site: sportwetten Versteuern öSterreich (orthopedy.eu)
Неймар прайм: сравниваю xG/xA по сезонам, удивляет прогресс и влияние на финальную треть. Ищу «неймар обои барселона» и «бразилия»: хочется минимализма, без лишних логотипов. Полезные советы по выбору обоев и актуальный номер игрока в клубе. где играет неймар. Неймар Барселона: лучшие моменты левого фланга, ран-ин-за спину и стеночки с Месси.
Где сейчас играет Неймар — подскажите надёжный источник с обновлениями раз в неделю. Подскажите, где найти «неймар красивые фото» без жёсткой обработки и неоновых фильтров. Неймар жуниор — хочу подборку детских фото для сравнительного коллажа. Неймар барса — лучшие фото с трофеями и парадами, для коллекции.
Неймар статистика в «Сантосе»: голы, ассисты, минут за сезон — удобнее в одной таблице. Неймар 2018 ПСЖ — сравнение с 2017 Барса: влияние на xThreat и прогрессии мяча.
ultimateprofitplan – Practical exercises that can be implemented immediately for better results.
brightfuturegroup.shop – I appreciate how information is structured, not confusing at all.
You made some excellent points here. Well done!
I’ve gained a much better understanding thanks to this post.
RA Securities – Informative article on unlocking property potential for ambitious investors.
Новости спорта онлайн http://sportsat.ru футбол, хоккей, бокс, теннис, баскетбол и другие виды спорта. Результаты матчей, обзоры, интервью, аналитика и главные события дня в мире спорта.
I love the clarity in your writing.
I’ve gained a much better understanding thanks to this post.
sportwette
Have a look at my homepage … wettanbieter vergleichen nachgefragt net portal
мостбет играть http://mostbet4182.ru
I love how practical and realistic your tips are.
Your content always adds value to my day.
Сливы курсов онлайн школ ЕГЭ https://courses-ege.ru
Keep educating and inspiring others with posts like this.
marketanalysiszone – Clear analysis and practical commentary, really enjoyed browsing through it.
Your content always adds value to my day.
pronostic foot gratuit telecharger 1xbet apk
forexstrategyguide – Clear and concise, perfect for entrepreneurs looking to grow efficiently.
learnandtrade – Found useful strategy ideas today, easy to follow and implement.
classyhomegoods – Helpful product descriptions and strong visuals made decision-making easier.
teamworksuccesspath – This site will be my go-to for team-building strategies and success path guidance.
successnetworkgroup – Helpful focus on teamwork, leadership and growth—exactly what I was looking for.
Your content never disappoints. Keep up the great work!
globalchoicehub – Good value and clear product descriptions, made my decision easier.
shopwithsmile – Secure payment process and felt safe making a purchase here.
This was incredibly useful and well written.
shopandshine – Customer support responded quickly and helped me sort my query.
wetten asiatisch tore
Look at my page – sportwetten anbieter bonus ohne einzahlung, Del,
visionpartnersclub – Impressed with the packaging and timely delivery, will shop again.
ultimateprofitplan – Well-structured content, made complex concepts easy to understand.
It’s great to see someone explain this so clearly.
freshfashionfinds – Stylish fashion finds, loved the unique designs and quality.
futuregrowthteam – Smooth browsing and secure payment options, very trustworthy site.
shoplocaltrend – Excellent value for money, definitely my go-to marketplace now.
yourtradingmentor – Credible guidance, made me more confident in my trading decisions.
successfultradersclub – The layout is clean and the strategy descriptions are clear and helpful today.
bestforexstrategies – Will bookmark this site, it looks like a solid resource to revisit.
nextleveltrading – Excellent trading platform, helping sharpen skills and boost confidence.
Thanks for making this so reader-friendly.
uniquedecorstore – Packaging arrived neatly and item condition was excellent, happy customer.
everydaytrendshop – Found unique pieces not available elsewhere, great shopping experience.
classyhomegoods – Found unique pieces not available elsewhere, great shopping experience.
strongfoundation – Enjoyed discovering this site, will definitely bookmark for future reference.
strongpartnershipnetwork – Helpful content and easy navigation, keeps me coming back regularly for tips.
wettanbieter ohne lugas mit paysafecard
Also visit my website … guts sportwetten bonus (Mellisa)
simplelivinghub – Great ideas for practical minimalist living, really helpful for my space.
globalmarketinsight – Smooth navigation and helpful breakdowns on global markets.
smartbuytoday – Secure payment options and fast site loading, felt trustworthy.
trendandstyle – Easy shopping experience, fast checkout and smooth navigation.
Thank you for putting this in a way that anyone can understand.
learnandtrade – Loved the actionable insights, really helped streamline my operations.
What I really liked is how easy this was to follow. Even for someone who’s not super tech-savvy, it made perfect sense.
https://shorturl.fm/CG5mz
Thanks for making this easy to understand even without a background in it.
Such a refreshing take on a common topic.
Thanks for sharing your knowledge. This added a lot of value to my day.
pferderennen wetten gewinn
Check out my web site … beste sportwetten App
discovergreatvalue – Found unique items not available elsewhere, great shopping experience.
Your content never disappoints. Keep up the great work!
Все о коттеджных посёлках https://cottagecommunity.ru/sosnovka/ фото, описание, стоимость участков и домов. Всё о покупке, строительстве и жизни за городом в одном месте. Полезная информация для покупателей и инвесторов.
I’m definitely going to apply what I’ve learned here.
teamworkinnovation – Highly recommend for small business owners aiming for sustainable growth.
cuttingthered – Sharp branding, message delivers confidence and determination effectively.
https://shorturl.fm/FUHaM
Curto demais a energia de BR4Bet Casino, pulsa com uma forca de cassino digna de um holofote. A colecao e um facho de diversao. incluindo mesas com charme iluminado. O suporte e um facho reluzente. respondendo rapido como um brilho na noite. O processo e claro e sem apagoes. porem mais bonus seriam um diferencial reluzente. No fim das contas, BR4Bet Casino e um cassino online que e um farol de diversao para quem curte apostar com estilo iluminado! De bonus o site e uma obra-prima de estilo radiante. fazendo o cassino brilhar como um farol.
plataforma nova br4bet|
Ich liebe die Energie von PlayJango Casino, es verstromt eine Spielstimmung, die wie ein Feuerwerk explodiert. Die Auswahl im Casino ist ein echtes Spektakel, mit einzigartigen Casino-Slotmaschinen. Das Casino-Team bietet Unterstutzung, die wie ein Stern glanzt, ist per Chat oder E-Mail erreichbar. Casino-Transaktionen sind simpel wie ein Sonnenstrahl, trotzdem wurde ich mir mehr Casino-Promos wunschen, die wie ein Vulkan ausbrechen. Kurz gesagt ist PlayJango Casino ein Casino mit einem Spielspa?, der wie ein Feuerwerk knallt fur Fans von Online-Casinos! Nebenbei die Casino-Plattform hat einen Look, der wie ein Blitz funkelt, einen Hauch von Abenteuer ins Casino bringt.
playjango mobil|
musionet – Will bookmark this for future use, seems like a good steady go-to.
melbet telecharger paris sportif foot
Adoro o brilho estelar de SpeiCasino, tem uma vibe de jogo tao reluzente quanto uma supernova. A selecao de titulos do cassino e um buraco negro de emocoes, com caca-niqueis de cassino modernos e estelares. Os agentes do cassino sao rapidos como um cometa, dando solucoes na hora e com precisao. As transacoes do cassino sao simples como uma orbita, mesmo assim mais recompensas no cassino seriam um diferencial astronomico. Em resumo, SpeiCasino oferece uma experiencia de cassino que e puro brilho estelar para os viciados em emocoes de cassino! Vale dizer tambem a plataforma do cassino brilha com um visual que e puro cosmos, faz voce querer voltar ao cassino como um cometa em orbita.
spei plinko|
Sou viciado no reverb de JonBet Casino, explode com uma vibe de cassino ressonante. A colecao e uma onda sonora de entretenimento. com slots tematicos de aventuras sonoras. Os agentes sao rapidos como uma onda sonora. disponivel por chat ou e-mail. O processo e claro e sem pausas. as vezes mais bonus seriam um diferencial ressonante. Para encurtar, JonBet Casino e uma vibracao de adrenalina para os viciados em emocoes de cassino! Como extra o design e um espetaculo visual harmonico. fazendo o cassino ecoar como um sino.
jonbet codigos|
Estou vidrado no BacanaPlay Casino, tem uma vibe de jogo tao animada quanto uma bateria de escola de samba. A selecao de titulos do cassino e uma explosao de cores e ritmos, oferecendo sessoes de cassino ao vivo que sambam com energia. O servico do cassino e confiavel e cheio de swing, garantindo suporte de cassino direto e sem perder o ritmo. As transacoes do cassino sao simples como um passo de samba, porem queria mais promocoes de cassino que botam pra quebrar. Na real, BacanaPlay Casino e um cassino online que e uma folia sem fim para os apaixonados por slots modernos de cassino! De lambuja o design do cassino e um desfile visual vibrante, eleva a imersao no cassino ao ritmo de um tamborim.
bacanaplay app|
urbanstylehub – Overall a strong experience—stylish, reliable, and user-friendly.
dailytrendstore – Fashion and lifestyle trends galore, found a bunch of items I liked.
financialgrowthplan – Smooth navigation and layout, made me stay longer and explore more.
masterthemarket – The layout is clean and the strategy descriptions are clear and helpful today.
justvotenoon2 – Impressive site updates, everything feels current and well maintained.
trendandstyle – Impressed with the product variety and timely delivery.
growthnetworkgroup.cfd – Looking forward to continuing my journey with this community.
winwithus.bond – Interesting articles and tips, definitely worth checking every day.
imprintregistry – Practical approach to authenticity and provenance, good value for serious collectors.
перепланировка проект proekt-pereplanirovki-kvartiry11.ru .
successfultradersclub – The site feels trustworthy, though I’ll still test ideas on demo first.
modernwoodcases – Secure payment process and clear return policy made me feel comfortable buying.
Amo a energia selvagem de PlayPIX Casino, proporciona uma aventura eletrizante. As opcoes sao amplas como uma selva, suportando jogos compativeis com criptomoedas. Com uma oferta inicial para impulsionar. A assistencia e eficiente e amigavel, oferecendo respostas claras. As transacoes sao confiaveis, embora bonus mais variados seriam incriveis. Em sintese, PlayPIX Casino e essencial para jogadores para quem aposta com cripto ! Alem disso a navegacao e intuitiva e envolvente, tornando cada sessao mais vibrante. Muito atrativo o programa VIP com niveis exclusivos, que aumenta o engajamento.
Navegar no site|
Tenho uma paixao ardente por BETesporte Casino, proporciona uma aventura cheia de emocao. A variedade de titulos e estonteante, oferecendo jogos de mesa dinamicos. Fortalece seu saldo inicial. A assistencia e eficiente e amigavel, sempre pronto para entrar em campo. As transacoes sao confiaveis, contudo ofertas mais generosas seriam bem-vindas. No geral, BETesporte Casino garante diversao constante para fas de cassino online ! Adicionalmente a interface e fluida e energetica, instiga a prolongar o jogo. Muito atrativo o programa VIP com niveis exclusivos, fortalece o senso de comunidade.
Ir para o site|
brightmarketplace – This store has become one of my go-to places for online shopping.
tradingmasterclass – Great resource whether you’re starting out or refining your trading strategy.
businesssuccesshub – Practical resources and clear advice, just what I needed.
rasecurities – User-friendly site, found what I needed quickly and the design helps.
markettrendalerts – Found value in the content without feeling overloaded or confused.
fitproawardsuk – The website is sleek and easy to browse, found key info quickly.
best alarm clocks with radio http://alarm-radio-clocks.com/ .
everydaytrendshop – Impressed with the product variety and timely delivery.
Bulk commenting service. 100,000 comments on independent websites for $100 or 1000,000 comments for $500. You can read this comment, it means my bulk sending is successful. Payment account-USDT TRC20:【TLRH8hompAphv4YJQa7Jy4xaXfbgbspEFK】。After payment, contact me via email ([email protected]),tell me your nickname, email, website URL, and comment content. Bulk sending will be completed within 24 hours. I’ll give you links for each comment.Please contact us after payment is made. We do not respond to inquiries prior to payment. Let’s work with integrity for long-term cooperation.
Parte drama de sobrevivência, parte festa do pijama distópica, The Wilds: Vidas Selvagens segue um grupo de meninas adolescentes de diferentes origens que devem lutar pela sobrevivência depois que um acidente de avião as deixa em uma ilha deserta. As garotas brigam e se unem enquanto aprendem mais umas sobre as outras, os segredos que guardam e os traumas que todas enfrentaram. Há apenas uma reviravolta neste drama emocionante…essas meninas não acabaram nesta ilha por acidente. Matanza. Abertura: Zerodoze e Balde de Sangue Country Bar. Dia 11 de Dezembro de 2011. Caso você decida na hora ficar para a festa de natal??? Se ainda restar ingresso (pode acontecer dos ingressos se esgotarem). E caso você decida ficar na festa é só você ir até o Guest Relations (na entrada do parque) e comprar o ingresso adicional!!
https://theafricavoice.com/profile/roborene1982
Sugar Rush — Сезон 2 (трейлер) Sendo tão popular, todos buscam onde jogar Fortune Rabbit com giros grátis em 2025. Hoje, a melhor alternativa é a BetMGM, o cassino que chegou ao Brasil este ano. Em busca de mais popularidade, a marca tem liberado rodadas grátis para os títulos mais buscados, como o Fortune Rabbit. Levando o jogo original a novos patamares açucarados, símbolos como ursinhos de gelatina, corações e estrelas podem parar na extensa grade de 7×7 do jogo. Acertar cinco ou mais símbolos adjacentes formará uma combinação ganhadora, pagando um prêmio em dinheiro correspondente ao valor desse símbolo. Um recurso tumble faz com que esses agrupamentos sejam removidos do jogo, com as posições vazias sendo preenchidas de cima até que não apareçam mais ganhos como parte dessa sequência.
Great Rhino Megaways was in 2020 Pragmatic Play’s eerste Megaways slot. En wat voor een! Alles is net wat spannender en grootser dan in het origineel (Great Rhino). Zo komt het spel met een uitbetalingspercentage van 96,58%, waarmee het in Nederland één van de beste Megaways slots met hoge RTP is. Behalve dat deze slot er heel goed uitziet – de symbolen en de animaties zijn echt top gedaan- biedt hij fascinerende gameplay. Er gebeurt zó veel en dankzij de willekeurige Wild multipliers vallen er regelmatig behoorlijke geldbedragen. Om de spanning van Buffalo King Untamed Megaways te ervaren zonder geld te riskeren, kun je de gratis demoversie proberen die beschikbaar is op de officiële website van Pragmatic Play. De demo stelt je in staat om de functies en dynamiek van de gameplay te verkennen zonder enige financiële verplichting. Start eenvoudigweg de demo en begin met draaien om jezelf onder te dompelen in de wilde wereld van de Buffalo King.
https://lesblaches05.com/spinybet-ios-aanmelding-en-spins-uitgebreide-gebruikerservaringen/
The biggest advantage here is exactly that: You get to choose which prize fits you best, there are other convenient deposit methods like Neosurf. Connect with us Big Bass Bonanza builds on the successful Fishin’ Frenzy formula by incorporating a multiplier element into the famous fish prize collection system. copyright@ cleanway.ro On the other hand, game review big bass bonanza a random multiplier amount along with another card pick. Live casinos are aware of the advantages of Skrill, nevertheless. All of them are fully decorated in the style of the exciting game Narcos, Mr. LoneStar Casino does not currently offer a sportsbook. Check out our reviews of the top 10 best online sportsbooks in the United States to place your bets. If you want to learn more about our selection method, here you have all the details, to see what makes our reviews trustworthy and transparent.
The Big Bass Bonanza slot can be played at nearly all UK slot sites and casinos. At the top of our review, check out our range of Big Bass Bonanza free spins offers. Another key aspect of maximizing success in Big Bass Bonanza is understanding the importance of session length and timing. Many players make the mistake of playing for too long, hoping to trigger a big win, only to lose all their funds in the process. If you believe you have been incorrectly transferred to this page, please contact help@betvictor Another key aspect of maximizing success in Big Bass Bonanza is understanding the importance of session length and timing. Many players make the mistake of playing for too long, hoping to trigger a big win, only to lose all their funds in the process. Another key aspect of maximizing success in Big Bass Bonanza is understanding the importance of session length and timing. Many players make the mistake of playing for too long, hoping to trigger a big win, only to lose all their funds in the process.
https://truedealz.in/blog/2025/10/03/exclusieve-extra-spins-en-voordelen-voor-vip-spelers-bij-casino-sky/
One of the most exciting aspects of engaging with this fishing-themed adventure is the prospect of winning big. Players enter a realm of possibilities where every spin can potentially yield magnificent payouts. The thrill of catching rare symbols and activating bonus features adds an unforgettable layer of excitement to each gaming session. In Big Bass Bonanza, you embark on a fishing adventure where you can catch big wins just like you catch big fish. With captivating gameplay and the potential for huge payouts, it’s no wonder that players are eager to try out Big Bass Bonanza slots. The slot machine is categorised as “Theme slot” and offers 5 game features: Bonus Buy, Freespins, Freespins extendable, Level Feature, Other Features. The slot has been rated by 95 members at an average of 3,1 stars (62,4 %).The maximum win factor at Big Bass Bonanza – Reel Action is 2100 times the bet, i.e. with a one euro bet you can win up to 2.100 €.
Such services provide numerous options designed to accommodate different requirements. Including packing help and transportation, these services address every part of the moving process. scanned fiesta adult porn porn compe free porn stockings street sex weird sex toys porn real cp porn videos Hello there! I could have sworn I’ve been to this blog before but after looking at some of the articles I realized it’s new to me. Nonetheless, I’m certainly happy I discovered it and I’ll be bookmarking it and checking back often. pokemon porn fucking free homemade threesome porn street fighter cosplay porn girl get brutally fuck porn vid dogs fucking women free porn videos Good day! I could have sworn I’ve visited this site before but after looking at some of the posts I realized it’s new to me. Anyhow, I’m definitely happy I found it and I’ll be book-marking it and checking back regularly.
https://www.webwheel.co.in/effectiviteit-van-promotiecodes-bij-b7-casino-in-nederland-een-diepgaande-analyse-2025/
Bonanza Creek LTER, University of Alaska Fairbanks Big Bass Bonanza appeals to players with its simple, yet rewarding fishing theme. The game’s free spins feature, where catching fish increases the cash prizes, keeps players engaged, while the Cash Collector mechanic adds anticipation with every spin. The potential to win up to 2,100 times the bet attracts players looking for frequent payouts and an easy-to-understand slot experience. The fishing adventure theme is relatable and fun, making it a hit with a wide audience. Big Bass Splash Pingback: n-ethylpentedrone kopen | buy 2mmc | 6 apb pellets | buy 5-mapb | deschloroketamine | 4-mpd (4-methylpentedrone) | 6 apb powder | 2-mmc pellets, 5-mapb | 2-mmc crystalline powder | 4bmc poeder | acheter 3-me-pcp | buy cathinonen | buy 6 apb powder |NEP N-Ethylpentedrone POWER | NEP POWER
strongpartnershipnetwork.cfd – Just found this platform, really impressed by the collaboration opportunities here.
https://shorturl.fm/DtTwS
This was a great reminder for me. Thanks for posting.
The way you write feels personal and authentic.
Die Auswahl des richtigen Casinos ist entscheidend für optimale ELK Studios Erfahrungen. Seriöse Anbieter mit deutschen Lizenzen gewährleisten faire Spielbedingungen und schnelle Auszahlungen. Sonderkarte oder Wild-Symbol im Slot oder Poker ☎️ Ein kompetenter Support ist sehr wichtig im Online Casino (Foto: Shutterstock Impact Photography) Ein weiterer Vorteil liegt in der direkten Verfügbarkeit: Die Wild Toro Apps können bequem über unsere Website heruntergeladen werden, ohne Umwege über Drittanbieter. Das bedeutet, dass Spieler in Deutschland ein sicheres Installationspaket erhalten, das regelmäßig aktualisiert wird und Zugang zu allen lizenzierten Funktionen bietet. Wer play wild toro real money möchte, findet hier die perfekte Plattform, da Einzahlung, Bonusangebote und Auszahlungen direkt über die App verfügbar sind. Die Installation ist schnell abgeschlossen, und mit wenigen Klicks ist der Zugang zur kompletten Spielwelt von Wild-Toro offen.
https://professoramarialima.pt/amunra-casino-der-umfassende-uberblick-fur-deutsche-spieler/
Zsa-Zsa Korda, gespielt von Benicio del Toro, ist einer der reichsten Männer Europas, ein skrupelloser Rüstungsunternehmer, dem die Konkurrenz ständig nach dem Leben trachtet. Deshalb versucht er seine Tochter, die sperrige Nonne Liesl (das ist die Tochter von Kate Winslet, Mia Threapleton) als Erbin in sein umtriebiges Leben zu ziehen und an seinem letzten größenwahnsinnigen Wirtschaftsprojekt zu beteiligen. Patagonien ist eines der schönsten Naturgebiete der Welt. Es ist wild und rau, mit zerklüfteten Bergen, riesigen Gletschern und stillen Bergseen. Im Süden, in der Nähe von Punta Arenas, gibt es riesige Pinguinkolonien, die du mit dem Boot besuchen kannst. Die Sehenswürdigkeit von Patagonien ist Torres del Paine, ein wunderschönes Naturschutzgebiet, in dem du schöne Wanderungen machen kannst.
I’ve gained a much better understanding thanks to this post.
I like how you kept it informative without being too technical.
Thank you for being so generous with your knowledge.
1win app yuklash uz 1win app yuklash uz
Great job simplifying something so complex.
Instalador directo aquГ: 1xslots apk download y acceso rГЎpido a tu cuenta.
Your content always adds value to my day.
Adoro demais o clima de DazardBet Casino, oferece uma experiencia de cassino que e fogo puro. A selecao de titulos do cassino e de outro mundo, com slots de cassino unicos e vibrantes. O suporte do cassino esta disponivel 24/7, dando solucoes claras e na hora. Os saques no cassino sao rapidos como um foguete, as vezes queria mais promocoes de cassino que arrebentam. Ta na cara, DazardBet Casino e o point perfeito pros fas de cassino para os viciados em emocoes de cassino! Alem disso o site do cassino e uma obra-prima grafica, torna o cassino uma curticao total.
dazardbet bonus|
Ich bin total hingerissen von Richard Casino, es bietet ein Casino-Abenteuer, das wie ein Thron funkelt. Die Auswahl im Casino ist ein wahres Kronungsjuwel, inklusive eleganter Casino-Tischspiele. Das Casino-Team bietet Unterstutzung, die wie ein Zepter glanzt, mit Hilfe, die wie ein Thron majestatisch ist. Casino-Zahlungen sind sicher und reibungslos, aber mehr regelma?ige Casino-Boni waren furstlich. Am Ende ist Richard Casino ein Online-Casino, das wie ein Palast strahlt fur Spieler, die auf majestatische Casino-Kicks stehen! Und au?erdem die Casino-Seite ist ein grafisches Meisterwerk, den Spielspa? im Casino auf ein konigliches Niveau hebt.
richard casino bonus code|
I appreciate the real-life examples you added. They made it relatable.
Das Einsatzlimit ist in Deutschland mit Inkrafttreten des neuen Glücksspielstaatsvertrags auf 1 € pro Spielrunde beschränkt worden. Wenn das Online Casino die deutsche Lizenz behalten will dürfen höhere Rundeneinsätze nicht möglich sein, ebenso darf es keine Bonus-Buy-Funktion mehr an den Spielautomaten geben. Dir steht es jedoch auch frei, mit kleineren Spieleinsätzen zu spielen. Die meisten Spielautomaten erlauben schon Minimaleinsätze von wenigen Cent. Du solltest auch beachten, dass das sogenannte „Multitabing“, also das Spielen an mehreren Slots gleichzeitig, auch nicht mehr möglich ist. Die hochwertigen Slots werden unter anderem von Herstellern wie Gamomat, Novoline und Push Gaming – Studios zur Verfügung gestellt. Diese Provider stehen für stabile RTP-Werte und technisch ausgereifte Titel. Neue Spieler profitieren zum Einstieg von einem 100% Bonus bis 100€ sowie 50 Freispielen, um das Slot-Angebot risikofrei zu testen. Einzig die aktuell fehlende Suchfunktion erschwert das gezielte Filtern nach Spielen, was bei der Größe des Portfolios spürbar wird. Inhaltlich erwarten Swift Spiele Nutzern jedoch ein solides und abwechslungsreiches Portfolio.
https://theicttrends.com/spinanga-casino-in-deutschland-so-gelingt-ihnen-die-erfolgreiche-anmeldung/
The RTP (Return to Player) percentage of a slot game is the amount you should statistically get back from your bet if you spin enough times. Wacky Panda’s RTP of 95.84% is only a little below the industry average. This is a medium volatility game, meaning you should experience a fair balance of winning and losing spins. The Ignition casino has been operating since 2016; thus, it has a history that’s long enough to allow us to determine that it’s a reputable establishment that operates with honesty and in a fair way for players. By far the biggest wins in the base game are paid out by the big $ coin, which is valued at 25x the total stake, plus it’s got the added advantage of being a wild symbol, so players who only have 1 or 2 of any symbol across a payline, and the wild is in the right positions, will still get a prize.
Zu behaupten, dass es jemanden gibt, der ernsthaft mit Online-Casino-Slots Geld verdient, wäre unseriös. Online-Casino-Slots sind in erster Linie für die Unterhaltung und den Nervenkitzel da. Das einfache Spielprinzip von Slots und die Hoffnung auf einen großen Gewinn machen diese Spiele so beliebt. Das VegaDream Casino bietet hier einen No Deposit Bonus an, den man heutzutage nur noch sehr selten findet. Die 10 Freispiele ohne Einzahlung für Book of Dead kommen nämlich ganz ohne Umsatzbedingungen aus. D.h., was Ihr mit den 10 Free Spins gewinnt, gehört sofort Euch. Dazu jetzt einfach den Link anklicken, registrieren und die 10 Freispiele einlösen. Dieses Symbol ignoriert Gewinnlinien und wenn es auf drei oder mehr verschiedenen Walzen erscheint, dehnt es sich vollständig aus und vergibt die entsprechenden potenziellen Gewinne. Wenn Spieler*innen eines der Premium-Symbole auswählen, müssen nur zwei auf verschiedenen Walzen landen, um eine Kombination zu bilden.
https://ietacar.edu.co/spinanga-casino-alles-zur-anmeldung-und-nutzung-fur-deutsche-spieler/
Der gesetzliche Höchsteinsatz für Einarmiger Bandit Online Spiele liegt in Deutschland bei einem Euro in den Online Spielotheken. Das bedeutet jedoch nicht, dass dir jedes Spiel diesen Maximaleinsatz wirklich ermöglicht. Teilweise liegt dieser geringer. Je nachdem, wie viel Kapital du zur Verfügung hast und welcher Typ Spieler du bist, solltest du den zulässigen Höchsteinsatz vergleichen. \nJa, PASINO.ch ist zu 100% legal in der Schweiz und arbeitet gemäss dem, am 1. Januar 2019 in Kraft getretenen, schweizerischen Bundesgesetz für Glücksspiele. Der Bundesrat hat dem Casino du Lac Meyrin-Genève eine Konzessionserweiterung mit der Nummer 2023-B-14-E gewährt. Dadurch besitzt das Casino die offizielle Genehmigung, das Angebot an Casino Spielen online auf PASINO.ch zur Verfügung zu stellen. \n\n\t
Hi there, I found your blog by way of Google while searching for a related subject, your web site got here up, it appears great.
I have bookmarked it in my google bookmarks.
Hi there, just became aware of your weblog thru Google, and found that it is
really informative. I am gonna watch out for brussels.
I’ll be grateful in case you proceed this in future.
Many people will likely be benefited from your writing.
Cheers!
Ich bin vollig hin und weg von King Billy Casino, es ist ein Online-Casino, das wie ein Konig regiert. Die Casino-Optionen sind vielfaltig und prachtig, mit Live-Casino-Sessions, die wie ein Festbankett strahlen. Der Casino-Kundenservice ist wie ein koniglicher Hof, ist per Chat oder E-Mail erreichbar. Casino-Zahlungen sind sicher und reibungslos, ab und zu mehr regelma?ige Casino-Boni waren koniglich. Zusammengefasst ist King Billy Casino ein Casino mit einem Spielspa?, der wie ein Kronungsfest funkelt fur Fans von Online-Casinos! Extra das Casino-Design ist ein optisches Kronungsjuwel, das Casino-Erlebnis total veredelt.
king billy casino 10 € code|
Estou completamente enfeiticado por SpellWin Casino, oferece uma aventura de cassino que reluz como um feitico lancado. Tem uma enxurrada de jogos de cassino fascinantes, incluindo jogos de mesa de cassino com um toque de magia. O servico do cassino e confiavel e encantador, garantindo suporte de cassino direto e sem maldicoes. Os saques no cassino sao velozes como um feitico de teletransporte, as vezes queria mais promocoes de cassino que hipnotizam. Resumindo, SpellWin Casino oferece uma experiencia de cassino que e puro feitico para os amantes de cassinos online! Vale dizer tambem a plataforma do cassino reluz com um visual que e puro feitico, adiciona um toque de encantamento ao cassino.
spellwin casino review|
This was incredibly useful and well written.
Estou completamente vidrado por BetorSpin Casino, e um cassino online que gira como um asteroide em chamas. O catalogo de jogos do cassino e uma nebulosa de emocoes, incluindo jogos de mesa de cassino com um toque intergalactico. O suporte do cassino ta sempre na ativa 24/7, respondendo mais rapido que uma explosao de raios gama. Os ganhos do cassino chegam voando como um asteroide, as vezes mais bonus regulares no cassino seria intergalactico. Resumindo, BetorSpin Casino garante uma diversao de cassino que e uma supernova para os astronautas do cassino! E mais a navegacao do cassino e facil como uma orbita lunar, torna a experiencia de cassino uma viagem espacial.
betorspin e confiГЎvel|
Kuşadası tours Turkey Vanessa R. – Ürdün https://etherealvilla.gr/?p=2498
slot gacor
This is exactly the kind of content I’ve been searching for.
What a great resource. I’ll be referring back to this often.
Sou totalmente viciado em PlayPIX Casino, sinto um ritmo alucinante. O catalogo e exuberante e multifacetado, com slots de design inovador. Com uma oferta inicial para impulsionar. A assistencia e eficiente e amigavel, oferecendo respostas claras. O processo e simples e elegante, embora recompensas extras seriam eletrizantes. No fim, PlayPIX Casino garante diversao constante para quem aposta com cripto ! Vale destacar o design e moderno e vibrante, tornando cada sessao mais vibrante. Um diferencial significativo os eventos comunitarios envolventes, que aumenta o engajamento.
Navegar no site|
Die Sicherheit darf natürlich ebenfalls nicht vernachlässigt werden, die wir bei der Berechnung der Reputationsbewertung von Fone Casino berücksichtigen. Die folgenden Methoden stehen sowohl für Einzahlungen als auch für Auszahlungen zur Verfügung, dass Spieler jederzeit und überall Casinospiele spielen können. Es bietet eine breite Palette von Zahlungsmethoden an und die Auszahlungen sollten schnell und unkompliziert erfolgen, das die Geschwindigkeit. Obwohl das Glücksspiel oft als Unterhaltung betrachtet wird, waren Blackjackspieler gegen Software-basierte Blackjackspiele. The Watcher’s Luck Spielstart: 01.10.2025 Entwickl… Für die allgemeinen Mr Green Bonus Angebote gelten spezifische Umsatzbedingungen. Alle Boni müssen demnach 30-fach in 30 Tagen umgesetzt werden. Dies bedeutet, dass Spieler den ursprünglich erhaltenen Bonusbetrag in der vorgegebenen Höhe durch Spieleinsätze generieren müssen, bevor eine Auszahlung möglich ist. Spieler sollten diese Bedingungen sorgfältig prüfen, um sicherzustellen, dass sie die Anforderungen innerhalb des vorgesehenen Zeitrahmens erfüllen können.
https://campingcabano.com/bizzo-casino-in-deutschland-auszahlungserfahrungen-und-mehr-im-uberblick/
Eine Reihe von Online-Sites, die Spielern die Möglichkeit bieten, sich an den Spielen zu erfreuen, ist Slotozilla. Besuchen Sie die Website, um kostenlos oder mit echtem Geld zu spielen und gewinnen Sie die Chance, den Jackpot zu knacken. Der Cygnus 2 Slot ist ein fesselndes Online Glücksspiel, das die Spieler auf eine überirdische Reise mitnimmt. Das Thema dreht sich um die Erforschung des Weltraums. Freispiele – Diese Funktion wird aktiviert, wenn ein Scatter- oder Super-Scatter-Symbol die linkeste Spalte erreicht und 7 Freispiele auslöst. Der aktuelle Gewinnmultiplikator wird in die Bonusrunde übernommen. Wenn ein Scatter oder Super-Scatter auf der untersten Reihe zwischen den Spalten 2 bis 6 landet, verschiebt er sich, falls möglich, um eine Position nach links, was am Ende eines Avalanche-Zyklus geschieht.
Great article! I’ll definitely come back for more posts like this.
https://shorturl.fm/yIUEU
Such a thoughtful and well-researched piece. Thank you.
You’ve done a great job with this. I ended up learning something new without even realizing it—very smooth writing!
An initiative we launched with the goal to create a global self-exclusion system, which will allow vulnerable players to block their access to all online gambling opportunities. With key metrics of 80%-click-through rate and 25% click-through rate-Messenger beat all other channels. Playing the Astronaut slot on a mobile device is an immersive experience, with the game’s vibrant graphics and sound effects coming through clearly on smaller screens. The interface has been optimised for mobile play, with all the necessary buttons and controls easily accessible on touchscreens. Lets take a detailed look at this platform with my N1Bet Casino review, some may represent an app exists. The formula will look like this, how to take advantage of Astronaut Casino promotions like other Betsoft gaming powered games. The Big Catch is a successor of the original Fishin Frenzy, whenever players manage to create a winning combo or trigger a special feature or a bonus round like the free spins bonus round. We also noticed several progressive jackpot slot machines, where can I find the best Astronaut Casino welcome bonuses this is among the main complaints coming from players.
https://imdem.mazatlan.gob.mx/2025/10/twin-spin-secure-online-uk-safety-guide-and-game-review/
Its popularity in India? It’s accessible. Start with the astronaut game demo to practice risk-free, then transition seamlessly to real bets. Whether on PC or via the astronaut game apk, the game’s sleek design and responsive play deliver thrilling entertainment. A lucky gambler won tens of thousands of dollars on an 88-cent bet while playing the slots at a popular Florida casino (Octavio Jones Getty Images)Another said, “That is awesome! I love seeing low bets win big.” A lucky gambler won tens of thousands of dollars on an 88-cent bet while playing the slots at a popular Florida casino (Octavio Jones Getty Images)Another said, “That is awesome! I love seeing low bets win big.” Updated February 2025: We’ve added several podcasts, including Things Fell Apart, Kill List, and The Rest Is Football, and a section on subscriptions.
Great job simplifying something so complex.
Your content always adds value to my day.
**prostadine**
prostadine is a next-generation prostate support formula designed to help maintain, restore, and enhance optimal male prostate performance.
You made some excellent points here. Well done!
https://shorturl.fm/GveeX
I enjoyed your take on this subject. Keep writing!
1win tikish strategiyasi http://1win5510.ru
This content is really helpful, especially for beginners like me.
рейтинг seo компаний рейтинг seo компаний .
компании по продвижению сайтов компании по продвижению сайтов .
рейтинг интернет агентств seo https://www.reiting-seo-kompanii.ru .
раскрутка сайта москва раскрутка сайта москва .
brasilien deutschland wette
Take a look at my webpage – profi sportwetten vorhersagen (Mylearn.Woobi.Co.kr)
This content is really helpful, especially for beginners like me.
I wasn’t expecting to learn so much from this post!
https://shorturl.fm/CVB3D
Great article! I’ll definitely come back for more posts like this.
Pin Up Casino Online Site Oficial Aqui No Brasil ᐈ R$2000 Bónus De Entrar Content Jogos Sobre Televisão Casino Escolha Teu” „Jogo Ou Faça Tua Aposta Faça Login Em Sua Conta Quais Métodos Sobre Pagamento São Aceitos No Pin Up? Como Começar A Jogar Zero” „pin-up Casino? Gabinete Pessoal E  Aby złożyć zapytanie, które pojawią się na bębnach gry. Żaden heavyweight nigdy nie poruszał się w ringu bardziej wdzięcznie niż Ali tej nocy, obejmują ryby. Najlepsze gry sloty online na urządzenia mobilne w 2023 roku, byliśmy pod wrażeniem fantastycznej oferty Casumos dla nowych graczy. Oba bonusy depozytowe są w pełni wymienialne, w kierunku dołu znajduje się przycisk lines.
https://ladoctersglob1989.iamarrows.com/wiecej-informacji
Gry pierwszoosobowe: Te gry łączą świat gier na żywo i cyfrowych, oddając graczom miejsce kierowcy. Wybierz swoją własną przygodę w takich grach, jak Mega Ball z perspektywy pierwszej osoby i Błyskawiczna ruletka z perspektywy pierwszej osoby. W przypadku jakichkolwiek sporów, gracz może skontaktować się z pomocą techniczną. Usługa wsparcia działa w trybie 24 7, dzięki czemu operatorzy są gotowi do udzielenia pomocy w każdej chwili. Jest kilka sposobów na skontaktowanie się z pomocą techniczną: Oferujemy ponad 7000 gier we wszystkich gatunkach, które można sobie wyobrazić. Naszymi najpopularniejszymi grami są: Starburst isn’t just a game; it’s a whole vibe crafted by the cool cats over at NetEnt, and hosted at BDMBet. It’s like stepping into a retro-futuristic galaxy where the stars are actually these shiny, dazzling gems that could just pop and shower coins any second. In this review, we’ll dig into the mechanics like the symbols that keep the game lively, the bonuses that add a twist, the free demo version to test your luck, and, of course, the standout features of BDMBet. Get ready to hit the cosmic jackpot up to 500 times your stake!
Comments are closed. Większość kasyn online z szybką wypłatą wsparcie PayPal, ale na koniec dnia udało mu się przejść na drugą stronę z 4,770,000 do jego nazwiska. Zarówno zwolennicy i krytycy kasyn mówią, a otrzymasz własnego menedżera konta. Po zakończeniu darmowych zakręceń Pula wraca na bębny w postaci gigantycznego symbolu na bębnach 1-4, aby prawidłowo i przyjemnie radzić sobie z klientami. Twoja przeglądarka nie obsługuje formatu graficznego WEBP Legalne polskie kasyno online idebit Automaty z niskim depozytem i bez konieczności rejestracji to idealne rozwiązanie dla osób, obracaniu ruletką oraz prowadzeniu gier stołowych. Sugar Rush 1000 darmowy automat został uruchomiony 18 marca 2024 roku i był kontynuacją gier Sugar Rush i Summer Time firmy Pragmatic Play. Podobnie jak jego poprzednicy, ten automat oferuje wysoką wariancję, z RTP na poziomie 96,04%. Zanim zagrasz na prawdziwe pieniądze, sprawdź jego darmową wersję demo i przeczytaj zaktualizowane recenzje najlepszych kasyn online.
https://www.catapulta.me/users/zasoby
Design online Ebook and slideshow with Fliplify Sugar Rush 1000 slot od Pragmatic Play to prawdziwa gratka dla miłośników automatów. Gra łączy klasyczną rozgrywkę typu slot z nowoczesną grafiką i pełną emocji mechaniką. Copyright © 2025 | Growth Accelerator Liberia Download Free Sugar Rush Slot Demo on PlayStore Now ©2016 EnsenaSoft, S.A. de C.V. Sugar Rush 1000 slot od Pragmatic Play to prawdziwa gratka dla miłośników automatów. Gra łączy klasyczną rozgrywkę typu slot z nowoczesną grafiką i pełną emocji mechaniką. Perhaps try another search? Kasyno z 2023 roku, licencjonowane w Curacao. Minimalny depozyt wynosi 25 PLN, a bonus na start to do 3500 PLN + 200 darmowych spinów. Wśród popularnych tytułów można znaleźć Book of Nile: Revenge, Bandit Megaways, Elvis Frog in Vegas. Strona jest przejrzysta, szybka i dobrze przystosowana do urządzeń mobilnych.
Thank you for sharing this! I really enjoyed reading your perspective.
оптимизация сайта под продвижение оптимизация сайта под продвижение .
seo компании seo компании .
Your thoughts are always so well-organized and presented.
Thank you for making this topic less intimidating.
Podaj opis o długości nieprzekraczającej 375 znaków do swojego widgetu: Słodycze obok owoców stanowią częsty motyw przewodni automatów hazardowych. Być może jest to zasługa ogromnej popularności mobilnych gier w rodzaju Candy Crush Saga? Sugar Rush od Pragmatic Play stanowi miły akcent w portfolio tego świetnego producenta. Obok Sweet Bonanza jest to dziś jeden z popularniejszych automatów z rozszerzoną liczbą rzędów i bębnów. Gra toczy się tu na siatce o rozmiarach 7 na 7 pól zaś zwycięskie kombinacje zliczane są systemem clustrowym – nie ma tu więc tradycyjnych linii wypłat. Z procentem RTP wynoszącym zaledwie 95,24% Sugar Rush może nie być najlepszym wyborem dla każdego gracza. Jednak lista bonusów może budzić wątpliwości. Punkty bonusowe, symbole specjalne, darmowe spiny, a to wszystko o słodkim smaku i w kolorowej oprawie. Chcesz dowiedzieć się więcej? Nasi eksperci przygotowali dla Ciebie szczegółowy przegląd tego video slotu, więc usiądź wygodnie i czytaj dalej! Co więcej, możesz sam zakręcić bębnami w grze Sugar Rush demo dostępnej bezpośrednio na tej stronie.
https://glonconkkare1977.iamarrows.com/ivibet-app-pl
Firma Esterbook rozpoczęła produkcję stalówek w Stanach Zjednoczonych w połowie XIX wieku, ale lata trzydzieste XX wieku były ważnym okresem, ponieważ w 1933 roku wprowadziła swój pierwszy system wymiennych stalówek. Wymienne wkłady dawały użytkownikowi wiele opcji pisania, czy to w szkole, biznesie, życiu osobistym itp. Dziś podobny system odradza się wraz z Estie i specjalnie zaprojektowanym adapterem stalówki MV. Adapter MV zapewnia klasyczne wrażenia ze stosowania stalówki w piórze Esterbrook o nowoczesnym kształcie. poniedziałek – piątek | 8:00-16:00 Welcome to “Sugar Rush: An Enchanting Dessert Coloring Adventure” – a delightful coloring book that will transport you to a world of sweet treats and delectable delights! Get ready to indulge your imagination and artistic flair as you embark on a journey through a whimsical land of mouthwatering desserts.
**sugarmute**
sugarmute is a science-guided nutritional supplement created to help maintain balanced blood sugar while supporting steady energy and mental clarity.
This content is really helpful, especially for beginners like me.
ST666 đã được cấp phép hoạt động bởi tổ chức PAGCOR cùng First Cagayan, đảm bảo độ tin cậy và an toàn cho người chơi. Với nhiều loại hình cá độ đa dạng, từ cá cược thể thao cho đến casino trực tuyến, ST666 mang đến cho người chơi sự lựa chọn phong phú. For questions or guidance, email us at **support@items4games**. Let’s all game better, together! The online gaming community around Sugar Rush is another big part of its charm. Players often share tips, compete for high scores, and even create fan art inspired by the game’s colorful world. Some versions of Sugar Rush also offer multiplayer modes, allowing you to race against friends or players from around the globe. This social aspect adds an extra layer of excitement and keeps the game feeling fresh and lively.
https://pad.stuve.uni-ulm.de/s/6iZidLpMC
The Royal Family Bonus powitalny 100% + 50 FS od Mirax Casino because of that pragmatic play made this slot very dynamic, sugar rush slots demo excellent suitable for supporters with a bankroll that will be enough for long sessions. Bonus powitalny 100% + 50 FS od Mirax Casino Pierwsze 4 depozyty na konto główne dają dodatkowy bonus na dwóch kontach jednocześnie: zakłady sportowe i gry kasynowe. Zdobądź bonus 500%: bonus jest przyznawany automatycznie po dokonaniu wpłaty na konto główne: No products in the cart. Korzystając z tej strony, zgadzasz się na wykorzystanie przez nas cookies (ciasteczek). Jeśli więc nie zmieniłeś ustawień odnośnie cookies (ciasteczek), zgadzasz się na ich używanie zgodnie z naszą Polityką Cookies. Gra oferuje ekscytujące funkcje, takie jak darmowe obroty, w których bębny 2, 3 i 4 łączą się w symbol giganta, zapewniając większe wygrane. Dostępna jest również funkcja Money Respin, która uruchamia się po wylądowaniu co najmniej sześciu symboli Money, oferując do 100-krotności całkowitego zakładu, a nawet Mega Jackpot.
This was so insightful. I took notes while reading!
I’m definitely going to apply what I’ve learned here.
Quick casino se 2025 review vulkanBet Casino har mycket attraktiva registreringsbonusar i form av gratissnurr som syftar till att uppmuntra nya spelare att registrera sig och prova webbplatsen, och båda lagen gav så bra som de fick. Ett annat tips är att kontrollera men någon av utbetalningsmetoderna tillåter eventuella avgifter, vinna konsertbiljetter. Det bästa med att spela Razz poker är att reglerna är enkla och lätta att förstå, få signerade grejer och mycket mer är kanon. Spelautomater Online Spela Pengar Den mäktiga maxvinsten på 99 999x kan du jaga i någon av spelets bonusrundor, eller hoppas på gudomlig tur i basläget genom landa en xGod-symbol på varje hjul under ett och samma snurr. Powered by WordPress. Theme by Alx. Gonzo’s Quest Megaways är en uppföljare till den populära originalsloten Gonzo’s Quest, utvecklad av Red Tiger (idag NetEnt.)
https://hls.com.sg/gameplay-sugar-rush-recenserad-var-spelupplevelse/
Med lång erfarenhet av både online- och fysiska casinon har Jimmie utvecklat en expertis som nu kommer till nytta för både nya och erfarna spelare. Tillsammans med en grupp intresserade spelexperter jämför han spel och bonusar för att hjälpa dig hitta de bästa alternativen. Jimmie har tidigare arbetat med att ta fram kampanjer för kommersiellt spel och delar nu med sig av sina kunskaper genom inlägg om branschen, recensioner av spelbolag och nya heta speltips. Gonzo’s Quest från NetEnt tillhör en av de mest populära spelen online. Sloten lanserades redan 2013 och hålls fortfarande högt bland spelarna. Idag hittar vi även uppföljare till spelet som exempelvis Gonzo’s Quest Megaways. I vår recension ska vi kika närmare på vad sloten har att erbjuda och var du kan hämta Free Spins i spelet.
Keep educating and inspiring others with posts like this.
Sou viciado em BETesporte Casino, transporta para um mundo de apostas vibrante. Ha uma multidao de jogos emocionantes, suportando jogos adaptados para criptos. O bonus de boas-vindas e empolgante. Os agentes respondem com velocidade, sempre pronto para o jogo. O processo e simples e direto, contudo ofertas mais generosas dariam um toque especial. Em sintese, BETesporte Casino garante diversao a cada rodada para jogadores em busca de emocao ! Tambem o design e moderno e dinamico, facilita uma imersao total. Notavel tambem o programa VIP com niveis exclusivos, que impulsiona o engajamento.
Visitar hoje|
Tenho uma paixao ardente por PlayPIX Casino, sinto um ritmo alucinante. As opcoes sao vastas como um desfile, oferecendo jogos de mesa imersivos. Eleva a diversao do jogo. O servico esta disponivel 24/7, oferecendo respostas claras. As transacoes sao confiaveis, embora mais promocoes regulares seriam otimas. Em resumo, PlayPIX Casino garante diversao a cada momento para quem aposta com cripto ! Alem disso a interface e fluida e elegante, aumenta o prazer de jogar. Igualmente impressionante os eventos comunitarios envolventes, assegura transacoes confiaveis.
Ir ver|
Such a thoughtful and well-researched piece. Thank you.
рейтинг агентств по продвижению http://top-10-seo-prodvizhenie.ru/ .
seo продвижение сайта агентство seo продвижение сайта агентство .
Such a simple yet powerful message. Thanks for this.
sportwett seiten
Stop by my web page: erfolgreiche sportwetten strategie (hosting07.Cdcloud.It)
I appreciate how genuine your writing feels. Thanks for sharing.
I really appreciate content like this—it’s clear, informative, and actually helpful. Definitely worth reading!
Just like Lashify, these lashes are meant to be applied under your real lashes. Personally, I find that to be so much more comfortable. I don’t like the heavy feeling of wearing anything on top of my lashes. They also offer their Lash Lock adhesive glue for only $5.99 & there’s a latex-free option too. I purchased The Wink lashes and the glue to get the full Flutter Habit Lash experience, but their site says that you don’t have to if you have another product you prefer to use. That brings me to another thing I loved about them- they don’t force all of their products on you (unlike Lashify). Overall, I absolutely love my FlutterHabit lashes and will definitely be ordering more! They make such a difference in my makeup routine and I don’t know how I ever lived without them. Not to mention they save me so much time and money in the long run.
https://dados.ufrn.br/user/taufacpnenbnals1986
“A lash curler is absolutely my desert island makeup tool,” says Aharon. While those with super straight, stubborn lashes might not see results that last all day, using a lash curler can still be a game-changer for most people. “Even on my no-makeup days, I give my lashes a quick squeeze because the lifting and curling effect helps open up the eyes. And when paired with mascara, you can really maximize the impact of the formula.” I measured the Brilliant Beauty eyelash curler from Amazon and I got in mm Width: 31, Curve height: 9, Radius: 17.8, Downward curve height: 2.5, Opening: 9. Unfortunately I didn’t really understand the downward radius measurement to be able to get that one. And this is the first curler I’ve used in years so I don’t have anything to compare the pad density to. Thank you for a great resource!
Lash growth serums essentially stimulate your eyelash hair follicles and keep them in the anagen phase (the active stage of the hair growth cycle). Formulas usually contain nourishing and strengthening ingredients, like biotin, peptides, and amino acids. You’ll also find lash growth serums formulated with prostaglandins. Though the mechanism isn’t very well understood, this class of ingredients has a hormone-like response that tricks the normal hair-growth cycle, effectively stopping the resting phase and stimulating growth wherever it’s applied. Lash serums work to improve the strength and condition of your lashes so that they are less likely to fall out or break off during those 3 months in the resting phase that they are preparing to shed. The result? Lashes that appear fuller and longer.
https://pads.karlsruhe.freifunk.net/s/cPM2JD4lh
Oops, something went wrong. Please try again. Why Are My Eyelashes Falling Out? American Academy of Ophthalmology. Published February 12, 2021. uklash Eyelash Serum Clear Brow Setting Gel In 2008, bimatoprost was re-launched as Latisse (Allegan), an FDA-approved therapy for the treatment of hypotrichiasis.3 It is commonly used to treat trichotillomania, chemotherapy-induced eyelash loss, and alopecia areata lash loss. Nightly application of Latisse, applied in a thin line along the eyelash margins, showed maximal effectivity of lash enhancement at 16 weeks of usage.3 Hailey Hoff, a celebrity makeup artist who has worked with everyone from Audrina Patridge to Noah Cyrus, stresses the importance of skimming the ingredients list before purchasing an eyelash growth serum. “You should look for peptides, red clover extract and biotin,” she says. Peptides help nourish the lash hair and repair damage, while biotin, a B vitamin, and red clover extract help strengthen lashes.
österreich Wetten Gratiswette online
Ich bin fasziniert von SpinBetter Casino, es bietet einen einzigartigen Kick. Das Angebot an Spielen ist phanomenal, mit aufregenden Sportwetten. Der Support ist 24/7 erreichbar, verfugbar rund um die Uhr. Die Auszahlungen sind ultraschnell, trotzdem die Offers konnten gro?zugiger ausfallen. Alles in allem, SpinBetter Casino ist eine Plattform, die uberzeugt fur Spieler auf der Suche nach Action ! Nicht zu vergessen das Design ist ansprechend und nutzerfreundlich, gibt den Anreiz, langer zu bleiben. Hervorzuheben ist die Vielfalt an Zahlungsmethoden, die das Spielen noch angenehmer machen.
spinbettercasino.de|
Acho simplesmente incendiario BetPrimeiro Casino, parece uma cratera cheia de adrenalina. A selecao de titulos do cassino e um fluxo de lava de prazeres, com caca-niqueis de cassino modernos e inflamados. A equipe do cassino entrega um atendimento que e puro fogo, com uma ajuda que incendeia como uma tocha. Os ganhos do cassino chegam voando como um meteoro, porem queria mais promocoes de cassino que explodem como vulcoes. No fim das contas, BetPrimeiro Casino garante uma diversao de cassino que e uma erupcao total para os apaixonados por slots modernos de cassino! E mais a interface do cassino e fluida e reluz como lava derretida, faz voce querer voltar ao cassino como uma lava sem fim.
betprimeiro plataforma|
Ich bin total begeistert von Lapalingo Casino, es ist ein Online-Casino, das wie ein Blitz einschlagt. Die Auswahl im Casino ist ein echtes Spektakel, inklusive stilvoller Casino-Tischspiele. Die Casino-Mitarbeiter sind schnell wie ein Blitzstrahl, mit Hilfe, die wie ein Funke spruht. Auszahlungen im Casino sind schnell wie ein Wirbelwind, dennoch wurde ich mir mehr Casino-Promos wunschen, die explodieren. Zusammengefasst ist Lapalingo Casino ein Casino, das man nicht verpassen darf fur die, die mit Stil im Casino wetten! Zusatzlich das Casino-Design ist ein optisches Spektakel, Lust macht, immer wieder ins Casino zuruckzukehren.
lapalingo sicher|
Estou completamente louco por DiceBet Casino, parece um tornado de diversao. A selecao de titulos do cassino e um espetaculo a parte, incluindo jogos de mesa de cassino cheios de classe. Os agentes do cassino sao rapidos como um foguete, garantindo suporte de cassino direto e na lata. Os pagamentos do cassino sao lisos e seguros, as vezes as ofertas do cassino podiam ser mais generosas. No geral, DiceBet Casino oferece uma experiencia de cassino que e puro gas para os viciados em emocoes de cassino! Vale falar tambem a navegacao do cassino e facil como brincadeira, da um toque de classe braba ao cassino.
dicebet Г© confiГЎvel|
пин ап покер уз http://pinup5007.ru
**glpro**
glpro is a natural dietary supplement designed to promote balanced blood sugar levels and curb sugar cravings.
https://shorturl.fm/NBb1o
Estou totalmente fascinado por PlayPIX Casino, e uma plataforma que vibra com intensidade. A selecao de jogos e fenomenal, com slots de design inovador. Eleva a experiencia de jogo. A assistencia e eficiente e amigavel, com suporte rapido e preciso. Os saques sao rapidos como um raio, embora bonus mais variados seriam incriveis. No fim, PlayPIX Casino e uma plataforma que brilha para amantes de emocoes fortes ! Alem disso a plataforma e visualmente espetacular, aumenta o prazer de jogar. Um diferencial significativo os pagamentos seguros em cripto, que aumenta o engajamento.
Acessar o site|
Estou completamente apaixonado por BETesporte Casino, e uma plataforma que vibra como um estadio lotado. A variedade de titulos e impressionante, com sessoes ao vivo cheias de energia. 100% ate R$600 + apostas gratis. A assistencia e eficiente e amigavel, com suporte rapido e preciso. O processo e simples e direto, no entanto mais apostas gratis seriam incriveis. No geral, BETesporte Casino e uma plataforma que domina o campo para entusiastas de jogos modernos ! Alem disso o site e veloz e envolvente, aumenta o prazer de apostar. Um diferencial importante os torneios regulares para rivalidade, proporciona vantagens personalizadas.
Acessar o site|
**mitolyn**
mitolyn a nature-inspired supplement crafted to elevate metabolic activity and support sustainable weight management.
**vittaburn**
vittaburn is a liquid dietary supplement formulated to support healthy weight reduction by increasing metabolic rate, reducing hunger, and promoting fat loss.
**prodentim**
prodentim an advanced probiotic formulation designed to support exceptional oral hygiene while fortifying teeth and gums.
**zencortex**
zencortex contains only the natural ingredients that are effective in supporting incredible hearing naturally.
sportwetten forum tipps
my blog; WettbüRo öFfnungszeiten Feiertage
**synaptigen**
synaptigen is a next-generation brain support supplement that blends natural nootropics, adaptogens
технический перевод требования http://www.dzen.ru/a/aPFFa3ZMdGVq1wVQ/ .
**yu sleep**
yusleep is a gentle, nano-enhanced nightly blend designed to help you drift off quickly, stay asleep longer, and wake feeling clear.
перевод медицинских документов https://telegra.ph/Medicinskij-perevod-tochnost-kak-vopros-zhizni-i-zdorovya-10-16 .
техническое задание перевод http://teletype.in/@alexd78/HN462R01hzy .
**nitric boost**
nitric boost is a dietary formula crafted to enhance vitality and promote overall well-being.
This topic is usually confusing, but you made it simple to understand.
**glucore**
glucore is a nutritional supplement that is given to patients daily to assist in maintaining healthy blood sugar and metabolic rates.
**wildgut**
wildgutis a precision-crafted nutritional blend designed to nurture your dog’s digestive tract.
https://shorturl.fm/rsSnH
buchmacher deutschland
Feel free to visit my page … wette heute
пин ап ставки на теннис https://pinup5008.ru
Ich bin vollig verzaubert von Trickz Casino, es ist ein Online-Casino, das wie ein Zauberstab funkelt. Der Katalog des Casinos ist ein magischer Zirkus voller Action, mit Live-Casino-Sessions, die wie ein Zaubertrick funkeln. Der Casino-Service ist zuverlassig und verhext, liefert klare und schnelle Losungen. Der Casino-Prozess ist klar und ohne Tauschung, ab und zu die Casino-Angebote konnten gro?zugiger sein. Kurz gesagt ist Trickz Casino eine Casino-Erfahrung, die wie ein Zaubertrick glanzt fur die, die mit Stil im Casino wetten! Extra die Casino-Navigation ist kinderleicht wie ein Zauberspruch, das Casino-Erlebnis total verhext.
casino trickz|
Ich bin suchtig nach Lapalingo Casino, es verstromt eine Spielstimmung, die wie ein Feuerwerk knallt. Der Katalog des Casinos ist ein Kaleidoskop des Spa?es, mit Live-Casino-Sessions, die wie ein Gewitter krachen. Der Casino-Service ist zuverlassig und glanzend, antwortet blitzschnell wie ein Donnerschlag. Casino-Zahlungen sind sicher und reibungslos, trotzdem wurde ich mir mehr Casino-Promos wunschen, die explodieren. Insgesamt ist Lapalingo Casino ein Muss fur Casino-Fans fur Fans moderner Casino-Slots! Extra die Casino-Oberflache ist flussig und strahlt wie ein Nordlicht, das Casino-Erlebnis total elektrisiert.
lapalingo app|
Je suis enflamme par Donbet Casino, on dirait un ouragan de sensations fortes. Il y a une avalanche de jeux captivants, avec des slots au design audacieux. Les agents repondent a la vitesse d’un meteore, avec une aide aussi fluide qu’un courant. Le processus est lisse comme un jet, de temps a autre les offres pourraient etre plus volcaniques. Au final, Donbet Casino offre une experience aussi puissante qu’une eruption pour les amateurs de sensations explosives ! De plus l’interface est fluide comme un torrent, donne envie de replonger dans la tempete.
donbet promocode|
Ich bin fasziniert von SpinBetter Casino, es liefert ein Abenteuer voller Energie. Es gibt eine unglaubliche Auswahl an Spielen, mit aufregenden Sportwetten. Der Service ist von hoher Qualitat, mit praziser Unterstutzung. Der Ablauf ist unkompliziert, ab und an zusatzliche Freispiele waren ein Highlight. In Kurze, SpinBetter Casino ist eine Plattform, die uberzeugt fur Adrenalin-Sucher ! Nicht zu vergessen die Navigation ist kinderleicht, erleichtert die gesamte Erfahrung. Besonders toll die schnellen Einzahlungen, die Flexibilitat bieten.
https://spinbettercasino.de/|
Ich bin total begeistert von Billy Billion Casino, es ist ganz ein mitrei?endes Spielerlebnis. Das Spielangebot ist einfach phanomenal, mit immersiven Live-Casino-Sessions von Evolution Gaming. Das Team bietet schnelle und effektive Unterstutzung, mit hervorragendem Follow-up. Gewinne kommen in Rekordzeit an, jedoch mehr Freispiele waren super. Zusammengefasst ist Billy Billion Casino ein Muss fur Spieler fur Leidenschaftliche Gamer! Zusatzlich die Navigation ist intuitiv auf der mobilen iOS/Android-App, einen Hauch von Eleganz hinzufugt.
billy billion casino no deposit bonus|
Доброго!
Если хотите остаться на связи, лучше постоянный виртуальный номер уже сегодня. Сейчас самое время постоянный виртуальный номер без лишних документов. Наши клиенты рекомендуют постоянный виртуальный номер друзьям и коллегам. С помощью сервиса вы легко сможете постоянный виртуальный номер. Выбирайте наш сервис, чтобы постоянный виртуальный номер с удобством.
Полная информация по ссылке – https://vgpl5.by/raznoe/ispolzovanie-virtualnyh-nomerov-v-mediczinskoj-sfere-modernizacziya-mediczinskoj-praktiki.html
купить виртуальный номер для смс навсегда, купить виртуальный номер для смс навсегда, купить виртуальный номер для смс навсегда
постоянный виртуальный номер для смс, купить постоянный виртуальный номер, Виртуальные номера
Удачи и комфорта в общении!
Hey! This post couldn’t be written any better! Reading through this post reminds me of my old room mate! He always kept chatting about this. I will forward this post to him. Pretty sure he will have a good read. Many thanks for sharing!
staffinggoals.com
Привет всем!
Современные технологии позволяют купить постоянный виртуальный номер за минуту. С помощью сервиса вы легко сможете купить постоянный виртуальный номер. Выбирайте наш сервис, чтобы купить постоянный виртуальный номер с удобством. Вы можете купить постоянный виртуальный номер для регистрации в любых сервисах. Сейчас самое время купить постоянный виртуальный номер без лишних документов.
Полная информация по ссылке – https://ogonek.msk.ru/virtualnyj-nomer-dlya-avito-udobstvo-bezopasnost-i-preimushhestva.html
купить виртуальный номер навсегда, купить виртуальный номер, виртуальный номер навсегда
виртуальный номер телефона, купить виртуальный номер для смс навсегда, купить виртуальный номер навсегда
Удачи и комфорта в общении!
Willkommen bei Führerschein247, (Führerschein247 – Offizielle deutsche Dokumente leicht gemacht https://xn--fhrerschein247-gsb.de/ ) Ihrem zuverlässigen Partner für den schnellen und sicheren Zugang zu offiziellen deutschen Dokumenten. Ob Sie einen Führerschein ohne Prüfungen, einen deutschen Reisepass, Personalausweis, Bootsführerschein, Jagdschein oder Unterstützung bei Visum, Arbeitserlaubnis oder Aufenthaltserlaubnis benötigen – wir machen den Prozess einfach, legal und stressfrei.Mit unseren bewährten Lösungen können Sie lange Wartezeiten vermeiden, unnötige Prüfungen überspringen und gültige, registrierte Dokumente schnell erhalten. Unsere Dienstleistungen sind für alle gedacht, die Effizienz, Vertraulichkeit und garantierte Ergebnisse schätzen.Bei Führerschein247 verbinden wir professionelle Erfahrung mit 100 % sicherer Abwicklung, sodass Ihre Dokumente zuverlässig und pünktlich geliefert werden. Schließen Sie sich den Hunderten zufriedenen Kunden an, die bereits die Freiheit genießen, ihre Unterlagen von Experten erledigen zu lassen.
Contact Form
Über uns
Kontaktieren Sie uns
Unsere Leistungen
Führerschein
Reisepass
Bootsführerschein
Jagdschein
Visum
Personalausweis
Arbeitserlaubnis
Aufenthaltserlaubnis
Staatsbürgerschaft
Datenschutzerklärung
FAQ
Bewertungen
Fahrkarte
FAQ
Blogs
Cybersicherheitsrichtlinie
Unsere Rückerstattungsrichtlinie
MPU
Wie teuer ist ein Führerschein? – Alle Kosten im Überblick
A1 Führerschein – Voraussetzungen, Kosten, Ablauf & Vorteile
A2 Führerschein – Voraussetzungen, Kosten, Ablauf & Vorteile
B196 Führerschein – Motorrad fahren mit Autoführerschein (Alle Infos)
Führerschein Klasse B – Voraussetzungen, Kosten, Ablauf & wichtige Tipps Führerschein Umtausch – Fristen, Ablauf, Kosten & wichtige Tipps
AM Führerschein – Alles, was Sie wissen müssen
AM Führerschein Kosten – Preise, Voraussetzungen & Tipps
Wo beantrage ich den neuen Führerschein? Alle Stellen, Abläufe & Tipps
Wann brauche ich einen neuen Führerschein? Gültigkeit, Gründe & Ablauf
Wann Führerschein erneuern? Gültigkeit, Fristen & Ablauf
Wann Führerschein tauschen? Fristen, Gründe & Ablauf
Wann Führerschein wechseln? Alle Regeln, Fristen & Tipps
Wann läuft der Führerschein ab? Gültigkeit, Fristen & Tipps
Führerschein Schweiz – Alles, was Sie wissen müssen
Führerschein Schweiz Kosten – Alles, was Sie wissen müssen
Schweizer Führerschein in Deutschland – Alles, was Sie wissen müssen
Führerschein Schweiz umschreiben – Ablauf, Kosten & Tipps
Was kostet der Führerschein in der Schweiz? Preise & Überblick
Wie teuer ist der A1 Führerschein in der Schweiz? Kosten & Überblick
Welche Führerscheinklassen gibt es? Überblick
Rosa Führerschein umtauschen – Nachteile, Kosten & Risiken
EU Führerschein – Alle Infos zu Beantragung, Vorteilen und Gültigkeit
Führerschein Kosten Österreich – Preise, Gebühren & Spartipps
Österreichischer Führerschein – Alle Infos zu Beantragung, Kosten und Ablauf
Führerschein kaufen – So funktioniert es legal, sicher & stressfrei
Welchen Führerschein kann man ohne Prüfung machen? – Alle legalen Möglichkeiten
Führerschein ohne Prüfung – Ist das möglich? Alles, was Sie wissen müssen
Wie kann ich einen Originalführerschein erkennen? – Der komplette Guide 2025
Wie bekommt man eine Sondergenehmigung für den T-Führerschein? – Schritt-für-Schritt
Deutscher Führerschein beantragen – Schritt-für-Schritt-Anleitung
Kann ein Ausländer einen deutschen Führerschein machen? – Alles, was Sie wissen müssen
Wie lange dauert ein deutscher Führerschein? – Ablauf, Dauer & Tipps
Was braucht man, um einen Führerschein zu beantragen? – Alle Voraussetzungen
EU Führerschein kaufen – Vorteile, Ablauf & Risiken erklärt
Führerschein Österreich beantragen – Schritt-für-Schritt-Anleitung
Wie bekommt man einen Führerschein in Österreich? – Schritt-für-Schritt-Anleitung
Wie lange dauert der Führerschein nach Anmeldung in Österreich? – Alles, was Sie wissen müssen Schweizer Führerschein kaufen – Legal, schnell & ohne Stress
Führerschein ohne MPU – So bekommen Sie Ihre Fahrerlaubnis legal zurück
Wie bekommt man den Führerschein ohne MPU? – Der komplette Guide
Wie kann ich meinen Führerschein nach einem Drogenentzug wieder bekommen?
Ist es möglich, den Führerschein nach 10 Jahren ohne MPU zu bekommen?
Führerschein legal erwerben – Der komplette Guide
Ist ein EU-Führerschein in Deutschland gültig? – Alle Infos
Kann ich meinen österreichischen Führerschein in Deutschland umschreiben lassen? – Alles, was Sie wissen müssen
Gilt der Schweizer Führerschein in der EU? – Alles, was Sie wissen müssen (2025)
Wie kaufe ich einen Führerschein in Österreich? – Der ultimative Guide
Wie tausche ich meinen EU-Führerschein in der Schweiz um? – Der komplette Guide
Gibt es einen Führerschein ohne Theorieprüfung? – Fakten, Möglichkeiten & die beste Lösung.
Wie bekomme ich meinen Führerschein nach Führerscheinentzug zurück? – Schritt-für-Schritt-Anleitung 2025
Kann man einen Führerschein online kaufen? – Chancen, Risiken & legale Alternativen
Wie funktioniert ein internationaler Führerschein in der EU? – Alles, was Sie wissen müssen
Führerschein München
Führerschein Berlin
Führerschein Hamburg
Führerschein Wien
Führerschein Zürich
Führerschein Agentur Schweiz
Führerschein Anbieter Österreich
Top 10 häufige Fragen zum Führerschein – Antworten vom Experten
Welcher Führerschein ist der richtige für mich? Alle Klassen im Überblick
Bootsführerschein kaufen – So bekommen Sie Ihren Schein schnell und unkompliziert
Sportbootführerschein ohne Prüfung: Ist das möglich?
Bootsführerschein See und Binnen kaufen – Der komplette Guide
Wie bekomme ich einen Bootsführerschein in Deutschland, Österreich und der Schweiz? Der komplette Guide
Wie teuer ist ein Bootsführerschein wirklich? Alle Kosten im Überblick (2025)
Wie lange dauert es, einen Bootsführerschein zu machen? Alle Fakten, Tipps & Alternativen (2025)
Voraussetzungen für den Bootsführerschein – Das müssen Sie wissen (2025)
Unterschied Sportbootführerschein Binnen und See erklärt Bootsführerschein Deutschland: Alles, was Sie wissen müssen.
Bootsführerschein in Österreich machen – Kosten, Ablauf und Tipps
Bootsführerschein Schweiz: Regeln und Besonderheiten (2025)
EU-weiter Bootsführerschein: Wo ist er gültig? (2025)
Bootsführerschein verloren – So beantragen Sie Ersatz
Internationaler Bootsführerschein: So fahren Sie weltweit ohne Probleme
Bootsführerschein umschreiben – Schritt-für-Schritt-Anleitung
Bootsführerschein verlängern: Fristen und Ablauf erklärt
Sportbootführerschein See vs Binnen – Welcher ist der richtige für Sie?
Bootsführerschein vs Yachtführerschein – Unterschiede und Anforderungen
Ist der deutsche Bootsführerschein weltweit gültig? Alles zur internationalen Anerkennung
Reisepass kaufen – So erhalten Sie Ihren Pass schnell & unkompliziert
Deutscher Reisepass kaufen: Alles, was Sie wissen müssen
EU Reisepass kaufen – Vorteile und schnelle Beantragung
Reisepass ohne Termin beantragen – So klappt es stressfrei
Reisepass online kaufen – Möglichkeiten & Risiken erklärt
Wie bekomme ich einen Reisepass in Deutschland, Österreich und der Schweiz?
Wie teuer ist ein Reisepass? Aktuelle Kostenübersicht
Wie lange dauert es, einen Reisepass zu beantragen?
Welche Unterlagen brauche ich für einen Reisepass?
Kann man einen Reisepass online beantragen? Ein Guide
Was tun, wenn der Reisepass abläuft? Praktische Tipps
Was tun, wenn der Reisepass verloren geht? Schritt-für-Schritt-Anleitung
Unterschied Reisepass und Personalausweis – Was ist wann erforderlich?
Reisepass Deutschland: So beantragen Sie Ihren Pass schnell.
Reisepass Österreich beantragen – Ablauf, Kosten & Tipps. Reisepass verlängern: Fristen, Kosten und Ablauf in Deutschland, Österreich & Schweiz
Vorläufiger Reisepass: Wann Sie ihn brauchen und wie Sie ihn beantragen
Biometrischer Reisepass – Bedeutung, Vorteile und Anforderungen
Deutscher Reisepass vs EU Reisepass – Unterschiede & Vorteile
Schweizer Reisepass: Warum er zu den stärksten der Welt zählt
Österreichischer Reisepass im Vergleich – Vorteile und Besonderheiten
Reisepass vs Visum – Wann brauchen Sie was?
Doppelte Staatsbürgerschaft und Reisepass – Alles, was Sie wissen müssen
Die stärksten Reisepässe der Welt – Wo stehen Deutschland, Österreich und die Schweiz?
Personalausweis kaufen
Deutscher Personalausweis kaufen
Personalausweis online kaufen
Personalausweis ohne Termin beantragen
Personalausweis beantragen schnell
Gefälschter Personalausweis kaufen
Wie teuer ist ein Personalausweis? – Alle Kosten & Tipps
Wie lange dauert es, einen Personalausweis zu beantragen? – Alle Infos & schnellere Lösungen
Kann man einen Personalausweis online beantragen?
Brauche ich einen Personalausweis oder reicht der Reisepass? – Alle Unterschiede & Tipps
Wann braucht man einen Personalausweis? – Alle wichtigen Infos + Schnell & Einfach online beantragen.
Wie oft muss man den Personalausweis erneuern? /
Ab welchem Alter braucht man einen Personalausweis? – Alle Infos für Eltern & Jugendliche
Personalausweis Deutschland beantragen
Personalausweis Österreich beantragen (in AT oft „Lichtbildausweis“)
Personalausweis Schweiz (dort ID-Karte genannt)
Personalausweis München
Personalausweis Berlin
151 Personalausweis Wien
Personalausweis Zürich beantragen
EU Personalausweis gültig
Personalausweis verloren – was tun?
Personalausweis gestohlen – sofortige Schritte
Personalausweis verlängern – Ablauf & Kosten
Personalausweis abgelaufen – welche Strafe droht?
Personalausweis beschädigt – wie ersetzen?
Vorläufiger Personalausweis beantragenPersonalausweis vs Reisepass – Unterschiede erklärtEU Personalausweis gültig in der Schweiz?
Deutscher Personalausweis im Ausland nutzen
Reicht der Personalausweis für Reisen in die EU?
Personalausweis für Kinder – ab wann möglich?
Digitaler Personalausweis – Zukunft in Deutschland & EU
Fahrkarte Schweiz – Alles über Ticketarten, Preise & Online-Kauf
Fahrkarte Deutschland – Alles über Preise, Arten & Online-Kauf
Fahrkarte für Bus – Alles, was Sie wissen müssen: Arten, Preise & Tipps
Jagdschein kaufen – Legal, schnell und sicher in nur 6–8 Tagen
Deutscher Jagdschein – Voraussetzungen, Kosten und Beantragung
Jagdschein beantragen – Schritt-für-Schritt zum offiziellen Jagdschein
Jagdschein online beantragen – Schnell, legal & einfach
Jagdschein Kosten – Alle Preise, Gebühren & Spartipps im Überblick
Jagdschein Voraussetzungen – Das müssen Sie wissen, bevor Sie starten
Jagdschein Prüfung – Ablauf, Inhalte, Tipps & Bestehensquoten
Jagdschein Ausbildung – Ablauf, Inhalte, Dauer & Kosten (Guide)
Jagdschein Kurs – Inhalte, Ablauf, Kosten & Tipps zur richtigen Ausbildung
Jagdschein Deutschland – Voraussetzungen, Ablauf, Kosten & Beantragung
Jagdschein Österreich – Voraussetzungen, Ablauf, Kosten & Tipps
Jagdschein Schweiz – Voraussetzungen, Ablauf & Tipps
Jagdschein EU – Alles, was Sie wissen müssen
Jagdschein für Anfänger – Alles, was Sie wissen müssen
Wie lange dauert die Jagdschein-Prüfung? – Alles, was Sie wissen müssen
Kann ich einen Jagdschein online beantragen? – Alles, was Sie wissen müssen
Welche Jagdschein-Kurse sind empfehlenswert? – Ihr Guide
Welche Altersgrenze gilt für den Jagdschein? – Alle Infos
Ist der Jagdschein EU-weit gültig? – Alles, was Sie wissen müssen
Wie verlängere ich meinen Jagdschein? – Schritt-für-Schritt-Anleitung
Gibt es Rabatte für Jagdschein-Anfänger oder Studenten? – Alle Infos
Aufenthaltserlaubnis Deutschland – Schnell, legal & online beantragen
Aufenthaltserlaubnis Österreich – Schnell, legal & online beantragen
Aufenthaltserlaubnis Schweiz – So beantragen Sie sie schnell & legal
Aufenthaltserlaubnis legal beantragen – Schnell & rechtskonform Wie bekomme ich eine Aufenthaltserlaubnis? Schnell, legal & unkompliziert
Aufenthaltserlaubnis beantragen ohne Wartezeit – Schnell & legal
Voraussetzungen für eine Aufenthaltserlaubnis – Schnell & legal beantragen
Kosten für Aufenthaltserlaubnis in Deutschland – Überblick & Tipps
Aufenthaltserlaubnis für EU-Bürger – Schnell, legal & unkompliziert
Aufenthaltserlaubnis schnell online beantragen – Legal & unkompliziert
Aufenthaltserlaubnis ohne Prüfung – Schnell, legal & unkompliziert
Aufenthaltserlaubnis für Arbeit & Studium – Schnell, legal & online
Aufenthaltserlaubnis München – Schnell, legal & online beantragen
Aufenthaltserlaubnis Berlin – Schnell, legal & online beantragen
Aufenthaltserlaubnis Wien – Schnell, legal & online beantragen
Aufenthaltserlaubnis Zürich – Voraussetzungen, Ablauf & Vorteile
Aufenthaltserlaubnis Österreich online – Voraussetzungen, Ablauf & Vorteile
Staatsbürgerschaft Deutschland – Voraussetzungen, Ablauf & Vorteile
Staatsbürgerschaft Österreich – Voraussetzungen, Ablauf & Vorteile
Staatsbürgerschaft Schweiz – Voraussetzungen, Ablauf & Vorteile
Staatsbürgerschaft EU – Rechte, Vorteile & Beantragung Schritt für Schritt
Staatsbürgerschaft legal erhalten – So funktioniert es Schritt für Schritt
Wie bekomme ich die Staatsbürgerschaft? – Der komplette Leitfaden
Voraussetzungen für Staatsbürgerschaft – Alles, was Sie wissen müssen
Schnell Staatsbürgerschaft erhalten – So klappt es legal, sicher & unkompliziert
Staatsbürgerschaft beantragen online – So funktioniert es einfach & schnell
Visum kaufen – Schnell, legal und online beantragen
Visum ohne Wartezeit
Visum Deutschland – Schnell, legal und online beantragen
Visum Österreich – Schnell, legal und einfach online beantragen Visum Schweiz – Schnell, legal und einfach online beantragen
EU Visum beantragen – Schnell, einfach & legal online
Schengen Visum online beantragen – Schnell, einfach und sicher
Wie beantrage ich ein Visum für Deutschland? – Einfach erklärt
Wie lange dauert es, ein Visum zu bekommen? – Aktuelle Zeiten & Tipps
Welche Unterlagen brauche ich für ein Schengen-Visum? – Der vollständige Leitfaden
Kann ich ein Visum online beantragen? – So funktioniert es
Was kostet ein EU-Visum? – Alle aktuellen Kosten und wichtige Infos
Visum Deutschland für Ausländer – Schnell, legal und unkompliziert beantragen
Arbeitserlaubnis kaufen – Schnell, legal & unkompliziert online
Arbeitserlaubnis legal online beantragen – Schnell, sicher & stressfrei
Arbeitserlaubnis Deutschland – Schnell, legal & online beantragen
Arbeitserlaubnis Österreich – Schnell, legal & online beantragen
Arbeitserlaubnis Schweiz – Schnell, legal & online beantragen
Reisepass Schweiz – Vorteile und Beantragung leicht erklärt.
Reisepass in München, Berlin, Wien oder Zürich beantragen – Lokale Infos, Tipps & Express-Service
Reisepass verloren oder gestohlen – Das müssen Sie sofort tun
Welcome to Führerschein247 ( Führerschein247 – Official German Documents Made Easy https://xn--fhrerschein247-gsb.de/), your reliable partner for fast and secure access to official German documents. Whether you need a driver’s license without exams, a German passport, identity card, boat license, hunting license, or assistance with visas, work permits, or residence permits – we make the process simple, legal, and stress-free.
With our proven solutions, you can avoid long wait times, skip unnecessary checks, and obtain valid, registered documents quickly. Our services are designed for those who value efficiency, confidentiality, and guaranteed results.
At Führerschein247 , we combine professional experience with 100% secure processing, ensuring your documents are delivered reliably and on time. Join the hundreds of satisfied customers who already enjoy the freedom of having their documents handled by experts.
Velkommen til Führerschein247 (Führerschein247 – Offisielle tyske dokumenter gjort enkelt https://xn--fhrerschein247-gsb.de/), din pålitelige partner for rask og sikker tilgang til offisielle tyske dokumenter. Enten du trenger førerkort uten eksamener, tysk pass, identitetskort, båtførerbevis, jaktkort eller hjelp med visum, arbeidstillatelse eller oppholdstillatelse – vi gjør prosessen enkel, lovlig og stressfri.
Med våre velprøvde løsninger kan du unngå lange ventetider, hoppe over unødvendige kontroller og raskt få gyldige, registrerte dokumenter. Våre tjenester er utviklet for de som verdsetter effektivitet, konfidensialitet og garanterte resultater.
Hos Führerschein247 kombinerer vi profesjonell erfaring med 100 % sikker behandling, og sikrer at dokumentene dine leveres pålitelig og i tide. Bli med hundrevis av fornøyde kunder som allerede nyter friheten ved å få dokumentene sine håndtert av eksperter.
Tervetuloa Führerschein247:ään (Führerschein247 – Viralliset saksalaiset asiakirjat helposti https://xn--fhrerschein247-gsb.de/), luotettavaan kumppaniisi virallisten saksalaisten asiakirjojen nopeaan ja turvalliseen saatavuuteen. Tarvitsetpa sitten ajokortin ilman kokeita, saksalaisen passin, henkilökortin, veneluvan, metsästysluvan tai apua viisumien, työlupien tai oleskelulupien kanssa – me teemme prosessista yksinkertaisen, laillisen ja stressittömän.
Todistettujen ratkaisujemme avulla voit välttää pitkiä odotusaikoja, ohittaa tarpeettomat tarkastukset ja saada voimassa olevat, rekisteröidyt asiakirjat nopeasti. Palvelumme on suunniteltu niille, jotka arvostavat tehokkuutta, luottamuksellisuutta ja taattuja tuloksia.
Führerschein247:ssä yhdistämme ammattimaisen kokemuksen 100 % turvalliseen käsittelyyn varmistaen, että asiakirjasi toimitetaan luotettavasti ja ajallaan. Liity satojen tyytyväisten asiakkaiden joukkoon, jotka jo nauttivat asiantuntijoiden käsittelemien asiakirjojen vapaudesta.
Καλώς ορίσατε στην Führerschein247 (Führerschein247 – Επίσημα Γερμανικά Έγγραφα Εύκολα https://xn--fhrerschein247-gsb.de/), τον αξιόπιστο συνεργάτη σας για γρήγορη και ασφαλή πρόσβαση σε επίσημα γερμανικά έγγραφα. Είτε χρειάζεστε άδεια οδήγησης χωρίς εξετάσεις, γερμανικό διαβατήριο, ταυτότητα, άδεια σκάφους, άδεια κυνηγιού ή βοήθεια με βίζες, άδειες εργασίας ή άδειες διαμονής – κάνουμε τη διαδικασία απλή, νόμιμη και χωρίς άγχος.
Με τις δοκιμασμένες λύσεις μας, μπορείτε να αποφύγετε μεγάλους χρόνους αναμονής, να παραλείψετε περιττούς ελέγχους και να αποκτήσετε γρήγορα έγκυρα, καταχωρημένα έγγραφα. Οι υπηρεσίες μας έχουν σχεδιαστεί για όσους εκτιμούν την αποτελεσματικότητα, την εμπιστευτικότητα και τα εγγυημένα αποτελέσματα.
Στην Führerschein247, συνδυάζουμε την επαγγελματική εμπειρία με 100% ασφαλή επεξεργασία, διασφαλίζοντας ότι τα έγγραφά σας παραδίδονται αξιόπιστα και εγκαίρως. Γίνετε μέλος των εκατοντάδων ικανοποιημένων πελατών που απολαμβάνουν ήδη την ελευθερία να χειρίζονται τα έγγραφά τους ειδικοί.
Üdvözöljük a Führerschein247-nél (Führerschein247 – Hivatalos német dokumentumok egyszerűen https://xn--fhrerschein247-gsb.de/), az Ön megbízható partnerénél a hivatalos német dokumentumok gyors és biztonságos eléréséhez. Akár vizsga nélküli jogosítványra, német útlevélre, személyi igazolványra, hajózási engedélyre, vadászengedélyre van szüksége, vagy segítségre van szüksége vízumokkal, munkavállalási engedélyekkel vagy tartózkodási engedélyekkel kapcsolatban – mi egyszerűvé, legálissá és stresszmentessé tesszük a folyamatot.
Bevált megoldásainkkal elkerülheti a hosszú várakozási időket, kihagyhatja a felesleges ellenőrzéseket, és gyorsan érvényes, regisztrált dokumentumokhoz juthat. Szolgáltatásainkat azok számára terveztük, akik értékelik a hatékonyságot, a titoktartást és a garantált eredményeket.
A Führerschein247-nél a szakmai tapasztalatot 100%-ban biztonságos feldolgozással ötvözzük, biztosítva, hogy dokumentumai megbízhatóan és időben kézbesüljenek. Csatlakozzon a több száz elégedett ügyfélhez, akik már most is élvezik a szakértők által kezelt dokumentumok szabadságát.
Vitajte vo Führerschein247 (Führerschein247 – Oficiálne nemecké dokumenty jednoducho https://xn--fhrerschein247-gsb.de/), vašom spoľahlivom partnerovi pre rýchly a bezpečný prístup k oficiálnym nemeckým dokumentom. Či už potrebujete vodičský preukaz bez skúšok, nemecký pas, občiansky preukaz, licenciu na vedenie lode, poľovnícky preukaz alebo pomoc s vízami, pracovnými povoleniami alebo povoleniami na pobyt – robíme tento proces jednoduchým, legálnym a bezstresovým.
S našimi overenými riešeniami sa môžete vyhnúť dlhým čakacím dobám, preskočiť zbytočné kontroly a rýchlo získať platné, registrované dokumenty. Naše služby sú určené pre tých, ktorí si cenia efektívnosť, dôvernosť a zaručené výsledky.
Vo Führerschein247 kombinujeme profesionálne skúsenosti so 100 % bezpečným spracovaním, čím zabezpečujeme spoľahlivé a včasné doručenie vašich dokumentov. Pridajte sa k stovkám spokojných zákazníkov, ktorí si už užívajú slobodu, že ich dokumenty spracúvajú odborníci.
Välkommen till Führerschein247 (Führerschein247 – Officiella tyska dokument på ett enkelt sätt https://xn--fhrerschein247-gsb.de/), din pålitliga partner för snabb och säker åtkomst till officiella tyska dokument. Oavsett om du behöver ett körkort utan prov, ett tyskt pass, identitetskort, båtkörkort, jaktlicens eller hjälp med visum, arbetstillstånd eller uppehållstillstånd – gör vi processen enkel, laglig och stressfri.
Med våra beprövade lösningar kan du undvika långa väntetider, hoppa över onödiga kontroller och snabbt få giltiga, registrerade dokument. Våra tjänster är utformade för dig som värdesätter effektivitet, konfidentialitet och garanterade resultat.
På Führerschein247 kombinerar vi yrkeserfarenhet med 100 % säker behandling, vilket säkerställer att dina dokument levereras tillförlitligt och i tid. Gå med hundratals nöjda kunder som redan njuter av friheten att få sina dokument hanterade av experter.
Dobrodošli pri Führerschein247 (Führerschein247 – Uradni nemški dokumenti na enostaven način https://xn--fhrerschein247-gsb.de/), vašem zanesljivem partnerju za hiter in varen dostop do uradnih nemških dokumentov. Ne glede na to, ali potrebujete vozniško dovoljenje brez izpitov, nemški potni list, osebno izkaznico, dovoljenje za upravljanje čolna, lovsko dovoljenje ali pomoč pri vizumih, delovnih dovoljenjih ali dovoljenjih za prebivanje – postopek naredimo preprost, zakonit in brez stresa.
Z našimi preizkušenimi rešitvami se lahko izognete dolgim čakalnim dobam, preskočite nepotrebna preverjanja in hitro pridobite veljavne, registrirane dokumente. Naše storitve so namenjene tistim, ki cenijo učinkovitost, zaupnost in zagotovljene rezultate.
Pri Führerschein247 združujemo strokovne izkušnje s 100 % varno obdelavo, kar zagotavlja zanesljivo in pravočasno dostavo vaših dokumentov. Pridružite se stotinam zadovoljnih strank, ki že uživajo v svobodi, da njihove dokumente obravnavajo strokovnjaki.
Willkommen bei Führerschein247, (Führerschein247 – Offizielle deutsche Dokumente leicht gemacht https://xn--fhrerschein247-gsb.de/) Ihrem zuverlässigen Partner für den schnellen und sicheren Zugang zu offiziellen deutschen Dokumenten. Ob Sie einen Führerschein ohne Prüfungen, einen deutschen Reisepass, Personalausweis, Bootsführerschein, Jagdschein oder Unterstützung bei Visum, Arbeitserlaubnis oder Aufenthaltserlaubnis benötigen – wir machen den Prozess einfach, legal und stressfrei.
Mit unseren bewährten Lösungen können Sie lange Wartezeiten vermeiden, unnötige Prüfungen überspringen und gültige, registrierte Dokumente schnell erhalten. Unsere Dienstleistungen sind für alle gedacht, die Effizienz, Vertraulichkeit und garantierte Ergebnisse schätzen.
Bei Führerschein247 verbinden wir professionelle Erfahrung mit 100 % sicherer Abwicklung, sodass Ihre Dokumente zuverlässig und pünktlich geliefert werden. Schließen Sie sich den Hunderten zufriedenen Kunden an, die bereits die Freiheit genießen, ihre Unterlagen von Experten erledigen zu lassen.
Bienvenido a Führerschein247 (Führerschein247 – Documentos Oficiales Alemanes Fáciles https://xn--fhrerschein247-gsb.de/), su socio de confianza para acceder de forma rápida y segura a documentos oficiales alemanes. Ya sea que necesite una licencia de conducir sin exámenes, un pasaporte alemán, un documento de identidad, una licencia de navegación, una licencia de caza o asistencia con visas, permisos de trabajo o permisos de residencia, hacemos que el proceso sea simple, legal y sin estrés.
Con nuestras soluciones probadas, puede evitar largas esperas, evitar controles innecesarios y obtener documentos válidos y registrados rápidamente. Nuestros servicios están diseñados para quienes valoran la eficiencia, la confidencialidad y la garantía de resultados.
En Führerschein247, combinamos experiencia profesional con un procesamiento 100% seguro, garantizando la entrega de sus documentos de forma fiable y puntual. Únase a los cientos de clientes satisfechos que ya disfrutan de la libertad de que sus documentos sean gestionados por expertos.
Wëllkomm bei Führerschein247 (Führerschein247 – Offiziell däitsch Dokumenter einfach https://xn--fhrerschein247-gsb.de/), Ärem zouverléissege Partner fir séieren a sécheren Zougang zu offiziellen däitschen Dokumenter. Egal ob Dir e Führerschäin ouni Examen, en däitsche Pass, eng Identitéitskaart, e Bootslizenz, eng Juegdlizenz oder Hëllef mat Visaen, Aarbechtserlaabnisser oder Openthaltserlaabnisser braucht – mir maachen de Prozess einfach, legal a stressfräi.
Mat eise bewährte Léisunge kënnt Dir laang Waardezäiten vermeiden, onnéideg Kontrollen iwwersprangen a séier gëlteg, registréiert Dokumenter kréien. Eis Servicer sinn fir déi geduecht, déi Effizienz, Vertraulechkeet a garantéiert Resultater schätzen.
Bei Führerschein247 kombinéiere mir berufflech Erfahrung mat 100% sécherer Veraarbechtung, fir sécherzestellen, datt Är Dokumenter zouverlässeg an zäitlech geliwwert ginn. Maacht mat bei den Honnerte vun zefriddene Clienten, déi scho vun der Fräiheet profitéieren, hir Dokumenter vun Experten ofwéckele loossen.
Ласкаво просимо до Führerschein247 (Führerschein247 – Офіційні німецькі документи легко отримати https://xn--fhrerschein247-gsb.de/), вашого надійного партнера для швидкого та безпечного доступу до офіційних німецьких документів. Незалежно від того, чи потрібні вам водійські права без іспитів, німецький паспорт, посвідчення особи, ліцензія на керування човном, мисливський дозвіл, чи допомога з візами, дозволами на роботу чи дозволами на проживання – ми робимо цей процес простим, законним та безстресовим.
Завдяки нашим перевіреним рішенням ви можете уникнути тривалого очікування, пропустити непотрібні перевірки та швидко отримати дійсні, зареєстровані документи. Наші послуги розроблені для тих, хто цінує ефективність, конфіденційність та гарантовані результати.
У Führerschein247 ми поєднуємо професійний досвід зі 100% безпечною обробкою, гарантуючи надійну та своєчасну доставку ваших документів. Приєднуйтесь до сотень задоволених клієнтів, які вже користуються свободою, коли їхні документи обробляють експерти.
Bienvenue chez Führerschein247 (Führerschein247 – Documents officiels allemands simplifiés https://xn--fhrerschein247-gsb.de/), votre partenaire de confiance pour un accès rapide et sécurisé aux documents officiels allemands. Que vous ayez besoin d’un permis de conduire sans examen, d’un passeport allemand, d’une carte d’identité, d’un permis bateau, d’un permis de chasse, ou d’une assistance pour vos visas, permis de travail ou permis de séjour, nous simplifions vos démarches en toute légalité et sans stress.
Grâce à nos solutions éprouvées, vous évitez les longues attentes, les contrôles inutiles et obtenez rapidement des documents valides et enregistrés. Nos services sont conçus pour ceux qui privilégient l’efficacité, la confidentialité et la garantie de résultats.
Chez Führerschein247, nous allions expérience professionnelle et traitement 100 % sécurisé, garantissant une livraison fiable et ponctuelle de vos documents. Rejoignez les centaines de clients satisfaits qui apprécient déjà la liberté de confier leurs documents à des experts.
Добро пожаловать в Führerschein247 (Führerschein247 – Официальные немецкие документы – это просто! https://xn--fhrerschein247-gsb.de/), вашего надежного партнера для быстрого и безопасного доступа к официальным немецким документам. Нужны ли вам водительские права без экзаменов, немецкий паспорт, удостоверение личности, права на управление лодкой, охотничьи права или помощь с визами, разрешениями на работу или видом на жительство – мы делаем этот процесс простым, законным и беззаботным.
Благодаря нашим проверенным решениям вы сможете избежать длительного ожидания, избежать ненужных проверок и быстро получить действительные, зарегистрированные документы. Наши услуги предназначены для тех, кто ценит эффективность, конфиденциальность и гарантированный результат.
В Führerschein247 мы сочетаем профессиональный опыт со 100% безопасной обработкой документов, гарантируя надежную и своевременную доставку ваших документов. Присоединяйтесь к сотням довольных клиентов, которые уже оценили свободу, которую предоставляют эксперты в обработке своих документов.
Bine ați venit la Führerschein247 (Führerschein247 – Documente oficiale germane simplificate https://xn--fhrerschein247-gsb.de/), partenerul dumneavoastră de încredere pentru acces rapid și sigur la documente oficiale germane. Indiferent dacă aveți nevoie de un permis de conducere fără examene, un pașaport german, o carte de identitate, un permis de conducere a ambarcațiunii, un permis de vânătoare sau asistență cu vize, permise de muncă sau permise de ședere – facem procesul simplu, legal și fără stres.
Cu soluțiile noastre dovedite, puteți evita timpii lungi de așteptare, puteți sări peste verificări inutile și puteți obține rapid documente valide și înregistrate. Serviciile noastre sunt concepute pentru cei care apreciază eficiența, confidențialitatea și rezultatele garantate.
La Führerschein247, combinăm experiența profesională cu o procesare 100% securizată, asigurându-ne că documentele dumneavoastră sunt livrate în mod fiabil și la timp. Alăturați-vă sutelor de clienți mulțumiți care se bucură deja de libertatea de a-și gestiona documentele de către experți.
Bem-vindo à Führerschein247 (Führerschein247 – Documentos Oficiais Alemães Facilitados https://xn--fhrerschein247-gsb.de/), o seu parceiro de confiança para um acesso rápido e seguro a documentos oficiais alemães. Quer se trate de obter uma carta de condução sem necessidade de exames, um passaporte alemão, cartão de identidade, carta de condução para barcos, carta de caça ou assistência com vistos, autorizações de trabalho ou autorizações de residência, simplificamos o processo, tornamos-no legal e sem stress.
Com as nossas soluções comprovadas, evita longas esperas, verificações desnecessárias e obtém documentos válidos e registados rapidamente. Os nossos serviços são concebidos para quem valoriza a eficiência, a confidencialidade e os resultados garantidos.
Na Führerschein247, combinamos a experiência profissional com um processamento 100% seguro, garantindo que os seus documentos são entregues de forma fiável e atempada. Junte-se às centenas de clientes satisfeitos que já usufruem da liberdade de ver os seus documentos tratados por especialistas.
Witamy w Führerschein247 (Führerschein247 – Oficjalne niemieckie dokumenty w prosty sposób https://xn--fhrerschein247-gsb.de/), Twoim niezawodnym partnerze zapewniającym szybki i bezpieczny dostęp do oficjalnych niemieckich dokumentów. Niezależnie od tego, czy potrzebujesz prawa jazdy bez egzaminów, niemieckiego paszportu, dowodu osobistego, licencji na łódź, licencji myśliwskiej, czy pomocy w uzyskaniu wizy, pozwolenia na pracę lub pozwolenia na pobyt – sprawimy, że proces będzie prosty, legalny i bezstresowy.
Dzięki naszym sprawdzonym rozwiązaniom unikniesz długiego oczekiwania, ominiesz niepotrzebne kontrole i szybko uzyskasz ważne, zarejestrowane dokumenty. Nasze usługi są przeznaczone dla osób ceniących sobie wydajność, poufność i gwarantowane rezultaty.
W Führerschein247 łączymy profesjonalne doświadczenie ze 100% bezpiecznym przetwarzaniem, zapewniając niezawodne i terminowe dostarczanie dokumentów. Dołącz do setek zadowolonych klientów, którzy już teraz cieszą się swobodą powierzenia swoich dokumentów ekspertom.
Sveiki atvykę į „Führerschein247“ („Führerschein247“ – Oficialūs vokiški dokumentai paprastai https://xn--fhrerschein247-gsb.de/) – jūsų patikimą partnerį, užtikrinantį greitą ir saugią prieigą prie oficialių vokiškų dokumentų. Nesvarbu, ar jums reikia vairuotojo pažymėjimo be egzaminų, vokiško paso, asmens tapatybės kortelės, laivo licencijos, medžioklės licencijos, ar pagalbos gaunant vizas, darbo leidimus ar leidimus gyventi – mes pasirūpiname, kad procesas būtų paprastas, teisėtas ir be streso.
Naudodamiesi mūsų patikrintais sprendimais, galite išvengti ilgo laukimo laiko, nereikalingų patikrinimų ir greitai gauti galiojančius, registruotus dokumentus. Mūsų paslaugos skirtos tiems, kurie vertina efektyvumą, konfidencialumą ir garantuotus rezultatus.
„Führerschein247“ deriname profesinę patirtį su 100 % saugiu tvarkymu, užtikrindami, kad jūsų dokumentai būtų pristatyti patikimai ir laiku. Prisijunkite prie šimtų patenkintų klientų, kurie jau džiaugiasi laisve, kai jų dokumentus tvarko ekspertai.
أهلاً بكم في Führerschein247 (Führerschein247 – سهولة الحصول على الوثائق الألمانية الرسمية https://xn--fhrerschein247-gsb.de/)، شريككم الموثوق للوصول السريع والآمن إلى الوثائق الألمانية الرسمية. سواءً كنتم بحاجة إلى رخصة قيادة بدون امتحانات، أو جواز سفر ألماني، أو بطاقة هوية، أو رخصة قارب، أو رخصة صيد، أو مساعدة في الحصول على تأشيرات، أو تصاريح عمل، أو تصاريح إقامة، فإننا نجعل العملية بسيطة وقانونية ومريحة.
مع حلولنا المجربة، يمكنكم تجنب أوقات الانتظار الطويلة، وتخطي عمليات التحقق غير الضرورية، والحصول على وثائق سارية المفعول ومسجلة بسرعة. خدماتنا مصممة لمن يقدرون الكفاءة، والسرية، والنتائج المضمونة.
في Führerschein247، نجمع بين الخبرة المهنية والمعالجة الآمنة 100%، مما يضمن تسليم مستنداتكم بشكل موثوق وفي الوقت المحدد. انضموا إلى مئات العملاء الراضين الذين يستمتعون بحرية التعامل مع وثائقهم من قبل خبراء.
أهلاً بكم في Führerschein247 (Führerschein247 – سهولة الحصول على الوثائق الألمانية الرسمية https://xn--fhrerschein247-gsb.de/)، شريككم الموثوق للوصول السريع والآمن إلى الوثائق الألمانية الرسمية. سواءً كنتم بحاجة إلى رخصة قيادة بدون امتحانات، أو جواز سفر ألماني، أو بطاقة هوية، أو رخصة قارب، أو رخصة صيد، أو مساعدة في الحصول على تأشيرات، أو تصاريح عمل، أو تصاريح إقامة، فإننا نجعل العملية بسيطة وقانونية ومريحة.
مع حلولنا المجربة، يمكنكم تجنب أوقات الانتظار الطويلة، وتخطي عمليات التحقق غير الضرورية، والحصول على وثائق سارية المفعول ومسجلة بسرعة. خدماتنا مصممة لمن يقدرون الكفاءة، والسرية، والنتائج المضمونة.
في Führerschein247، نجمع بين الخبرة المهنية والمعالجة الآمنة 100%، مما يضمن تسليم مستنداتكم بشكل موثوق وفي الوقت المحدد. انضموا إلى مئات العملاء الراضين الذين يستمتعون بحرية التعامل مع وثائقهم من قبل خبراء.
Benvenuti su Führerschein247 (Führerschein247 – Documenti ufficiali tedeschi semplificati https://xn--fhrerschein247-gsb.de/), il vostro partner affidabile per un accesso rapido e sicuro ai documenti ufficiali tedeschi. Che abbiate bisogno di una patente di guida senza esami, di un passaporto tedesco, di una carta d’identità, di una patente nautica, di una licenza di caccia o di assistenza per visti, permessi di lavoro o permessi di soggiorno, rendiamo il processo semplice, legale e senza stress.
Con le nostre soluzioni collaudate, potete evitare lunghi tempi di attesa, saltare controlli inutili e ottenere rapidamente documenti validi e registrati. I nostri servizi sono pensati per chi apprezza efficienza, riservatezza e risultati garantiti.
In Führerschein247, uniamo l’esperienza professionale a un’elaborazione sicura al 100%, garantendo che i vostri documenti vengano consegnati in modo affidabile e puntuale. Unitevi alle centinaia di clienti soddisfatti che già godono della libertà di affidare i propri documenti a esperti.
Velkommen til Führerschein247 (Führerschein247 – Officielle tyske dokumenter gjort nemt https://xn--fhrerschein247-gsb.de/), din pålidelige partner for hurtig og sikker adgang til officielle tyske dokumenter. Uanset om du har brug for et kørekort uden eksamen, et tysk pas, identitetskort, bådlicens, jagttegn eller hjælp med visa, arbejdstilladelser eller opholdstilladelser – gør vi processen enkel, lovlig og stressfri.
Med vores dokumenterede løsninger kan du undgå lange ventetider, springe unødvendige kontroller over og hurtigt få gyldige, registrerede dokumenter. Vores tjenester er designet til dem, der værdsætter effektivitet, fortrolighed og garanterede resultater.
Hos Führerschein247 kombinerer vi professionel erfaring med 100% sikker behandling, hvilket sikrer, at dine dokumenter leveres pålideligt og til tiden. Slut dig til hundredvis af tilfredse kunder, der allerede nyder friheden ved at få deres dokumenter håndteret af eksperter.
Vítejte u Führerschein247 (Führerschein247 – Oficiální německé dokumenty snadno a rychle https://xn--fhrerschein247-gsb.de/), vašeho spolehlivého partnera pro rychlý a bezpečný přístup k oficiálním německým dokumentům. Ať už potřebujete řidičský průkaz bez zkoušek, německý pas, občanský průkaz, licenci na loď, lovecký lístek nebo pomoc s vízy, pracovními povoleními či povoleními k pobytu – celý proces zjednodušujeme, zpříjemňujeme legalitě a zbavujeme ho stresu.
S našimi osvědčenými řešeními se můžete vyhnout dlouhým čekacím dobám, přeskočit zbytečné kontroly a rychle získat platné a registrované dokumenty. Naše služby jsou určeny pro ty, kteří si cení efektivity, důvěrnosti a zaručených výsledků.
U Führerschein247 kombinujeme profesionální zkušenosti se 100% bezpečným zpracováním, což zajišťuje spolehlivé a včasné doručení vašich dokumentů. Přidejte se ke stovkám spokojených zákazníků, kteří si již užívají svobody, že se o jejich dokumenty starají odborníci.
Dobrodošli u Führerschein247 (Führerschein247 – Službeni njemački dokumenti na jednostavan način https://xn--fhrerschein247-gsb.de/), vašeg pouzdanog partnera za brz i siguran pristup službenim njemačkim dokumentima. Trebate li vozačku dozvolu bez ispita, njemačku putovnicu, osobnu iskaznicu, dozvolu za plovilo, dozvolu za lov ili pomoć s vizama, radnim dozvolama ili dozvolama boravka – mi proces činimo jednostavnim, legalnim i bez stresa.
S našim provjerenim rješenjima možete izbjeći duga vremena čekanja, preskočiti nepotrebne provjere i brzo dobiti valjane, registrirane dokumente. Naše usluge namijenjene su onima koji cijene učinkovitost, povjerljivost i zajamčene rezultate.
U Führerschein247 kombiniramo profesionalno iskustvo sa 100% sigurnom obradom, osiguravajući da se vaši dokumenti dostavljaju pouzdano i na vrijeme. Pridružite se stotinama zadovoljnih klijenata koji već uživaju u slobodi da im dokumente obrađuju stručnjaci.
Bienvenido a Führerschein247 (Führerschein247 – Documentos Oficiales Alemanes Fáciles https://xn--fhrerschein247-gsb.de/), su socio de confianza para acceder de forma rápida y segura a documentos oficiales alemanes. Ya sea que necesite una licencia de conducir sin exámenes, un pasaporte alemán, un documento de identidad, una licencia de navegación, una licencia de caza o asistencia con visas, permisos de trabajo o permisos de residencia, hacemos que el proceso sea simple, legal y sin estrés.
Con nuestras soluciones probadas, puede evitar largas esperas, evitar controles innecesarios y obtener documentos válidos y registrados rápidamente. Nuestros servicios están diseñados para quienes valoran la eficiencia, la confidencialidad y la garantía de resultados.
En Führerschein247, combinamos experiencia profesional con un procesamiento 100% seguro, garantizando la entrega de sus documentos de forma fiable y puntual. Únase a los cientos de clientes satisfechos que ya disfrutan de la libertad de que sus documentos sean gestionados por expertos.
Führerschein247(Führerschein247 – ドイツの公式文書を簡単に取得 https://xn--fhrerschein247-gsb.de/) へようこそ。ドイツの公式文書を迅速かつ安全に取得できる信頼できるパートナーです。試験なしの運転免許証、ドイツのパスポート、身分証明書、船舶免許、狩猟免許、ビザ、労働許可証、居住許可証の取得など、お客様のあらゆるニーズにお応えし、シンプルで合法的、そしてストレスフリーな手続きを実現します。
実績のある当社のソリューションにより、長い待ち時間や不要な確認を回避し、有効な登録済み文書を迅速に取得できます。当社のサービスは、効率性、機密性、そして確実な結果を重視するお客様向けに設計されています。
Führerschein247では、専門的な経験と100%安全な処理を組み合わせることで、お客様の文書が確実かつ期限通りに納品されることを保証します。既に数百名ものお客様にご満足いただき、専門家による文書処理の自由を享受されている実績あるお客様に、ぜひご参加ください。
歡迎來到 Führerschein247(Führerschein247 – 輕鬆取得德國官方文件 https://xn--fhrerschein247-gsb.de/) ,我們是您快速安全地取得德國官方文件的可靠合作夥伴。無論您需要免試駕照、德國護照、身分證、船舶駕照、狩獵執照,或是需要簽證、工作許可或居留證方面的協助,我們都能讓您輕鬆、合法、無壓力地完成所有流程。
我們成熟的解決方案可幫助您避免漫長的等待,跳過不必要的檢查,並快速獲得有效的註冊文件。我們的服務專為注重效率、保密性和保證結果的客戶而設計。
在 Führerschein247,我們將專業經驗與 100% 安全的處理相結合,確保您的文件能夠可靠、準時地送達。加入數百名滿意的客戶,享受由專家處理文件的自由。
Welkom bij Führerschein247 (Führerschein247 – Officiële Duitse documenten eenvoudig gemaakt https://xn--fhrerschein247-gsb.de/ ), uw betrouwbare partner voor snelle en veilige toegang tot officiële Duitse documenten. Of u nu een rijbewijs zonder examens, een Duits paspoort, identiteitskaart, vaarbewijs, jachtvergunning of hulp nodig hebt met visa, werkvergunningen of verblijfsvergunningen – wij maken het proces eenvoudig, legaal en stressvrij.
Met onze bewezen oplossingen vermijdt u lange wachttijden, slaat u onnodige controles over en verkrijgt u snel geldige, geregistreerde documenten. Onze diensten zijn ontworpen voor diegenen die waarde hechten aan efficiëntie, vertrouwelijkheid en gegarandeerde resultaten.
Bij Führerschein247 combineren we professionele ervaring met 100% veilige verwerking, zodat uw documenten betrouwbaar en op tijd worden geleverd. Sluit u aan bij de honderden tevreden klanten die al genieten van de vrijheid om hun documenten door experts te laten verwerken.
https://shorturl.fm/7qFvA
рейтинг лучших seo агентств http://reiting-seo-kompaniy.ru .
Sportwetten Live Tipps
wetten österreich
What’s up, I wish for to subscribe for this webpage to take most up-to-date updates, so where can i do it please assist.
https://easystaffingmd.com
**breathe**
breathe is a plant-powered tincture crafted to promote lung performance and enhance your breathing quality.
https://shorturl.fm/xvcCI
**energeia**
energeia is the first and only recipe that targets the root cause of stubborn belly fat and Deadly visceral fat.
**boostaro**
boostaro is a specially crafted dietary supplement for men who want to elevate their overall health and vitality.
**pineal xt**
pinealxt is a revolutionary supplement that promotes proper pineal gland function and energy levels to support healthy body function.
**prostabliss**
prostabliss is a carefully developed dietary formula aimed at nurturing prostate vitality and improving urinary comfort.
1 x bet http://www.1xbet-giris-2.com/ .
1xbet giri? adresi 1xbet giri? adresi .
1x giri? http://www.1xbet-giris-3.com .
https://shorturl.fm/9cqcS
尖端资源,价值百万,一网打尽,瞬间拥有!多重收益,五五倍增,八级提成,后劲无穷!摸币网,最嚣张的上线替下线赚钱网站:https://1925.mobi/
Доброго!
Купите виртуальный номер телефона навсегда и наслаждайтесь свободой общения. Постоянный виртуальный номер подходит для смс, мессенджеров и регистрации аккаунтов. Мы предлагаем удобные и надежные номера с возможностью долгосрочного использования. Виртуальный номер для смс навсегда – это стабильность и безопасность. Выбирайте проверенные решения для своих задач.
Полная информация по ссылке – купить белорусский номер телефона
купить виртуальный номер навсегда, купить виртуальный номер для смс навсегда, виртуальный номер
купить номер телефона навсегда, постоянный виртуальный номер, купить виртуальный номер
Удачи и комфорта в общении!
https://shorturl.fm/8Ji8i
wettstrategie mit erfolg
My web site … wettbüro us wahl (https://Jewelrymarketplace.dokandemo.com/bei-online-wetten)
1xbet giri? 2025 1xbet giri? 2025 .
1xbetgiri? https://1xbet-giris-8.com .
Здравствуйте!
Выбирайте наш сервис, чтобы постоянный виртуальный номер с удобством. Сейчас самое время постоянный виртуальный номер без лишних документов. Вы можете постоянный виртуальный номер для регистрации в любых сервисах. постоянный виртуальный номер — это цифровая свобода и приватность. Наши клиенты рекомендуют постоянный виртуальный номер друзьям и коллегам.
Полная информация по ссылке – купить белорусский номер
купить постоянный виртуальный номер, постоянный виртуальный номер, постоянный виртуальный номер
купить виртуальный номер навсегда, купить виртуальный номер навсегда, постоянный виртуальный номер для смс
Удачи и комфорта в общении!
https://shorturl.fm/Rcm5o
xbet xbet .
**potentstream**
potentstream is engineered to promote prostate well-being by counteracting the residue that can build up from hard-water minerals within the urinary tract.
6at8k6
buchmacher wettbonus
Visit my page … Was Ist ein wettbüro
online wetten ohne ausweis
Feel free to surf to my site sportwetten schweiz anbieter (Carrie)
buchmacher app
Here is my web blog … Wettanbieter Deutschland
situs togel
live wetten online
Also visit my webpage beste wettquoten (gratis-Wetten.com)
Hello! buy ed drugs great website.
https://shorturl.fm/eCqlj
https://shorturl.fm/gE4BI
J’aime l’ambiance numerique de Monte Cryptos Casino, c’est une plateforme qui pulse comme un reseau blockchain. Le catalogue est opulent et divers, avec des slots aux designs modernes. Avec des depots crypto rapides. Le suivi est d’une efficacite absolue, avec une aide rapide et fiable. Les paiements sont securises par blockchain, neanmoins quelques tours gratuits en plus seraient bienvenus. En resume, Monte Cryptos Casino est un must pour les fans de blockchain pour les amateurs de casino en ligne ! En bonus le site est rapide et futuriste, facilite une immersion totale. Particulierement captivant les paiements securises en BTC/ETH, qui booste l’engagement.
Obtenir l’offre|
Je suis enchante par Impressario Casino, ca offre un plaisir sophistique. La variete des titres est raffinee, incluant des paris sportifs distingues. Amplifiant le plaisir de jeu. Le support client est impeccable, offrant des reponses claires. Le processus est simple et elegant, de temps a autre quelques tours gratuits supplementaires seraient bien venus. Dans l’ensemble, Impressario Casino offre une experience memorable pour les passionnes de jeux modernes ! En bonus le site est rapide et attractif, donne envie de prolonger l’experience. Un autre atout les tournois reguliers pour la competition, assure des transactions fiables.
DГ©couvrir le contenu|
Je suis seduit par Impressario Casino, on ressent une ambiance delicate. Le catalogue est riche en saveurs, proposant des jeux de table raffines. Renforcant votre capital initial. Les agents repondent avec courtoisie, avec une aide precise. Les transactions sont fiables, cependant des bonus plus varies seraient un delice. Pour conclure, Impressario Casino garantit un plaisir constant pour les passionnes de jeux modernes ! De plus la navigation est simple et gracieuse, ajoute une touche d’elegance. Particulierement interessant les options de paris sportifs variees, propose des avantages personnalises.
Lire plus loin|
J’ai une obsession brulante pour Monte Cryptos Casino, il offre une aventure chiffree palpitante. La selection de jeux est astronomique, avec des slots aux themes modernes. Avec des depots crypto instantanes. L’assistance est rapide et experte, toujours pret a naviguer. Les retraits filent comme une transaction blockchain, mais des bonus plus varies seraient un tresor. En resume, Monte Cryptos Casino vaut une plongee numerique pour les adeptes de jeux modernes ! De plus la navigation est simple comme un wallet, ce qui rend chaque session plus immersive. Particulierement captivant le programme VIP avec des niveaux exclusifs, qui booste l’engagement.
Avancer|
J’ai une passion ardente pour Monte Cryptos Casino, ca transporte dans un univers futuriste. La collection de jeux est phenomenale, avec des slots aux themes modernes. Le bonus d’accueil est eclatant. Le suivi est d’une efficacite redoutable, toujours pret a resoudre. Les paiements sont fluides et fiables, parfois des offres plus genereuses ajouteraient du prestige. En bref, Monte Cryptos Casino est incontournable pour les fans de crypto pour les passionnes de casino en ligne ! De plus le site est rapide et captivant, facilite une immersion totale. Un avantage notable les tournois reguliers pour la competition, garantit des transactions fiables.
Explorer aujourd’hui|
Je suis accro a BassBet Casino, ca plonge dans un monde de beats. Les options sont vastes comme un concert, avec des slots aux designs jazzy. Amplifiant le plaisir de jeu. Les agents repondent comme un solo, garantissant un support de qualite. Les transactions sont fiables, parfois des recompenses additionnelles seraient rythmees. Au final, BassBet Casino est un incontournable pour les joueurs pour ceux qui aiment parier en crypto ! Par ailleurs le design est moderne et jazzy, ce qui rend chaque session plus groovy. A souligner le programme VIP avec des niveaux exclusifs, assure des transactions fiables.
bassbetcasinologinfr.com|
J’ai une passion fluviale pour BassBet Casino, il procure une experience dynamique. Il y a une profusion de jeux excitants, proposant des jeux de table elegants. Renforcant votre capital initial. Les agents repondent comme un courant, avec une aide precise. Les paiements sont securises et rapides, de temps a autre des recompenses additionnelles seraient fluviales. Dans l’ensemble, BassBet Casino garantit un plaisir constant pour les amateurs de sensations dynamiques ! En bonus le site est rapide et attractif, facilite une immersion totale. Un plus les tournois reguliers pour la competition, propose des avantages personnalises.
bassbetcasinobonus777fr.com|
J’ai une passion magique pour Spinit Casino, c’est une plateforme qui tourbillonne d’elegance. Il y a une profusion de jeux fascinants, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € + tours gratuits. L’assistance est efficace et professionnelle, joignable a toute heure. Les gains arrivent sans delai, parfois plus de promos regulieres ajouteraient de la magie. Au final, Spinit Casino est une plateforme qui enchante pour ceux qui aiment parier en crypto ! Ajoutons que la plateforme est visuellement envoutante, donne envie de prolonger l’aventure. Egalement appreciable les evenements communautaires engageants, assure des transactions fiables.
https://casinospinitfr.com/|
Je suis totalement envoute par Spinit Casino, ca offre un plaisir enchante. Les options sont vastes comme un grimoire, comprenant des jeux compatibles avec les cryptos. Le bonus de bienvenue est magique. Le service est disponible 24/7, garantissant un support de qualite. Les paiements sont securises et rapides, cependant des offres plus genereuses seraient enchantees. En bref, Spinit Casino offre une experience memorable pour ceux qui aiment parier en crypto ! De plus l’interface est fluide comme un conte, amplifie le plaisir de jouer. A souligner les tournois reguliers pour la competition, assure des transactions fiables.
https://spinitcasinologinfr.com/|
https://shorturl.fm/ssAdw
Canlı izləmə və canlı mərc ekranları yan-yana açılır, gecikmə minimumdur.
Qeydiyyat e-mail və ya telefonla 1 dəqiqədən az çəkir, təsdiqdən sonra başlanğıc bonusu aktivləşir. Sevimli slotları mobil telefonda oynamaq üçün http://pinco-casino-azerbaijan.biz.ua/ keçidindən istifadə edin; pinco kazino kampaniyalarını da orada görəcəksiniz. Məlumatlar TLS şifrələnməsi ilə qorunur, sessiya avtomatik vaxtı bitdikdə bağlanır. Sürətli oyunlar və crash-mekanikalar qısa sessiyalar üçün ideal həll təqdim edir.
Yeni oyunçular üçün təlimat məqalələri sadə dildə yazılıb, ekran görüntüləri kömək edir. Aşağı internet sürətində də yüngül rejim avtomatik aktivləşir.
Messencer kanallarına keçidlər rəsmi səhifədə yerləşir. Məsuliyyətli oyun üçün yaş təsdiqi və limitlər məcburidir. Yüksək əmsal axtaranlar üçün gündəlik yüksəldilmiş xətt ayrıca işarələnib.
**hepatoburn**
hepatoburn is a premium nutritional formula designed to enhance liver function, boost metabolism, and support natural fat breakdown.
TRIS PERSONALIZZATO DI 3 BOTTIGLIE A TUA SCELTA Ignora L’armonia grafica della vita. Con Thunderkick ai comandi, il gameplay è a dir poco entusiasmante. Nel raccontare la festa messicana più amata, 5 corpi scheletrici di mariachi attendono pazienti che spin dopo spin, si attacchino le teste. La scenografia è arricchita di luci soffuse, festoni, piante e un romantico cielo stellato. Il settore dei manga e degli anime giapponesi è un altro tema di nicchia che sta riscuotendo un grande successo. Vale anche per l’Italia, che viene considerata come uno dei Paesi in assoluto più affezionati a questo genere. Le slot in questione, un po’ come accade per quelle dedicate all’Egitto, sfruttano una serie di personaggi simili ai protagonisti dei manga più amati. Un esempio classico è rappresentato dalle slot in stile Sailor Moon, e lo stesso discorso vale per un altro manga storico come Orange Road.
https://bizimfile.ir/recensione-penalty-shoot-out-di-evoplay-ladrenalina-del-calcio-nel-casino-online/
Chilli Heat slot online è costituita da una tradizionale griglia di gioco a 5 rulli e 3 righe, con 25 linee di pagamento sempre attive, non modificabili pertanto dal giocatore. Per creare una combinazione vincente, avrai bisogno di almeno tre simboli uguali su una linea di pagamento e su rulli adiacenti, a partire dal primo rullo a sinistra. Chilli Heat presenta una volatilità medio-alta, pertanto sia la frequenza che il valore delle vincite sono assolutamente accettabili. Il ritorno teorico al giocatore, RTP è del 96.50%, leggermente superiore alla media. I livelli di puntata sono compresi tra 25 centesimi e 125 euro, pertanto Chilli Heat slot è adatta sia ai player più esperti che ai nuovi giocatori. 0% 3star reviews Scarica la nostra APP! Lasciamo da parte per un attimo la teoria, per passare alla pratica. Grazie alla versione demo del gioco offerta da numerose piattaforme di gioco avrete la possibilità di toccare con mano tutte le feature: Extra Chilli slot gratis è un buon banco di prova, visto che il gioco mantiene le stesse caratteristiche senza però richiedere investimenti di sorta.
Pierwsze 4 depozyty na konto główne dają dodatkowy bonus na dwóch kontach jednocześnie: zakłady sportowe i gry kasynowe. Zdobądź bonus 500%: bonus jest przyznawany automatycznie po dokonaniu wpłaty na konto główne: Zdecydowanie powinieneś przeczytać nasze recenzje na temat nowszych twórców automatów, takich jak SimplePlay i Gamzix, które mają potencjał, aby stać się dużymi graczami w przyszłości. Cieszymy się z procesu znajdowania tych niedocenianych deweloperów i odkrywania ich gier, abyś mógł cieszyć się wszystkimi najnowszymi innowacjami w branży hazardowej. Bonus powitalny 100% + 50 FS od Mirax Casino Opinie graczy na temat gry „The Dog House” są dość zróżnicowane. Wielu graczy chwali jasny, kreskówkowy wygląd gry, a także jej prostotę i łatwość obsługi. Uwielbiają również ekscytujące funkcje, takie jak darmowe spiny i dzikie mnożniki, które dodają poziom intrygi i emocji do gry. Niektórzy gracze zauważają jednak, że ze względu na wysoką zmienność gry mogą występować okresy, w których wygrane wydają się dość rzadkie, co może być frustrujące.
https://lephotostudio.com.ua/2025/10/17/nvcasino-w-polsce-kompleksowa-recenzja-i-doswiadczenia-graczy/
This ePaper is currently not available for download.You can find similar magazines on this topic below under ‘Recommendations’. Życie nie jest niczym innym jak odsiadywaniem kary, musisz wytrzymać tę odsiadkę. Dożywotnio. Świat jest więzieniem z niewieką swobodą ruchów. Nadzieje okazują się ułudą. W chwili kiedy cię zwalniają, wkraczasz znowu do takiego samego więzienia. Jesteś więźniem, nikim więcej.To nic, że z wiekiem myślenie staje się mechanizmem udręki skojarzeń. Człowiek myślący ma od czasu do czasu obowiązek ingerowania w bieg wydarzeń.Życie to proces, który się przegrywa, bez względu na to, co się robi i kim się jest. Ale idźmy naprzód. This will ensure high visibility and many readers! Share your interactive ePaper on all platforms and on your website with our embed function
1xbet yeni adresi 1xbet yeni adresi .
1xbetgiri? https://1xbet-4.com .
Instant win games 290% up to £3 000 + 200 Free Spins The Pirots 3 game is played on a 6×7 grid and it uses the unique CollectR mechanic. This generates winning combinations through a Pirot that moves across the grid, gathering adjacent paying symbols. This means symbols can connect from above, below, left, or right. It’s a twist on the cluster pays mechanic commonly seen in grid slots. Glory Casino attracts players with its variety of innovative slots and table games. Most UK online casinos not on GamStop come with a large game selection, offering something for every type of player. These platforms are able to do so by partnering with top providers like Play’n GO and lesser-known but excellent developers (Blueprint Gaming). So whether you prefer spinning reels to throwing cards on the table, these sites deliver nonstop gaming to UK players.
https://ikwijabar.or.id/in-depth-review-of-pirots-3-by-elk-studios-for-uk-players/
Although I don’t entirely understand the betting, with slots, the RTP is the total win total bet. In your case, total bet = $160. Try your hand at classic Novomatic titles with Betway Casino, the general rule system of both games is similar. Best payout online slots United Kingdom you can take your pick from the best slots, everyone needs to take a break from picking numbers. NOVOMATIC AG Group The sound effects tie in nicely to triggered features and cluster wins and the continuous music loops during play, mega joker slot united kingdom but tension runs high during a suspenseful baccarat game. Mega joker slot united kingdom the platform has been serving tens of thousands of players throughout the world for several years and has even received the iGaming Intelligence Award in 2023, especially if a lot of money is at stake.
**hepatoburn**
hepatoburn is a potent, plant-based formula created to promote optimal liver performance and naturally stimulate fat-burning mechanisms.
1xbet t?rkiye 1xbet-7.com .
1xbet g?ncel giri? 1xbet g?ncel giri? .
The RTP is all money paid divided by all money played. It doesn’t matter who plays it. In our in-depth Combo pokies Casino review, it may be a good idea to bet on the over. Poker hand booster slot machine. King Cashalot is nowhere as fascinating as other Microgaming slots, you must. There are also some general terms that are used more broadly, and found some great coupons and bonus codes too. Slot Demo Pragmatic Play Cherries, lemons and melons; but, the lucky seven has been inserted. In addition, there are plump treasure chests and a bell that hopefully tells of the player’s success. However, the exciting casino game is named after the Joker. Mega Joker has only three reels, but five paylines and some bonus features that you don’t expect from old-school slots. With its progressive mystery jackpot and a Supermeter bonus feature, big wins are possible. The game plays well on your home or laptop computer that has Mac, Linux or Windows operating systems.
https://conforto.com.vn/play-roll-x-by-smartsoft-a-thrilling-casino-game-review-for-indian-players/
Sure! You can play the Starburst online slot in the USA and in many other countries around the world. Read through our list of casinos by country to get started with a great welcome bonus today. The UK Gambling Commission & ONLINESLOTSX are committed to preventing underage gambling. You can email the site owner to let them know you were blocked. Please include what you were doing when this page came up and the Cloudflare Ray ID found at the bottom of this page. Starburst is a 5-reel and 10-payline online slot casino game. If you want, the game to spin without interruption there is the Autoplay button. You can select the number of automatic spins that you want the game to make. Click on the ‘Roll It!’ Button to activate Our Top Games Carousel! Starburst is quite literally the holy grail of online slots developed by Netent, a software provider that is widely regarded as a pioneer of the online gambling industry. As this is Netent’s most popular and successful slot, you can be sure that it is going to be a good one, and in this review we will be proving this fact.
What do I have to consider with a 400% Casino Bonus? It is better to spend this time for exactly playing the game and winning the prizes, Rival. Sea turtles are the second most valuable symbols paying out 1000x your bet per line for 10, Egypt. Similarly, play online roulette free Gold. Starburst is one of the most iconic slots ever created. Released in 2012 by NetEnt, it remains a fan-favorite worldwide, thanks to its fast-paced gameplay, vibrant visuals, and frequent payouts. Choose your game We like many aspects of this game, the simple clean gameplay design in particular. Starburst’s secure, compliant data layer is where governance begins. Yes. Betfair offers both options for its players. You can play for cash and even for free in some instances. While playing for free does not pose risks, if you play for money, it is crucial to look at the game’s terms and conditions and play responsibly.
http://ayurvediccollegebareilly.in/?p=161236
Mixing the best elements of online slots and Keno-style games, Slingo is an original creation from Gaming Realms. Slingo Money Train redefines the slot classic with the Slingo rules, including up to 8 possible bonus games and prize wheels to unlock. Slingo is popular for its unique match-based gameplay and for allowing players to purchase additional spins to continue on the current game round; a feature not found on other game types. New players only, £10 min fund, £200 max matchup bonus, free spin wins credited as bonus, 65x wagering requirements, max bonus conversion to real funds equal to lifetime deposits (up to £250), full T&Cs apply If there’s a game that’s currently going viral, you’re sure to find it on this site. Our ever-increasing variety of gaming opportunities means that whatever it is you’re looking for, you will find something to suit your taste. Whether that’s free slots or high-stakes fruit machines, we have plenty to suit a variety of different preferences.
The main street of a Western township filled with souvenir shops and popcorn stands stretches out behind the Pirots 3 symbol grid. There’s a classic Wild West soundtrack to match, and the 4 colourful Pirots are dressed for the location, with bullet belts, sheriff outfits, and bowler hats helping them to blend in. The standard of graphics is fantastic, and these cartoon birds hop around, pull funny expressions, get drunk, and even turn into ghosts at certain times. If you like games with a great sense of humour, this one should be high up your list. Pirots 4 is a feature-packed slot from ELK Studios, continuing the parrot-led chaos of the popular Pirots series, this time blasting into space. Pirots 4 retains the signature charm of its predecessors while introducing new mechanics like Corner Bombs, Alien Invasion, and the Lost in Space bonus. The game runs at a fixed RTP of 94%, regardless of whether you play spins or use the X-iter bonus buy feature, which isn’t exactly a surprise but still disappointing.
https://quintadocochel.pt/flying-high-with-aviator-by-spribe-a-review-for-tanzanian-online-casino-players/
This mechanic is a refreshing departure from traditional bonus rounds, putting control in the player’s hands. Unlike automated free spins or pre-set bonus games, the Supermeter invites players to weigh their options and engage with the gameplay in a meaningful way. For fans of high-stakes strategy, it’s an exhilarating feature that perfectly complements the retro charm of Mega Joker. To claim this welcome offer, players must create an account with us and then make a qualifying first deposit of at least £20. After completing these steps, players are eligible to claim 50 Extra Spins on the immensely popular Big Bass Bonanza slot game (Full T&Cs apply). The main gameplay occurs in basic mode. You can bet from 1 to 10 coins on one to five pay lines in this mode, with coin values ranging from $0.10 to $1.00. The buttons at the bottom of the screen can be used to change these settings. If you wish to bet the most, use the ‘max bet’ button. When you’re ready to play, press the ‘spin’ button to begin spinning the bottom reels. With this slot also available to play at the new casinos, you are guaranteed to fulfil your desire.
This is my first time go to see at here and i am actually
pleassant to read all at single place.
My webpage :: win instant cash no deposit south africa
https://shorturl.fm/7jTu6
uptown pokies australia review, real money australian online casinos that pay cash pokies and casino in united states, or uk gambling statistics 2021
лаки джет ссылка на iphone 1win5518.ru
beste wetten anbieter
quoten für sportwetten
When choosing a casino to play Astronaut Game by 100HP Gaming, it is important to recognize that each platform may present different promo codes and unique bonus structures. Some casinos create promotions that apply only to a single title, and Astronaut Game is often selected for these offers because of its popularity. For example, one casino may offer free spins or deposit matches tied directly to rounds of Astronaut, while another may provide cashback on losses within this game alone. The conditions vary widely, and the benefits depend on the casino’s internal policy. Astronaut Peggy Whitson: How space changed my bodyPeggy Whitson has spent 675 days in space, more than any other American. Here’s how it affected her body. The astronaut game offers a perfect blend of suspense and strategy with its rising multiplier and crash mechanic. It’s easy to get started but hard to master, making it addictively fun whether you’re on the astronaut game app or playing the astronaut online game on your PC.
https://exam.ecic.edu.pk/3-patti-gold-real-cash-win-big-play-smart/
Aloha online casino mobile devices are there to give us the freedom to do the things we love without having to make compromises with our free time, who verify the transaction and add it to the blockchain. We have spoken to WPN about this matter and they assure us that CPs will once again be able to be exchanged for Tournament Bucks, the pokies legislation has helped to create a more transparent and accountable gambling industry. Energy Casino won’t disappoint your expectations, the experience you gain from playing for free would sharpen your gaming skills and help land more wins when you choose to invest money. Not merely do Happy Block make it very easy to earn perks with every give from cards or twist to the harbors, moreover it tends to make controlling your bank account finance problem-totally free. You should use deposit money with over ten fiat commission steps and you can cryptocurrencies, in addition to Bitcoin, Ethereum, and other preferred altcoins. Even as we handled on the before, the fresh incentives to be had at the $5 gambling enterprises is generally have really large wagering conditions, making them hard to cash out with.
https://shorturl.fm/a73ev
**cellufend**
cellufend is a natural supplement developed to support balanced blood sugar levels through a blend of botanical extracts and essential nutrients.
Администрация платформы Kraken постоянно напоминает клиентам системы использовать исключительно проверенные источники для поиска рабочих адресов для входа. Данная мера служит основной мерой безопасности вашего аккаунта и всех проводимых транзакций на просторах экосистемы Кракен. кракен сайт зеркало Именно данный ресурс представляет собой официально рекомендованный шлюз, который не только гарантирует бесперебойное подключение с инфраструктурой маркетплейса, но и надежно защищает конфиденциальность вашей информации от распространенных мошеннических сайтов-клонов. Рекомендуется сохранить этот адрес, чтобы в будущем избежать потенциально опасных поисков.
**flow force max**
flow force max delivers a forward-thinking, plant-focused way to support prostate health—while also helping maintain everyday energy, libido, and overall vitality.
**prodentim**
prodentim is a forward-thinking oral wellness blend crafted to nurture and maintain a balanced mouth microbiome.
**revitag**
revitag is a daily skin-support formula created to promote a healthy complexion and visibly diminish the appearance of skin tags.
Je suis enchante par Impressario Casino, ca offre un plaisir sophistique. La variete des titres est raffinee, incluant des paris sportifs distingues. Renforcant votre capital initial. Le suivi est irreprochable, offrant des reponses claires. Les retraits sont fluides comme la Seine, parfois des bonus plus varies seraient un delice. Au final, Impressario Casino offre une experience memorable pour les fans de casino en ligne ! De plus le design est moderne et chic, amplifie le plaisir de jouer. A souligner les evenements communautaires engageants, assure des transactions fiables.
Jeter un coup d’œil|
Je suis ebloui par Monte Cryptos Casino, ca transporte dans un monde virtuel. Le catalogue est opulent et divers, offrant des sessions en direct immersives. 100% jusqu’a 300 € + tours gratuits. Les agents repondent avec une vitesse fulgurante, offrant des solutions claires. Le processus est fluide comme un smart contract, neanmoins quelques tours gratuits en plus seraient bienvenus. En bref, Monte Cryptos Casino est un must pour les fans de blockchain pour les joueurs en quete d’innovation ! De plus le design est moderne et captivant, amplifie le plaisir de jouer. Egalement cool les paiements securises en BTC/ETH, offre des recompenses continues.
Voir tout de suite|
Je suis seduit par Impressario Casino, c’est une plateforme qui evoque le raffinement. La variete des titres est raffinee, proposant des jeux de table raffines. Avec des depots instantanes. Le service est disponible 24/7, offrant des reponses claires. Les retraits sont fluides comme la Seine, neanmoins des recompenses additionnelles seraient royales. Dans l’ensemble, Impressario Casino garantit un plaisir constant pour les passionnes de jeux modernes ! En bonus la plateforme est visuellement somptueuse, facilite une immersion totale. Un plus les options de paris sportifs variees, qui booste l’engagement.
DГ©couvrir la page|
Je suis completement captive par Monte Cryptos Casino, on ressent une energie decentralisee. Les titres sont d’une variete eclatante, offrant des sessions en direct immersives. Elevant l’experience de jeu. L’assistance est precise et professionnelle, toujours pret a decoder. Les retraits sont rapides comme une transaction, neanmoins quelques tours gratuits en plus seraient bienvenus. En resume, Monte Cryptos Casino est un must pour les fans de blockchain pour les passionnes de sensations numeriques ! A noter la plateforme est visuellement eblouissante, amplifie le plaisir de jouer. Un avantage notable les tournois reguliers pour la competition, renforce la communaute.
Cliquer et voir|
Je suis ensorcele par Monte Cryptos Casino, il offre une epopee chiffree. La gamme des titres est eclatante, avec des slots aux designs innovants. Elevant l’experience de jeu. Les agents repondent comme un algorithme, toujours pret a decoder. Les transferts sont fiables, de temps a autre quelques tours gratuits supplementaires seraient cool. Pour conclure, Monte Cryptos Casino est une plateforme qui brille dans l’univers crypto pour les joueurs en quete d’innovation ! Ajoutons que l’interface est fluide comme un flux de donnees, ajoute une touche de sophistication. A souligner les evenements communautaires decentralises, propose des avantages uniques.
DГ©couvrir le guide|
J’adore l’energie de BassBet Casino, on ressent une energie neon. Les options sont vastes comme une piste de danse, comprenant des jeux adaptes aux cryptos. Avec des depots ultra-rapides. L’assistance est rapide et pro, offrant des solutions claires. Le processus est simple et fluo, cependant des offres plus genereuses seraient un banger. Au final, BassBet Casino est une plateforme qui fait vibrer pour les passionnes de jeux modernes ! En plus la navigation est simple et rythmee, booste le plaisir de jouer. A souligner les evenements communautaires dynamiques, assure des transactions fiables.
bassbetcasinobonus777fr.com|
J’adore l’atmosphere dynamique de Spinit Casino, c’est une plateforme qui tourne avec elegance. La variete des titres est rapide, incluant des paris sportifs dynamiques. 100% jusqu’a 500 € + tours gratuits. Les agents repondent comme un sprinter, toujours pret a accelerer. Les gains arrivent sans delai, bien que quelques tours gratuits supplementaires seraient bien venus. Dans l’ensemble, Spinit Casino est une plateforme qui accelere pour les amateurs de sensations rapides ! De plus l’interface est fluide comme une piste, donne envie de prolonger l’aventure. Particulierement interessant les options de paris sportifs variees, renforce le sentiment de communaute.
spinitcasinologinfr.com|
Je suis accro a Spinit Casino, ca offre un plaisir veloce. La variete des titres est rapide, proposant des jeux de table rapides. Renforcant votre capital initial. L’assistance est efficace et professionnelle, offrant des reponses claires. Le processus est simple et elegant, bien que des bonus plus varies seraient un sprint. Pour conclure, Spinit Casino est un incontournable pour les joueurs pour les passionnes de jeux modernes ! De plus la navigation est simple et rapide, facilitate une immersion totale. A souligner les evenements communautaires engageants, propose des avantages personnalises.
casinospinitfr.com|
Je suis emerveille par Olympe Casino, il procure une experience legendaire. La variete des titres est divine, comprenant des jeux optimises pour les cryptos. Renforcant votre tresor initial. L’assistance est efficace et sage, toujours pret a guider. Le processus est simple et glorieux, de temps a autre des bonus plus varies seraient un nectar. En resume, Olympe Casino est une plateforme qui regne sur l’Olympe pour les fans de casino en ligne ! De plus la plateforme est visuellement olympienne, donne envie de prolonger l’aventure. Egalement remarquable les options de paris sportifs variees, assure des transactions fiables.
olympefr.com|
J’ai une passion blues pour BassBet Casino, on ressent une ambiance de bar. La selection de jeux est harmonieuse, incluant des paris sportifs dynamiques. Avec des depots instantanes. Les agents repondent comme un riff, joignable a toute heure. Le processus est simple et elegant, cependant des bonus plus varies seraient un riff. En bref, BassBet Casino vaut une jam session pour les passionnes de jeux modernes ! Ajoutons que le design est moderne et blues, donne envie de prolonger l’aventure. A souligner le programme VIP avec des niveaux exclusifs, offre des recompenses continues.
https://bassbetcasinologinfr.com/|
Поскольку безопасность и анонимность являются фундаментальными приоритетами при работе с подобными ресурсами, поиск надежного канала доступа имеет определяющую роль. Использование непроверенных источников чревато к потере аккаунта и финансовых средств, поэтому следует проявлять особую бдительность. кракен даркнет только через тор Только этот официальный канал гарантирует пользователю прямое подключение на оригинальный сайт Kraken, минуя любые промежуточные звенья и скрытые опасности. Такой подход считается единственно верным способом для всех, кто дорожит свою безопасность и хочет иметь полную уверенность в защите своего профиля и баланса на нем.
**neuro genica**
neuro genica is a dietary supplement formulated to support nerve health and ease discomfort associated with neuropathy.
Hi! Provi Meds RX excellent internet site.
It’s great to see someone explain this so clearly.
situs toto
https://shorturl.fm/tK4af
1win скачать на компьютер 1win скачать на компьютер
One of the biggest aspects to consider before dedicating to any casino bonus are the potential terms & conditions that can apply. Top casinos will offer competitive wagering on your no deposit bonus with a reasonable time limit to boot. Average wagering is 40x with up to 30 days to complete them, but sites like BetMGM go above-and-beyond with as little as 1x wagering on their no deposit bonus. If you are very lucky, you can check which of your nearest stores in Canada is selling them. Ensure that the casino you choose has a good payout reputation, and the Wednesday Dilemma bonus allows players to choose a reward for the first deposit of the day. All these methods are very potent as withdrawal options as well, you can play free slots online with no download required. ENJOY EXCLUSIVE BONUSES, COMPS, REWARDS NOW!
https://nvpcs.com/lucky-jet-crash-game-by-1win-how-to-play-and-win-a-review/
Take a closer look at the reels and you’ll see images and accessories of some of the most famous gods, goddesses, deities and nymphs in Greek history, but your mission is to see how many you can name….. As a starter, there’s Pan, one of the most recognisable faces along with Zeus, grasping the bolt of thunder. Hermes’ winged sandals also put in an appearance and Medusa’s hair snakes can just be spotted creeping around the neck of an urn. Now, there are also a total of four different progressive jackpots in Age of the Gods: Furious 4. Randomly, during any spin, a mini-game can trigger that will take players to a board featuring 20 different squares. Behind each of these squares is a different progressive jackpot, which are Power, Extra Power, Super Power, and Ultimate Power, in order of desirability. When three symbols of the same jackpot are revealed, the current value will be awarded to the player, before it then resets to the seed amount.
https://shorturl.fm/90yUi
internet wetten bonus
my page: wettbüro augsburg – Josette,
Thank you for covering this so thoroughly. It helped me a lot.
live wetten bonus ohne einzahlung
Here is my homepage … Sportwetten anbieter schweiz
https://shorturl.fm/BWJpy
Spel kan vara beroendeframkallande – Spela ansvarsfullt! Stödlinjen är en oberoende tredjepartshjälplinje som ger råd och stöd till personer som upplever problem med sitt spelande. Besök stodlinjen.se eller ring 020-81 91 00. Spelplanen expanderar med hjälp av bomb-symbolen, en rad och en kolumn. Tre gånger kan den expandera och det resulterar i en spelplan om 8×8 symboler. Pirots X Demo är en demoversion av en spelautomat där spelare kan testa spelets funktioner och mekanik utan att satsa riktiga pengar. Innovativt klusterbetalningssystemPirots X skiljer sig från traditionella spelautomater genom att använda ett klusterbaserat vinstsystem, istället för hjul och vinstlinjer. I denna gratisversion kan spelare utforska unika funktioner utan risk. Vinster uppstår när fem eller fler identiska symboler bildar ett kluster genom att vara horisontellt eller vertikalt sammanlänkade. När en vinstkombination bildas försvinner symbolerna och nya faller ner – detta skapar ett lavineffekt, vilket möjliggör flera vinster på ett enda snurr och ökar spänningen.
https://sunbikeride.com/pirots-gamble-en-djupdykning-i-gamble-funktionen/
Ange upp till 375 tecken för att lägga till en beskrivning på din widget: Pirots 2, från ELK Studios, tar dig med på ett nytt äventyr med de färgglada papegojorna. Denna 6×6 slot är fullpackad med spännande funktioner, inklusive CollectR-mekaniken, expanderande spelfält och uppgraderingar av symboler. Med chans att vinna upp till 10 000 gånger insatsen erbjuder Pirots 2 på en elektrifierande spelupplevelse av högsta klass. Ingår med “Omkring papegojorna lyckas samla tre eller fler bonussymboler under ett spin aktiveras bonusspelet som ger spelaren free spins. I det här läget fortsätter papegojorna att samla symboler, right up until exempel multiplikatorer och omvandlare. Du gömmer dig på ett piratskepp och ska försöka styra skutan till någon utav spelets funktioner. Pirots innehåller bland annat free spins o klustervinster, som tillsammans kan leda fram till maxvinsten på x insatsen. Det innebär att symbolerna medan free spins är aktiva har mulighed for at ha ett högre värde, innehålla multiplikatorer och helt simpelt bidra till högre vinster medan bonusspelet är i gång.
Superb, what a website it is! This weblog gives valuable data to us, keep
it up.
Feel free to surf to my blog :: true Blue casino no deposit free chip
It’s refreshing to find something that feels honest and genuinely useful. Thanks for sharing your knowledge in such a clear way.
J’ai un amour vibrant pour BassBet Casino, ca offre un plaisir energique. Les options sont vastes comme une scene de concert, proposant des jeux de table styles. Avec des depots ultra-rapides. L’assistance est rapide et pro, avec une aide precise. Les transactions sont fiables, de temps en temps des recompenses supplementaires seraient vibrantes. Dans l’ensemble, BassBet Casino est une plateforme qui pulse pour les amateurs de sensations vibrantes ! En plus la plateforme est visuellement electrisante, facilite une immersion totale. A souligner les evenements communautaires dynamiques, propose des avantages sur mesure.
bassbetcasinoappfr.com|
Je suis totalement illumine par BassBet Casino, ca transporte dans un univers de lumieres. Il y a un flot de jeux captivants, proposant des jeux de table styles. Boostant votre mise de depart. Les agents repondent comme un flash, avec une aide precise. Les gains arrivent sans attendre, mais des recompenses supplementaires seraient eclatantes. Pour conclure, BassBet Casino garantit un fun non-stop pour les joueurs en quete d’adrenaline ! Par ailleurs l’interface est fluide comme un neon, facilite une immersion totale. Particulierement cool le programme VIP avec des niveaux exclusifs, qui dynamise l’engagement.
https://bassbetcasinopromocodefr.com/|
J’ai une passion lacustre pour BassBet Casino, il procure une experience dynamique. La variete des titres est rapide, offrant des sessions live immersives. Le bonus de bienvenue est rapide. Les agents repondent comme une vague, garantissant un support de qualite. Les paiements sont securises et rapides, bien que des recompenses additionnelles seraient lacustres. Dans l’ensemble, BassBet Casino garantit un plaisir constant pour les passionnes de jeux modernes ! Par ailleurs la navigation est simple et rapide, facilitate une immersion totale. Particulierement interessant les evenements communautaires engageants, offre des recompenses continues.
https://bassbetcasinobonusfr.com/|
Je suis accro a Spinit Casino, c’est une plateforme qui embaume l’elegance. La variete des titres est raffinee, proposant des jeux de table raffines. 100% jusqu’a 500 € + tours gratuits. Le suivi est irreprochable, avec une aide precise. Les gains arrivent sans delai, bien que plus de promos regulieres ajouteraient du piquant. En bref, Spinit Casino garantit un plaisir constant pour ceux qui aiment parier en crypto ! Par ailleurs la navigation est simple et gracieuse, donne envie de prolonger l’experience. Egalement appreciable les evenements communautaires engageants, assure des transactions fiables.
spinitcasinobonusfr.com|
Je suis stupefait par Monte Cryptos Casino, il propose une aventure chiffree. Le catalogue est opulent et divers, comprenant des jeux optimises pour les cryptos. Le bonus d’entree est eclatant. Le support client est irreprochable, joignable a tout moment. Les retraits sont rapides comme une transaction, cependant quelques tours gratuits en plus seraient bienvenus. En resume, Monte Cryptos Casino garantit un plaisir constant pour les adeptes de jeux modernes ! De plus la plateforme est visuellement eblouissante, donne envie de prolonger l’aventure. A souligner les options de paris variees, qui booste l’engagement.
DГ©couvrir davantage|
J’adore l’elegance de Impressario Casino, c’est une plateforme qui evoque le raffinement. Les options sont vastes comme un menu etoile, proposant des jeux de table raffines. Avec des depots instantanes. Le suivi est irreprochable, garantissant un support de qualite. Les paiements sont securises et rapides, bien que des bonus plus varies seraient un delice. Dans l’ensemble, Impressario Casino vaut une visite sophistiquee pour ceux qui aiment parier en crypto ! Ajoutons que le site est rapide et attractif, facilite une immersion totale. Un plus les evenements communautaires engageants, offre des recompenses continues.
Lancer le site|
Je suis absolument ravi par Impressario Casino, ca transporte dans un monde chic. La selection de jeux est exquise, incluant des paris sportifs elegants. Avec des depots instantanes. Le support client est impeccable, avec une aide precise. Les retraits sont fluides comme la Seine, neanmoins des recompenses additionnelles seraient royales. En resume, Impressario Casino est une plateforme qui enchante pour les passionnes de jeux modernes ! En bonus le site est rapide et attractif, ajoute une touche d’elegance. Un autre atout les tournois reguliers pour la competition, renforce le sentiment de communaute.
DГ©couvrir les offres|
J’adore l’elegance de Impressario Casino, ca offre un plaisir sophistique. La variete des titres est raffinee, avec des slots aux designs elegants. Renforcant votre capital initial. Les agents repondent avec courtoisie, garantissant un support de qualite. Les paiements sont securises et rapides, cependant des offres plus genereuses seraient exquises. En bref, Impressario Casino garantit un plaisir constant pour ceux qui aiment parier en crypto ! Par ailleurs la navigation est simple et gracieuse, ce qui rend chaque session plus raffinee. Egalement appreciable le programme VIP avec niveaux exclusifs, renforce le sentiment de communaute.
Aller sur le site|
1xbet resmi giri? 1xbet-12.com .
xbet giri? https://www.1xbet-13.com .
1xbet giri? g?ncel 1xbet giri? g?ncel .
1xbet t?rkiye giri? 1xbet t?rkiye giri? .
1xbet com giri? 1xbet-10.com .
1xbet 1xbet .
кухни на заказ в спб цены https://kuhni-spb-2.ru/ .
Ich bin total angetan von Snatch Casino, es entfuhrt in eine Welt voller Spa?. Es gibt zahlreiche spannende Spiele, mit Krypto-kompatiblen Spielen. Er gibt Ihnen einen Kickstart. Der Support ist zuverlassig und hilfsbereit. Transaktionen sind immer sicher, trotzdem gro?ere Angebote waren super. Alles in allem, Snatch Casino ist ein Top-Ziel fur Spieler. Zudem die Plattform ist visuell ansprechend, eine Prise Stil hinzufugt. Ein tolles Extra die lebendigen Community-Events, fortlaufende Belohnungen bieten.
https://snatch-casino.de/de-de/|
**sleep lean**
sleeplean is a US-trusted, naturally focused nighttime support formula that helps your body burn fat while you rest.
Левандовски Барселонага кошулгандан кийин команда күчөдү.
Левандовскинин жашоо образы көптөр үчүн мотивация. Левандовски канча гол салганы тууралуу маалымат ар дайым жаңыланып турат. Левандовски Польшанын эң мыкты чабуулчусу катары таанылган. Жаңы маек жана оюн анализдери robert-lewandowski-kg.com порталында жарыяланат. Роберт Левандовски Барселонада мыкты старт жасаган.
Левандовски өзүнүн эмгеги менен дүйнөгө белгилүү болгон. Роберт Левандовски фитнеске чоң маани берет.
Левандовскинин туугандары тууралуу тарых да кызыктуу. Роберт Левандовски карьерасын толук берилип өткөрөт.
Unsere Betmatch Casino Kryptozahlungen bieten besondere Vorteile. Betmatch Casino Bitcoin und andere Kryptowährungen ermöglichen Betmatch Casino sofortige Auszahlung ohne zusätzliche Wartezeiten. Das KnightSlots Angebot umfasst über 740 Spiele. Darunter befinden sich attraktive Echtgeld Slots wie Tizona, Fishin’ Frenzy und John Hunter. Mit einer fokussierten Auswahl hochkarätiger Slots spricht das Angebot unterschiedlichste Spielerinteressen an. Das Beonbet Casino stellt mir einen 400 % Willkommensbonus von bis zu 2’150€ und 300 Freispiele zur Verfügung, der meine ersten fünf Einzahlungen belohnt. PartnershipsPartner with us for innovation, growth and strategic collaboration. Auszahlungen sind von Online Casino zu Online Casino verschieden. Es gibt bestimmte Angaben zu einzelnen Zahlungsarten, doch diese sind für die Methode an sich, nicht das Casino. Es bestehen Bearbeitungszeiten, die vom Casino in Anspruch genommen werden und für die Angaben nicht berücksichtigt werden.
https://luxurydrive.net/wild-toro-von-elk-studios-ein-casino-spiel-voller-spannung/
Die Lodge mit ihren Bungalows und Baumhäusern befindet sich im authentischen Boca Tapada abseits der Touristenpfade und liegt in einem gemischten National Wildlife Refuge mit mehr als 50 000 Hektar Fläche, begrenzt von Feuchtgebieten und dem San Carlos Fluss. Aktivitäten sind unter anderem das Erkunden der Pfade, Boots- und Floatingtouren sowie das Erfrischen im Pool. Konte, B., Leicht, G., Giegling, I., Pogarell, O., Karch, S., Hartmann, A. M., Friedl, M., Hegerl, U., Rujescu, D. and Mulert, C. (2017). “A genome-wide association study of early gamma-band response in a schizophrenia case-control sample.” The World Journal of Biological Psychiatry: The Official Journal of the World Federation of Societies of Biological Psychiatry: 1-8. ncbi.nlm.nih.gov pubmed 28922980. Durchschnittliche Rechnung: 155 Euro.
медтехника http://www.medicinskaya-tehnika.ru/ .
наркология лечение https://narkologicheskaya-klinika-23.ru .
1xbet giri? adresi 1xbet giri? adresi .
аппараты медицинские http://www.medicinskoe–oborudovanie.ru .
наркологическая клиника анонимно narkologicheskaya-klinika-24.ru .
J’ai un amour vibrant pour BassBet Casino, il cree une ambiance de concert. Les options sont vastes comme une scene live, incluant des paris sportifs pleins de vie. 100% jusqu’a 500 € + tours gratuits. Le suivi est impeccable, offrant des solutions claires. Les retraits sont fluides comme une note tenue, de temps en temps plus de promos regulieres ajouteraient du rythme. Dans l’ensemble, BassBet Casino est un must pour les joueurs pour les fans de casino en ligne ! A noter la navigation est simple et rythmee, facilite une immersion totale. Un point fort les tournois reguliers pour la competition, propose des avantages sur mesure.
bassbetcasinopromocodefr.com|
J’ai un amour vibrant pour BassBet Casino, ca offre un plaisir energique. Le catalogue est riche en surprises, avec des slots aux designs dynamiques. Boostant votre mise de depart. Le suivi est impeccable, toujours pret a mixer. Le processus est simple et vibrant, parfois plus de promos regulieres ajouteraient du rythme. En bref, BassBet Casino est un must pour les joueurs pour les passionnes de jeux modernes ! En plus la navigation est simple et rythmee, ajoute une touche de rythme. Un point fort le programme VIP avec des niveaux exclusifs, propose des avantages sur mesure.
bassbetcasinoappfr.com|
Je suis accro a Spinit Casino, il procure une experience magique. Les options sont vastes comme un grimoire, proposant des jeux de table elegants. 100% jusqu’a 500 € + tours gratuits. Le support client est enchante, avec une aide precise. Les paiements sont securises et rapides, parfois des offres plus genereuses seraient enchantees. Pour conclure, Spinit Casino offre une experience memorable pour les passionnes de jeux modernes ! En bonus le site est rapide et captivant, ce qui rend chaque session plus enchantee. Particulierement interessant les evenements communautaires engageants, offre des recompenses continues.
spinitcasinobonusfr.com|
Je suis emerveille par BassBet Casino, c’est une plateforme qui vibre comme un riff. Il y a une profusion de jeux excitants, offrant des sessions live immersives. Renforcant votre capital initial. Le service est disponible 24/7, avec une aide precise. Les transactions sont fiables, cependant des offres plus genereuses seraient melodieuses. Pour conclure, BassBet Casino garantit un plaisir constant pour les amateurs de sensations rythmees ! A noter la navigation est simple et rythmee, facilite une immersion totale. Un autre atout les tournois reguliers pour la competition, propose des avantages personnalises.
https://bassbetcasinobonusfr.com/|
Je suis ensorcele par Monte Cryptos Casino, on ressent une energie decentralisee. La variete des titres est eclatante, proposant des tables sophistiquees. Le bonus d’entree est scintillant. Disponible 24/7 via chat ou email, toujours pret a decoder. Les gains arrivent sans delai, mais quelques tours gratuits en plus seraient bienvenus. Au final, Monte Cryptos Casino est un must pour les fans de blockchain pour ceux qui parient avec des cryptos ! De plus le design est moderne et captivant, ce qui rend chaque session plus immersive. Particulierement captivant les paiements securises en BTC/ETH, propose des avantages uniques.
Tenter sa chance|
J’adore l’elegance de Impressario Casino, ca transporte dans un monde gourmand. La variete des titres est raffinee, avec des slots aux designs elegants. Avec des depots instantanes. L’assistance est efficace et professionnelle, joignable a toute heure. Les gains arrivent sans delai, neanmoins des offres plus genereuses seraient exquises. Au final, Impressario Casino garantit un plaisir constant pour ceux qui aiment parier en crypto ! Ajoutons que l’interface est fluide comme un banquet, ce qui rend chaque session plus raffinee. Egalement appreciable les evenements communautaires engageants, offre des recompenses continues.
Aller voir|
J’aime l’ambiance futuriste de Monte Cryptos Casino, il procure une aventure virtuelle. Il y a une profusion de jeux captivants, avec des slots aux themes innovants. Le bonus d’accueil est eclatant. Le support client est stellaire, joignable a tout moment. Les transferts sont fiables, de temps a autre plus de promos regulieres dynamiseraient l’experience. Dans l’ensemble, Monte Cryptos Casino vaut une exploration virtuelle pour ceux qui parient avec des cryptos ! A noter le design est moderne et captivant, ajoute une touche de sophistication. Egalement cool les tournois reguliers pour la competition, qui booste l’engagement.
Emmenez-moi lГ -bas|
No jogo Book of Dead, Rich Wilde vai até o Egito Antigo em busca de fortunas em uma experiência que promete muita emoção e diversão. E sabe do melhor? Você é o convidado de honra para embarcar nessa jornada. Se a sua dúvida é relacionada ao RTP (Retorno ao Jogador) do Book of Dead, saiba que ele é considerado padrão ao comparado aos demais jogos de caça-níqueis do mercado, atingindo uma média de 96%. Por último, mas não menos importante, a BetMGM Brasil tem uma oferta de rodadas grátis para seus clientes que fazem parte do plano de fidelidade da plataforma. Inscreva-se Para Receber Atualizações Sem Depósito e Rodadas Grátis Sua interface possui 5 rolos verticais com símbolos variados, e o objetivo do jogo é posicionar combinações iguais, conforme as 10 linhas de pagamentos disponíveis. Os ícones da temática do Egito Antigo, são os mais valiosos, proporcionando os maiores pagamentos. É um jogo que além de ofertar a versão demo, disponibiliza apostas mais flexíveis.
https://www.nobleventurefinancial.com/2025/10/09/review-do-sugar-rush-diversao-doce-e-ganhos-reais-no-cassino-online/
O jogo nos oferece uma experiência confortável, e sua interface além de interativa e bem intuitiva, oferece uma ótima qualidade nos melhores cassinos online, nos envolvendo em toda a trama desta aventura do explorador Rich Wild. Cookies analíticos são usados para entender como os visitantes interagem com o site. Esses cookies ajudam a fornecer informações sobre as métricas do número de visitantes, taxa de rejeição, origem do tráfego, etc. O CoinPoker é o melhor casino sem requisitos KYC, pois oferece um grande bónus de boas-vindas, serviços bancários seguros, levantamentos rápidos e mais de 1.500 jogos de slot machine. O TG.Casino está em segundo lugar e compete pelo título de melhor casino anónimo. Home » Jogos por Cointelegraph Brasil » Melhores Slots para Jogar em 2025: Guia Completo de Caça-níqueis » Book of Dead: Guia Como jogar Estratégias e Melhores Cassinos
Ao utilizar o código Betclic no registo pode realizar uma primeira aposta sem risco até 50€, ou seja, uma aposta grátis exclusiva com o código promocional Betclic JOGOBET. Faça um depósito de 10€ e uma aposta com odds mínimas de 1.20 para desbloquear as ofertas. Use ainda o seu codigo promocional betclic para explorar a secção de betclic apostas com um saldo extra. R$ 00,00 da Play’n Go This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data.
https://www.mbuzzsport.com/review-do-big-bass-bonanza-atracao-irresistivel-para-jogadores-brasileiros/
O Book of Ra é um jogo de slot popular que possui muitos prós e alguns contras. Com gráficos impressionantes e uma trilha sonora envolvente, este jogo oferece uma experiência de jogo imersiva. If you aren’t ready to go tomb raiding with Rich Wilde using real money just yet, you can try the Book of Dead DEMO version! Access to the demo mode takes just a few clicks: login to your EnergyCasino account, search for Book of Dead and hover over the thumbnail to display the grey DEMO button. You can adjust your wager to suit your playstyle, and you will have plenty of virtual funds available to fully enjoy the experience of Play’n GO’s Ancient Egypt Book of Dead online casino slot. O caça níquel grátis Book of Dead é um dos mais marcantes já criados, e qualquer fã de caça-níqueis tem que experimentá-lo pelo menos uma vez. Se você considerar dar uma chance, aqui você deixamos uma revisão caça níquel Book of Dead, os prós e contras do jogo, uma comparação com outros caça-níqueis do Egito e os melhores cassinos que você pode jogar por dinheiro real.
J’ai une affection particuliere pour Impressario Casino, il procure une experience distinguee. La selection de jeux est exquise, comprenant des jeux compatibles avec les cryptos. Amplifiant le plaisir de jeu. Le service est disponible 24/7, avec une aide precise. Les gains arrivent sans delai, parfois des recompenses additionnelles seraient royales. En resume, Impressario Casino offre une experience memorable pour les fans de casino en ligne ! De plus le design est moderne et chic, amplifie le plaisir de jouer. Particulierement interessant le programme VIP avec niveaux exclusifs, assure des transactions fiables.
DГ©couvrir les faits|
J’ai une affection pour Impressario Casino, il procure une experience exquise. La selection de jeux est somptueuse, avec des slots aux designs elegants. Amplifiant le plaisir de jeu. Le service est disponible 24/7, toujours pret a servir. Les paiements sont securises et rapides, bien que des recompenses additionnelles seraient royales. En resume, Impressario Casino garantit un plaisir constant pour les joueurs en quete d’excitation ! Ajoutons que la plateforme est visuellement somptueuse, ce qui rend chaque session plus raffinee. Un plus le programme VIP avec niveaux exclusifs, offre des recompenses continues.
Aller plus loin|
https://shorturl.fm/kssPW
Até recentemente, havia diversas maneiras de obter rodadas grátis sem depósito no Brasil: como recompensa após fazer o cadastro e também como parte de ofertas promocionais frequentes como rodas de prêmios, torneios e bônus em jogos da semana. BÔNUS DE ATÉ R$4000 Copyright © 2024 SlotsCalendar, todos os direitos reservados. SlotsCalendar não é responsável pela validade de qualquer oferta listada no site. Recomendamos vivamente que verifique os T&Cs de todos os casinos mencionados antes de registar uma conta ou fazer um depósito. A idade mínima para jogar é 18 anos. Jogue com responsabilidade. Se você deseja se aventurar no Book of Dead e ainda contar com a chance de ganhos em dinheiro, é simples. Basta seguir os passos abaixo: Os bônus sem depósito são uma ótima maneira de dar as boas-vindas para novos jogadores. Isso permite com que os iniciantes, que ainda não entendem muito sobre os jogos online, se familiarizem com as opções que o cassino online oferece. Sem essas vantagens as chances de confusão e de perder muito dinheiro são muito grandes. Por isso, para novos usuários, as melhores opções de cassino são aqueles que oferecem bônus sem depósito.
https://fincalabradores.com/big-bass-bonanza-analise-do-rtp-e-jogabilidade/
A simplicidade da slot Book of Dead nota-se na única Ronda Bónus que possui, a de Jogadas Grátis. Para isso, o jogador terá de obter uma combinação de no mínimo três Book of Dead, não interessando a sua posição nos rolos. Isto despoleta uma sequência de rodadas grátis, até atingir o prémio máximo. A cada novos símbolos Scatter, serão adicionadas mais 10 rodadas grátis! Existem vários jogos online de casino, com grande foco nas slot machines. Estes jogos simples e dinâmicos surgem às centenas ou milhares em cada site. Vários casinos também oferecem jogos de mesa, onde se incluem a roleta e blackjack, banca francesa ou poker. Bem-vindo ao portal de informações sobre a Lottu Bet!Se você está em busca de uma plataforma confiável para se divertir sem preocupação, chegou ao lugar certo. Em breve, a Lottubet estará operando no Brasil, e além de ser autorizada para funcionar oficialmente pela Secretaria de Prêmios e Apostas do Ministério da Fazenda, a Lottu Bet vai inaugurar um novo conceito de diversão online.Esqueça tudo que você já viu em um cassino online e esteja pronto para experimentar a plataforma Lottubet que está chegando novinha para você. Na Lottubet plataforma, você vai vivenciar uma experiência de jogo única, leve, divertida, de alta qualidade e com jogos que prometem momentos de pura emoção e adrenalina.
pferderennen krefeld wetten
Also visit my web page … sportwetten tipps anbieter
bet wetten online (Chad) sportwetten neu
tipp wetten heute in deutschland
ob1jdh
schweiz Pferderennen Dortmund Wetten
mostbet официальный сайт регистрация http://mostbet12031.ru
Ich bin begeistert von der Welt bei Snatch Casino, es verspricht pure Spannung. Die Auswahl ist einfach unschlagbar, mit immersiven Live-Dealer-Spielen. Der Bonus fur Neukunden ist attraktiv. Erreichbar 24/7 per Chat oder E-Mail. Die Zahlungen sind sicher und zuverlassig, trotzdem regelma?igere Promos wurden das Spiel aufwerten. Im Gro?en und Ganzen, Snatch Casino bietet ein unvergessliches Erlebnis. Zusatzlich die Oberflache ist glatt und benutzerfreundlich, jeden Moment aufregender macht. Ein starker Vorteil die vielfaltigen Wettmoglichkeiten, reibungslose Transaktionen sichern.
Snatch Casino|
J’adore l’ame soul de BassBet Casino, ca offre un plaisir melodique. Les options sont vastes comme une scene live, avec des slots aux designs soul. Avec des depots ultra-rapides. Les agents repondent avec un groove parfait, garantissant un service de haute qualite. Les paiements sont securises et instantanes, de temps en temps des bonus plus varies seraient une melodie. Dans l’ensemble, BassBet Casino est un must pour les joueurs pour les passionnes de jeux modernes ! A noter le site est rapide et captivant, booste le plaisir de jouer. Particulierement cool le programme VIP avec des niveaux exclusifs, qui dynamise l’engagement.
bassbetcasinopromocodefr.com|
J’adore l’atmosphere dynamique de Spinit Casino, on ressent une ambiance de piste. Les options sont vastes comme une course, avec des slots aux designs veloces. Avec des depots instantanes. Le service est disponible 24/7, garantissant un support de qualite. Les paiements sont securises et rapides, de temps a autre des recompenses additionnelles seraient rapides. Au final, Spinit Casino offre une experience memorable pour les amateurs de sensations rapides ! De plus la plateforme est visuellement veloce, donne envie de prolonger l’aventure. Particulierement interessant les tournois reguliers pour la competition, propose des avantages personnalises.
https://casinospinitfr.com/|
Je suis totalement envoute par BassBet Casino, c’est une plateforme qui vibre comme un riff. Le catalogue est riche et varie, incluant des paris sportifs dynamiques. Amplifiant le plaisir de jeu. Le support client est melodieux, joignable a toute heure. Les transactions sont fiables, cependant quelques tours gratuits supplementaires seraient bien venus. En resume, BassBet Casino offre une experience memorable pour les fans de casino en ligne ! Par ailleurs le site est rapide et attractif, donne envie de prolonger l’aventure. Egalement appreciable les options de paris sportifs variees, qui booste l’engagement.
bassbetcasinobonusfr.com|
Je suis totalement envoute par Spinit Casino, ca offre un plaisir enchante. Le catalogue est riche et varie, proposant des jeux de table elegants. Amplifiant le plaisir de jeu. Le support client est enchante, joignable a toute heure. Les gains arrivent sans delai, de temps a autre des recompenses additionnelles seraient narratives. Au final, Spinit Casino offre une experience memorable pour les passionnes de jeux modernes ! A noter la plateforme est visuellement envoutante, ajoute une touche de mystere. Un plus les evenements communautaires engageants, propose des avantages personnalises.
https://spinitcasinobonusfr.com/|
Je suis absolument captive par Monte Cryptos Casino, il propose une odyssee chiffree. La variete des titres est eclatante, offrant des sessions en direct immersives. Avec des depots crypto rapides. Les agents repondent avec une vitesse fulgurante, toujours pret a decoder. Les transferts sont fiables, mais quelques tours gratuits en plus seraient bienvenus. Dans l’ensemble, Monte Cryptos Casino est un must pour les fans de blockchain pour les adeptes de jeux modernes ! A noter la navigation est simple comme un wallet, ce qui rend chaque session plus immersive. Un avantage notable les options de paris variees, qui booste l’engagement.
Cliquer pour les infos|
Je suis ensorcele par Monte Cryptos Casino, il propose une odyssee chiffree. La selection de jeux est astronomique, avec des slots aux designs modernes. Le bonus d’entree est scintillant. Les agents repondent avec une vitesse fulgurante, offrant des solutions claires. Les paiements sont securises par blockchain, mais des offres plus genereuses ajouteraient du charme. Au final, Monte Cryptos Casino garantit un plaisir constant pour les passionnes de sensations numeriques ! Ajoutons que la plateforme est visuellement eblouissante, donne envie de prolonger l’aventure. Un atout cle le programme VIP avec des niveaux exclusifs, renforce la communaute.
Plongez-y|
J’ai une passion brulante pour Impressario Casino, il evoque un tapis rouge scintillant. Le catalogue est riche et varie, incluant des paris sportifs dynamiques. Illuminant l’experience de jeu. Disponible 24/7 via chat ou email, toujours pret a briller. Les transactions sont fiables, de temps en temps plus de promotions regulieres ajouteraient du prestige. Au final, Impressario Casino est une plateforme qui captive pour les adeptes de jeux modernes ! De plus l’interface est fluide comme un film, amplifie le plaisir de jouer. Un point fort le programme VIP avec des niveaux exclusifs, qui dynamise l’engagement.
http://www.casinoimpressariofr.com|
Je suis absolument seduit par Monte Cryptos Casino, ca offre un plaisir numerique unique. Les options sont vastes comme un reseau, avec des slots aux themes innovants. Avec des depots crypto rapides. Le suivi est irreprochable, garantissant un service de pointe. Les retraits sont rapides comme une transaction blockchain, mais plus de promos regulieres dynamiseraient l’experience. Pour conclure, Monte Cryptos Casino offre une experience inoubliable pour les adeptes de jeux modernes ! Par ailleurs la plateforme est visuellement eblouissante, facilite une immersion totale. Particulierement captivant les options de paris variees, qui booste l’engagement.
Ouvrir ici|
you’re in point of fact a good webmaster. The web site loading velocity is amazing. It sort of feels that you’re doing any distinctive trick. Also, The contents are masterpiece. you’ve done a wonderful task in this matter!
https://kra42c.com
Hi! canadian pharmacies online good internet site.
Keep educating and inspiring others with posts like this.
code promo 1xbet togo The variations are endless: “code bonus 1xbet,” “1xbet code promo pari gratuit,” “1xbet bonus de bienvenue 2026,” and “bonus de bienvenue 1xbet.” These phrases denote a desire for diverse bonus types. There are country-specific demands like “Code promo 1xbet Afrique du Sud.”
Your writing style makes complex ideas so easy to digest.
https://shorturl.fm/w24pk
**memorylift**
memorylift is an innovative dietary formula designed to naturally nurture brain wellness and sharpen cognitive performance.
мостбет букмекерская контора мостбет букмекерская контора
I like how you kept it informative without being too technical.
наркологическая клиника наркологическая клиника .
наркологическая служба http://www.narkologicheskaya-klinika-25.ru .
обмазочная гидроизоляция цена работы за м2 http://www.gidroizolyaciya-cena-7.ru .
What’s up to every , as I am actually eager of reading this web site’s post to be updated regularly. It consists of good material.
kra42 at
Hi, how have you been lately?
https://shorturl.fm/W2Erk
https://shorturl.fm/EBZmk
sportwetten
Feel free to surf to my blog; wetten unter freunden app
наркологическая платная клиника наркологическая платная клиника .
We absolutely love your blog and find most of your post’s to be precisely what I’m looking for. can you offer guest writers to write content to suit your needs? I wouldn’t mind writing a post or elaborating on many of the subjects you write concerning here. Again, awesome web log!
kra41 cc
J’adore l’harmonie de Olympe Casino, on ressent une energie divine. Les options sont vastes comme un orchestre, proposant des jeux de table glorieux. Avec des depots rapides. Le service est disponible 24/7, avec une aide precise. Les retraits sont rapides comme une melodie, neanmoins des bonus plus varies seraient un nectar. En bref, Olympe Casino garantit un plaisir divin pour les amateurs de sensations mythiques ! A noter la navigation est simple comme un oracle, facilite une immersion totale. Particulierement captivant les options de paris sportifs variees, renforce le sentiment de communaute.
https://olympefr.com/|
https://shorturl.fm/YcK7V
Ich bin begeistert von der Welt bei Cat Spins Casino, es bietet eine dynamische Erfahrung. Das Angebot an Titeln ist riesig, mit spannenden Sportwetten-Angeboten. Er gibt Ihnen einen Kickstart. Der Service ist immer zuverlassig. Zahlungen sind sicher und schnell, jedoch ein paar zusatzliche Freispiele waren klasse. Im Gro?en und Ganzen, Cat Spins Casino garantiert langanhaltenden Spa?. Au?erdem die Oberflache ist glatt und benutzerfreundlich, eine Prise Stil hinzufugt. Ein gro?artiges Plus die dynamischen Community-Events, ma?geschneiderte Vorteile liefern.
Weiterlesen|
Ich freue mich riesig uber Cat Spins Casino, es begeistert mit Dynamik. Das Angebot an Titeln ist riesig, mit modernen Slots in ansprechenden Designs. Der Bonus ist wirklich stark. Der Kundensupport ist erstklassig. Transaktionen sind zuverlassig und klar, dennoch zusatzliche Freispiele waren willkommen. In Summe, Cat Spins Casino sorgt fur ununterbrochenen Spa?. Daruber hinaus die Navigation ist einfach und klar, zum Bleiben einladt. Ein starkes Feature sind die sicheren Krypto-Transaktionen, sichere Zahlungen garantieren.
Website erkunden|
Ich bin beeindruckt von Cat Spins Casino, es schafft eine mitrei?ende Stimmung. Es gibt eine Fulle an aufregenden Titeln, mit traditionellen Tischspielen. Er gibt Ihnen einen tollen Boost. Der Support ist effizient und professionell. Die Zahlungen sind sicher und effizient, jedoch haufigere Promos wurden begeistern. Letztlich, Cat Spins Casino ist ein absolutes Highlight. Hinzu kommt die Navigation ist klar und flussig, eine tiefe Immersion ermoglicht. Ein starker Vorteil sind die zuverlassigen Krypto-Zahlungen, personliche Vorteile bereitstellen.
Weiter lesen|
Ich habe eine Leidenschaft fur Cat Spins Casino, es verspricht ein einzigartiges Abenteuer. Es gibt zahlreiche spannende Spiele, mit Live-Sportwetten. Mit blitzschnellen Einzahlungen. Der Kundendienst ist ausgezeichnet. Gewinne werden schnell uberwiesen, allerdings gro?zugigere Angebote waren klasse. Letztlich, Cat Spins Casino ist ein Muss fur Spieler. Daruber hinaus die Navigation ist klar und flussig, einen Hauch von Eleganz hinzufugt. Ein bemerkenswertes Feature die haufigen Turniere fur mehr Spa?, individuelle Vorteile liefern.
Webseite besuchen|
J’ai une passion debordante pour Ruby Slots Casino, on ressent une ambiance festive. La variete des jeux est epoustouflante, offrant des experiences de casino en direct. Avec des depots rapides et faciles. Les agents repondent avec rapidite. Les transactions sont fiables et efficaces, parfois des offres plus importantes seraient super. En conclusion, Ruby Slots Casino assure un fun constant. En bonus le site est fluide et attractif, ajoute une touche de dynamisme. A signaler le programme VIP avec des recompenses exclusives, garantit des paiements rapides.
DГ©couvrir la page|
J’adore le dynamisme de Ruby Slots Casino, il procure une sensation de frisson. La selection de jeux est impressionnante, proposant des jeux de casino traditionnels. Avec des depots fluides. Le support est pro et accueillant. Le processus est fluide et intuitif, quelquefois des recompenses supplementaires dynamiseraient le tout. Globalement, Ruby Slots Casino est un endroit qui electrise. Notons egalement la plateforme est visuellement dynamique, apporte une energie supplementaire. Un point cle les tournois reguliers pour la competition, propose des avantages sur mesure.
Rejoindre maintenant|
Je ne me lasse pas de Sugar Casino, ca donne une vibe electrisante. On trouve une profusion de jeux palpitants, avec des slots aux graphismes modernes. 100% jusqu’a 500 € avec des spins gratuits. Les agents repondent avec rapidite. Les retraits sont simples et rapides, par moments des bonus plus frequents seraient un hit. En resume, Sugar Casino merite une visite dynamique. A mentionner l’interface est fluide comme une soiree, ajoute une touche de dynamisme. Particulierement fun les competitions regulieres pour plus de fun, assure des transactions fiables.
Rejoindre maintenant|
Je suis bluffe par Sugar Casino, c’est une plateforme qui pulse avec energie. La bibliotheque est pleine de surprises, incluant des paris sur des evenements sportifs. Il donne un elan excitant. Le service est disponible 24/7. Le processus est transparent et rapide, par moments des recompenses supplementaires seraient parfaites. Pour conclure, Sugar Casino offre une aventure inoubliable. Par ailleurs la plateforme est visuellement electrisante, ajoute une vibe electrisante. Un avantage notable les competitions regulieres pour plus de fun, qui dynamise l’engagement.
Aller au site|
Je suis emerveille par Ruby Slots Casino, ca invite a plonger dans le fun. La variete des jeux est epoustouflante, proposant des jeux de cartes elegants. Il rend le debut de l’aventure palpitant. Le support est rapide et professionnel. Les transactions sont toujours fiables, cependant des bonus diversifies seraient un atout. En bref, Ruby Slots Casino est un must pour les passionnes. A mentionner le design est moderne et energique, permet une plongee totale dans le jeu. Un avantage notable le programme VIP avec des niveaux exclusifs, assure des transactions fiables.
Voir plus|
https://shorturl.fm/Flhk3
Thanks for including real user stories — very relatable.
отделка подвала отделка подвала .
наплавляемая гидроизоляция цена наплавляемая гидроизоляция цена .
Hmm is anyone else encountering problems with the images on this blog loading? I’m trying to determine if its a problem on my end or if it’s the blog. Any feed-back would be greatly appreciated.
https://www.madelyncovey.com/?p=74622
https://shorturl.fm/Q489j
You bring a fresh voice to a well-covered topic.
Practical advice that’s easy to implement. Much appreciated.
During our Pirots 4 slot review, we noticed a few exciting symbol prizes. Players have four birds that can move around the grid to collect symbols, with paying symbols consisting of gems, coins and wilds. The gems can be upgraded to higher levels, up to a maximum payout level of 7. Slots are the most popular games found on most of the casino’s game library. You’ll find various slots not on GamStop, from classic 3-reel fruit machines to feature-packed titles with attractive themes. Then, there are the jackpots and innovative mechanics like Megaways or cluster pays. Blast off with ELK Studios’ latest installment in the wildly entertaining Pirots series. And this time, the birds are going galactic. Pirots 4 takes the classic CollectR engine and launches it into space with an upgraded grid, more complex symbol transformations, and a cast of birds that could easily star in their own animated movie.
https://huzzaz.com/createdby/IntelligentAddr
We are a premium supplier of slots, scratchcards and instant win games to the online gaming industry. For people who find it even more convenient to use their smartphones to play scratch cards, we offer our mobile site that serves as a platform to help you enjoy those games, anywhere and anytime. Our easy to comprehend and amazing user interface makes it quite an easy breeze to play a game and have a go at your luck and fortune. No more do you have to visit a casino venue to enjoy feature-laden Scratch Cards Online. We offer everything right at the comforts of your own home. You should be aware of the low returns before you play, but if it’s acceptable, then you will find the Pirots 2 slot to be a highly entertaining game. The cartoon graphics and great animations are a real highlight, and it’s filled with innovative features.
торкретирование цена торкретирование цена .
Your tips are practical and easy to apply. Thanks a lot!
What I really liked is how easy this was to follow. Even for someone who’s not super tech-savvy, it made perfect sense.
no deposit bonus sportwetten
Look at my web site; wer ist der beste wettanbieter (cineveracruz.Com.br)
https://chester.bet/ – Новости спорта,Онлайн трансляции спортивных матчей,Спорт,Футбол,Хоккей,Баскетбол,Теннис,Волейбол,Авто-мото-вело спорт,Прогнозы на спорт
Je suis captive par Olympe Casino, ca offre un plaisir melodieux. Les options sont vastes comme un orchestre, offrant des sessions live immortelles. Le bonus de bienvenue est divin. Le service est disponible 24/7, garantissant un support celeste. Les gains arrivent sans delai, bien que des recompenses supplementaires seraient eternelles. Dans l’ensemble, Olympe Casino est un incontournable pour les joueurs pour les joueurs en quete d’epopee ! Par ailleurs l’interface est fluide comme un nectar, ajoute une touche de mythologie. Un plus divin les paiements securises en crypto, offre des recompenses eternelles.
https://olympefr.com/|
Hi it’s me, I am also visiting this website regularly, this site is actually pleasant and the people are truly sharing fastidious thoughts.
https://ckyaudit.com/melbet-rabochee-zerkalo-skachat-na-android-2025/
It’s always a good idea to choose a high RTP slot machine, as this could mean that you have a higher chance of a win! Some of our top high RTP slots include Mega Joker, 1429 Uncharted Seas and Big Bass Bonanza. Ideally, look for games with an RTP of 97% or higher. The world of online gaming is vast, filled with various themes and narratives waiting to draw players in. One such captivating option is the Mega Joker slot machine. With its vibrant visuals and engaging gameplay, it has become a beloved choice among avid slot enthusiasts. This article will explore the unique features, gameplay mechanics, and strategies to maximize your winnings on this enthralling game. To make the most of your experience with the Mega Joker slot machine, consider these winning strategies: NOVOMATIC AG Group No id casino United Kingdom but remember, the custodian reveals the Players cards. You can expect to play some quality slot games from the likes of NetEnt, and Atlanta Falcons have also come close to losing theirs recently.
https://tbpenergy.com/aviator-jetx-the-crash-game-revolution/
What’s even better about this feature, is that the Twin Reels can expand to become triplet, quadruplet or even quintuplet reels. This can make for some enormous payouts to lucky players. In fact, the maximum win at the time of writing is a staggering 270,000 coins, worth up to hundreds of thousands of pounds. Not bad for a slot with no progressive jackpot and only one special feature. Yes, online casinos really pay out. All of the casino games and slots available on Red Casino are real money games. That means you play with real money for the chance to win real money, and you get to keep what you win. Twin Spin offers an exciting twist in the world of online gaming, much like the flexibility available at casinos without Spelpaus, where players can enjoy gaming without self-exclusion restrictions.
So simple, yet so impactful. Well written!
cd clock radio alarm-radio-clocks.com .
Ich freue mich sehr uber Cat Spins Casino, es entfuhrt in eine Welt voller Spa?. Es gibt eine Fulle an aufregenden Titeln, mit interaktiven Live-Spielen. Der Bonus fur Neukunden ist attraktiv. Erreichbar 24/7 per Chat oder E-Mail. Die Zahlungen sind sicher und effizient, gelegentlich zusatzliche Freispiele waren willkommen. Im Gro?en und Ganzen, Cat Spins Casino ist definitiv einen Besuch wert. Nebenbei die Navigation ist klar und flussig, das Spielvergnugen steigert. Ein gro?er Pluspunkt sind die zuverlassigen Krypto-Zahlungen, sichere Zahlungen garantieren.
Jetzt stöbern|
Ich bin total hingerissen von Cat Spins Casino, es ist ein Hotspot fur Spielspa?. Es gibt eine Fulle an aufregenden Titeln, mit stilvollen Tischspielen. 100 % bis zu 500 € plus Freispiele. Der Support ist professionell und schnell. Der Prozess ist einfach und transparent, aber ein paar Freispiele mehr waren super. Alles in allem, Cat Spins Casino sorgt fur ununterbrochenen Spa?. Nebenbei ist das Design modern und einladend, eine immersive Erfahrung ermoglicht. Ein bemerkenswertes Feature sind die sicheren Krypto-Zahlungen, regelma?ige Boni bieten.
Mit dem Lesen beginnen|
продвижение французского сайта цена optimizaciya-i-seo-prodvizhenie-sajtov-moskva.ru .
Ich bin suchtig nach Cat Spins Casino, es entfuhrt in eine Welt voller Nervenkitzel. Es gibt eine Fulle an aufregenden Titeln, mit klassischen Tischspielen. Er macht den Einstieg unvergesslich. Der Support ist zuverlassig und hilfsbereit. Der Prozess ist einfach und transparent, trotzdem gro?ere Boni waren ein Highlight. Letztlich, Cat Spins Casino bietet ein gro?artiges Erlebnis. Daruber hinaus die Navigation ist klar und flussig, eine Note von Eleganz hinzufugt. Ein bemerkenswertes Extra die regelma?igen Wettbewerbe fur Spannung, zuverlassige Transaktionen sichern.
Details prГјfen|
Ich habe einen Narren gefressen an Cat Spins Casino, es sorgt fur ein fesselndes Erlebnis. Es gibt eine beeindruckende Anzahl an Titeln, mit aufregenden Live-Casino-Erlebnissen. Der Bonus ist wirklich stark. Der Support ist schnell und freundlich. Gewinne kommen ohne Verzogerung, ab und zu gro?zugigere Angebote waren klasse. Letztlich, Cat Spins Casino garantiert dauerhaften Spielspa?. Zusatzlich die Plattform ist visuell ansprechend, das Spielerlebnis steigert. Ein starkes Plus sind die sicheren Krypto-Transaktionen, zuverlassige Transaktionen sichern.
Zum Ansehen klicken|
мелбет онлайн ставки на спорт мелбет онлайн ставки на спорт .
раскрутка сайта москва раскрутка сайта москва .
I appreciated the formatting — easy to skim and still informative.
стратегия продвижения блог http://statyi-o-marketinge6.ru/ .
J’adore le dynamisme de Sugar Casino, il offre une experience dynamique. La variete des jeux est epoustouflante, avec des machines a sous visuellement superbes. Il propulse votre jeu des le debut. Disponible a toute heure via chat ou email. Les gains arrivent en un eclair, en revanche quelques tours gratuits en plus seraient geniaux. En fin de compte, Sugar Casino est un must pour les passionnes. Ajoutons aussi le design est moderne et energique, donne envie de continuer l’aventure. A souligner les paiements securises en crypto, qui motive les joueurs.
Entrer maintenant|
J’adore la vibe de Ruby Slots Casino, il cree une experience captivante. On trouve une gamme de jeux eblouissante, avec des machines a sous aux themes varies. Avec des depots fluides. Le support est efficace et amical. Les retraits sont ultra-rapides, cependant plus de promotions frequentes boosteraient l’experience. En conclusion, Ruby Slots Casino est un incontournable pour les joueurs. En complement l’interface est intuitive et fluide, ce qui rend chaque session plus palpitante. Egalement genial les nombreuses options de paris sportifs, propose des privileges personnalises.
AccГ©der Г la page|
Je suis enthousiasme par Sugar Casino, ca pulse comme une soiree animee. Il y a une abondance de jeux excitants, offrant des sessions live immersives. Il donne un elan excitant. Le service client est excellent. Les transactions sont toujours securisees, cependant quelques tours gratuits supplementaires seraient cool. En resume, Sugar Casino assure un fun constant. En bonus l’interface est fluide comme une soiree, ce qui rend chaque moment plus vibrant. Particulierement fun les competitions regulieres pour plus de fun, offre des recompenses regulieres.
Poursuivre la lecture|
Je suis totalement conquis par Ruby Slots Casino, on y trouve une vibe envoutante. Le choix est aussi large qu’un festival, comprenant des jeux optimises pour Bitcoin. Il offre un demarrage en fanfare. Le service client est de qualite. Les retraits sont lisses comme jamais, occasionnellement des recompenses supplementaires seraient parfaites. Pour finir, Ruby Slots Casino est un lieu de fun absolu. D’ailleurs le design est moderne et attrayant, ajoute une touche de dynamisme. Un atout le programme VIP avec des avantages uniques, assure des transactions fluides.
DГ©couvrir maintenant|
value wetten strategie
Here is my site Sichere Wette
Je suis sous le charme de Ruby Slots Casino, ca invite a plonger dans le fun. Le choix de jeux est tout simplement enorme, avec des machines a sous aux themes varies. Avec des depots instantanes. Le support client est irreprochable. Les transactions sont d’une fiabilite absolue, bien que des offres plus importantes seraient super. En somme, Ruby Slots Casino garantit un plaisir constant. Notons egalement la plateforme est visuellement captivante, apporte une energie supplementaire. Un plus les transactions crypto ultra-securisees, qui dynamise l’engagement.
DГ©couvrir les faits|
BetMGM Casino is the best slot site for real money, offering 1,000+ games, exclusive jackpots and a $1,500 bonus. Other top choices include Caesars (great UI, $2,500 bonus), bet365 (high RTP slots) and FanDuel (fast payouts). All are legal, secure and packed with high-RTP games like Book of 99 and Mega Joker. High RTP, exciting Supermeter mode, and progressive jackpots create an excellent gaming experience and the will for massive real money wins for Aussie users. He is alone with a route on his faithful machine, but in this case it also adds the cash value to the credit balance. Not to say that theres anything wrong, respin joker slots welcome bonus the platform offers cashback bonuses to new customers. You can see the full terms and privacy policy on the site, Blitzspins offers additional promotions for existing users.
https://kumad.org/christmas-big-bass-bonanza-play-canadian-holiday-fun/
The free spin collection fun doesn’t end there. Any Fruit Win during free spins will top-up your free spins tally by the totals above. Not to be left out, the Card Suits also join in the fun once the Free Spins Bonus has begun, adding spins to your total as follows: Fruit Shop is a typical fruity theme slot machine from NetEnt with plenty of modern features thrown in to keep your gameplay and those fruit symbols fresh and entertaining. The slot comes with 15 paylines and enhanced multipliers throughout with a top prize of 630x your stake. Colourful graphics and an energetic pace add to the in-game features to make it even more fun to play. With its classic fruit-slot feel and modern twist, it’s got all right elements for fabulous fun, so why not give it a go? A platform created to showcase all of our efforts aimed at bringing the vision of a safer and more transparent online gambling industry to reality.
Select from an enormous sort of various other themes and acquire you to perfect games. Since the interest in casino ports became, so performed the necessity for sets one to provided not merely profits and also entertainment. The web resulted in then exploration of various position classes, gives players an array of possibilities today. When you fill all ranks to your reels to your exact same game signs, the bonus Rewin feature tend to turn on. While the white ends to the an eco-friendly field of the wheel, you’ll victory a different award on the entire display! So it extra function finishes when the site visitors white productivity to the red-colored business, or if you winnings six minutes consecutively. For players who prefer to play Mega Joker online on the go, Mega Joker offers excellent mobile compatibility. Whether you’re using a smartphone or tablet, you can enjoy the same high-quality gaming experience as on a desktop. The game performs seamlessly across various devices, ensuring that all features, including those that trigger randomly, are just as accessible and thrilling on mobile as they are on larger screens.
https://svcppondy.ac.in/sweet-bonanza-india-a-hit-among-indian-players/
Celebrate the Spookiest Season at LuckyWins with Daily Rewards between October 23rd – October 31st, 2023! Ultimate Treasures Await in Lucky Mystery Halloween Pumpkins! Log into your account each day between the 23rd and 31st of October, make at least one deposit, each day of the campaign to receive your Halloween Mystery Pumpkins of the day. Once you have made your daily deposit you will get access to the Lucky Halloween Mystery Pumpkins of the day. Unlock the chest and reveal your fate! You can find up to 100 Free Spins! Dare to Deposit, Choose Your Pumpkin, and Unveil your Lucky Halloween Surprises! Promo runs from July 1,2025 to December 31,2025 only. Promo runs from July 1,2025 to December 31,2025 only. Twin Spin Megaways is played on six reels and has Megaways power which boosts the payline to a groovy 117,649 possible ways to win. Each of the reels can have between two and seven symbols on each spin and the closer to seven you get, the more Megaways lines are activated. Wins start from matching three symbols or more on adjoining reels.
Play Real Casino Slots Online In Uk Needless to mention, this five- line, multi coin gaming machine is different from others because it boasts two sets of three reels, which are used in varying ways. You may really go crazy with its supermeter mode, thus taking gambling to a completely new level. It is also enjoyable to see that both sets of reels offer different symbols, so you will never feel bored with the ordinary icons. Therefore, on the bottom reels you will notice cherries, bells, lemons, Jokers, and treasure chests whilst the top ones include green 7’s, grapes, and oranges. Mega joker slot uk and to top things off and help players continue to visit, it comes with the standard package. Claiming more than one bonus offer at the same time, gambling was tackled by more than half of the population based on immorality and the aforementioned prohibition of gambling houses and strict regulation of lotteries were still intact.
https://bnb-housekeeping.co.uk/2025/10/08/why-did-the-chicken-cross-the-road-a-british-dive-into-chicken-road-by-inout/
Performance cookies are used to understand and analyze the key performance indexes of the website which helps in delivering a better user experience for the visitors. What you want to look at is RTP (Return to Player). That’s basically the way in which the house edge gets displayed for slots. No matter how you look at it, in the long run, the casino will always come out on top. However, the short-term outcome of slots is random, so you have the best slot machine odds if you play a slot that has an RTP of 97% or higher. The minimum amount players can withdraw is limited to IDR 50.000 and there is no maximum withdrawal limit, Nero’s Fortune is not a very popular slot. Also look out for no wager requirements as a bonus, players can bag gifts that include. No deposit bonus with spins. We hope these clear up any queries and that youll be in a position where you can dive right in and start playing, but to actually give you real recommendations that you can depend on. Now this is what we call a good deal, win real money casino if you use multiple browsers or devices you will need to execute this opt-out on each browser or device. However, it is only the start of what is an incredible starter package.
Rather than adopting standard win lines, the five reels in Twin Spin offer 243 ways to win. This not only means the chances of a win line are high, but that they’re easy to spot, since any three or more consecutive symbols delivers a prize. Betting starts from as little as 0.25 with a maximum of 125 per spin. You can bet up to 10 coins per line. For your convenience, you can make use of the handy Max Bet button and Auto Play feature to speed up the betting process. The energy of Twin Spin Deluxe will appeal to players who like fast-paced games as this certainly has a vibrant feel to it. Many NetEnt fans will recognise this style straight away with its 6 reel and 5 row layout with the cluster pays feature. This style of play has its enthusiasts so there is no shortage of gamblers looking to try their luck on this slot! The modern music and neon colours contrast with the classic fruit machine symbols to create an interesting and intriguing combination. Payouts offer 10,000 coins as a jackpot which should also encourage new players to try this energetic game.
https://staging.ajcreativeimaging.com/2025/10/08/chicken-crossing-road-casino-top-uk-picks/
Your personal data will be used to support your experience throughout this website, to manage access to your account, and for other purposes described in our privacy policy. It seems so facile – that such a ruse (and in the fruit-machine industry there are many, as I’m to discover) should be so effective. But effective it is, and to such an extent that if anyone is celebrating, it should be the people who created this avenue of misfortune. The gaming-machine industry is thriving in the UK despite of – or possibly, because of – the recession. The total fruit-machine market is up almost 15% in the past year. It was up the year before, too, from 234,000 to 261,000 machines. Once you’ve played all the hits in Big Hits Blazinator, more big wins are in store for you. Other slots with similar themes include:
блог интернет-маркетинга https://statyi-o-marketinge7.ru .
wetten dass heute live stream
My website – sicherste sportwetten strategie
Ich habe eine Leidenschaft fur Cat Spins Casino, es bietet ein mitrei?endes Spielerlebnis. Die Spielauswahl ist ein echtes Highlight, mit Slots in modernem Look. Mit schnellen Einzahlungen. Der Service ist von hochster Qualitat. Gewinne kommen sofort an, in seltenen Fallen haufigere Promos wurden begeistern. Kurz und bundig, Cat Spins Casino ist perfekt fur Casino-Liebhaber. Ubrigens die Navigation ist unkompliziert, das Spielerlebnis bereichert. Ein starkes Plus ist das VIP-Programm mit exklusiven Stufen, zuverlassige Transaktionen sichern.
Jetzt Г¶ffnen|
Ich schatze die Energie bei Cat Spins Casino, es verspricht ein einzigartiges Abenteuer. Das Angebot ist ein Traum fur Spieler, mit eleganten Tischspielen. 100 % bis zu 500 € mit Freispielen. Die Mitarbeiter antworten prazise. Gewinne kommen sofort an, jedoch mehr Bonusoptionen waren top. Insgesamt, Cat Spins Casino ist ideal fur Spielbegeisterte. Zusatzlich die Oberflache ist glatt und benutzerfreundlich, das Vergnugen maximiert. Ein super Vorteil die lebendigen Community-Events, ma?geschneiderte Privilegien liefern.
Cat Spins|
Ich bin ein gro?er Fan von Cat Spins Casino, es bietet ein immersives Erlebnis. Die Spielesammlung ist uberwaltigend, mit Slots in modernem Look. 100 % bis zu 500 € inklusive Freispiele. Der Support ist professionell und schnell. Gewinne werden ohne Wartezeit uberwiesen, dennoch gro?ere Angebote waren super. Insgesamt, Cat Spins Casino bietet ein einmaliges Erlebnis. Zusatzlich die Plattform ist optisch ein Highlight, eine Prise Stil hinzufugt. Ein bemerkenswertes Feature die haufigen Turniere fur Wettbewerb, exklusive Boni bieten.
Jetzt klicken|
Ich bin suchtig nach Cat Spins Casino, es ladt zu spannenden Spielen ein. Es gibt eine enorme Vielfalt an Spielen, mit immersiven Live-Dealer-Spielen. Mit sofortigen Einzahlungen. Der Service ist immer zuverlassig. Auszahlungen sind einfach und schnell, trotzdem mehr Bonusoptionen waren top. Letztlich, Cat Spins Casino ist definitiv einen Besuch wert. Ubrigens die Oberflache ist glatt und benutzerfreundlich, was jede Session spannender macht. Ein gro?artiges Plus ist das VIP-Programm mit einzigartigen Belohnungen, die Gemeinschaft starken.
Eintreten|
Ich bin beeindruckt von Cat Spins Casino, es entfuhrt in eine Welt voller Spa?. Die Spiele sind abwechslungsreich und fesselnd, mit eleganten Tischspielen. Er sorgt fur einen starken Einstieg. Der Kundendienst ist hervorragend. Die Zahlungen sind sicher und zuverlassig, in seltenen Fallen mehr Bonusangebote waren ideal. Alles in allem, Cat Spins Casino ist ein absolutes Highlight. Ubrigens die Seite ist zugig und ansprechend, zum Weiterspielen animiert. Ein super Vorteil ist das VIP-Programm mit besonderen Vorteilen, die die Gemeinschaft starken.
Jetzt klicken|
I appreciate the depth and clarity of this post.
J’adore l’energie de Sugar Casino, il offre une experience dynamique. Les titres proposes sont d’une richesse folle, proposant des jeux de table classiques. Le bonus de bienvenue est genereux. Le support est pro et accueillant. Le processus est simple et transparent, quelquefois plus de promotions variees ajouteraient du fun. En conclusion, Sugar Casino vaut une exploration vibrante. Par ailleurs la navigation est intuitive et lisse, ce qui rend chaque moment plus vibrant. A signaler le programme VIP avec des privileges speciaux, qui stimule l’engagement.
Ouvrir le site|
J’ai un faible pour Ruby Slots Casino, c’est une plateforme qui deborde de dynamisme. Les options sont aussi vastes qu’un horizon, incluant des paris sportifs pleins de vie. Il amplifie le plaisir des l’entree. Les agents sont rapides et pros. Les transactions sont d’une fiabilite absolue, rarement quelques tours gratuits en plus seraient geniaux. Pour finir, Ruby Slots Casino offre une aventure memorable. A souligner le site est fluide et attractif, amplifie le plaisir de jouer. Particulierement interessant les tournois frequents pour l’adrenaline, assure des transactions fiables.
Visiter le site|
Je suis enthousiasme par Sugar Casino, on y trouve une energie contagieuse. La selection de jeux est impressionnante, incluant des options de paris sportifs dynamiques. Il booste votre aventure des le depart. Disponible a toute heure via chat ou email. Les paiements sont securises et instantanes, en revanche plus de promotions frequentes boosteraient l’experience. En resume, Sugar Casino offre une aventure inoubliable. Ajoutons aussi la navigation est simple et intuitive, ajoute une vibe electrisante. Un avantage les transactions crypto ultra-securisees, cree une communaute soudee.
Aller sur le site|
J’ai un faible pour Ruby Slots Casino, il procure une sensation de frisson. Les options de jeu sont infinies, offrant des sessions live palpitantes. Le bonus de depart est top. Les agents sont rapides et pros. Les transactions sont toujours securisees, en revanche des bonus varies rendraient le tout plus fun. Dans l’ensemble, Ruby Slots Casino est un choix parfait pour les joueurs. Ajoutons aussi le design est tendance et accrocheur, permet une immersion complete. Un bonus les evenements communautaires pleins d’energie, propose des avantages uniques.
DГ©couvrir maintenant|
J’ai un veritable coup de c?ur pour Sugar Casino, c’est une plateforme qui deborde de dynamisme. Le catalogue de titres est vaste, incluant des options de paris sportifs dynamiques. Avec des depots rapides et faciles. Les agents repondent avec rapidite. Les paiements sont securises et rapides, a l’occasion des bonus diversifies seraient un atout. Pour finir, Sugar Casino vaut une visite excitante. A souligner le design est tendance et accrocheur, incite a prolonger le plaisir. Un avantage les transactions en crypto fiables, offre des bonus constants.
Voir le site|
https://znakavto.com/
C’est tout ce que vous devez savoir pour commencer à jouer, simple non ? Chaque progression dans le vortex est aléatoire, cela veut dire que vous pouvez être décalé entre les éléments. La Planque du Joueur a regroupé 5 jeux des casinos proposant des bonus sans dépôt gratuits, offrant un RTP élevé. Vortex Casino ne facilite pas la prise de contact. Les joueurs ne peuvent pas compter sur des représentants disponibles 24h 24 et 7j 7 pour gérer toutes sortes de questions ou de problèmes. Un service de chat en direct gratuit n’est toujours pas disponible sur le site Web du casino et dans le logiciel, permettant aux joueurs de se connecter avec des spécialistes du support directement sur le Web. Les joueurs peuvent également appeler le casino en utilisant un numéro de téléphone gratuit en France ou un numéro de téléphone international, ou simplement envoyer un courriel au casino et obtenir une réponse dans les 24 heures dans la plupart des cas.
https://migovo.com.ua/2025/10/08/ou-jouer-a-jetx-en-france-decouvrez-les-meilleurs-casinos-en-ligne/
Nous pensons certainement que c’est peu probable, Touch my Bingo. À ce jour, je travaille dans le milieu des casinos en ligne. Depuis plus jeune, j’adore les jeux d’argent et à de nombreuses reprises, j’ai acheté un billet de loto au tabac du coin jusqu’à découvrir les casinos en ligne. J’y ai joué plusieurs années, jusqu’à ce qu’une entreprise du casino me remarque. Ayant quelques talents d’écriture, j’ai commencé à travailler pour French-Eyes. J’écris des avis de casino et quelques autres articles à ce sujet. Je m’occupe aussi de notre équipe de rédacteurs. Qui aurait dit qu’un jour je ferais de ma passion, mon travail à temps plein ? Tous les mécanismes de Diamond Vortex sont nouveaux, mais tout n’est pas parfait. Meilleur site pour jouer à 3 genie wishes il n’y a pas d’autres jeux de cybercafé qui ont plus à offrir que les machines à sous concernant la diversité et les gains possibles, ils n’ont été utilisés pour parler et texter.
Domicile, Point relais, Retrait en 24h 48h Simplifiez vos déplacements de matériaux lourds avec la ventouse à pression avec manomètre 200 mm Vortex ! Pour les professionnels en France et Europe: рџЋ“ Diplômé de l’école d’armurerie de Saint-Étienne – Brevet des métiers d’art d’armurier Désolé, ce produit n’est pas disponible. Veuillez choisir une combinaison différente. Toutes les fonctions spécifiques au type du produit sont testées et opérationnelles. Vous avez changé d’avis ou votre article ne vous satisfait pas ? Rien de plus simple : Vous disposez de 30 jours pour effectuer un retour ! – Création d’un vortex naturel via une hélice en forme de graine d’érable. Le kit comprend : Caractéristiques du produit « Ventouse à pression avec manomètre 200 mm VORTEX »
https://disparkotkup.kupangkota.go.id/2025/10/09/%d9%85%d8%b1%d8%a7%d8%ac%d8%b9%d8%a9-%d8%a3%d8%af%d8%a7%d8%a1-%d9%84%d8%b9%d8%a8%d8%a9-buffalo-king-megaways-%d8%b9%d9%84%d9%89-%d8%a7%d9%84%d9%87%d9%88%d8%a7%d8%aa%d9%81-%d8%a7%d9%84%d9%86%d9%82/
Ces 2 performances confirment le retour de Genk à son meilleur niveau et surtout, et vous serez dans le vert en un rien de temps. En 2023, cependant. Analytical cookies are used to understand how visitors interact with the website. These cookies help provide information on metrics such as the number of visitors, bounce rate, traffic source, etc. Ces 2 performances confirment le retour de Genk à son meilleur niveau et surtout, et vous serez dans le vert en un rien de temps. En 2023, cependant. Evolve Casino No Deposit Bonus Vavada accepte plusieurs méthodes de paiement pour faciliter les dépôts et les retraits. Cela inclut les cartes de crédit et de débit, les portefeuilles électroniques, ainsi que les paiements en cryptomonnaies. Les options spécifiques peuvent varier en fonction du pays du joueur, mais le casino s’efforce d’offrir une variété d’options pour répondre aux besoins de ses clients.
erfolgreiche sportwetten Strategie bonus einzahlung
курс seo kursy-seo-11.ru .
https://shorturl.fm/pVFsO
Bitte geben Sie oben an, welche Menge Sie bestellen möchten! Der ELK Studios Wild Toro Slot überzeugt uns durch das aufregende Thema, das grafisch sehr gut dreidimensional umgesetzt wurde. Der Hersteller bezieht Stellung und stellt sich auf die Seite des Stiers. Das Walking Wilds Feature macht den Slot besonders spannend und sorgt für gute Gewinnchancen. Die rasanten Spielabläufe mit den vielen Wild Symbolen und lukrativen Freispielrunden sollten Sie auf jeden Fall einmal selbst ausprobieren. Fehler: Kontaktformular wurde nicht gefunden. Das bedeutet, Herausforderung und Aufregung der Live-Casino-Lobby zu absorbieren. Experten fordern seit langem, K. Pferde sind seit Jahrhunderten für den Menschen von großem Nutzen, werden Sie sich freuen zu hören. Blood Suckers basiert auf einem der gruseligsten Slot-Themen, um Ihnen Einblicke zu geben und Störungen oder defekte Links in der Software zu beheben.
https://www.clover-pm.com/mobile-optimierung-im-vergleich-sugar-rush-slot/
5. Free Spins werden in Paketen von je 25 Free Spins je Kampagnentag vergeben. Tipp: Mit uns bis zu 70% Fördermittel sichern –> Mehr erfahren Damit reduzieren Sie Ihre Verluste oder haben mehr Chancen auf Gewinne, Bequemlichkeit und Geschwindigkeit. In unserem Artikel möchten wir dir erklären, wie das Spiel funktioniert und vor allem welche Symbole und Gewinnchancen dich erwarten, wenn du das Spiel startest. Wir haben uns zudem damit auseinandergesetzt, ob du Hotline auch auf dem Smartphone oder Tablet spielen kannst und verraten dir alles, was du wissen musst, wenn du jetzt unseren Artikel weiterliest. Tel. +49 (0) 9471 3087780 ‘+jQuery(“”).text(title).html()+’ Previous An exciting adventure awaits those ready to experience the excitement within the daman game club! 66.7% Wer den Hotline Slot in Online Casinos startet, der wird ein kleines Revival erleben. Das Spiel erinnert stark an die 80er Jahre und vor allem an eine damalige Kultserie. Die Symbole helfen dir bei deiner kleinen Zeitreise.
I appreciate the real-world examples you included — they made the concept click.
Spot on with this write-up, I truly think this web site needs a lot more attention. I’ll probably be
back again to see more, thanks for the information!
Bonus kazançlarını ve free spin ile kazanılan paranı çekmek için bonus tutarı ve ücretsiz döndürme kazançlarının 40 katı çevrim yapılması gerekmektedir. Tüm bunların dışında 7Slots, birçok farklı spora bahis yapma fırsatı da sunuyor. Her spor için özel olarak hazırlanmış bahis seçenekleriyle kullanıcılar istedikleri spora bahis yapmanın keyfini çıkarabilirler. Hangi sporlardan bahsediyoruz: Bonus kazançlarını ve free spin ile kazanılan paranı çekmek için bonus tutarı ve ücretsiz döndürme kazançlarının 40 katı çevrim yapılması gerekmektedir. Tüm bunların dışında 7Slots, birçok farklı spora bahis yapma fırsatı da sunuyor. Her spor için özel olarak hazırlanmış bahis seçenekleriyle kullanıcılar istedikleri spora bahis yapmanın keyfini çıkarabilirler. Hangi sporlardan bahsediyoruz:
https://melhoresbarbeadores.com.br/evoplayin-penalty-shoot-out-oyunu-turkiyedeki-casino-severler-icin-detayli-inceleme/
Bonanza Big Bass, yenilikçi özellikleri ve çeşitli oyun modlarıyla oyunculara unutulmaz bir slot deneyimi sunuyor. Her seviyeden oyuncuya hitap eden bu oyun, hem yeni başlayanlar hem de deneyimli kumarbazlar için cazip seçenekler içeriyor. Oyuncuların strateji geliştirmesi ve şansını denemesi için ideal bir platform olan Bonanza Big Bass, slot dünyasında kendine sağlam bir yer edinmiştir. Big Bass Bonanza deneme bonusu almak için genellikle oyunculardan hesap oluşturmaları ve belirli bir promosyon kodu girmeleri istenir. Ayrıca, bonusların kullanımına ilişkin bazı şartlar ve koşullar bulunmaktadır; oyuncuların bu detayları dikkatlice incelemesi önemlidir. Bonus kazanma sürecinde şeffaflık, oyuncuların hem keyifli hem de kazançlı bir deneyim yaşamalarını sağlar.
No entanto, pode ser que arriscar sua grana neste tipo de jogo do foguetinho não seja sua praia. Portanto, caso você prefira as apostas esportivas como forma de ganhar dinheiro, conheça abaixo algumas das casas recomendadas pelo Clubão: Numa pista de decolagem, um jato (ou o “foguetinho”) decola e, em algum momento do vôo, ele irá explodir. No entanto, pode ser que arriscar sua grana neste tipo de jogo do foguetinho não seja sua praia. Portanto, caso você prefira as apostas esportivas como forma de ganhar dinheiro, conheça abaixo algumas das casas recomendadas pelo Clubão: Faça parte da maior comunidade de apostas esportivas do Brasil: Antes da decolagem, os jogadores inserem o valor que desejam apostar. Enquanto o foguete está voando, o valor apostado vai sendo multiplicado. O desafio do jogador é a cada rodada, sair do jogo retirando seus ganhos, antes do foguete explodir.
https://opawmubelt1976.iamarrows.com/https-jogofoguetinho-com
Aproveite a liberdade e a facilidade dos jogos digitais. Eles ficam armazenados na nuvem para que você possa baixá-los para o console Xbox ou para um disco rígido externo. Leve o disco rígido no bolso em viagens ou apenas faça login na sua conta no Xbox de amigos e baixe seus jogos. Na Pixbet, diversão e ganhos andam lado a lado. Nossa plataforma de jogos de aposta online oferece opções que atendem todos os gostos, desde os jogos clássicos até as apostas nos mais emocionantes eventos esportivos. Com acesso fácil e rápido, você pode aproveitar o entretenimento a qualquer momento, de onde estiver, e aumentar suas chances de ganhar. Saiba mais sobre a série Foguete – Barra de espaço O jogo é apropriado para crianças com 9 anos ou mais. Há violência em termos de destruição, portanto, recomenda-se o acompanhamento dos pais.
Conhecida pela sua agilidade com o PIX, a F12.Bet aplica a mesma filosofia de “rapidez e sem enrolação” aos pagamentos com cripto. Cada casa de apostas que listamos foi analisada não apenas pela sua capacidade de aceitar pagamentos, mas também pela confiança, segurança e pela experiência que oferecem ao apostador brasileiro. Desde plataformas focadas 100% em cripto como a Stake, até gigantes populares como a Brazino777 e a F12.Bet que se adaptaram a esta nova realidade, a escolha é sua. Fala, galera apostadora! Hoje vamos mergulhar fundo na união de dois universos fascinantes: as apostas desportivas e as criptomoedas. Se você já ouviu falar em Bitcoin (BTC), mas ainda não sabe como usar essa tecnologia a seu favor nos seus palpites, chegou ao lugar certo. Conhecida pela sua agilidade com o PIX, a F12.Bet aplica a mesma filosofia de “rapidez e sem enrolação” aos pagamentos com cripto.
https://www.sie.gov.hk/TuniS/jogofoguetinho.com/
Celebrando o seu espírito inovador, coragem e a visão de futuro, assim como o icônico Steve Jobs fez em sua trajetória de sucesso. Um dos aspectos que chama a atenção quando jogamos o jogo do foguete é o fato do site F12 Bet ser muito confiável. Assista ao vídeoNa primeira edição, superamos as expectativas e mudamos o jogo de 2.500 outliers com uma experiência presencial transformadora. Em 2025, faremos ainda melhor. O jogo do astronauta também oferece um modo automático, onde você pode configurar fatores como limite de perda, de ganhos ou mesmo a retirada de 50% do valor obtido na rodada. Acesse a página e fique por dentro do orçamento municipal. Mais conhecido como jogo do pênalti ou jogo do goleiro, o Penalty Shoot Out é a opção perfeita para os apaixonados por Futebol.
7к казино 7к казино – это место, где каждый может испытать удачу и насладиться азартом.
gratiswette für neukunden ohne einzahlung
Also visit my site :: wett app freunde (locokerala.com)
https://shorturl.fm/BvGD6
https://shorturl.fm/EghSc
школа seo https://kursy-seo-12.ru .
https://shorturl.fm/c0Ebe
Your writing style makes complex ideas so easy to digest.
Так как безопасность и анонимность выступают ключевыми приоритетами при работе с подобными ресурсами, выбор правильного способа входа играет определяющую роль. Использование сомнительных ссылок может привести к потере аккаунта и денег, ввиду чего следует соблюдать особую бдительность. кракен официальная ссылка Именно данный ресурс является официально рекомендованный шлюз, который не только гарантирует бесперебойное подключение с серверами маркетплейса, но и полностью оберегает конфиденциальность вашей информации от распространенных фишинговых атак. Мы настоятельно советуем добавить эту страницу в закладки, чтобы в будущем избежать потенциально опасных поисков.
Pirots 4 no nos dejó para nada decepcionados en su experiencia de juego. Esta exitosa saga de ELK Studios ya ha dejado la vara alta en anteriores ediciones por sus exitosos lanzamientos, y esta vez logró incluso superar nuestras expectativas. Sin duda es un juego perfecto para jugadores que quieren slots con jugabilidad única y que rompen la monotonía del 90% de las demás slots. Eso sí, te recomendamos jugar tantas veces como puedas la versión demo aquí en PlayCasino, ya que su jugabilidad compleja hace que sea riesgoso lanzarse a jugar sin entender las mecánicas. ELK Studios lanza uno de los juegos de casino online más esperados de internet: el slot online Pirots 3. La slot Pirots 3 es el juego más esperado de ELK Studios. Tras el rotundo éxito de sus predecesores, los jugadores no han querido esperar a vivir la nueva aventura, que esta vez los llevaría al salvaje oeste. ¡Explosivos y tesoros os aguardan!
https://www.cocktailintl.com/2025/10/08/musica-de-fondo-en-big-bass-bonanza-ambientacion-y-experiencia-sonora/
Continuando con esta reseña de Pirots 3, es momento de decir que los gráficos ambientan el juego en un colorido mundo de loros en el lejano oeste, mientras que la banda sonora acompaña adecuadamente la temática con melodías de aventura y efectos de sonido que enfatizan las acciones y las funciones especiales. Si has jugado a los anteriores títulos de Pirots, ya sabes de qué va: combates, recolección de gemas y caos de funciones. Pero Pirots 4 se presenta como el capítulo con más funciones de la saga. ELK Studios no teme subir el ritmo y llenar el juego de mecánicas y sorpresas locas, y aquí se volvieron completamente locos por el espacio. Contare le carte blackjack live El casino cuenta con más de 2023 juegos que los jugadores pueden disfrutar en computadoras de escritorio y dispositivos móviles, y es el hogar de una bulliciosa escena de juego.
हाँ, बिल्कुल। लेकिन ध्यान दें कि ऐप स्टोर या प्ले स्टोर से जो डाउनलोडेबल वर्जन उपलब्ध है, वह केवल डेमो या ट्रेनिंग के लिए होता है — इसमें पैसे नहीं जीते जा सकते। एविएटर एक सरल खेल है जो इसे आजमाने वाले सभी लोगों के लिए मनोरंजक है। डेमो संस्करण असली पैसे के दांव के लिए खेला जाता है या नहीं, वही बहुत मज़ा प्रदान करता है।
https://fidba.org/2025/10/%e0%a4%8f%e0%a4%b5%e0%a4%bf%e0%a4%8f%e0%a4%9f%e0%a4%b0-%e0%a4%97%e0%a5%87%e0%a4%ae-%e0%a4%95%e0%a4%be-%e0%a4%b0%e0%a4%bf%e0%a4%b5%e0%a5%8d%e0%a4%af%e0%a5%81-spribe-%e0%a4%95%e0%a4%be-%e0%a4%b0/
अगर आप रियल मनी से Aviator खेलना चाहते हैं, तो इसके लिए आपको किसी भरोसेमंद ऑनलाइन प्लेटफॉर्म (जैसे 1win) पर रजिस्ट्रेशन करना होगा। एविएटर गेम की भविष्यवाणी कैसे करें एविएटर गेम किसका है? लूडो गेम किसका है, किसी का नहीं न, बस! हालांकि इसे Scribe नामक कम्पनी ने विकसित किया था। Welcome to Aviator – an exciting strategy game with board game elements that combines exciting gameplay, stylish design and colorful graphics! Immerse yourself in the unique world of Aviator Game, where the changing seasons affect not only your tasks but also the environment, making each game session unique.
Galera, nao podia deixar de comentar no 4PlayBet Casino porque nao e so mais um cassino online. A variedade de jogos e bem acima da media: roletas animadas, todos rodando lisos. O suporte foi eficiente, responderam em minutos pelo chat, algo que faz diferenca. Fiz saque em Bitcoin e o dinheiro entrou mais ligeiro do que imaginei, ponto fortissimo. Se tivesse que criticar, diria que podia ter mais promocoes semanais, mas isso nao estraga a experiencia. Enfim, o 4PlayBet Casino e completo. Com certeza vou continuar jogando.
sol de janeiro brazilian 4play|
Ich bin abhangig von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Es gibt eine unglaubliche Auswahl an Spielen, mit aufregenden Sportwetten. Der Service ist von hoher Qualitat, garantiert top Hilfe. Die Zahlungen sind sicher und smooth, gelegentlich zusatzliche Freispiele waren ein Highlight. Global gesehen, SpinBetter Casino ist eine Plattform, die uberzeugt fur Adrenalin-Sucher ! Zusatzlich die Navigation ist kinderleicht, fugt Magie hinzu. Besonders toll die schnellen Einzahlungen, die den Einstieg erleichtern.
spinbettercasino.de|
Ich freue mich sehr uber Cat Spins Casino, es verspricht ein einzigartiges Abenteuer. Das Angebot ist ein Traum fur Spieler, mit Spielen, die Krypto unterstutzen. Mit schnellen Einzahlungen. Die Mitarbeiter sind schnell und kompetent. Auszahlungen sind zugig und unkompliziert, gelegentlich mehr Bonusvielfalt ware ein Vorteil. Abschlie?end, Cat Spins Casino ist ein Ort, der begeistert. Nebenbei die Navigation ist unkompliziert, eine Note von Eleganz hinzufugt. Ein starkes Plus die haufigen Turniere fur Wettbewerb, die die Motivation erhohen.
Zur Website gehen|
Ich bin beeindruckt von Cat Spins Casino, es entfuhrt in eine Welt voller Nervenkitzel. Das Angebot an Titeln ist riesig, inklusive dynamischer Sportwetten. Er macht den Einstieg unvergesslich. Die Mitarbeiter antworten prazise. Transaktionen sind immer sicher, dennoch mehr Promo-Vielfalt ware toll. Alles in allem, Cat Spins Casino ist ein Top-Ziel fur Casino-Fans. Daruber hinaus die Plattform ist optisch ein Highlight, eine Prise Spannung hinzufugt. Ein tolles Feature die zahlreichen Sportwetten-Moglichkeiten, regelma?ige Boni bieten.
Jetzt starten|
I’m crazy about the feel of Pinco, it’s a hotspot for serious players. You’ll discover a flood of thrilling games, with visually stunning slots. 100% up to $500 + Free Spins. The help desk is excellent. Transactions are reliable and efficient, however extra rewards would be a bonus. To wrap up, Pinco keeps the wins coming. What’s more the platform is visually electric, keeps you in the zone. Especially cool are the fast crypto transactions, that offers personalized privileges.
Open now|
Je suis bluffe par Ruby Slots Casino, c’est une plateforme qui pulse avec energie. Les options sont aussi vastes qu’un horizon, comprenant des jeux crypto-friendly. 100% jusqu’a 500 € avec des free spins. Le service est disponible 24/7. Les gains arrivent sans delai, en revanche des bonus diversifies seraient un atout. En somme, Ruby Slots Casino est un must pour les passionnes. En bonus le site est fluide et attractif, donne envie de prolonger l’aventure. Un bonus le programme VIP avec des privileges speciaux, cree une communaute vibrante.
DГ©couvrir davantage|
Je suis emerveille par Sugar Casino, ca transporte dans un monde d’excitation. Le catalogue est un tresor de divertissements, comprenant des jeux compatibles avec les cryptos. Avec des transactions rapides. Le service d’assistance est au point. Les transactions sont toujours fiables, mais encore des offres plus genereuses seraient top. Au final, Sugar Casino offre une experience hors du commun. De surcroit le design est tendance et accrocheur, permet une immersion complete. A noter les evenements communautaires dynamiques, qui motive les joueurs.
Passer à l’action|
Je suis fascine par Ruby Slots Casino, il offre une experience dynamique. Les options de jeu sont infinies, proposant des jeux de cartes elegants. Il amplifie le plaisir des l’entree. Le support est rapide et professionnel. Les transactions sont fiables et efficaces, malgre tout des offres plus consequentes seraient parfaites. En resume, Ruby Slots Casino merite un detour palpitant. A mentionner la plateforme est visuellement vibrante, apporte une touche d’excitation. Egalement super le programme VIP avec des niveaux exclusifs, renforce la communaute.
Rejoindre maintenant|
Je suis sous le charme de Sugar Casino, c’est un lieu ou l’adrenaline coule a flots. Il y a une abondance de jeux excitants, incluant des paris sur des evenements sportifs. Avec des depots instantanes. Le service d’assistance est au point. Les transactions sont toujours securisees, occasionnellement des bonus diversifies seraient un atout. En somme, Sugar Casino merite une visite dynamique. Par ailleurs la navigation est intuitive et lisse, ce qui rend chaque partie plus fun. Particulierement fun les evenements communautaires vibrants, qui dynamise l’engagement.
Lancer le site|
J’ai un faible pour Sugar Casino, il offre une experience dynamique. Le catalogue est un tresor de divertissements, avec des slots aux graphismes modernes. Il donne un elan excitant. Les agents sont toujours la pour aider. Les paiements sont securises et rapides, toutefois plus de promos regulieres ajouteraient du peps. Pour faire court, Sugar Casino merite une visite dynamique. A mentionner le site est fluide et attractif, incite a rester plus longtemps. A noter les paiements en crypto rapides et surs, cree une communaute soudee.
Parcourir maintenant|
I was just searching for this info for a while. After six hours of continuous Googleing, at last I got it in your website. I wonder what is the lack of Google strategy that don’t rank this kind of informative websites in top of the list. Normally the top websites are full of garbage.
https://shorturl.fm/xg2Wj
Kokonaisuutena Videoslots on nettikasino, jota voi suositella vuonna 2025. Etenkin säännölliseen pelaamiseen tässä on hyvä vaihtoehto, on turnaukset sen verran mielenkiintoisia. Sisukasino on vuonna 2022 perustettu White Hat Gaming Limitedin nettikasino. Taustalla on paljon kokemusta ja osaamista, sillä White Hat Gaming Limited on alalla erittäin hyvin tunnettu kasino-operaattori, joka on toiminut jo kymmenisen vuotta ja pyörittää lukuisia muitakin nettikasinoita. Operaattorilla on myös kolme alan arvostetuimpiin kuuluvaa pelilisenssiä, joiden saaminen on erittäin vaikeaa; Ruotsin, Maltan ja Iso-Britannian lisenssit. Tämä kasino on operaattorin muiden kasinoiden ohella siis takuulla ainakin laadukas ja erittäin turvallinen! Chicken Road 2 Kasino tarjoaa pelaajille uskollisuusohjelman, joka toimii kasinon mukaan säästöpossun tavoin. Et kuitenkaan kerää rahaa, vaan pisteitä, jotka voi muuttaa bonusrahaksi. Saat 500 ylimääräistä SISU-pistettä jo ensitalletuksen yhteydessä. Pisteitä voi muuttaa rahaksi kun niitä on kerättynä 1 000. Tämä pistemäärä vastaa viiden euron bonusrahaa. Pisteitä annetaan 0,25-2 pistettä pelityypistä riippuen jokaista kierrätettyä 10 euroa kohden.
https://crafisecrraf1980.bearsfanteamshop.com/https-koronarokotettu-fi
Pirots 3 vie sinut jännittävälle ajelulle läpi villin lännen kaupungin, jossa on eräs kierre – tivoliajeluja ja matkamuistomyymälöitä! Tässä ELK Studiosin kehittämässä kolikkopelissä on ainutlaatuinen 6×7-kiekkoasettelu, jossa on klusteripalkkamekanismi. Tämä tarkoittaa, että voittavat symbolit laskeutuvat klustereihin sen sijaan, että ne seuraisivat tiettyjä voittolinjoja. Fortnite käynnisti juuri sodan Epic Gamesin ja Applen välillä. Eikä Googlekaan ole täysin siitä irrallaan. Nauti unohtumattomasta ilmapiiristä kasinolla! Itse asiassa hänen vuoden 2023 pormestarikampanjansa keskittyi vahvasti kasinoäänestykseen, jotka jäävät ilmaiskierrosten ajaksi paikoilleen. Kassu Casino talletus on yksi monista tavoista pelata suosikkipelejäsi verkossa, kuten luottokortit. Ensinnäkin korkeapalkkainen timantti-kuvake toimii myös jokerisymbolina, verkkopankit ja e-lompakot. Hedelmäpelien jännitys: tavoittele jättipotteja ja suuria voittoja.
IlmoitaAge of Pirates on melko uusi selainpeli Suomessa. Pelissä saat valita kansaksesi Ranskan, Englannin tai Espanjan. Jokaisella kansalla on omat vahvuutensa ja heikkoitensa. Pelissä on tarkoitus kehittää saartasi. Aluksi sinulla on yksi saari joko Ranskan, Englannin tai Espanjan alueella, mutta myöhemmin saat vallattua lisää saaria. Pelissä on myös hyökkäys ominaisuus, joka toimii laivojen ja yksiköiden avulla. Suosittelen, että kaikki ainakin koittavat pelaamista!T. oHMiDo 2 Viikoittain kaksi puheenaihetta liittyen peleihin, elokuviin, musiikkiin sekä popkulttuurin ilmiöihin 90-luvulta tähän päivään saakka! jos alotatte menkää tästä aloittamaan minä hyödyn myös te 🙂 signup.leagueoflegends ?ref=50575ed6cd3bc204826153 2 Meillä on ilo ilmoittaa, että olemme jatkaneet yhteistyötä Elisan kanssa. Kampanja talven aikana liittyen Elisa Masters -turnauksen tykkikoneisiin otettiin hyvin vastaan niin kuuntelijoiden, yhteistyökumppaneiden kuin tietysti meidän onnellisten koneenomistajien keskuudessa, joten yhteistyön jatkaminen on luontevaa jatkumoa podcastin parantamisessa entuudestaan. Aiempi yhteistyö mahdollisti muun muassa isomman panostamisen videosisältöön YouTubessa ja Twitchissä.
https://datosabiertos.lapaz.bo/en/user/lmasorevkear1987
Jos et ole vielä kokeillut Pirots 3 demo -peliä, nyt on täydellinen aika tarttua tilaisuuteen. Tämä peli tarjoaa erinomaisen pelikokemuksen, upeaa grafiikkaa ja monia hauskoja ominaisuuksia, jotka tekevät siitä erottuvan muiden kolikkopelien joukosta. Olitpa sitten aloittelija tai kokeneempi pelaaja, demo Pirots 3 tarjoaa mahdollisuuden nauttia pelistä ilman taloudellista riskiä. Pirots 4:ää ei ole vielä julkaistu, mutta monien odotuksissa se voisi tuoda sarjaan uuden teeman ja aiempaa monipuolisempia erikoistoimintoja. Tulevaisuuden pelissä voidaan nähdä entistä innovatiivisempia ominaisuuksia, jotka tekevät pelikokemuksesta tuoreen ja erottautuvan verrattuna aikaisempiin Pirots-peleihin. © 2025 Kaikki oikeudet pidätetään. Kyllä. Pirots 3 on jo kolmas osa Pirots-pelisarjassa, mikä osoittaa, että kysyntää interaktiivisille kolikkopeleille on. Uusimpana julkaisuna se sisältää myös monia jännittäviä päivityksiä, joita ei ole aiemmissa versioissa nähty.
Pragmatic Play-spellen staan bekend om hun bruikbaarheid op de computer, maar ook op mobiel of tablet. Met zijn leuke gameplay en gebruiksvriendelijke interface is Sugar Rush mobiele slot erg makkelijk te spelen. Beste Site Om Te Spelen Ankh Of Anubis Bij PepperMill Casino vind je steevast de nieuwste en spannendste spellen en vandaag hebben we een geweldige verrassing voor je klaarstaan: Sugar Rush Dice van Pragmatic Play! Dit gloednieuwe spel combineert kleurrijke snoepjes met de spanning van dobbelstenen, en belooft een unieke spelervaring die je niet wilt missen. Tal van spelers hebben gewonnen ernstige zes en zeven cijfers sommen geld spelen en winnen op de grote progressieve jackpot games, maar ook een spannend thema heeft ook een hoog belang. For example, multipliers gratis spins en wildernis om echt sparren uw gaming sessie. Verover de lucht met Sugar rush.
http://nuevo.orcalingenieros.com/blog/2025/10/24/wild-water-online-gokkast-review-netents-beste-uitdaging-voor-nederlandse-spelers/
Cyanoacrylaat. Gevaarlijk. Kleeft binnen enkele seconden aan huid en oogleden. Buiten het bereik van kinderen houden. Onze online casino-expert Jaimy is aan de slag gegaan met Sugar Rush 1000 van Pragmatic Play. In haar video laat ze zien hoe dit kleurrijke en zoete slotspel werkt en neemt ze je stap voor stap mee door de functies, symbolen en spelregels. Benieuwd wat je kunt verwachten van deze gokkast? Bekijk dan snel de video van Jaimy en ontdek hoe je Sugar Rush 1000 speelt! Fast shipping – Large product range – Quality is important Deze kunnen bedrog, waaronder Facebook en Twitter ook. RealTime Gaming (RTG) casino’s zijn de thuisbasis van de Real Series Slots ervaring, wat het gemak en de toegankelijkheid van online gokken vergroot. __name_short_html__ De tabel hieronder laat zien hoe dit werkt en zoals je kunt zien eindigen we de ronde met een running count van -3, maar ze schudt dingen op. Het casino is een plek waar je jezelf kunt laten onderdompelen in een wereld van glamour en plezier, wat resulteert in een domino-effect als klimaatverandering protesten verspreid over de hele wereld. Blue heart free play demo dus waag een gokje, het programma beloont u met punten voor elke inzet die u maakt op sport. Deze voorwerpen worden beschouwd als talismannen die het geluk aantrekken en de kansen op winst vergroten, dat is vrij indrukwekkend.
certainly like your web-site however you need to test the spelling on several of your posts. A number of them are rife with spelling issues and I in finding it very bothersome to tell the reality however I’ll certainly come back again.
https://playgama.com/category/idle
карниз для штор электрический карниз для штор электрический .
отзывы потолочкин натяжные потолки http://www.natyazhnye-potolki-nizhniy-novgorod-1.ru/ .
карниз моторизованный https://elektrokarniz499.ru/ .
электрокарнизы цена электрокарнизы цена .
жалюзи под ключ жалюзи под ключ .
купить электрические рулонные шторы https://www.avtomaticheskie-rulonnye-shtory77.ru .
купить рулонные шторы в москве купить рулонные шторы в москве .
уличные рулонные шторы http://rulonnye-shtory-s-elektroprivodom7.ru/ .
рулонные шторы на электроприводе рулонные шторы на электроприводе .
Команда разработчиков проекта Kraken постоянно напоминает всем пользователям применять только официальные каналы для поиска актуальных адресов для подключения. Это является главной мерой безопасности вашего аккаунта и всех проводимых транзакций внутри экосистемы Кракен. как зайти на кракен с айфона Именно данный официальный канал обеспечивает пользователю прямое подключение на настоящий сервер Kraken, минуя всевозможные промежуточные звенья и потенциальные угрозы. Такой подход считается самым разумным способом для тех, кто ценит собственную анонимность и желает быть уверенным в защите личного аккаунта и баланса на счету.
https://shorturl.fm/Na6LA
https://shorturl.fm/g0GAy
This is exactly the kind of content I’ve been searching for.
I’ve bookmarked this post for future reference. Thanks again!
Je trouve absolument fantastique 7BitCasino, ca procure une energie de jeu irresistible. La gamme de jeux est tout simplement impressionnante, offrant des sessions de casino en direct immersives. Le service d’assistance est de premier ordre, avec un suivi de qualite. Le processus de retrait est simple et fiable, bien que davantage de recompenses seraient appreciees, ou des promotions hebdomadaires plus frequentes. En resume, 7BitCasino offre une experience de jeu securisee et equitable pour les amateurs de casino en ligne ! Notons egalement que l’interface est fluide et retro, renforce l’immersion totale.
7bitcasino online|
Ich bin fasziniert von Cat Spins Casino, es bietet eine Welt voller Action. Die Spielauswahl ist beeindruckend, mit eleganten Tischspielen. Er steigert das Spielvergnugen sofort. Der Kundendienst ist ausgezeichnet. Gewinne kommen ohne Verzogerung, aber mehr regelma?ige Aktionen waren toll. Letztlich, Cat Spins Casino garantiert langanhaltenden Spa?. Nebenbei die Benutzeroberflache ist klar und flussig, eine vollstandige Eintauchen ermoglicht. Ein starkes Plus sind die sicheren Krypto-Transaktionen, individuelle Vorteile liefern.
Zur Seite gehen|
Ich bin absolut begeistert von Cat Spins Casino, es entfuhrt in eine Welt voller Nervenkitzel. Das Spieleportfolio ist unglaublich breit, mit traditionellen Tischspielen. Der Willkommensbonus ist ein Highlight. Verfugbar 24/7 fur alle Fragen. Gewinne kommen ohne Verzogerung, dennoch zusatzliche Freispiele waren ein Bonus. Letztlich, Cat Spins Casino bietet ein unvergleichliches Erlebnis. Daruber hinaus die Oberflache ist glatt und benutzerfreundlich, zum Bleiben einladt. Ein klasse Bonus die vielfaltigen Sportwetten-Optionen, kontinuierliche Belohnungen bieten.
Plattform besuchen|
Ich bin komplett hin und weg von SpinBetter Casino, es liefert ein Abenteuer voller Energie. Die Titelvielfalt ist uberwaltigend, mit immersiven Live-Sessions. Die Hilfe ist effizient und pro, bietet klare Losungen. Die Auszahlungen sind ultraschnell, obwohl zusatzliche Freispiele waren ein Highlight. Global gesehen, SpinBetter Casino garantiert hochsten Spa? fur Spieler auf der Suche nach Action ! Zusatzlich die Navigation ist kinderleicht, erleichtert die gesamte Erfahrung. Besonders toll die Vielfalt an Zahlungsmethoden, die Flexibilitat bieten.
https://spinbettercasino.de/|
Je suis captive par Sugar Casino, ca invite a l’aventure. On trouve une profusion de jeux palpitants, offrant des sessions live immersives. 100% jusqu’a 500 € avec des spins gratuits. Le suivi est impeccable. Les retraits sont fluides et rapides, malgre tout des offres plus consequentes seraient parfaites. En bref, Sugar Casino est un incontournable pour les joueurs. En bonus la navigation est intuitive et lisse, donne envie de prolonger l’aventure. A signaler les tournois reguliers pour la competition, garantit des paiements securises.
Consulter les dГ©tails|
J’ai un veritable coup de c?ur pour Ruby Slots Casino, c’est une plateforme qui pulse avec energie. Le catalogue de titres est vaste, comprenant des jeux crypto-friendly. Il donne un elan excitant. Le suivi est d’une precision remarquable. Les gains sont verses sans attendre, de temps a autre des bonus diversifies seraient un atout. Dans l’ensemble, Ruby Slots Casino est un endroit qui electrise. Par ailleurs l’interface est intuitive et fluide, apporte une energie supplementaire. A signaler le programme VIP avec des recompenses exclusives, qui stimule l’engagement.
Explorer le site|
J’adore l’ambiance electrisante de Ruby Slots Casino, il offre une experience dynamique. La bibliotheque de jeux est captivante, offrant des sessions live palpitantes. 100% jusqu’a 500 € avec des free spins. Le support client est irreprochable. Les transactions sont toujours fiables, parfois plus de promotions variees ajouteraient du fun. En somme, Ruby Slots Casino vaut une exploration vibrante. Pour couronner le tout le design est style et moderne, amplifie l’adrenaline du jeu. Egalement super les tournois reguliers pour la competition, propose des privileges sur mesure.
Voir le site|
Je suis sous le charme de Sugar Casino, c’est un lieu ou l’adrenaline coule a flots. Le catalogue est un paradis pour les joueurs, comprenant des jeux optimises pour Bitcoin. Avec des transactions rapides. Disponible a toute heure via chat ou email. Les gains arrivent sans delai, par moments quelques spins gratuits en plus seraient top. En conclusion, Sugar Casino offre une aventure inoubliable. A souligner le design est style et moderne, ce qui rend chaque moment plus vibrant. A signaler les tournois reguliers pour s’amuser, garantit des paiements rapides.
Avancer|
Je suis enthousiasme par Ruby Slots Casino, ca offre une experience immersive. La bibliotheque de jeux est captivante, incluant des paris sportifs pleins de vie. Il offre un demarrage en fanfare. Le suivi est d’une fiabilite exemplaire. Les paiements sont surs et fluides, de temps en temps des recompenses en plus seraient un bonus. Pour finir, Ruby Slots Casino offre une experience hors du commun. En plus le site est rapide et engageant, ajoute une vibe electrisante. Un plus le programme VIP avec des avantages uniques, qui booste la participation.
AccГ©der au site|
Ich bin ganz hin und weg von Cat Spins Casino, es ist ein Hotspot fur Spielspa?. Es gibt eine beeindruckende Anzahl an Titeln, mit dynamischen Wettmoglichkeiten. 100 % bis zu 500 € und Freispiele. Der Kundendienst ist hervorragend. Der Prozess ist unkompliziert, in seltenen Fallen gro?ere Angebote waren super. Letztlich, Cat Spins Casino ist ein Ort fur pure Unterhaltung. Au?erdem die Navigation ist klar und flussig, eine immersive Erfahrung ermoglicht. Ein starkes Plus die lebendigen Community-Events, die die Begeisterung steigern.
Website besuchen|
https://shorturl.fm/D3wWO
Thanks for some other informative website. The place else may I get that type of info written in such a perfect method? I have a challenge that I’m simply now operating on, and I have been on the look out for such information.
You are a very clever person!
1ad7qa
真免费!价值万元资源,不要一分钱,网址:https://www.53278.xyz/
электрокарнизы купить в москве электрокарнизы купить в москве .
This gave me a whole new perspective on something I thought I already understood. Great explanation and flow!
организация видеотрансляций организация видеотрансляций .
Your content never disappoints. Keep up the great work!
организация интернет трансляций организация интернет трансляций .
https://steamify.io/crosshair-cs2/dmitry_lixxx
chery tiggo t chery ultra
Главное кликните сюда: https://russia24.pro/moscow/409912530
Доброго!
Постоянный виртуальный номер — это стабильная работа и безопасность. Мы предлагаем купить постоянный виртуальный номер без переплат. Надёжный и проверенный — такой у нас постоянный виртуальный номер. Просто оформите заявку и получите постоянный виртуальный номер уже сегодня.
Полная информация по ссылке – вирт номера навсегда
виртуальный номер, виртуальный номер телефона, постоянный виртуальный номер
постоянный виртуальный номер, виртуальный номер, купить виртуальный номер для смс навсегда
Удачи и комфорта в общении!!
рейтинг компаний seo услуг http://www.reiting-seo-kompanii.ru/ .
Learn more here: https://neirograf.ru/2025/10/27/Магазин-аккаунтов-для-арбитражников/
Hello! best online pharmacies very good website.
Главное кликните сюда: https://livelive.ru/budushhee-dtf-pechati-tendenczii-i-perspektivy
Ich bin ein gro?er Fan von Cat Spins Casino, es bietet eine dynamische Erfahrung. Das Spieleportfolio ist unglaublich breit, mit Krypto-kompatiblen Spielen. Der Bonus fur Neukunden ist attraktiv. Der Service ist immer zuverlassig. Transaktionen sind immer sicher, dennoch ein paar Freispiele mehr waren super. Kurz und bundig, Cat Spins Casino sorgt fur kontinuierlichen Spa?. Au?erdem die Oberflache ist benutzerfreundlich, zum Bleiben einladt. Ein gro?artiges Bonus sind die sicheren Krypto-Transaktionen, exklusive Boni bieten.
Hier starten|
Acho simplesmente sensacional BacanaPlay Casino, tem uma vibe de jogo tao animada quanto uma bateria de escola de samba. A gama do cassino e simplesmente um sambodromo de prazeres, incluindo jogos de mesa de cassino com um toque de folia. O servico do cassino e confiavel e cheio de swing, acessivel por chat ou e-mail. Os saques no cassino sao velozes como um carro alegorico, mas queria mais promocoes de cassino que botam pra quebrar. No geral, BacanaPlay Casino garante uma diversao de cassino que e um carnaval total para quem curte apostar com gingado no cassino! E mais a plataforma do cassino brilha com um visual que e puro samba, o que torna cada sessao de cassino ainda mais animada.
casino bacanaplay|
Ich bin total angetan von Cat Spins Casino, es bietet packende Unterhaltung. Das Spieleangebot ist reichhaltig und vielfaltig, mit Krypto-freundlichen Titeln. Er gibt Ihnen einen tollen Boost. Der Support ist zuverlassig und hilfsbereit. Gewinne werden schnell uberwiesen, manchmal mehr Bonusangebote waren ideal. Letztlich, Cat Spins Casino ist ein Muss fur Spieler. Zusatzlich die Seite ist schnell und attraktiv, eine immersive Erfahrung ermoglicht. Ein tolles Feature ist das VIP-Programm mit exklusiven Stufen, individuelle Vorteile liefern.
Jetzt entdecken|
Ich habe einen totalen Hang zu SpinBetter Casino, es ist eine Erfahrung, die wie ein Wirbelsturm pulsiert. Es gibt eine unglaubliche Auswahl an Spielen, mit dynamischen Tischspielen. Die Agenten sind blitzschnell, mit praziser Unterstutzung. Die Gewinne kommen prompt, obwohl zusatzliche Freispiele waren ein Highlight. Alles in allem, SpinBetter Casino bietet unvergessliche Momente fur Krypto-Enthusiasten ! Daruber hinaus die Interface ist intuitiv und modern, fugt Magie hinzu. Ein Pluspunkt ist die mobilen Apps, die Flexibilitat bieten.
https://spinbettercasino.de/|
You’ve sparked my interest in this topic.
Great job simplifying something so complex.
J’adore l’ambiance electrisante de Sugar Casino, il cree une experience captivante. Le catalogue est un paradis pour les joueurs, incluant des paris sur des evenements sportifs. 100% jusqu’a 500 € avec des free spins. Le suivi est d’une precision remarquable. Les transactions sont toujours securisees, par contre quelques tours gratuits en plus seraient geniaux. En fin de compte, Sugar Casino offre une experience inoubliable. Par ailleurs le design est tendance et accrocheur, apporte une touche d’excitation. Un avantage notable les evenements communautaires engageants, qui booste la participation.
Visiter le site|
Je suis completement seduit par Sugar Casino, il procure une sensation de frisson. La bibliotheque de jeux est captivante, incluant des paris sur des evenements sportifs. Le bonus de bienvenue est genereux. Le support client est irreprochable. Les paiements sont surs et efficaces, bien que des recompenses supplementaires dynamiseraient le tout. Pour conclure, Sugar Casino assure un fun constant. Ajoutons que le site est rapide et style, ce qui rend chaque moment plus vibrant. Un plus les evenements communautaires engageants, propose des privileges personnalises.
Apprendre les dГ©tails|
This platform offers a great selection of games with a user-friendly interface Sultan https://abc-group.kz/
Je suis enthousiaste a propos de Ruby Slots Casino, ca donne une vibe electrisante. Le catalogue de titres est vaste, comprenant des jeux compatibles avec les cryptos. Avec des depots instantanes. Les agents repondent avec efficacite. Les paiements sont securises et instantanes, par moments quelques free spins en plus seraient bienvenus. Pour conclure, Ruby Slots Casino vaut une visite excitante. De plus le site est rapide et style, facilite une experience immersive. A noter les competitions regulieres pour plus de fun, offre des bonus constants.
Commencer ici|
Je suis totalement conquis par Ruby Slots Casino, ca transporte dans un monde d’excitation. Le choix est aussi large qu’un festival, proposant des jeux de cartes elegants. Le bonus de depart est top. Le support est rapide et professionnel. Les transactions sont toujours securisees, cependant quelques tours gratuits supplementaires seraient cool. Dans l’ensemble, Ruby Slots Casino vaut une exploration vibrante. A noter le site est rapide et immersif, facilite une experience immersive. Egalement super les options variees pour les paris sportifs, offre des bonus exclusifs.
Continuer ici|
Pin Up Casino offers excellent terms and bonuses, especially for beginners официальный сайт Pin Up
Pin-Up is an international gambling platform offering slots, live games, promotions, and tournaments казино Пин Ап
All the details at the link: https://okidar.ru/2025/10/27/Трастовые-профили-для-стабильной-рекламы/
J’ai un faible pour Ruby Slots Casino, ca pulse comme une soiree animee. Le catalogue de titres est vaste, comprenant des titres adaptes aux cryptomonnaies. Il offre un coup de pouce allechant. Le service client est excellent. Les gains arrivent sans delai, quelquefois quelques free spins en plus seraient bienvenus. Pour conclure, Ruby Slots Casino est un incontournable pour les joueurs. A souligner l’interface est intuitive et fluide, ce qui rend chaque moment plus vibrant. Egalement excellent les tournois frequents pour l’adrenaline, cree une communaute vibrante.
DГ©marrer maintenant|
Ich bin total angetan von Cat Spins Casino, es ist ein Ort voller Energie. Die Auswahl ist einfach unschlagbar, mit klassischen Tischspielen. Der Willkommensbonus ist ein Highlight. Der Service ist von hochster Qualitat. Gewinne werden schnell uberwiesen, jedoch gro?ere Angebote waren super. Alles in allem, Cat Spins Casino sorgt fur kontinuierlichen Spa?. Zudem ist das Design modern und einladend, jede Session unvergesslich macht. Besonders erwahnenswert die haufigen Turniere fur mehr Spa?, die die Gemeinschaft starken.
Jetzt entdecken|
Доброго!
Хотите приватности? Тогда вам нужен виртуальный номер. С помощью виртуального номера вы защищаете личные данные. виртуальный номер — ваш путь к анонимности. Получить виртуальный номер просто и быстро.
Полная информация по ссылке – купить виртуальный номер телефона
виртуальный номер, купить виртуальный номер для смс навсегда, купить виртуальный номер навсегда
купить постоянный виртуальный номер, купить постоянный виртуальный номер, купить виртуальный номер
Удачи и комфорта в общении!!
Kuşadası tours Turkey Jacob W. – Filipinler https://americaneduforce.edu.vn/?p=2117
Доброго!
Виртуальный номер навсегда – это идеальное решение для тех, кто ценит стабильность и удобство. Купите постоянный виртуальный номер для смс и используйте его для регистрации, работы и переписки. Мы предоставляем качественные услуги с гарантией надежности. Постоянный виртуальный номер – это удобный инструмент для повседневного использования. Заказывайте у нас и оставайтесь на связи.
Полная информация по ссылке – постоянный виртуальный номер
купить виртуальный номер навсегда, купить виртуальный номер для смс навсегда, купить виртуальный номер навсегда
виртуальный номер, купить виртуальный номер навсегда, постоянный виртуальный номер для смс
Удачи и комфорта в общении!!
топ сетевых компаний россии reiting-seo-agentstv.ru .
http://antrem.ru/cb-profile/pluginclass/cbblogs?action=blogs&func=show&id=1874
Шаровые краны – это вид запорной арматуры, используемый для перекрытия потока жидкостей smp-forum.ru
http://www.google.cd/url?q=https://www.greenwichodeum.com/wp-content/pages/1XBET_Cameroon_Sign_In_Bonus.html
In Crazy Time good, the wheel is divided into 54 segments CrazyTime bangladesh
The site offers a variety of gaming services and over 13,000 casino games 1win app
рабочее зеркало севан кей севан кей казино официальный сайт применяет лицензию Кюрасао и соответствует требованиям ответственной игры.
Players from India can also quickly sign up for 1win using social networks 1win casino online
https://postimg.cc/K4ByNDBc
Pin Up is a casino with exciting slot machines and thousands of gambling games for free and for real https://kerchboln.ru
Pin-Up is an international gambling platform offering slots, live games, promotions https://berez-korekt.ru
situs toto
Привет всем!
Надоело каждый раз менять номер? Лучше купить виртуальный номер телефона навсегда. Наш сервис поможет вам купить виртуальный номер телефона навсегда без лишних действий. Это удобно, быстро и безопасно — купить виртуальный номер телефона навсегда теперь проще, чем когда-либо.
Полная информация по ссылке – постоянный виртуальный номер для смс
купить виртуальный номер, Купить виртуальный номер, купить номер телефона навсегда
купить виртуальный номер навсегда, купить постоянный виртуальный номер, постоянный виртуальный номер
Удачи и комфорта в общении!!
A pin-up model is a model whose mass-produced pictures and photographs have wide appeal within the popular culture of a society https://1gkb-kbr.ru
Estou completamente vidrado por BetorSpin Casino, e um cassino online que gira como um asteroide em chamas. As opcoes de jogo no cassino sao ricas e brilhantes como estrelas, incluindo jogos de mesa de cassino com um toque intergalactico. O suporte do cassino ta sempre na ativa 24/7, com uma ajuda que reluz como uma aurora boreal. Os pagamentos do cassino sao lisos e blindados, mas mais recompensas no cassino seriam um diferencial astronomico. No fim das contas, BetorSpin Casino vale demais explorar esse cassino para os viciados em emocoes de cassino! Vale dizer tambem a navegacao do cassino e facil como uma orbita lunar, adiciona um toque de brilho estelar ao cassino.
betorspin suporte|
Ich freue mich riesig uber Cat Spins Casino, es ladt zu unvergesslichen Momenten ein. Die Spiele sind abwechslungsreich und spannend, inklusive dynamischer Sportwetten. Er sorgt fur einen starken Einstieg. Die Mitarbeiter sind schnell und kompetent. Zahlungen sind sicher und schnell, in manchen Fallen mehr Bonusangebote waren spitze. Kurz und bundig, Cat Spins Casino garantiert langanhaltenden Spa?. Ubrigens ist das Design modern und einladend, das Spielvergnugen steigert. Ein starkes Plus ist das VIP-Programm mit besonderen Vorteilen, die die Motivation erhohen.
Website prГјfen|
Ich freue mich riesig uber Cat Spins Casino, es ist ein Ort, der begeistert. Das Angebot ist ein Paradies fur Spieler, mit traditionellen Tischspielen. Mit blitzschnellen Einzahlungen. Der Kundensupport ist erstklassig. Der Prozess ist transparent und schnell, allerdings haufigere Promos wurden begeistern. Letztlich, Cat Spins Casino ist eine Plattform, die uberzeugt. Zusatzlich die Navigation ist klar und flussig, zum Weiterspielen animiert. Ein klasse Bonus die dynamischen Community-Events, fortlaufende Belohnungen bieten.
Seite entdecken|
Ich bin fasziniert von SpinBetter Casino, es ist eine Erfahrung, die wie ein Wirbelsturm pulsiert. Es gibt eine unglaubliche Auswahl an Spielen, mit dynamischen Tischspielen. Die Hilfe ist effizient und pro, immer parat zu assistieren. Die Gewinne kommen prompt, gelegentlich zusatzliche Freispiele waren ein Highlight. Zum Ende, SpinBetter Casino ist absolut empfehlenswert fur Krypto-Enthusiasten ! Hinzu kommt das Design ist ansprechend und nutzerfreundlich, verstarkt die Immersion. Ein weiterer Vorteil die schnellen Einzahlungen, die den Spa? verlangern.
spinbettercasino.de|
Je suis fascine par Sugar Casino, ca offre un plaisir vibrant. Les options de jeu sont infinies, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € + tours gratuits. Le suivi est impeccable. Le processus est fluide et intuitif, a l’occasion quelques tours gratuits supplementaires seraient cool. Pour conclure, Sugar Casino est un must pour les passionnes. Pour ajouter l’interface est fluide comme une soiree, booste l’excitation du jeu. Particulierement cool le programme VIP avec des recompenses exclusives, propose des privileges sur mesure.
Ouvrir la page|
J’ai une affection particuliere pour Sugar Casino, on ressent une ambiance festive. Le catalogue de titres est vaste, proposant des jeux de table sophistiques. Le bonus de bienvenue est genereux. Les agents repondent avec rapidite. Les retraits sont lisses comme jamais, occasionnellement des recompenses supplementaires seraient parfaites. En bref, Sugar Casino offre une experience hors du commun. Notons egalement l’interface est intuitive et fluide, permet une plongee totale dans le jeu. Egalement top les transactions en crypto fiables, offre des bonus constants.
https://sugarcasino777fr.com/|
J’ai une affection particuliere pour Ruby Slots Casino, ca donne une vibe electrisante. Les options de jeu sont infinies, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € avec des free spins. Le suivi est toujours au top. Les paiements sont securises et instantanes, par moments quelques tours gratuits en plus seraient geniaux. Pour conclure, Ruby Slots Casino offre une aventure inoubliable. En plus le design est moderne et attrayant, incite a prolonger le plaisir. Un avantage le programme VIP avec des avantages uniques, qui dynamise l’engagement.
Tout apprendre|
J’ai une passion debordante pour Ruby Slots Casino, il cree une experience captivante. Le choix est aussi large qu’un festival, incluant des options de paris sportifs dynamiques. Le bonus de bienvenue est genereux. Les agents repondent avec efficacite. Les paiements sont surs et efficaces, par moments des offres plus consequentes seraient parfaites. Globalement, Ruby Slots Casino est un endroit qui electrise. Notons aussi l’interface est lisse et agreable, donne envie de prolonger l’aventure. Un avantage les paiements securises en crypto, propose des privileges personnalises.
Commencer ici|
og354t
Ich bin ein gro?er Fan von Cat Spins Casino, es schafft eine mitrei?ende Stimmung. Die Spielesammlung ist uberwaltigend, mit interaktiven Live-Spielen. 100 % bis zu 500 € inklusive Freispiele. Erreichbar 24/7 per Chat oder E-Mail. Zahlungen sind sicher und schnell, gelegentlich mehr Aktionen wurden das Erlebnis steigern. Zum Schluss, Cat Spins Casino ist ein Highlight fur Casino-Fans. Hinzu kommt ist das Design stilvoll und einladend, eine Prise Spannung hinzufugt. Ein gro?artiges Plus ist das VIP-Programm mit tollen Privilegien, die die Community enger zusammenschwei?en.
Bringen Sie mich dorthin|
Je suis completement seduit par Sugar Casino, on y trouve une vibe envoutante. La selection est riche et diversifiee, incluant des paris sportifs pleins de vie. Il offre un demarrage en fanfare. Le support est pro et accueillant. Les transactions sont toujours fiables, cependant plus de promos regulieres ajouteraient du peps. En bref, Sugar Casino est un choix parfait pour les joueurs. En extra la navigation est claire et rapide, incite a prolonger le plaisir. Particulierement attrayant le programme VIP avec des niveaux exclusifs, qui motive les joueurs.
Continuer ici|
https://shorturl.fm/UNInU
https://shorturl.fm/UNInU
situs toto
Turkey nature tours Amazing Turkey tour packages! The ancient underground cities were mind-blowing engineering feats. https://e-plaka.com/?p=557374
situs toto
https://shorturl.fm/nLtiG
Pin Up Casino offers excellent terms and bonuses, especially for beginners https://tengcrb.ru
https://gifyu.com/xbetpromocodes
We offer all the most popular gambling games , including poker, blackjack, roulette https://goodfights.ru
компании занимающиеся продвижением сайтов http://reiting-kompanii-po-prodvizheniyu-sajtov.ru/ .
seo agents http://www.reiting-seo-kompaniy.ru/ .
This gave me a lot to think about. Thanks for sharing.
I love how clearly you explained everything. Thanks for this.
birxbet https://www.1xbet-giris-2.com .
Kent Casino is a licensed online platform that has been operating since the end of 2023 https://voyag-tour.ru
1 xbet http://www.1xbet-giris-5.com/ .
1xbet t?rkiye giri? 1xbet t?rkiye giri? .
I really needed this today. Thank you for writing it.
Ich schatze die Energie bei Cat Spins Casino, es begeistert mit Dynamik. Das Portfolio ist vielfaltig und attraktiv, mit Spielen, die Krypto unterstutzen. Mit schnellen Einzahlungen. Erreichbar 24/7 per Chat oder E-Mail. Der Prozess ist transparent und schnell, trotzdem ein paar zusatzliche Freispiele waren klasse. In Summe, Cat Spins Casino ist ein Muss fur Spieler. Au?erdem ist das Design stilvoll und einladend, was jede Session spannender macht. Ein starkes Plus ist das VIP-Programm mit exklusiven Stufen, kontinuierliche Belohnungen bieten.
Loslegen|
Galera, resolvi contar como foi no 4PlayBet Casino porque foi muito alem do que imaginei. A variedade de jogos e de cair o queixo: roletas animadas, todos bem otimizados ate no celular. O suporte foi atencioso, responderam em minutos pelo chat, algo que faz diferenca. Fiz saque em PIX e o dinheiro entrou em minutos, ponto fortissimo. Se tivesse que criticar, diria que mais brindes fariam falta, mas isso nao estraga a experiencia. Pra concluir, o 4PlayBet Casino e parada obrigatoria pra quem gosta de cassino. Eu ja voltei varias vezes.
como fazer para imprimir pelo celular motog 4play|
Ich bin beeindruckt von Cat Spins Casino, es bietet packende Unterhaltung. Es gibt eine Fulle an aufregenden Titeln, mit packenden Live-Casino-Optionen. Mit blitzschnellen Einzahlungen. Der Service ist von hochster Qualitat. Gewinne werden ohne Wartezeit uberwiesen, dennoch zusatzliche Freispiele waren ein Bonus. Insgesamt, Cat Spins Casino bietet ein einmaliges Erlebnis. Daruber hinaus die Benutzeroberflache ist klar und flussig, das Spielerlebnis steigert. Ein bemerkenswertes Feature ist das VIP-Programm mit tollen Privilegien, die die Gemeinschaft starken.
Hier fortfahren|
Ich bin abhangig von SpinBetter Casino, es fuhlt sich an wie ein Strudel aus Freude. Es gibt eine unglaubliche Auswahl an Spielen, mit Spielen, die fur Kryptos optimiert sind. Die Hilfe ist effizient und pro, verfugbar rund um die Uhr. Der Ablauf ist unkompliziert, trotzdem zusatzliche Freispiele waren ein Highlight. Zum Ende, SpinBetter Casino ist eine Plattform, die uberzeugt fur Adrenalin-Sucher ! Au?erdem das Design ist ansprechend und nutzerfreundlich, gibt den Anreiz, langer zu bleiben. Ein weiterer Vorteil die Sicherheit der Daten, die Flexibilitat bieten.
https://spinbettercasino.de/|
Je suis fascine par Ruby Slots Casino, c’est une plateforme qui pulse avec energie. La gamme est variee et attrayante, avec des machines a sous visuellement superbes. Il propulse votre jeu des le debut. Disponible a toute heure via chat ou email. Les gains sont transferes rapidement, occasionnellement des offres plus consequentes seraient parfaites. Pour finir, Ruby Slots Casino offre une aventure inoubliable. De surcroit le site est rapide et engageant, ajoute une vibe electrisante. A mettre en avant les options variees pour les paris sportifs, assure des transactions fiables.
Explorer maintenant|
Je suis fascine par Sugar Casino, ca invite a l’aventure. Le choix de jeux est tout simplement enorme, proposant des jeux de table sophistiques. Avec des depots rapides et faciles. Le service est disponible 24/7. Les paiements sont surs et fluides, malgre tout des bonus diversifies seraient un atout. Pour conclure, Sugar Casino est un choix parfait pour les joueurs. Notons aussi le site est rapide et engageant, booste le fun du jeu. Egalement top les tournois reguliers pour s’amuser, renforce le lien communautaire.
Essayer|
J’adore l’ambiance electrisante de Sugar Casino, on ressent une ambiance de fete. Les options sont aussi vastes qu’un horizon, comprenant des jeux compatibles avec les cryptos. 100% jusqu’a 500 € avec des free spins. Disponible 24/7 pour toute question. Les retraits sont lisses comme jamais, a l’occasion des bonus plus frequents seraient un hit. En bref, Sugar Casino vaut une exploration vibrante. Pour couronner le tout l’interface est lisse et agreable, ce qui rend chaque partie plus fun. Un bonus les evenements communautaires engageants, propose des avantages sur mesure.
Tout apprendre|
J’adore la vibe de Sugar Casino, ca transporte dans un monde d’excitation. Les titres proposes sont d’une richesse folle, avec des machines a sous aux themes varies. Il rend le debut de l’aventure palpitant. Le suivi est d’une fiabilite exemplaire. Les retraits sont fluides et rapides, malgre tout des bonus varies rendraient le tout plus fun. En fin de compte, Sugar Casino est un endroit qui electrise. Notons aussi le design est style et moderne, facilite une immersion totale. A signaler les tournois frequents pour l’adrenaline, propose des avantages sur mesure.
Plonger dedans|
Logging into Pin Up Casino is just the first step to the adventure https://mbou40.ru
https://www.meetyourmarkets.com/1xbet-promo-code-today-india-free
mostbet.com вход mostbet12033.ru
http://www.travelnews24.ru/88801-dublikat-ukrainskix-nomerov
потолочкин натяжные потолки нижний новгород отзывы http://www.natyazhnye-potolki-nizhniy-novgorod-1.ru .
интернет агентство digital интернет агентство digital .
Hi there to every one, it’s truly a good for me to pay a quick visit this site, it consists of important Information.
https://www.thepropelinitiative.org/melbet-2025-apkmelbet-obzor-bk/
1xbet t?rkiye giri? 1xbet t?rkiye giri? .
Ich schatze die Spannung bei Cat Spins Casino, es schafft eine elektrisierende Atmosphare. Die Auswahl ist so gro? wie ein Casino-Floor, mit stilvollen Tischspielen. Der Willkommensbonus ist ein Highlight. Der Service ist von hochster Qualitat. Auszahlungen sind schnell und reibungslos, von Zeit zu Zeit mehr Promo-Vielfalt ware toll. Zusammenfassend, Cat Spins Casino sorgt fur ununterbrochenen Spa?. Nebenbei die Navigation ist klar und flussig, das Vergnugen maximiert. Ein Hauptvorteil ist das VIP-Programm mit exklusiven Stufen, die die Community enger zusammenschwei?en.
Mehr entdecken|
Pin Up is a great bookmaker ! I’ve been playing for a long time and am always happy https://mbou40.ru
The Gods of Gold slot machine at Pin Up Casino also works https://mbou40.ru
https://shorturl.fm/fUyDv
https://shorturl.fm/BQObf
mostbet kz скачать mostbet kz скачать
Ich bin suchtig nach Cat Spins Casino, es bietet eine dynamische Erfahrung. Die Auswahl ist so gro? wie ein Casino-Floor, mit Live-Sportwetten. Der Willkommensbonus ist ein Highlight. Erreichbar rund um die Uhr. Die Zahlungen sind sicher und sofortig, gelegentlich gro?ere Boni waren ein Highlight. Im Gro?en und Ganzen, Cat Spins Casino garantiert langanhaltenden Spa?. Au?erdem die Plattform ist visuell ansprechend, einen Hauch von Eleganz hinzufugt. Ein klasse Bonus die lebendigen Community-Events, das die Motivation steigert.
Vertiefen|
Je trouve absolument fantastique 7BitCasino, ca ressemble a une energie de jeu irresistible. Le catalogue est incroyablement vaste, offrant des sessions de casino en direct immersives. Le support est ultra-reactif et professionnel, repondant en un clin d’?il. Les gains sont verses en un temps record, occasionnellement j’aimerais plus d’offres promotionnelles, comme des offres de cashback plus avantageuses. Globalement, 7BitCasino offre une experience de jeu securisee et equitable pour ceux qui aiment parier avec des cryptomonnaies ! Notons egalement que l’interface est fluide et retro, facilite chaque session de jeu.
resena 7bitcasino|
You made some excellent points here. Well done!
https://shorturl.fm/QWpKK
I love the clarity in your writing.
https://103news.com/english/374151472/
Ich bin fasziniert von Cat Spins Casino, es schafft eine elektrisierende Atmosphare. Die Spielesammlung ist uberwaltigend, mit spannenden Sportwetten-Angeboten. Der Willkommensbonus ist gro?zugig. Der Support ist professionell und schnell. Die Zahlungen sind sicher und zuverlassig, gelegentlich ein paar zusatzliche Freispiele waren klasse. Alles in allem, Cat Spins Casino ist ein Muss fur Spieler. Hinzu kommt die Seite ist zugig und ansprechend, das Spielerlebnis bereichert. Besonders erwahnenswert ist das VIP-Programm mit tollen Privilegien, die Community enger verbinden.
Tauchen Sie ein|
Hi colleagues, how is the whole thing, and what you wish for to say regarding this piece of writing, in my view its really awesome for me.
https://www.hamishedarmiyan.com/melbet-skachat-na-android-besplatno-2025/
http://www.google.com.br/url?q=https://astra-hotel.ch/articles/meilleur_code_promotionnel_pour_melbet_bonus.html
https://shorturl.fm/tYQ8n
https://www.haphong.edu.vn/post/l%E1%BB%8Bch-khai-gi%E1%BA%A3ng-ielts-th%C3%A1ng-8-%C6%B0u-%C4%91%C3%A3i-ng%E1%BA%ADp-tr%C3%A0n
The availability of natural light significantly impacts the quality https://telegra.ph/Archivio-Storico-Terremoti-per-Comune-in-Italia-11-02
https://kvadropack-kupit.ru
https://www.animaljobsdirect.com/employers/3861887-code-promo-linebet-crash
Je suis enthousiasme par Wild Robin Casino, c’est une plateforme qui pulse avec energie. Les jeux proposes sont d’une diversite folle, proposant des jeux de table sophistiques. Il donne un elan excitant. Le service est disponible 24/7. Les paiements sont securises et rapides, occasionnellement quelques tours gratuits supplementaires seraient cool. Globalement, Wild Robin Casino est une plateforme qui pulse. A noter la plateforme est visuellement electrisante, ajoute une touche de dynamisme. Egalement genial les nombreuses options de paris sportifs, assure des transactions fluides.
http://www.wildrobincasinofr.com|
J’ai une affection particuliere pour Frumzi Casino, ca invite a plonger dans le fun. Les options de jeu sont infinies, incluant des paris sportifs en direct. Le bonus initial est super. Les agents repondent avec rapidite. Le processus est simple et transparent, par contre plus de promos regulieres ajouteraient du peps. Globalement, Frumzi Casino est un immanquable pour les amateurs. En plus le design est moderne et attrayant, apporte une touche d’excitation. Particulierement interessant les nombreuses options de paris sportifs, offre des recompenses continues.
https://frumzicasinologinfr.com/|
Je suis bluffe par Wild Robin Casino, il propose une aventure palpitante. Les options de jeu sont infinies, comprenant des jeux crypto-friendly. 100% jusqu’a 500 € + tours gratuits. Le suivi est toujours au top. Les retraits sont simples et rapides, par moments des recompenses en plus seraient un bonus. En somme, Wild Robin Casino garantit un amusement continu. A mentionner le site est rapide et immersif, amplifie l’adrenaline du jeu. A mettre en avant les transactions en crypto fiables, qui dynamise l’engagement.
Visiter la plateforme|
Je suis completement seduit par Wild Robin Casino, ca donne une vibe electrisante. La selection est riche et diversifiee, avec des slots aux graphismes modernes. Il offre un demarrage en fanfare. Les agents sont rapides et pros. Les paiements sont surs et efficaces, mais encore des recompenses en plus seraient un bonus. En fin de compte, Wild Robin Casino vaut une visite excitante. Notons aussi l’interface est intuitive et fluide, apporte une touche d’excitation. Un bonus les options de paris sportifs variees, offre des bonus exclusifs.
Aller sur le site web|
J’ai une passion debordante pour Frumzi Casino, ca donne une vibe electrisante. Le choix de jeux est tout simplement enorme, incluant des paris sur des evenements sportifs. 100% jusqu’a 500 € avec des spins gratuits. Le service d’assistance est au point. Les retraits sont ultra-rapides, par moments des offres plus genereuses rendraient l’experience meilleure. En bref, Frumzi Casino merite un detour palpitant. A souligner la plateforme est visuellement dynamique, permet une plongee totale dans le jeu. Particulierement cool les transactions en crypto fiables, qui stimule l’engagement.
Lire les dГ©tails|
J’ai une passion debordante pour Cheri Casino, ca offre un plaisir vibrant. La selection est riche et diversifiee, comprenant des jeux crypto-friendly. Il propulse votre jeu des le debut. Disponible 24/7 par chat ou email. Les transactions sont d’une fiabilite absolue, parfois quelques tours gratuits supplementaires seraient cool. Au final, Cheri Casino assure un divertissement non-stop. En extra l’interface est intuitive et fluide, booste l’excitation du jeu. Un point cle les options de paris sportifs diversifiees, offre des recompenses continues.
Plonger dedans|
Je suis totalement conquis par Cheri Casino, ca pulse comme une soiree animee. Les options de jeu sont incroyablement variees, offrant des experiences de casino en direct. Il rend le debut de l’aventure palpitant. Le support est pro et accueillant. Les gains sont transferes rapidement, de temps a autre des bonus varies rendraient le tout plus fun. En somme, Cheri Casino offre une aventure inoubliable. Ajoutons aussi le design est moderne et energique, incite a rester plus longtemps. A noter les tournois reguliers pour la competition, qui booste la participation.
Aller sur le site web|
Je suis captive par Instant Casino, ca transporte dans un univers de plaisirs. La gamme est variee et attrayante, incluant des options de paris sportifs dynamiques. Il offre un coup de pouce allechant. Le suivi est toujours au top. Les transactions sont fiables et efficaces, toutefois plus de promotions frequentes boosteraient l’experience. En conclusion, Instant Casino offre une aventure memorable. A signaler le site est fluide et attractif, ce qui rend chaque session plus palpitante. Un point fort le programme VIP avec des avantages uniques, assure des transactions fiables.
Lire plus|
Je suis accro a Instant Casino, on y trouve une energie contagieuse. Les options de jeu sont incroyablement variees, comprenant des titres adaptes aux cryptomonnaies. 100% jusqu’a 500 € avec des free spins. Le suivi est d’une precision remarquable. Les gains arrivent en un eclair, bien que des recompenses supplementaires dynamiseraient le tout. En conclusion, Instant Casino garantit un plaisir constant. Ajoutons aussi l’interface est simple et engageante, ajoute une touche de dynamisme. A souligner les evenements communautaires dynamiques, propose des privileges personnalises.
Voir maintenant|
Kaş tours Turkey Jasmine W. – Mısır https://www.dewanconsultants.com/?p=7332
situs toto
What i don’t realize is if truth be told how you are now
not actually a lot more well-favored than you might be
right now. You are very intelligent. You understand therefore significantly on the subject of this
subject, produced me in my view imagine it from numerous various angles.
Its like women and men aren’t interested except it is one thing to do with Girl
gaga! Your individual stuffs great. All the time take care of it up!
Pin Up Casino offers excellent terms and bonuses, especially for beginners. You’ll find slots официальный сайт Pin Up
https://spark.ru/user/152056/blog/205608/kak-i-zachem-izgotavlivayut-dublikati-nomerov-na-avto
https://shorturl.fm/oioXy
согласование перепланировки в нежилом здании http://pereplanirovka-nezhilogo-pomeshcheniya16.ru/ .
согласовать перепланировку нежилого помещения https://www.pereplanirovka-nezhilogo-pomeshcheniya17.ru .
экскаватор погрузчик москва https://arenda-ekskavatora-pogruzchika-1.ru .
согласование перепланировок нежилых помещений pereplanirovka-nezhilogo-pomeshcheniya18.ru .
смартвэй официальный сайт смвэй sajt-smart-way.ru .
Je suis enthousiaste a propos de Wild Robin Casino, ca transporte dans un univers de plaisirs. On trouve une gamme de jeux eblouissante, proposant des jeux de casino traditionnels. Il propulse votre jeu des le debut. Le support est fiable et reactif. Le processus est fluide et intuitif, bien que quelques tours gratuits supplementaires seraient cool. Globalement, Wild Robin Casino offre une experience hors du commun. Par ailleurs le design est tendance et accrocheur, donne envie de continuer l’aventure. Un avantage les options de paris sportifs variees, renforce le lien communautaire.
Plonger dedans|
J’adore l’energie de Frumzi Casino, il cree un monde de sensations fortes. On trouve une profusion de jeux palpitants, incluant des paris sportifs pleins de vie. Il booste votre aventure des le depart. Le suivi est d’une fiabilite exemplaire. Les retraits sont simples et rapides, en revanche plus de promos regulieres dynamiseraient le jeu. En conclusion, Frumzi Casino offre une experience inoubliable. En complement le design est moderne et attrayant, ajoute une vibe electrisante. Egalement genial les options de paris sportifs variees, qui dynamise l’engagement.
Explorer le site web|
Je suis sous le charme de Wild Robin Casino, ca transporte dans un monde d’excitation. La bibliotheque de jeux est captivante, offrant des sessions live immersives. Il amplifie le plaisir des l’entree. Le suivi est impeccable. Le processus est simple et transparent, toutefois plus de promos regulieres dynamiseraient le jeu. Pour finir, Wild Robin Casino assure un divertissement non-stop. Notons aussi la plateforme est visuellement vibrante, ce qui rend chaque session plus excitante. Particulierement attrayant les options de paris sportifs variees, qui dynamise l’engagement.
Aller voir|
https://xbetcodeprom.blogspot.com/2025/11/1xbet-promo-code-2026-130-for-new.html
Je suis enthousiasme par Wild Robin Casino, on ressent une ambiance de fete. Le choix de jeux est tout simplement enorme, offrant des sessions live palpitantes. Il booste votre aventure des le depart. Le suivi est impeccable. Les paiements sont securises et rapides, de temps en temps des recompenses supplementaires seraient parfaites. Pour faire court, Wild Robin Casino vaut une exploration vibrante. En bonus la plateforme est visuellement vibrante, donne envie de continuer l’aventure. Un avantage les evenements communautaires engageants, offre des bonus constants.
VГ©rifier ceci|
Je suis fascine par Instant Casino, c’est une plateforme qui pulse avec energie. Les options de jeu sont incroyablement variees, proposant des jeux de casino traditionnels. Il offre un coup de pouce allechant. Le service d’assistance est au point. Les retraits sont fluides et rapides, quelquefois quelques tours gratuits en plus seraient geniaux. En somme, Instant Casino est un incontournable pour les joueurs. De surcroit la navigation est simple et intuitive, amplifie le plaisir de jouer. Egalement top les paiements en crypto rapides et surs, propose des avantages sur mesure.
Visiter le site|
J’ai une affection particuliere pour Cheri Casino, c’est une plateforme qui deborde de dynamisme. Les options sont aussi vastes qu’un horizon, comprenant des jeux compatibles avec les cryptos. Le bonus de depart est top. Les agents repondent avec efficacite. Les gains sont transferes rapidement, de temps en temps quelques tours gratuits supplementaires seraient cool. Pour conclure, Cheri Casino est un endroit qui electrise. A noter le site est rapide et immersif, facilite une experience immersive. Egalement excellent les evenements communautaires pleins d’energie, renforce la communaute.
Cliquer maintenant|
J’adore la vibe de Cheri Casino, ca offre une experience immersive. Il y a une abondance de jeux excitants, incluant des options de paris sportifs dynamiques. Le bonus initial est super. Le service client est excellent. Le processus est simple et transparent, mais encore des bonus varies rendraient le tout plus fun. Pour faire court, Cheri Casino est une plateforme qui fait vibrer. En bonus la navigation est fluide et facile, permet une immersion complete. A noter les paiements securises en crypto, renforce le lien communautaire.
Commencer ici|
Je suis totalement conquis par Cheri Casino, on y trouve une vibe envoutante. La bibliotheque de jeux est captivante, proposant des jeux de casino traditionnels. Le bonus de bienvenue est genereux. Le support client est irreprochable. Les transactions sont toujours securisees, neanmoins quelques tours gratuits supplementaires seraient cool. En resume, Cheri Casino est un endroit qui electrise. Pour completer la plateforme est visuellement captivante, incite a rester plus longtemps. Un element fort les paiements securises en crypto, propose des privileges personnalises.
Entrer|
Je suis accro a Frumzi Casino, ca donne une vibe electrisante. La bibliotheque est pleine de surprises, proposant des jeux de table sophistiques. Il donne un elan excitant. Les agents sont rapides et pros. Les paiements sont surs et efficaces, par contre des recompenses additionnelles seraient ideales. Globalement, Frumzi Casino est un lieu de fun absolu. Ajoutons aussi l’interface est fluide comme une soiree, apporte une touche d’excitation. Egalement genial les options de paris sportifs variees, offre des recompenses regulieres.
Plongez-y|
Je suis fascine par Instant Casino, ca offre une experience immersive. La bibliotheque est pleine de surprises, avec des machines a sous visuellement superbes. Le bonus initial est super. Le service client est de qualite. Les transactions sont fiables et efficaces, en revanche plus de promos regulieres dynamiseraient le jeu. Pour finir, Instant Casino garantit un plaisir constant. Par ailleurs la plateforme est visuellement vibrante, donne envie de continuer l’aventure. Un atout les options variees pour les paris sportifs, propose des avantages uniques.
Consulter les dГ©tails|
Pin-Up is an international gambling platform offering slots, live games, promotions, and tournaments. Services играть в Пин Ап казино
Keep on writing, great job!
топ 10 казино
https://shorturl.fm/fnDjs
Free spins in Pin-Up are reel spins that guarantee you a win. Plus, you can win even more казино Pin Up
https://shorturl.fm/ousDj
https://www.highbarfitness.com/profile/herewon21425739/profile
Watch online videos from Pin Up Casino official website играть в Пин Ап казино
https://shorturl.fm/Kef9R
https://shorturl.fm/0dqs9
Gates Of Olympus gra na prawdziwe pieniądze zdecydowanie wyróżnia się na tle konkurencji. Kilka unikalnych nowinek i jackpot pozwalają na świetną zabawę przez długie godziny. Pogodny, lecz równocześnie motywujący soundtrack dodaje całej scenerii kolorytu i jeszcze bardziej pozwala nam wczuć się w klimat starożytnej Grecji. Brakuje tutaj jedynie opcji Gamble, jednak i tak znajdziemy tutaj mnóstwo innych opcji. Dobra, słuchajcie, miłośnicy slotów! Gates of Olympus to niesamowita przygoda prosto z starożytnej Grecji. Gotowi stawić czoła samemu Zeusowi? Oto jak grać: Masz ochotę na coś słodkiego? Zajrzyj więc do Energy Casino i spróbuj gry na cukierkowym slocie Sweet Feast! Słodka kraina czarów już na Ciebie czeka. Bonusy i darmowe spiny w grze Gates of Olympus to klucz do niesamowitych wygranych i ekscytujących emocji. Gracze, którzy wybiorą ten ulubiony slot w kasynie Vulkan Vegas mogą cieszyć się różnorodnymi bonusami, które zwiększają ich szanse na sukces.
https://gadgetguides.org/jak-skutecznie-wyplacic-srodki-z-aplikacji-casinia-poradnik-dla-polskich-graczy/
Proces oceny i wyboru kasyn do współpracy jest niezwykle rygorystyczny. Bierzemy pod uwagę wiele czynników, takich jak: licencja i nadzór, różnorodność gier i dostawców, metody płatności, programy lojalnościowe i bonusy, obsługa klienta oraz bezpieczeństwo i uczciwa gra. Profesjonalizm. Doświadczenie. Niezawodność. Wiele interaktywnych gier dostępnych jest w wersjach demonstracyjnych, co pozwala na darmowe testowanie i nabieranie doświadczenia bez ryzyka. Planowana jest także dedykowana aplikacja mobilna na Android i iOS. Nasza decyzja pozostanie ostateczna i nie możemy dostarczyć żadnych dalszych dowodów na prośbę Juli, który koncentruje się na ekskluzywnych automatach do gier. Nie ma opłat za transakcje konsumenckie, które musisz wysłać. Graj w blackjacka za darmo na swoim telefonie z Androidem.
https://shorturl.fm/96GGP
Paris sportifs avec 1xbet rdc apk : pre-match & live, statistiques, cash-out, builder de paris. Bonus d’inscription, programme fidelite, appli mobile. Depots via M-Pesa/Airtel Money. Informez-vous sur la reglementation. 18+, jouez avec moderation.
J’adore l’ambiance electrisante de Wild Robin Casino, c’est une plateforme qui pulse avec energie. Les titres proposes sont d’une richesse folle, proposant des jeux de cartes elegants. Le bonus initial est super. Le support est fiable et reactif. Les paiements sont securises et instantanes, mais des offres plus importantes seraient super. En bref, Wild Robin Casino est une plateforme qui fait vibrer. A souligner le design est moderne et attrayant, donne envie de continuer l’aventure. Un point fort les options de paris sportifs variees, cree une communaute soudee.
https://wildrobincasinopromocodefr.com/|
Je suis epate par Frumzi Casino, il offre une experience dynamique. Il y a une abondance de jeux excitants, comprenant des jeux compatibles avec les cryptos. Il donne un elan excitant. Le support client est irreprochable. Les transactions sont fiables et efficaces, bien que quelques tours gratuits supplementaires seraient cool. En conclusion, Frumzi Casino est un immanquable pour les amateurs. Par ailleurs la navigation est claire et rapide, ajoute une vibe electrisante. Un atout les evenements communautaires engageants, renforce la communaute.
Passer à l’action|
J’ai un faible pour Frumzi Casino, on ressent une ambiance festive. Les options de jeu sont incroyablement variees, incluant des options de paris sportifs dynamiques. Il offre un coup de pouce allechant. Le support est rapide et professionnel. Les transactions sont fiables et efficaces, a l’occasion des offres plus importantes seraient super. En fin de compte, Frumzi Casino garantit un plaisir constant. En complement la navigation est intuitive et lisse, permet une plongee totale dans le jeu. Un avantage notable les evenements communautaires engageants, propose des avantages sur mesure.
VГ©rifier ceci|
Je suis accro a Instant Casino, il propose une aventure palpitante. On trouve une profusion de jeux palpitants, comprenant des titres adaptes aux cryptomonnaies. Le bonus d’inscription est attrayant. Les agents repondent avec efficacite. Les retraits sont ultra-rapides, en revanche des bonus plus varies seraient un plus. En resume, Instant Casino est une plateforme qui fait vibrer. En bonus la plateforme est visuellement captivante, amplifie l’adrenaline du jeu. Un element fort les tournois frequents pour l’adrenaline, assure des transactions fluides.
Avancer|
Je suis epate par Cheri Casino, c’est une plateforme qui pulse avec energie. Il y a une abondance de jeux excitants, comprenant des jeux compatibles avec les cryptos. Il rend le debut de l’aventure palpitant. Disponible a toute heure via chat ou email. Les transactions sont fiables et efficaces, cependant des bonus plus varies seraient un plus. Au final, Cheri Casino est un must pour les passionnes. En plus l’interface est fluide comme une soiree, amplifie le plaisir de jouer. A mettre en avant les evenements communautaires dynamiques, garantit des paiements securises.
AccГ©der maintenant|
Kasyno Vavada oferuje szeroką gamę najwyżej ocenianych gier slotowych, które z pewnością zadowolą wszystkich graczy, od początkujących po doświadczonych weteranów. Niezależnie od tego, czy wolisz progresywne jackpoty, ekscytujące funkcje bonusowe czy urzekające motywy, każdy znajdzie coś dla siebie. Dzięki popularnym tytułom, takim jak Book of Dead, Starburst i Mega Moolah, a także wielu innym ekscytującym opcjom, możesz spodziewać się najwyższej klasy wrażeń z gry z dużymi nagrodami w kasynie Vavada. Więc na co czekać? Zakręć bębnami i zobacz, dokąd zaprowadzi Cię szczęście! In at the edge of the forest Number of guests: 11 people Ta strona internetowa korzysta z plik\u00f3w cookie w celu realizacji us\u0142ug zgodnie z Polityk\u0105 Cookie. – Wycofać zgodę na otrzymywanie e-maili marketingingowych, spersonalizowanych usług lub polityki danych jako całości.
https://tekno.trade/2025/10/31/pelna-analiza-lemon-casino-wyplaty-limity-i-szybkosc-realizacji-transakcji/
Vox Casino Poland słynie w branży ze swoich bonusów i promocji. Trudno się temu dziwić, jako że kasyno regularnie dokłada wszelkich starań, aby jego oferta wyprzedzała konkurencję o przysłowiowy krok — albo i więcej. W ofercie bonusowej są wspaniałe bonusy powitalne, turnieje, premie od doładowania, darmowe spiny, Vox Casino program lojalnościowy, koło fortuny i wiele innych atrakcji, które znacząco poprawiają wrażenia z grania w tym kasynie. Mеtоdа рłаtnоśсі Kategorie gier obejmują przede wszystkim sloty, gry z jackpotami, klasyczne gry stołowe, a także dynamicznie rozwijającą się sekcję gier typu crash instant. Największe wrażenie robi jednak kasyno na żywo, które oferuje ponad 200 stołów z prawdziwymi krupierami. Gracze mogą spróbować swoich sił w popularnych tytułach, takich jak Speed Roulette, Blackjack VIP czy 32 Card.
Poznaj nowy, lepszy sposób sterowania Umieszczanie domków, jak również pozyskiwanie kolonistów oraz produkcja towarów mają swój cel. Każda karta zawiera imię boga oraz jego wymagania. Na zakończenie zabawy wszyscy gracze otrzymują punkty za spełnienie warunków określonych przez antyczne bóstwa. Dla przykładu rolnik powiązany z Minerwą zapewnia trzy punkty za każde miasto dostarczające zboże, w którym gracz wybudował placówkę. Mars z kolei dostarcza dwa punkty za każdego kolonistę: pieszego oraz statek. Przy dwóch kartach z imieniem Marsa i pięciu kolonistach suma otrzymanych punktów wynosi 20. Analogiczne kalkulacje wykonywane są dla Jupitera, Saturna, Merkurego oraz Westy, oczywiście zgodnie z kryteriami zawartymi na kartach. Jak miał na imię słynny pruski teoretyk wojskowy, który napisał swoje dzieło po zakończeniu wojen napoleońskich?
https://eddesignworks.com/2025/10/31/lemoncasino-kompleksowa-recenzja-z-perspektywy-polskiego-gracza/
Jak widzisz, oferta automatów to prawdziwa feeria stylów, unikalnych funkcji i realnych szans na pokaźne wygrane. Od ponadczasowych klasyków po innowacyjne mechaniki – każdy tytuł dostarczy Ci niezapomnianych wrażeń, a co najważniejsze, jest dostępny zarówno na Twoim komputerze, jak i na urządzeniach mobilnych. Gates Of Olympus Super Scatter Oczywiście każdego gracza interesuje pytanie, jak wygrać na slocie Gates of Olympus. Niemożliwe jest udzielenie jednoznacznej odpowiedzi na to pytanie, ponieważ sam automat działa w oparciu o generator liczb losowych. Dlatego nie ma sposobu, aby zagwarantować 100% wygranej, ale można zwiększyć swoje szanse na wygraną. Pierwszą rzeczą, którą należy zrobić, jest zapoznanie się z tabelą wypłat. W tej grze środki trafiają na konto gracza za pojawienie się następujących symboli:
Je suis completement seduit par Wild Robin Casino, ca invite a l’aventure. La selection est riche et diversifiee, proposant des jeux de casino traditionnels. Le bonus de bienvenue est genereux. Le service client est excellent. Les retraits sont simples et rapides, occasionnellement plus de promotions variees ajouteraient du fun. En somme, Wild Robin Casino merite une visite dynamique. Pour ajouter l’interface est lisse et agreable, ce qui rend chaque moment plus vibrant. Egalement top le programme VIP avec des niveaux exclusifs, assure des transactions fiables.
DГ©couvrir la page|
I absolutely love your blog and find many of your post’s to be just what I’m looking for.
Do you offer guest writers to write content to suit your needs?
I wouldn’t mind producing a post or elaborating
on a few of the subjects you write regarding here. Again, awesome weblog!
J’adore l’energie de Instant Casino, on y trouve une vibe envoutante. Le catalogue est un paradis pour les joueurs, avec des slots aux graphismes modernes. Avec des depots instantanes. Le suivi est d’une precision remarquable. Les gains sont transferes rapidement, en revanche plus de promos regulieres dynamiseraient le jeu. En somme, Instant Casino est un endroit qui electrise. En extra la navigation est intuitive et lisse, incite a prolonger le plaisir. Egalement top les options variees pour les paris sportifs, assure des transactions fiables.
Voir plus|
J’ai un veritable coup de c?ur pour Cheri Casino, c’est une plateforme qui pulse avec energie. Le catalogue est un paradis pour les joueurs, offrant des tables live interactives. Avec des depots instantanes. Les agents repondent avec rapidite. Les transactions sont toujours securisees, a l’occasion des offres plus genereuses rendraient l’experience meilleure. Dans l’ensemble, Cheri Casino est un incontournable pour les joueurs. Par ailleurs l’interface est lisse et agreable, amplifie le plaisir de jouer. Egalement excellent les evenements communautaires pleins d’energie, propose des avantages uniques.
AccГ©der maintenant|
J’ai une passion debordante pour Frumzi Casino, ca offre une experience immersive. Les options de jeu sont infinies, incluant des options de paris sportifs dynamiques. Avec des transactions rapides. Le support est efficace et amical. Les paiements sont securises et rapides, en revanche des offres plus genereuses rendraient l’experience meilleure. Pour conclure, Frumzi Casino est un immanquable pour les amateurs. A mentionner la plateforme est visuellement vibrante, booste l’excitation du jeu. Egalement top les transactions en crypto fiables, offre des recompenses regulieres.
https://frumzicasinopromofr.com/|
Je suis emerveille par Instant Casino, c’est une plateforme qui deborde de dynamisme. Le catalogue de titres est vaste, offrant des tables live interactives. 100% jusqu’a 500 € avec des spins gratuits. Les agents repondent avec rapidite. Les retraits sont ultra-rapides, de temps en temps des bonus diversifies seraient un atout. En fin de compte, Instant Casino merite un detour palpitant. En complement le design est moderne et attrayant, facilite une experience immersive. Particulierement interessant les options de paris sportifs variees, propose des privileges personnalises.
Avancer|
Plateforme parifoot rd congo : pronos fiables, comparateur de cotes multi-books, tendances du marche, cash-out, statistiques avancees. Depots via M-Pesa/Airtel Money, support francophone, retraits securises. Pariez avec moderation.
Онлайн казино Україна пропонують бонуси за реєстрацію. Офіційні ігрові автомати працюють лише в ліцензійних казино.
Легальні онлайн казино гарантують підтримку 24/7. Хочете офіційні автомати без «скручених» результатів? Перелік тут — офіційні ігрові автомати. Казино з українським інтерфейсом легко зрозуміти навіть новачкам.
Казино з українським інтерфейсом має зрозумілу навігацію. Онлайн казино України пропонують величезний вибір ігор. Казино онлайн Україна дає змогу грати без ризиків. Онлайн казино України пропонують акції та фріспіни щотижня. Кращі казино України пропонують високий RTP і чесну гру.
http://www.google.co.id/url?q=https://clubcoma.org/blog/1xbet_promo_code___welcome_bonus_1.html
uludag holiday 2024 William G. ★★☆☆☆ Souvenir shops stops felt pushy. Reduced tour time at actual sites. Minimize commercial breaks! https://keyclue.ae/budget-istanbul-tours-affordable-adventures-in-turkey/
So simple, yet so impactful. Well written!
This topic is usually confusing, but you made it simple to understand.
Bezoek het nummer 1 legale online casino en win grow Pin Up casino
Оформите онлайн-займ https://zaimy-57.ru без визита в офис: достаточно паспорта, проверка за минуты. Выдача на карту, кошелёк или счёт. Прозрачный договор, напоминания о платеже, безопасность данных, акции для новых клиентов. Сравните предложения и выберите выгодно.
услуги экскаватора в москве arenda-ekskavatora-pogruzchika-2.ru .
Обновлено сегодня: https://fotoredaktor.top
1xbet resmi sitesi http://www.1xbet-giris-9.com/ .
студия для самостоятельной записи студия для самостоятельной записи .
International vip escorts in Paris agency is a unique combination of a concierge service in the sphere of personal relationships, leisure, acquaintances and scouting for modeling and dating.
Finding a stunning, sophisticated and hypnotically charming russian escort Dubai that will satisfy all of your sensual impulses has never been this simple.
Pin Up Casino is a licensed gaming establishment that upholds this reputation, therefore, all gamblers играть в Пин Ап казино that will satisfy all of your sensual impulses has never been this simple.
The official Azino 777 website offers, first and foremost, the opportunity to play your favorite games https://bimmer71.ru
mostbet.com https://www.mostbet12035.ru
Lorsqu’il s’agit de logiciels frauduleux tentant de tromper les utilisateurs, on peut remettre en question l’authenticité de Vortex Momentum. Cependant, notre logiciel est méticuleusement conçu par une équipe d’économistes, de mathématiciens et de développeurs estimés. Grâce à des recherches approfondies, Vortex Momentum utilise des stratégies de trading avancées et des protocoles de gestion des risques robustes, offrant aux investisseurs des bénéfices quotidiens constants. Les données suivantes peuvent être utilisées pour vous suivre dans plusieurs apps et sites web appartenant à d’autres sociétés : L’indicateur Vortex est basé sur le principe selon lequel la direction du mouvement des prix est liée à la force relative des mouvements de prix positifs et négatifs. La ligne +DI mesure la force de la tendance haussière, tandis que la ligne -DI mesure la force de la tendance baissière. Les deux lignes sont ensuite combinées pour créer la ligne Vortex Indicator. Lorsque la ligne de l’indicateur Vortex passe au-dessus de la ligne médiane, c’est un signal haussier, et lorsqu’elle passe en dessous de la ligne médiane, c’est un signal baissier.
https://terrasantanoticias.com.br/2025/10/31/guide-complet-pour-bien-debuter-sur-le-casino-en-ligne-cashed/
Jouer gates of olympus en ligne cependant, conformément à l’article 50 du Décret-loi 3 de. Il est peut-être sorti depuis un certain temps maintenant, le fichier de compte doe correspondant 56a-b est ouvert et les points accumulés pendant le jeu du dispositif de jeu 34 sont attribués à ce fichier. Il reste encore plus de 40 événements, vous pouvez toujours activer une Super Mise pour doubler vos chances de tours gratuits. Souvent, la smartwatch Samsung Galaxy Gear a également accès à la première machine à sous mobile en ligne créée par Microgaming. Tous les 9 et 10 sont retirés des jeux et vous pouvez Doubler, mais avec une couche magnétique de mystère ajoutée avec le motif du crâne sur chaque symbole. Donc, vous devez effectuer un dépôt pour jouer aux jeux de Casino. Olympus Gate clusters gagnants et fonctionnalité avalanche je vous recommande vivement de rejoindre également Cherry Gold Casino, puis télécharger un nouveau jeu et commencer à jouer pour profiter de tas d’argent.
Azino777 is a licensed online casino, a leader among its peers across the RuNet . Playing at Azino777 https://deztep.ru
обзор казино
http://www.travelnews24.ru/88801-dublikat-ukrainskix-nomerov
Hi, always i used to check website posts here early in the break of day, for the reason that i enjoy to learn more and more.
кракен маркетплейс
Je suis enthousiasme par Wild Robin Casino, il cree un monde de sensations fortes. Les options de jeu sont incroyablement variees, comprenant des jeux optimises pour Bitcoin. Il donne un elan excitant. Le support est efficace et amical. Les paiements sont surs et fluides, par contre quelques tours gratuits supplementaires seraient cool. En conclusion, Wild Robin Casino est une plateforme qui pulse. En extra le design est moderne et energique, amplifie l’adrenaline du jeu. Egalement genial les paiements securises en crypto, cree une communaute soudee.
DГ©couvrir les offres|
J’adore l’energie de Frumzi Casino, il cree une experience captivante. Il y a un eventail de titres captivants, offrant des tables live interactives. Il amplifie le plaisir des l’entree. Le service est disponible 24/7. Les retraits sont simples et rapides, bien que des recompenses en plus seraient un bonus. Dans l’ensemble, Frumzi Casino est une plateforme qui fait vibrer. De plus l’interface est intuitive et fluide, apporte une touche d’excitation. Un atout les evenements communautaires pleins d’energie, offre des recompenses regulieres.
DГ©couvrir maintenant|
Je suis enthousiasme par Cheri Casino, ca donne une vibe electrisante. Les options de jeu sont infinies, comprenant des jeux compatibles avec les cryptos. Avec des transactions rapides. Le suivi est d’une precision remarquable. Les gains arrivent sans delai, a l’occasion quelques spins gratuits en plus seraient top. En conclusion, Cheri Casino merite une visite dynamique. Pour completer la plateforme est visuellement electrisante, ajoute une touche de dynamisme. Un atout le programme VIP avec des niveaux exclusifs, qui stimule l’engagement.
DГ©couvrir les faits|
J’ai une passion debordante pour Frumzi Casino, c’est une plateforme qui pulse avec energie. Le choix de jeux est tout simplement enorme, avec des slots aux graphismes modernes. Avec des depots instantanes. Disponible 24/7 pour toute question. Les paiements sont securises et instantanes, cependant des bonus plus frequents seraient un hit. Pour finir, Frumzi Casino offre une experience inoubliable. Ajoutons que le design est tendance et accrocheur, booste le fun du jeu. Un avantage le programme VIP avec des avantages uniques, qui stimule l’engagement.
En savoir plus|
J’adore le dynamisme de Instant Casino, il offre une experience dynamique. La selection est riche et diversifiee, avec des machines a sous aux themes varies. Avec des depots rapides et faciles. Le suivi est impeccable. Les gains sont transferes rapidement, mais des recompenses en plus seraient un bonus. En resume, Instant Casino offre une experience inoubliable. Par ailleurs la navigation est claire et rapide, donne envie de prolonger l’aventure. Particulierement attrayant les paiements en crypto rapides et surs, renforce la communaute.
Avancer|
J’adore la vibe de Wild Robin Casino, ca transporte dans un univers de plaisirs. Le catalogue est un tresor de divertissements, avec des machines a sous visuellement superbes. Avec des depots rapides et faciles. Disponible 24/7 pour toute question. Les paiements sont surs et fluides, parfois des recompenses en plus seraient un bonus. En bref, Wild Robin Casino vaut une exploration vibrante. Ajoutons aussi la navigation est simple et intuitive, ce qui rend chaque partie plus fun. Particulierement cool les evenements communautaires engageants, cree une communaute vibrante.
Tout apprendre|
Je suis totalement conquis par Instant Casino, il procure une sensation de frisson. Le catalogue est un tresor de divertissements, comprenant des titres adaptes aux cryptomonnaies. Le bonus de depart est top. Les agents repondent avec efficacite. Les retraits sont simples et rapides, mais encore quelques free spins en plus seraient bienvenus. En conclusion, Instant Casino merite un detour palpitant. D’ailleurs la plateforme est visuellement dynamique, ce qui rend chaque session plus excitante. Un plus le programme VIP avec des recompenses exclusives, propose des avantages uniques.
Visiter pour plus|
Je suis enthousiaste a propos de Instant Casino, on y trouve une vibe envoutante. Le catalogue est un paradis pour les joueurs, proposant des jeux de table classiques. Avec des depots rapides et faciles. Le support client est irreprochable. Les gains arrivent sans delai, toutefois des bonus plus frequents seraient un hit. En somme, Instant Casino est un must pour les passionnes. De surcroit la navigation est claire et rapide, permet une plongee totale dans le jeu. Particulierement interessant les options de paris sportifs variees, propose des privileges personnalises.
http://www.casinoinstantfr.com|
J’adore l’ambiance electrisante de Cheri Casino, ca offre un plaisir vibrant. Le catalogue de titres est vaste, comprenant des jeux crypto-friendly. 100% jusqu’a 500 € avec des free spins. Disponible 24/7 pour toute question. Les paiements sont securises et rapides, cependant quelques tours gratuits en plus seraient geniaux. En conclusion, Cheri Casino garantit un plaisir constant. Par ailleurs le design est moderne et attrayant, apporte une touche d’excitation. A noter le programme VIP avec des niveaux exclusifs, cree une communaute vibrante.
Aller sur le site|
Je suis totalement conquis par Frumzi Casino, ca invite a l’aventure. Il y a une abondance de jeux excitants, avec des slots aux graphismes modernes. Le bonus initial est super. Les agents sont rapides et pros. Le processus est clair et efficace, mais des bonus plus frequents seraient un hit. En fin de compte, Frumzi Casino offre une experience inoubliable. En complement le site est rapide et engageant, amplifie l’adrenaline du jeu. Particulierement attrayant les paiements securises en crypto, cree une communaute soudee.
Aller au site|
v4r0ix
https://shorturl.fm/4xQbA
https://www.dennisdemo.com/articles/melbet-%D0%BF%D1%80%D0%BE%D0%BC%D0%BE%D0%BA%D0%BE%D0%B4-%D0%BD%D0%B0-%D1%84%D1%80%D0%B8%D1%81%D0%BF%D0%B8%D0%BD%D1%8B that will satisfy all of your sensual impulses has never been this simple.
What a helpful and well-structured post. Thanks a lot!
I appreciate the real-life examples you added. They made it relatable.
аренда мебели корпоратив Корпоративная мебель для корпоративов. Элегантное решение и решение под ключ.
https://www.orkhonschool.edu.mn/single-post/2018/10/24/certification-award-ceremony?commentId=cf2dabf6-8582-4b37-8b5a-6dad45c49faf
мебель в аренду в москве Аренда мебели в городе на нужный период. Лояльные тарифы и простой заказ.
https://shorturl.fm/FNCXX
https://shorturl.fm/anDjw
https://nashforum.listbb.ru/viewtopic.php?f=2&t=41888
https://mebel-rental.ru Рабочие столы для мастер-классов. Эргономичные стулья напрокат.
A working Pinko Casino mirror is more than just a tool, it’s a lifeline in an ocean of restrictions Pinco casino
Check out a review of the official Pinco Casino website https://xn--31-dlchfb3bxd.xn--p1ai
Senator Elizabeth Warren will remain one of the most important voices in American politics https://plisio.net/th/blog/cold-wallet-crypto
http://www.mebel-rental.ru Аренда качелей садовых для garden party. Подвесные диваны в аренду.
Great article! I’ll definitely come back for more posts like this.
I love how well-organized and detailed this post is.
You’ve sparked my interest in this topic.
https://www.mebel-rental.ru Аренда обогревателей с мебелью для холодного времени. Газовые обогреватели организуем.
https://bonbone.ru/catalogue/sms/673394
Search For More… We are constantly showing banners about important news regarding events and product launches. Please turn AdBlock off in order to see these areas. Please enable Strictly Necessary Cookies first so that we can save your preferences! Gates of Olympus is a synthesis of exciting themes, impressive graphics, and innovative technologies. This game transports its participants to an exciting journey through the world of ancient Greek mythology, where they interact with the gods of Olympus and explore their magnificent kingdom. Each element, from symbols to background images and animation effects, is created with high precision and attention to detail. Vivid and bright colors, majestic decorations, and the creation of an atmospheric feel enhance the user’s visual perception. Top-performing Prosperity Link™ MLP add extra thrills to your floor with exciting new titles.
https://ulimwengufabricators.com/buffalo-king-megaways-review-roaming-the-reels-in-the-uk/
To learn how to add music to a video on an iPhone, all you need to do is download PowerDirector and upload the video you want to overlay with music. Next, you’ll tap on Audio and either select Music or opt to use another audio editing tool built into the app. ✅ Personalize your soundtrack: Have a specific song in mind? SubMagic lets you add your own music to videos in iphone, offering a personalized touch that sets your content apart. Whether it’s a copyrighted tune you have the rights to use or a unique piece you’ve created, adding it to your video is just a click away. Describe your idea, and let your Agent handle everything — from storyboarding to video editing. No, but you can use our all-in-one editor to add several audio tracks such as background music, voiceovers, and sound effects and control the volume of each track separately.
CapCut is a freemium app developed by Bytedance. Similar to other apps like iMyFone Filme and Filme Lite, this was created to accompany the simple video-editing capabilities of TikTok, a social networking mobile app where users create, watch, and share videos. That’s our complete walk-through VlogNow tutorial. We covered everything you need to know to create professional videos and speed up your video editing process using VN Video Editor. Uptodown is a multi-platform app store specialized in Android. Our goal is to provide free and open access to a large catalog of apps without restrictions, while providing a legal distribution platform accessible from any browser, and also through its official native app. VN Video Editor is a powerful yet easy-to-use tool for anyone looking to create professional videos on a budget. Whether you’re a beginner or an experienced editor, VN offers all the features you need — from trimming clips to adding keyframe animations and green screen effects.
https://promptm.com/2025/10/24/buffalo-king-megaways-review-a-wild-ride-for-uk-players/
Aug 17, 2025Version 8.7.20Added AI Video Beauty: Switch between Natural, Young, Delicate, Glamour and more — one tap for flawless refinement!Added D3D Camera to Live2D: Make the whole image more vivid!Added Video Drafts: Automatically saved to prevent loss!Added INS Pet Ⅳ, Light to Effect. Make photos more atmospheric. David is a Los Angeles-based video creator, educator, and marketer. He has 12 years of experience in the creative and tech space. He attended the prestigious American Film Institute in Hollywood and has directed numerous award-winning films and series, including the Primetime Emmy-winning new media series, Acting Dead. He’s lectured on video creation and post-production in universities around the world. He has helped improve and grow numerous tech companies’ marketing and video strategies. Now, he’s sharing his years of experience and knowledge with you.
производство верхней одежды санкт петербург https://arbuztech.ru .
пошив пижам на заказ http://www.miniatelie.ru/ .
Hi! propecia online pharmacy great internet site.
https://shorturl.fm/fWTAn
J’adore l’energie de Viggoslots Casino, on ressent une ambiance festive. Les options de jeu sont incroyablement variees, incluant des paris sportifs en direct. 100% jusqu’a 500 € plus des tours gratuits. Le support est efficace et amical. Les paiements sont securises et instantanes, neanmoins des offres plus importantes seraient super. Au final, Viggoslots Casino offre une experience hors du commun. En bonus le site est fluide et attractif, ajoute une vibe electrisante. Particulierement fun les tournois frequents pour l’adrenaline, offre des bonus constants.
Viggoslots|
J’adore l’energie de Betzino Casino, on ressent une ambiance de fete. La bibliotheque de jeux est captivante, proposant des jeux de casino traditionnels. Il booste votre aventure des le depart. Les agents repondent avec efficacite. Les transactions sont toujours securisees, par moments quelques free spins en plus seraient bienvenus. Pour finir, Betzino Casino est un choix parfait pour les joueurs. En plus l’interface est lisse et agreable, permet une immersion complete. Egalement excellent les transactions en crypto fiables, offre des recompenses regulieres.
http://www.casinobetzinofr.com|
Je suis bluffe par Betzino Casino, ca invite a l’aventure. Le catalogue de titres est vaste, avec des machines a sous aux themes varies. 100% jusqu’a 500 € avec des free spins. Les agents repondent avec rapidite. Le processus est simple et transparent, parfois des recompenses en plus seraient un bonus. En resume, Betzino Casino offre une aventure inoubliable. De surcroit le design est tendance et accrocheur, incite a rester plus longtemps. Un point fort le programme VIP avec des avantages uniques, renforce la communaute.
Betzino|
J’adore l’energie de Betzino Casino, on ressent une ambiance de fete. La bibliotheque de jeux est captivante, offrant des experiences de casino en direct. Avec des depots instantanes. Les agents sont rapides et pros. Les transactions sont fiables et efficaces, mais plus de promos regulieres ajouteraient du peps. En fin de compte, Betzino Casino merite une visite dynamique. En complement la plateforme est visuellement vibrante, facilite une experience immersive. Particulierement cool les evenements communautaires engageants, propose des avantages uniques.
Visiter maintenant|
Je suis bluffe par Viggoslots Casino, on ressent une ambiance de fete. Les options de jeu sont incroyablement variees, offrant des tables live interactives. Il offre un coup de pouce allechant. Le suivi est d’une fiabilite exemplaire. Les transactions sont d’une fiabilite absolue, mais encore des recompenses additionnelles seraient ideales. Globalement, Viggoslots Casino assure un fun constant. Notons egalement le site est rapide et engageant, booste le fun du jeu. Un plus les tournois frequents pour l’adrenaline, offre des bonus exclusifs.
Apprendre les dГ©tails|
Je ne me lasse pas de Posido Casino, il cree une experience captivante. On trouve une profusion de jeux palpitants, avec des slots aux graphismes modernes. Il propulse votre jeu des le debut. Le suivi est d’une precision remarquable. Le processus est transparent et rapide, a l’occasion plus de promotions variees ajouteraient du fun. Globalement, Posido Casino garantit un plaisir constant. A mentionner la navigation est simple et intuitive, ajoute une touche de dynamisme. Particulierement attrayant les tournois reguliers pour la competition, offre des recompenses continues.
Lire la suite|
Je suis totalement conquis par Cheri Casino, il offre une experience dynamique. La bibliotheque est pleine de surprises, avec des slots aux graphismes modernes. Avec des depots fluides. Disponible 24/7 par chat ou email. Les retraits sont fluides et rapides, mais quelques tours gratuits supplementaires seraient cool. Dans l’ensemble, Cheri Casino est une plateforme qui pulse. Pour completer la navigation est intuitive et lisse, facilite une immersion totale. Particulierement interessant les evenements communautaires engageants, propose des privileges sur mesure.
Savoir plus|
J’ai une passion debordante pour Posido Casino, ca donne une vibe electrisante. On trouve une gamme de jeux eblouissante, proposant des jeux de casino traditionnels. Avec des depots fluides. Le suivi est d’une precision remarquable. Les gains sont verses sans attendre, rarement des bonus varies rendraient le tout plus fun. Pour finir, Posido Casino offre une aventure inoubliable. Ajoutons que la navigation est intuitive et lisse, apporte une touche d’excitation. A mettre en avant les tournois frequents pour l’adrenaline, propose des avantages uniques.
AccГ©der au site|
J’adore l’energie de Vbet Casino, ca invite a plonger dans le fun. Le catalogue est un paradis pour les joueurs, comprenant des jeux compatibles avec les cryptos. Avec des depots rapides et faciles. Le service est disponible 24/7. Les paiements sont securises et rapides, de temps en temps plus de promos regulieres ajouteraient du peps. Au final, Vbet Casino est une plateforme qui pulse. De plus le site est rapide et engageant, ce qui rend chaque partie plus fun. Un avantage notable les paiements en crypto rapides et surs, garantit des paiements rapides.
https://vbetcasinobonusfr.com/|
https://mebel-rental.ru VIP мебель для ночных клубов. Диваны для клубов в аренду.
Оформите займ https://zaimy-86.ru онлайн без визита в офис — быстро, безопасно и официально. Деньги на карту за несколько минут, круглосуточная обработка заявок, честные условия и поддержка клиентов 24/7.
https://shorturl.fm/mhYln
https://www.mebel-rental.ru Прокат артистической мебели для музыкантов. Служебная мебель в наличии.
This game is closely linked to Pragmatic Play’s Sweet Bonanza as the two games have similar gameplay. Both utilise the Tumble feature and have random multipliers with a wide range of potential values. Both offer players an ante bet setting which, when activated, doubles the chance of landing free spins. You’ll find plenty of streamers and player forums comparing the two games and trying to figure out which one is best! The game has a max win of 5,000x and is a high volatility game. More on this later. Looking for bonus codes for Gates of Olympus? This is the place for you – CasinoBonusCo has special bonus codes for this slot game by Pragmatic Play, which takes you to the ancient Greek setting of the gods. This news content may be integrated into any legitimate news gathering and publishing effort. Linking is permitted.
https://riwayat.ca/408/buffalo-king-megaways-a-uk-players-casino-game-review/
You are able to find and try out, Yggdrasil will continue to prosper over the next few quarters which might reflect in the upcoming 2023 B2B and International Gaming Awards. While checking the casino, gates of Olympus game casinos online and they have an event which they organize together or also with their neighbours. Gates of Olympus game android installation slots will be appreciated by high rollers and everyone who likes games with original mechanics, by registering and depositing for the first time. What is the RTP of Gates of Olympus?The game offers a 96.5% RTP, aligning with industry standards. Gates of Olympus is a Greek mythology-themed slot game developed by Pragmatic Play, one of the industry’s most respected names in slot machine game software. It’s no surprise that Gates of Olympus enjoys immense popularity, as it delivers the same high-quality gameplay that bettors have come to expect from Pragmatic Play’s other titles.
http://www.google.tn/url?q=https://aviator-game.su/
Russian and CIS technical industry standards, norms and regulations, specifications and technical publications both in Russian and English Russian standards
https://www.4shared.com/u/kIrQCQ3p/folmipirzi.html
Оформите займ https://zaimy-59.ru онлайн без визита в офис — быстро, безопасно и официально. Деньги на карту за несколько минут, круглосуточная обработка заявок, честные условия и поддержка клиентов 24/7.
https://1.kupitiblog.ru/10/forums/topic/aviator-igra-skachat-na-telefon/
бонусы без отыгрыша за регистрацию
Инвестируйте в будущее с профессионалами! ПИФы – это готовые решения для роста вашего капиталa https://tutvot.com
Die Vielfalt der Slots und Casinos, die sie anbieten, ist wirklich beeindruckend und verwirrend zugleich. Während die meisten von ihnen Standardanzahlungen akzeptieren, bieten andere zu niedrige Einsätze an. Viele Spieler zweifeln an ihrem Wert. Daher benötigen sie einen Leitfaden, um zu lernen, wie sie Slots sicher auswählen und welche Strategien sie anwenden sollten. With all of these slots to choose from, it can be hard to find the best Stake slots for your playing style. These are the things to bear in mind when making your choice: Effektives Finanzmanagement ist der Schlüssel zu langfristigem Erfolg in allen Bereichen, die mit finanziellen Risiken verbunden sind. Schwankungen und Verlustperioden sind unvermeidlich; eine solide Strategie schützt vor dem Ruin und ermöglicht es, das Potenzial für Gewinne langfristig zu nutzen. Das gilt natürlich auch für den Glücksspiel-Sektor.
https://empunion.iugaza.edu.ps/2025/10/frumzi-im-check-ein-ausfuhrlicher-blick-auf-den-deutschen-online-casino-favoriten/
Witchcraft Academy demonstriert uns die Leistungsfähigkeit des Designteams von NetEnt. Es ist ein Spielautomat für PC und mobile Geräte mit wirklich tollen Grafiken und Animationen, die in einen einfach zu spielenden Spielautomaten gepackt wurden. Das Ziel des Spiels ist es, die Tür zum Bonusverlies zu öffnen, wo Sie das Schicksal Ihrer Bonusrunde in die Hände eines jungen Zauberers oder einer Hexe legen müssen, um Wild-Walzen, Sticky WIlds und Multiplikatoren in Ihr Freispiel zu bringen. casin online6 5Carnival Cashhabanero€62,Dieser Slot ist eindeutig dem italienischen Nationalgericht Pizza gewidmet.Die Auszahlungsrate des Fancy Fruits Double Rush Slots liegt bei 96,um weitere Details zum jeweiligen Bonus zu erhalten.roulette online puntata minima 10 centesimiMark Seibert”,verantwortungsbewusst verhalten.Kein Wunder also,fishin frenzy game provider
You always deliver high-quality information. Thanks again!
скрытый алкоголизм http://www.narkologicheskaya-klinika-23.ru/ .
Great points, well supported by facts and logic.
анонимный наркологический центр анонимный наркологический центр .
1xbet giri? 2025 1xbet giri? 2025 .
экстренное вытрезвление в москве http://narkologicheskaya-klinika-27.ru .
литокол гидроизоляция цена https://gidroizolyaciya-cena-7.ru .
II.II Foreskin Duo Ich möchte diesen grässlichen Kampf nur erwähnen, weil FromSoft die Gruppenkämpfe angepasst hat. Ähnlich wie die Dämonen in Dark Souls 3 wechseln nun auch die Doppelbosse in ER zwischen einem aggressiven und einem passiven Part. Ist ein Gegner offensiver, hält sich der andere eher zurück. Das macht die Kämpfe dynamischer und verhindert, dass dich die RNG in ausweglose Situationen manövriert. Zwar landet der Spieler immer mal wieder in einer Attacke, weil sich beide Bosse zu perfekt abgestimmt haben, aber die teils unfaire parallele AI zu Release-Zeiten ist definitiv verschwunden. Preiset Marika. Brettspiel-Tipps Spiele-Tipps: Kind, Familie & Freunde Welches Bauwerk ist höher: das Wembley-Stadion oder die Cheopspyramide? Was ist schwerer: eine Ein-Euro-Münze oder ein Teelöffel Salz? In „Schätz it if you can“ sortieren die Ratenden nach und nach neun Antworten in eine Reihenfolge. Wer am Zug ist, darf die Einschätzung des vorigen Spielers anzweifeln.
https://metscco.saudi360inc.com/2025/10/22/wazamba-casino-im-test-erfahrungen-und-einblicke-fur-deutsche-spieler/
Aber erstmal zu den Fakten: Die Spielbank ist u. a. im Besitz der deutschen Glücksspiellizenz. Im Verlauf unseres bwin Tests klären wir: Ist die Spielo bwin seriös oder ist bwin Betrug? Zum Schluss kommen wir zu einem Fazit unserer bwin Erfahrungen. Viel Freude mit den einzelnen Abschnitten! Wir haben das Spiel nicht nur getestet, um dir zu berichten, was dich für spannende neue Features erwarten, sondern dir nachfolgend eine Anleitung zusammengestellt. Wenn du die einzelnen Schritte berücksichtigst, dann kannst du sicherstellen, dass du problemlos im Browser spielen kannst. Nachdem es sich um Echtgeld handelt, mit dem du spielen möchtest, solltest du immer auf deine Sicherheit achten und nur bei seriösen Anbietern spielen, die du auf unserer Webseite findest. Danach kommen die Streamingdienste für Musik und Videos. Bei den Videos ist wohl Netflix die bekannsteste und beliebteste Plattform. Aber auch auf vielen anderen Streaming-Plattformen wie DAZN ist die Bezahlung per Handy möglich. Bei der Musik müssen wir allen voran natürlich Spotify nennen, wo man das Abo auch bequem per Handyrechnung bezahlen kann.
Entdecken Sie die besten Weinverkostungen in Wien auf weinverkostung nahe wien.
Die osterreichische Hauptstadt bietet eine einzigartige Mischung aus Tradition und Moderne.
Die Weinverkostungen in Wien sind perfekt fur Kenner und Neulinge. Zusatzlich gibt es oft kulinarische Begleitungen, die den Genuss erhohen.
#### **2. Die besten Orte fur Weinverkostungen**
In Wien gibt es zahlreiche Lokale und Weinguter, die Verkostungen anbieten. Das Weinmuseum im Stadtzentrum ist ein idealer Ausgangspunkt fur Weinliebhaber.
Einige Winzer veranstalten Fuhrungen durch ihre Kellereien. Dabei erfahren Besucher mehr uber die Herstellung der Weine.
#### **3. Wiener Weinsorten und ihre Besonderheiten**
Wiener Weine sind vor allem fur ihre Vielfalt bekannt. Rote Weine wie der Blaue Zweigelt gewinnen immer mehr an Beliebtheit.
Die Bodenbeschaffenheit und das Klima pragen den Geschmack. Die warmen Sommer sorgen fur vollmundige Aromen.
#### **4. Tipps fur eine gelungene Weinverkostung**
Eine gute Vorbereitung macht die Verkostung noch angenehmer. Ein neutraler Geschmack im Mund vor der Verkostung verbessert das Erlebnis.
Gruppenverkostungen bringen zusatzlichen Spa?. Viele Veranstalter bieten thematische Verkostungen an.
—
### **Spin-Template fur den Artikel**
#### **1. Einfuhrung in die Weinverkostung in Wien**
Dabei lernen Gaste die Besonderheiten der regionalen Rebsorten kennen.
#### **2. Die besten Orte fur Weinverkostungen**
In Wien gibt es zahlreiche Lokale und Weinguter, die Verkostungen anbieten.
#### **3. Wiener Weinsorten und ihre Besonderheiten**
Auch der fruchtige Grune Veltliner zahlt zu den bekanntesten Wei?weinen der Region.
#### **4. Tipps fur eine gelungene Weinverkostung**
Gemeinsames Diskutieren uber die Aromen fordert den Austausch.
https://easlist.golocaly.online/1xbet-free-bet-code-2026-1xsun200-e130/
https://livescores.biz/
https://shorturl.fm/xWQD1
J’adore la vibe de Betzino Casino, il propose une aventure palpitante. La gamme est variee et attrayante, avec des machines a sous visuellement superbes. Avec des depots rapides et faciles. Les agents repondent avec efficacite. Les retraits sont fluides et rapides, bien que des recompenses additionnelles seraient ideales. Au final, Betzino Casino est une plateforme qui pulse. A noter la plateforme est visuellement dynamique, donne envie de prolonger l’aventure. Particulierement attrayant le programme VIP avec des privileges speciaux, offre des bonus exclusifs.
Voir la page|
Je suis bluffe par Viggoslots Casino, on ressent une ambiance festive. Les jeux proposes sont d’une diversite folle, avec des machines a sous visuellement superbes. Le bonus de depart est top. Le suivi est impeccable. Les gains sont verses sans attendre, mais plus de promos regulieres ajouteraient du peps. En conclusion, Viggoslots Casino offre une experience hors du commun. En complement la navigation est fluide et facile, ce qui rend chaque session plus excitante. Un avantage les evenements communautaires engageants, offre des recompenses regulieres.
Visiter la page web|
Je suis sous le charme de Viggoslots Casino, on y trouve une energie contagieuse. La bibliotheque est pleine de surprises, offrant des sessions live immersives. 100% jusqu’a 500 € + tours gratuits. Disponible a toute heure via chat ou email. Le processus est clair et efficace, de temps a autre des offres plus importantes seraient super. Dans l’ensemble, Viggoslots Casino garantit un amusement continu. Par ailleurs le design est moderne et energique, apporte une energie supplementaire. A mettre en avant les transactions en crypto fiables, cree une communaute vibrante.
https://viggoslotscasino777fr.com/|
J’ai une passion debordante pour Betzino Casino, c’est une plateforme qui deborde de dynamisme. Le choix est aussi large qu’un festival, proposant des jeux de casino traditionnels. Le bonus d’inscription est attrayant. Le service est disponible 24/7. Les transactions sont toujours fiables, mais encore des recompenses en plus seraient un bonus. Au final, Betzino Casino est une plateforme qui pulse. Pour couronner le tout la navigation est intuitive et lisse, facilite une immersion totale. Un plus les tournois frequents pour l’adrenaline, garantit des paiements securises.
VГ©rifier ceci|
Je suis epate par Betzino Casino, il cree une experience captivante. La variete des jeux est epoustouflante, offrant des tables live interactives. Avec des depots instantanes. Le suivi est impeccable. Les transactions sont d’une fiabilite absolue, malgre tout plus de promos regulieres dynamiseraient le jeu. En conclusion, Betzino Casino offre une aventure inoubliable. En bonus la navigation est claire et rapide, donne envie de prolonger l’aventure. Particulierement fun les options variees pour les paris sportifs, assure des transactions fiables.
AccГ©der maintenant|
Je suis totalement conquis par Vbet Casino, il procure une sensation de frisson. La bibliotheque est pleine de surprises, offrant des experiences de casino en direct. Il propulse votre jeu des le debut. Le support est fiable et reactif. Les transactions sont fiables et efficaces, occasionnellement des recompenses en plus seraient un bonus. Pour conclure, Vbet Casino assure un divertissement non-stop. Pour ajouter le design est moderne et attrayant, ce qui rend chaque partie plus fun. A signaler les evenements communautaires dynamiques, garantit des paiements securises.
Aller voir|
Je suis enthousiasme par Posido Casino, il procure une sensation de frisson. La gamme est variee et attrayante, incluant des paris sur des evenements sportifs. Le bonus d’inscription est attrayant. Disponible 24/7 par chat ou email. Les gains sont transferes rapidement, mais des offres plus genereuses seraient top. En bref, Posido Casino merite un detour palpitant. En extra le site est rapide et immersif, amplifie l’adrenaline du jeu. Un point fort les paiements en crypto rapides et surs, propose des privileges sur mesure.
Essayer|
J’ai une passion debordante pour Vbet Casino, c’est une plateforme qui deborde de dynamisme. Les jeux proposes sont d’une diversite folle, avec des machines a sous aux themes varies. Le bonus de bienvenue est genereux. Les agents repondent avec efficacite. Les retraits sont ultra-rapides, occasionnellement des bonus varies rendraient le tout plus fun. Au final, Vbet Casino est un must pour les passionnes. A noter le site est rapide et immersif, ce qui rend chaque session plus palpitante. Particulierement interessant les evenements communautaires dynamiques, offre des bonus exclusifs.
DГ©couvrir le web|
Je suis enthousiaste a propos de Vbet Casino, il offre une experience dynamique. Les titres proposes sont d’une richesse folle, avec des machines a sous aux themes varies. 100% jusqu’a 500 € avec des spins gratuits. Le suivi est impeccable. Les retraits sont simples et rapides, neanmoins des recompenses en plus seraient un bonus. Au final, Vbet Casino vaut une exploration vibrante. En bonus la navigation est claire et rapide, booste l’excitation du jeu. A mettre en avant les paiements securises en crypto, assure des transactions fluides.
http://www.vbetcasinobonusfr.com|
Je suis sous le charme de Posido Casino, il offre une experience dynamique. On trouve une gamme de jeux eblouissante, comprenant des jeux crypto-friendly. Il donne un avantage immediat. Les agents repondent avec rapidite. Les transactions sont toujours fiables, quelquefois plus de promos regulieres dynamiseraient le jeu. Pour faire court, Posido Casino merite une visite dynamique. Ajoutons aussi la navigation est fluide et facile, facilite une experience immersive. A signaler les transactions crypto ultra-securisees, assure des transactions fluides.
Voir plus|
https://shorturl.fm/F89th
лучшие seo компании reiting-seo-kompanii.ru .
https://magazin-prestige.in.ua/
http://www.google.co.jp/url?q=https://vodazone.ru/image/pgs/index.php?1win-promokod.html
This game uses the Megaways betting mechanic, which offers up to 117,649 ways to win. The popular Dog House slot returns with a Megaways twist. Trusted Pragmatic Play casinos typically include the Dog House Megaways. Each reel of the game can have 2 to 7 symbols, which affects the number of win ways, creating up to 117,649 possible ways to win. The maximum win is an impressive 12,305x your stake, and the bet ranges between €20 and €100. Peergame Casino No Deposit Bonus 100 Free Spins There are three other VIP levels, you might think that these are the same bonuses as those found in bitcoin slots. The second half of free spins are added 24 hours after the deposit, Good Girl Bad Girl. The best part is that there are so many slot games online exclusive to online casinos, Bewitched. Realm of Poseidon to be a highly volatile slot, free spins bonuses and more – this gorgeous website is capable of serving it all to you in a flash-based environment that’s unfortunately not available via download or mobile.
http://lakshaa.com/sugar-rush-slot-review-pragmatic-play-for-canadian-players/
Basic Game Info The graph shows the distribution of the multiplier hit frequency. In other words, the probability of different win multipliers to drop. It allows you to estimate the most frequent multipliers in The Dog House Megaways, and how frequently they are awarded during Free Spins. This website is using a security service to protect itself from online attacks. The action you just performed triggered the security solution. There are several actions that could trigger this block including submitting a certain word or phrase, a SQL command or malformed data. COPYRIGHT © 2015 – 2025. All rights reserved to Pragmatic Play, a Veridian (Gibraltar) Limited investment. Any and all content included on this website or incorporated by reference is protected by international copyright laws. The graph shows the distribution of the multiplier hit frequency. In other words, the probability of different win multipliers to drop. It allows you to estimate the most frequent multipliers in The Dog House Megaways, and how frequently they are awarded during Free Spins.
http://www.autoradioservice.ru/stati/ukrali-nomera-kak-postupit.html
https://www.proizvoditeli-rossii.ru/transport/avtoaksessuary/21568-dublikaty-gos-nomerov-vip-dublikat
торкретирование москва http://torkretirovanie-1.ru/ .
ремонт подвального помещения ремонт подвального помещения .
наплавляемая гидроизоляция цена за м2 работа http://gidroizolyaciya-cena-8.ru .
наркологическое отделение наркологии narkologicheskaya-klinika-23.ru .
1xbet turkiye 1xbet turkiye .
платная наркологическая клиника платная наркологическая клиника .
горизонтальные жалюзи с электроприводом горизонтальные жалюзи с электроприводом .
наркологические клиники москвы наркологические клиники москвы .
карниз моторизованный elektrokarniz797.ru .
подвал дома ремонт https://gidroizolyaciya-cena-7.ru .
электрокарнизы цена электрокарнизы цена .
надежное казино Устали от ограничений? Мобильное казино – это ваш билет в мир развлечений без лишних хлопот. Благодаря современным технологиям, вы можете наслаждаться всеми преимуществами настоящего казино прямо со своего мобильного устройства. Быстрый доступ, интуитивно понятный интерфейс и возможность играть в любое удобное время – вот что делает мобильные казино такими популярными.
Попробуйте сами и убедитесь, насколько легко и увлекательно играть на ходу!
https://filesharingshop.com/news/keep2share-paypal-buy-keep2share-premium-from-reseller
ставки на спорт бишкек ставки на спорт бишкек
Very useful tips! I’m excited to implement them soon.
Posts like this are why I keep coming back. It’s rare to find content that’s simple, practical, and not full of fluff.
Je suis captive par Viggoslots Casino, ca transporte dans un monde d’excitation. La variete des jeux est epoustouflante, proposant des jeux de table classiques. Il offre un coup de pouce allechant. Les agents repondent avec efficacite. Les transactions sont d’une fiabilite absolue, par ailleurs quelques free spins en plus seraient bienvenus. En fin de compte, Viggoslots Casino offre une aventure inoubliable. D’ailleurs l’interface est lisse et agreable, ajoute une vibe electrisante. Particulierement interessant les tournois reguliers pour s’amuser, renforce la communaute.
Touchez ici|
J’adore l’energie de Viggoslots Casino, ca invite a l’aventure. La variete des jeux est epoustouflante, incluant des paris sportifs en direct. Avec des depots fluides. Le suivi est d’une fiabilite exemplaire. Les gains sont transferes rapidement, mais encore quelques tours gratuits supplementaires seraient cool. En fin de compte, Viggoslots Casino est un immanquable pour les amateurs. Par ailleurs la navigation est claire et rapide, booste le fun du jeu. Egalement genial le programme VIP avec des privileges speciaux, offre des recompenses regulieres.
Apprendre comment|
Je suis enthousiaste a propos de Betzino Casino, ca invite a plonger dans le fun. Le catalogue est un paradis pour les joueurs, offrant des experiences de casino en direct. 100% jusqu’a 500 € + tours gratuits. Le support client est irreprochable. Les gains sont verses sans attendre, a l’occasion des recompenses supplementaires seraient parfaites. En resume, Betzino Casino offre une aventure inoubliable. En extra le design est style et moderne, donne envie de prolonger l’aventure. Particulierement attrayant les options de paris sportifs diversifiees, offre des bonus constants.
http://www.betzinocasino365fr.com|
Je suis sous le charme de Viggoslots Casino, c’est une plateforme qui pulse avec energie. Les options de jeu sont incroyablement variees, proposant des jeux de table sophistiques. Le bonus de depart est top. Le support client est irreprochable. Les gains sont transferes rapidement, bien que plus de promotions variees ajouteraient du fun. En somme, Viggoslots Casino merite une visite dynamique. Notons egalement la plateforme est visuellement vibrante, ce qui rend chaque session plus palpitante. A mettre en avant les nombreuses options de paris sportifs, garantit des paiements rapides.
Parcourir le site|
J’ai une affection particuliere pour Betzino Casino, il procure une sensation de frisson. Les jeux proposes sont d’une diversite folle, offrant des sessions live palpitantes. 100% jusqu’a 500 € avec des spins gratuits. Le suivi est toujours au top. Les gains sont verses sans attendre, malgre tout quelques free spins en plus seraient bienvenus. En resume, Betzino Casino est un immanquable pour les amateurs. Ajoutons que le design est style et moderne, ajoute une touche de dynamisme. Particulierement attrayant les tournois reguliers pour s’amuser, propose des privileges personnalises.
Aller Г la page|
ремонт в подвале gidroizolyaciya-cena-8.ru .
https://shorturl.fm/zCJnZ
торкретирование стен торкретирование стен .
гидроизоляция подвала под ключ http://www.gidroizolyaciya-podvala-cena.ru .
Pinco giriş üçün link yeniləndi. Canlı oyunları izləmək və mərclər etmək üçün pinko casino istifadə et. Pinco az linkləri daim yenilənir.
Pinco oyunlarını dostlarla paylaş.
электрокарниз двухрядный https://elektrokarniz797.ru/ .
J’adore la vibe de Vbet Casino, on ressent une ambiance de fete. Il y a une abondance de jeux excitants, proposant des jeux de table classiques. 100% jusqu’a 500 € avec des free spins. Disponible a toute heure via chat ou email. Les gains arrivent en un eclair, neanmoins des bonus varies rendraient le tout plus fun. En bref, Vbet Casino merite un detour palpitant. Notons egalement la navigation est fluide et facile, incite a prolonger le plaisir. Un point cle les evenements communautaires vibrants, garantit des paiements securises.
Commencer Г lire|
Je suis emerveille par Posido Casino, ca transporte dans un univers de plaisirs. Les titres proposes sont d’une richesse folle, avec des slots aux designs captivants. Il donne un avantage immediat. Disponible 24/7 pour toute question. Les paiements sont securises et instantanes, par ailleurs quelques tours gratuits supplementaires seraient cool. Dans l’ensemble, Posido Casino est une plateforme qui fait vibrer. En bonus le site est rapide et engageant, booste le fun du jeu. Particulierement interessant les options de paris sportifs diversifiees, propose des privileges personnalises.
En savoir plus|
J’ai une passion debordante pour Vbet Casino, on ressent une ambiance festive. La variete des jeux est epoustouflante, avec des machines a sous aux themes varies. 100% jusqu’a 500 € plus des tours gratuits. Le support est fiable et reactif. Les retraits sont simples et rapides, parfois des recompenses en plus seraient un bonus. En bref, Vbet Casino merite un detour palpitant. Notons egalement l’interface est simple et engageante, booste l’excitation du jeu. Egalement excellent le programme VIP avec des avantages uniques, offre des recompenses regulieres.
Commencer Г explorer|
J’adore le dynamisme de Posido Casino, on ressent une ambiance festive. Les titres proposes sont d’une richesse folle, comprenant des titres adaptes aux cryptomonnaies. 100% jusqu’a 500 € plus des tours gratuits. Le suivi est d’une fiabilite exemplaire. Les retraits sont fluides et rapides, neanmoins des recompenses en plus seraient un bonus. Pour conclure, Posido Casino assure un fun constant. En extra le site est fluide et attractif, incite a rester plus longtemps. Egalement super les evenements communautaires engageants, offre des bonus constants.
Explorer le site|
Je suis enthousiaste a propos de Posido Casino, ca invite a l’aventure. La selection est riche et diversifiee, avec des machines a sous visuellement superbes. Il offre un demarrage en fanfare. Le service client est excellent. Les paiements sont securises et rapides, de temps en temps plus de promos regulieres dynamiseraient le jeu. Pour finir, Posido Casino est un choix parfait pour les joueurs. A souligner le site est rapide et engageant, incite a prolonger le plaisir. Un element fort les transactions en crypto fiables, assure des transactions fluides.
Plonger dedans|
электрокарнизы цена электрокарнизы цена .
наркологический частный центр http://narkologicheskaya-klinika-27.ru/ .
ремонт в подвале http://gidroizolyaciya-cena-7.ru/ .
центр наркологической помощи центр наркологической помощи .
анонимная наркология narkologicheskaya-klinika-23.ru .
1xbet t?rkiye giri? 1xbet t?rkiye giri? .
производство женской одежды санкт петербург http://www.arbuztech.ru .
пошив пижам оптом https://www.miniatelie.ru .
теннис букмекерская скачать http://www.mostbet12036.ru
наплавляемая гидроизоляция цена наплавляемая гидроизоляция цена .
карниз с приводом http://www.elektrokarniz797.ru .
электрокарниз купить в москве электрокарниз купить в москве .
гидроизоляция подвала снаружи цены http://www.gidroizolyaciya-podvala-cena.ru .
торкретирование бетона цена м2 https://torkretirovanie-1.ru/ .
https://shorturl.fm/j81T1
электрокранизы http://www.elektrokarniz-kupit.ru .
электрокарнизы в москве электрокарнизы в москве .
электрожалюзи на заказ http://elektricheskie-zhalyuzi97.ru/ .
https://shorturl.fm/6MIKg
https://www.johnkerryandsons.co.uk/index.php?route=journal3/blog/post&journal_blog_post_id=18
https://cgmood.com/strat-egies
Je suis accro a Betzino Casino, ca pulse comme une soiree animee. Le choix de jeux est tout simplement enorme, incluant des paris sportifs pleins de vie. 100% jusqu’a 500 € avec des spins gratuits. Le support est efficace et amical. Les gains arrivent en un eclair, mais encore des bonus varies rendraient le tout plus fun. En bref, Betzino Casino offre une experience inoubliable. A noter le site est rapide et immersif, ce qui rend chaque session plus palpitante. Un avantage notable les tournois reguliers pour s’amuser, propose des avantages sur mesure.
DГ©couvrir dГЁs maintenant|
карниз для штор электрический карниз для штор электрический .
益群网:终身分红,逆向推荐,不拉下线,也有钱赚!尖端资源,价值百万,一网打尽,瞬间拥有!多重收益,五五倍增,八级提成,后劲无穷!网址:1199.pw
жалюзи для пластиковых окон с электроприводом http://elektricheskie-zhalyuzi97.ru/ .
электрокарниз двухрядный цена http://www.elektrokarniz777.ru/ .
At Wellton Property, we offer access to a curated portfolio of North Cyprus https://www.hudsonvalleytraveler.com/Redirect?redirect_url=https://welltonproperty.com
J’adore le dynamisme de Viggoslots Casino, il cree un monde de sensations fortes. Les jeux proposes sont d’une diversite folle, comprenant des jeux crypto-friendly. Il booste votre aventure des le depart. Les agents sont toujours la pour aider. Les gains arrivent en un eclair, par ailleurs des offres plus consequentes seraient parfaites. En resume, Viggoslots Casino offre une aventure inoubliable. Par ailleurs le design est tendance et accrocheur, ce qui rend chaque session plus excitante. Un plus les options variees pour les paris sportifs, garantit des paiements securises.
DГ©couvrir les faits|
J’adore le dynamisme de Viggoslots Casino, on y trouve une energie contagieuse. On trouve une gamme de jeux eblouissante, offrant des sessions live palpitantes. Il amplifie le plaisir des l’entree. Disponible 24/7 par chat ou email. Le processus est clair et efficace, mais encore plus de promos regulieres dynamiseraient le jeu. Pour finir, Viggoslots Casino offre une aventure inoubliable. A noter la plateforme est visuellement electrisante, facilite une immersion totale. Egalement excellent les paiements en crypto rapides et surs, renforce le lien communautaire.
Continuer ici|
Je suis enthousiaste a propos de Viggoslots Casino, ca offre une experience immersive. La bibliotheque de jeux est captivante, avec des machines a sous visuellement superbes. Le bonus de bienvenue est genereux. Disponible 24/7 pour toute question. Les transactions sont d’une fiabilite absolue, parfois des recompenses supplementaires seraient parfaites. Pour conclure, Viggoslots Casino garantit un plaisir constant. Pour ajouter le site est fluide et attractif, booste le fun du jeu. A mettre en avant les options variees pour les paris sportifs, qui booste la participation.
Aller sur le web|
Je suis totalement conquis par Betzino Casino, ca pulse comme une soiree animee. La selection est riche et diversifiee, comprenant des jeux optimises pour Bitcoin. Le bonus de depart est top. Le suivi est impeccable. Les gains sont transferes rapidement, par contre quelques spins gratuits en plus seraient top. Globalement, Betzino Casino offre une experience hors du commun. De plus l’interface est lisse et agreable, permet une immersion complete. Un plus les evenements communautaires dynamiques, qui dynamise l’engagement.
Aller sur le web|
Your advice is exactly what I needed right now.
This was a great reminder for me. Thanks for posting.
Je suis accro a Vbet Casino, il offre une experience dynamique. On trouve une profusion de jeux palpitants, offrant des experiences de casino en direct. Avec des depots fluides. Le suivi est d’une fiabilite exemplaire. Les transactions sont toujours fiables, de temps a autre quelques spins gratuits en plus seraient top. En conclusion, Vbet Casino vaut une visite excitante. En bonus l’interface est intuitive et fluide, apporte une energie supplementaire. Particulierement cool les options variees pour les paris sportifs, qui motive les joueurs.
DГ©couvrir le web|
Je suis sous le charme de Vbet Casino, on ressent une ambiance de fete. Le catalogue est un paradis pour les joueurs, comprenant des jeux compatibles avec les cryptos. Avec des depots rapides et faciles. Le support est rapide et professionnel. Les gains arrivent sans delai, par contre des bonus plus varies seraient un plus. Pour faire court, Vbet Casino est un incontournable pour les joueurs. En plus le site est rapide et style, ajoute une touche de dynamisme. A mettre en avant les evenements communautaires engageants, qui stimule l’engagement.
Ouvrir le site|
promocore.click – Pages loaded fast, images appeared sharp, and formatting stayed consistent.
Je suis totalement conquis par Posido Casino, c’est une plateforme qui pulse avec energie. Il y a une abondance de jeux excitants, comprenant des titres adaptes aux cryptomonnaies. Avec des depots instantanes. Le support client est irreprochable. Les paiements sont surs et fluides, par contre plus de promos regulieres ajouteraient du peps. En conclusion, Posido Casino est un endroit qui electrise. A souligner le design est moderne et energique, apporte une energie supplementaire. Particulierement fun les transactions crypto ultra-securisees, offre des bonus constants.
Visiter en ligne|
Сайт dj-controllers.ru предоставляет подробные обзоры, профессиональные советы и актуальную информацию о DJ-контроллерах, помогая выбрать и использовать лучшее оборудование для микширования и выступлений https://dj-controllers.ru/
https://inkbunny.net/robertspoon
Je suis sous le charme de Posido Casino, on y trouve une energie contagieuse. Les options de jeu sont infinies, avec des machines a sous visuellement superbes. Il offre un coup de pouce allechant. Le service est disponible 24/7. Le processus est simple et transparent, quelquefois des offres plus genereuses seraient top. Dans l’ensemble, Posido Casino merite une visite dynamique. Pour couronner le tout la plateforme est visuellement captivante, amplifie le plaisir de jouer. Un avantage notable les options de paris sportifs diversifiees, offre des recompenses regulieres.
Ouvrir la page|
Je suis captive par Posido Casino, ca invite a plonger dans le fun. On trouve une gamme de jeux eblouissante, offrant des sessions live palpitantes. Avec des transactions rapides. Disponible 24/7 pour toute question. Les gains sont transferes rapidement, neanmoins quelques tours gratuits supplementaires seraient cool. En fin de compte, Posido Casino est un endroit qui electrise. A noter le design est moderne et attrayant, amplifie l’adrenaline du jeu. Un bonus les tournois reguliers pour s’amuser, assure des transactions fluides.
DГ©couvrir plus|
So simple, yet so impactful. Well written!
Posts like this are why I keep coming back. It’s rare to find content that’s simple, practical, and not full of fluff.
автоматические карнизы автоматические карнизы .
бамбуковые электрожалюзи elektricheskie-zhalyuzi97.ru .
электрокарниз двухрядный цена http://www.elektrokarniz777.ru/ .
Je suis enthousiasme par Betzino Casino, on ressent une ambiance festive. La selection de jeux est impressionnante, comprenant des jeux crypto-friendly. 100% jusqu’a 500 € + tours gratuits. Le suivi est toujours au top. Les retraits sont lisses comme jamais, par contre plus de promotions variees ajouteraient du fun. Au final, Betzino Casino merite un detour palpitant. A souligner la navigation est fluide et facile, booste le fun du jeu. Un avantage le programme VIP avec des avantages uniques, renforce la communaute.
http://www.betzinocasinobonusfr.com|
https://shorturl.fm/PhxCr
I always spent my half an hour to read this blog’s articles or reviews daily
along with a mug of coffee.
https://shorturl.fm/rIZl2
топ-10 казино с бонусами за регистрацию
https://shorturl.fm/Ob1rk
Je suis enthousiasme par Betway Casino, il propose une aventure palpitante. La selection de jeux est impressionnante, offrant des sessions live palpitantes. Avec des depots fluides. Le support est rapide et professionnel. Les gains sont verses sans attendre, par ailleurs quelques spins gratuits en plus seraient top. Au final, Betway Casino offre une experience hors du commun. A souligner la plateforme est visuellement vibrante, donne envie de continuer l’aventure. Un element fort les transactions en crypto fiables, qui motive les joueurs.
Commencer Г dГ©couvrir|
рулонные шторки на окна рулонные шторки на окна .
рулонные шторы в москве рулонные шторы в москве .
рольшторы на окна купить в москве rulonnye-shtory-s-elektroprivodom7.ru .
bahis siteler 1xbet bahis siteler 1xbet .
1xbet g?ncel http://www.1xbet-giris-2.com/ .
1xbet g?ncel 1xbet g?ncel .
поставка медоборудования medoborudovanie-postavka.ru .
1xbet com giri? https://www.1xbet-giris-4.com .
1xbet yeni adresi 1xbet yeni adresi .
медтехника medicinskaya-tehnika.ru .
студия для самостоятельной записи студия для самостоятельной записи .
онлайн трансляции заказать https://zakazat-onlayn-translyaciyu5.ru .
перепланировка нежилого здания pereplanirovka-nezhilogo-pomeshcheniya16.ru .
https://shorturl.fm/Nv6jj
перепланировка в нежилом помещении pereplanirovka-nezhilogo-pomeshcheniya16.ru .
поставка медицинского оборудования поставка медицинского оборудования .
рулонные шторки на окна рулонные шторки на окна .
1xbet guncel 1xbet guncel .
Je suis totalement conquis par Belgium Casino, ca invite a l’aventure. Le catalogue est un tresor de divertissements, offrant des experiences de casino en direct. Il donne un avantage immediat. Les agents repondent avec rapidite. Les gains arrivent sans delai, par ailleurs plus de promotions frequentes boosteraient l’experience. En bref, Belgium Casino offre une aventure inoubliable. En plus la plateforme est visuellement vibrante, booste l’excitation du jeu. Egalement super les evenements communautaires vibrants, garantit des paiements securises.
DГ©couvrir les offres|
J’adore l’ambiance electrisante de Belgium Casino, il cree une experience captivante. Les titres proposes sont d’une richesse folle, incluant des paris sportifs en direct. Avec des depots fluides. Le support est rapide et professionnel. Les retraits sont fluides et rapides, neanmoins des recompenses additionnelles seraient ideales. En conclusion, Belgium Casino est un lieu de fun absolu. Par ailleurs la navigation est intuitive et lisse, ce qui rend chaque moment plus vibrant. Particulierement cool les options variees pour les paris sportifs, propose des privileges sur mesure.
Explorer le site|
J’ai une affection particuliere pour Betway Casino, on ressent une ambiance de fete. Les jeux proposes sont d’une diversite folle, avec des machines a sous aux themes varies. Il amplifie le plaisir des l’entree. Disponible 24/7 pour toute question. Les gains sont verses sans attendre, occasionnellement des recompenses supplementaires seraient parfaites. Dans l’ensemble, Betway Casino est un endroit qui electrise. Par ailleurs la navigation est fluide et facile, amplifie l’adrenaline du jeu. Egalement genial les transactions crypto ultra-securisees, qui stimule l’engagement.
https://betwaycasino366fr.com/|
Je suis sous le charme de Betway Casino, ca donne une vibe electrisante. Les options de jeu sont infinies, comprenant des jeux compatibles avec les cryptos. Le bonus d’inscription est attrayant. Disponible a toute heure via chat ou email. Les retraits sont simples et rapides, neanmoins des bonus plus frequents seraient un hit. Dans l’ensemble, Betway Casino est un endroit qui electrise. De surcroit le site est fluide et attractif, ajoute une touche de dynamisme. A souligner les nombreuses options de paris sportifs, propose des privileges sur mesure.
DГ©couvrir|
1xbet resmi http://1xbet-15.com .
медтехника http://medicinskaya-tehnika.ru .
запись подкастов запись подкастов .
организация онлайн трансляций цена https://www.zakazat-onlayn-translyaciyu5.ru .
Je suis sous le charme de Gamdom Casino, ca offre une experience immersive. La bibliotheque est pleine de surprises, avec des machines a sous visuellement superbes. Il propulse votre jeu des le debut. Le support est fiable et reactif. Les paiements sont surs et fluides, cependant des recompenses additionnelles seraient ideales. En somme, Gamdom Casino assure un divertissement non-stop. En complement la plateforme est visuellement dynamique, apporte une energie supplementaire. Egalement excellent les tournois reguliers pour s’amuser, qui booste la participation.
https://gamdomcasino366fr.com/|
Howdy! online pharmacy propecia excellent website.
J’ai une affection particuliere pour Betify Casino, ca offre un plaisir vibrant. Il y a un eventail de titres captivants, comprenant des jeux crypto-friendly. Avec des depots instantanes. Disponible 24/7 par chat ou email. Les retraits sont simples et rapides, par moments quelques spins gratuits en plus seraient top. Pour finir, Betify Casino vaut une visite excitante. Notons aussi la plateforme est visuellement dynamique, ajoute une touche de dynamisme. Un avantage notable les evenements communautaires vibrants, propose des privileges personnalises.
Emmenez-moi lГ -bas|
J’adore l’ambiance electrisante de Gamdom Casino, il procure une sensation de frisson. La bibliotheque de jeux est captivante, comprenant des jeux compatibles avec les cryptos. Avec des depots rapides et faciles. Le support est efficace et amical. Les gains arrivent sans delai, mais encore des bonus plus varies seraient un plus. Pour finir, Gamdom Casino est un immanquable pour les amateurs. Notons aussi la navigation est fluide et facile, donne envie de continuer l’aventure. A souligner les nombreuses options de paris sportifs, offre des bonus exclusifs.
Plonger dedans|
https://shorturl.fm/HTTNF
рулонные шторы это avtomaticheskie-rulonnye-shtory1.ru .
рольшторы заказать rulonnye-shtory-s-elektroprivodom7.ru .
1x giri? http://www.1xbet-giris-2.com .
one x bet one x bet .
J’adore la vibe de Betify Casino, on ressent une ambiance festive. Il y a un eventail de titres captivants, avec des machines a sous visuellement superbes. Avec des depots rapides et faciles. Disponible 24/7 par chat ou email. Les transactions sont fiables et efficaces, de temps en temps des recompenses en plus seraient un bonus. Pour finir, Betify Casino est un endroit qui electrise. En plus la plateforme est visuellement captivante, ce qui rend chaque partie plus fun. A mettre en avant les options variees pour les paris sportifs, qui motive les joueurs.
Emmenez-moi lГ -bas|
1xbet com giri? 1xbet-giris-4.com .
Фриспины в казино Бездепозитные бонусы – это отличная возможность попробовать свои силы в онлайн-казино без риска для собственных средств. Однако, прежде чем активировать бонус, внимательно ознакомьтесь с его условиями, чтобы избежать разочарований в будущем. Удачи в игре!
согласование перепланировки нежилого помещения в жилом доме https://pereplanirovka-nezhilogo-pomeshcheniya16.ru .
поставка медицинского оборудования поставка медицинского оборудования .
1xbet guncel 1xbet guncel .
рулонные шторы на большие окна рулонные шторы на большие окна .
медтехника https://www.medicinskaya-tehnika.ru .
1xbet tr giri? http://www.1xbet-15.com .
https://shorturl.fm/OWKRM
аренда студии для записи подкаста studiya-podkastov-spb4.ru .
J’adore le dynamisme de Betway Casino, on y trouve une vibe envoutante. La selection de jeux est impressionnante, incluant des paris sportifs pleins de vie. Avec des depots instantanes. Le support est fiable et reactif. Les retraits sont simples et rapides, en revanche plus de promotions frequentes boosteraient l’experience. Dans l’ensemble, Betway Casino est un lieu de fun absolu. A mentionner le site est fluide et attractif, permet une plongee totale dans le jeu. Egalement super les competitions regulieres pour plus de fun, assure des transactions fiables.
Visiter aujourd’hui|
заказать трансляцию конференции https://www.zakazat-onlayn-translyaciyu5.ru .
birxbet birxbet .
рулонные шторы с направляющими купить http://www.avtomaticheskie-rulonnye-shtory1.ru .
1xbet yeni giri? http://www.1xbet-giris-2.com/ .
1x lite https://1xbet-giris-4.com .
Pinco casino bonusları mükəmməldir. Canlı yayımlar üçün rəsmi ünvan pinco casino. Pinco az linkləri daim yenilənir.
Pinco-da oyun çox rahatdır.
https://shorturl.fm/3tOof
Начните писать эссе с ИИ-помощником прямо сейчас. Сервис предложит план, примеры и формулировки, чтобы вы могли быстро создать качественный черновик лучшие ии для написания эссе
Современные нейросети стали мощным инструментом для подготовки учебных работ. Они анализируют тысячи источников, чтобы помочь вам написать хорошо структурированный и уникальный реферат как попросить чат gpt написать реферат
Such a refreshing take on a common topic.
I wasn’t sure what to expect at first, but this turned out to be surprisingly useful. Thanks for taking the time to put this together.
Создайте качественный реферат в разы быстрее. Нейросеть соберет и структурирует информацию из разных источников, вам останется лишь проверить и оформить работу нейросеть рефератов для студентов
Discover exquisite Austrian wines at schaumwein verkostung and immerse yourself in Vienna’s vibrant wine culture.
Wien begeistert mit seiner langen Weintradition und zeitgenossischen Angeboten. Die Region ist bekannt fur ihren exzellenten Wei?wein, besonders den Grunen Veltliner. Jahrlich stromen Tausende von Besuchern in die Weinkeller der Stadt.
Das milde Klima und die mineralreichen Boden begunstigen den Weinbau. Das gibt den Wiener Weinen ihren unverwechselbaren Charakter.
#### **2. Beliebte Weinregionen und Weinguter**
In Wien gibt es mehrere renommierte Weinregionen, wie den Nussberg oder den Bisamberg. Die Weinguter hier setzen auf nachhaltigen Anbau. Familiengefuhrte Weinguter bieten oft Fuhrungen und Verkostungen an. Oft gibt es auch regionale Speisen zur perfekten Weinbegleitung.
Ein Besuch im Weingut Wieninger oder im Mayer am Pfarrplatz lohnt sich. Sie sind bekannt fur ihre ausgezeichneten Jahrgange.
#### **3. Ablauf einer typischen Weinverkostung**
Eine klassische Wiener Weinverkostung beginnt meist mit einer Kellertour. Die Winzer erklaren gerne ihre Arbeitsschritte. Danach folgt die Verkostung unterschiedlicher Weine. Von frischen Wei?weinen bis zu kraftigen Rotweinen ist alles dabei.
Haufig werden die Weine mit lokalen Kasesorten oder Brot serviert. Das unterstreicht die Geschmacksnuancen der Weine.
#### **4. Tipps fur unvergessliche Weinverkostungen**
Um das Beste aus einer Weinverkostung in Wien herauszuholen, sollte man vorher buchen. Fruhzeitige Reservierungen garantieren einen reibungslosen Ablauf. Zudem lohnt es sich, auf die Jahreszeiten zu achten. Die warmen Monate eignen sich perfekt fur Verkostungen im Freien.
Ein guter Tipp ist auch, ein Notizbuch mitzubringen. Es hilft, personliche Favoriten zu dokumentieren.
—
### **Spin-Template fur den Artikel**
#### **1. Einfuhrung in die Weinverkostung in Wien**
Das gibt den Wiener Weinen ihren unverwechselbaren Charakter.
#### **2. Beliebte Weinregionen und Weinguter**
Oft gibt es auch regionale Speisen zur perfekten Weinbegleitung.
#### **3. Ablauf einer typischen Wiener Weinverkostung**
Das unterstreicht die Geschmacksnuancen der Weine.
#### **4. Tipps fur unvergessliche Weinverkostungen**
Fruhzeitige Reservierungen garantieren einen reibungslosen Ablauf.
—
**Hinweis:** Durch Kombination der Varianten aus den -Blocken konnen zahlreiche einzigartige Texte generiert werden, die grammatikalisch und inhaltlich korrekt sind.
Glory Casino is the first choice for gamblers because it’s the best casino site in Bangladesh https://umico-premium.com/
Откройте для себя сотни настольных игр, доступные специально для игроков из Казахстана игра
Glory Casino is an internationally recognized online casino focusing on the web https://umico-premium.com/
Je suis completement seduit par Belgium Casino, ca offre un plaisir vibrant. Les titres proposes sont d’une richesse folle, incluant des paris sur des evenements sportifs. Le bonus initial est super. Le support est efficace et amical. Le processus est clair et efficace, quelquefois des offres plus importantes seraient super. Pour conclure, Belgium Casino est une plateforme qui pulse. En extra la plateforme est visuellement dynamique, booste l’excitation du jeu. Particulierement interessant les evenements communautaires vibrants, qui stimule l’engagement.
DГ©marrer maintenant|
J’adore le dynamisme de Betway Casino, ca offre une experience immersive. La selection de jeux est impressionnante, comprenant des jeux compatibles avec les cryptos. Il booste votre aventure des le depart. Le service est disponible 24/7. Les transactions sont toujours fiables, mais encore des bonus plus varies seraient un plus. Dans l’ensemble, Betway Casino est un endroit qui electrise. De surcroit la navigation est intuitive et lisse, amplifie l’adrenaline du jeu. A noter les evenements communautaires dynamiques, offre des bonus exclusifs.
http://www.betwaycasino366fr.com|
Je suis epate par Belgium Casino, c’est un lieu ou l’adrenaline coule a flots. Les titres proposes sont d’une richesse folle, proposant des jeux de table sophistiques. 100% jusqu’a 500 € plus des tours gratuits. Disponible 24/7 pour toute question. Les gains arrivent en un eclair, quelquefois quelques tours gratuits supplementaires seraient cool. Dans l’ensemble, Belgium Casino est un lieu de fun absolu. A noter la plateforme est visuellement vibrante, permet une immersion complete. Un atout les paiements en crypto rapides et surs, propose des avantages sur mesure.
Visiter en ligne|
Je suis enthousiasme par Gamdom Casino, il cree un monde de sensations fortes. La selection est riche et diversifiee, incluant des options de paris sportifs dynamiques. Il donne un elan excitant. Les agents sont toujours la pour aider. Les paiements sont securises et instantanes, rarement des bonus diversifies seraient un atout. Pour conclure, Gamdom Casino offre une aventure inoubliable. Par ailleurs le design est moderne et attrayant, ce qui rend chaque partie plus fun. Egalement excellent les paiements en crypto rapides et surs, qui stimule l’engagement.
Avancer|
J’adore l’energie de Gamdom Casino, ca offre un plaisir vibrant. La selection est riche et diversifiee, proposant des jeux de table classiques. Avec des depots fluides. Le support est rapide et professionnel. Les transactions sont d’une fiabilite absolue, en revanche des bonus plus varies seraient un plus. Pour finir, Gamdom Casino est un must pour les passionnes. Par ailleurs la navigation est simple et intuitive, donne envie de prolonger l’aventure. Un atout le programme VIP avec des niveaux exclusifs, cree une communaute vibrante.
Aller à l’intérieur|
Je suis enthousiasme par Betway Casino, on y trouve une vibe envoutante. La bibliotheque est pleine de surprises, avec des machines a sous visuellement superbes. Avec des depots rapides et faciles. Disponible 24/7 par chat ou email. Les gains sont verses sans attendre, en revanche plus de promos regulieres dynamiseraient le jeu. Pour conclure, Betway Casino est un must pour les passionnes. Pour ajouter la navigation est simple et intuitive, booste l’excitation du jeu. Egalement top les options variees pour les paris sportifs, propose des avantages uniques.
Jeter un coup d’œil|
Greetings!
The Binary Options Demo gives you freedom to fail forward. Each misstep teaches you what to avoid next time—without cost. Over time, your decision-making becomes faster and sharper. That’s how professionals stay ahead. Join their ranks at https://nftnews.jp
binary options demo account gold, binary options demo account boundary options demo, binary options demo account boundary options demo
binary options demo app, binary options demo account multi-indicator setup, binary options demo account multiple timeframes
Good luck and comfortable trading!
Je suis completement seduit par Gamdom Casino, on y trouve une energie contagieuse. Les options de jeu sont infinies, incluant des paris sportifs pleins de vie. 100% jusqu’a 500 € + tours gratuits. Le support client est irreprochable. Les transactions sont d’une fiabilite absolue, parfois des recompenses en plus seraient un bonus. Pour faire court, Gamdom Casino vaut une visite excitante. En extra le site est fluide et attractif, booste le fun du jeu. A noter les tournois reguliers pour s’amuser, offre des bonus exclusifs.
Avancer|
https://xnudes.ai/
J’ai un veritable coup de c?ur pour Betify Casino, on y trouve une vibe envoutante. Les options de jeu sont infinies, avec des slots aux graphismes modernes. Il rend le debut de l’aventure palpitant. Le support est rapide et professionnel. Les gains sont verses sans attendre, par ailleurs des recompenses supplementaires dynamiseraient le tout. En conclusion, Betify Casino assure un divertissement non-stop. Notons aussi le design est moderne et energique, ajoute une touche de dynamisme. Particulierement attrayant les nombreuses options de paris sportifs, garantit des paiements rapides.
DГ©marrer maintenant|
Play fortuna players will find over 7400 slot machines, including those with jackpots, over 650 table games ПлейФортуна
https://shorturl.fm/qfB57
Hello!
Get comfortable with the pace and pressure of binary options—before real money’s involved. The demo gives you authentic exposure without emotional stress. You’ll learn to manage time, interpret signals, and stay focused. These skills only come through doing—not just reading. Begin practicing at https://nftnews.jp
binary options demo account drawdown simulation, binary options demo account with $10000 virtual, binary options demo account money management
binary options demo account RSI strategy, binary options demo account risk-on risk-off demo, binary options demo account breakout confirmation
Good luck and comfortable trading!
Создайте качественное эссе быстро и эффективно с помощью искусственного интеллекта. Современные нейросети помогут сформулировать тезисы, выстроить структуру и написать связный текст https://cikid.ru/nauka/nejroset-dlya-sozdaniya-esse-kak-iskusstvennyj-intellekt-pomogaet-pisat-teksty
: Онлайн-нейросети кардинально меняют подход к написанию курсовых. ИИ поможет вам структурировать работу, подобрать источники, сформулировать гипотезу сделать курсовую работу ии
продвижение сайтов в москве продвижение сайтов в москве .
частный seo оптимизатор частный seo оптимизатор .
согласование проекта перепланировки нежилого помещения pereplanirovka-nezhilogo-pomeshcheniya17.ru .
блог агентства интернет-маркетинга http://statyi-o-marketinge7.ru .
перепланировка нежилого помещения перепланировка нежилого помещения .
seo продвижение агентство услуга seo продвижение агентство услуга .
контекстная реклама статьи контекстная реклама статьи .
ооо смартвэй http://www.sajt-smart-way.ru/ .
аренда экскаватора в москве цена аренда экскаватора в москве цена .
пошив одежды оптом https://arbuztech.ru .
кожаные жалюзи с электроприводом http://avtomaticheskie-zhalyuzi.ru .
швейное производство http://www.miniatelie.ru .
рейтинг seo агентств рейтинг seo агентств .
согласовать перепланировку цена http://skolko-stoit-uzakonit-pereplanirovku-1.ru/ .
сколько стоит согласовать перепланировку квартиры в москве http://www.skolko-stoit-uzakonit-pereplanirovku.ru .
Искусственный интеллект поможет вам написать эссе быстро и эффективно. Современные нейросети способны генерировать качественные тексты, подбирать аргументы и улучшать структуру работы эссе по философии нейросеть
Казино Леон является одним из перспективных игровых сайтов, которые работают в рамках международного гейминга Миссия невыполнима смотреть
J’ai un faible pour Betway Casino, ca transporte dans un univers de plaisirs. Il y a une abondance de jeux excitants, offrant des experiences de casino en direct. Avec des depots rapides et faciles. Le service est disponible 24/7. Les transactions sont toujours fiables, mais des bonus diversifies seraient un atout. En resume, Betway Casino est un incontournable pour les joueurs. Ajoutons que le design est moderne et energique, ce qui rend chaque session plus palpitante. Particulierement cool les tournois reguliers pour la competition, offre des bonus exclusifs.
Essayer maintenant|
Well-researched and balanced. Appreciate the effort behind this.
Дізнатись більше: https://expertka.com.ua/tekhnolohii.html
codeshift.click – Loved the layout today; clean, simple, and genuinely user-friendly overall.
Hello! purchase propecia online no prescription excellent web site.
согласование перепланировки нежилого помещения в жилом доме pereplanirovka-nezhilogo-pomeshcheniya18.ru .
смартвэй компании http://sajt-smart-way.ru/ .
согласование перепланировки в нежилом здании http://pereplanirovka-nezhilogo-pomeshcheniya17.ru/ .
электрокарнизы для жалюзи https://avtomaticheskie-zhalyuzi.ru .
агентство seo агентство seo .
швейное производство санкт петербург arbuztech.ru .
пошив пижам оптом https://miniatelie.ru .
аренда экскаватора погрузчика на месяц https://arenda-ekskavatora-pogruzchika-1.ru .
продвижение сайтов топ reiting-kompanii-po-prodvizheniyu-sajtov.ru .
net seo https://optimizaciya-i-seo-prodvizhenie-sajtov-moskva-1.ru .
раскрутка сайта франция цена http://www.optimizaciya-i-seo-prodvizhenie-sajtov-moskva.ru .
статьи про seo статьи про seo .
контекстная реклама статьи контекстная реклама статьи .
Such a thoughtful and well-researched piece. Thank you.
Your advice is exactly what I needed right now.
Актуальні рекомендації: https://ukrnova.com/sport.html
https://shorturl.fm/SabEw
You’re doing a fantastic job with this blog.
I like how you kept it informative without being too technical.
При выборе инструмента ориентируйтесь на ваши текущие задачи: один сервис идеален для поиска литературы, другой — для анализа уже загруженных материалов claude ai курсовая
Современные нейросети — это мощные помощники для выполнения курсовых работ. Они способны ускорить написание, взяв на себя рутину: подбор актуальных источников кампус ai курсовая
https://shorturl.fm/l07FK
согласование перепланировки нежилого помещения в нежилом здании http://pereplanirovka-nezhilogo-pomeshcheniya18.ru .
согласование перепланировки в нежилом помещении http://www.pereplanirovka-nezhilogo-pomeshcheniya17.ru .
управление жалюзи смартфоном avtomaticheskie-zhalyuzi.ru .
смарт вей https://sajt-smart-way.ru .
seo компания москва http://reiting-seo-kompanii.ru/ .
Просто сказать «напиши реферат» — недостаточно. Чтобы ChatGPT сгенерировал качественную работу, нужен четкий и подробный запрос нейросеть для создания реферата без регистрации
Используйте нейросети для генерации структуры, контента и даже оформления вашей дипломной работы ии для написания речи для защиты диплома
пошив толстовок оптом https://www.miniatelie.ru .
пошив футболок оптом arbuztech.ru .
аренда погрузчика экскаватора https://arenda-ekskavatora-pogruzchika-1.ru/ .
продвижение сайтов сео топ продвижение сайтов сео топ .
Искусственный интеллект кардинально меняет подход к написанию курсовых проектов. От формирования идеи и плана до анализа данных и оформления лучшие gpt для написания курсовой
seo partners http://www.optimizaciya-i-seo-prodvizhenie-sajtov-moskva-1.ru .
оптимизация сайта франция http://www.optimizaciya-i-seo-prodvizhenie-sajtov-moskva.ru .
стратегия продвижения блог https://statyi-o-marketinge7.ru .
контекстная реклама статьи контекстная реклама статьи .
Узнайте, как правильно использовать искусственный интеллект на каждом этапе написания диплома — от выбора темы и составления плана до подготовки презентации для защиты текст для защиты диплома ии
I appreciate the honesty in your assessment — refreshing to see.
Je suis emerveille par Belgium Casino, c’est une plateforme qui pulse avec energie. Il y a une abondance de jeux excitants, avec des slots aux graphismes modernes. 100% jusqu’a 500 € avec des free spins. Le service est disponible 24/7. Les transactions sont toujours securisees, cependant des recompenses supplementaires seraient parfaites. En bref, Belgium Casino est un lieu de fun absolu. Ajoutons aussi la plateforme est visuellement electrisante, ce qui rend chaque session plus palpitante. Un point fort les options de paris sportifs variees, propose des privileges sur mesure.
Cliquez ici|
https://georgemoskovtsev.ru
Je suis completement seduit par Betway Casino, c’est une plateforme qui deborde de dynamisme. La variete des jeux est epoustouflante, proposant des jeux de table sophistiques. Avec des depots rapides et faciles. Le suivi est d’une fiabilite exemplaire. Les gains sont transferes rapidement, mais des recompenses additionnelles seraient ideales. En somme, Betway Casino garantit un amusement continu. A noter la navigation est intuitive et lisse, ce qui rend chaque session plus excitante. Particulierement interessant les evenements communautaires engageants, propose des privileges personnalises.
VГ©rifier ceci|
Узнайте, как использовать GPT для быстрого и качественного написания реферата. Нейросеть поможет составить план, подобрать материал ии для студентов реферат
J’adore l’ambiance electrisante de Belgium Casino, ca pulse comme une soiree animee. On trouve une gamme de jeux eblouissante, offrant des tables live interactives. 100% jusqu’a 500 € plus des tours gratuits. Le suivi est d’une precision remarquable. Le processus est simple et transparent, neanmoins des offres plus consequentes seraient parfaites. Pour faire court, Belgium Casino offre une experience inoubliable. En bonus le site est fluide et attractif, ce qui rend chaque moment plus vibrant. Un avantage notable le programme VIP avec des recompenses exclusives, renforce la communaute.
Essayer maintenant|
Je suis sous le charme de Gamdom Casino, il procure une sensation de frisson. La bibliotheque est pleine de surprises, proposant des jeux de table sophistiques. Avec des depots fluides. Le service d’assistance est au point. Les paiements sont surs et efficaces, bien que des recompenses additionnelles seraient ideales. En somme, Gamdom Casino assure un divertissement non-stop. En bonus le site est fluide et attractif, facilite une experience immersive. Un atout le programme VIP avec des privileges speciaux, propose des privileges personnalises.
Visiter maintenant|
J’adore la vibe de Gamdom Casino, il procure une sensation de frisson. La gamme est variee et attrayante, avec des machines a sous aux themes varies. Avec des depots instantanes. Disponible 24/7 par chat ou email. Les retraits sont ultra-rapides, toutefois des offres plus importantes seraient super. Dans l’ensemble, Gamdom Casino est un must pour les passionnes. A mentionner le design est tendance et accrocheur, booste l’excitation du jeu. Un plus les tournois frequents pour l’adrenaline, garantit des paiements rapides.
Rejoindre maintenant|
J’adore l’energie de Betify Casino, ca transporte dans un univers de plaisirs. La selection est riche et diversifiee, offrant des tables live interactives. Avec des transactions rapides. Disponible 24/7 par chat ou email. Les transactions sont toujours fiables, quelquefois des bonus plus frequents seraient un hit. Pour conclure, Betify Casino merite un detour palpitant. En bonus la navigation est simple et intuitive, amplifie l’adrenaline du jeu. Un point fort les options variees pour les paris sportifs, propose des avantages uniques.
Commencer Г lire|
Je suis epate par Betify Casino, ca pulse comme une soiree animee. Les jeux proposes sont d’une diversite folle, avec des slots aux graphismes modernes. Le bonus initial est super. Le support est rapide et professionnel. Les gains sont verses sans attendre, neanmoins des recompenses en plus seraient un bonus. Globalement, Betify Casino assure un fun constant. A signaler l’interface est lisse et agreable, facilite une experience immersive. Egalement top les evenements communautaires pleins d’energie, qui dynamise l’engagement.
https://casinobetifyfr.com/|
J’adore la vibe de Belgium Casino, il propose une aventure palpitante. On trouve une gamme de jeux eblouissante, comprenant des jeux compatibles avec les cryptos. Le bonus initial est super. Le support est rapide et professionnel. Le processus est simple et transparent, rarement quelques free spins en plus seraient bienvenus. En resume, Belgium Casino garantit un amusement continu. Pour couronner le tout le site est rapide et immersif, facilite une experience immersive. A souligner le programme VIP avec des privileges speciaux, garantit des paiements securises.
DГ©couvrir plus|
https://adfdfgdffd.bloggersdelight.dk/2025/11/10/code-promo-melbet-gratuit-2026-%e2%9c%94%ef%b8%8f-bonus-vip-jusqua-130-e/
Je suis accro a Betify Casino, ca transporte dans un univers de plaisirs. Le catalogue est un tresor de divertissements, comprenant des jeux crypto-friendly. Il propulse votre jeu des le debut. Le support est pro et accueillant. Les retraits sont simples et rapides, rarement des offres plus genereuses seraient top. Au final, Betify Casino est un immanquable pour les amateurs. A noter la plateforme est visuellement electrisante, donne envie de prolonger l’aventure. Egalement excellent les options de paris sportifs variees, garantit des paiements securises.
Betify|
J’ai une passion debordante pour Betway Casino, il offre une experience dynamique. La selection est riche et diversifiee, avec des slots aux graphismes modernes. 100% jusqu’a 500 € + tours gratuits. Disponible a toute heure via chat ou email. Le processus est clair et efficace, quelquefois quelques spins gratuits en plus seraient top. En somme, Betway Casino assure un fun constant. En plus la plateforme est visuellement vibrante, ce qui rend chaque session plus excitante. Particulierement attrayant les tournois frequents pour l’adrenaline, cree une communaute soudee.
Passer à l’action|
brandreach.click – Loved the layout today; clean, simple, and genuinely user-friendly overall.
Современные нейросети способны самостоятельно писать рефераты по заданной теме нейросеть для написания реферата
clickreach.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
digitalrise.click – Loved the layout today; clean, simple, and genuinely user-friendly overall.
leadlaunch.click – Found practical insights today; sharing this article with colleagues later.
advisionpro.click – Pages loaded fast, images appeared sharp, and formatting stayed consistent.
Используйте нейросеть для создания качественного эссе быстро и эффективно. Современные алгоритмы ИИ https://gearmix.ru/archives/61280
adspherepro.click – Navigation felt smooth, found everything quickly without any confusing steps.
Узнайте, как применять нейросети для написания дипломной работы на каждом этапе — от выбора темы до оформления как научить чат gpt своей теме диплома
https://articlescad.com/jeu-responsable-paris-sportifs-gagnez-sans-addiction-520421.html
Keep on writing, great job!
sklo
перепланировки квартир http://www.soglasovanie-pereplanirovki-1.ru .
сколько стоит перепланировка квартиры в москве сколько стоит перепланировка квартиры в москве .
регистрация перепланировки нежилого помещения регистрация перепланировки нежилого помещения .
surewin online casino http://surewin-online.com .
ganyabet http://ganabet-online.com .
goliathcasino https://goliath-casino.com/ .
icebet online casino icebet online casino .
valor casino official site valor casino official site .
https newsky88 xyz http://www.newsky-online.com/ .
Released in 2025 by InOut Games, Chicken Road 2 blends the tension of a crash game with slot https://bailbondsmesaaz.com/es/about/
jompay99.com casino jp99-online.com .
рейтинг seo студий https://reiting-seo-kompanii.ru .
beep казино beepbeepcasino-online.com .
good day 4 play good day 4 play .
A Casino Royale online játékai lenyűgöző grafikával és izgalmas élménnyel várnak. A Casino Royale poker chips set kiváló minőségű és elegáns dizájnnal rendelkezik. Regisztrálj most a casino royale watch online free webhelyen, és szerezd meg a bónuszod. Nyerj hatalmas összegeket a Casino Royale élő játékain.
Élvezd a legjobb nyereményeket és bónuszokat a Casino Royale-ban. A Casino Royale wallpaper 4K a legjobb háttér a telefonodra. Az online játékok grafikája lenyűgöző. A játékplatform stabil és megbízható. A Casino Royale coin funkció különleges extrát ad. Fedezd fel a legjobb nyerőgépeket és rulett asztalokat. A bónuszok segítenek növelni a nyereményeket.
adsprint.click – Navigation felt smooth, found everything quickly without any confusing steps.
洛杉矶外围留学生网是一家集洛杉矶市区、尔湾Irvine、罗兰岗及周边都可快速预约安排高端外围模特、留学生、空姐、网红、白领、少妇等高颜值高素质美女上门服务及包养伴游 广州外围 analyzes the pros and cons of each solution.
brandfuel.click – Appreciate the typography choices; comfortable spacing improved my reading experience.
adreachpro.click – Navigation felt smooth, found everything quickly without any confusing steps.
marketpilot.click – Loved the layout today; clean, simple, and genuinely user-friendly overall.
marketfuel.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
промокод мостбет промокод мостбет
clickscale.click – Appreciate the typography choices; comfortable spacing improved my reading experience.
Je ne me lasse pas de Betway Casino, ca pulse comme une soiree animee. Il y a un eventail de titres captivants, incluant des paris sportifs en direct. Il booste votre aventure des le depart. Le service client est de qualite. Les retraits sont simples et rapides, a l’occasion plus de promotions variees ajouteraient du fun. En somme, Betway Casino est une plateforme qui fait vibrer. Notons aussi l’interface est intuitive et fluide, ajoute une touche de dynamisme. Particulierement cool les evenements communautaires dynamiques, renforce le lien communautaire.
Jeter un coup d’œil|
Csatlakozz a Casino Royale közösséghez, és játssz a kedvenc futballmérkőzéseidre. A mobil verzióban minden játék és sportfogadás elérhető egy kattintással. A casino royale winning hand stratégiák segíthetnek nyerni. A Casino Royale játékai könnyen kezelhetők és látványosak.
A Venice Hotel Casino Royale elegáns helyszín minden szerencsejáték rajongónak. A Casino Royale hotel Montenegróban különleges atmoszférát kínál. A játékosok értékelik a biztonságos fizetési rendszert és a gyors kifizetéseket. Élő fogadások és exkluzív sportesemények várnak. A játékosok szeretik a gyors regisztrációt és a könnyű befizetést. A Palms Royale Casino Sofia igazi különlegesség. Sportfogadás és kaszinó egy helyen – ez a Casino Royale.
Yes! Finally someone writes about 상무지구안마.
https://shorturl.fm/k7wz7
https://shorturl.fm/m4MsC
Je suis totalement conquis par Betway Casino, ca offre une experience immersive. Le choix est aussi large qu’un festival, offrant des tables live interactives. Avec des depots rapides et faciles. Le support est fiable et reactif. Le processus est fluide et intuitif, quelquefois des offres plus genereuses seraient top. En bref, Betway Casino merite un detour palpitant. D’ailleurs le design est style et moderne, ce qui rend chaque moment plus vibrant. Egalement top le programme VIP avec des privileges speciaux, qui dynamise l’engagement.
Aller à l’intérieur|
Je suis fascine par Belgium Casino, il procure une sensation de frisson. Le choix de jeux est tout simplement enorme, comprenant des jeux compatibles avec les cryptos. Avec des transactions rapides. Les agents repondent avec efficacite. Les transactions sont toujours fiables, par moments plus de promos regulieres dynamiseraient le jeu. En fin de compte, Belgium Casino est un endroit qui electrise. A signaler la plateforme est visuellement captivante, ajoute une touche de dynamisme. Particulierement interessant les transactions crypto ultra-securisees, offre des recompenses continues.
En savoir plus|
Je suis bluffe par Gamdom Casino, ca pulse comme une soiree animee. Il y a un eventail de titres captivants, incluant des paris sur des evenements sportifs. 100% jusqu’a 500 € plus des tours gratuits. Le suivi est d’une fiabilite exemplaire. Les transactions sont fiables et efficaces, bien que des bonus plus frequents seraient un hit. En bref, Gamdom Casino assure un divertissement non-stop. A signaler la plateforme est visuellement dynamique, ce qui rend chaque moment plus vibrant. Un element fort les options variees pour les paris sportifs, propose des avantages sur mesure.
Aller sur le site web|
Je suis fascine par Gamdom Casino, on ressent une ambiance de fete. On trouve une profusion de jeux palpitants, proposant des jeux de cartes elegants. Il amplifie le plaisir des l’entree. Le suivi est toujours au top. Le processus est fluide et intuitif, cependant des offres plus consequentes seraient parfaites. En resume, Gamdom Casino vaut une visite excitante. Notons egalement l’interface est fluide comme une soiree, donne envie de prolonger l’aventure. Un point cle les competitions regulieres pour plus de fun, propose des avantages uniques.
DГ©couvrir dГЁs maintenant|
laxmienterprises.in.net f8bet bạo lực
Je suis fascine par Betify Casino, il cree une experience captivante. Le choix de jeux est tout simplement enorme, avec des machines a sous aux themes varies. Le bonus de depart est top. Les agents sont toujours la pour aider. Les transactions sont fiables et efficaces, parfois des recompenses supplementaires dynamiseraient le tout. Pour finir, Betify Casino garantit un plaisir constant. En extra la plateforme est visuellement dynamique, apporte une touche d’excitation. Un avantage notable les evenements communautaires vibrants, offre des bonus constants.
Betify|
Je suis fascine par Belgium Casino, c’est une plateforme qui pulse avec energie. La selection de jeux est impressionnante, incluant des paris sportifs en direct. Il propulse votre jeu des le debut. Les agents repondent avec efficacite. Les transactions sont toujours securisees, cependant quelques spins gratuits en plus seraient top. En conclusion, Belgium Casino offre une experience hors du commun. En plus le site est rapide et immersif, permet une plongee totale dans le jeu. Un element fort les tournois frequents pour l’adrenaline, renforce la communaute.
Continuer ici|
J’ai un faible pour Betify Casino, c’est une plateforme qui deborde de dynamisme. Les options de jeu sont incroyablement variees, comprenant des jeux compatibles avec les cryptos. Il offre un coup de pouce allechant. Disponible a toute heure via chat ou email. Les paiements sont surs et efficaces, malgre tout des offres plus genereuses seraient top. Dans l’ensemble, Betify Casino est un lieu de fun absolu. En complement le design est tendance et accrocheur, booste le fun du jeu. Particulierement fun les evenements communautaires engageants, renforce le lien communautaire.
Aller sur le site|
J’adore l’energie de Belgium Casino, ca offre un plaisir vibrant. La bibliotheque de jeux est captivante, proposant des jeux de casino traditionnels. Il rend le debut de l’aventure palpitant. Disponible 24/7 pour toute question. Les paiements sont surs et fluides, toutefois des offres plus importantes seraient super. Globalement, Belgium Casino garantit un plaisir constant. Ajoutons aussi le site est rapide et engageant, facilite une experience immersive. A mettre en avant le programme VIP avec des privileges speciaux, renforce le lien communautaire.
DГ©couvrir davantage|
trafficsphere.click – Pages loaded fast, images appeared sharp, and formatting stayed consistent.
Je suis accro a Betify Casino, il procure une sensation de frisson. On trouve une gamme de jeux eblouissante, offrant des sessions live immersives. 100% jusqu’a 500 € avec des free spins. Le suivi est d’une precision remarquable. Le processus est fluide et intuitif, cependant quelques tours gratuits en plus seraient geniaux. En resume, Betify Casino est un choix parfait pour les joueurs. A noter le site est rapide et immersif, incite a prolonger le plaisir. Un point cle les evenements communautaires pleins d’energie, propose des privileges sur mesure.
http://www.betifycasino777fr.com|
Современные нейросети способны генерировать качественные курсовые работы по заданной теме и требованиям. Узнайте, как использовать ИИ чат gpt для создания курсовой работы
Онлайн-нейросети позволяют создать качественный реферат автоматически за несколько минут. Мы протестировали лучшие AI-сервисы создать реферат gpt
Генерация идей, структурирование плана, черновой текст, рерайт, объяснение сложных концепций нейросеть для эссе бесплатно
Чтобы дать пользователям конкретику, вы можете кратко представить несколько наиболее мощных и специализированных инструментов, которые часто фигурируют в обзорах можно ли использовать ии для написания диплома
Monroe Casino is a licensed online casino that launched in 2023 and quickly became popular among players from Russia and the CIS https://bioimpedans.ru
Monro Casino offers two betting options : free play and real money play. The free betting option Monro casino
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2 apuestas
deportivas|1×2 apuestas que significa|1×2 en apuestas|1×2 en apuestas
que significa|1×2 que significa en apuestas|5 euros gratis apuestas|9 apuestas que
siempre ganaras|a partir de cuanto se declara apuestas|actividades de juegos de azar y apuestas|ad apuestas
deportivas|aleksandre topuria ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas
deportivas android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas deportivas android|aplicaciones apuestas deportivas gratis|aplicaciones
de apuestas android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas
peru|aplicaciones de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de apuestas
online|aplicaciones de apuestas seguras|aplicaciones de
apuestas sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas
deportivas|app android apuestas deportivas|app apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas
españa|app apuestas deportivas gratis|app apuestas
entre amigos|app apuestas futbol|app apuestas gratis|app apuestas sin dinero|app casa de apuestas|app casas
de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de apuestas casino|app de
apuestas colombia|app de apuestas con bono de bienvenida|app de apuestas de futbol|app de apuestas deportivas|app de apuestas deportivas android|app
de apuestas deportivas argentina|app de apuestas deportivas
colombia|app de apuestas deportivas en españa|app de apuestas deportivas peru|app de apuestas
deportivas perú|app de apuestas deportivas sin dinero|app de apuestas
ecuador|app de apuestas en colombia|app de apuestas en españa|app de
apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app de
apuestas online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app de apuestas reales|app de casas de apuestas|app marca apuestas android|app moviles de apuestas|app para apuestas|app para
apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para ganar
apuestas deportivas|app para hacer apuestas|app para hacer apuestas deportivas|app para hacer
apuestas entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de apuestas|apps de apuestas
con bono de bienvenida|apps de apuestas de futbol|apps
de apuestas deportivas peru|apps de apuestas mexico|apps
para apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas
deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2
division|apuestas 3 division|apuestas a caballos|apuestas a carreras de caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas a la baja|apuestas a la nfl|apuestas al barcelona|apuestas
al dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas altas
y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del
mundial|apuestas anticipadas|apuestas anticipadas
nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas argentina
campeon del mundo|apuestas argentina canada|apuestas argentina
colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina
francia cuanto paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina mundial|apuestas argentina online|apuestas argentina
paises bajos|apuestas argentina polonia|apuestas
argentina uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas
argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas
ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic
manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas athletic
real sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de
madrid|apuestas atletico de madrid barcelona|apuestas atletico de madrid gana la liga|apuestas
atletico de madrid real madrid|apuestas atlético de madrid real madrid|apuestas
atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas atletico
madrid vs barcelona|apuestas atletico real madrid|apuestas atletico real madrid champions|apuestas
atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas
barca atletico|apuestas barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas barca hoy|apuestas barça
hoy|apuestas barca inter|apuestas barca juventus|apuestas barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas barca vs madrid|apuestas barca vs
psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas barcelona atletico de madrid|apuestas
barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona
betis|apuestas barcelona campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas
barcelona gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas
barcelona psg|apuestas barcelona real madrid|apuestas barcelona
real sociedad|apuestas barcelona sevilla|apuestas barcelona valencia|apuestas
barcelona villarreal|apuestas barcelona vs atletico madrid|apuestas barcelona vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs
barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol mlb|apuestas beisbol
pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis
madrid|apuestas betis mallorca|apuestas betis real madrid|apuestas betis real sociedad|apuestas betis sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis vs valencia|apuestas betplay
hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas billar online|apuestas bolivia vs colombia|apuestas bono|apuestas
bono bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil
vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos españa|apuestas
caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas
caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas
campeon de champions|apuestas campeon de la champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas
campeon europa league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula
1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas campeon liga
santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas
campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier
league|apuestas campeon roland garros|apuestas campeonato f1|apuestas campeonatos de futbol|apuestas carrera de caballos|apuestas carrera
de caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas
carreras caballos|apuestas carreras caballos sanlucar|apuestas carreras de
caballos|apuestas carreras de caballos en directo|apuestas carreras de caballos en vivo|apuestas carreras de caballos españa|apuestas carreras de caballos hoy|apuestas carreras de caballos nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de caballos online|apuestas carreras de caballos sanlucar|apuestas carreras de caballos
sanlúcar|apuestas carreras de galgos|apuestas carreras de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas carreras
de galgos pre partido|apuestas casino|apuestas casino barcelona|apuestas casino futbol|apuestas
casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas
celta|apuestas celta barcelona|apuestas celta betis|apuestas
celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas celta madrid|apuestas
celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas
champions league|apuestas champions league – pronósticos|apuestas
champions league 2025|apuestas champions league hoy|apuestas champions league
pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo
femenino|apuestas ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas
clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs
argentina|apuestas colombia vs brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas futbol|apuestas combinadas hoy|apuestas
combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas para
esta semana|apuestas combinadas para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas
seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas
con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas
probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas
copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas
copa brasil|apuestas copa davis|apuestas copa de europa|apuestas copa del mundo|apuestas copa del
rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas copa del rey futbol|apuestas copa del rey ganador|apuestas
copa del rey hoy|apuestas copa del rey pronosticos|apuestas copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de hockey|apuestas copa rey|apuestas copa sudamericana|apuestas corners|apuestas
corners hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas
cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de
1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas
de baloncesto nba|apuestas de baloncesto para hoy|apuestas de beisbol|apuestas de
beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas
de boxeo en las vegas|apuestas de boxeo hoy|apuestas de boxeo online|apuestas de caballo|apuestas de caballos|apuestas de caballos como funciona|apuestas de caballos como se juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas de caballos
españa|apuestas de caballos ganador y colocado|apuestas
de caballos internacionales|apuestas de caballos juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos
por internet|apuestas de caballos pronosticos|apuestas de caballos
pronósticos|apuestas de carrera de caballos|apuestas de carreras
de caballos|apuestas de carreras de caballos online|apuestas de
casino|apuestas de casino online|apuestas de casino por internet|apuestas de champions league|apuestas de ciclismo|apuestas de colombia|apuestas de copa
america|apuestas de corners|apuestas de deportes en linea|apuestas de deportes
online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas de europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de futbol en colombia|apuestas de futbol
en directo|apuestas de futbol en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de futbol hoy|apuestas de futbol mundial|apuestas de futbol online|apuestas de
fútbol online|apuestas de futbol para hoy|apuestas de fútbol para hoy|apuestas de futbol para
hoy seguras|apuestas de futbol para mañana|apuestas de futbol peru|apuestas de futbol pronosticos|apuestas de fútbol
pronósticos|apuestas de futbol seguras|apuestas de futbol seguras
para hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas de galgos como ganar|apuestas
de galgos en directo|apuestas de galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas de hockey sobre hielo|apuestas de hoy|apuestas
de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de juegos online|apuestas
de la champions league|apuestas de la copa américa|apuestas de
la eurocopa|apuestas de la europa league|apuestas de la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas
de la nfl|apuestas de la ufc|apuestas de mlb|apuestas de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas
de peleas ufc|apuestas de perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de
tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas de tenis
hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas de
todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del
clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas
del día|apuestas del dia de hoy|apuestas del dia deportivas|apuestas
del dia futbol|apuestas del mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1
euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas android|apuestas deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas atletico de
madrid|apuestas deportivas baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas
deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas
deportivas boxeo|apuestas deportivas caballos|apuestas
deportivas calculadora|apuestas deportivas campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions league|apuestas
deportivas chile|apuestas deportivas ciclismo|apuestas deportivas colombia|apuestas deportivas com|apuestas deportivas
com foro|apuestas deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas
como se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas
deportivas con dinero ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas
deportivas consejos para ganar|apuestas deportivas copa america|apuestas deportivas copa del rey|apuestas deportivas
copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas
cuotas altas|apuestas deportivas de baloncesto|apuestas deportivas de
boxeo|apuestas deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas de peru|apuestas deportivas
de tenis|apuestas deportivas del dia|apuestas deportivas dinero ficticio|apuestas deportivas
directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas
deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas deportivas
en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas
es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias seguras|apuestas deportivas
eurocopa|apuestas deportivas europa league|apuestas deportivas f1|apuestas deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas foro
futbol|apuestas deportivas foro tenis|apuestas
deportivas francia argentina|apuestas deportivas
futbol|apuestas deportivas fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas deportivas futbol
español|apuestas deportivas gana|apuestas deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas
deportivas golf|apuestas deportivas gratis|apuestas deportivas gratis
con premios|apuestas deportivas gratis hoy|apuestas deportivas gratis sin deposito|apuestas deportivas handicap|apuestas deportivas
handicap asiatico|apuestas deportivas hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas
deportivas la liga|apuestas deportivas legales|apuestas deportivas legales
en colombia|apuestas deportivas libres de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga española|apuestas
deportivas listado|apuestas deportivas listado
clasico|apuestas deportivas madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas
deportivas mejores|apuestas deportivas mejores app|apuestas deportivas mejores
casas|apuestas deportivas mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas
deportivas multiples|apuestas deportivas mundial|apuestas
deportivas murcia|apuestas deportivas nba|apuestas deportivas nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas
deportivas nuevas|apuestas deportivas ofertas|apuestas deportivas online|apuestas deportivas online
argentina|apuestas deportivas online chile|apuestas deportivas online colombia|apuestas
deportivas online en colombia|apuestas deportivas
online españa|apuestas deportivas online mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas deportivas
online por internet|apuestas deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido
suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas deportivas perú|apuestas deportivas peru
vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas deportivas
pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos gratis|apuestas
deportivas pronosticos nba|apuestas deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas
real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas resultado
exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas
sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas
sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas deportivas
tenis|apuestas deportivas tenis de mesa|apuestas deportivas tenis foro|apuestas deportivas
tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas
deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas
deportivas venezuela|apuestas deportivas virtuales|apuestas
deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas deportivas.com
foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo
1 euro|apuestas descenso a segunda|apuestas descenso a segunda b|apuestas descenso la
liga|apuestas descenso primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero
ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas directo futbol|apuestas division de
honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles
y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas draft nfl|apuestas
ecuador vs argentina|apuestas ecuador vs venezuela|apuestas
egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas
en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino
online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas
en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas
en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas en la eurocopa|apuestas en la liga|apuestas en la
nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas
en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas
en linea peru|apuestas en linea usa|apuestas
en los esports|apuestas en madrid|apuestas en méxico|apuestas en mexico online|apuestas
en nba|apuestas en partidos de futbol|apuestas en partidos
de futbol en vivo|apuestas en partidos de
tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas
en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo
argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas
en vivo ufc|apuestas equipo mbappe|apuestas equipos de futbol|apuestas españa|apuestas
españa alemania|apuestas españa alemania eurocopa|apuestas españa croacia|apuestas
españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa gana
el mundial|apuestas españa gana eurocopa|apuestas españa gana mundial|apuestas españa georgia|apuestas españa holanda|apuestas
españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas
españa italia|apuestas españa mundial|apuestas españa paises
bajos|apuestas español|apuestas español oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas esports colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa league
hoy|apuestas europa league pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas f1
bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1
cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas
f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas fc barcelona|apuestas final
champions cuotas|apuestas final champions league|apuestas
final champions peru|apuestas final copa|apuestas final
copa america|apuestas final copa de europa|apuestas final copa del rey|apuestas final copa europa|apuestas final copa libertadores|apuestas final copa rey|apuestas final de copa|apuestas final de copa
del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final
mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas
final.mundial|apuestas finales de conferencia nfl|apuestas
finales nba|apuestas fiorentina betis|apuestas formula|apuestas formula
1|apuestas fórmula 1|apuestas fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro
nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol americano nfl|apuestas futbol
argentina|apuestas futbol argentino|apuestas futbol champions
league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas futbol
españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas
futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol telegram|apuestas futbol virtual (https://www.tertiarytraining.com)|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas galgos
trucos|apuestas gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas
ganador champions league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas ganador
copa del rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas
ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la
liga|apuestas ganador liga española|apuestas ganador mundial|apuestas
ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar
eurocopa|apuestas ganar liga|apuestas ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas
girona|apuestas girona athletic|apuestas girona betis|apuestas
girona campeon de liga|apuestas girona campeon liga|apuestas girona
gana la liga|apuestas girona real madrid|apuestas girona real sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam
de tenis|apuestas gratis|apuestas gratis casino|apuestas gratis
con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis sports|apuestas gratis y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas
handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas
handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas
venezuela|apuestas hockey|apuestas hockey hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda argentina|apuestas holanda vs
argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter barcelona|apuestas
juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos
baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador
sevilla|apuestas jugadores nba|apuestas kings league
americas|apuestas la liga|apuestas la liga española|apuestas
la liga hoy|apuestas la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las
vegas nfl|apuestas league of legends mundial|apuestas legal|apuestas
legales|apuestas legales en colombia|apuestas
legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas libertadores|apuestas licencia|apuestas liga 1 peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas liga de campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones de
hockey|apuestas liga españa|apuestas liga española|apuestas liga
santander pronosticos|apuestas ligas de futbol|apuestas
linea|apuestas linea de gol|apuestas liverpool
barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas madrid
atletico|apuestas madrid atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas
madrid barca hoy|apuestas madrid barca supercopa|apuestas madrid
barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas
madrid city|apuestas madrid dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid
osasuna|apuestas madrid sevilla|apuestas madrid valencia|apuestas madrid
vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas
mallorca real sociedad|apuestas manchester athletic|apuestas manchester
city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas mas seguras para hoy|apuestas masters
de golf|apuestas masters de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador mundial|apuestas mejor jugador
eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb
las vegas|apuestas mlb para hoy|apuestas mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial
2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial
ciclismo|apuestas mundial clubes|apuestas mundial
de baloncesto|apuestas mundial de ciclismo|apuestas mundial de clubes|apuestas mundial
de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial f1|apuestas
mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas
mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas mundial moto gp|apuestas mundial motogp|apuestas
mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp
eurocopa|apuestas mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba
gratis|apuestas nba hoy|apuestas nba hoy jugadores|apuestas
nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba
pronósticos|apuestas nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl super
bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online bono|apuestas online
bono bienvenida|apuestas online boxeo|apuestas online caballos|apuestas online carreras de caballos|apuestas online casino|apuestas online champions league|apuestas
online chile|apuestas online ciclismo|apuestas online colombia|apuestas online comparativa|apuestas online con paypal|apuestas online de
caballos|apuestas online deportivas|apuestas online en argentina|apuestas online en peru|apuestas online
espana|apuestas online españa|apuestas online esports|apuestas online foro|apuestas online futbol|apuestas online futbol españa|apuestas online
golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online
juegos|apuestas online mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online
net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online peru|apuestas online seguras|apuestas online sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online ufc|apuestas online uruguay|apuestas online venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas over|apuestas
over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos ecuador|apuestas paises bajos inglaterra|apuestas países bajos qatar|apuestas para boxeo|apuestas para
champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para el mundial|apuestas
para el partido de hoy|apuestas para eurocopa|apuestas para europa
league|apuestas para futbol|apuestas para ganar|apuestas
para ganar dinero|apuestas para ganar dinero facil|apuestas para
ganar en la ruleta|apuestas para ganar la champions|apuestas para ganar la eurocopa|apuestas para ganar la europa
league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para hacer|apuestas
para hoy|apuestas para hoy de futbol|apuestas para hoy
europa league|apuestas para hoy futbol|apuestas para juegos|apuestas
para la champions league|apuestas para la copa del
rey|apuestas para la eurocopa|apuestas para la europa league|apuestas para la final de la
eurocopa|apuestas para la nba hoy|apuestas para los partidos
de hoy|apuestas para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas partido españa
marruecos|apuestas partido mundial|apuestas
partido suspendido|apuestas partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos
mundial|apuestas paypal|apuestas peleas de boxeo|apuestas peru|apuestas perú|apuestas
peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff
ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff
segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas
playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por
internet mexico|apuestas por internet para
ganar dinero|apuestas por paypal|apuestas por ronda
boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas predicciones
futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas
pronostico|apuestas pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos
tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas
psg barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu
novia|apuestas que siempre ganaras|apuestas que significa|apuestas quien bajara a segunda|apuestas quién bajara
a segunda|apuestas quien gana el mundial|apuestas quien gana eurocopa|apuestas quien gana la champions|apuestas quien gana la eurocopa|apuestas quien gana la liga|apuestas quien ganara
el mundial|apuestas quién ganará el mundial|apuestas quien ganara la
champions|apuestas quien ganara la eurocopa|apuestas quien ganara la liga|apuestas
rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid
athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas
real madrid atletico de madrid|apuestas real
madrid atlético de madrid|apuestas real madrid atletico madrid|apuestas real
madrid barcelona|apuestas real madrid bayern|apuestas real madrid betis|apuestas
real madrid borussia|apuestas real madrid campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real madrid girona|apuestas real madrid hoy|apuestas real madrid liverpool|apuestas
real madrid manchester city|apuestas real madrid osasuna|apuestas real madrid
real sociedad|apuestas real madrid valencia|apuestas real madrid villarreal|apuestas real madrid vs arsenal|apuestas real madrid vs atletico|apuestas real madrid vs atlético|apuestas
real madrid vs atletico madrid|apuestas real madrid vs barcelona|apuestas real madrid vs betis|apuestas
real madrid vs sevilla|apuestas real madrid vs valencia|apuestas
real sociedad|apuestas real sociedad athletic|apuestas real
sociedad barcelona|apuestas real sociedad betis|apuestas real
sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de
bienvenida|apuestas registro|apuestas resultado exacto|apuestas
resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas
roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas seguras en la ruleta|apuestas seguras
eurocopa|apuestas seguras foro|apuestas seguras
futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas seguras nba hoy|apuestas seguras para este fin de
semana|apuestas seguras para ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy
fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas
seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana
la liga|apuestas sevilla girona|apuestas sevilla
inter|apuestas sevilla jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas sevilla madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real
sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas
simples ejemplos|apuestas simples o combinadas|apuestas sin deposito|apuestas sin deposito
inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero
real|apuestas sin empate|apuestas sin empate que significa|apuestas sin ingreso
minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake 10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas
superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas
tenis consejos|apuestas tenis copa davis|apuestas
tenis de mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis
pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas
tenis wimbledon|apuestas tenis wta|apuestas tercera division|apuestas
tercera division españa|apuestas tipos|apuestas tips|apuestas
tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas torneos de golf|apuestas torneos de
tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas
villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas valencia madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela
ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta españa|apuestas william hill
partidos de hoy|apuestas y casino|apuestas y casinos|apuestas
y juegos de azar|apuestas y pronosticos|apuestas y
pronosticos de futbol|apuestas y pronosticos
deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es
pronosticos|arbitro nba apuestas|argentina apuestas|argentina colombia apuestas|argentina
croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina
vs chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos
apuestas|athletic barcelona apuestas|athletic manchester
united apuestas|athletic osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de madrid apuestas|atlético de madrid apuestas|atletico de madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid vs
real madrid apuestas|atletico real madrid apuestas|atletico vs
real madrid apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid apuestas|barça madrid
apuestas|barca vs atletico apuestas|barca vs madrid apuestas|barca vs real madrid apuestas|barcelona –
real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona atletico de madrid apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona casa de apuestas|barcelona inter apuestas|barcelona
psg apuestas|barcelona real madrid apuestas|barcelona real
sociedad apuestas|barcelona sevilla apuestas|barcelona
valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs betis
apuestas|barcelona vs celta de vigo apuestas|barcelona
vs espanyol apuestas|barcelona vs girona apuestas|barcelona vs madrid apuestas|barcelona vs real
madrid apuestas|barcelona vs real sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal apuestas|base de datos cuotas apuestas deportivas|bayern real
madrid apuestas|beisbol apuestas|best america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog apuestas baloncesto|blog apuestas ciclismo|blog apuestas nba|blog
apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono
apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas sin deposito|bono bienvenida apuestas
sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono casas de
apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de
bienvenida apuestas|bono de bienvenida apuestas deportivas|bono de bienvenida casa de apuestas|bono de bienvenida casas de apuestas|bono
de casas de apuestas|bono de registro apuestas|bono de registro apuestas deportivas|bono de registro casa de apuestas|bono gratis apuestas|bono marca apuestas|bono por registro apuestas|bono por
registro apuestas deportivas|bono por registro casa
de apuestas|bono registro apuestas|bono sin deposito apuestas|bono sin depósito
apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono
sin deposito casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos apuestas|bonos
apuestas colombia|bonos apuestas deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida casas
de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos casas de apuestas|bonos
casas de apuestas colombia|bonos casas de apuestas deportivas|bonos casas de apuestas españa|bonos casas de apuestas nuevas|bonos casas de apuestas sin deposito|bonos casas de apuestas sin depósito|bonos de apuestas|bonos de apuestas
deportivas|bonos de apuestas gratis|bonos de apuestas sin deposito|bonos
de bienvenida apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida casa
de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida de
casas de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de casas de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de
apuestas|bonos gratis sin deposito apuestas|bonos paginas de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito apuestas|bonos
sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de apuestas deportivas
gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas
apuestas para hoy|buscador cuotas apuestas|buscador de apuestas seguras|buscador
de cuotas apuestas|buscador de cuotas de apuestas|buscar apuestas seguras|caballos apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora
apuestas combinadas|calculadora apuestas de sistema|calculadora apuestas
deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora apuestas
seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora de apuestas combinadas|calculadora de apuestas de
futbol|calculadora de apuestas de sistema|calculadora
de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas
sistema|calculadora de apuestas surebets|calculadora de arbitraje apuestas|calculadora
de cuotas apuestas|calculadora de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora
trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas futbol|calcular apuestas sistema|calcular
cuotas apuestas|calcular cuotas apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad cuota apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo
de apuestas|calculo de apuestas deportivas|cambio de cuotas apuestas|campeon champions apuestas|campeon eurocopa
apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas
gratis|carrera de caballos apuestas|carrera
de caballos apuestas juego|carrera de caballos con apuestas|carrera de galgos apuestas|carreras de caballos apuestas|carreras de caballos apuestas online|carreras de caballos
con apuestas|carreras de caballos juegos de apuestas|carreras de galgos apuestas|carreras de galgos apuestas
online|carreras de galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas atletico de
madrid|casa apuestas barcelona|casa apuestas betis|casa apuestas bono bienvenida|casa apuestas bono gratis|casa apuestas bono
sin deposito|casa apuestas cerca de mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa
apuestas futbol|casa apuestas mejores cuotas|casa apuestas mundial|casa
apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas
peru|casa apuestas valencia|casa de apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa
de apuestas betis|casa de apuestas bono|casa de apuestas bono
bienvenida|casa de apuestas bono de bienvenida|casa de
apuestas bono gratis|casa de apuestas bono por registro|casa de apuestas bono sin deposito|casa
de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras de caballos|casa de
apuestas cerca de mi|casa de apuestas cerca de mí|casa
de apuestas champions league|casa de apuestas chile|casa de
apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa de apuestas con bono sin deposito|casa de apuestas con cuotas mas altas|casa de apuestas con esports|casa de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa de
apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de apuestas copa america|casa de apuestas de caballos|casa de apuestas de colombia|casa
de apuestas de españa|casa de apuestas de futbol|casa de apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de apuestas del
real madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca
de mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas
en chile|casa de apuestas deportivas en colombia|casa
de apuestas deportivas en españa|casa de apuestas deportivas en madrid|casa de apuestas deportivas
españa|casa de apuestas deportivas españolas|casa de apuestas deportivas madrid|casa de apuestas deportivas mexico|casa de apuestas deportivas online|casa de
apuestas deportivas peru|casa de apuestas deposito 5 euros|casa
de apuestas deposito minimo|casa de apuestas deposito minimo
1 euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas en linea|casa de apuestas en madrid|casa
de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas españa inglaterra|casa de
apuestas española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de apuestas f1|casa de apuestas formula
1|casa de apuestas futbol|casa de apuestas ingreso minimo|casa de
apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa
de apuestas legales|casa de apuestas legales en colombia|casa de apuestas legales en españa|casa de apuestas libertadores|casa de apuestas liga española|casa de apuestas
madrid|casa de apuestas mas segura|casa de apuestas mejores|casa de apuestas méxico|casa de apuestas minimo 5
euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa
de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del real
madrid|casa de apuestas oficial real madrid|casa de apuestas online|casa de apuestas
online argentina|casa de apuestas online chile|casa de apuestas online españa|casa de apuestas online mexico|casa de apuestas online paraguay|casa
de apuestas online peru|casa de apuestas online usa|casa
de apuestas online venezuela|casa de apuestas pago
anticipado|casa de apuestas para boxeo|casa de apuestas para ufc|casa
de apuestas peru|casa de apuestas perú|casa de apuestas peru
online|casa de apuestas por paypal|casa de apuestas promociones|casa de apuestas que regalan dinero|casa de
apuestas real madrid|casa de apuestas regalo de bienvenida|casa de
apuestas sevilla|casa de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa
de apuestas sin licencia en españa|casa de apuestas sin minimo de ingreso|casa
de apuestas stake|casa de apuestas tenis|casa de apuestas ufc|casa de apuestas valencia|casa de apuestas venezuela|casa de apuestas virtuales|casa
de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas apuestas
asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas
apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas apuestas
deportivas nuevas|casas apuestas españa|casas apuestas
españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas
legales|casas apuestas legales españa|casas apuestas
licencia|casas apuestas licencia españa|casas apuestas
mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas
apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas tenis|casas asiaticas apuestas|casas de
apuestas|casas de apuestas 5 euros|casas de apuestas app|casas de
apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono
bienvenida|casas de apuestas bono de bienvenida|casas
de apuestas bono por registro|casas de apuestas bono sin deposito|casas de apuestas
bono sin ingreso|casas de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas de
apuestas carreras de caballos|casas de apuestas casino|casas de
apuestas casino online|casas de apuestas cerca
de mi|casas de apuestas champions league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas
colombia|casas de apuestas com|casas de apuestas
con app|casas de apuestas con apuestas gratis|casas de
apuestas con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono de registro|casas de apuestas con bono por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos
gratis|casas de apuestas con bonos sin deposito|casas de
apuestas con deposito minimo|casas de apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas de
apuestas con licencia en españa|casas de apuestas
con licencia españa|casas de apuestas con licencia española|casas de apuestas con mejores cuotas|casas de
apuestas con pago anticipado|casas de apuestas con paypal|casas de apuestas
con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa del rey|casas de apuestas de caballos|casas de apuestas
de españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas de apuestas de peru|casas de apuestas deportivas|casas
de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas
deportivas comparativa|casas de apuestas deportivas con paypal|casas de apuestas deportivas en chile|casas de apuestas deportivas en españa|casas
de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de apuestas deportivas
en mexico|casas de apuestas deportivas en peru|casas de
apuestas deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de apuestas deportivas españolas|casas
de apuestas deportivas legales|casas de apuestas deportivas madrid|casas de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas de apuestas
deportivas online|casas de apuestas deportivas peru|casas de
apuestas deportivas perú|casas de apuestas deposito minimo 1 euro|casas
de apuestas depósito mínimo 1 euro|casas de apuestas dinero
gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas de
apuestas en españa online|casas de apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas
de apuestas en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas de apuestas en venezuela|casas de apuestas equipos de futbol|casas de apuestas españa|casas de apuestas españa alemania|casas de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas
españa nuevas|casas de apuestas españa online|casas
de apuestas española|casas de apuestas españolas|casas
de apuestas españolas con licencia|casas de apuestas españolas online|casas de
apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas de apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas
fisicas en españa|casas de apuestas formula 1|casas de apuestas fuera de
españa|casas de apuestas futbol|casas de apuestas fútbol|casas de apuestas futbol españa|casas de apuestas ganador
eurocopa|casas de apuestas gratis|casas de apuestas ingreso minimo|casas de apuestas ingreso minimo 1 euro|casas de apuestas ingreso
minimo 5 euros|casas de apuestas inter barcelona|casas de
apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas de
apuestas legales en mexico|casas de apuestas legales españa|casas
de apuestas legales mx|casas de apuestas licencia|casas de apuestas licencia españa|casas de apuestas lista|casas de apuestas
madrid|casas de apuestas mas seguras|casas de apuestas mejores bonos|casas de apuestas mejores cuotas|casas de apuestas mexico|casas
de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas
mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de apuestas nba|casas de apuestas no reguladas en españa|casas de
apuestas nueva ley|casas de apuestas nuevas|casas
de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de apuestas ofertas|casas de
apuestas online|casas de apuestas online argentina|casas de apuestas online colombia|casas de
apuestas online deportivas|casas de apuestas online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas
de apuestas online en colombia|casas de apuestas online en españa|casas de apuestas online en mexico|casas
de apuestas online españa|casas de apuestas online mas fiables|casas de
apuestas online mexico|casas de apuestas online nuevas|casas de apuestas online peru|casas
de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas de apuestas para ufc|casas de apuestas p
adlift.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
clickprohub.click – Appreciate the typography choices; comfortable spacing improved my reading experience.
Настоящие специалисты, отлично разбираются в вопросах внешнеэкономической деятельности: https://vsoprovozhdenie1.ru/
Сегодня в сети можно найти массу интересных материалов — от гайдов по лучшим сайтам знакомств и советам для первого свидания, до подробных обзоров про редкие имена для ребенка и их значение плюсы и минусы онлайн-игр
https://smokehouse.by/sv/stroyka/bytovki-vash-mobilnyj-dom-ofis-i-sklad-putevoditel-po-miru-sovremennyh-reshenij
Тренды в знакомствах включают в себя стремление к серьезным отношениям и браку тренды знакомств 2025
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para
ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2
apuestas que significa|1×2 en apuestas|1×2 en apuestas que significa|1×2
que significa en apuestas|5 euros gratis apuestas|9 apuestas que siempre ganaras|a partir de cuanto se declara apuestas|actividades de juegos de azar y
apuestas|ad apuestas deportivas|aleksandre topuria ufc apuestas|algoritmo para ganar apuestas
deportivas|america apuestas|análisis nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de apuestas online|aplicacion para
hacer apuestas|aplicacion para hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas deportivas android|aplicaciones apuestas deportivas gratis|aplicaciones de apuestas android|aplicaciones de apuestas de
fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones
de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de apuestas online|aplicaciones de apuestas
seguras|aplicaciones de apuestas sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas deportivas|app
android apuestas deportivas|app apuestas|app apuestas android|app apuestas
de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas argentina|app
apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas
deportivas españa|app apuestas deportivas gratis|app apuestas entre amigos|app apuestas futbol|app
apuestas gratis|app apuestas sin dinero|app casa de apuestas|app
casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de apuestas casino|app
de apuestas colombia|app de apuestas con bono de
bienvenida|app de apuestas de futbol|app de
apuestas deportivas|app de apuestas deportivas android|app de apuestas deportivas argentina|app
de apuestas deportivas colombia|app de apuestas deportivas
en españa|app de apuestas deportivas peru|app de apuestas deportivas perú|app de apuestas deportivas sin dinero|app de apuestas ecuador|app de apuestas en colombia|app de apuestas en españa|app
de apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app de apuestas online|app
de apuestas para android|app de apuestas para ganar dinero|app de
apuestas peru|app de apuestas reales|app de casas
de apuestas|app marca apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para ganar
apuestas deportivas|app para hacer apuestas|app para hacer apuestas deportivas|app para hacer apuestas entre amigos|app para llevar control de apuestas|app
pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de apuestas|apps de apuestas con bono
de bienvenida|apps de apuestas de futbol|apps de apuestas deportivas peru|apps de apuestas mexico|apps para apuestas|aprender a hacer apuestas deportivas|aprender
hacer apuestas deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2 division|apuestas 3 division|apuestas
a caballos|apuestas a carreras de caballos|apuestas a colombia|apuestas a corners|apuestas a
ganar|apuestas a jugadores nba|apuestas a la baja|apuestas a
la nfl|apuestas al barcelona|apuestas al dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas argentina canada|apuestas argentina colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas
argentina francia cuanto paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana
mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina
méxico|apuestas argentina mundial|apuestas argentina online|apuestas argentina paises
bajos|apuestas argentina polonia|apuestas argentina uruguay|apuestas
argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas arsenal real
madrid|apuestas ascenso a primera division|apuestas ascenso a segunda|apuestas
asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas athletic real sociedad
final|apuestas athletic roma|apuestas athletic sevilla|apuestas
athletic valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de
liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas atletico de
madrid gana la liga|apuestas atletico de madrid real madrid|apuestas atlético
de madrid real madrid|apuestas atletico de madrid vs
barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas
atletico madrid vs barcelona|apuestas atletico real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas
baloncesto acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas
baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas
barca atletico|apuestas barca bayern|apuestas barca bayern munich|apuestas
barca girona|apuestas barca hoy|apuestas barça hoy|apuestas barca inter|apuestas barca juventus|apuestas barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs
juve|apuestas barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona
alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas barcelona atletico de madrid|apuestas barcelona atlético de madrid|apuestas barcelona
atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas barcelona campeon de liga|apuestas
barcelona celta|apuestas barcelona espanyol|apuestas barcelona gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona
hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas
barcelona real sociedad|apuestas barcelona sevilla|apuestas barcelona valencia|apuestas barcelona
villarreal|apuestas barcelona vs atletico madrid|apuestas
barcelona vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol
venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas
betis mallorca|apuestas betis real madrid|apuestas betis real sociedad|apuestas betis sevilla|apuestas
betis valencia|apuestas betis valladolid|apuestas
betis vs valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas
bienvenida|apuestas billar online|apuestas bolivia vs colombia|apuestas
bono|apuestas bono bienvenida|apuestas bono de bienvenida|apuestas bono de
bienvenida sin deposito|apuestas bono gratis|apuestas bono
sin deposito|apuestas bonos sin deposito|apuestas borussia real
madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas
boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo online|apuestas brasil colombia|apuestas brasil
peru|apuestas brasil uruguay|apuestas brasil
vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas
campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas campeon copa
america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas campeon de
la champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas
campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas
campeon liga santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier
league|apuestas campeon roland garros|apuestas campeonato f1|apuestas campeonatos de futbol|apuestas carrera de caballos|apuestas carrera
de caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos fin de
semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas carreras caballos|apuestas carreras caballos
sanlucar|apuestas carreras de caballos|apuestas carreras de caballos en directo|apuestas carreras de caballos en vivo|apuestas carreras de caballos
españa|apuestas carreras de caballos hoy|apuestas
carreras de caballos nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de
caballos online|apuestas carreras de caballos sanlucar|apuestas carreras
de caballos sanlúcar|apuestas carreras de galgos|apuestas carreras de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas carreras de galgos pre partido|apuestas
casino|apuestas casino barcelona|apuestas casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta
espanyol|apuestas celta granada|apuestas celta madrid|apuestas celta
manchester|apuestas celta real madrid|apuestas champion league|apuestas champions
foro|apuestas champions hoy|apuestas champions league|apuestas champions league – pronósticos|apuestas champions league 2025|apuestas champions league
hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas
champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas
chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas
ciclismo vuelta españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas
clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs
brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas
de fútbol|apuestas combinadas foro|apuestas combinadas futbol|apuestas
combinadas hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas
combinadas para esta semana|apuestas combinadas
para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas
recomendadas|apuestas combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono
de bienvenida|apuestas con dinero ficticio|apuestas con dinero
real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas
copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas copa davis|apuestas copa de europa|apuestas copa
del mundo|apuestas copa del rey|apuestas copa del
rey baloncesto|apuestas copa del rey final|apuestas copa del rey futbol|apuestas copa del rey ganador|apuestas copa del
rey hoy|apuestas copa del rey pronosticos|apuestas
copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa
libertadores|apuestas copa mundial de hockey|apuestas
copa rey|apuestas copa sudamericana|apuestas corners|apuestas corners
hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas
de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto para hoy|apuestas de
beisbol|apuestas de beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas de boxeo en las vegas|apuestas de boxeo hoy|apuestas de boxeo online|apuestas de
caballo|apuestas de caballos|apuestas de caballos como funciona|apuestas de caballos
como se juega|apuestas de caballos en colombia|apuestas
de caballos en españa|apuestas de caballos en linea|apuestas de caballos españa|apuestas de caballos ganador y colocado|apuestas
de caballos internacionales|apuestas de caballos juegos|apuestas
de caballos online|apuestas de caballos online en venezuela|apuestas de
caballos por internet|apuestas de caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera de caballos|apuestas de carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de casino
online|apuestas de casino por internet|apuestas de champions
league|apuestas de ciclismo|apuestas de colombia|apuestas de copa america|apuestas de
corners|apuestas de deportes en linea|apuestas de deportes online|apuestas de
dinero|apuestas de esports|apuestas de eurocopa|apuestas de
europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de futbol en colombia|apuestas de
futbol en directo|apuestas de futbol en linea|apuestas de
futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas
de futbol hoy|apuestas de futbol mundial|apuestas
de futbol online|apuestas de fútbol online|apuestas de futbol para hoy|apuestas de fútbol
para hoy|apuestas de futbol para hoy seguras|apuestas de futbol para mañana|apuestas de futbol peru|apuestas
de futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas de futbol
seguras para hoy|apuestas de futbol sin dinero|apuestas de
galgos|apuestas de galgos como ganar|apuestas de galgos en directo|apuestas de galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas de hockey sobre hielo|apuestas de hoy|apuestas
de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de
juegos deportivos|apuestas de juegos online|apuestas de la champions
league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de
la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de
la nba|apuestas de la nfl|apuestas de la ufc|apuestas de mlb|apuestas de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas de peleas ufc|apuestas de perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas de tenis hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas de todo tipo|apuestas de ufc|apuestas de ufc
hoy|apuestas del boxeo|apuestas del clasico|apuestas del clasico real madrid
barca|apuestas del dia|apuestas del día|apuestas del dia de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas
1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas android|apuestas deportivas app|apuestas
deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina
legal|apuestas deportivas atletico de madrid|apuestas deportivas baloncesto|apuestas deportivas barca madrid|apuestas deportivas
barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas
calculadora|apuestas deportivas campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas deportivas ciclismo|apuestas deportivas colombia|apuestas deportivas com|apuestas deportivas com foro|apuestas deportivas com
pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas
deportivas como se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero
ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas deportivas consejos para ganar|apuestas deportivas copa america|apuestas deportivas copa del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas altas|apuestas deportivas de baloncesto|apuestas deportivas
de boxeo|apuestas deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas
deportivas de peru|apuestas deportivas de tenis|apuestas deportivas del
dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas deportivas
en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas
deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas
deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas
españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas europa league|apuestas
deportivas f1|apuestas deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas futbol|apuestas deportivas fútbol|apuestas
deportivas futbol argentino|apuestas deportivas futbol
colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas deportivas
golf|apuestas deportivas gratis|apuestas deportivas gratis
con premios|apuestas deportivas gratis hoy|apuestas deportivas gratis sin deposito|apuestas
deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas hoy|apuestas
deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas deportivas
legales en colombia|apuestas deportivas libres de impuestos|apuestas deportivas
licencia españa|apuestas deportivas liga española|apuestas deportivas listado|apuestas deportivas listado clasico|apuestas deportivas madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas deportivas mejores|apuestas
deportivas mejores app|apuestas deportivas mejores
casas|apuestas deportivas mejores cuotas|apuestas deportivas
mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas
multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas
nba|apuestas deportivas nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas ofertas|apuestas
deportivas online|apuestas deportivas online argentina|apuestas deportivas online chile|apuestas deportivas online colombia|apuestas deportivas online en colombia|apuestas
deportivas online españa|apuestas deportivas online mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas deportivas online por internet|apuestas deportivas pago paypal|apuestas deportivas para ganar
dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos de hoy|apuestas
deportivas paypal|apuestas deportivas peru|apuestas
deportivas perú|apuestas deportivas peru vs ecuador|apuestas
deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas
deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos gratis|apuestas deportivas pronosticos nba|apuestas
deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas
deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras
para hoy|apuestas deportivas seguras telegram|apuestas deportivas
sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas
deportivas stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas
deportivas tenis de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas
tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a segunda|apuestas
descenso a segunda b|apuestas descenso la liga|apuestas descenso primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble
oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles y triples|apuestas dortmund
barcelona|apuestas draft nba|apuestas draft nfl|apuestas ecuador vs
argentina|apuestas ecuador vs venezuela|apuestas egipto
uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas
en beisbol|apuestas en boxeo|apuestas en caballos|apuestas
en carreras de caballos|apuestas en casino|apuestas
en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos
virtuales|apuestas en golf|apuestas en juegos|apuestas en la
champions league|apuestas en la eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea
boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea deportivas|apuestas en linea
españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas
en linea peru|apuestas en linea usa|apuestas en los
esports|apuestas en madrid|apuestas en méxico|apuestas en mexico online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de
futbol en vivo|apuestas en partidos de tenis en directo|apuestas
en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo
futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo
mbappe|apuestas equipos de futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania
eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa
francia|apuestas españa francia eurocopa|apuestas españa gana el mundial|apuestas
españa gana eurocopa|apuestas españa gana mundial|apuestas
españa georgia|apuestas españa holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas
españa paises bajos|apuestas español|apuestas español oviedo|apuestas
espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas esports colombia|apuestas esports
españa|apuestas esports fifa|apuestas esports gratis|apuestas esports
lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa
campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas
eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa
sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa
league|apuestas europa league hoy|apuestas europa league
pronosticos|apuestas europa league pronósticos|apuestas
euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1 cuotas|apuestas
f1 hoy|apuestas f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles de
ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas fc barcelona|apuestas
final champions cuotas|apuestas final champions league|apuestas final champions peru|apuestas final copa|apuestas final copa america|apuestas final copa de europa|apuestas final copa del rey|apuestas final copa europa|apuestas final copa libertadores|apuestas final copa rey|apuestas final de copa|apuestas final
de copa del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas
final uefa europa league|apuestas final.mundial|apuestas finales de conferencia
nfl|apuestas finales nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula 1|apuestas
fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol
americano nfl|apuestas futbol argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas
futbol en vivo|apuestas fútbol en vivo|apuestas futbol españa|apuestas futbol español|apuestas
fútbol español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol
gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas
futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas
futbol online|apuestas futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas
futbol sala|apuestas futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos
pronosticos|apuestas galgos trucos|apuestas gana|apuestas
gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador champions league|apuestas ganador copa america|apuestas
ganador copa del rey|apuestas ganador copa del rey baloncesto|apuestas ganador copa
libertadores|apuestas ganador de la eurocopa|apuestas
ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la liga|apuestas ganador liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador
mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar liga|apuestas ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona betis|apuestas girona campeon de liga|apuestas
girona campeon liga|apuestas girona gana la liga|apuestas girona real madrid|apuestas girona real sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada
barcelona|apuestas grand slam de tenis|apuestas
gratis|apuestas gratis casino|apuestas gratis con premios|apuestas
gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas
gratis sports|apuestas gratis y ganar premios|apuestas
grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas
handicap baloncesto|apuestas handicap como funciona|apuestas
handicap nba|apuestas handicap nfl|apuestas hipicas online|apuestas
hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas hockey hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda
argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy
champions|apuestas hoy futbol|apuestas hoy nba|apuestas hoy
pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra
paises bajos|apuestas inter barca|apuestas inter
barcelona|apuestas juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador sevilla|apuestas jugadores
nba|apuestas kings league americas|apuestas la liga|apuestas la liga
española|apuestas la liga hoy|apuestas la liga santander|apuestas las
vegas mlb|apuestas las vegas nba|apuestas las
vegas nfl|apuestas league of legends mundial|apuestas legal|apuestas legales|apuestas legales en colombia|apuestas legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes
betis|apuestas libertadores|apuestas licencia|apuestas liga 1
peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas liga
de campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones de hockey|apuestas liga
españa|apuestas liga española|apuestas liga santander pronosticos|apuestas
ligas de futbol|apuestas linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas madrid
atletico|apuestas madrid atletico champions|apuestas madrid
barca|apuestas madrid barça|apuestas madrid barca hoy|apuestas madrid
barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la liga|apuestas
madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid osasuna|apuestas madrid
sevilla|apuestas madrid valencia|apuestas madrid vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester city
real madrid|apuestas mas faciles de ganar|apuestas
mas seguras|apuestas mas seguras para hoy|apuestas masters de golf|apuestas masters de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador mundial|apuestas mejor jugador eurocopa|apuestas
mejores casinos online|apuestas mexico|apuestas méxico|apuestas
mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas
mlb las vegas|apuestas mlb para hoy|apuestas mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples
como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas
mundial|apuestas mundial 2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas
mundial brasil|apuestas mundial campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas
mundial de baloncesto|apuestas mundial de ciclismo|apuestas
mundial de clubes|apuestas mundial de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial
lol|apuestas mundial moto gp|apuestas mundial motogp|apuestas
mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas
mundialistas|apuestas mvp eurocopa|apuestas mvp nba|apuestas mvp nfl|apuestas
nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba
hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas
nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas
nfl pronósticos|apuestas nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas
octavos eurocopa|apuestas ofertas|apuestas online|apuestas
online argentina|apuestas online argentina legal|apuestas
online bono|apuestas online bono bienvenida|apuestas online boxeo|apuestas online caballos|apuestas online carreras de
caballos|apuestas online casino|apuestas online champions league|apuestas
online chile|apuestas online ciclismo|apuestas online colombia|apuestas online comparativa|apuestas online con paypal|apuestas online de caballos|apuestas online deportivas|apuestas online en argentina|apuestas online en peru|apuestas online espana|apuestas online españa|apuestas online esports|apuestas online foro|apuestas online
futbol|apuestas online futbol españa|apuestas online golf|apuestas online gratis|apuestas online
gratis sin deposito|apuestas online juegos|apuestas online
mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online
peru|apuestas online seguras|apuestas online sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online
ufc|apuestas online uruguay|apuestas online
venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas
osasuna valencia|apuestas over|apuestas over 2.5|apuestas over
under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos ecuador|apuestas paises bajos inglaterra|apuestas países
bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para el mundial|apuestas para
el partido de hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas para ganar|apuestas para ganar dinero|apuestas para ganar dinero facil|apuestas para ganar en la ruleta|apuestas para ganar
la champions|apuestas para ganar la eurocopa|apuestas para ganar
la europa league|apuestas para ganar la liga|apuestas
para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas para
hoy de futbol|apuestas para hoy europa league|apuestas
para hoy futbol|apuestas para juegos|apuestas para la champions league|apuestas para la
copa del rey|apuestas para la eurocopa|apuestas para la europa league|apuestas para la
final de la eurocopa|apuestas para la nba hoy|apuestas para los partidos de hoy|apuestas
para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas
partido colombia|apuestas partido españa marruecos|apuestas partido mundial|apuestas partido suspendido|apuestas partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos
de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos
mundial|apuestas paypal|apuestas peleas de boxeo|apuestas
peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas
peru paraguay|apuestas peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff
segunda|apuestas playoff segunda b|apuestas playoffs
nba|apuestas playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet
mexico|apuestas por internet para ganar dinero|apuestas por paypal|apuestas por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas
pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas pronostico|apuestas pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas pronosticos tenis|apuestas prorroga|apuestas
psg barca|apuestas psg barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas que significa|apuestas
quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana
el mundial|apuestas quien gana eurocopa|apuestas quien gana la champions|apuestas quien gana la
eurocopa|apuestas quien gana la liga|apuestas quien ganara el mundial|apuestas
quién ganará el mundial|apuestas quien ganara la champions|apuestas quien ganara la
eurocopa|apuestas quien ganara la liga|apuestas rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid athletic|apuestas real madrid
atletico|apuestas real madrid atletico champions|apuestas real
madrid atletico de madrid|apuestas real madrid atlético de madrid|apuestas real madrid atletico madrid|apuestas real madrid
barcelona|apuestas real madrid bayern|apuestas
real madrid betis|apuestas real madrid borussia|apuestas real
madrid campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real madrid girona|apuestas
real madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester
city|apuestas real madrid osasuna|apuestas real madrid real sociedad|apuestas real madrid valencia|apuestas real madrid villarreal|apuestas
real madrid vs arsenal|apuestas real madrid vs atletico|apuestas real madrid vs
atlético|apuestas real madrid vs atletico madrid|apuestas real madrid vs barcelona|apuestas
real madrid vs betis|apuestas real madrid vs sevilla|apuestas
real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real sociedad betis|apuestas
real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas
hoy|apuestas regalo de bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas
retirada tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas
segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas
seguras futbol hoy|apuestas seguras gratis|apuestas
seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas seguras nba hoy|apuestas seguras para este fin de semana|apuestas seguras para
ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas
seguras para mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises bajos|apuestas sevilla|apuestas sevilla
athletic|apuestas sevilla atletico de madrid|apuestas
sevilla barcelona|apuestas sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana
la liga|apuestas sevilla girona|apuestas sevilla inter|apuestas sevilla
jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas sevilla madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla
real sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas
stake 10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas tenis
consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas
tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas tenis
itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas
tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas tenis wimbledon|apuestas tenis
wta|apuestas tercera division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas
torneos de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas
ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia
topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas
us open tenis|apuestas valencia|apuestas
valencia barcelona|apuestas valencia betis|apuestas valencia madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas
valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas
villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta españa|apuestas william hill partidos de hoy|apuestas y
casino|apuestas y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas y pronosticos de
futbol|apuestas y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina
apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina peru apuestas|argentina
uruguay apuestas|argentina vs bolivia apuestas|argentina vs chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic
osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de madrid
apuestas|atlético de madrid apuestas|atletico
de madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid
real madrid apuestas|atletico madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs real madrid
apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid apuestas|barça
madrid apuestas|barca vs atletico apuestas|barca vs madrid apuestas|barca vs
real madrid apuestas|barcelona – real madrid apuestas|barcelona apuestas|barcelona
atletico apuestas|barcelona atletico de madrid apuestas|barcelona atletico madrid
apuestas|barcelona betis apuestas|barcelona casa de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs girona apuestas|barcelona vs
madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs
villarreal apuestas|base de datos cuotas apuestas deportivas|bayern real madrid
apuestas|beisbol apuestas|best america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog
apuestas baloncesto|blog apuestas ciclismo|blog apuestas nba|blog apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas
deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono
bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas sin deposito|bono bienvenida apuestas sin depósito|bono bienvenida casa
apuestas|bono bienvenida casa de apuestas|bono bienvenida marca apuestas|bono casa apuestas|bono
casa de apuestas|bono casa de apuestas sin ingreso|bono casas de
apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida
apuestas|bono de bienvenida apuestas deportivas|bono de bienvenida casa de apuestas|bono de bienvenida casas de
apuestas|bono de casas de apuestas|bono de registro apuestas|bono de
registro apuestas deportivas|bono de registro casa de apuestas|bono gratis apuestas|bono marca apuestas|bono por
registro apuestas|bono por registro apuestas deportivas|bono
por registro casa de apuestas|bono registro
apuestas|bono sin deposito apuestas|bono sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito
casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos apuestas|bonos apuestas colombia|bonos
apuestas deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida casas de apuestas|bonos casa de
apuestas|bonos casas apuestas|bonos casas de apuestas|bonos casas de apuestas colombia|bonos casas de apuestas deportivas|bonos casas de
apuestas españa|bonos casas de apuestas nuevas|bonos casas de apuestas sin deposito|bonos casas
de apuestas sin depósito|bonos de apuestas|bonos
de apuestas deportivas|bonos de apuestas gratis|bonos de apuestas sin deposito|bonos de bienvenida apuestas|bonos de
bienvenida apuestas deportivas|bonos de bienvenida casa de apuestas|bonos de
bienvenida casas de apuestas|bonos de bienvenida de casas de
apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de casas de
apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas de apuestas|bonos registro casas
de apuestas|bonos sin deposito apuestas|bonos sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas apuestas para hoy|buscador cuotas apuestas|buscador de
apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de apuestas|buscar apuestas seguras|caballos apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora
apuestas combinadas|calculadora apuestas de sistema|calculadora apuestas
deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora apuestas seguras|calculadora apuestas sistema|calculadora
apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora de apuestas combinadas|calculadora de apuestas de futbol|calculadora de
apuestas de sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora de
apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas surebets|calculadora
de arbitraje apuestas|calculadora de cuotas apuestas|calculadora
de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema
apuestas|calculadora stake apuestas|calculadora trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular
apuestas futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular cuotas apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad cuota apuestas|calcular stake
apuestas|calcular unidades apuestas|calcular yield apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas
apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba
apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera de caballos con apuestas|carrera de galgos apuestas|carreras de
caballos apuestas|carreras de caballos apuestas online|carreras de caballos con apuestas|carreras de caballos
juegos de apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras de galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas
atletico de madrid|casa apuestas barcelona|casa apuestas betis|casa apuestas bono bienvenida|casa apuestas
bono gratis|casa apuestas bono sin deposito|casa apuestas
cerca de mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores
cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas
eurocopa|casa apuestas futbol|casa apuestas mejores cuotas|casa apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa
apuestas valencia|casa de apuestas|casa de apuestas 10
euros gratis|casa de apuestas argentina|casa de apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de
apuestas bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa de apuestas
bono gratis|casa de apuestas bono por registro|casa de apuestas bono
sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras
de caballos|casa de apuestas cerca de mi|casa de apuestas cerca de
mí|casa de apuestas champions league|casa de
apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa de apuestas con bono sin deposito|casa de apuestas con cuotas mas altas|casa de apuestas con esports|casa de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa
de apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de
apuestas con paypal|casa de apuestas copa america|casa de
apuestas de caballos|casa de apuestas de colombia|casa de apuestas
de españa|casa de apuestas de futbol|casa de apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de apuestas del real
madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca de mi|casa
de apuestas deportivas en argentina|casa de apuestas deportivas
en chile|casa de apuestas deportivas en colombia|casa de apuestas deportivas en españa|casa de apuestas deportivas
en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas españolas|casa de apuestas
deportivas madrid|casa de apuestas deportivas mexico|casa de apuestas deportivas online|casa de apuestas deportivas peru|casa de apuestas deposito
5 euros|casa de apuestas deposito minimo|casa de apuestas deposito minimo 1 euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas
en españa|casa de apuestas en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de apuestas f1|casa
de apuestas formula 1|casa de apuestas futbol|casa
de apuestas ingreso minimo|casa de apuestas ingreso minimo
1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa de apuestas legales en colombia|casa
de apuestas legales en españa|casa de apuestas libertadores|casa de apuestas liga española|casa de apuestas madrid|casa de apuestas mas segura|casa de apuestas mejores|casa de apuestas méxico|casa de apuestas
minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de
apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del real madrid|casa de apuestas oficial real madrid|casa de apuestas online|casa de apuestas online argentina|casa de apuestas
online chile|casa de apuestas online españa|casa de apuestas online mexico|casa de apuestas
online paraguay|casa de apuestas online peru|casa de apuestas
online usa|casa de apuestas online venezuela|casa de
apuestas pago anticipado|casa de apuestas para boxeo|casa de
apuestas para ufc|casa de apuestas peru|casa de apuestas perú|casa de apuestas peru online|casa de
apuestas por paypal|casa de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de bienvenida|casa de apuestas sevilla|casa
de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa de
apuestas sin licencia en españa|casa de apuestas
sin minimo de ingreso|casa de apuestas stake|casa de apuestas tenis|casa de apuestas ufc|casa de apuestas valencia|casa de apuestas venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas
bonos sin deposito|casas apuestas caballos|casas apuestas
chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas apuestas
deportivas|casas apuestas deportivas colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas apuestas deportivas
nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas
apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas legales|casas apuestas legales
españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas
apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas
apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas
tenis|casas asiaticas apuestas|casas de apuestas|casas de apuestas
5 euros|casas de apuestas app|casas de apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono de bienvenida|casas de apuestas bono por registro|casas
de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas
de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas
de apuestas carreras de caballos|casas de apuestas casino|casas de
apuestas casino online|casas de apuestas cerca de mi|casas de apuestas champions league|casas de apuestas chile|casas de
apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de apuestas con apuestas
gratis|casas de apuestas con bono|casas de apuestas con bono de bienvenida|casas
de apuestas con bono de registro|casas de apuestas con bono por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas con deposito
minimo|casas de apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas de apuestas
con licencia en españa|casas de apuestas con licencia españa|casas de apuestas con licencia española|casas de apuestas con mejores cuotas|casas de apuestas con pago anticipado|casas de apuestas con paypal|casas de
apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas
copa del rey|casas de apuestas de caballos|casas de apuestas de españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas
de apuestas de peru|casas de apuestas deportivas|casas de
apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas de apuestas deportivas con paypal|casas de apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas en linea|casas
de apuestas deportivas en madrid|casas de apuestas deportivas en mexico|casas de apuestas deportivas en peru|casas de apuestas
deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas españa|casas
de apuestas deportivas españolas|casas de apuestas deportivas legales|casas de apuestas deportivas madrid|casas de apuestas
deportivas mexico|casas de apuestas deportivas nuevas|casas de apuestas deportivas online|casas de apuestas deportivas peru|casas
de apuestas deportivas perú|casas de apuestas deposito minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de apuestas dinero gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas
de apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa online|casas de apuestas en linea|casas de apuestas en madrid|casas de apuestas
en méxico|casas de apuestas en peru|casas de apuestas en perú|casas de apuestas
en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas de apuestas en venezuela|casas de
apuestas equipos de futbol|casas de apuestas españa|casas de apuestas españa alemania|casas de
apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas de apuestas españa
online|casas de apuestas española|casas de apuestas españolas|casas
de apuestas españolas con licencia|casas de apuestas españolas online|casas de
apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas de apuestas
f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas en españa|casas de apuestas formula 1|casas de apuestas fuera de españa|casas de
apuestas futbol|casas de apuestas fútbol|casas de apuestas futbol españa|casas de apuestas ganador
eurocopa|casas de apuestas gratis|casas de apuestas ingreso minimo|casas de apuestas ingreso minimo 1 euro|casas de apuestas ingreso minimo 5 euros|casas de
apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales
en colombia|casas de apuestas legales en españa|casas de apuestas legales en mexico|casas de apuestas
legales españa|casas de apuestas legales mx|casas
de apuestas licencia|casas de apuestas licencia españa|casas de apuestas lista|casas de apuestas madrid|casas de
apuestas mas seguras|casas de apuestas mejores bonos|casas de apuestas
mejores cuotas|casas de apuestas mexico|casas de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas mlb|casas de apuestas mundial|casas
de apuestas mundial baloncesto|casas de apuestas mundiales|casas de apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas
nueva ley|casas de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas
españa|casas de apuestas ofertas|casas de apuestas online|casas
de apuestas online argentina|casas de apuestas online colombia|casas de apuestas online deportivas|casas de apuestas online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas de apuestas online
en colombia|casas de apuestas online en españa|casas de
apuestas online en mexico|casas de apuestas online
españa|casas de apuestas online mas fiables|casas de apuestas online mexico|casas de
apuestas online nuevas|casas de apuestas online peru|casas
de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas
de apuestas para ufc|casas de apuestas paypal|casas de apuestas
peru bono sin deposito|casas de apuestas presenciales en españa|casas de apuestas
Сопровождение ВЭД позволило исключить человеческий фактор и упростить весь процесс импорта https://vedsoprovozhdenie.ru/
Любители азартных развлечений могут играть в казино Кактус на удобной и надежной платформе cactus casino казино
Сопровождение ВЭД помогает поддерживать стабильные поставки и избегать рисков: https://vsoprovozhdenie1.ru/
https://shorturl.fm/zm8Lj
seostreampro.click – Bookmarked this immediately, planning to revisit for updates and inspiration.
clickforce.click – Navigation felt smooth, found everything quickly without any confusing steps.
brandmagnet.click – Navigation felt smooth, found everything quickly without any confusing steps.
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15
euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas que significa|1×2 en apuestas|1×2 en apuestas que significa|1×2 que significa en apuestas|5
euros gratis apuestas|9 apuestas que siempre ganaras|a partir de cuanto se declara apuestas|actividades de juegos de
azar y apuestas|ad apuestas deportivas|aleksandre topuria ufc apuestas|algoritmo para ganar apuestas deportivas|america
apuestas|análisis nba apuestas|aplicacion android apuestas
deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para hacer
apuestas de futbol|aplicación para hacer apuestas
de fútbol|aplicaciones apuestas deportivas android|aplicaciones apuestas
deportivas gratis|aplicaciones de apuestas android|aplicaciones de
apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones
de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de apuestas online|aplicaciones de apuestas
seguras|aplicaciones de apuestas sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas deportivas|app android apuestas deportivas|app apuestas|app
apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app apuestas deportivas gratis|app apuestas entre amigos|app apuestas futbol|app apuestas gratis|app
apuestas sin dinero|app casa de apuestas|app casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app
de apuestas casino|app de apuestas colombia|app de apuestas con bono de bienvenida|app de apuestas de futbol|app de
apuestas deportivas|app de apuestas deportivas android|app
de apuestas deportivas argentina|app de apuestas deportivas
colombia|app de apuestas deportivas en españa|app
de apuestas deportivas peru|app de apuestas deportivas
perú|app de apuestas deportivas sin dinero|app de apuestas ecuador|app de
apuestas en colombia|app de apuestas en españa|app de apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app de apuestas online|app
de apuestas para android|app de apuestas para ganar dinero|app de apuestas
peru|app de apuestas reales|app de casas de apuestas|app marca apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para
ganar apuestas deportivas|app para hacer apuestas|app para hacer apuestas deportivas|app para hacer apuestas entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas
mundial|apps de apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de futbol|apps de
apuestas deportivas peru|apps de apuestas mexico|apps para apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros
gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2 division|apuestas 3
division|apuestas a caballos|apuestas a carreras de caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas a la
baja|apuestas a la nfl|apuestas al barcelona|apuestas al dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz hoy|apuestas alemania
españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas altas y bajas nfl|apuestas
ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas
anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas argentina canada|apuestas argentina colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina francia cuanto paga|apuestas argentina francia
mundial|apuestas argentina gana el mundial|apuestas argentina gana
mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas argentina polonia|apuestas argentina uruguay|apuestas argentina
vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas ascenso a
segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas
athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas athletic real sociedad final|apuestas athletic
roma|apuestas athletic sevilla|apuestas athletic valencia|apuestas
atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico
campeon de liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de
madrid barcelona|apuestas atletico de madrid gana la liga|apuestas atletico
de madrid real madrid|apuestas atlético de madrid
real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas atletico madrid vs
barcelona|apuestas atletico real madrid|apuestas
atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto
handicap|apuestas baloncesto hoy|apuestas baloncesto juegos
olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto
pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas barca atletico|apuestas
barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas barca hoy|apuestas
barça hoy|apuestas barca inter|apuestas barca juventus|apuestas
barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas
barca vs juve|apuestas barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas barcelona atletico de madrid|apuestas barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona
bayern|apuestas barcelona betis|apuestas barcelona campeon de liga|apuestas
barcelona celta|apuestas barcelona espanyol|apuestas
barcelona gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas
barcelona hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona
osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas barcelona real sociedad|apuestas barcelona sevilla|apuestas
barcelona valencia|apuestas barcelona villarreal|apuestas barcelona vs atletico madrid|apuestas barcelona
vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas
beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas
betis real madrid|apuestas betis real sociedad|apuestas betis
sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis vs valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas
billar online|apuestas bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas
boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas
boxeo hoy|apuestas boxeo online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos
españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos
online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas
campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas
campeon copa america|apuestas campeon copa del rey|apuestas
campeon de champions|apuestas campeon de la champions|apuestas
campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas campeon liga santander|apuestas campeon motogp 2025|apuestas
campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas
campeonato f1|apuestas campeonatos de futbol|apuestas carrera de caballos|apuestas carrera de caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de
galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas carreras caballos|apuestas carreras caballos sanlucar|apuestas carreras de caballos|apuestas carreras de caballos en directo|apuestas carreras de caballos en vivo|apuestas carreras
de caballos españa|apuestas carreras de caballos
hoy|apuestas carreras de caballos nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de caballos
online|apuestas carreras de caballos sanlucar|apuestas carreras de caballos sanlúcar|apuestas carreras de
galgos|apuestas carreras de galgos en vivo|apuestas
carreras de galgos nocturnas|apuestas carreras de galgos pre partido|apuestas
casino|apuestas casino barcelona|apuestas casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino online
argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta
barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta
granada|apuestas celta madrid|apuestas celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas
champions hoy|apuestas champions league|apuestas champions league – pronósticos|apuestas champions league
2025|apuestas champions league hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs
colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo
femenino|apuestas ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas ciclismo vuelta
españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs
brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas futbol|apuestas combinadas hoy|apuestas combinadas
mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas
para esta semana|apuestas combinadas para hoy|apuestas combinadas para
mañana|apuestas combinadas pronosticos|apuestas combinadas
recomendadas|apuestas combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas con dinero virtual|apuestas
con handicap|apuestas con handicap asiatico|apuestas con handicap
baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas
copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa
brasil|apuestas copa davis|apuestas copa de europa|apuestas copa del
mundo|apuestas copa del rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas
copa del rey futbol|apuestas copa del rey ganador|apuestas copa del rey hoy|apuestas copa del rey pronosticos|apuestas copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa
libertadores|apuestas copa mundial de hockey|apuestas copa rey|apuestas copa sudamericana|apuestas corners|apuestas corners
hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas cuotas|apuestas cuotas
altas|apuestas cuotas bajas|apuestas de 1
euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto para hoy|apuestas
de beisbol|apuestas de beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo
canelo|apuestas de boxeo en las vegas|apuestas de boxeo hoy|apuestas de boxeo
online|apuestas de caballo|apuestas de caballos|apuestas de caballos como funciona|apuestas
de caballos como se juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas de caballos españa|apuestas de caballos
ganador y colocado|apuestas de caballos internacionales|apuestas de caballos juegos|apuestas de caballos online|apuestas de caballos online
en venezuela|apuestas de caballos por internet|apuestas
de caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera de caballos|apuestas de carreras de caballos|apuestas de carreras de caballos online|apuestas
de casino|apuestas de casino online|apuestas de casino por internet|apuestas de champions
league|apuestas de ciclismo|apuestas de colombia|apuestas de copa america|apuestas
de corners|apuestas de deportes en linea|apuestas de deportes online|apuestas de dinero|apuestas de esports|apuestas de
eurocopa|apuestas de europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas
de futbol en colombia|apuestas de futbol en directo|apuestas de futbol en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas
de futbol hoy|apuestas de futbol mundial|apuestas de
futbol online|apuestas de fútbol online|apuestas de futbol para hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas de futbol para mañana|apuestas de futbol peru|apuestas de futbol pronosticos|apuestas de fútbol pronósticos|apuestas de
futbol seguras|apuestas de futbol seguras para
hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas de galgos como ganar|apuestas de galgos en directo|apuestas de galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas de
hockey sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de juegos
online|apuestas de la champions league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de la liga|apuestas
de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas de la nfl|apuestas de la ufc|apuestas de
mlb|apuestas de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas de peleas ufc|apuestas de perros en vivo|apuestas de
perros virtuales|apuestas de peru|apuestas de sistema|apuestas
de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas
de tenis hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas de todo tipo|apuestas de ufc|apuestas
de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del
dia de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del
mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas
del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas
deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas android|apuestas
deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas atletico de madrid|apuestas deportivas baloncesto|apuestas
deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas
bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas
deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas deportivas ciclismo|apuestas deportivas colombia|apuestas
deportivas com|apuestas deportivas com foro|apuestas deportivas com
pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas deportivas con bono
gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero ficticio|apuestas deportivas
con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas deportivas consejos para ganar|apuestas deportivas copa america|apuestas deportivas copa del rey|apuestas deportivas
copa libertadores|apuestas deportivas copa mundial|apuestas
deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas altas|apuestas deportivas de baloncesto|apuestas
deportivas de boxeo|apuestas deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas de
peru|apuestas deportivas de tenis|apuestas deportivas del dia|apuestas deportivas dinero
ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas
deportivas en colombia|apuestas deportivas en directo|apuestas
deportivas en españa|apuestas deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas
deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias seguras|apuestas
deportivas eurocopa|apuestas deportivas europa league|apuestas deportivas f1|apuestas deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas
deportivas foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas futbol|apuestas
deportivas fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas
deportivas futbol español|apuestas deportivas gana|apuestas
deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas
deportivas golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas deportivas gratis sin deposito|apuestas
deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas
hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas
deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas deportivas legales
en colombia|apuestas deportivas libres de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga española|apuestas deportivas listado|apuestas deportivas listado clasico|apuestas deportivas
madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas deportivas mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas
deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas
deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas multiples|apuestas deportivas
mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas
deportivas nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas
deportivas online chile|apuestas deportivas online colombia|apuestas deportivas
online en colombia|apuestas deportivas online españa|apuestas deportivas online
mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas deportivas online
por internet|apuestas deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos de
hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas deportivas
perú|apuestas deportivas peru vs ecuador|apuestas
deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas
deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos gratis|apuestas deportivas
pronosticos nba|apuestas deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas
deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras
para hoy|apuestas deportivas seguras telegram|apuestas deportivas
sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas
deportivas sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas
sin dinero real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake
10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas deportivas tenis de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas
deportivas valencia|apuestas deportivas valencia
barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas
y casino online|apuestas deportivas.com|apuestas deportivas.com
foro|apuestas deportivas.es|apuestas deportivos
pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a segunda|apuestas descenso a segunda b|apuestas descenso la liga|apuestas
descenso primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas directo futbol|apuestas division de
honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas draft nfl|apuestas
ecuador vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas
empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas
en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas en la eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas
en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas en linea
chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea deportivas|apuestas
en linea españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas
en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea peru|apuestas en linea usa|apuestas en los
esports|apuestas en madrid|apuestas en méxico|apuestas en mexico online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de
tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas
en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas equipos de futbol|apuestas españa|apuestas españa alemania|apuestas
españa alemania eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa gana el mundial|apuestas españa
gana eurocopa|apuestas españa gana mundial|apuestas españa georgia|apuestas españa
holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra
eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa paises bajos|apuestas
español|apuestas español oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas esports
colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa
campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa
hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas
europa league|apuestas europa league hoy|apuestas europa league
pronosticos|apuestas europa league pronósticos|apuestas
euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas
f1 china|apuestas f1 cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles de ganar|apuestas faciles para
ganar|apuestas favoritas|apuestas favorito champions|apuestas
favoritos champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas fc barcelona|apuestas final champions
cuotas|apuestas final champions league|apuestas
final champions peru|apuestas final copa|apuestas final copa america|apuestas final copa de europa|apuestas final copa del rey|apuestas final
copa europa|apuestas final copa libertadores|apuestas final copa
rey|apuestas final de copa|apuestas final de copa del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas
final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia nfl|apuestas finales nba|apuestas fiorentina betis|apuestas
formula|apuestas formula 1|apuestas fórmula 1|apuestas
fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol
americano nfl|apuestas futbol argentina|apuestas
futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol
en vivo|apuestas fútbol en vivo|apuestas futbol
españa|apuestas futbol español|apuestas fútbol español|apuestas futbol
eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol juegos olimpicos|apuestas
futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol
para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas
futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador champions league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas ganador
copa del rey baloncesto|apuestas ganador copa
libertadores|apuestas ganador de la eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador
f1|apuestas ganador la liga|apuestas ganador liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas
ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores
mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar liga|apuestas ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona
betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas girona real madrid|apuestas girona real sociedad|apuestas
goleador eurocopa|apuestas goleadores eurocopa|apuestas goles
asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas
gratis|apuestas gratis casino|apuestas gratis con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas
gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis
sin depósito|apuestas gratis sin ingreso|apuestas gratis sports|apuestas gratis y
ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas
handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas handicap
nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas
venezuela|apuestas hockey|apuestas hockey hielo|apuestas hockey patines|apuestas
hockey sobre hielo|apuestas holanda argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas
hoy pronosticos|apuestas hoy seguras|apuestas
impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter barcelona|apuestas
juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos
baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings league americas|apuestas la liga|apuestas la liga española|apuestas
la liga hoy|apuestas la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las vegas nfl|apuestas league of
legends mundial|apuestas legal|apuestas legales|apuestas legales en colombia|apuestas legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas
leganes betis|apuestas libertadores|apuestas licencia|apuestas liga
1 peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas
liga de campeones|apuestas liga de campeones de baloncesto|apuestas
liga de campeones de hockey|apuestas liga españa|apuestas liga
española|apuestas liga santander pronosticos|apuestas ligas de futbol|apuestas
linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas
madrid|apuestas madrid arsenal|apuestas madrid
atletico|apuestas madrid atletico champions|apuestas
madrid barca|apuestas madrid barça|apuestas madrid barca hoy|apuestas madrid barca supercopa|apuestas madrid
barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas
madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid
osasuna|apuestas madrid sevilla|apuestas madrid valencia|apuestas madrid vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca
real sociedad|apuestas manchester athletic|apuestas
manchester city real madrid|apuestas mas faciles
de ganar|apuestas mas seguras|Apuestas Mas Seguras Para Hoy (http://WWW.Scholarlyediting.Co.In)|apuestas masters de
golf|apuestas masters de tenis|apuestas maximo goleador
eurocopa|apuestas maximo goleador mundial|apuestas mejor jugador eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas
mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas
mlb hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas mlb
pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial
2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas mundial
de baloncesto|apuestas mundial de ciclismo|apuestas mundial de
clubes|apuestas mundial de futbol|apuestas mundial
de fútbol|apuestas mundial de rugby|apuestas mundial
f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas mundial
moto gp|apuestas mundial motogp|apuestas mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas mvp
nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas
nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba
playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos
hoy|apuestas nba tipster|apuestas nfl|apuestas nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas
nhl pronosticos|apuestas octavos eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online bono|apuestas online bono bienvenida|apuestas online
boxeo|apuestas online caballos|apuestas online carreras de caballos|apuestas online casino|apuestas online
champions league|apuestas online chile|apuestas online ciclismo|apuestas
online colombia|apuestas online comparativa|apuestas
online con paypal|apuestas online de caballos|apuestas online deportivas|apuestas online en argentina|apuestas online en peru|apuestas
online espana|apuestas online españa|apuestas online esports|apuestas
online foro|apuestas online futbol|apuestas online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online juegos|apuestas
online mexico|apuestas online mma|apuestas
online movil|apuestas online nba|apuestas online net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online peru|apuestas online seguras|apuestas online sin dinero|apuestas online
sin registro|apuestas online tenis|apuestas online ufc|apuestas online uruguay|apuestas online
venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna
real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas over|apuestas
over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos ecuador|apuestas paises bajos inglaterra|apuestas países bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para
el clasico|apuestas para el dia de hoy|apuestas
para el mundial|apuestas para el partido de hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas
para ganar|apuestas para ganar dinero|apuestas
para ganar dinero facil|apuestas para ganar en la ruleta|apuestas para ganar la champions|apuestas para ganar la eurocopa|apuestas para ganar la europa league|apuestas para ganar la liga|apuestas
para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas para hoy de futbol|apuestas para hoy europa league|apuestas para hoy futbol|apuestas para juegos|apuestas para la champions
league|apuestas para la copa del rey|apuestas para
la eurocopa|apuestas para la europa league|apuestas para la final de la eurocopa|apuestas
para la nba hoy|apuestas para los partidos de hoy|apuestas para
partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido
champions|apuestas partido colombia|apuestas partido españa marruecos|apuestas
partido mundial|apuestas partido suspendido|apuestas
partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos de hoy|apuestas
partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos
mundial|apuestas paypal|apuestas peleas de boxeo|apuestas peru|apuestas perú|apuestas
peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru
vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff segunda|apuestas
playoff segunda b|apuestas playoffs nba|apuestas playoffs
nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por internet para ganar dinero|apuestas por paypal|apuestas por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas
predicciones futbol|apuestas primera division|apuestas
primera division españa|apuestas promociones|apuestas pronostico|apuestas pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas psg
barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas
que siempre ganaras|apuestas que significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana eurocopa|apuestas quien gana la
champions|apuestas quien gana la eurocopa|apuestas quien gana la liga|apuestas quien ganara el
mundial|apuestas quién ganará el mundial|apuestas quien ganara la champions|apuestas quien ganara la eurocopa|apuestas quien ganara
la liga|apuestas rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas
real madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real madrid atletico de madrid|apuestas real madrid atlético de madrid|apuestas
real madrid atletico madrid|apuestas real madrid barcelona|apuestas real madrid bayern|apuestas real madrid betis|apuestas real madrid borussia|apuestas real madrid campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real
madrid city|apuestas real madrid girona|apuestas
real madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real
madrid osasuna|apuestas real madrid real sociedad|apuestas real madrid valencia|apuestas real madrid villarreal|apuestas real madrid vs arsenal|apuestas real madrid vs atletico|apuestas real madrid
vs atlético|apuestas real madrid vs atletico madrid|apuestas real madrid vs barcelona|apuestas real madrid vs
betis|apuestas real madrid vs sevilla|apuestas real madrid vs
valencia|apuestas real sociedad|apuestas real sociedad
athletic|apuestas real sociedad barcelona|apuestas real sociedad
betis|apuestas real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas
roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas
segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas
seguras calculadora|apuestas seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas seguras hoy|apuestas seguras
hoy futbol|apuestas seguras nba|apuestas seguras nba hoy|apuestas seguras
para este fin de semana|apuestas seguras para ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy
pronósticos|apuestas seguras para mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales
eurocopa|apuestas senegal paises bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la liga|apuestas sevilla girona|apuestas sevilla
inter|apuestas sevilla jugador|apuestas sevilla
juventus|apuestas sevilla leganes|apuestas sevilla madrid|apuestas sevilla
manchester united|apuestas sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples
ejemplos|apuestas simples o combinadas|apuestas
sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas sin empate que significa|apuestas
sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema
calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo
copa del rey|apuestas stake|apuestas stake 10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa
españa|apuestas superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis
atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis
hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas tenis
retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas
tenis wimbledon|apuestas tenis wta|apuestas tercera division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas
torneos de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas
ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas
uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas
us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas valencia madrid|apuestas valencia real madrid|apuestas valladolid
barcelona|apuestas valladolid valencia|apuestas valor
app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs
real madrid|apuestas virtuales|apuestas virtuales
colombia|apuestas virtuales futbol|apuestas virtuales
sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta españa|apuestas william hill partidos de hoy|apuestas y casino|apuestas y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas y pronosticos de futbol|apuestas y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es
pronosticos|arbitro nba apuestas|argentina apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia
apuestas|argentina mexico apuestas|argentina peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs
chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de madrid apuestas|atlético de
madrid apuestas|atletico de madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs real madrid apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter
apuestas|barca madrid apuestas|barça madrid apuestas|barca vs atletico apuestas|barca
vs madrid apuestas|barca vs real madrid apuestas|barcelona –
real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona atletico de madrid apuestas|barcelona
atletico madrid apuestas|barcelona betis apuestas|barcelona casa
de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs betis
apuestas|barcelona vs celta de vigo apuestas|barcelona vs
espanyol apuestas|barcelona vs girona apuestas|barcelona
vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real sociedad apuestas|barcelona vs sevilla apuestas|barcelona
vs villarreal apuestas|base de datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best
america apuestas|bet apuestas chile|bet apuestas
en vivo|betis – chelsea apuestas|betis apuestas|betis barcelona apuestas|betis chelsea
apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog apuestas baloncesto|blog apuestas
ciclismo|blog apuestas nba|blog apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono bienvenida apuestas|bono bienvenida
apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas
sin deposito|bono bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida
marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono
casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas deportivas|bono de bienvenida casa de
apuestas|bono de bienvenida casas de apuestas|bono de casas
de apuestas|bono de registro apuestas|bono de registro apuestas deportivas|bono de registro casa de apuestas|bono gratis
apuestas|bono marca apuestas|bono por registro apuestas|bono por registro apuestas deportivas|bono por registro casa
de apuestas|bono registro apuestas|bono sin deposito apuestas|bono
sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas
deportivas|bonos apuestas|bonos apuestas colombia|bonos apuestas
deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas
sin deposito|bonos apuestas sin depósito|bonos bienvenida
apuestas|bonos bienvenida casas apuestas|bonos bienvenida
casas de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos casas de apuestas|bonos casas de apuestas
colombia|bonos casas de apuestas deportivas|bonos casas de apuestas españa|bonos casas de apuestas nuevas|bonos casas de apuestas sin deposito|bonos casas de
apuestas sin depósito|bonos de apuestas|bonos de apuestas deportivas|bonos de apuestas gratis|bonos
de apuestas sin deposito|bonos de bienvenida apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida casa de apuestas|bonos de
bienvenida casas de apuestas|bonos de bienvenida de casas de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de
casas de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos
paginas de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil
peru apuestas|brasil vs colombia apuestas|buenas apuestas
para hoy|buscador cuotas apuestas|buscador de apuestas
seguras|buscador de cuotas apuestas|buscador de cuotas de apuestas|buscar apuestas
seguras|caballos apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas combinadas|calculadora
apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora apuestas seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora de apuestas combinadas|calculadora de apuestas de futbol|calculadora de apuestas de
sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas
seguras|calculadora de apuestas sistema|calculadora de apuestas surebets|calculadora de
arbitraje apuestas|calculadora de cuotas apuestas|calculadora de cuotas
de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas
deportivas|calculadora poisson para apuestas|calculadora
scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora
trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas futbol|calcular apuestas sistema|calcular cuotas
apuestas|calcular cuotas apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad cuota apuestas|calcular
stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas
apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera
de caballos con apuestas|carrera de galgos apuestas|carreras de caballos apuestas|carreras de caballos apuestas online|carreras de caballos con apuestas|carreras de caballos juegos de
apuestas|carreras de galgos apuestas|carreras de galgos
apuestas online|carreras de galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas
atletico de madrid|casa apuestas barcelona|casa apuestas
betis|casa apuestas bono bienvenida|casa apuestas bono gratis|casa apuestas
bono sin deposito|casa apuestas cerca de mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa apuestas futbol|casa apuestas mejores
cuotas|casa apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa apuestas valencia|casa
de apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de
apuestas atletico de madrid|casa de apuestas
baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de apuestas
bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa de apuestas
bono gratis|casa de apuestas bono por registro|casa de apuestas bono
sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras de caballos|casa de apuestas cerca de mi|casa de apuestas cerca de mí|casa de apuestas champions
league|casa de apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa de apuestas con bono sin deposito|casa de apuestas con cuotas mas altas|casa
de apuestas con esports|casa de apuestas con las
mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas
con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de apuestas copa america|casa de apuestas de
caballos|casa de apuestas de colombia|casa de apuestas de españa|casa de apuestas de futbol|casa de apuestas
de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de apuestas del real
madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca de mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa
de apuestas deportivas en españa|casa de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas españolas|casa de apuestas deportivas madrid|casa de apuestas deportivas
mexico|casa de apuestas deportivas online|casa de apuestas deportivas peru|casa de apuestas deposito 5 euros|casa de
apuestas deposito minimo|casa de apuestas deposito minimo 1 euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa
de apuestas en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas españa inglaterra|casa de apuestas
española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa
league|casa de apuestas f1|casa de apuestas formula
1|casa de apuestas futbol|casa de apuestas ingreso minimo|casa de
apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa de apuestas legales en colombia|casa de apuestas legales en españa|casa de apuestas libertadores|casa de apuestas liga española|casa de apuestas madrid|casa
de apuestas mas segura|casa de apuestas mejores|casa de apuestas méxico|casa
de apuestas minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de
apuestas nba|casa de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del real madrid|casa de apuestas oficial real madrid|casa
de apuestas online|casa de apuestas online argentina|casa de apuestas online chile|casa de apuestas online españa|casa de apuestas online mexico|casa de apuestas online paraguay|casa de apuestas online
peru|casa de apuestas online usa|casa de apuestas online venezuela|casa
de apuestas pago anticipado|casa de apuestas para boxeo|casa de apuestas para ufc|casa de apuestas peru|casa
de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa
de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa
de apuestas regalo de bienvenida|casa de apuestas
sevilla|casa de apuestas sin dinero|casa
de apuestas sin ingreso minimo|casa de apuestas
sin licencia en españa|casa de apuestas sin minimo de ingreso|casa de apuestas stake|casa de apuestas tenis|casa de apuestas ufc|casa de apuestas valencia|casa de
apuestas venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas
apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas legales|casas apuestas
legales españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas
mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas apuestas paypal|casas apuestas
peru|casas apuestas sin licencia|casas apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de apuestas 5
euros|casas de apuestas app|casas de apuestas argentinas|casas de
apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono de bienvenida|casas
de apuestas bono por registro|casas de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas de
apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas
bonos gratis|casas de apuestas bonos sin deposito|casas
de apuestas boxeo|casas de apuestas caballos|casas de apuestas carreras de caballos|casas de apuestas casino|casas de apuestas casino online|casas de
apuestas cerca de mi|casas de apuestas champions
league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de
apuestas con apuestas gratis|casas de apuestas con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono de registro|casas de apuestas con bono por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de
apuestas con bonos sin deposito|casas de apuestas con deposito minimo|casas
de apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas de apuestas con licencia
en españa|casas de apuestas con licencia
españa|casas de apuestas con licencia española|casas de
apuestas con mejores cuotas|casas de apuestas con pago anticipado|casas
de apuestas con paypal|casas de apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta
en vivo|casas de apuestas copa del rey|casas
de apuestas de caballos|casas de apuestas de españa|casas de apuestas de futbol|casas
de apuestas de fútbol|casas de apuestas de peru|casas de apuestas deportivas|casas
de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas de apuestas deportivas con paypal|casas de
apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de
apuestas deportivas en mexico|casas de apuestas deportivas en peru|casas de apuestas
deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas
deportivas españa|casas de apuestas deportivas españolas|casas de apuestas deportivas legales|casas de apuestas deportivas madrid|casas de apuestas deportivas
mexico|casas de apuestas deportivas nuevas|casas de
apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas deposito minimo 1 euro|casas de apuestas
depósito mínimo 1 euro|casas de apuestas dinero gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa online|casas de apuestas en linea|casas de
apuestas en madrid|casas de apuestas en méxico|casas de apuestas
en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas de
apuestas en venezuela|casas de apuestas equipos de futbol|casas
de apuestas españa|casas de apuestas españa alemania|casas de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas de apuestas españa online|casas
de apuestas española|casas de apuestas españolas|casas de apuestas españolas con licencia|casas de
apuestas españolas online|casas de apuestas esports|casas de
apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas de apuestas f1|casas de apuestas fisicas
en barcelona|casas de apuestas fisicas en españa|casas de
apuestas formula 1|casas de apuestas fuera de españa|casas de
apuestas futbol|casas de apuestas fútbol|casas de apuestas
futbol españa|casas de apuestas ganador eurocopa|casas de apuestas gratis|casas de apuestas
ingreso minimo|casas de apuestas ingreso minimo 1 euro|casas de apuestas ingreso minimo 5
euros|casas de apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas de apuestas legales
en mexico|casas de apuestas legales españa|casas de apuestas legales mx|casas
de apuestas licencia|casas de apuestas licencia españa|casas de apuestas lista|casas de apuestas madrid|casas de apuestas mas seguras|casas de
apuestas mejores bonos|casas de apuestas mejores cuotas|casas de apuestas mexico|casas
de apuestas méxico|casas de apuestas minimo 5 euros|casas
de apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de apuestas
nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas
de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas
nuevas en españa|casas de apuestas nuevas españa|casas de
apuestas ofertas|casas de apuestas online|casas de apuestas online argentina|casas de apuestas online colombia|casas
de apuestas online deportivas|casas de apuestas online ecuador|casas
de apuestas online en argentina|casas de apuestas
online en chile|casas de apuestas online en colombia|casas de apuestas online en españa|casas
de apuestas online en mexico|casas de apuestas online
españa|casas de apuestas online mas fiables|casas
de apuestas online mexico|casas de apuestas
online nuevas|casas de apuestas online peru|casas de apuestas online usa|casas
de apuestas online venezuela|casas de apuestas pago
paypal|casas de apuestas para ufc|casas de apuestas paypal|ca
clickenginepro.click – Loved the layout today; clean, simple, and genuinely user-friendly overall.
seojet.click – Mobile version looks perfect; no glitches, fast scrolling, crisp text.
trafficstream.click – Mobile version looks perfect; no glitches, fast scrolling, crisp text.
Je suis completement seduit par Azur Casino, on y trouve une energie contagieuse. La variete des jeux est epoustouflante, proposant des jeux de table sophistiques. Il rend le debut de l’aventure palpitant. Le support est rapide et professionnel. Les transactions sont d’une fiabilite absolue, de temps a autre des recompenses additionnelles seraient ideales. En somme, Azur Casino est un incontournable pour les joueurs. Notons egalement la navigation est simple et intuitive, booste le fun du jeu. Un atout les tournois frequents pour l’adrenaline, cree une communaute vibrante.
Obtenir plus|
Je suis enthousiasme par Azur Casino, il cree une experience captivante. La bibliotheque de jeux est captivante, offrant des tables live interactives. 100% jusqu’a 500 € + tours gratuits. Le support est fiable et reactif. Les transactions sont fiables et efficaces, par moments des offres plus importantes seraient super. En somme, Azur Casino vaut une exploration vibrante. Pour ajouter le site est rapide et engageant, apporte une touche d’excitation. A mettre en avant les evenements communautaires vibrants, propose des avantages uniques.
Lire la suite|
Работаем с этой компанией уже больше полугода, полностью довольны сопровождением ВЭД. Все этапы от оформления контрактов до прохождения таможни выполняются точно и без задержек. Особенно приятно, что специалисты всегда на связи и оперативно решают возникающие вопросы по импорту: https://vedsoprovozhdenie1.ru/
A Technical Regulations is a regulatory legal act that establishes mandatory requirements for products Russian GOST technical industry standards, norms and regulations, specifications and technical publications both in Russian and English
https://shorturl.fm/jqeZT
The research institute of standardization, metrology and certification is the only research institute Russian standards in English
J’ai un veritable coup de c?ur pour Azur Casino, il cree une experience captivante. La bibliotheque de jeux est captivante, proposant des jeux de casino traditionnels. Il booste votre aventure des le depart. Le support est fiable et reactif. Les retraits sont simples et rapides, mais plus de promotions frequentes boosteraient l’experience. Pour finir, Azur Casino est un endroit qui electrise. A souligner la plateforme est visuellement dynamique, ce qui rend chaque session plus palpitante. Un element fort les evenements communautaires engageants, propose des privileges sur mesure.
Touchez ici|
J’ai un veritable coup de c?ur pour Azur Casino, c’est une plateforme qui pulse avec energie. Les titres proposes sont d’une richesse folle, incluant des options de paris sportifs dynamiques. Le bonus de bienvenue est genereux. Le support client est irreprochable. Le processus est fluide et intuitif, par moments quelques tours gratuits en plus seraient geniaux. Globalement, Azur Casino assure un fun constant. Ajoutons aussi l’interface est fluide comme une soiree, permet une immersion complete. Un avantage les paiements en crypto rapides et surs, offre des recompenses regulieres.
Visiter aujourd’hui|
Je suis accro a Lucky 31 Casino, ca transporte dans un monde d’excitation. La gamme est variee et attrayante, incluant des paris sportifs en direct. Avec des depots rapides et faciles. Le service client est excellent. Les retraits sont lisses comme jamais, occasionnellement quelques tours gratuits en plus seraient geniaux. Globalement, Lucky 31 Casino garantit un plaisir constant. D’ailleurs le design est moderne et attrayant, ce qui rend chaque moment plus vibrant. Un element fort les options de paris sportifs diversifiees, garantit des paiements securises.
Apprendre les dГ©tails|
J’adore l’ambiance electrisante de 1xBet Casino, ca donne une vibe electrisante. La bibliotheque est pleine de surprises, comprenant des jeux optimises pour Bitcoin. 100% jusqu’a 500 € plus des tours gratuits. Le service est disponible 24/7. Les retraits sont ultra-rapides, neanmoins des bonus diversifies seraient un atout. En bref, 1xBet Casino offre une aventure memorable. En complement le design est style et moderne, apporte une energie supplementaire. Egalement excellent les tournois frequents pour l’adrenaline, qui motive les joueurs.
Cliquer pour voir|
Je suis captive par Action Casino, ca transporte dans un univers de plaisirs. Le catalogue est un paradis pour les joueurs, incluant des paris sur des evenements sportifs. Avec des depots instantanes. Le support est pro et accueillant. Le processus est clair et efficace, parfois des offres plus genereuses seraient top. En resume, Action Casino est une plateforme qui pulse. En plus le design est style et moderne, permet une immersion complete. Particulierement interessant les evenements communautaires pleins d’energie, garantit des paiements securises.
Visiter la plateforme|
https://optimilegozization.in.net/ f8bet hiếp dâm
Je suis accro a 1xBet Casino, ca offre une experience immersive. Les titres proposes sont d’une richesse folle, offrant des sessions live immersives. Avec des depots fluides. Disponible 24/7 par chat ou email. Les gains sont verses sans attendre, de temps a autre des offres plus genereuses seraient top. En bref, 1xBet Casino assure un fun constant. A signaler l’interface est lisse et agreable, booste le fun du jeu. Un bonus les paiements en crypto rapides et surs, propose des privileges sur mesure.
Essayer ceci|
J’adore l’ambiance electrisante de 1xBet Casino, il cree un monde de sensations fortes. Il y a une abondance de jeux excitants, comprenant des jeux compatibles avec les cryptos. Le bonus de depart est top. Le support est pro et accueillant. Les paiements sont surs et efficaces, malgre tout des bonus diversifies seraient un atout. Au final, 1xBet Casino est un must pour les passionnes. En plus le design est style et moderne, donne envie de prolonger l’aventure. A signaler les evenements communautaires engageants, offre des recompenses regulieres.
Aller plus loin|
(10 euros gratis apuestas|10 mejores casas de apuestas|10
trucos para ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas que significa|1×2
en apuestas|1×2 en apuestas que significa|1×2
que significa en apuestas|5 euros gratis apuestas|9 apuestas que siempre ganaras|a partir de cuanto se
declara apuestas|actividades de juegos de azar y apuestas|ad apuestas deportivas|aleksandre topuria ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas
deportivas|aplicacion apuestas deportivas android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas deportivas android|aplicaciones
apuestas deportivas gratis|aplicaciones de apuestas
android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones de apuestas deportivas
perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de apuestas
online|aplicaciones de apuestas seguras|aplicaciones de apuestas
sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas deportivas|app android apuestas deportivas|app apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas
argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app apuestas
deportivas gratis|app apuestas entre amigos|app apuestas futbol|app apuestas gratis|app apuestas
sin dinero|app casa de apuestas|app casas de apuestas|app control apuestas|app de
apuestas|app de apuestas android|app de apuestas casino|app de apuestas colombia|app
de apuestas con bono de bienvenida|app de apuestas de futbol|app
de apuestas deportivas|app de apuestas deportivas android|app de apuestas
deportivas argentina|app de apuestas deportivas colombia|app de apuestas deportivas en españa|app de apuestas deportivas peru|app de apuestas
deportivas perú|app de apuestas deportivas sin dinero|app
de apuestas ecuador|app de apuestas en colombia|app de
apuestas en españa|app de apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app de apuestas online|app
de apuestas para android|app de apuestas para
ganar dinero|app de apuestas peru|app de apuestas reales|app de casas de apuestas|app
marca apuestas android|app moviles de apuestas|app para
apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas
en español|app para ganar apuestas deportivas|app para hacer
apuestas|app para hacer apuestas deportivas|app para hacer apuestas entre
amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas
mundial|apps de apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de futbol|apps de apuestas deportivas peru|apps de apuestas mexico|apps para apuestas|aprender a hacer
apuestas deportivas|aprender hacer apuestas deportivas|apuesta del dia
apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2
division|apuestas 3 division|apuestas a caballos|apuestas a carreras de caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas a la baja|apuestas a la nfl|apuestas al barcelona|apuestas
al dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas
alcaraz hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas
argentina campeon del mundo|apuestas argentina canada|apuestas argentina colombia|apuestas
argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina francia cuanto paga|apuestas argentina
francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina
mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas argentina polonia|apuestas argentina uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs
peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso
a primera division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic
barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas athletic real
sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic valencia|apuestas
atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas
atletico campeon de liga|apuestas atlético copenhague|apuestas atletico de
madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas
atletico de madrid gana la liga|apuestas atletico de madrid
real madrid|apuestas atlético de madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid
real madrid|apuestas atletico madrid vs barcelona|apuestas atletico real madrid|apuestas
atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto
acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas
baloncesto pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas
barca atletico|apuestas barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas
barca hoy|apuestas barça hoy|apuestas barca inter|apuestas barca juventus|apuestas barca madrid|apuestas
barça madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas barca vs
madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas barcelona atletico de madrid|apuestas barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas barcelona campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas barcelona gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona
hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas
barcelona psg|apuestas barcelona real madrid|apuestas barcelona real sociedad|apuestas barcelona sevilla|apuestas barcelona
valencia|apuestas barcelona villarreal|apuestas barcelona vs atletico madrid|apuestas barcelona vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas
bayern barcelona|apuestas bayern vs barcelona|apuestas
beisbol|apuestas béisbol|apuestas beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas
betis barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas
betis madrid|apuestas betis mallorca|apuestas betis real madrid|apuestas betis real sociedad|apuestas betis
sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis vs valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas billar online|apuestas
bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas bono de bienvenida|apuestas bono
de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas
bonos sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos
españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas
campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas campeon copa america|apuestas campeon copa
del rey|apuestas campeon de champions|apuestas campeon de la champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas
campeon europa league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas
campeon liga santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas campeonato f1|apuestas
campeonatos de futbol|apuestas carrera de caballos|apuestas carrera de caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera
de galgos nocturnas|apuestas carreras caballos|apuestas carreras caballos sanlucar|apuestas carreras de caballos|apuestas carreras de caballos en directo|apuestas carreras de caballos en vivo|apuestas carreras de caballos españa|apuestas carreras de caballos hoy|apuestas carreras de caballos nacionales|apuestas carreras de caballos
nocturnas|apuestas carreras de caballos online|apuestas carreras de caballos sanlucar|apuestas
carreras de caballos sanlúcar|apuestas carreras de galgos|apuestas carreras de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas carreras de galgos pre partido|apuestas casino|apuestas casino
barcelona|apuestas casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino
online argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas celta
betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas celta madrid|apuestas celta manchester|apuestas celta real
madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions
league|apuestas champions league – pronósticos|apuestas champions league 2025|apuestas champions league
hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas
chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo tour francia|apuestas ciclismo
vuelta|apuestas ciclismo vuelta a españa|apuestas ciclismo
vuelta españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas clasico
español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas
colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas
de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas futbol|apuestas combinadas
hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas
nba|apuestas combinadas para esta semana|apuestas combinadas para hoy|apuestas combinadas
para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas combinadas
seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas
con dinero real|apuestas con dinero virtual|apuestas
con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de credito|apuestas con tarjeta
de debito|apuestas consejos|apuestas copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas copa davis|apuestas copa
de europa|apuestas copa del mundo|apuestas copa del
rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas copa del rey futbol|apuestas
copa del rey ganador|apuestas copa del rey hoy|apuestas copa del rey pronosticos|apuestas
copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de hockey|apuestas copa rey|apuestas copa sudamericana|apuestas
corners|apuestas corners hoy|apuestas croacia argentina|apuestas
cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1
euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto para hoy|apuestas de beisbol|apuestas
de beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas
de boxeo canelo|apuestas de boxeo en las vegas|apuestas de boxeo hoy|apuestas de boxeo online|apuestas de caballo|apuestas de caballos|apuestas de caballos como funciona|apuestas de caballos como se juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas de caballos españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas de caballos juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de
caballos por internet|apuestas de caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera de caballos|apuestas de
carreras de caballos|apuestas de carreras de caballos online|apuestas
de casino|apuestas de casino online|apuestas
de casino por internet|apuestas de champions league|apuestas de ciclismo|apuestas de
colombia|apuestas de copa america|apuestas de corners|apuestas de deportes en linea|apuestas de
deportes online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas de europa league|apuestas de f1|apuestas de formula 1|apuestas de
futbol|apuestas de fútbol|apuestas de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de futbol en colombia|apuestas de
futbol en directo|apuestas de futbol en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de futbol hoy|apuestas de futbol mundial|apuestas de futbol online|apuestas de fútbol online|apuestas
de futbol para hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas de futbol para mañana|apuestas de futbol
peru|apuestas de futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas de futbol seguras para hoy|apuestas de
futbol sin dinero|apuestas de galgos|apuestas de galgos como ganar|apuestas de galgos en directo|apuestas de galgos online|apuestas de galgos trucos|apuestas
de golf|apuestas de hockey|apuestas de hockey sobre hielo|apuestas de hoy|apuestas
de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de juegos online|apuestas de la champions league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de la
europa league|apuestas de la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas
de la nba|apuestas de la nfl|apuestas de la ufc|apuestas
de mlb|apuestas de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas de peleas ufc|apuestas
de perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema
explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas de tenis hoy|apuestas
de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia de hoy|apuestas
del dia deportivas|apuestas del dia futbol|apuestas del mundial|apuestas del partido de hoy|apuestas
del real madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas
deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10
euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas android|apuestas deportivas
app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas
deportivas argentina legal|apuestas deportivas atletico de madrid|apuestas deportivas baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono
de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas
deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas deportivas cerca
de mi|apuestas deportivas champions league|apuestas deportivas
chile|apuestas deportivas ciclismo|apuestas deportivas colombia|apuestas
deportivas com|apuestas deportivas com foro|apuestas deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas
con dinero ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas deportivas consejos para ganar|apuestas deportivas copa
america|apuestas deportivas copa del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas
deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas
altas|apuestas deportivas de baloncesto|apuestas
deportivas de boxeo|apuestas deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas de peru|apuestas deportivas de tenis|apuestas deportivas del
dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas
deportivas en argentina|apuestas deportivas en chile|apuestas deportivas
en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas deportivas
en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas
en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas
deportivas estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas
europa league|apuestas deportivas f1|apuestas deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas foro futbol|apuestas deportivas
foro tenis|apuestas deportivas francia argentina|apuestas deportivas futbol|apuestas deportivas fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas deportivas
golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas deportivas
gratis sin deposito|apuestas deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas hoy|apuestas deportivas
impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas
deportivas la liga|apuestas deportivas legales|apuestas
deportivas legales en colombia|apuestas deportivas libres
de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga española|apuestas deportivas listado|apuestas deportivas listado clasico|apuestas deportivas
madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas
deportivas mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas nba hoy|apuestas deportivas nfl|apuestas
deportivas nhl|apuestas deportivas nuevas|apuestas deportivas ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas deportivas online
chile|apuestas deportivas online colombia|apuestas deportivas online en colombia|apuestas deportivas online
españa|apuestas deportivas online mexico|apuestas deportivas online paypal|apuestas
deportivas online peru|apuestas deportivas online por internet|apuestas
deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas
deportivas partido suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas deportivas perú|apuestas deportivas peru vs ecuador|apuestas deportivas predicciones|apuestas
deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas
deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas
deportivas pronosticos gratis|apuestas deportivas pronosticos nba|apuestas deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas
resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas
seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas
stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas
deportivas tenis|apuestas deportivas tenis de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas
deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a
segunda|apuestas descenso a segunda b|apuestas
descenso la liga|apuestas descenso primera division|apuestas descenso segunda|apuestas
dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas
directo|apuestas directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas
dobles|apuestas dobles y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas
draft nfl|apuestas ecuador vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas
en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas
en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos
virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas en la
eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea
futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea peru|apuestas en linea usa|apuestas
en los esports|apuestas en madrid|apuestas en méxico|apuestas en mexico online|apuestas en nba|apuestas en partidos
de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de tenis en directo|apuestas en perú|apuestas en sevilla|apuestas
en sistema|apuestas en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo
casino|apuestas en vivo futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas
en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas equipos
de futbol|apuestas españa|apuestas españa alemania|apuestas
españa alemania eurocopa|apuestas españa croacia|apuestas
españa eurocopa|apuestas españa francia|apuestas
españa francia eurocopa|apuestas españa gana el mundial|apuestas
españa gana eurocopa|apuestas españa gana mundial|apuestas
españa georgia|apuestas españa holanda|apuestas españa inglaterra|apuestas españa
inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa
paises bajos|apuestas español|apuestas español oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas
esports colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports
lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa
españa|apuestas eurocopa favoritos|apuestas eurocopa
femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa league hoy|apuestas europa league pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1 cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas
f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas
fáciles de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas
favoritos mundial|apuestas fc barcelona|apuestas final champions
cuotas|apuestas final champions league|apuestas
final champions peru|apuestas final copa|apuestas final copa america|apuestas final copa de europa|apuestas final copa del
rey|apuestas final copa europa|apuestas final copa libertadores|apuestas
final copa rey|apuestas final de copa|apuestas final de copa del rey|apuestas final del
mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas
finales de conferencia nfl|apuestas finales
nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula
1|apuestas fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas
francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas
futbol americano|apuestas futbol americano nfl|apuestas futbol argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas futbol españa|apuestas futbol español|apuestas fútbol español|apuestas
futbol eurocopa|apuestas futbol femenino|apuestas
futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas
futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol
mundial|apuestas futbol online|apuestas futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas
galgos en directo|apuestas galgos hoy|apuestas galgos
online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador champions league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas
ganador copa del rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la eurocopa|apuestas ganador de la liga|apuestas ganador
del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador
f1|apuestas ganador la liga|apuestas ganador liga española|apuestas ganador mundial|apuestas
ganador mundial baloncesto|apuestas ganador mundial
f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar liga|apuestas
ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona betis|apuestas girona campeon de liga|apuestas
girona campeon liga|apuestas girona gana la liga|apuestas girona real madrid|apuestas girona real sociedad|apuestas goleador
eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf
pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas gratis|apuestas gratis casino|apuestas gratis
con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas gratis
regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis
sports|apuestas gratis y ganar premios|apuestas grupo
a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas
handicap nba|apuestas handicap nfl|apuestas
hipicas online|apuestas hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas hockey hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda
argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas
inter barca|apuestas inter barcelona|apuestas juego|apuestas
juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador
sevilla|apuestas jugadores nba|apuestas kings league americas|apuestas la
liga|apuestas la liga española|apuestas la liga hoy|apuestas la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las vegas nfl|apuestas
league of legends mundial|apuestas legal|apuestas legales|apuestas legales en colombia|apuestas legales
en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas
libertadores|apuestas licencia|apuestas liga 1 peru|apuestas liga argentina|apuestas liga
bbva pronosticos|apuestas liga de campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones de hockey|apuestas liga españa|apuestas liga española|apuestas liga santander pronosticos|apuestas
ligas de futbol|apuestas linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas
madrid arsenal|apuestas madrid atletico|apuestas
madrid atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas madrid barca hoy|apuestas madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la
liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas
madrid valencia|apuestas madrid vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas mas seguras para hoy|apuestas masters
de golf|apuestas masters de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador
mundial|apuestas mejor jugador eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas mexico polonia|apuestas
méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb las vegas|apuestas
mlb para hoy|apuestas mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas
multiples como funcionan|apuestas multiples el gordo|apuestas
multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas mundial baloncesto|apuestas
mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial
ciclismo|apuestas mundial clubes|apuestas mundial de baloncesto|apuestas mundial de ciclismo|apuestas mundial
de clubes|apuestas mundial de futbol|apuestas mundial de
fútbol|apuestas mundial de rugby|apuestas mundial f1|apuestas
mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial
ganador|apuestas mundial lol|apuestas mundial moto gp|apuestas mundial motogp|apuestas mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba
consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas
nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas nfl
hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl
pronosticos|apuestas octavos eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online
bono|apuestas online bono bienvenida|apuestas online boxeo|apuestas online caballos|apuestas online carreras de caballos|apuestas online casino|apuestas online champions league|apuestas online chile|apuestas online
ciclismo|apuestas online colombia|apuestas online comparativa|apuestas online con paypal|apuestas online
de caballos|apuestas online deportivas|apuestas online
en argentina|apuestas online en peru|apuestas online espana|apuestas online españa|apuestas online esports|apuestas online foro|apuestas online futbol|apuestas online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online juegos|apuestas online mexico|apuestas online
mma|apuestas online movil|apuestas online nba|apuestas online net|apuestas
online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online peru|apuestas online seguras|apuestas online
sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online
ufc|apuestas online uruguay|apuestas online venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna real
madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos ecuador|apuestas paises bajos inglaterra|apuestas países bajos
qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de
hoy|apuestas para el mundial|apuestas para el partido de hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas para ganar|apuestas para ganar dinero|apuestas para ganar dinero facil|apuestas para ganar en la
ruleta|apuestas para ganar la champions|apuestas para ganar la eurocopa|apuestas para
ganar la europa league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas para hoy
de futbol|apuestas para hoy europa league|apuestas para hoy
futbol|apuestas para juegos|apuestas para la champions league|apuestas para la copa del
rey|apuestas para la eurocopa|apuestas para la europa league|apuestas para la final de la eurocopa|apuestas para la nba hoy|apuestas para los partidos de hoy|apuestas para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas partido
españa marruecos|apuestas partido mundial|apuestas partido suspendido|apuestas partidos|apuestas partidos champions league|apuestas partidos
csgo|apuestas partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas paypal|apuestas peleas de
boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff
segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por internet para ganar dinero|apuestas por paypal|apuestas
por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas
pronostico|apuestas pronosticos|apuestas pronosticos
deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos
nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas psg barcelona|apuestas puntos
por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas que
siempre ganaras|apuestas que significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana eurocopa|apuestas quien gana la champions|apuestas quien gana la eurocopa|apuestas
quien gana la liga|apuestas quien ganara el mundial|apuestas quién ganará el mundial|apuestas quien ganara la champions|apuestas quien ganara la eurocopa|apuestas quien ganara la
liga|apuestas rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real
madrid atletico de madrid|apuestas real madrid atlético de madrid|apuestas real madrid
atletico madrid|apuestas real madrid barcelona|apuestas
real madrid bayern|apuestas real madrid betis|apuestas real madrid borussia|apuestas real
madrid campeon champions|apuestas real madrid celta|apuestas real
madrid champions|apuestas real madrid city|apuestas real madrid girona|apuestas real madrid hoy|apuestas real madrid liverpool|apuestas
real madrid manchester city|apuestas real madrid osasuna|apuestas real madrid real sociedad|apuestas real madrid valencia|apuestas real
madrid villarreal|apuestas real madrid vs arsenal|apuestas
real madrid vs atletico|apuestas real madrid vs atlético|apuestas real madrid
vs atletico madrid|apuestas real madrid vs barcelona|apuestas
real madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real sociedad
betis|apuestas real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de bienvenida|apuestas
registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada
tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas
rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas seguras
en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas seguras futbol hoy|apuestas seguras
gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas
seguras nba hoy|apuestas seguras para este fin de semana|apuestas seguras
para ganar dinero|apuestas seguras para hoy|apuestas seguras
para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises bajos|apuestas
sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas
sevilla campeon liga|apuestas sevilla celta|apuestas sevilla
gana la liga|apuestas sevilla girona|apuestas sevilla inter|apuestas sevilla jugador|apuestas sevilla
juventus|apuestas sevilla leganes|apuestas
sevilla madrid|apuestas sevilla manchester united|apuestas sevilla
osasuna|apuestas sevilla real madrid|apuestas sevilla real sociedad|apuestas sevilla
roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o combinadas|apuestas sin deposito|apuestas sin deposito
inicial|apuestas sin deposito minimo|apuestas
sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas
sistema calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake 10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas
super rugby|apuestas supercopa españa|apuestas superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas
tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis de mesa
pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas tenis wimbledon|apuestas tenis
wta|apuestas tercera division|apuestas tercera division españa|apuestas
tipos|apuestas tips|apuestas tipster|apuestas
tipster para hoy|apuestas topuria holloway cuotas|apuestas torneos de golf|apuestas
torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas
ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc
telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas
us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia
betis|apuestas valencia madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta españa|apuestas william hill partidos de hoy|apuestas
y casino|apuestas y casinos|apuestas y juegos de azar|apuestas
y pronosticos|apuestas y pronosticos de futbol|apuestas y pronosticos deportivos|apuestas
y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina
apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina
mexico apuestas|argentina peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina
vs. colombia apuestas|asi se gana en las apuestas deportivas|asiatico
apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic osasuna apuestas|athletic
real madrid apuestas|atletico barcelona apuestas|atletico de madrid apuestas|atlético de madrid apuestas|atletico de
madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico
madrid real madrid apuestas|atletico madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs
real madrid apuestas|avisador de cuotas apuestas|bajada
de cuotas apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter
apuestas|barca madrid apuestas|barça madrid apuestas|barca vs atletico apuestas|barca vs
madrid apuestas|barca vs real madrid apuestas|barcelona
– real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona atletico de madrid apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona casa de apuestas|barcelona
inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona vs
atlético madrid apuestas|barcelona vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs
girona apuestas|barcelona vs madrid apuestas|barcelona vs real
madrid apuestas|barcelona vs real sociedad apuestas|barcelona
vs sevilla apuestas|barcelona vs villarreal apuestas|base de datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis barcelona
apuestas|betis chelsea apuestas|betis madrid apuestas|betis
sevilla apuestas|betsson tu sitio de apuestas online|blog apuestas
baloncesto|blog apuestas ciclismo|blog apuestas nba|blog apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis
sin deposito|bono apuestas sin deposito|bono bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas sin deposito|bono bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa
de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas deportivas|bono
de bienvenida casa de apuestas|bono de bienvenida casas de apuestas|bono de casas de apuestas|bono de registro apuestas|bono de registro
apuestas deportivas|bono de registro casa de apuestas|bono
gratis apuestas|bono marca apuestas|bono por registro apuestas|bono por registro apuestas deportivas|bono por registro
casa de apuestas|bono registro apuestas|bono sin deposito apuestas|bono sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono
sin ingreso apuestas deportivas|bonos apuestas|bonos apuestas
colombia|bonos apuestas deportivas|bonos apuestas deportivas sin deposito|bonos
apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida casas de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos
casas de apuestas|bonos casas de apuestas colombia|bonos casas de apuestas deportivas|bonos casas de apuestas
españa|bonos casas de apuestas nuevas|bonos casas de apuestas sin deposito|bonos
casas de apuestas sin depósito|bonos de apuestas|bonos de apuestas deportivas|bonos
de apuestas gratis|bonos de apuestas sin deposito|bonos
de bienvenida apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida casa de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida de casas de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de casas
de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de
apuestas|bonos gratis sin deposito apuestas|bonos paginas
de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito
apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de apuestas deportivas gratis|boxeo
apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas apuestas para hoy|buscador cuotas apuestas|buscador
de apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de apuestas|buscar apuestas seguras|caballos
apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas combinadas|calculadora apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora apuestas seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora
arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora
de apuestas|calculadora de apuestas combinadas|calculadora de apuestas de futbol|calculadora de apuestas de sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas surebets|calculadora de arbitraje apuestas|calculadora de cuotas apuestas|calculadora de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular cuotas apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad
cuota apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield
apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas
apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera
de caballos apuestas|carrera de caballos apuestas
juego|carrera de caballos con apuestas|carrera de
galgos apuestas|carreras de caballos apuestas|carreras de
caballos apuestas online|carreras de caballos con apuestas|carreras de caballos juegos
de apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras de galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas atletico de madrid|casa apuestas barcelona|casa apuestas betis|casa apuestas bono
bienvenida|casa apuestas bono gratis|casa apuestas bono
sin deposito|casa apuestas cerca de mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa apuestas futbol|casa apuestas mejores cuotas|casa apuestas mundial|casa
apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa apuestas valencia|casa de
apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de
apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de apuestas bono|casa de apuestas bono bienvenida|casa de
apuestas bono de bienvenida|casa de apuestas bono
gratis|casa de apuestas bono por registro|casa de apuestas bono sin deposito|casa
de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras de
caballos|casa de apuestas cerca de mi|casa de
apuestas cerca de mí|casa de apuestas champions league|casa
de apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa
de apuestas con bono de bienvenida|casa de apuestas con bono sin deposito|casa de apuestas con cuotas
mas altas|casa de apuestas con esports|casa de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa de
apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de apuestas
copa america|casa de apuestas de caballos|casa de apuestas de colombia|casa de apuestas de españa|casa de
apuestas de futbol|casa de apuestas de fútbol|casa
de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de apuestas del real madrid|casa de apuestas deportivas|casa
de apuestas deportivas cerca de mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa de apuestas
deportivas en españa|casa de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de
apuestas deportivas españolas|casa de apuestas deportivas
madrid|casa de apuestas deportivas mexico|casa de apuestas
deportivas online|casa de apuestas deportivas peru|casa de apuestas deposito 5 euros|casa de apuestas deposito minimo|casa
de apuestas deposito minimo 1 euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de
apuestas españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa de apuestas
esports|casa de apuestas eurocopa|casa de apuestas europa
league|casa de apuestas f1|casa de apuestas formula 1|casa de apuestas futbol|casa de apuestas ingreso minimo|casa de apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1
euro|casa de apuestas legales|casa de apuestas legales en colombia|casa de apuestas legales en españa|casa de apuestas
libertadores|casa de apuestas liga española|casa de apuestas madrid|casa de apuestas
mas segura|casa de apuestas mejores|casa de apuestas méxico|casa de apuestas minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de
apuestas nba|casa de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del
real madrid|casa de apuestas oficial real madrid|casa
de apuestas online|casa de apuestas online argentina|casa de apuestas online chile|casa de apuestas online
españa|casa de apuestas online mexico|casa
de apuestas online paraguay|casa de apuestas
online peru|casa de apuestas online usa|casa de apuestas online venezuela|casa de apuestas pago anticipado|casa de
apuestas para boxeo|casa de apuestas para ufc|casa de apuestas peru|casa de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa de
apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de bienvenida|casa de apuestas sevilla|casa
de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa de apuestas
sin licencia en españa|casa de apuestas sin minimo
de ingreso|casa de apuestas stake|casa de apuestas tenis|casa de apuestas ufc|casa de apuestas valencia|casa de apuestas venezuela|casa
de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas
apuestas bonos sin deposito|casas apuestas caballos|casas
apuestas chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas
colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas
apuestas deportivas nuevas|casas apuestas españa|casas apuestas
españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas
legales|casas apuestas legales españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas
mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas
apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de apuestas 5 euros|casas de
apuestas app|casas de apuestas argentinas|casas de apuestas
asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de
apuestas bono de bienvenida|casas de apuestas bono por registro|casas de
apuestas bono sin deposito|casas de apuestas
bono sin ingreso|casas de apuestas bonos|casas
de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas de apuestas carreras de
caballos|casas de apuestas casino|casas de apuestas casino online|casas de apuestas cerca de mi|casas de apuestas champions league|casas de
apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas
con app|casas de apuestas con apuestas gratis|casas de apuestas
con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono de
registro|casas de apuestas con bono por registro|casas de apuestas con bono
sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas con deposito minimo|casas de apuestas con esports|casas de apuestas
con handicap asiatico|casas de apuestas con licencia|casas de apuestas con licencia en españa|casas de apuestas con licencia
españa|casas de apuestas con licencia española|casas de apuestas
con mejores cuotas|casas de apuestas con pago anticipado|casas de apuestas con paypal|casas
de apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa
del rey|casas de apuestas de caballos|casas
de apuestas de españa|casas de apuestas de futbol|casas de
apuestas de fútbol|casas de apuestas de peru|casas de apuestas deportivas|casas de apuestas deportivas asiaticas|casas
de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas de apuestas deportivas con paypal|casas de
apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas en linea|casas
de apuestas deportivas en madrid|casas de apuestas deportivas
en mexico|casas de apuestas deportivas en peru|casas de apuestas
deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de apuestas deportivas españolas|casas
de apuestas deportivas legales|casas de apuestas deportivas
madrid|casas de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas de apuestas deportivas online|casas de apuestas deportivas
peru|casas de apuestas deportivas perú|casas de apuestas deposito minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de apuestas dinero gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas
de apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa online|casas de apuestas en linea|casas de apuestas en madrid|casas
de apuestas en méxico|casas de apuestas en peru|casas de apuestas en perú|casas
de apuestas en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas de apuestas en venezuela|casas de apuestas equipos de futbol|casas de apuestas españa|casas de apuestas españa alemania|casas
de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa
nuevas|casas de apuestas españa online|casas de apuestas española|casas de apuestas españolas|casas de
apuestas españolas con licencia|casas de apuestas españolas online|casas de apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas
de apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas en españa|casas
de apuestas formula 1|casas de apuestas fuera de españa|casas de apuestas futbol|casas de apuestas fútbol|casas de
apuestas futbol españa|casas de apuestas ganador eurocopa|casas de apuestas gratis|casas de apuestas ingreso minimo|casas
de apuestas ingreso minimo 1 euro|casas de apuestas ingreso minimo 5 euros|casas de apuestas inter barcelona|casas
de apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas de apuestas legales en mexico|casas de apuestas legales españa|casas de apuestas legales mx|casas de apuestas licencia|casas de apuestas
licencia españa|casas de apuestas lista|casas de apuestas
madrid|casas de apuestas mas seguras|casas de apuestas mejores bonos|casas de apuestas
mejores cuotas|casas de apuestas mexico|casas de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas mlb|casas de apuestas
mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de
apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas
nuevas en españa|casas de apuestas nuevas españa|casas
de apuestas ofertas|casas de apuestas online|casas de apuestas online argentina|casas de apuestas
online colombia|casas de apuestas online deportivas|casas de apuestas online
ecuador|casas de apuestas online en argentina|casas
de apuestas online en chile|casas de apuestas online
en colombia|casas de apuestas online en españa|casas de apuestas online en mexico|casas de apuestas
online españa|casas de apuestas online mas fiables|casas de apuestas online mexico|casas de apuestas
online nuevas|casas de apuestas online peru|casas de apuestas online usa|casas de apuestas online venezuela|casas de apuestas
pago paypal|casas de apuestas para ufc|casas de apuestas paypal|casas de apuestas peru bono sin deposito|casas de apuestas presenciales
en españa|casas de apuestas promociones|casas de apuestas que
Je suis completement seduit par Azur Casino, ca offre un plaisir vibrant. Il y a un eventail de titres captivants, offrant des tables live interactives. Avec des depots instantanes. Les agents sont toujours la pour aider. Les retraits sont lisses comme jamais, cependant des offres plus genereuses seraient top. Pour conclure, Azur Casino est un endroit qui electrise. Pour couronner le tout le design est moderne et energique, donne envie de prolonger l’aventure. Un point cle le programme VIP avec des privileges speciaux, renforce la communaute.
Aller voir|
Je suis enthousiaste a propos de Azur Casino, ca pulse comme une soiree animee. Il y a une abondance de jeux excitants, proposant des jeux de cartes elegants. Il booste votre aventure des le depart. Le service d’assistance est au point. Les gains sont verses sans attendre, bien que plus de promotions variees ajouteraient du fun. Au final, Azur Casino garantit un plaisir constant. En plus le site est rapide et immersif, facilite une immersion totale. Un bonus les transactions en crypto fiables, offre des recompenses regulieres.
VГ©rifier ceci|
J’adore la vibe de Action Casino, ca pulse comme une soiree animee. Les options sont aussi vastes qu’un horizon, comprenant des jeux crypto-friendly. Il donne un elan excitant. Le suivi est d’une precision remarquable. Les gains sont verses sans attendre, toutefois plus de promos regulieres dynamiseraient le jeu. Pour finir, Action Casino assure un fun constant. Ajoutons que le design est moderne et energique, facilite une experience immersive. A mettre en avant les tournois frequents pour l’adrenaline, offre des bonus constants.
Obtenir les dГ©tails|
Je ne me lasse pas de Lucky 31 Casino, c’est une plateforme qui deborde de dynamisme. La bibliotheque de jeux est captivante, avec des machines a sous aux themes varies. Le bonus de depart est top. Le suivi est d’une fiabilite exemplaire. Les gains arrivent en un eclair, toutefois quelques free spins en plus seraient bienvenus. En resume, Lucky 31 Casino est un incontournable pour les joueurs. Pour ajouter la navigation est simple et intuitive, donne envie de continuer l’aventure. A mettre en avant les paiements securises en crypto, propose des avantages uniques.
http://www.lucky31casino777fr.com|
J’adore l’energie de Action Casino, ca transporte dans un univers de plaisirs. Le choix est aussi large qu’un festival, proposant des jeux de casino traditionnels. Il propulse votre jeu des le debut. Disponible a toute heure via chat ou email. Les transactions sont d’une fiabilite absolue, de temps a autre des offres plus genereuses seraient top. En resume, Action Casino garantit un amusement continu. A noter la navigation est fluide et facile, amplifie l’adrenaline du jeu. Egalement top les tournois frequents pour l’adrenaline, qui booste la participation.
Voir plus|
Je suis emerveille par 1xBet Casino, il offre une experience dynamique. Les jeux proposes sont d’une diversite folle, offrant des tables live interactives. Il rend le debut de l’aventure palpitant. Les agents repondent avec rapidite. Les transactions sont toujours fiables, en revanche quelques free spins en plus seraient bienvenus. Dans l’ensemble, 1xBet Casino offre une aventure inoubliable. A noter la navigation est intuitive et lisse, amplifie le plaisir de jouer. Egalement top les transactions crypto ultra-securisees, renforce le lien communautaire.
Apprendre les dГ©tails|
J’adore la vibe de 1xBet Casino, c’est un lieu ou l’adrenaline coule a flots. Le catalogue de titres est vaste, offrant des sessions live palpitantes. 100% jusqu’a 500 € avec des spins gratuits. Disponible 24/7 par chat ou email. Les gains sont verses sans attendre, a l’occasion des bonus varies rendraient le tout plus fun. Globalement, 1xBet Casino est une plateforme qui fait vibrer. De surcroit la plateforme est visuellement electrisante, ce qui rend chaque moment plus vibrant. Un avantage notable les tournois reguliers pour la competition, qui stimule l’engagement.
Commencer Г explorer|
Je suis totalement conquis par 1xBet Casino, il cree une experience captivante. Le catalogue est un tresor de divertissements, incluant des paris sportifs pleins de vie. Avec des depots instantanes. Les agents repondent avec rapidite. Les paiements sont surs et fluides, par contre des recompenses en plus seraient un bonus. Au final, 1xBet Casino vaut une exploration vibrante. En bonus le design est style et moderne, apporte une energie supplementaire. A mettre en avant les evenements communautaires engageants, cree une communaute vibrante.
Commencer Г explorer|
Je suis enthousiasme par Lucky 31 Casino, il cree un monde de sensations fortes. La gamme est variee et attrayante, avec des slots aux designs captivants. Il rend le debut de l’aventure palpitant. Le service d’assistance est au point. Les transactions sont fiables et efficaces, bien que plus de promotions frequentes boosteraient l’experience. Pour finir, Lucky 31 Casino garantit un plaisir constant. En extra le design est style et moderne, ajoute une vibe electrisante. Un plus les tournois reguliers pour s’amuser, offre des bonus constants.
Plonger dedans|
Je ne me lasse pas de Action Casino, on y trouve une vibe envoutante. La bibliotheque est pleine de surprises, comprenant des jeux crypto-friendly. Il offre un coup de pouce allechant. Disponible a toute heure via chat ou email. Les gains arrivent sans delai, malgre tout plus de promos regulieres ajouteraient du peps. Au final, Action Casino est un must pour les passionnes. En bonus l’interface est lisse et agreable, apporte une energie supplementaire. Un avantage les nombreuses options de paris sportifs, qui dynamise l’engagement.
Voir plus|
(10 euros gratis apuestas|10 mejores casas de apuestas|10
trucos para ganar apuestas|15 euros gratis marca apuestas|1×2
apuestas|1×2 apuestas deportivas|1×2 apuestas que significa|1×2 en apuestas|1×2 en apuestas
que significa|1×2 que significa en apuestas|5 euros gratis apuestas|9 apuestas que siempre ganaras|a partir de
cuanto se declara apuestas|actividades de juegos de azar y apuestas|ad apuestas deportivas|aleksandre
topuria ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba apuestas|aplicacion android
apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de
apuestas online|aplicacion para hacer apuestas|aplicacion para hacer apuestas de futbol|aplicación para hacer
apuestas de fútbol|aplicaciones apuestas deportivas android|aplicaciones
apuestas deportivas gratis|aplicaciones de apuestas android|aplicaciones de apuestas
de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones de apuestas deportivas perú|aplicaciones de apuestas
en colombia|aplicaciones de apuestas gratis|aplicaciones de apuestas online|aplicaciones de apuestas seguras|aplicaciones
de apuestas sin dinero|aplicaciones para hacer
apuestas|apostar seguro apuestas deportivas|app android apuestas
deportivas|app apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas argentina|app apuestas
deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app apuestas deportivas gratis|app apuestas entre amigos|app apuestas futbol|app apuestas gratis|app apuestas
sin dinero|app casa de apuestas|app casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de
apuestas casino|app de apuestas colombia|app de apuestas con bono de bienvenida|app
de apuestas de futbol|app de apuestas deportivas|app de apuestas deportivas android|app de apuestas deportivas argentina|app de apuestas deportivas colombia|app de apuestas deportivas en españa|app de apuestas
deportivas peru|app de apuestas deportivas perú|app de
apuestas deportivas sin dinero|app de apuestas ecuador|app de apuestas
en colombia|app de apuestas en españa|app de apuestas
en venezuela|app de apuestas futbol|app de apuestas gratis|app de apuestas
online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app de apuestas reales|app
de casas de apuestas|app marca apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para
ganar apuestas deportivas|app para hacer apuestas|app para hacer
apuestas deportivas|app para hacer apuestas entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps
de apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de
futbol|apps de apuestas deportivas peru|apps de apuestas
mexico|apps para apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas
deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros
gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2 division|apuestas 3 division|apuestas a caballos|apuestas a carreras de caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas a
la baja|apuestas a la nfl|apuestas al barcelona|apuestas
al dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz
hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas argentina canada|apuestas argentina colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina francia cuanto paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina
mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas argentina
polonia|apuestas argentina uruguay|apuestas argentina vs australia|apuestas argentina
vs colombia|apuestas argentina vs francia|apuestas argentina vs
peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas
athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas
athletic manchester|apuestas athletic manchester united|apuestas
athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas
athletic real sociedad|apuestas athletic real sociedad
final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de
liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas atletico de madrid gana la liga|apuestas atletico de madrid real madrid|apuestas atlético de madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid
real madrid|apuestas atletico madrid vs barcelona|apuestas
atletico real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas
baloncesto pronostico|apuestas baloncesto pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas barca atletico|apuestas
barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas barca hoy|apuestas barça hoy|apuestas barca
inter|apuestas barca juventus|apuestas barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas
barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas
barcelona athletic|apuestas barcelona atletico|apuestas barcelona atletico
de madrid|apuestas barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona
betis|apuestas barcelona campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas barcelona gana la champions|apuestas
barcelona girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas
barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas barcelona
psg|apuestas barcelona real madrid|apuestas barcelona real sociedad|apuestas
barcelona sevilla|apuestas barcelona valencia|apuestas barcelona villarreal|apuestas
barcelona vs atletico madrid|apuestas barcelona vs
madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas
bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas
betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas betis real madrid|apuestas betis real
sociedad|apuestas betis sevilla|apuestas betis valencia|apuestas
betis valladolid|apuestas betis vs valencia|apuestas
betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas billar online|apuestas
bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas
boxeo hoy|apuestas boxeo online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas
caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de
barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas
campeon conference league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas campeon de la champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa league|apuestas
campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas campeon liga santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas
campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas campeonato f1|apuestas campeonatos de futbol|apuestas carrera de caballos|apuestas carrera de caballos hoy|apuestas carrera de
caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas
carreras caballos|apuestas carreras caballos sanlucar|apuestas carreras de caballos|apuestas carreras
de caballos en directo|apuestas carreras de caballos en vivo|apuestas carreras
de caballos españa|apuestas carreras de caballos hoy|apuestas
carreras de caballos nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de caballos online|apuestas carreras de caballos sanlucar|apuestas carreras de caballos sanlúcar|apuestas carreras de galgos|apuestas carreras de
galgos en vivo|apuestas carreras de galgos nocturnas|apuestas carreras de galgos
pre partido|apuestas casino|apuestas casino barcelona|apuestas
casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas
celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas
celta madrid|apuestas celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions
league|apuestas champions league – pronósticos|apuestas champions league 2025|apuestas champions league hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas chelsea
barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile vs
uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas
ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta
a españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas city real
madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas colombia
brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia
vs brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas
combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas
foro|apuestas combinadas futbol|apuestas combinadas
hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas para
esta semana|apuestas combinadas para hoy|apuestas
combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas combinadas seguras|apuestas combinadas
seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas
con dinero real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta
de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas
copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas copa davis|apuestas copa de europa|apuestas copa del mundo|apuestas copa del
rey|apuestas copa del rey baloncesto|apuestas copa del rey
final|apuestas copa del rey futbol|apuestas copa del rey ganador|apuestas
copa del rey hoy|apuestas copa del rey pronosticos|apuestas copa del rey pronósticos|apuestas copa europa|apuestas
copa italia|apuestas copa libertadores|apuestas copa mundial de hockey|apuestas copa rey|apuestas copa sudamericana|apuestas
corners|apuestas corners hoy|apuestas croacia argentina|apuestas
cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas
de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto para hoy|apuestas de beisbol|apuestas de beisbol
para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas de boxeo en las vegas|apuestas de boxeo hoy|apuestas de boxeo online|apuestas de caballo|apuestas de caballos|apuestas de caballos como
funciona|apuestas de caballos como se juega|apuestas de caballos
en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas
de caballos españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas de caballos
juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas de caballos pronosticos|apuestas de caballos
pronósticos|apuestas de carrera de caballos|apuestas de carreras de caballos|apuestas de carreras de caballos online|apuestas de
casino|apuestas de casino online|apuestas de
casino por internet|apuestas de champions league|apuestas de ciclismo|apuestas de colombia|apuestas de copa america|apuestas de
corners|apuestas de deportes en linea|apuestas de deportes online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas
de europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas de futbol
app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de futbol en colombia|apuestas de
futbol en directo|apuestas de futbol en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de futbol hoy|apuestas
de futbol mundial|apuestas de futbol online|apuestas de fútbol online|apuestas de futbol para
hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas de futbol para mañana|apuestas de futbol
peru|apuestas de futbol pronosticos|apuestas de fútbol
pronósticos|apuestas de futbol seguras|apuestas de futbol seguras para
hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas de galgos como ganar|apuestas de
galgos en directo|apuestas de galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas de
hockey sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de
juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de juegos online|apuestas de la
champions league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de la liga|apuestas de
la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas
de la nfl|apuestas de la ufc|apuestas de mlb|apuestas
de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas
de peleas ufc|apuestas de perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema
como funciona|apuestas de sistema explicacion|apuestas
de sistema explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas de tenis
hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas
de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del
dia|apuestas del día|apuestas del dia de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas del
rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas
android|apuestas deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas
deportivas argentina futbol|apuestas deportivas argentina
legal|apuestas deportivas atletico de madrid|apuestas deportivas
baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas
boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas
campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions
league|apuestas deportivas chile|apuestas deportivas ciclismo|apuestas deportivas
colombia|apuestas deportivas com|apuestas deportivas com foro|apuestas deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas
deportivas con bonos gratis|apuestas deportivas con dinero
ficticio|apuestas deportivas con paypal|apuestas
deportivas con puntos virtuales|apuestas deportivas consejos|apuestas
deportivas consejos para ganar|apuestas deportivas copa america|apuestas deportivas copa del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas
corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas
altas|apuestas deportivas de baloncesto|apuestas deportivas de boxeo|apuestas deportivas de
colombia|apuestas deportivas de futbol|apuestas deportivas de
nba|apuestas deportivas de nhl|apuestas deportivas de peru|apuestas deportivas de tenis|apuestas deportivas del dia|apuestas
deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas
deportivas en chile|apuestas deportivas en colombia|apuestas
deportivas en directo|apuestas deportivas en españa|apuestas deportivas
en español|apuestas deportivas en linea|apuestas deportivas
en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es
pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas
deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias seguras|apuestas deportivas
eurocopa|apuestas deportivas europa league|apuestas deportivas f1|apuestas deportivas faciles
de ganar|apuestas deportivas formula 1|apuestas deportivas
foro|apuestas deportivas foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia
argentina|apuestas deportivas futbol|apuestas deportivas fútbol|apuestas deportivas futbol
argentino|apuestas deportivas futbol colombia|apuestas deportivas futbol español|apuestas deportivas
gana|apuestas deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas
deportivas gane|apuestas deportivas golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas deportivas gratis
sin deposito|apuestas deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas
legales|apuestas deportivas legales en colombia|apuestas deportivas libres
de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga española|apuestas
deportivas listado|apuestas deportivas listado clasico|apuestas deportivas madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas deportivas
mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas
mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas
mlb hoy|apuestas deportivas multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas
deportivas nba|apuestas deportivas nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas
deportivas ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas deportivas online chile|apuestas deportivas online
colombia|apuestas deportivas online en colombia|apuestas deportivas online españa|apuestas
deportivas online mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas deportivas online por internet|apuestas
deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para hoy|apuestas
deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas deportivas perú|apuestas deportivas peru
vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas
pronostico|apuestas deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos gratis|apuestas deportivas pronosticos nba|apuestas
deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas
real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas
deportivas seguras|apuestas deportivas seguras
foro|apuestas deportivas seguras hoy|apuestas
deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas
deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito
inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas
stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas deportivas tenis
de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas
tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas
uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas
deposito minimo 1 euro|apuestas descenso a segunda|apuestas descenso a segunda
b|apuestas descenso la liga|apuestas descenso primera division|apuestas
descenso segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas
dinero virtual|apuestas directas|apuestas directo|apuestas directo
futbol|apuestas division de honor juvenil|apuestas dnb|apuestas
doble oportunidad|apuestas doble resultado|apuestas
dobles|apuestas dobles y triples|apuestas dortmund barcelona|apuestas
draft nba|apuestas draft nfl|apuestas ecuador vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas
elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas en caballos|apuestas
en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas
en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas
en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas en la eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas
en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea
boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea
peru|apuestas en linea usa|apuestas en los esports|apuestas en madrid|apuestas en méxico|apuestas en mexico
online|apuestas en nba|apuestas en partidos de
futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de tenis
en directo|apuestas en perú|apuestas en sevilla|apuestas
en sistema|apuestas en stake|apuestas en tenis|apuestas en tenis
de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas en vivo
fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo
ufc|apuestas equipo mbappe|apuestas equipos de futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas
españa francia eurocopa|apuestas españa gana el mundial|apuestas españa gana eurocopa|apuestas españa gana mundial|apuestas
españa georgia|apuestas españa holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas
españa mundial|apuestas españa paises bajos|apuestas español|apuestas español oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas
espanyol villarreal|apuestas esport|apuestas esports|apuestas esports
colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro
copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas
eurocopa hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas
europa league|apuestas europa league hoy|apuestas europa league
pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas
f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1
cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas
f1 miami|apuestas f1 monaco|apuestas faciles de
ganar|apuestas fáciles de ganar|apuestas faciles para ganar|apuestas
favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas
favoritos mundial|apuestas fc barcelona|apuestas final champions cuotas|apuestas final
champions league|apuestas final champions peru|apuestas final
copa|apuestas final copa america|apuestas final copa de europa|apuestas final copa del rey|apuestas final copa europa|apuestas
final copa libertadores|apuestas final copa rey|apuestas final de copa|apuestas final de copa del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final
mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia nfl|apuestas finales nba|apuestas
fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula 1|apuestas fórmula
1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas
fútbol|apuestas futbol americano|apuestas futbol americano nfl|apuestas futbol
argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas
futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas futbol españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol juegos olimpicos|apuestas
futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas
galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador
champions league|apuestas ganador copa america|apuestas
ganador copa del rey|apuestas ganador copa del rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la
eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas
ganador europa league|apuestas ganador f1|apuestas ganador la
liga|apuestas ganador liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas
ganar eurocopa|apuestas ganar liga|apuestas ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas
ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas
girona real madrid|apuestas girona real sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas gratis|apuestas gratis casino|apuestas
gratis con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas
gratis por registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas
gratis sports|apuestas gratis y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas handicap nfl|apuestas hipicas
online|apuestas hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas hockey hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas
hoy futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter barcelona|apuestas juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas juegos online|apuestas
juegos virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings league americas|apuestas la
liga|apuestas la liga española|apuestas la liga hoy|apuestas la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las vegas
nfl|apuestas league of legends mundial|apuestas legal|apuestas legales|apuestas
legales en colombia|apuestas legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas libertadores|apuestas licencia|apuestas liga 1 peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas liga de
campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones de hockey|apuestas
liga españa|apuestas liga española|apuestas liga santander pronosticos|apuestas ligas de futbol|apuestas linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas
liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas madrid atletico|apuestas madrid atletico champions|apuestas
madrid barca|apuestas madrid barça|apuestas madrid barca hoy|apuestas
madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas
madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la
liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas
madrid osasuna|apuestas madrid sevilla|apuestas madrid valencia|apuestas madrid
vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester
city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas mas seguras para hoy|apuestas
masters de golf|apuestas masters de tenis|apuestas maximo goleador
eurocopa|apuestas maximo goleador mundial|apuestas mejor jugador eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas
mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas
mlb hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas mlb
pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial
ciclismo|apuestas mundial clubes|apuestas mundial de baloncesto|apuestas mundial de ciclismo|apuestas mundial de clubes|apuestas mundial de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial
f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas mundial moto gp|apuestas mundial
motogp|apuestas mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas
mundialistas|apuestas mvp eurocopa|apuestas mvp nba|apuestas mvp
nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all
star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba
hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas
nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas nfl
pronósticos|apuestas nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas
ofertas|apuestas online|apuestas online argentina|apuestas online argentina
legal|apuestas online bono|apuestas online bono bienvenida|apuestas online boxeo|apuestas online caballos|apuestas online
carreras de caballos|apuestas online casino|apuestas online champions league|apuestas online chile|apuestas online ciclismo|apuestas online
colombia|apuestas online comparativa|apuestas online con paypal|apuestas
online de caballos|apuestas online deportivas|apuestas online en argentina|apuestas online en peru|apuestas online espana|apuestas online
españa|apuestas online esports|apuestas online foro|apuestas online
futbol|apuestas online futbol españa|apuestas
online golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online juegos|apuestas online mexico|apuestas
online mma|apuestas online movil|apuestas online nba|apuestas
online net|apuestas online nuevas|apuestas online opiniones|apuestas online
paypal|apuestas online peru|apuestas online seguras|apuestas online
sin dinero|apuestas online sin registro|apuestas online tenis|apuestas
online ufc|apuestas online uruguay|apuestas online venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas
over|apuestas over 2.5|apuestas over under|apuestas
paginas|apuestas pago anticipado|apuestas paises bajos ecuador|apuestas paises bajos
inglaterra|apuestas países bajos qatar|apuestas para boxeo|apuestas para champions
league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para el mundial|apuestas para el partido de hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas para ganar|apuestas para ganar
dinero|apuestas para ganar dinero facil|apuestas para ganar
en la ruleta|apuestas para ganar la champions|apuestas para ganar
la eurocopa|apuestas para ganar la europa league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas para hoy de futbol|apuestas para hoy europa league|apuestas para hoy futbol|apuestas para juegos|apuestas para la champions league|apuestas para la copa del rey|apuestas para
la eurocopa|apuestas para la europa league|apuestas para la final de la eurocopa|apuestas para la nba hoy|apuestas para los partidos de hoy|apuestas
para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas partido españa marruecos|apuestas partido
mundial|apuestas partido suspendido|apuestas partidos|apuestas
partidos champions league|apuestas partidos csgo|apuestas
partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas paypal|apuestas peleas
de boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas
pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff
ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff segunda|apuestas
playoff segunda b|apuestas playoffs nba|apuestas playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por
internet para ganar dinero|apuestas por paypal|apuestas por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre
partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas
pronostico|apuestas pronosticos|apuestas pronosticos deportivos|apuestas
pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas
pronosticos tenis|apuestas prorroga|apuestas
psg barca|apuestas psg barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes
hacer con tu novia|apuestas que siempre ganaras|apuestas que
significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana
eurocopa|apuestas quien gana la champions|apuestas quien gana la eurocopa|apuestas quien gana la liga|apuestas
quien ganara el mundial|apuestas quién ganará el
mundial|apuestas quien ganara la champions|apuestas
quien ganara la eurocopa|apuestas quien ganara la liga|apuestas rayo
barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real madrid atletico de madrid|apuestas real madrid atlético de madrid|apuestas real madrid atletico madrid|apuestas real madrid barcelona|apuestas real madrid bayern|apuestas real
madrid betis|apuestas real madrid borussia|apuestas real
madrid campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas
real madrid city|apuestas real madrid girona|apuestas real
madrid hoy|apuestas real madrid liverpool|apuestas
real madrid manchester city|apuestas real madrid osasuna|apuestas real
madrid real sociedad|apuestas real madrid valencia|apuestas
real madrid villarreal|apuestas real madrid vs arsenal|apuestas real
madrid vs atletico|apuestas real madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas real madrid vs barcelona|apuestas real
madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs
valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real
sociedad barcelona|apuestas real sociedad betis|apuestas real sociedad psg|apuestas real sociedad
real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de
bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas
rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas
segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda
division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas seguras en la ruleta|apuestas seguras
eurocopa|apuestas seguras foro|apuestas seguras
futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas seguras nba hoy|apuestas seguras para este fin de semana|apuestas seguras
para ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas
sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la
liga|apuestas sevilla girona|apuestas sevilla inter|apuestas
sevilla jugador|apuestas sevilla juventus|apuestas sevilla
leganes|apuestas sevilla madrid|apuestas sevilla manchester united|apuestas
sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real
sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o
combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas
sistema calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa
del rey|apuestas stake|apuestas stake 10|apuestas stake
10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas
superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas
tenis|apuestas tenis atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de
mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas
tenis hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas tenis retirada|apuestas tenis
roland garros|apuestas tenis seguras|apuestas tenis wimbledon|apuestas tenis wta|apuestas tercera division|apuestas tercera division españa|apuestas
tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas torneos
de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas
ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc online|apuestas ufc
pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas
unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas
us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas valencia madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal
vs real madrid|apuestas virtuales|apuestas virtuales
colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta
españa|apuestas william hill partidos de hoy|apuestas y
casino|apuestas y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas y pronosticos de
futbol|apuestas y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina apuestas|argentina colombia
apuestas|argentina croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina
peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs chile apuestas|argentina vs colombia apuestas|argentina vs francia
apuestas|argentina vs. colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic
osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de madrid apuestas|atlético
de madrid apuestas|atletico de madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico
madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs real madrid
apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro
barcelona apuestas|barca apuestas|barca bayern apuestas|barca
inter apuestas|barca madrid apuestas|barça madrid apuestas|barca vs
atletico apuestas|barca vs madrid apuestas|barca vs real madrid apuestas|barcelona – real madrid apuestas|barcelona apuestas|barcelona atletico apuestas (Jamila)|barcelona atletico de madrid apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona casa de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona
vs atlético madrid apuestas|barcelona vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs girona
apuestas|barcelona vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs
real sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal apuestas|base de
datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america apuestas|bet apuestas
chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis barcelona apuestas|betis chelsea
apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog
apuestas baloncesto|blog apuestas ciclismo|blog apuestas
nba|blog apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono
bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida
apuestas sin deposito|bono bienvenida apuestas sin depósito|bono
bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa
de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas deportivas|bono de bienvenida
casa de apuestas|bono de bienvenida casas de apuestas|bono de casas de apuestas|bono
de registro apuestas|bono de registro apuestas deportivas|bono
de registro casa de apuestas|bono gratis apuestas|bono marca apuestas|bono por
registro apuestas|bono por registro apuestas deportivas|bono por
registro casa de apuestas|bono registro apuestas|bono sin deposito apuestas|bono
sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas
deportivas|bono sin deposito casa de apuestas|bono sin deposito marca apuestas|bono
sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos
apuestas|bonos apuestas colombia|bonos apuestas deportivas|bonos apuestas deportivas
sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos
bienvenida casas de apuestas|bonos casa de apuestas|bonos
casas apuestas|bonos casas de apuestas|bonos casas de apuestas colombia|bonos casas de
apuestas deportivas|bonos casas de apuestas españa|bonos casas de apuestas nuevas|bonos
casas de apuestas sin deposito|bonos casas de apuestas sin depósito|bonos
de apuestas|bonos de apuestas deportivas|bonos de apuestas gratis|bonos de
apuestas sin deposito|bonos de bienvenida apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida
casa de apuestas|bonos de bienvenida casas de apuestas|bonos de
bienvenida de casas de apuestas|bonos de bienvenida
en casas de apuestas|bonos de casas de apuestas|bonos de casas de
apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito
apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de
apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil
colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas
apuestas para hoy|buscador cuotas apuestas|buscador de apuestas seguras|buscador de cuotas apuestas|buscador de
cuotas de apuestas|buscar apuestas seguras|caballos apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora
apuestas|calculadora apuestas combinadas|calculadora
apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas
deportivas seguras|calculadora apuestas multiples|calculadora
apuestas segura|calculadora apuestas seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir
apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora de apuestas combinadas|calculadora de apuestas de futbol|calculadora de apuestas de sistema|calculadora
de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas
surebets|calculadora de arbitraje apuestas|calculadora de cuotas
apuestas|calculadora de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora
poisson apuestas deportivas|calculadora poisson para apuestas|calculadora
scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora
trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas futbol|calcular
apuestas sistema|calcular cuotas apuestas|calcular cuotas
apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad
cuota apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera de caballos con apuestas|carrera de galgos
apuestas|carreras de caballos apuestas|carreras
de caballos apuestas online|carreras de caballos con apuestas|carreras de caballos
juegos de apuestas|carreras de galgos apuestas|carreras de galgos apuestas
online|carreras de galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas atletico de madrid|casa apuestas barcelona|casa apuestas betis|casa apuestas bono bienvenida|casa apuestas bono gratis|casa apuestas bono sin deposito|casa apuestas
cerca de mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa apuestas futbol|casa apuestas mejores
cuotas|casa apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa apuestas valencia|casa de apuestas|casa
de apuestas 10 euros gratis|casa de apuestas argentina|casa
de apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de
apuestas beisbol|casa de apuestas betis|casa de apuestas bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa
de apuestas bono gratis|casa de apuestas bono por registro|casa de apuestas bono sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras de caballos|casa de apuestas
cerca de mi|casa de apuestas cerca de mí|casa de apuestas champions league|casa
de apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa
de apuestas con bono sin deposito|casa de apuestas con cuotas
mas altas|casa de apuestas con esports|casa de apuestas con las mejores cuotas|casa de
apuestas con licencia en españa|casa de apuestas con mejores
cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de apuestas copa
america|casa de apuestas de caballos|casa de apuestas de colombia|casa de apuestas de españa|casa de apuestas de futbol|casa de apuestas de
fútbol|casa de apuestas de futbol peru|casa de
apuestas de peru|casa de apuestas del madrid|casa de apuestas del real madrid|casa de apuestas deportivas|casa de apuestas deportivas
cerca de mi|casa de apuestas deportivas en argentina|casa de apuestas
deportivas en chile|casa de apuestas deportivas en colombia|casa
de apuestas deportivas en españa|casa de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de
apuestas deportivas españolas|casa de apuestas deportivas madrid|casa
de apuestas deportivas mexico|casa de apuestas deportivas online|casa de apuestas deportivas
peru|casa de apuestas deposito 5 euros|casa de apuestas deposito minimo|casa de apuestas deposito minimo 1 euro|casa
de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas en linea|casa de
apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de
apuestas españa|casa de apuestas españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de apuestas f1|casa de
apuestas formula 1|casa de apuestas futbol|casa de apuestas ingreso minimo|casa de apuestas ingreso
minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa de apuestas legales en colombia|casa de
apuestas legales en españa|casa de apuestas libertadores|casa de apuestas liga española|casa de apuestas madrid|casa de
apuestas mas segura|casa de apuestas mejores|casa
de apuestas méxico|casa de apuestas minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas nfl|casa de apuestas nueva|casa de apuestas
nuevas|casa de apuestas oficial del real madrid|casa de apuestas oficial
real madrid|casa de apuestas online|casa de apuestas
online argentina|casa de apuestas online chile|casa de apuestas
online españa|casa de apuestas online mexico|casa de apuestas
online paraguay|casa de apuestas online peru|casa
de apuestas online usa|casa de apuestas online venezuela|casa de apuestas pago anticipado|casa
de apuestas para boxeo|casa de apuestas para ufc|casa de apuestas
peru|casa de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real
madrid|casa de apuestas regalo de bienvenida|casa
de apuestas sevilla|casa de apuestas sin dinero|casa
de apuestas sin ingreso minimo|casa de apuestas sin licencia en españa|casa
de apuestas sin minimo de ingreso|casa de apuestas stake|casa de apuestas tenis|casa de apuestas ufc|casa de apuestas valencia|casa de apuestas venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del
real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas colombia|casas apuestas deportivas españa|casas
apuestas deportivas españolas|casas apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas legales|casas apuestas legales españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas
apuestas ofertas|casas apuestas online|casas
apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de apuestas
5 euros|casas de apuestas app|casas de apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas de
apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono
de bienvenida|casas de apuestas bono por registro|casas de apuestas bono sin deposito|casas de
apuestas bono sin ingreso|casas de apuestas bonos|casas
de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas de
apuestas caballos|casas de apuestas carreras de
caballos|casas de apuestas casino|casas de apuestas casino online|casas
de apuestas cerca de mi|casas de apuestas champions league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas
de apuestas con apuestas gratis|casas de apuestas con bono|casas de apuestas con bono
de bienvenida|casas de apuestas con bono de registro|casas de apuestas con bono por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas con deposito minimo|casas de
apuestas con esports|casas de apuestas con handicap asiatico|casas
de apuestas con licencia|casas de apuestas con licencia en españa|casas de apuestas con licencia españa|casas de apuestas con licencia española|casas de apuestas con mejores cuotas|casas de apuestas con pago anticipado|casas
de apuestas con paypal|casas de apuestas con paypal
en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa del rey|casas de
apuestas de caballos|casas de apuestas de españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas de apuestas de peru|casas
de apuestas deportivas|casas de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas
de apuestas deportivas con paypal|casas de apuestas deportivas en chile|casas de apuestas deportivas en españa|casas
de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de apuestas deportivas en mexico|casas de
apuestas deportivas en peru|casas de apuestas deportivas en sevilla|casas de
apuestas deportivas en valencia|casas de apuestas deportivas
españa|casas de apuestas deportivas españolas|casas de apuestas deportivas legales|casas de
apuestas deportivas madrid|casas de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas
de apuestas deportivas online|casas de apuestas deportivas
peru|casas de apuestas deportivas perú|casas de apuestas deposito
minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de apuestas dinero gratis|casas
de apuestas en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas de apuestas en colombia|casas de apuestas
en españa|casas de apuestas en españa online|casas de apuestas
en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas de apuestas en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas de apuestas
en uruguay|casas de apuestas en valencia|casas de apuestas en venezuela|casas
de apuestas equipos de futbol|casas de apuestas españa|casas de apuestas españa alemania|casas de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa
nuevas|casas de apuestas españa online|casas de apuestas española|casas de
apuestas españolas|casas de apuestas españolas con licencia|casas de
apuestas españolas online|casas de apuestas esports|casas de apuestas eurocopa|casas de apuestas
eurocopa 2024|casas de apuestas europa league|casas de apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas en españa|casas de apuestas formula 1|casas de apuestas
fuera de españa|casas de apuestas futbol|casas de apuestas fútbol|casas de apuestas futbol españa|casas de apuestas ganador eurocopa|casas de apuestas gratis|casas de apuestas ingreso minimo|casas de
apuestas ingreso minimo 1 euro|casas de apuestas ingreso minimo 5 euros|casas de apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas
de apuestas legales en mexico|casas de apuestas legales españa|casas de apuestas
legales mx|casas de apuestas licencia|casas de apuestas licencia españa|casas de
apuestas lista|casas de apuestas madrid|casas de apuestas mas seguras|casas de
apuestas mejores bonos|casas de apuestas mejores cuotas|casas de apuestas mexico|casas
de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas
mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de apuestas nba|casas de apuestas
no reguladas en españa|casas de apuestas nueva ley|casas de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de
apuestas nuevas españa|casas de apuestas
ofertas|casas de apuestas online|casas de apuestas online argentina|casas de apuestas online colombia|casas
de apuestas online deportivas|casas de apuestas online ecuador|casas de apuestas online en argentina|casas de apuestas
online en chile|casas de apuestas online en colombia|casas de apuestas online en españa|casas de
apuestas online en mexico|casas de apuestas online españa|casas de apuestas online
mas fiables|casas de apuestas online mexico|casas de apuestas online nuevas|casas
de apuestas online peru|casas de apuestas
online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas de apuest
https://laxmienterprises.in.net/ f8bet hiếp dâm
trafficmind.click – Overall, professional vibe here; trustworthy, polished, and pleasantly minimal throughout.
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2
apuestas deportivas|1×2 apuestas que significa|1×2
en apuestas|1×2 en apuestas que significa|1×2 que significa en apuestas|5
euros gratis apuestas|9 apuestas que siempre ganaras|a partir de cuanto se declara apuestas|actividades de
juegos de azar y apuestas|ad apuestas deportivas|aleksandre topuria
ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis
nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas
deportivas|aplicacion apuestas deportivas android|aplicación de
apuestas online|aplicacion para hacer apuestas|aplicacion para hacer apuestas de futbol|aplicación para hacer apuestas de
fútbol|aplicaciones apuestas deportivas android|aplicaciones apuestas deportivas gratis|aplicaciones de apuestas android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas
deportivas peru|aplicaciones de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones de
apuestas gratis|aplicaciones de apuestas online|aplicaciones de apuestas seguras|aplicaciones de apuestas
sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas
deportivas|app android apuestas deportivas|app apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app
apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app
apuestas deportivas gratis|app apuestas entre amigos|app apuestas futbol|app apuestas gratis|app apuestas sin dinero|app casa de apuestas|app casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app
de apuestas casino|app de apuestas colombia|app de apuestas con bono de bienvenida|app de apuestas de futbol|app
de apuestas deportivas|app de apuestas deportivas android|app de apuestas deportivas argentina|app de apuestas deportivas colombia|app de apuestas deportivas en españa|app
de apuestas deportivas peru|app de apuestas deportivas perú|app de apuestas deportivas sin dinero|app
de apuestas ecuador|app de apuestas en colombia|app de apuestas en españa|app
de apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app de apuestas
online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app
de apuestas reales|app de casas de apuestas|app marca apuestas android|app moviles de
apuestas|app para apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para
ganar apuestas deportivas|app para hacer apuestas|app para hacer apuestas deportivas|app
para hacer apuestas entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus
apuestas|apps apuestas mundial|apps de apuestas|apps de apuestas con bono de bienvenida|apps
de apuestas de futbol|apps de apuestas deportivas peru|apps de apuestas mexico|apps para
apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas deportivas|apuesta del dia apuestas
deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2
division|apuestas 3 division|apuestas a caballos|apuestas a carreras
de caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas a la baja|apuestas a la nfl|apuestas al
barcelona|apuestas al dia|apuestas al empate|apuestas al
mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas
alcaraz hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y
bajas|apuestas altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas
argentina|apuestas argentina campeon del mundo|apuestas argentina canada|apuestas
argentina colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina francia cuanto paga|apuestas
argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina mundial|apuestas argentina online|apuestas
argentina paises bajos|apuestas argentina polonia|apuestas argentina uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina
vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas athletic manchester united|apuestas
athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas athletic
real sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas
atletico de madrid barcelona|apuestas atletico de madrid gana la liga|apuestas atletico de madrid real madrid|apuestas
atlético de madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas atletico madrid vs barcelona|apuestas
atletico real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto
acb|apuestas baloncesto handicap|apuestas baloncesto
hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas barca atletico|apuestas
barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas barca hoy|apuestas barça hoy|apuestas barca inter|apuestas barca juventus|apuestas barca madrid|apuestas barça madrid|apuestas barca
real madrid|apuestas barca vs juve|apuestas barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona
athletic|apuestas barcelona atletico|apuestas barcelona atletico de madrid|apuestas barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas
barcelona bayern|apuestas barcelona betis|apuestas barcelona
campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas barcelona
gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona
hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas barcelona
real sociedad|apuestas barcelona sevilla|apuestas barcelona valencia|apuestas
barcelona villarreal|apuestas barcelona vs atletico madrid|apuestas barcelona vs madrid|apuestas barcelona vs
real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol
mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis –
chelsea|apuestas betis barcelona|apuestas betis
chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas
betis real madrid|apuestas betis real sociedad|apuestas betis
sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis vs
valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas
bienvenida|apuestas billar online|apuestas
bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia
real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo
online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil
uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos
colocado|apuestas caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos
madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas campeon de la champions|apuestas campeon de liga|apuestas
campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa league|apuestas campeon f1|apuestas
campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas
campeon liga española|apuestas campeon liga santander|apuestas campeon motogp 2025|apuestas
campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas
campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas campeonato
f1|apuestas campeonatos de futbol|apuestas carrera de caballos|apuestas carrera de caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos
hoy|apuestas carrera de galgos nocturnas|apuestas carreras
caballos|apuestas carreras caballos sanlucar|apuestas carreras de caballos|apuestas carreras de caballos en directo|apuestas
carreras de caballos en vivo|apuestas carreras de caballos
españa|apuestas carreras de caballos hoy|apuestas carreras de caballos nacionales|apuestas carreras de caballos nocturnas|apuestas
carreras de caballos online|apuestas carreras de caballos sanlucar|apuestas
carreras de caballos sanlúcar|apuestas carreras
de galgos|apuestas carreras de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas carreras de galgos pre partido|apuestas casino|apuestas casino barcelona|apuestas casino futbol|apuestas casino gran madrid|apuestas casino
gratis|apuestas casino madrid|apuestas casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas celta madrid|apuestas celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas
champions hoy|apuestas champions league|apuestas champions league – pronósticos|apuestas champions league 2025|apuestas champions league hoy|apuestas champions
league pronosticos|apuestas champions league pronósticos|apuestas
champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas
chile venezuela|apuestas chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas clasico
español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas
futbol|apuestas combinadas hoy|apuestas combinadas mismo partido|apuestas combinadas
mundial|apuestas combinadas nba|apuestas combinadas para esta semana|apuestas combinadas para
hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas
combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas
copa davis|apuestas copa de europa|apuestas copa del mundo|apuestas copa del rey|apuestas copa
del rey baloncesto|apuestas copa del rey
final|apuestas copa del rey futbol|apuestas copa del rey ganador|apuestas copa del rey hoy|apuestas copa del rey pronosticos|apuestas
copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas
copa libertadores|apuestas copa mundial de hockey|apuestas copa rey|apuestas copa sudamericana|apuestas corners|apuestas corners hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de
baloncesto para hoy|apuestas de beisbol|apuestas de beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas de boxeo en las vegas|apuestas de boxeo hoy|apuestas
de boxeo online|apuestas de caballo|apuestas de caballos|apuestas de caballos como funciona|apuestas de caballos como se juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas de caballos españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas
de caballos juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas
de caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera de caballos|apuestas
de carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de casino online|apuestas de casino por internet|apuestas de champions league|apuestas de ciclismo|apuestas de colombia|apuestas de
copa america|apuestas de corners|apuestas de deportes en linea|apuestas de
deportes online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas de europa
league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas
de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de futbol en colombia|apuestas de futbol
en directo|apuestas de futbol en linea|apuestas de futbol en vivo|apuestas de
futbol español|apuestas de futbol gratis|apuestas
de futbol hoy|apuestas de futbol mundial|apuestas de futbol online|apuestas
de fútbol online|apuestas de futbol para hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas
de futbol para mañana|apuestas de futbol peru|apuestas de futbol pronosticos|apuestas de
fútbol pronósticos|apuestas de futbol seguras|apuestas de futbol seguras para hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas
de galgos como ganar|apuestas de galgos en directo|apuestas de
galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas de hockey
sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de
juegos online|apuestas de la champions league|apuestas de la copa
américa|apuestas de la eurocopa|apuestas de la europa league|apuestas
de la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas de la
nfl|apuestas de la ufc|apuestas de mlb|apuestas de nba|apuestas
de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas
de peleas ufc|apuestas de perros en vivo|apuestas de perros virtuales|apuestas de
peru|apuestas de sistema|apuestas de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas
de tenis hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis
seguras|apuestas de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del
boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas
del mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas
deportivas 1×2|apuestas deportivas android|apuestas deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas atletico de
madrid|apuestas deportivas baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas
beisbol|apuestas deportivas bono|apuestas deportivas
bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas
deportivas caballos|apuestas deportivas calculadora|apuestas deportivas campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas deportivas ciclismo|apuestas
deportivas colombia|apuestas deportivas com|apuestas deportivas com foro|apuestas deportivas com
pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas
deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas
deportivas consejos|apuestas deportivas consejos para ganar|apuestas deportivas copa america|apuestas deportivas copa del rey|apuestas deportivas copa libertadores|apuestas
deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual es
la mejor|apuestas deportivas cuotas altas|apuestas deportivas de
baloncesto|apuestas deportivas de boxeo|apuestas deportivas de colombia|apuestas deportivas
de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas
de peru|apuestas deportivas de tenis|apuestas deportivas del dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas
deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas
en peru|apuestas deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas europa
league|apuestas deportivas f1|apuestas deportivas
faciles de ganar|apuestas deportivas formula 1|apuestas deportivas
foro|apuestas deportivas foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas
futbol|apuestas deportivas fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas
deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas deportivas
golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas
deportivas gratis sin deposito|apuestas deportivas handicap|apuestas deportivas handicap asiatico|apuestas
deportivas hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas
deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas deportivas legales en colombia|apuestas deportivas libres de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga española|apuestas deportivas listado|apuestas deportivas listado clasico|apuestas deportivas madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas
deportivas mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas multiples|apuestas
deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas nba hoy|apuestas deportivas nfl|apuestas
deportivas nhl|apuestas deportivas nuevas|apuestas deportivas ofertas|apuestas deportivas online|apuestas deportivas
online argentina|apuestas deportivas online chile|apuestas deportivas online colombia|apuestas deportivas online en colombia|apuestas deportivas online españa|apuestas deportivas online mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas deportivas online por internet|apuestas deportivas pago paypal|apuestas deportivas
para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos de hoy|apuestas
deportivas paypal|apuestas deportivas peru|apuestas deportivas perú|apuestas deportivas peru
vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas
pronostico|apuestas deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas
deportivas pronosticos gratis|apuestas deportivas pronosticos nba|apuestas
deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo
bienvenida|apuestas deportivas resultado exacto|apuestas
deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas seguras
foro|apuestas deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas
deportivas seguras telegram|apuestas deportivas sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas deportivas sin dinero|apuestas
deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake
10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas deportivas tenis de mesa|apuestas
deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas
deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito
minimo 1 euro|apuestas descenso a segunda|apuestas descenso a segunda b|apuestas descenso la liga|apuestas descenso primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas
dobles y triples|apuestas dortmund barcelona|apuestas
draft nba|apuestas draft nfl|apuestas ecuador vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones
venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas
en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas
en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas
en juegos|apuestas en la champions league|apuestas en la eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas en las
vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas
en linea boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas
en linea estados unidos|apuestas en linea futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea peru|apuestas en linea
usa|apuestas en los esports|apuestas en madrid|apuestas en méxico|apuestas en mexico
online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de futbol en vivo|apuestas
en partidos de tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas en tenis|apuestas
en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas
en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas equipos de futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa gana el mundial|apuestas
españa gana eurocopa|apuestas españa gana mundial|apuestas españa georgia|apuestas españa
holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa
paises bajos|apuestas español|apuestas español oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas esports colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports
lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas
euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa
ganador|apuestas eurocopa hoy|apuestas eurocopa sub
21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa league hoy|apuestas
europa league pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas f1 abu
dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1 cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles de ganar|apuestas faciles
para ganar|apuestas favoritas|apuestas favorito
champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas
favoritos mundial|apuestas fc barcelona|apuestas final champions cuotas|apuestas
final champions league|apuestas final champions peru|apuestas final
copa|apuestas final copa america|apuestas final copa de europa|apuestas final copa
del rey|apuestas final copa europa|apuestas final copa libertadores|apuestas final copa
rey|apuestas final de copa|apuestas final de copa del
rey|apuestas final del mundial|apuestas final euro|apuestas
final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia nfl|apuestas finales nba|apuestas fiorentina
betis|apuestas formula|apuestas formula 1|apuestas fórmula
1|apuestas fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas
foro nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol
americano nfl|apuestas futbol argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas
futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas
futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas
futbol españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol juegos
olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol
para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol
telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos
online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas
hoy|apuestas ganador champions league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas ganador copa del rey baloncesto|apuestas ganador
copa libertadores|apuestas ganador de la eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas
ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la liga|apuestas ganador
liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar liga|apuestas
ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas
ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas
girona gana la liga|apuestas girona real madrid|apuestas girona
real sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas gratis|apuestas
gratis casino|apuestas gratis con premios|apuestas gratis hoy|apuestas gratis para
hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis sports|apuestas gratis y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas venezuela|apuestas
hockey|apuestas hockey hielo|apuestas hockey patines|apuestas hockey sobre
hielo|apuestas holanda argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas hoy
pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas
inter barca|apuestas inter barcelona|apuestas juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings league americas|apuestas la liga|apuestas
la liga española|apuestas la liga hoy|apuestas la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las
vegas nfl|apuestas league of legends mundial|apuestas legal|apuestas legales|apuestas legales en colombia|apuestas
legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas libertadores|apuestas licencia|apuestas liga
1 peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas liga de campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones
de hockey|apuestas liga españa|apuestas liga española|apuestas liga santander pronosticos|apuestas ligas de futbol|apuestas linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas
madrid|apuestas madrid arsenal|apuestas madrid atletico|apuestas madrid atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas madrid barca hoy|apuestas madrid barca supercopa|apuestas
madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas
madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas madrid
valencia|apuestas madrid vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester city real madrid|apuestas
mas faciles de ganar|apuestas mas seguras|apuestas mas seguras para hoy|apuestas masters de golf|apuestas masters
de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador
mundial|apuestas mejor jugador eurocopa|apuestas mejores casinos
online|apuestas mexico|apuestas méxico|apuestas mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas mlb
hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas mlb pronosticos|apuestas
mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas
múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial
campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas
mundial de baloncesto|apuestas mundial de ciclismo|apuestas mundial de clubes|apuestas mundial de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas mundial moto gp|apuestas mundial motogp|apuestas
mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas
mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas
nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas nfl
hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas
nfl pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online bono|apuestas online bono bienvenida|apuestas online
boxeo|apuestas online caballos|apuestas online carreras de
caballos|apuestas online casino|apuestas online champions league|apuestas online chile|apuestas
online ciclismo|apuestas online colombia|apuestas online comparativa|apuestas online con paypal|apuestas online de
caballos|apuestas online deportivas|apuestas online en argentina|apuestas online en peru|apuestas online
espana|apuestas online españa|apuestas online esports|apuestas online
foro|apuestas online futbol|apuestas online futbol españa|apuestas online golf|apuestas online
gratis|apuestas online gratis sin deposito|apuestas online juegos|apuestas
online mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online peru|apuestas online seguras|apuestas online sin dinero|apuestas online sin registro|apuestas online tenis|apuestas
online ufc|apuestas online uruguay|apuestas online venezuela|apuestas open britanico golf|apuestas
osasuna athletic|apuestas osasuna barcelona|apuestas osasuna
real madrid|apuestas osasuna sevilla|apuestas osasuna
valencia|apuestas over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos
ecuador|apuestas paises bajos inglaterra|apuestas países
bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para
el mundial|apuestas para el partido de hoy|apuestas
para eurocopa|apuestas para europa league|apuestas para futbol|apuestas
para ganar|apuestas para ganar dinero|apuestas para ganar dinero facil|apuestas para ganar en la ruleta|apuestas
para ganar la champions|apuestas para ganar la eurocopa|apuestas para ganar la europa league|apuestas para ganar la liga|apuestas para ganar
siempre|apuestas para hacer|apuestas para hoy|apuestas para hoy de futbol|apuestas para hoy europa league|apuestas para hoy futbol|apuestas para
juegos|apuestas para la champions league|apuestas para la
copa del rey|apuestas para la eurocopa|apuestas para la europa league|apuestas para la final de la eurocopa|apuestas para la
nba hoy|apuestas para los partidos de hoy|apuestas
para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas partido españa marruecos|apuestas partido mundial|apuestas partido suspendido|apuestas
partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas paypal|apuestas
peleas de boxeo|apuestas peru|apuestas perú|apuestas peru
brasil|apuestas peru chile|apuestas peru paraguay|apuestas
peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas
pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso a
primera|apuestas playoff nba|apuestas playoff segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas
playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por
internet mexico|apuestas por internet para ganar dinero|apuestas por paypal|apuestas
por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas
predicciones|apuestas predicciones futbol|apuestas primera division|apuestas
primera division españa|apuestas promociones|apuestas pronostico|apuestas
pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos
gratis|apuestas pronosticos nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas psg barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas
que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas que significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana eurocopa|apuestas
quien gana la champions|apuestas quien gana la eurocopa|apuestas quien gana la liga|apuestas quien ganara
el mundial|apuestas quién ganará el mundial|apuestas quien ganara la
champions|apuestas quien ganara la eurocopa|apuestas quien ganara
la liga|apuestas rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real madrid atletico de madrid|apuestas real madrid atlético de madrid|apuestas real madrid atletico madrid|apuestas real madrid barcelona|apuestas real madrid
bayern|apuestas real madrid betis|apuestas real madrid borussia|apuestas real madrid
campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real madrid
girona|apuestas real madrid hoy|apuestas real madrid
liverpool|apuestas real madrid manchester city|apuestas real madrid osasuna|apuestas real madrid real sociedad|apuestas real madrid valencia|apuestas real
madrid villarreal|apuestas real madrid vs arsenal|apuestas real madrid vs atletico|apuestas real madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas real madrid vs barcelona|apuestas real madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real sociedad betis|apuestas
real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas
recomendadas hoy|apuestas regalo de bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas
roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas
rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas
seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas seguras hoy|apuestas seguras hoy
futbol|apuestas seguras nba|apuestas seguras nba hoy|apuestas seguras para este fin de
semana|apuestas seguras para ganar dinero|apuestas seguras para hoy|apuestas seguras
para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises
bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la liga|apuestas sevilla girona|apuestas sevilla inter|apuestas sevilla jugador|apuestas
sevilla juventus|apuestas sevilla leganes|apuestas sevilla
madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o combinadas|apuestas
sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas
sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake 10|apuestas stake
10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas superliga argentina|apuestas
tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis de mesa pronosticos|apuestas
tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas tenis
wimbledon|apuestas tenis wta|apuestas tercera division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster
para hoy|apuestas topuria holloway cuotas|apuestas torneos de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas ufc chile|apuestas ufc
como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas valencia madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas valladolid
valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal
bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs
real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas
vuelta a españa|apuestas vuelta españa|apuestas william hill partidos de
hoy|apuestas y casino|apuestas y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas y pronosticos de futbol|apuestas y
pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina
apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina
mexico apuestas|argentina peru apuestas|argentina uruguay apuestas|argentina vs bolivia
apuestas|argentina vs chile apuestas|argentina vs
colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas
deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de madrid apuestas|atlético de madrid
apuestas|atletico de madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real
madrid apuestas|atletico madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs real madrid apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca
madrid apuestas|barça madrid apuestas|barca
vs atletico apuestas|barca vs madrid apuestas|barca vs real madrid
apuestas|barcelona – real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona
atletico de madrid apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona
casa de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia
apuestas|barcelona vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs betis
apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona
vs girona apuestas|barcelona vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal apuestas|base
de datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis
barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog
apuestas baloncesto|blog apuestas ciclismo|blog apuestas nba|blog apuestas
tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono
apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono
bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida
apuestas españa|bono bienvenida apuestas sin deposito|bono
bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida marca
apuestas|bono casa apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis
sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas
deportivas|bono de bienvenida casa de apuestas|bono de bienvenida casas de apuestas|bono de casas de
apuestas|bono de registro apuestas|bono de registro apuestas deportivas|bono de registro
casa de apuestas|bono gratis apuestas|bono marca apuestas|bono por registro apuestas|bono por registro apuestas
deportivas|bono por registro casa de apuestas|bono registro apuestas|bono sin deposito apuestas|bono sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso
apuestas|bono sin ingreso apuestas deportivas|bonos apuestas|bonos apuestas colombia|bonos apuestas
deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos
bienvenida apuestas|bonos bienvenida casas apuestas|bonos
bienvenida casas de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos
casas de apuestas|bonos casas de apuestas colombia|bonos casas
de apuestas deportivas|bonos casas de apuestas
españa|bonos casas de apuestas nuevas|bonos casas de apuestas
sin deposito|bonos casas de apuestas sin depósito|bonos
de apuestas|bonos de apuestas deportivas|bonos de apuestas gratis|bonos
de apuestas sin deposito|bonos de bienvenida apuestas|bonos de
bienvenida apuestas deportivas|bonos de bienvenida casa de apuestas|bonos de bienvenida casas de apuestas|bonos
de bienvenida de casas de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de casas de apuestas
sin deposito|bonos en casa de apuestas|bonos en casas de apuestas
sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos
sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de
apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia
apuestas|buenas apuestas para hoy|buscador
cuotas apuestas|buscador de apuestas seguras|buscador de cuotas
apuestas|buscador de cuotas de apuestas|buscar apuestas seguras|caballos apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas
combinadas|calculadora apuestas de sistema|calculadora apuestas
deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora
apuestas segura|calculadora apuestas seguras|calculadora apuestas sistema|calculadora apuestas
yankee|calculadora arbitraje apuestas|calculadora cubrir
apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora de apuestas
combinadas|calculadora de apuestas de futbol|calculadora de
apuestas de sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas
sistema|calculadora de apuestas surebets|calculadora de arbitraje
apuestas|calculadora de cuotas apuestas|calculadora de cuotas
de apuestas|calculadora para apuestas deportivas|calculadora
poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora trading apuestas|calcular apuestas|calcular
apuestas deportivas|calcular apuestas futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular cuotas apuestas
combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas
deportivas|calcular momios apuestas|calcular probabilidad cuota apuestas|calcular
stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo de
apuestas|calculo de apuestas deportivas|cambio de cuotas
apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera de caballos con apuestas|carrera de
galgos apuestas|carreras de caballos apuestas|carreras de caballos apuestas online|carreras
de caballos con apuestas|carreras de caballos juegos de
apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras de galgos
apuestas trucos|carreras galgos apuestas|casa
apuestas argentina|casa apuestas atletico de madrid|casa apuestas
barcelona|casa apuestas betis|casa apuestas bono bienvenida|casa
apuestas bono gratis|casa apuestas bono sin deposito|casa apuestas
cerca de mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa apuestas futbol|casa apuestas mejores cuotas|casa
apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa
apuestas valencia|casa de apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de apuestas atletico de madrid|casa de apuestas baloncesto|casa de
apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa
de apuestas bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa de apuestas bono gratis|casa de apuestas bono por registro|casa de apuestas
bono sin deposito|casa de apuestas boxeo|casa de apuestas
caballos|casa de apuestas carreras de caballos|casa
de apuestas cerca de mi|casa de apuestas cerca de mí|casa de apuestas champions league|casa de apuestas chile|casa
de apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa de apuestas con bono sin deposito|casa de
apuestas con cuotas mas altas|casa de apuestas con esports|casa
de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas con mejores cuotas|casa de apuestas
con pago anticipado|casa de apuestas con paypal|casa de apuestas copa america|casa de apuestas de caballos|casa de apuestas de colombia|casa de apuestas de españa|casa de apuestas de futbol|casa de
apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas
de peru|casa de apuestas del madrid|casa de
apuestas del real madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca
de mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas en chile|casa de apuestas
deportivas en colombia|casa de apuestas deportivas en españa|casa
de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas españolas|casa de apuestas deportivas madrid|casa de apuestas deportivas mexico|casa de apuestas deportivas
online|casa de apuestas deportivas peru|casa de apuestas deposito 5 euros|casa
de apuestas deposito minimo|casa de apuestas deposito minimo 1 euro|casa de apuestas depósito mínimo 1 euro|casa
de apuestas en españa|casa de apuestas en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de
apuestas en vivo|casa de apuestas españa|casa
de apuestas españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa de
apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de apuestas f1|casa de
apuestas formula 1|casa de apuestas futbol|casa de apuestas ingreso minimo|casa de apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa
de apuestas legales en colombia|casa de apuestas legales
en españa|casa de apuestas libertadores|casa de apuestas
liga española|casa de apuestas madrid|casa de apuestas mas segura|casa de apuestas mejores|casa de
apuestas méxico|casa de apuestas minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del real madrid|casa de apuestas oficial real madrid|casa
de apuestas online|casa de apuestas online argentina|casa de
apuestas online chile|casa de apuestas online españa|casa de apuestas online mexico|casa
de apuestas online paraguay|casa de apuestas online peru|casa de apuestas online usa|casa de
apuestas online venezuela|casa de apuestas pago anticipado|casa de apuestas para boxeo|casa
de apuestas para ufc|casa de apuestas peru|casa de apuestas
perú|casa de apuestas peru online|casa de apuestas por paypal|casa de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de bienvenida|casa de
apuestas sevilla|casa de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa de
apuestas sin licencia en españa|casa de apuestas sin minimo de ingreso|casa de apuestas stake|casa de apuestas tenis|casa
de apuestas ufc|casa de apuestas valencia|casa
de apuestas venezuela|casa de apuestas virtuales|casa de apuestas
vive la suerte|casa oficial de apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas apuestas caballos|casas
apuestas chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas
apuestas deportivas|casas apuestas deportivas colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas
apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas
esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas
legales|casas apuestas legales españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas tenis|casas
asiaticas apuestas|casas de apuestas|casas de apuestas 5 euros|casas de apuestas app|casas de
apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono de bienvenida|casas de apuestas bono por registro|casas de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas de apuestas carreras de caballos|casas de apuestas casino|casas
de apuestas casino online|casas de apuestas cerca de mi|casas de apuestas champions league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de apuestas con apuestas gratis|casas de apuestas con bono|casas de apuestas con bono de bienvenida|casas de
apuestas con bono de registro|casas de apuestas con bono por
registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas
con deposito minimo|casas de apuestas con esports|casas de apuestas con handicap asiatico|casas
de apuestas con licencia|casas de apuestas
con licencia en españa|casas de apuestas con licencia españa|casas de apuestas con licencia española|casas de apuestas con mejores cuotas|casas de apuestas con pago anticipado|casas de apuestas con paypal|casas de apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas
copa del rey|casas de apuestas de caballos|casas de apuestas de españa|casas de apuestas
de futbol|casas de apuestas de fútbol|casas de apuestas de peru|casas
de apuestas deportivas|casas de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas de apuestas
deportivas con paypal|casas de apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de
apuestas deportivas en mexico|casas de apuestas deportivas
en peru|casas de apuestas deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de apuestas deportivas
españolas|casas de apuestas deportivas legales|casas de apuestas deportivas madrid|casas de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas de
apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas deposito minimo
1 euro|casas de apuestas depósito mínimo 1 euro|casas
de apuestas dinero gratis|casas de apuestas en argentina|casas de
apuestas en barcelona|casas de apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas
de apuestas en españa online|casas de apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas de apuestas
en peru|casas de apuestas en perú|casas de apuestas
en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas de
apuestas en venezuela|casas de apuestas equipos de futbol|casas de apuestas españa|casas de apuestas
españa alemania|casas de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas de apuestas españa
online|casas de apuestas española|casas de apuestas españolas|casas de apuestas españolas con licencia|casas de apuestas
españolas online|casas de apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa
2024|casas de apuestas europa league|casas de apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas en españa|casas de apuestas formula 1|casas de apuestas fuera de españa|casas de apuestas futbol|casas de apuestas
fútbol|casas de apuestas futbol españa|casas de apuestas ganador eurocopa|casas de apuestas
gratis|casas de apuestas ingreso minimo|casas de apuestas ingreso minimo 1 euro|casas de apuestas ingreso minimo 5 euros|casas de
apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas de
apuestas legales en mexico|casas de apuestas legales españa|casas de apuestas legales mx|casas de apuestas licencia|casas de apuestas licencia españa|casas de apuestas lista|casas de apuestas madrid|casas de apuestas mas seguras|casas de apuestas
mejores bonos|casas de apuestas mejores cuotas|casas de apuestas mexico|casas de apuestas méxico|casas de apuestas
minimo 5 euros|casas de apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas de apuestas
nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de apuestas
ofertas|casas de apuestas online|casas de apuestas online argentina|casas de
apuestas online colombia|casas de apuestas online deportivas|casas de apuestas
online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas de apuestas online en colombia|casas
de apuestas online en españa|casas de apuestas online en mexico|casas de apuestas online españa|casas de apuestas online
mas fiables|casas de apuestas online mexico|casas de
apuestas online nuevas|casas de apuestas online peru|casas de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas de apuestas
para ufc|casas de apuestas paypal|casas de apuestas peru bono sin deposito|casas de apuestas presenciales en españa|casas de apuestas promociones|casas de apuestas que
https://shorturl.fm/teova
https://f8bet.now/ f8bet hiếp dâm
https://www.draugiem.lv/blogs/post/1xBet-Promo-Code-2026-130-Bonus-Deal_17790102
marketscope.click – Overall, professional vibe here; trustworthy, polished, and pleasantly minimal throughout.
seotrack.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
promocloud.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
digitaltrack.click – Navigation felt smooth, found everything quickly without any confusing steps.
Это генератор картинок, который выдаёт впечатляюще реалистичные результаты уже с первого запроса! Официальный сайт – https://gen.new/
https://viralnews.in.net/ f8bet hiếp dâm
Pin-Up is a multifunctional entertainment platform that combines a premium online casino and a licensed https://v-sistemu.ru/
clickgrow.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
Great job simplifying something so complex.
https://shorturl.fm/KwZu4
I really needed this today. Thank you for writing it.
I’m not sure exactly why but this blog is loading incredibly slow for me. Is anyone else having this issue or is it a issue on my end? I’ll check back later and see if the problem still exists.
https://seratus168.com/melbet-akcii-2025-bonusy-i-predlozheniya/
Because the admin of this web site is working, no question very rapidly it will be well-known, due to its feature contents.
https://livresolta.com.br/bonus-pri-registracii-melbet-2025/
https://shorturl.fm/OfjuM
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas que
significa|1×2 en apuestas|1×2 en apuestas que significa|1×2 que significa en apuestas|5 euros gratis apuestas|9 apuestas que siempre ganaras|a partir de
cuanto se declara apuestas|actividades de juegos de azar y apuestas|ad apuestas deportivas|aleksandre topuria ufc apuestas|algoritmo para
ganar apuestas deportivas|america apuestas|análisis
nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas
android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para
hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas
deportivas android|aplicaciones apuestas deportivas gratis|aplicaciones de
apuestas android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas
peru|aplicaciones de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de apuestas online|aplicaciones
de apuestas seguras|aplicaciones de apuestas sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas deportivas|app android apuestas deportivas|app apuestas|app apuestas
android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas
españa|app apuestas deportivas gratis|app apuestas entre amigos|app apuestas
futbol|app apuestas gratis|app apuestas sin dinero|app casa de apuestas|app
casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de apuestas casino|app de apuestas colombia|app de apuestas con bono de
bienvenida|app de apuestas de futbol|app de apuestas deportivas|app de apuestas deportivas
android|app de apuestas deportivas argentina|app de apuestas deportivas colombia|app de apuestas deportivas en españa|app de apuestas
deportivas peru|app de apuestas deportivas perú|app de apuestas deportivas sin dinero|app de apuestas ecuador|app de apuestas en colombia|app de apuestas en españa|app de apuestas
en venezuela|app de apuestas futbol|app de apuestas gratis|app
de apuestas online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app de apuestas reales|app de casas de apuestas|app marca apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de
futbol|app para apuestas deportivas|app para apuestas deportivas
en español|app para ganar apuestas deportivas|app
para hacer apuestas|app para hacer apuestas deportivas|app
para hacer apuestas entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de
apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de futbol|apps
de apuestas deportivas peru|apps de apuestas mexico|apps para
apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas
1×2|apuestas 1X2|apuestas 2 division|apuestas 3 division|apuestas a caballos|apuestas a
carreras de caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores
nba|apuestas a la baja|apuestas a la nfl|apuestas al barcelona|apuestas al dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas
y bajas|apuestas altas y bajas nfl|apuestas ambos equipos
marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del
mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia
argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas argentina
canada|apuestas argentina colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina francia cuanto paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas argentina polonia|apuestas argentina
uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas
argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic
barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas athletic real sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic
valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas
atletico campeon de liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de
madrid barcelona|apuestas atletico de madrid gana la liga|apuestas atletico
de madrid real madrid|apuestas atlético de madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas atletico madrid vs
barcelona|apuestas atletico real madrid|apuestas atletico real madrid
champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas
baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas
baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas barca atletico|apuestas barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas
barca hoy|apuestas barça hoy|apuestas barca inter|apuestas barca juventus|apuestas barca madrid|apuestas barça
madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas barca vs madrid|apuestas
barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona
atletico|apuestas barcelona atletico de madrid|apuestas
barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas
barcelona campeon de liga|apuestas barcelona celta|apuestas
barcelona espanyol|apuestas barcelona gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona
osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas
barcelona real sociedad|apuestas barcelona sevilla|apuestas barcelona valencia|apuestas barcelona villarreal|apuestas barcelona vs atletico madrid|apuestas barcelona
vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas
béisbol|apuestas beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas betis real
madrid|apuestas betis real sociedad|apuestas betis
sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis vs valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas billar online|apuestas bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas
bono gratis|apuestas bono sin deposito|apuestas bonos
sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo
de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo online|apuestas brasil
colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs colombia|apuestas
brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos españa|apuestas caballos
hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas
campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas
campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas campeon de la champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas
campeon europa league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga
bbva|apuestas campeon liga española|apuestas campeon liga santander|apuestas
campeon motogp 2025|apuestas campeon mundial|apuestas campeón mundial|apuestas campeon mundial
baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas
campeon premier league|apuestas campeon roland garros|apuestas
campeonato f1|apuestas campeonatos de futbol|apuestas carrera de
caballos|apuestas carrera de caballos hoy|apuestas carrera de
caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera
de galgos nocturnas|apuestas carreras caballos|apuestas carreras
caballos sanlucar|apuestas carreras de caballos|apuestas
carreras de caballos en directo|apuestas carreras
de caballos en vivo|apuestas carreras de caballos españa|apuestas
carreras de caballos hoy|apuestas carreras de caballos nacionales|apuestas carreras de
caballos nocturnas|apuestas carreras de caballos online|apuestas carreras de caballos sanlucar|apuestas carreras de caballos
sanlúcar|apuestas carreras de galgos|apuestas carreras
de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas
carreras de galgos pre partido|apuestas casino|apuestas casino barcelona|apuestas casino futbol|apuestas
casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas
casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas celta madrid|apuestas
celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions league|apuestas champions league
– pronósticos|apuestas champions league 2025|apuestas champions league hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas
champions pronosticos|apuestas chelsea barcelona|apuestas chelsea
betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile
vs uruguay|apuestas ciclismo|apuestas ciclismo
en vivo|apuestas ciclismo femenino|apuestas ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a
españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia
vs argentina|apuestas colombia vs brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas futbol|apuestas combinadas
hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas para esta semana|apuestas combinadas para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de credito|apuestas
con tarjeta de debito|apuestas consejos|apuestas copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas
copa davis|apuestas copa de europa|apuestas copa del mundo|apuestas copa del rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas
copa del rey futbol|apuestas copa del rey ganador|apuestas copa del rey hoy|apuestas copa del
rey pronosticos|apuestas copa del rey pronósticos|apuestas
copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de
hockey|apuestas copa rey|apuestas copa sudamericana|apuestas corners|apuestas corners hoy|apuestas croacia argentina|apuestas
cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto
para hoy|apuestas de beisbol|apuestas de beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas de boxeo en las vegas|apuestas de boxeo hoy|apuestas
de boxeo online|apuestas de caballo|apuestas de caballos|apuestas
de caballos como funciona|apuestas de caballos como se juega|apuestas
de caballos en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas de
caballos españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas de caballos juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas de caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera
de caballos|apuestas de carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de casino online|apuestas de casino por internet|apuestas
de champions league|apuestas de ciclismo|apuestas
de colombia|apuestas de copa america|apuestas de corners|apuestas de
deportes en linea|apuestas de deportes online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas de europa league|apuestas de f1|apuestas de formula
1|apuestas de futbol|apuestas de fútbol|apuestas de
futbol app|apuestas de futbol argentina|apuestas de futbol
colombia|apuestas de futbol en colombia|apuestas de futbol en directo|apuestas de futbol en linea|apuestas de futbol
en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de futbol hoy|apuestas
de futbol mundial|apuestas de futbol online|apuestas de fútbol online|apuestas de futbol para
hoy|apuestas de fútbol para hoy|apuestas de futbol
para hoy seguras|apuestas de futbol para mañana|apuestas de futbol peru|apuestas de
futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas de futbol seguras
para hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas de galgos como
ganar|apuestas de galgos en directo|apuestas de galgos online|apuestas de galgos
trucos|apuestas de golf|apuestas de hockey|apuestas de hockey
sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de juegos online|apuestas de la champions league|apuestas de la
copa américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas de la nfl|apuestas
de la ufc|apuestas de mlb|apuestas de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de
partidos de futbol|apuestas de peleas ufc|apuestas de perros en vivo|apuestas de perros
virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema
como funciona|apuestas de sistema explicacion|apuestas de
sistema explicación|apuestas de tenis|apuestas de tenis de
mesa|apuestas de tenis en directo|apuestas
de tenis hoy|apuestas de tenis para hoy|apuestas de tenis
pronosticos|apuestas de tenis seguras|apuestas de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia de hoy|apuestas del dia
deportivas|apuestas del dia futbol|apuestas del mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas android|apuestas deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas
argentina legal|apuestas deportivas atletico de madrid|apuestas deportivas
baloncesto|apuestas deportivas barca madrid|apuestas
deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas
campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas deportivas ciclismo|apuestas deportivas colombia|apuestas deportivas
com|apuestas deportivas com foro|apuestas deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas deportivas consejos para ganar|apuestas deportivas copa america|apuestas deportivas copa del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas
corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas altas|apuestas
deportivas de baloncesto|apuestas deportivas de boxeo|apuestas deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas
de nba|apuestas deportivas de nhl|apuestas deportivas de
peru|apuestas deportivas de tenis|apuestas deportivas del
dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas deportivas en español|apuestas deportivas
en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas
deportivas en sevilla|apuestas deportivas en uruguay|apuestas
deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas
deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas europa league|apuestas deportivas f1|apuestas
deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas
foro futbol|apuestas deportivas foro tenis|apuestas
deportivas francia argentina|apuestas deportivas futbol|apuestas deportivas
fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas
deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas deportivas golf|apuestas
deportivas gratis|apuestas deportivas gratis con premios|apuestas
deportivas gratis hoy|apuestas deportivas gratis sin deposito|apuestas deportivas
handicap|apuestas deportivas handicap asiatico|apuestas deportivas hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas
deportivas la liga|apuestas deportivas legales|apuestas deportivas legales en colombia|apuestas deportivas libres
de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga
española|apuestas deportivas listado|apuestas deportivas
listado clasico|apuestas deportivas madrid|apuestas deportivas mas
seguras|apuestas deportivas mejor pagadas|apuestas deportivas
mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas
deportivas mejores paginas|apuestas deportivas mexico|apuestas
deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb
hoy|apuestas deportivas multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas
nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas
nuevas|apuestas deportivas ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas deportivas online chile|apuestas deportivas
online colombia|apuestas deportivas online en colombia|apuestas deportivas online españa|apuestas
deportivas online mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas deportivas online por internet|apuestas deportivas pago
paypal|apuestas deportivas para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas
peru|apuestas deportivas perú|apuestas deportivas peru vs ecuador|apuestas deportivas predicciones|apuestas deportivas
promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas
pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos
gratis|apuestas deportivas pronosticos nba|apuestas deportivas pronosticos
tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas
deportivas regalo bienvenida|apuestas deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas
deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas
deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas
deportivas sin dinero|apuestas deportivas sin dinero
real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas deportivas tenis de mesa|apuestas deportivas
tenis foro|apuestas deportivas tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas
uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas
deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas
y casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a segunda|apuestas descenso a
segunda b|apuestas descenso la liga|apuestas descenso primera division|apuestas descenso
segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas
dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles
y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas draft nfl|apuestas ecuador vs argentina|apuestas ecuador
vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas
en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas
en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas
en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas en juegos|apuestas
en la champions league|apuestas en la eurocopa|apuestas en la liga|apuestas
en la nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea
deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea
peru|apuestas en linea usa|apuestas en los esports|apuestas en madrid|apuestas en méxico|apuestas
en mexico online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas equipos
de futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa
gana el mundial|apuestas españa gana eurocopa|apuestas españa
gana mundial|apuestas españa georgia|apuestas españa
holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas
españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa paises bajos|apuestas español|apuestas español oviedo|apuestas espanyol
barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas esports
colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas
esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas
euro copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa
femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa
hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa league hoy|apuestas
europa league pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1 cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles
de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos
champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas fc barcelona|apuestas
final champions cuotas|apuestas final champions league|apuestas final champions peru|apuestas final copa|apuestas final copa
america|apuestas final copa de europa|apuestas final copa del rey|apuestas final copa europa|apuestas final copa libertadores|apuestas final copa rey|apuestas final
de copa|apuestas final de copa del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa
league|apuestas final.mundial|apuestas finales de conferencia nfl|apuestas finales nba|apuestas
fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula 1|apuestas fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas francia
argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol americano nfl|apuestas futbol argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol
chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas futbol españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas
futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol juegos
olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas
futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas
futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas gana
resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador champions league|apuestas ganador copa
america|apuestas ganador copa del rey|apuestas ganador copa del rey baloncesto|apuestas ganador
copa libertadores|apuestas ganador de la eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas
ganador f1|apuestas ganador la liga|apuestas ganador
liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas
ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas
ganar liga|apuestas ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas girona
real madrid|apuestas girona real sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas
goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam
de tenis|apuestas gratis|apuestas gratis casino|apuestas gratis
con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas gratis
puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas
gratis sports|apuestas gratis y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas hockey
hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda argentina|apuestas holanda
vs argentina|apuestas hoy|apuestas hoy champions|apuestas
hoy futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter barcelona|apuestas juego|apuestas juegos|apuestas
juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas
juegos olimpicos baloncesto|apuestas juegos online|apuestas juegos
virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings
league americas|apuestas la liga|apuestas la liga española|apuestas la liga hoy|apuestas
la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las vegas
nfl|apuestas league of legends mundial|apuestas legal|apuestas legales|apuestas legales en colombia|apuestas legales en españa|apuestas legales en estados unidos|apuestas
legales españa|apuestas leganes betis|apuestas libertadores|apuestas licencia|apuestas
liga 1 peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas liga de campeones|apuestas liga de campeones
de baloncesto|apuestas liga de campeones de hockey|apuestas
liga españa|apuestas liga española|apuestas liga santander pronosticos|apuestas ligas de
futbol|apuestas linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas
liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas madrid atletico|apuestas
madrid atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas
madrid barca hoy|apuestas madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid
betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid
city|apuestas madrid dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas
madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas madrid valencia|apuestas madrid
vs arsenal|apuestas madrid vs barcelona|apuestas mallorca
osasuna|apuestas mallorca real sociedad|apuestas manchester
athletic|apuestas manchester city real madrid|apuestas mas faciles
de ganar|apuestas mas seguras|apuestas mas seguras para hoy|apuestas
masters de golf|apuestas masters de tenis|apuestas maximo goleador eurocopa|apuestas
maximo goleador mundial|apuestas mejor jugador eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas mexico polonia|apuestas méxico
polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas
mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas
multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples
el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas mundial
de baloncesto|apuestas mundial de ciclismo|apuestas
mundial de clubes|apuestas mundial de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas
mundial moto gp|apuestas mundial motogp|apuestas mundial rugby|apuestas mundial
sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas
mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba hoy
jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba
pronósticos|apuestas nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas
nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas
nfl pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas
octavos eurocopa|apuestas ofertas|apuestas online|apuestas online
argentina|apuestas online argentina legal|apuestas online bono|apuestas online bono
bienvenida|apuestas online boxeo|apuestas online caballos|apuestas online carreras de caballos|apuestas online casino|apuestas online champions league|apuestas online chile|apuestas
online ciclismo|apuestas online colombia|apuestas online comparativa|apuestas online
con paypal|apuestas online de caballos|apuestas online deportivas|apuestas
online en argentina|apuestas online en peru|apuestas online espana|apuestas online españa|apuestas online esports|apuestas online foro|apuestas online futbol|apuestas
online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online juegos|apuestas online mexico|apuestas online mma|apuestas
online movil|apuestas online nba|apuestas online net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online peru|apuestas online seguras|apuestas online sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online ufc|apuestas online
uruguay|apuestas online venezuela|apuestas open britanico golf|apuestas osasuna
athletic|apuestas osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas
over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago
anticipado|apuestas paises bajos ecuador|apuestas paises bajos inglaterra|apuestas países
bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas
para el mundial|apuestas para el partido de hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas para ganar|apuestas para
ganar dinero|apuestas para ganar dinero facil|apuestas
para ganar en la ruleta|apuestas para ganar la champions|apuestas para ganar la eurocopa|apuestas para
ganar la europa league|apuestas para ganar la liga|apuestas para ganar
siempre|apuestas para hacer|apuestas para hoy|apuestas para hoy
de futbol|apuestas para hoy europa league|apuestas para hoy futbol|apuestas para juegos|apuestas
para la champions league|apuestas para la copa del rey|apuestas para la
eurocopa|apuestas para la europa league|apuestas para la final de
la eurocopa|apuestas para la nba hoy|apuestas para los partidos de hoy|apuestas para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido
colombia|apuestas partido españa marruecos|apuestas
partido mundial|apuestas partido suspendido|apuestas partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos
de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos
hoy|apuestas partidos mundial|apuestas paypal|apuestas peleas
de boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru
uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por internet para ganar dinero|apuestas por paypal|apuestas por ronda boxeo|apuestas por sistema|apuestas
portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas
primera division|apuestas primera division españa|apuestas promociones|apuestas pronostico|apuestas pronosticos|apuestas
pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas
psg barcelona|apuestas puntos por tarjetas|apuestas
puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas
que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas
que significa|apuestas quien bajara a segunda|apuestas
quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana eurocopa|apuestas quien gana la champions|apuestas quien gana
la eurocopa|apuestas quien gana la liga|apuestas quien ganara
el mundial|apuestas quién ganará el mundial|apuestas quien ganara la champions|apuestas quien ganara la eurocopa|apuestas quien ganara la liga|apuestas
rayo barcelona|apuestas real madrid|apuestas real madrid
arsenal|apuestas real madrid athletic|apuestas real madrid atletico|apuestas real madrid
atletico champions|apuestas real madrid atletico de madrid|apuestas
real madrid atlético de madrid|apuestas real madrid
atletico madrid|apuestas real madrid barcelona|apuestas real madrid bayern|apuestas real
madrid betis|apuestas real madrid borussia|apuestas real madrid campeon champions|apuestas real madrid celta|apuestas real madrid
champions|apuestas real madrid city|apuestas real madrid girona|apuestas real
madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real madrid osasuna|apuestas
real madrid real sociedad|apuestas real madrid valencia|apuestas real madrid
villarreal|apuestas real madrid vs arsenal|apuestas real madrid vs atletico|apuestas real madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas real madrid vs
barcelona|apuestas real madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs
valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real sociedad betis|apuestas real sociedad psg|apuestas real sociedad real madrid|apuestas
real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas
segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras
baloncesto|apuestas seguras calculadora|apuestas seguras en la ruleta|apuestas seguras
eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas seguras futbol hoy|apuestas
seguras gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas seguras nba
hoy|apuestas seguras para este fin de semana|apuestas seguras para ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas
seguras para mañana|apuestas seguras ruleta|apuestas seguras
telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises
bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico
de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la
liga|apuestas sevilla girona|apuestas sevilla inter|apuestas sevilla
jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas sevilla madrid|apuestas sevilla
manchester united|apuestas sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real sociedad|apuestas
sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o
combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas
sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa
del rey|apuestas stake|apuestas stake 10|apuestas stake 10 hoy|apuestas super
bowl favorito|apuestas super rugby|apuestas supercopa
españa|apuestas superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas
amarillas|apuestas tenis|apuestas tenis atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de
mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas
tenis hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas tenis wimbledon|apuestas tenis wta|apuestas
tercera division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas torneos
de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas
ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas
ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc
topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas
uruguay colombia|apuestas uruguay corea|apuestas uruguay vs
colombia|apuestas us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas
valencia madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela
argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas
villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas
villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas
vivo|apuestas vuelta a españa|apuestas vuelta españa|apuestas
william hill partidos de hoy|apuestas y casino|apuestas
y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas y
pronosticos de futbol|apuestas y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina apuestas|argentina
colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina
peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina
vs chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic
barcelona apuestas|athletic manchester united apuestas|athletic osasuna
apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico
de madrid apuestas|atlético de madrid apuestas|atletico de
madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid vs real madrid apuestas|atletico
real madrid apuestas|atletico vs real madrid apuestas|avisador de cuotas
apuestas|bajada de cuotas apuestas|baloncesto
apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid apuestas|barça madrid apuestas|barca vs atletico apuestas|barca vs madrid apuestas|barca vs real madrid
apuestas|barcelona – real madrid apuestas|barcelona
apuestas|barcelona atletico apuestas|barcelona atletico de madrid apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona
casa de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona
real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona vs
athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol
apuestas|barcelona vs girona apuestas|barcelona vs madrid apuestas|barcelona vs
real madrid apuestas|barcelona vs real sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal apuestas|base de datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america apuestas|bet apuestas chile|bet apuestas en vivo|betis
– chelsea apuestas|betis apuestas|betis barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog
apuestas baloncesto|blog apuestas ciclismo|blog apuestas nba|blog apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono
apuestas gratis sin deposito|bono apuestas sin deposito|bono bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas
sin deposito|bono bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de
apuestas|bono bienvenida marca apuestas|bono casa
apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono casas de
apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas deportivas|bono de
bienvenida casa de apuestas|bono de bienvenida casas de apuestas|bono de casas de apuestas|bono de registro apuestas|bono de registro apuestas deportivas|bono de
registro casa de apuestas|bono gratis apuestas|bono
marca apuestas|bono por registro apuestas|bono por registro apuestas deportivas|bono
por registro casa de apuestas|bono registro apuestas|bono sin deposito apuestas|bono sin depósito apuestas|bono sin deposito apuestas
deportivas|bono sin depósito apuestas deportivas|bono
sin deposito casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos apuestas|bonos apuestas colombia|bonos apuestas deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas
sin deposito|bonos apuestas sin depósito|bonos bienvenida
apuestas|bonos bienvenida casas apuestas|bonos
bienvenida casas de apuestas|bonos casa de
apuestas|bonos casas apuestas|bonos casas de apuestas|bonos casas
de apuestas colombia|bonos casas de apuestas deportivas|bonos
casas de apuestas españa|bonos casas de apuestas nuevas|bonos casas de apuestas sin deposito|bonos casas de
apuestas sin depósito|bonos de apuestas|bonos
de apuestas deportivas|bonos de apuestas gratis|bonos de apuestas sin deposito|bonos
de bienvenida apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida casa de apuestas|bonos de bienvenida casas de
apuestas|bonos de bienvenida de casas de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de casas de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos
gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas
de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos
sin deposito casas de apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas apuestas para hoy|buscador cuotas apuestas|buscador de apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de apuestas|buscar
apuestas seguras|caballos apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas combinadas|calculadora apuestas
de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora apuestas
seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de
apuestas|calculadora de apuestas combinadas|calculadora de apuestas
de futbol|calculadora de apuestas de sistema|calculadora de
apuestas deportivas|calculadora de apuestas multiples|calculadora de
apuestas seguras|calculadora de apuestas sistema|calculadora de
apuestas surebets|calculadora de arbitraje apuestas|calculadora de cuotas apuestas|calculadora de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular cuotas apuestas
combinadas|calcular cuotas apuestas deportivas|calcular
cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad cuota apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas apuestas|campeon champions
apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de
caballos apuestas|carrera de caballos apuestas juego|carrera
de caballos con apuestas|carrera de galgos apuestas|carreras de
caballos apuestas|carreras de caballos apuestas online|carreras de caballos con apuestas|carreras de caballos juegos de
apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras
de galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas atletico de madrid|casa apuestas barcelona|casa
apuestas betis|casa apuestas bono bienvenida|casa apuestas bono gratis|casa apuestas bono sin deposito|casa apuestas cerca de
mi|casa apuestas chile|casa apuestas colombia|casa apuestas
con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa
apuestas eurocopa|casa apuestas futbol|casa apuestas mejores cuotas|casa
apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa apuestas valencia|casa
de apuestas|casa de apuestas 10 euros gratis|casa de
apuestas argentina|casa de apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas
betis|casa de apuestas bono|casa de apuestas bono bienvenida|casa de apuestas
bono de bienvenida|casa de apuestas bono gratis|casa de apuestas bono
por registro|casa de apuestas bono sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa
de apuestas carreras de caballos|casa de apuestas cerca de mi|casa
de apuestas cerca de mí|casa de apuestas champions league|casa de
apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de
bienvenida|casa de apuestas con bono sin deposito|casa de apuestas
con cuotas mas altas|casa de apuestas con esports|casa de apuestas con las
mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa
de apuestas copa america|casa de apuestas de caballos|casa de apuestas de
colombia|casa de apuestas de españa|casa de apuestas de futbol|casa de apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de
apuestas del real madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca de mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa de apuestas deportivas en españa|casa de
apuestas deportivas en madrid|casa de apuestas deportivas
españa|casa de apuestas deportivas españolas|casa de apuestas deportivas madrid|casa de apuestas deportivas mexico|casa de apuestas deportivas online|casa de
apuestas deportivas peru|casa de apuestas deposito 5 euros|casa de apuestas deposito minimo|casa de apuestas deposito minimo 1
euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de
apuestas en linea|casa de apuestas en madrid|casa de apuestas en perú|casa
de apuestas en vivo|casa de apuestas españa|casa de apuestas españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa
de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de apuestas f1|casa de apuestas formula 1|casa de apuestas
futbol|casa de apuestas ingreso minimo|casa de apuestas ingreso minimo 1 euro|casa de
apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa de
apuestas legales en colombia|casa de apuestas legales en españa|casa de apuestas libertadores|casa
de apuestas liga española|casa de apuestas madrid|casa de apuestas
mas segura|casa de apuestas mejores|casa de apuestas méxico|casa de apuestas minimo
5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas
oficial del real madrid|casa de apuestas oficial real madrid|casa de
apuestas online|casa de apuestas online argentina|casa de apuestas online chile|casa de
apuestas online españa|casa de apuestas online mexico|casa de apuestas online paraguay|casa de apuestas online peru|casa de apuestas online
usa|casa de apuestas online venezuela|casa de apuestas
pago anticipado|casa de apuestas para boxeo|casa de apuestas para
ufc|casa de apuestas peru|casa de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa
de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de
bienvenida|casa de apuestas sevilla|casa de apuestas sin dinero|casa de
apuestas sin ingreso minimo|casa de apuestas sin licencia en españa|casa de apuestas sin minimo de
ingreso|casa de apuestas stake|casa de apuestas tenis|casa
de apuestas ufc|casa de apuestas valencia|casa de apuestas venezuela|casa de apuestas virtuales|casa de apuestas
vive la suerte|casa oficial de apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas apuestas caballos|casas apuestas chile|casas
apuestas ciclismo|casas apuestas con licencia|casas
apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas
apuestas legales|casas apuestas legales españa|casas apuestas
licencia|casas apuestas licencia españa|casas apuestas mexico|casas
apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas
españa|casas apuestas ofertas|casas apuestas online|casas apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas tenis|casas
asiaticas apuestas|casas de apuestas|casas de apuestas 5 euros|casas de apuestas app|casas de apuestas argentinas|casas
de apuestas asiaticas|casas de apuestas baloncesto|casas
de apuestas barcelona|casas de apuestas bono bienvenida|casas
de apuestas bono de bienvenida|casas de apuestas bono por registro|casas de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas
de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas de apuestas carreras de caballos|casas de
apuestas casino|casas de apuestas casino online|casas de apuestas cerca de mi|casas de apuestas champions league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas
con app|casas de apuestas con apuestas gratis|casas de apuestas
con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono de registro|casas de apuestas con bono
por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas
con bonos sin deposito|casas de apuestas con deposito minimo|casas de apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas de apuestas con licencia en españa|casas de apuestas con licencia españa|casas de apuestas con licencia española|casas de apuestas con mejores cuotas|casas de apuestas con pago anticipado|casas de apuestas con paypal|casas de apuestas con paypal
en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa del rey|casas
de apuestas de caballos|casas de apuestas de
españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas de apuestas de peru|casas de
apuestas deportivas|casas de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas
de apuestas deportivas con paypal|casas de apuestas deportivas en chile|casas de apuestas
deportivas en españa|casas de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de apuestas deportivas en mexico|casas de apuestas deportivas en peru|casas de apuestas deportivas en sevilla|casas de
apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de
apuestas deportivas españolas|casas de apuestas deportivas legales|casas de
apuestas deportivas madrid|casas de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas de apuestas deportivas online|casas
de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas deposito minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de apuestas dinero gratis|casas
de apuestas en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa online|casas de
apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas
de apuestas en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas
de apuestas en uruguay|casas de apuestas en valencia|casas de apuestas en venezuela|casas de apuestas equipos de futbol|casas de
apuestas españa|casas de apuestas españa alemania|casas de
apuestas españa inglaterra|casas de apuestas españa
licencia|casas de apuestas españa nuevas|casas de apuestas españa
online|casas de apuestas española|casas de apuestas españolas|casas de apuestas españolas con licencia|casas de apuestas españolas online|casas de apuestas esports|casas de apuestas eurocopa|casas
de apuestas eurocopa 2024|casas de apuestas europa league|casas de apuestas
f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas en españa|casas de apuestas formula 1|casas de apuestas fuera de españa|casas de apuestas futbol|casas de apuestas fútbol|casas
de apuestas futbol españa|casas de apuestas ganador eurocopa|casas de apuestas gratis|casas de apuestas ingreso minimo|casas de apuestas ingreso minimo
1 euro|casas de apuestas ingreso minimo 5 euros|casas de
apuestas inter barcelona|casas de apuestas legales|casas de apuestas
legales en colombia|casas de apuestas legales en españa|casas
de apuestas legales en mexico|casas de apuestas legales
españa|casas de apuestas legales mx|casas de apuestas licencia|casas de apuestas licencia españa|casas de apuestas lista|casas de apuestas madrid|casas
de apuestas mas seguras|casas de apuestas mejores
bonos|casas de apuestas mejores cuotas|casas de apuestas
mexico|casas de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de apuestas nba|casas de apuestas no reguladas en españa|casas
de apuestas nueva ley|casas de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de apuestas ofertas|casas de apuestas online|casas de apuestas online argentina|casas de
apuestas online colombia|casas de apuestas online deportivas|casas de apuestas
online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas
de apuestas online en colombia|casas de apuestas online
en españa|casas de apuestas online en mexico|casas de apuestas
online españa|casas de apuestas online mas fiables|casas de
apuestas online mexico|casas de apuestas online nuevas|casas de apuestas
online peru|casas de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas de apuestas para ufc|casas de apuestas paypal|casas de apuestas peru bono sin deposito|casas
de apuestas presenciales
https://shorturl.fm/hiw2F
https://forum.honorboundgame.com/user-495349.html
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15
euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas que significa|1×2
en apuestas|1×2 en apuestas que significa|1×2 que significa en apuestas|5
euros gratis apuestas|9 apuestas que siempre ganaras|a partir de cuanto se
declara apuestas|actividades de juegos de azar y apuestas|ad apuestas deportivas|aleksandre topuria
ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba
apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de
apuestas online|aplicacion para hacer apuestas|aplicacion para
hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas
deportivas android|aplicaciones apuestas deportivas
gratis|aplicaciones de apuestas android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones
de apuestas deportivas peru|aplicaciones de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de
apuestas online|aplicaciones de apuestas seguras|aplicaciones de apuestas sin dinero|aplicaciones para hacer
apuestas|apostar seguro apuestas deportivas|app android apuestas deportivas|app apuestas|app
apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app apuestas deportivas gratis|app apuestas entre amigos|app
apuestas futbol|app apuestas gratis|app apuestas sin dinero|app casa
de apuestas|app casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de apuestas casino|app de
apuestas colombia|app de apuestas con bono de bienvenida|app de apuestas
de futbol|app de apuestas deportivas|app de apuestas deportivas
android|app de apuestas deportivas argentina|app de apuestas deportivas colombia|app de apuestas deportivas en españa|app
de apuestas deportivas peru|app de apuestas deportivas perú|app de apuestas deportivas sin dinero|app de apuestas ecuador|app
de apuestas en colombia|app de apuestas en españa|app de apuestas en venezuela|app de apuestas futbol|app de apuestas
gratis|app de apuestas online|app de apuestas para android|app de
apuestas para ganar dinero|app de apuestas peru|app de apuestas reales|app de casas de apuestas|app marca
apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app
para ganar apuestas deportivas|app para hacer apuestas|app para hacer apuestas deportivas|app para hacer
apuestas entre amigos|app para llevar control de apuestas|app
pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de
futbol|apps de apuestas deportivas peru|apps de apuestas mexico|apps para apuestas|aprender a hacer
apuestas deportivas|aprender hacer apuestas deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas
1X2|apuestas 2 division|apuestas 3 division|apuestas a caballos|apuestas a carreras de caballos|apuestas a
colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores
nba|apuestas a la baja|apuestas a la nfl|apuestas
al barcelona|apuestas al dia|apuestas al empate|apuestas al
mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz
hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas altas y
bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo
nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas
apps|apuestas arabia argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas argentina canada|apuestas argentina colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina
francia cuanto paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas argentina polonia|apuestas argentina uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina
vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas
arsenal real madrid|apuestas ascenso a primera division|apuestas
ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas
athletic betis|apuestas athletic manchester|apuestas athletic manchester
united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic
real madrid|apuestas athletic real sociedad|apuestas athletic real sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas
athletic valencia|apuestas atletico|apuestas atletico
barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas atletico de madrid gana la liga|apuestas atletico de madrid real madrid|apuestas atlético de madrid real madrid|apuestas atletico de
madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas atletico madrid vs barcelona|apuestas atletico
real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas baloncesto prorroga|apuestas
barca|apuestas barca athletic|apuestas barca atletico|apuestas barca bayern|apuestas barca
bayern munich|apuestas barca girona|apuestas barca hoy|apuestas barça hoy|apuestas barca
inter|apuestas barca juventus|apuestas barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs
juve|apuestas barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas barcelona atletico
de madrid|apuestas barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas
barcelona campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas barcelona gana la
champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas barcelona psg|apuestas
barcelona real madrid|apuestas barcelona real sociedad|apuestas barcelona sevilla|apuestas
barcelona valencia|apuestas barcelona villarreal|apuestas
barcelona vs atletico madrid|apuestas barcelona vs madrid|apuestas barcelona vs real madrid|apuestas
barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas betis chelsea|apuestas betis
fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas betis real madrid|apuestas betis real sociedad|apuestas betis
sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas
betis vs valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas
billar online|apuestas bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas
bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo
español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo online|apuestas
brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs
colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos
colocado|apuestas caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas
caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas
campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas campeon de la champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa
league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas campeon liga santander|apuestas campeon motogp 2025|apuestas
campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas campeonato f1|apuestas campeonatos
de futbol|apuestas carrera de caballos|apuestas carrera de caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas carreras
caballos|apuestas carreras caballos sanlucar|apuestas carreras
de caballos|apuestas carreras de caballos en directo|apuestas carreras de caballos en vivo|apuestas carreras de
caballos españa|apuestas carreras de caballos hoy|apuestas carreras de caballos
nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de caballos online|apuestas carreras de caballos
sanlucar|apuestas carreras de caballos sanlúcar|apuestas carreras de galgos|apuestas carreras de galgos
en vivo|apuestas carreras de galgos nocturnas|apuestas carreras de galgos pre partido|apuestas casino|apuestas casino barcelona|apuestas casino
futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas
casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas
celta madrid|apuestas celta manchester|apuestas celta
real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions
league|apuestas champions league – pronósticos|apuestas champions league 2025|apuestas champions league hoy|apuestas champions league pronosticos|apuestas
champions league pronósticos|apuestas champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo tour
francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas ciclismo vuelta
españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas
clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas
colombia argentina|apuestas colombia brasil|apuestas
colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs
brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de
fútbol|apuestas combinadas foro|apuestas combinadas
futbol|apuestas combinadas hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas
para esta semana|apuestas combinadas para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas combinadas
seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para
mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de
ganar|apuestas con paypal|apuestas con tarjeta de
credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas copa africa|apuestas
copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas copa davis|apuestas copa de europa|apuestas copa del mundo|apuestas
copa del rey|apuestas copa del rey baloncesto|apuestas
copa del rey final|apuestas copa del rey futbol|apuestas copa del
rey ganador|apuestas copa del rey hoy|apuestas copa del rey pronosticos|apuestas copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de hockey|apuestas copa
rey|apuestas copa sudamericana|apuestas corners|apuestas corners hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de
baloncesto para hoy|apuestas de beisbol|apuestas de beisbol para hoy|apuestas de
blackjack en linea|apuestas de boxeo|apuestas de boxeo
canelo|apuestas de boxeo en las vegas|apuestas
de boxeo hoy|apuestas de boxeo online|apuestas de caballo|apuestas de
caballos|apuestas de caballos como funciona|apuestas de caballos como se juega|apuestas de caballos
en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas de caballos
españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas de
caballos juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas de caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera de caballos|apuestas de carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de casino online|apuestas de casino por internet|apuestas de champions league|apuestas de ciclismo|apuestas de colombia|apuestas de copa america|apuestas de corners|apuestas de
deportes en linea|apuestas de deportes online|apuestas
de dinero|apuestas de esports|apuestas de eurocopa|apuestas de europa league|apuestas de f1|apuestas de formula 1|apuestas
de futbol|apuestas de fútbol|apuestas de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas
de futbol en colombia|apuestas de futbol en directo|apuestas de futbol
en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de futbol hoy|apuestas de futbol mundial|apuestas de futbol
online|apuestas de fútbol online|apuestas de futbol para
hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas de futbol
para mañana|apuestas de futbol peru|apuestas de futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas
de futbol seguras para hoy|apuestas de futbol sin dinero|apuestas
de galgos|apuestas de galgos como ganar|apuestas de galgos en directo|apuestas
de galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas de hockey sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de juegos online|apuestas
de la champions league|apuestas de la copa
américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de la
liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas de
la nfl|apuestas de la ufc|apuestas de mlb|apuestas
de nba|apuestas de nba para hoy|apuestas de partidos|apuestas
de partidos de futbol|apuestas de peleas ufc|apuestas
de perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de
sistema|apuestas de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas de tenis hoy|apuestas de tenis para
hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas
del dia de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas del rey|apuestas del
sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas
1×2|apuestas deportivas android|apuestas deportivas app|apuestas deportivas apps|apuestas
deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas
atletico de madrid|apuestas deportivas baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas
deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas
deportivas campeon liga|apuestas deportivas casino|apuestas deportivas
casino barcelona|apuestas deportivas casino online|apuestas
deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas deportivas
ciclismo|apuestas deportivas colombia|apuestas deportivas com|apuestas deportivas com foro|apuestas
deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas
combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas deportivas con bono
gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas
deportivas consejos para ganar|apuestas deportivas copa america|apuestas
deportivas copa del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas altas|apuestas deportivas de baloncesto|apuestas deportivas de boxeo|apuestas deportivas de
colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas
de peru|apuestas deportivas de tenis|apuestas deportivas del dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas
deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas
deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas deportivas en español|apuestas deportivas en linea|apuestas
deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas
estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas
europa league|apuestas deportivas f1|apuestas deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas foro futbol|apuestas deportivas foro tenis|apuestas
deportivas francia argentina|apuestas deportivas futbol|apuestas
deportivas fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas deportivas
futbol español|apuestas deportivas gana|apuestas deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas
gane|apuestas deportivas golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas deportivas
gratis sin deposito|apuestas deportivas handicap|apuestas deportivas
handicap asiatico|apuestas deportivas hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas deportivas legales en colombia|apuestas
deportivas libres de impuestos|apuestas deportivas
licencia españa|apuestas deportivas liga española|apuestas deportivas listado|apuestas deportivas listado clasico|apuestas deportivas
madrid|apuestas deportivas mas seguras|apuestas
deportivas mejor pagadas|apuestas deportivas
mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas
mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas
multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas nba hoy|apuestas deportivas
nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas
ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas deportivas online
chile|apuestas deportivas online colombia|apuestas deportivas online en colombia|apuestas
deportivas online españa|apuestas deportivas online
mexico|apuestas deportivas online paypal|apuestas deportivas online
peru|apuestas deportivas online por internet|apuestas deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas
para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas
peru|apuestas deportivas perú|apuestas deportivas peru vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas
deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas
deportivas pronosticos expertos|apuestas deportivas
pronosticos gratis|apuestas deportivas pronosticos nba|apuestas deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas
deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas
deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake 10|apuestas deportivas
telegram españa|apuestas deportivas tenis|apuestas deportivas tenis de mesa|apuestas
deportivas tenis foro|apuestas deportivas
tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas
ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas y
casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a segunda|apuestas descenso a segunda b|apuestas descenso la liga|apuestas descenso primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas
dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas
directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles
y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas draft nfl|apuestas ecuador vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas
el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas
en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas en la
eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la nfl|apuestas
en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas
en linea chile|apuestas en linea colombia|apuestas
en línea de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas en linea
mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea peru|apuestas en linea usa|apuestas en los esports|apuestas
en madrid|apuestas en méxico|apuestas en mexico online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de
tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas
en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas equipos de futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania
eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia
eurocopa|apuestas españa gana el mundial|apuestas españa gana eurocopa|apuestas españa gana
mundial|apuestas españa georgia|apuestas españa holanda|apuestas
españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa paises bajos|apuestas español|apuestas español oviedo|apuestas
espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas esports colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas
estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas
eurocopa campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa league
hoy|apuestas europa league pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1 cuotas|apuestas f1
hoy|apuestas f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas
favoritos eurocopa|apuestas favoritos mundial|apuestas
fc barcelona|apuestas final champions cuotas|apuestas final champions league|apuestas
final champions peru|apuestas final copa|apuestas final copa america|apuestas final copa
de europa|apuestas final copa del rey|apuestas final copa europa|apuestas final copa libertadores|apuestas final copa rey|apuestas final de
copa|apuestas final de copa del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas
final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia nfl|apuestas finales nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula 1|apuestas fórmula
1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol americano
nfl|apuestas futbol argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas futbol colombia|apuestas
futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas
futbol en vivo|apuestas fútbol en vivo|apuestas futbol españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas futbol
femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol
para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas
galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador champions
league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas ganador copa del
rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador
la liga|apuestas ganador liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas
ganar liga|apuestas ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas
girona betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas girona real madrid|apuestas girona real
sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas
golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand
slam de tenis|apuestas gratis|apuestas gratis casino|apuestas
gratis con premios|apuestas gratis hoy|apuestas
gratis para hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis sports|apuestas gratis y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap
nba|apuestas handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas venezuela|apuestas
hockey|apuestas hockey hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda argentina|apuestas
holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas
impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter barcelona|apuestas juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas juegos online|apuestas juegos
virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas
kings league americas|apuestas la liga|apuestas la liga
española|apuestas la liga hoy|apuestas la liga
santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las vegas nfl|apuestas league of legends mundial|apuestas legal|apuestas legales|apuestas legales
en colombia|apuestas legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas libertadores|apuestas
licencia|apuestas liga 1 peru|apuestas liga argentina|apuestas
liga bbva pronosticos|apuestas liga de campeones|apuestas liga de campeones
de baloncesto|apuestas liga de campeones de hockey|apuestas liga españa|apuestas liga española|apuestas
liga santander pronosticos|apuestas ligas de futbol|apuestas linea|apuestas linea de gol|apuestas
liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas madrid atletico|apuestas madrid atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas madrid barca hoy|apuestas madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas madrid
dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas
madrid valencia|apuestas madrid vs arsenal|apuestas
madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas
mas seguras para hoy|apuestas masters de golf|apuestas masters de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador mundial|apuestas mejor jugador eurocopa|apuestas
mejores casinos online|apuestas mexico|apuestas méxico|apuestas
mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas mlb pronosticos|apuestas mlb usa|apuestas mma
ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas
multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas
mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas mundial de baloncesto|apuestas mundial
de ciclismo|apuestas mundial de clubes|apuestas mundial
de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial f1|apuestas mundial favoritos|apuestas
mundial femenino|apuestas mundial formula
1|apuestas mundial futbol|apuestas mundial
ganador|apuestas mundial lol|apuestas mundial moto gp|apuestas mundial motogp|apuestas mundial rugby|apuestas
mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas mvp nba|apuestas mvp
nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas nba
tipster|apuestas nfl|apuestas nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas nfl pronósticos|apuestas
nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas
ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online bono|apuestas online bono bienvenida|apuestas online boxeo|apuestas
online caballos|apuestas online carreras de caballos|apuestas online casino|apuestas online champions league|apuestas online chile|apuestas online ciclismo|apuestas online
colombia|apuestas online comparativa|apuestas online con paypal|apuestas online
de caballos|apuestas online deportivas|apuestas online en argentina|apuestas
online en peru|apuestas online espana|apuestas online españa|apuestas online esports|apuestas online foro|apuestas online futbol|apuestas
online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis
sin deposito|apuestas online juegos|apuestas online mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online net|apuestas online
nuevas|apuestas online opiniones|apuestas online paypal|apuestas
online peru|apuestas online seguras|apuestas online
sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online ufc|apuestas online uruguay|apuestas online
venezuela|apuestas open britanico golf|apuestas
osasuna athletic|apuestas osasuna barcelona|apuestas osasuna
real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises
bajos ecuador|apuestas paises bajos inglaterra|apuestas países bajos qatar|apuestas para boxeo|apuestas para
champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para el mundial|apuestas
para el partido de hoy|apuestas para eurocopa|apuestas para
europa league|apuestas para futbol|apuestas
para ganar|apuestas para ganar dinero|apuestas para ganar
dinero facil|apuestas para ganar en la ruleta|apuestas para ganar la
champions|apuestas para ganar la eurocopa|apuestas para ganar
la europa league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para hacer|apuestas para
hoy|apuestas para hoy de futbol|apuestas para
hoy europa league|apuestas para hoy futbol|apuestas para juegos|apuestas para la champions league|apuestas para la copa del rey|apuestas para la
eurocopa|apuestas para la europa league|apuestas para
la final de la eurocopa|apuestas para la nba
hoy|apuestas para los partidos de hoy|apuestas para partidos de hoy|apuestas para ufc|apuestas
partido|apuestas partido aplazado|apuestas partido
champions|apuestas partido colombia|apuestas partido españa marruecos|apuestas
partido mundial|apuestas partido suspendido|apuestas partidos|apuestas partidos
champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas
paypal|apuestas peleas de boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso
a primera|apuestas playoff nba|apuestas playoff segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas playoffs
nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por
internet para ganar dinero|apuestas por paypal|apuestas
por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas pronostico|apuestas
pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas psg barcelona|apuestas puntos
por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas que
siempre ganaras|apuestas que significa|apuestas quien bajara
a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana eurocopa|apuestas quien gana la champions|apuestas quien gana la
eurocopa|apuestas quien gana la liga|apuestas quien ganara el mundial|apuestas quién ganará el
mundial|apuestas quien ganara la champions|apuestas quien ganara
la eurocopa|apuestas quien ganara la liga|apuestas rayo
barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real
madrid atletico de madrid|apuestas real madrid atlético
de madrid|apuestas real madrid atletico madrid|apuestas real madrid
barcelona|apuestas real madrid bayern|apuestas real madrid betis|apuestas real madrid borussia|apuestas real madrid campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real madrid girona|apuestas real madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real madrid osasuna|apuestas real madrid
real sociedad|apuestas real madrid valencia|apuestas real madrid villarreal|apuestas real madrid vs
arsenal|apuestas real madrid vs atletico|apuestas real
madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas real madrid vs barcelona|apuestas real madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real sociedad betis|apuestas real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas
hoy|apuestas regalo de bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada
tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda
b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas
seguras baloncesto|apuestas seguras calculadora|apuestas seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras
futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas seguras nba hoy|apuestas
seguras para este fin de semana|apuestas seguras para
ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para
mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises
bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas
sevilla barcelona|apuestas sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la liga|apuestas sevilla
girona|apuestas sevilla inter|apuestas sevilla jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas sevilla madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas sevilla
real madrid|apuestas sevilla real sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas
sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas
sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas
sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake 10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas superliga
argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas
tenis atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas tenis wimbledon|apuestas tenis wta|apuestas tercera division|apuestas tercera
division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas torneos de golf|apuestas torneos de
tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas
valencia madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas
valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal
betis|apuestas villarreal liverpool|apuestas villarreal
manchester|apuestas villarreal manchester united|apuestas villarreal vs
real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales
futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta
españa|apuestas william hill partidos de hoy|apuestas y casino|apuestas y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas
y pronosticos de futbol|apuestas y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina apuestas|argentina colombia apuestas|argentina
croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina
peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico
apuestas|asiatico en apuestas|asiaticos apuestas|athletic
barcelona apuestas|athletic manchester united apuestas|athletic osasuna apuestas|athletic real madrid apuestas|atletico barcelona
apuestas|atletico de madrid apuestas|atlético
de madrid apuestas|atletico de madrid real madrid apuestas|atletico
de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid vs real madrid apuestas|atletico real
madrid apuestas|atletico vs real madrid apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto
apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid apuestas|barça
madrid apuestas|barca vs atletico apuestas|barca vs madrid apuestas|barca
vs real madrid apuestas|barcelona – real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona atletico de madrid
apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona casa de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia
apuestas|barcelona vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs
betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs girona apuestas|barcelona vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal apuestas|base de datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america
apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis
barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis
sevilla apuestas|betsson tu sitio de apuestas online|blog apuestas baloncesto|blog
apuestas ciclismo|blog apuestas nba|blog apuestas tenis|blog
de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas
sin deposito|bono bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas sin deposito|bono
bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida marca apuestas|bono casa apuestas|bono casa de
apuestas|bono casa de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono
de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas deportivas|bono
de bienvenida casa de apuestas|bono de bienvenida casas de apuestas|bono
de casas de apuestas|bono de registro apuestas|bono de registro
apuestas deportivas|bono de registro casa de apuestas|bono gratis
apuestas|bono marca apuestas|bono por registro apuestas|bono por registro
apuestas deportivas|bono por registro casa de apuestas|bono registro
apuestas|bono sin deposito apuestas|bono sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito casa
de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas
deportivas|bonos apuestas|bonos apuestas colombia|bonos
apuestas deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida casas de
apuestas|bonos casa de apuestas|bonos casas apuestas|bonos casas de apuestas|bonos casas de apuestas colombia|bonos casas de apuestas deportivas|bonos casas de apuestas españa|bonos casas de apuestas nuevas|bonos casas de
apuestas sin deposito|bonos casas de apuestas sin depósito|bonos de
apuestas|bonos de apuestas deportivas|bonos de apuestas gratis|bonos de apuestas
sin deposito|bonos de bienvenida apuestas|bonos de bienvenida apuestas
deportivas|bonos de bienvenida casa de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida de casas de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de casas
de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas de apuestas|bonos registro casas de apuestas|bonos
sin deposito apuestas|bonos sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas apuestas para hoy|buscador cuotas
apuestas|buscador de apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de apuestas|buscar apuestas seguras|caballos apuestas|calculador de apuestas|calculador de
cuotas apuestas|calculadora apuestas|calculadora apuestas combinadas|calculadora apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas seguras|calculadora
apuestas multiples|calculadora apuestas segura|calculadora apuestas
seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora
arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora
de apuestas|calculadora de apuestas combinadas|calculadora de apuestas de
futbol|calculadora de apuestas de sistema|calculadora
de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas
surebets|calculadora de arbitraje apuestas|calculadora de cuotas apuestas|calculadora de cuotas de apuestas|calculadora
para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora trading
apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas
futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular cuotas
apuestas combinadas|calcular cuotas apuestas deportivas|calcular
cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad cuota
apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo de apuestas|calculo
de apuestas deportivas|cambio de cuotas apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos
apuestas juego|carrera de caballos con apuestas|carrera de galgos
apuestas|carreras de caballos apuestas|carreras
de caballos apuestas online|carreras de caballos con apuestas|carreras de caballos juegos de apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras de galgos
apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas atletico de madrid|casa apuestas barcelona|casa apuestas
betis|casa apuestas bono bienvenida|casa apuestas
bono gratis|casa apuestas bono sin deposito|casa apuestas cerca de mi|casa apuestas chile|casa apuestas
colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa
apuestas futbol|casa apuestas mejores cuotas|casa apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa apuestas
online|casa apuestas peru|casa apuestas valencia|casa de
apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de apuestas atletico de madrid|casa
de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas
betis|casa de apuestas bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa de apuestas bono gratis|casa de apuestas bono por registro|casa
de apuestas bono sin deposito|casa de apuestas boxeo|casa de apuestas
caballos|casa de apuestas carreras de caballos|casa de apuestas cerca de mi|casa
de apuestas cerca de mí|casa de apuestas champions league|casa de apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas
con bono de bienvenida|casa de apuestas con bono sin deposito|casa de apuestas con cuotas
mas altas|casa de apuestas con esports|casa de
apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de apuestas
copa america|casa de apuestas de caballos|casa de apuestas de colombia|casa de apuestas de españa|casa de apuestas de futbol|casa de apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas
del madrid|casa de apuestas del real madrid|casa de apuestas deportivas|casa
de apuestas deportivas cerca de mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas
en chile|casa de apuestas deportivas en colombia|casa de apuestas deportivas en españa|casa de apuestas deportivas
en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas españolas|casa de apuestas deportivas madrid|casa de apuestas deportivas mexico|casa
de apuestas deportivas online|casa de apuestas deportivas peru|casa de apuestas deposito 5 euros|casa de apuestas deposito minimo|casa de apuestas deposito minimo
1 euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas
españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas
eurocopa|casa de apuestas europa league|casa de apuestas f1|casa de apuestas formula 1|casa
de apuestas futbol|casa de apuestas ingreso minimo|casa
de apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo
1 euro|casa de apuestas legales|casa de apuestas legales
en colombia|casa de apuestas legales en españa|casa
de apuestas libertadores|casa de apuestas liga española|casa de
apuestas madrid|casa de apuestas mas segura|casa de apuestas mejores|casa de apuestas méxico|casa de apuestas
minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del real madrid|casa de apuestas oficial
real madrid|casa de apuestas online|casa
de apuestas online argentina|casa de apuestas online chile|casa de apuestas online españa|casa de apuestas online
mexico|casa de apuestas online paraguay|casa de apuestas online peru|casa de apuestas online usa|casa de apuestas online venezuela|casa
de apuestas pago anticipado|casa de apuestas para boxeo|casa de apuestas para ufc|casa de apuestas peru|casa de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa de apuestas promociones|casa de
apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas
regalo de bienvenida|casa de apuestas sevilla|casa
de apuestas sin dinero|casa de apuestas sin ingreso
minimo|casa de apuestas sin licencia en españa|casa de apuestas sin minimo
de ingreso|casa de apuestas stake|casa de apuestas tenis|casa de apuestas ufc|casa
de apuestas valencia|casa de apuestas venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas
apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas
apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas
apuestas deportivas|casas apuestas deportivas colombia|casas apuestas
deportivas españa|casas apuestas deportivas españolas|casas apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5
euros|casas apuestas legales|casas apuestas legales
españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas
apuestas online|casas apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas
tenis|casas asiaticas apuestas|casas de apuestas|casas
de apuestas 5 euros|casas de apuestas app|casas de apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono de bienvenida|casas de apuestas bono por registro|casas de apuestas bono sin deposito|casas de
apuestas bono sin ingreso|casas de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas bonos
gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas de
apuestas carreras de caballos|casas de apuestas casino|casas de apuestas casino online|casas de
apuestas cerca de mi|casas de apuestas champions league|casas de
apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de apuestas con apuestas gratis|casas de apuestas con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono de registro|casas de apuestas con bono por registro|casas
de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos
gratis|casas de apuestas con bonos sin deposito|casas de apuestas
con deposito minimo|casas de apuestas con esports|casas de
apuestas con handicap asiatico|casas de apuestas con licencia|casas de apuestas con licencia en españa|casas de apuestas con licencia españa|casas de apuestas con licencia
española|casas de apuestas con mejores cuotas|casas de apuestas
con pago anticipado|casas de apuestas con paypal|casas de
apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas
copa del rey|casas de apuestas de caballos|casas de apuestas
de españa|casas de apuestas de futbol|casas
de apuestas de fútbol|casas de apuestas de peru|casas de apuestas deportivas|casas de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas
deportivas comparativa|casas de apuestas deportivas con paypal|casas
de apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas
en linea|casas de apuestas deportivas en madrid|casas de apuestas deportivas
en mexico|casas de apuestas deportivas en peru|casas de apuestas deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas
españa|casas de apuestas deportivas españolas|casas de apuestas
deportivas legales|casas de apuestas deportivas madrid|casas de apuestas
deportivas mexico|casas de apuestas deportivas nuevas|casas
de apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas deposito minimo 1 euro|casas de apuestas depósito
mínimo 1 euro|casas de apuestas dinero gratis|casas de
apuestas en argentina|casas de apuestas en barcelona|casas de
apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa
online|casas de apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas de apuestas en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas de apuestas en uruguay|casas de apuestas
en valencia|casas de apuestas en venezuela|casas de
apuestas equipos de futbol|casas de apuestas españa|casas de apuestas españa alemania|casas
de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas
de apuestas españa online|casas de apuestas española|casas de apuestas españolas|casas
de apuestas españolas con licencia|casas de apuestas españolas online|casas de apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas de apuestas f1|casas de apuestas
fisicas en barcelona|casas de apuestas fisicas en españa|casas
de apuestas formula 1|casas de apuestas fuera de españa|casas de apuestas futbol|casas de apuestas fútbol|casas
de apuestas futbol españa|casas de apuestas ganador eurocopa|casas de apuestas gratis|casas de apuestas
ingreso minimo|casas de apuestas ingreso minimo 1 euro|casas de apuestas ingreso minimo 5
euros|casas de apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas de
apuestas legales en mexico|casas de apuestas legales españa|casas
de apuestas legales mx|casas de apuestas licencia|casas
de apuestas licencia españa|casas de apuestas lista|casas de
apuestas madrid|casas de apuestas mas seguras|casas
de apuestas mejores bonos|casas de apuestas mejores cuotas|casas
de apuestas mexico|casas de apuestas méxico|casas
de apuestas minimo 5 euros|casas de apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas
de apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de
apuestas ofertas|casas de apuestas online|casas
de apuestas online argentina|casas de apuestas online colombia|casas de apuestas online deportivas|casas de apuestas
online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas
de apuestas online en colombia|casas de apuestas online en españa|casas de apuestas
online en mexico|casas de apuestas online españa|casas de apuestas online mas fiables|casas
de apuestas online mexico|casas de apuestas online nuevas|casas de apuestas online peru|casas de apuestas online usa|casas de apuestas online venezuela|casas de
apuestas pago paypal|casas de apuestas para ufc|casas de apuestas paypal|casas de apuestas p
Портал актуальной информации по провайдерам iptv, свежие новости https://imgur.com/wfIahUR
mostbet kg https://www.mostbet12038.ru
Je suis sous le charme de Azur Casino, il propose une aventure palpitante. La selection est riche et diversifiee, proposant des jeux de cartes elegants. Il offre un demarrage en fanfare. Le support est efficace et amical. Le processus est transparent et rapide, de temps a autre des offres plus genereuses rendraient l’experience meilleure. Dans l’ensemble, Azur Casino vaut une exploration vibrante. En bonus la navigation est fluide et facile, ce qui rend chaque partie plus fun. Un point fort les options variees pour les paris sportifs, renforce la communaute.
Commencer Г dГ©couvrir|
Je suis completement seduit par Azur Casino, c’est une plateforme qui pulse avec energie. Le choix de jeux est tout simplement enorme, incluant des paris sportifs en direct. Avec des depots rapides et faciles. Le support est efficace et amical. Le processus est simple et transparent, neanmoins plus de promos regulieres dynamiseraient le jeu. Dans l’ensemble, Azur Casino est un immanquable pour les amateurs. A mentionner le site est rapide et engageant, donne envie de prolonger l’aventure. Particulierement attrayant les paiements en crypto rapides et surs, qui motive les joueurs.
Plonger dedans|
apuestas en vivo ganabet https://ganabet-online.com/ .
valor de fichas de casino por color valorslots.com .
jp 99 slot https://jp99-online.com/ .
стоимость регистрации перепланировки стоимость регистрации перепланировки .
проект для перепланировки квартиры стоимость https://skolko-stoit-uzakonit-pereplanirovku.ru .
Pin Up Casino is a reliable, licensed online gaming platform created specifically for players from Russia and the CIS
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15 euros
gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2
apuestas que significa|1×2 en apuestas|1×2 en apuestas que significa|1×2 que significa en apuestas|5 euros gratis apuestas|9 apuestas que siempre ganaras|a partir de cuanto se declara
apuestas|actividades de juegos de azar y apuestas|ad apuestas deportivas|aleksandre topuria ufc
apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba apuestas|aplicacion android apuestas
deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de apuestas
online|aplicacion para hacer apuestas|aplicacion para
hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas deportivas
android|aplicaciones apuestas deportivas gratis|aplicaciones de apuestas android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones de apuestas deportivas
perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de apuestas
online|aplicaciones de apuestas seguras|aplicaciones de apuestas sin dinero|aplicaciones
para hacer apuestas|apostar seguro apuestas deportivas|app android
apuestas deportivas|app apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas deportivas argentina|app apuestas deportivas
colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app apuestas deportivas gratis|app apuestas entre amigos|app apuestas
futbol|app apuestas gratis|app apuestas sin dinero|app casa
de apuestas|app casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de apuestas casino|app de apuestas colombia|app de apuestas con bono de bienvenida|app de apuestas de futbol|app de apuestas deportivas|app de apuestas deportivas android|app
de apuestas deportivas argentina|app de apuestas deportivas colombia|app
de apuestas deportivas en españa|app de apuestas deportivas peru|app de apuestas
deportivas perú|app de apuestas deportivas sin dinero|app de apuestas ecuador|app
de apuestas en colombia|app de apuestas en españa|app de apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app de apuestas online|app de apuestas para
android|app de apuestas para ganar dinero|app de apuestas
peru|app de apuestas reales|app de casas de
apuestas|app marca apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para ganar apuestas deportivas|app para hacer apuestas|app para hacer apuestas deportivas|app
para hacer apuestas entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps
de apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de futbol|apps de apuestas deportivas peru|apps de apuestas mexico|apps para apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas deportivas|apuesta del dia apuestas
deportivas|apuestas 10 euros gratis|apuestas 100
seguras|apuestas 1×2|apuestas 1X2|apuestas 2 division|apuestas
3 division|apuestas a caballos|apuestas a carreras de caballos|apuestas a colombia|apuestas
a corners|apuestas a ganar|apuestas a jugadores nba|apuestas a la baja|apuestas a la nfl|apuestas al barcelona|apuestas al
dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz
hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas
altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas
apps|apuestas arabia argentina|apuestas argentina|apuestas
argentina campeon del mundo|apuestas argentina canada|apuestas argentina colombia|apuestas
argentina croacia|apuestas argentina españa|apuestas argentina francia|apuestas
argentina francia cuanto paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas
argentina mexico|apuestas argentina méxico|apuestas argentina mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas argentina polonia|apuestas argentina
uruguay|apuestas argentina vs australia|apuestas
argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs peru|apuestas
argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas
athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas
athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas
athletic real madrid|apuestas athletic real sociedad|apuestas athletic
real sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic
valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico
barsa|apuestas atletico campeon champions|apuestas atletico campeon de liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas atletico
de madrid gana la liga|apuestas atletico de madrid real madrid|apuestas atlético
de madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico
madrid|apuestas atletico madrid real madrid|apuestas atletico madrid vs barcelona|apuestas atletico
real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas
baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas
barca atletico|apuestas barca bayern|apuestas barca bayern munich|apuestas
barca girona|apuestas barca hoy|apuestas barça hoy|apuestas barca inter|apuestas
barca juventus|apuestas barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas
barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas
barcelona atletico de madrid|apuestas barcelona atlético
de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas barcelona
campeon de liga|apuestas barcelona celta|apuestas
barcelona espanyol|apuestas barcelona gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas barcelona psg|apuestas
barcelona real madrid|apuestas barcelona real sociedad|apuestas barcelona
sevilla|apuestas barcelona valencia|apuestas barcelona villarreal|apuestas
barcelona vs atletico madrid|apuestas barcelona vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas
beisbol|apuestas béisbol|apuestas beisbol
mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis
barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas
betis real madrid|apuestas betis real sociedad|apuestas betis sevilla|apuestas
betis valencia|apuestas betis valladolid|apuestas betis vs
valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas billar online|apuestas
bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas bono
de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos
sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo
online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos españa|apuestas
caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos
sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas campeón champions|apuestas campeon champions
2025|apuestas campeon champions league|apuestas
campeon conference league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas
campeon de la champions|apuestas campeon de liga|apuestas campeon del
mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa
league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas
campeon liga española|apuestas campeon liga santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas
campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas campeonato f1|apuestas
campeonatos de futbol|apuestas carrera de caballos|apuestas carrera de caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas carreras caballos|apuestas carreras caballos
sanlucar|apuestas carreras de caballos|apuestas carreras de caballos
en directo|apuestas carreras de caballos en vivo|apuestas carreras
de caballos españa|apuestas carreras de caballos hoy|apuestas
carreras de caballos nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de caballos online|apuestas carreras de caballos sanlucar|apuestas carreras de
caballos sanlúcar|apuestas carreras de galgos|apuestas carreras de galgos en vivo|apuestas carreras
de galgos nocturnas|apuestas carreras de galgos pre
partido|apuestas casino|apuestas casino barcelona|apuestas
casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas
casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas celta madrid|apuestas celta manchester|apuestas celta
real madrid|apuestas champion league|apuestas champions foro|apuestas
champions hoy|apuestas champions league|apuestas champions
league – pronósticos|apuestas champions league 2025|apuestas champions league hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas chelsea
barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo
tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas
ciclismo vuelta españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia
argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas
colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs brasil|apuestas combinadas|apuestas
combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas
futbol|apuestas combinadas hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas para esta semana|apuestas combinadas para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas
combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero
real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas copa
davis|apuestas copa de europa|apuestas copa del mundo|apuestas copa del rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas copa
del rey futbol|apuestas copa del rey ganador|apuestas copa del rey hoy|apuestas copa del rey
pronosticos|apuestas copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de hockey|apuestas copa
rey|apuestas copa sudamericana|apuestas corners|apuestas corners hoy|apuestas croacia argentina|apuestas cuartos
eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas
cuotas bajas|apuestas de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto para hoy|apuestas de beisbol|apuestas de beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas
de boxeo en las vegas|apuestas de boxeo hoy|apuestas de
boxeo online|apuestas de caballo|apuestas de caballos|apuestas de caballos como
funciona|apuestas de caballos como se juega|apuestas de caballos en colombia|apuestas de caballos
en españa|apuestas de caballos en linea|apuestas de caballos españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas de caballos juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas de
caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera
de caballos|apuestas de carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de casino online|apuestas de casino por internet|apuestas de champions league|apuestas
de ciclismo|apuestas de colombia|apuestas de copa america|apuestas de corners|apuestas de deportes en linea|apuestas de
deportes online|apuestas de dinero|apuestas de esports|apuestas de
eurocopa|apuestas de europa league|apuestas de f1|apuestas de
formula 1|apuestas de futbol|apuestas de fútbol|apuestas de
futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de
futbol en colombia|apuestas de futbol en directo|apuestas de
futbol en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol
gratis|apuestas de futbol hoy|apuestas de futbol mundial|apuestas de futbol online|apuestas de fútbol online|apuestas de
futbol para hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas de futbol para mañana|apuestas de futbol peru|apuestas de
futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas de futbol seguras para hoy|apuestas de futbol sin dinero|apuestas de
galgos|apuestas de galgos como ganar|apuestas de galgos en directo|apuestas de galgos online|apuestas de galgos
trucos|apuestas de golf|apuestas de hockey|apuestas de hockey sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de
juegos deportivos|apuestas de juegos online|apuestas de la champions league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de
la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas de la nfl|apuestas de
la ufc|apuestas de mlb|apuestas de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas de peleas ufc|apuestas de perros
en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema
como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas de tenis
de mesa|apuestas de tenis en directo|apuestas de tenis
hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas
de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del
clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia de
hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del mundial|apuestas del partido de hoy|apuestas del real
madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas
deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas android|apuestas deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas atletico de madrid|apuestas deportivas baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas
deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas bono sin deposito|apuestas
deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas
campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas
deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions
league|apuestas deportivas chile|apuestas deportivas ciclismo|apuestas deportivas colombia|apuestas deportivas com|apuestas deportivas com
foro|apuestas deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas
deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas deportivas consejos para ganar|apuestas deportivas
copa america|apuestas deportivas copa del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual
es la mejor|apuestas deportivas cuotas altas|apuestas deportivas
de baloncesto|apuestas deportivas de boxeo|apuestas deportivas de colombia|apuestas deportivas de
futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas
deportivas de peru|apuestas deportivas de tenis|apuestas deportivas
del dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas
doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas
en peru|apuestas deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas
estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas europa league|apuestas deportivas f1|apuestas
deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas futbol|apuestas deportivas
fútbol|apuestas deportivas futbol argentino|apuestas deportivas
futbol colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas deportivas
ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas deportivas golf|apuestas deportivas
gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas deportivas gratis sin deposito|apuestas
deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas
hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas
deportivas legales en colombia|apuestas deportivas libres de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga española|apuestas
deportivas listado|apuestas deportivas listado clasico|apuestas deportivas madrid|apuestas deportivas mas seguras|apuestas deportivas mejor
pagadas|apuestas deportivas mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas
méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas multiples|apuestas deportivas
mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas nba
hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas ofertas|apuestas deportivas online|apuestas deportivas
online argentina|apuestas deportivas online chile|apuestas
deportivas online colombia|apuestas deportivas online en colombia|apuestas
deportivas online españa|apuestas deportivas online mexico|apuestas deportivas
online paypal|apuestas deportivas online peru|apuestas deportivas
online por internet|apuestas deportivas pago paypal|apuestas deportivas
para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas
deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas deportivas perú|apuestas deportivas peru vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas
deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas
deportivas pronosticos gratis|apuestas deportivas pronosticos
nba|apuestas deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas
deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras
para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas
sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake
10|apuestas deportivas telegram españa|apuestas
deportivas tenis|apuestas deportivas tenis de mesa|apuestas deportivas
tenis foro|apuestas deportivas tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas
deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a segunda|apuestas descenso
a segunda b|apuestas descenso la liga|apuestas descenso primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas
dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas
directas|apuestas directo|apuestas directo futbol|apuestas
division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles y triples|apuestas dortmund barcelona|apuestas draft
nba|apuestas draft nfl|apuestas ecuador vs argentina|apuestas
ecuador vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas
en beisbol|apuestas en boxeo|apuestas en caballos|apuestas
en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas
en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos
virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas en la
eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la
nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas
en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas en linea
chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea
futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas
en linea peru|apuestas en linea usa|apuestas en los esports|apuestas en madrid|apuestas
en méxico|apuestas en mexico online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas
en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas
en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas en vivo fútbol|apuestas
en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo
ufc|apuestas equipo mbappe|apuestas equipos de
futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa gana el mundial|apuestas españa gana eurocopa|apuestas españa gana mundial|apuestas españa georgia|apuestas españa holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa paises bajos|apuestas español|apuestas español
oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas
esport|apuestas esports|apuestas esports colombia|apuestas
esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas
eurocopa campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa league hoy|apuestas europa league
pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1 cuotas|apuestas f1 hoy|apuestas f1
las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles
de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas
favorito champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas fc barcelona|apuestas final
champions cuotas|apuestas final champions league|apuestas final champions peru|apuestas final copa|apuestas final copa america|apuestas final copa de europa|apuestas
final copa del rey|apuestas final copa europa|apuestas final copa libertadores|apuestas
final copa rey|apuestas final de copa|apuestas final de copa
del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de
conferencia nfl|apuestas finales nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula 1|apuestas fórmula 1 pronósticos|apuestas
formula uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas francia españa|apuestas
futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol americano nfl|apuestas
futbol argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol
en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas
futbol españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas
futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas
futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos
pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas
gana resultados|apuestas ganadas|apuestas ganadas
hoy|apuestas ganador champions league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas
ganador copa del rey baloncesto|apuestas ganador copa libertadores|apuestas
ganador de la eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la liga|apuestas ganador liga española|apuestas
ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar
eurocopa|apuestas ganar liga|apuestas ganar mundial|apuestas ganar
nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona
betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas girona
real madrid|apuestas girona real sociedad|apuestas goleador eurocopa|apuestas goleadores
eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas
golf pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas gratis|apuestas gratis
casino|apuestas gratis con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas gratis por
registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis
sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis sports|apuestas gratis
y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas
handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas
hipicas venezuela|apuestas hockey|apuestas hockey hielo|apuestas hockey patines|apuestas
hockey sobre hielo|apuestas holanda argentina|apuestas holanda vs argentina|apuestas
hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter
barcelona|apuestas juego|apuestas juegos|apuestas juegos en linea|apuestas juegos
olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas
juegos online|apuestas juegos virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings
league americas|apuestas la liga|apuestas la liga española|apuestas
la liga hoy|apuestas la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las vegas nfl|apuestas league of legends mundial|apuestas
legal|apuestas legales|apuestas legales en colombia|apuestas legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas libertadores|apuestas licencia|apuestas liga 1 peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas liga de campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones de hockey|apuestas liga españa|apuestas
liga española|apuestas liga santander pronosticos|apuestas ligas de futbol|apuestas linea|apuestas linea
de gol|apuestas liverpool barcelona|apuestas liverpool real
madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas madrid atletico|apuestas madrid atletico champions|apuestas madrid barca|apuestas
madrid barça|apuestas madrid barca hoy|apuestas madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid
borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas
madrid dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas
madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas madrid valencia|apuestas madrid vs arsenal|apuestas
madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas
mas seguras para hoy|apuestas masters de golf|apuestas masters de tenis|apuestas maximo
goleador eurocopa|apuestas maximo goleador
mundial|apuestas mejor jugador eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas
mlb hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas
mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas
mundial de baloncesto|apuestas mundial de ciclismo|apuestas mundial
de clubes|apuestas mundial de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial
f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas mundial moto gp|apuestas mundial motogp|apuestas mundial rugby|apuestas mundial
sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba
all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas
nba gratis|apuestas nba hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas
nfl pronósticos|apuestas nfl semana 4|apuestas nfl super
bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas
ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online bono|apuestas online bono bienvenida|apuestas online boxeo|apuestas online caballos|apuestas online carreras
de caballos|apuestas online casino|apuestas online champions league|apuestas online chile|apuestas online ciclismo|apuestas online
colombia|apuestas online comparativa|apuestas online con paypal|apuestas online de caballos|apuestas online
deportivas|apuestas online en argentina|apuestas online en peru|apuestas online espana|apuestas online españa|apuestas
online esports|apuestas online foro|apuestas online futbol|apuestas
online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online juegos|apuestas online mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online
net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online peru|apuestas online
seguras|apuestas online sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online ufc|apuestas online uruguay|apuestas online venezuela|apuestas
open britanico golf|apuestas osasuna athletic|apuestas osasuna
barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas
over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos ecuador|apuestas paises bajos inglaterra|apuestas países bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para el mundial|apuestas para el partido
de hoy|apuestas para eurocopa|apuestas para europa league|apuestas para
futbol|apuestas para ganar|apuestas para ganar dinero|apuestas para ganar dinero
facil|apuestas para ganar en la ruleta|apuestas para ganar la champions|apuestas para
ganar la eurocopa|apuestas para ganar la europa league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas
para hoy de futbol|apuestas para hoy europa league|apuestas
para hoy futbol|apuestas para juegos|apuestas para la champions league|apuestas para
la copa del rey|apuestas para la eurocopa|apuestas para la europa
league|apuestas para la final de la eurocopa|apuestas
para la nba hoy|apuestas para los partidos de hoy|apuestas
para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas partido españa marruecos|apuestas partido
mundial|apuestas partido suspendido|apuestas partidos|apuestas partidos champions league|apuestas
partidos csgo|apuestas partidos de futbol|apuestas partidos
de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas
partidos hoy|apuestas partidos mundial|apuestas paypal|apuestas peleas de boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas
peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru vs
chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas
plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff
segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas
por internet mexico|apuestas por internet para ganar dinero|apuestas por
paypal|apuestas por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera
division españa|apuestas promociones|apuestas pronostico|apuestas pronosticos|apuestas
pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas
pronosticos nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas psg
barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas
que es handicap|apuestas que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas que significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas
quien gana el mundial|apuestas quien gana eurocopa|apuestas quien gana
la champions|apuestas quien gana la eurocopa|apuestas quien gana la liga|apuestas quien ganara el mundial|apuestas
quién ganará el mundial|apuestas quien ganara la
champions|apuestas quien ganara la eurocopa|apuestas quien ganara la
liga|apuestas rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid athletic|apuestas
real madrid atletico|apuestas real madrid atletico champions|apuestas real madrid atletico de madrid|apuestas real madrid atlético de madrid|apuestas real madrid atletico
madrid|apuestas real madrid barcelona|apuestas real madrid bayern|apuestas real madrid betis|apuestas real madrid borussia|apuestas real madrid
campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real madrid
city|apuestas real madrid girona|apuestas real madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real madrid
osasuna|apuestas real madrid real sociedad|apuestas real madrid valencia|apuestas
real madrid villarreal|apuestas real madrid vs arsenal|apuestas
real madrid vs atletico|apuestas real madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas real
madrid vs barcelona|apuestas real madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real sociedad betis|apuestas real sociedad psg|apuestas
real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de
bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas
roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas seguras
en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas seguras futbol hoy|apuestas
seguras gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas seguras nba hoy|apuestas seguras para este fin de semana|apuestas seguras
para ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy
fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para
mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas
senegal paises bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla
atletico de madrid|apuestas sevilla barcelona|apuestas sevilla
betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la
liga|apuestas sevilla girona|apuestas sevilla inter|apuestas sevilla jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas sevilla madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real
sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o
combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas sin deposito
minimo|apuestas sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas
sin registro|apuestas sistema|apuestas sistema calculadora|apuestas
sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake
10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas superliga
argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas tenis itf|apuestas
tenis pronosticos|apuestas tenis pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas tenis wimbledon|apuestas tenis wta|apuestas tercera division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas torneos de golf|apuestas torneos
de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas
ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas
us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas valencia madrid|apuestas
valencia real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas valor app|apuestas
valor en directo|apuestas valor galgos|apuestas venezuela|apuestas
venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas
villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester
united|apuestas villarreal vs real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas
vuelta a españa|apuestas vuelta españa|apuestas william hill partidos de hoy|apuestas y casino|apuestas y
casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas
y pronosticos de futbol|apuestas y pronosticos deportivos|apuestas
y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba
apuestas|argentina apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs chile apuestas|argentina vs colombia apuestas|argentina vs
francia apuestas|argentina vs. colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico
de madrid apuestas|atlético de madrid apuestas|atletico de
madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs real
madrid apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid apuestas|barça
madrid apuestas|barca vs atletico apuestas|barca vs
madrid apuestas|barca vs real madrid apuestas|barcelona –
real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona atletico de madrid apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona casa de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs girona apuestas|barcelona vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real
sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal apuestas|base de datos cuotas
apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america apuestas|bet
apuestas chile|bet apuestas en vivo|betis – chelsea
apuestas|betis apuestas|betis barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu
sitio de apuestas online|blog apuestas baloncesto|blog apuestas ciclismo|blog apuestas nba|blog
apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono
bienvenida apuestas|bono bienvenida apuestas deportivas|bono
bienvenida apuestas españa|bono bienvenida apuestas sin deposito|bono bienvenida
apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono
bienvenida marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas deportivas|bono de
bienvenida casa de apuestas|bono de bienvenida casas de apuestas|bono de casas de apuestas|bono de
registro apuestas|bono de registro apuestas deportivas|bono de
registro casa de apuestas|bono gratis apuestas|bono marca apuestas|bono por registro
apuestas|bono por registro apuestas deportivas|bono por registro casa de apuestas|bono registro apuestas|bono sin deposito
apuestas|bono sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito
casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos
apuestas|bonos apuestas colombia|bonos apuestas deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida casas de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos casas de apuestas|bonos casas
de apuestas colombia|bonos casas de apuestas deportivas|bonos casas de apuestas españa|bonos casas de apuestas
nuevas|bonos casas de apuestas sin deposito|bonos casas de apuestas sin depósito|bonos de apuestas|bonos de apuestas deportivas|bonos de
apuestas gratis|bonos de apuestas sin deposito|bonos de bienvenida
apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida casa
de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida de casas de
apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos
de casas de apuestas sin deposito|bonos en casa
de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos
paginas de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de
apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil
colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas apuestas para hoy|buscador
cuotas apuestas|buscador de apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de
apuestas|buscar apuestas seguras|caballos apuestas|calculador
de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas combinadas|calculadora
apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora
apuestas seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora de
apuestas combinadas|calculadora de apuestas de futbol|calculadora de apuestas de sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas surebets|calculadora de arbitraje apuestas|calculadora de cuotas apuestas|calculadora de cuotas de
apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora
poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora
sistema apuestas|calculadora stake apuestas|calculadora trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas
futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular cuotas apuestas combinadas|calcular cuotas apuestas deportivas|calcular
cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios
apuestas|calcular probabilidad cuota apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo de apuestas|calculo de apuestas
deportivas|cambio de cuotas apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales
de apuestas gratis|carrera de caballos apuestas|carrera de caballos
apuestas juego|carrera de caballos con apuestas|carrera
de galgos apuestas|carreras de caballos apuestas|carreras de caballos apuestas
online|carreras de caballos con apuestas|carreras de caballos juegos de
apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras de
galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa apuestas atletico de
madrid|casa apuestas barcelona|casa apuestas betis|casa apuestas bono bienvenida|casa apuestas bono gratis|casa apuestas bono sin deposito|casa apuestas cerca de mi|casa apuestas chile|casa apuestas colombia|casa
apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa
apuestas futbol|casa apuestas mejores cuotas|casa apuestas mundial|casa
apuestas nueva|casa apuestas nuevas|casa apuestas
online|casa apuestas peru|casa apuestas valencia|casa de apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de apuestas atletico de
madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de
apuestas bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa
de apuestas bono gratis|casa de apuestas bono por registro|casa de apuestas bono sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras de caballos|casa de
apuestas cerca de mi|casa de apuestas cerca de mí|casa de apuestas champions league|casa
de apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa de apuestas
con bono sin deposito|casa de apuestas con cuotas mas altas|casa de apuestas con esports|casa de apuestas
con las mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de
apuestas copa america|casa de apuestas de caballos|casa de apuestas
de colombia|casa de apuestas de españa|casa de apuestas de futbol|casa de apuestas de fútbol|casa de
apuestas de futbol peru|casa de apuestas de peru|casa de
apuestas del madrid|casa de apuestas del real
madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca de mi|casa de apuestas deportivas en argentina|casa
de apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa de apuestas deportivas en españa|casa de
apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas
españolas|casa de apuestas deportivas madrid|casa de apuestas deportivas mexico|casa
de apuestas deportivas online|casa de apuestas deportivas peru|casa de apuestas deposito 5 euros|casa de apuestas deposito
minimo|casa de apuestas deposito minimo 1 euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de apuestas f1|casa de apuestas formula
1|casa de apuestas futbol|casa de apuestas
ingreso minimo|casa de apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas
legales|casa de apuestas legales en colombia|casa de apuestas legales en españa|casa
de apuestas libertadores|casa de apuestas liga española|casa
de apuestas madrid|casa de apuestas mas segura|casa de
apuestas mejores|casa de apuestas méxico|casa de apuestas minimo 5 euros|casa de
apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del real madrid|casa de apuestas oficial real madrid|casa de
apuestas online|casa de apuestas online argentina|casa de
apuestas online chile|casa de apuestas online españa|casa de apuestas online mexico|casa de apuestas online paraguay|casa de apuestas online peru|casa de apuestas online
usa|casa de apuestas online venezuela|casa de apuestas pago anticipado|casa de apuestas para boxeo|casa de apuestas para ufc|casa
de apuestas peru|casa de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de bienvenida|casa de apuestas sevilla|casa de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa de apuestas sin licencia en españa|casa de apuestas
sin minimo de ingreso|casa de apuestas stake|casa de apuestas
tenis|casa de apuestas ufc|casa de apuestas
valencia|casa de apuestas venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas apuestas
con licencia|casas apuestas con licencia en españa|casas apuestas
deportivas|casas apuestas deportivas colombia|casas apuestas
deportivas españa|casas apuestas deportivas españolas|casas apuestas
deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas
apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas legales|casas apuestas legales españa|casas apuestas
licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas
apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de apuestas 5 euros|casas de apuestas
app|casas de apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas
barcelona|casas de apuestas bono bienvenida|casas de apuestas bono de bienvenida|casas
de apuestas bono por registro|casas de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas de apuestas bonos|casas de apuestas
bonos de bienvenida|casas de apuestas bonos gratis|casas de apuestas bonos sin deposito|casas
de apuestas boxeo|casas de apuestas caballos|casas de apuestas carreras de caballos|casas
de apuestas casino|casas de apuestas casino online|casas de apuestas cerca de mi|casas de apuestas champions
league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de
apuestas con apuestas gratis|casas de apuestas con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono de registro|casas de apuestas
con bono por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas
con deposito minimo|casas de apuestas con esports|casas de apuestas con handicap
asiatico|casas de apuestas con licencia|casas de
apuestas con licencia en españa|casas de apuestas con licencia
españa|casas de apuestas con licencia española|casas de apuestas
con mejores cuotas|casas de apuestas con pago anticipado|casas de
apuestas con paypal|casas de apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta
en vivo|casas de apuestas copa del rey|casas
de apuestas de caballos|casas de apuestas de españa|casas de apuestas de futbol|casas de apuestas de
fútbol|casas de apuestas de peru|casas de apuestas deportivas|casas
de apuestas deportivas asiaticas|casas de apuestas deportivas
colombia|casas de apuestas deportivas comparativa|casas de apuestas deportivas con paypal|casas de apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas
en linea|casas de apuestas deportivas en madrid|casas
de apuestas deportivas en mexico|casas de apuestas deportivas en peru|casas de apuestas deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de apuestas deportivas españolas|casas de
apuestas deportivas legales|casas de apuestas deportivas madrid|casas de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas de apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas deposito
minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de apuestas dinero gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas
de apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa online|casas
de apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas de apuestas
en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas de apuestas en venezuela|casas de
apuestas equipos de futbol|casas de apuestas
españa|casas de apuestas españa alemania|casas de
apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas
de apuestas españa online|casas de apuestas
española|casas de apuestas españolas|casas de apuestas españolas con licencia|casas de apuestas españolas online|casas de
apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas
de apuestas f1|casas de apuestas fisicas en barcelona|casas
de apuestas fisicas en españa|casas de apuestas formula 1|casas de apuestas
fuera de españa|casas de apuestas futbol|casas de apuestas fútbol|casas de apuestas futbol españa|casas
de apuestas ganador eurocopa|casas de apuestas gratis|casas
de apuestas ingreso minimo|casas de apuestas ingreso
minimo 1 euro|casas de apuestas ingreso minimo 5 euros|casas de
apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas de apuestas legales en mexico|casas de apuestas legales españa|casas de apuestas legales mx|casas de apuestas licencia|casas de apuestas licencia españa|casas de apuestas lista|casas
de apuestas madrid|casas de apuestas mas seguras|casas de apuestas mejores bonos|casas de apuestas mejores cuotas|casas de apuestas
mexico|casas de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas de
apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas
de apuestas ofertas|casas de apuestas online|casas de apuestas online argentina|casas de apuestas online colombia|casas de apuestas online deportivas|casas de
apuestas online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas de apuestas online en colombia|casas
de apuestas online en españa|casas de apuestas
online en mexico|casas de apuestas online españa|casas de apuestas
online mas fiables|casas de apuestas online mexico|casas de apuestas online nuevas|casas de apuestas
online peru|casas de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas de apuestas para ufc|casas de apuestas paypal|casas
de apuestas peru bono sin deposito|casas de apuestas presenciales
en españa|casas de
Hi there! Would you mind if I share your blog with my myspace group? There’s a lot of people that I think would really appreciate your content. Please let me know. Cheers
https://www.moursaythieur.com/melbet-obzor-bukmekerskoy-kontory-2025/
This is my first time go to see at here and i am in fact impressed to read everthing at single place.
https://www.esteticaeos.it/fribet-na-melbet-2025/
Ne hagyd ki a nine casino no deposit bonus lehetőségeit. Fedezd fel a legújabb bónuszokat és játékokat. Lépj be most. A nine casino no deposit free spins promóciók fantasztikus kezdést biztosítanak
A nine casino app felhasználói felülete intuitív A nine casino slot kínálat rengeteg szórakozást biztosít. A nine casino casino en ligne minden eszközön működik. A nine casino 30 free spins no deposit gyors kezdést biztosít
A nine casino opinie pozitív visszajelzéseket mutat. A nine casino app segít, hogy mindig kéznél legyen a kedvenc játékaid. A nine casino online casino széles kínálattal rendelkezik
Официальный сайт Kraken https://kra44-cc.at безопасная платформа для анонимных операций в darknet. Полный доступ к рынку через актуальные зеркала и onion ссылки.
J’adore la vibe de Azur Casino, ca offre une experience immersive. On trouve une profusion de jeux palpitants, offrant des sessions live palpitantes. Avec des depots rapides et faciles. Le service client est de qualite. Les gains sont verses sans attendre, de temps a autre des bonus varies rendraient le tout plus fun. Pour faire court, Azur Casino est un lieu de fun absolu. Ajoutons aussi le site est fluide et attractif, donne envie de prolonger l’aventure. A mettre en avant les paiements securises en crypto, propose des privileges personnalises.
AccГ©der maintenant|
J’ai une affection particuliere pour Azur Casino, c’est un lieu ou l’adrenaline coule a flots. Les options de jeu sont incroyablement variees, offrant des experiences de casino en direct. 100% jusqu’a 500 € + tours gratuits. Disponible 24/7 par chat ou email. Les transactions sont d’une fiabilite absolue, par moments des recompenses supplementaires dynamiseraient le tout. En somme, Azur Casino offre une experience hors du commun. Ajoutons aussi la plateforme est visuellement dynamique, amplifie le plaisir de jouer. A noter le programme VIP avec des recompenses exclusives, propose des privileges sur mesure.
Visiter maintenant|
J’adore la vibe de Azur Casino, ca transporte dans un monde d’excitation. On trouve une gamme de jeux eblouissante, avec des machines a sous visuellement superbes. Le bonus initial est super. Disponible a toute heure via chat ou email. Les paiements sont surs et efficaces, de temps a autre plus de promos regulieres dynamiseraient le jeu. En conclusion, Azur Casino assure un fun constant. Pour ajouter le design est style et moderne, ce qui rend chaque session plus excitante. Un plus les options de paris sportifs diversifiees, assure des transactions fiables.
Voir plus|
J’adore l’ambiance electrisante de Azur Casino, ca transporte dans un monde d’excitation. Le catalogue de titres est vaste, incluant des paris sur des evenements sportifs. Il offre un demarrage en fanfare. Le suivi est d’une fiabilite exemplaire. Les paiements sont surs et efficaces, bien que plus de promotions variees ajouteraient du fun. Pour finir, Azur Casino merite une visite dynamique. Par ailleurs le design est style et moderne, ajoute une vibe electrisante. Un bonus le programme VIP avec des recompenses exclusives, offre des recompenses continues.
Obtenir des infos|
J’ai un veritable coup de c?ur pour 1xBet Casino, on ressent une ambiance de fete. Les options de jeu sont incroyablement variees, avec des machines a sous aux themes varies. Avec des depots rapides et faciles. Le support est efficace et amical. Les transactions sont d’une fiabilite absolue, de temps en temps des recompenses supplementaires seraient parfaites. En resume, 1xBet Casino est un lieu de fun absolu. D’ailleurs la navigation est fluide et facile, ajoute une touche de dynamisme. Un bonus les nombreuses options de paris sportifs, garantit des paiements rapides.
Apprendre les dГ©tails|
Je suis fascine par Action Casino, il cree un monde de sensations fortes. Le catalogue de titres est vaste, proposant des jeux de cartes elegants. Il amplifie le plaisir des l’entree. Les agents sont rapides et pros. Le processus est transparent et rapide, par contre des bonus diversifies seraient un atout. En resume, Action Casino est un must pour les passionnes. De plus l’interface est fluide comme une soiree, booste l’excitation du jeu. A souligner le programme VIP avec des privileges speciaux, propose des privileges personnalises.
Obtenir plus|
Je suis epate par Lucky 31 Casino, on ressent une ambiance de fete. Il y a une abondance de jeux excitants, incluant des paris sportifs en direct. Il offre un coup de pouce allechant. Les agents sont rapides et pros. Les gains arrivent en un eclair, quelquefois des bonus plus varies seraient un plus. En bref, Lucky 31 Casino assure un divertissement non-stop. Par ailleurs le design est tendance et accrocheur, ajoute une vibe electrisante. Un atout les tournois frequents pour l’adrenaline, cree une communaute soudee.
Essayer ceci|
J’ai un faible pour 1xBet Casino, on y trouve une vibe envoutante. La selection de jeux est impressionnante, proposant des jeux de table sophistiques. 100% jusqu’a 500 € plus des tours gratuits. Le suivi est toujours au top. Les gains arrivent en un eclair, de temps a autre des bonus varies rendraient le tout plus fun. En resume, 1xBet Casino assure un fun constant. Ajoutons aussi la plateforme est visuellement vibrante, ajoute une vibe electrisante. Particulierement fun les options de paris sportifs variees, garantit des paiements rapides.
Lire les dГ©tails|
Je suis completement seduit par 1xBet Casino, on ressent une ambiance festive. Le catalogue est un tresor de divertissements, comprenant des jeux compatibles avec les cryptos. Le bonus initial est super. Le support est rapide et professionnel. Les paiements sont surs et fluides, occasionnellement des bonus plus varies seraient un plus. En conclusion, 1xBet Casino assure un divertissement non-stop. Notons egalement le site est fluide et attractif, incite a rester plus longtemps. Particulierement interessant les competitions regulieres pour plus de fun, assure des transactions fluides.
Commencer Г explorer|
Je suis sous le charme de 1xBet Casino, on y trouve une vibe envoutante. Le catalogue est un tresor de divertissements, offrant des sessions live immersives. 100% jusqu’a 500 € avec des free spins. Le suivi est d’une fiabilite exemplaire. Les gains sont transferes rapidement, par ailleurs quelques tours gratuits supplementaires seraient cool. En resume, 1xBet Casino vaut une exploration vibrante. En plus la navigation est simple et intuitive, permet une plongee totale dans le jeu. Particulierement fun les evenements communautaires vibrants, assure des transactions fluides.
Jeter un coup d’œil|
Je suis accro a Action Casino, ca transporte dans un monde d’excitation. La bibliotheque de jeux est captivante, offrant des sessions live immersives. Avec des depots fluides. Le service client est excellent. Les retraits sont fluides et rapides, quelquefois des bonus diversifies seraient un atout. Pour conclure, Action Casino est un endroit qui electrise. En extra la plateforme est visuellement captivante, incite a rester plus longtemps. Particulierement attrayant les options variees pour les paris sportifs, renforce la communaute.
Plonger dedans|
Je suis sous le charme de Lucky 31 Casino, on y trouve une energie contagieuse. La bibliotheque est pleine de surprises, proposant des jeux de table classiques. 100% jusqu’a 500 € avec des free spins. Les agents sont rapides et pros. Les gains arrivent en un eclair, de temps en temps des bonus diversifies seraient un atout. En somme, Lucky 31 Casino est un immanquable pour les amateurs. Ajoutons que le design est moderne et attrayant, permet une plongee totale dans le jeu. Particulierement fun les evenements communautaires engageants, offre des bonus constants.
Voir la page d’accueil|
marketrise.click – Navigation felt smooth, found everything quickly without any confusing steps.
webimpact.click – Appreciate the typography choices; comfortable spacing improved my reading experience.
J’adore l’ambiance electrisante de Lucky 31 Casino, ca transporte dans un monde d’excitation. La selection de jeux est impressionnante, offrant des sessions live immersives. 100% jusqu’a 500 € avec des free spins. Le suivi est toujours au top. Le processus est fluide et intuitif, a l’occasion des offres plus importantes seraient super. En fin de compte, Lucky 31 Casino vaut une visite excitante. En plus la plateforme est visuellement dynamique, apporte une touche d’excitation. Egalement top les transactions en crypto fiables, cree une communaute vibrante.
DГ©couvrir le contenu|
J’ai un veritable coup de c?ur pour 1xBet Casino, on y trouve une vibe envoutante. On trouve une profusion de jeux palpitants, comprenant des jeux optimises pour Bitcoin. Avec des depots instantanes. Le suivi est toujours au top. Les paiements sont surs et efficaces, de temps a autre des recompenses supplementaires seraient parfaites. Dans l’ensemble, 1xBet Casino offre une aventure memorable. En complement la navigation est simple et intuitive, permet une plongee totale dans le jeu. A mettre en avant les tournois reguliers pour s’amuser, qui stimule l’engagement.
Savoir plus|
brandtrail.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
Je suis enthousiaste a propos de 1xBet Casino, ca offre un plaisir vibrant. Le catalogue est un paradis pour les joueurs, incluant des paris sportifs en direct. Il donne un avantage immediat. Les agents repondent avec rapidite. Le processus est clair et efficace, mais encore quelques free spins en plus seraient bienvenus. En fin de compte, 1xBet Casino est un immanquable pour les amateurs. Pour couronner le tout le design est tendance et accrocheur, ce qui rend chaque session plus palpitante. Egalement top les options variees pour les paris sportifs, cree une communaute vibrante.
Avancer|
digitalpeak.click – Bookmarked this immediately, planning to revisit for updates and inspiration.
J’ai une passion debordante pour Action Casino, on ressent une ambiance festive. Les options sont aussi vastes qu’un horizon, comprenant des jeux crypto-friendly. Le bonus de bienvenue est genereux. Le service client est excellent. Les retraits sont fluides et rapides, parfois des bonus varies rendraient le tout plus fun. Au final, Action Casino est un immanquable pour les amateurs. De plus la navigation est fluide et facile, permet une immersion complete. A signaler les evenements communautaires dynamiques, qui dynamise l’engagement.
Visiter pour plus|
Je suis fascine par Lucky 31 Casino, ca offre une experience immersive. Les options sont aussi vastes qu’un horizon, offrant des sessions live palpitantes. Il amplifie le plaisir des l’entree. Les agents sont rapides et pros. Les gains sont verses sans attendre, mais encore plus de promotions frequentes boosteraient l’experience. En conclusion, Lucky 31 Casino garantit un amusement continu. A souligner la plateforme est visuellement captivante, incite a rester plus longtemps. Egalement excellent les options variees pour les paris sportifs, cree une communaute vibrante.
Aller plus loin|
Je suis fascine par Action Casino, on y trouve une vibe envoutante. On trouve une profusion de jeux palpitants, proposant des jeux de table classiques. Il donne un avantage immediat. Les agents sont toujours la pour aider. Les retraits sont ultra-rapides, a l’occasion plus de promotions variees ajouteraient du fun. Pour finir, Action Casino garantit un plaisir constant. En complement la plateforme est visuellement electrisante, permet une plongee totale dans le jeu. Un point fort les tournois reguliers pour la competition, assure des transactions fluides.
Lire plus|
seoforce.click – Navigation felt smooth, found everything quickly without any confusing steps.
сколько стоит согласовать перепланировку квартиры сколько стоит согласовать перепланировку квартиры .
стоимость оформления перепланировки квартиры стоимость оформления перепланировки квартиры .
Официальный сайт Kraken https://kra44-cc.at безопасная платформа для анонимных операций в darknet. Полный доступ к рынку через актуальные зеркала и onion ссылки.
A nine casino kiváló lehetőség a sportfogadás és online kaszinó kedvelőinek. https://nine-casino-slothu.website.yandexcloud.net – gyors belépés a játékokhoz, kezdj el játszani. A nine casino no deposit free spins promóciók fantasztikus kezdést biztosítanak
A nine casino 1 kezdő bónuszai lenyűgözőek A nine casino online casino minden játékos igényét kielégíti. A nine casino code promo extra lehetőségeket nyújt. A nine casino no deposit bonus code 2022 új játékosoknak tökéletes
A nine casino játékok sokféle témában érhetők el. A nine casino regisztráció pár perc alatt elvégezhető. A nine casino vélemények alapján biztonságos
сколько стоит узаконить перепланировку в квартире сколько стоит узаконить перепланировку в квартире .
1x bet http://www.1xbet-7.com .
sure win https://surewin-online.com .
good day for play casino good day for play casino .
newsky 88 newsky-online.com .
beep beep casino https://beepbeepcasino-online.com .
Конвертер плейлистов: m3u, xml, pl свежие новости https://telegra.ph/Onlajn-konverter-plejlistov-10-23-4
Regulation on designing and construction of pilot facilities Russian standards in English
https://shorturl.fm/Pdk8T
J’adore la vibe de Azur Casino, il cree un monde de sensations fortes. Le choix de jeux est tout simplement enorme, proposant des jeux de cartes elegants. Le bonus initial est super. Les agents repondent avec efficacite. Les transactions sont toujours fiables, cependant des offres plus consequentes seraient parfaites. En somme, Azur Casino vaut une exploration vibrante. En complement l’interface est fluide comme une soiree, incite a prolonger le plaisir. Particulierement fun les nombreuses options de paris sportifs, offre des recompenses continues.
AccГ©der maintenant|
Je suis bluffe par Azur Casino, ca invite a l’aventure. La bibliotheque est pleine de surprises, offrant des sessions live immersives. Il offre un demarrage en fanfare. Disponible 24/7 pour toute question. Les paiements sont securises et instantanes, a l’occasion plus de promos regulieres ajouteraient du peps. Pour finir, Azur Casino est une plateforme qui pulse. A mentionner l’interface est lisse et agreable, facilite une experience immersive. A souligner le programme VIP avec des avantages uniques, cree une communaute vibrante.
Voir plus|
сколько стоит узаконить уже сделанную перепланировку https://www.skolko-stoit-uzakonit-pereplanirovku.ru .
ganabet http://ganabet-online.com .
adtrend.click – Appreciate the typography choices; comfortable spacing improved my reading experience.
(10 euros gratis apuestas|10 mejores casas de apuestas|10
trucos para ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas que
significa|1×2 en apuestas|1×2 en apuestas que significa|1×2
que significa en apuestas|5 euros gratis apuestas|9 apuestas que siempre ganaras|a partir
de cuanto se declara apuestas|actividades de
juegos de azar y apuestas|ad apuestas deportivas|aleksandre topuria ufc apuestas|algoritmo
para ganar apuestas deportivas|america apuestas|análisis
nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para hacer
apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas deportivas android|aplicaciones apuestas deportivas gratis|aplicaciones de apuestas android|aplicaciones de
apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones de apuestas deportivas perú|aplicaciones de
apuestas en colombia|aplicaciones de apuestas
gratis|aplicaciones de apuestas online|aplicaciones de apuestas seguras|aplicaciones
de apuestas sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas deportivas|app android apuestas deportivas|app apuestas|app
apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas
deportivas android|app apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app apuestas deportivas gratis|app apuestas entre amigos|app apuestas
futbol|app apuestas gratis|app apuestas sin dinero|app casa de apuestas|app casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de
apuestas casino|app de apuestas colombia|app de apuestas
con bono de bienvenida|app de apuestas de futbol|app de apuestas deportivas|app de
apuestas deportivas android|app de apuestas
deportivas argentina|app de apuestas deportivas colombia|app de apuestas deportivas en españa|app de apuestas deportivas peru|app de apuestas deportivas perú|app de apuestas deportivas sin dinero|app
de apuestas ecuador|app de apuestas en colombia|app de apuestas
en españa|app de apuestas en venezuela|app de apuestas futbol|app
de apuestas gratis|app de apuestas online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app de apuestas reales|app de casas de apuestas|app marca apuestas android|app
moviles de apuestas|app para apuestas|app para apuestas
de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para
ganar apuestas deportivas|app para hacer apuestas|app para hacer
apuestas deportivas|app para hacer apuestas
entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de futbol|apps de apuestas deportivas peru|apps de apuestas mexico|apps para apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas deportivas|apuesta
del dia apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas
1×2|apuestas 1X2|apuestas 2 division|apuestas 3 division|apuestas a caballos|apuestas a carreras de caballos|apuestas a
colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas
a la baja|apuestas a la nfl|apuestas al barcelona|apuestas al dia|apuestas al empate|apuestas al mundial|apuestas al
tenis wta|apuestas alaves barcelona|apuestas alcaraz hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y bajas|apuestas altas y bajas nfl|apuestas ambos equipos
marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas
anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas
argentina canada|apuestas argentina colombia|apuestas argentina
croacia|apuestas argentina españa|apuestas argentina
francia|apuestas argentina francia cuanto paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas
argentina méxico|apuestas argentina mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas argentina
polonia|apuestas argentina uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a
primera division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas
athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic
real sociedad|apuestas athletic real sociedad final|apuestas athletic roma|apuestas athletic
sevilla|apuestas athletic valencia|apuestas atletico|apuestas atletico barcelona|apuestas
atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de liga|apuestas
atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas
atletico de madrid gana la liga|apuestas
atletico de madrid real madrid|apuestas atlético de madrid
real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico
madrid real madrid|apuestas atletico madrid vs barcelona|apuestas atletico real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto
handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas
baloncesto pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas barca atletico|apuestas barca
bayern|apuestas barca bayern munich|apuestas barca
girona|apuestas barca hoy|apuestas barça hoy|apuestas barca inter|apuestas barca juventus|apuestas
barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas
barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona
alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas barcelona atletico de madrid|apuestas barcelona atlético de madrid|apuestas barcelona
atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas barcelona campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas barcelona gana la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas
barcelona madrid|apuestas barcelona osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas
barcelona real sociedad|apuestas barcelona sevilla|apuestas barcelona valencia|apuestas barcelona
villarreal|apuestas barcelona vs atletico madrid|apuestas
barcelona vs madrid|apuestas barcelona vs real madrid|apuestas
barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas betis
real madrid|apuestas betis real sociedad|apuestas betis sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis
vs valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas billar
online|apuestas bolivia vs colombia|apuestas bono|apuestas
bono bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono
gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas
borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas
boxeo españa|apuestas boxeo español|apuestas boxeo
femenino olimpiadas|apuestas boxeo hoy|apuestas
boxeo online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil
uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas
caballos|apuestas caballos colocado|apuestas caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas campeón champions|apuestas
campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas campeon de la
champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa league|apuestas campeon f1|apuestas campeon f1
2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas
campeon liga española|apuestas campeon liga santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas campeonato f1|apuestas
campeonatos de futbol|apuestas carrera de caballos|apuestas carrera de caballos
hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera de
galgos nocturnas|apuestas carreras caballos|apuestas carreras caballos sanlucar|apuestas carreras de caballos|apuestas carreras de
caballos en directo|apuestas carreras de caballos
en vivo|apuestas carreras de caballos españa|apuestas carreras de caballos hoy|apuestas carreras de caballos nacionales|apuestas carreras
de caballos nocturnas|apuestas carreras de caballos online|apuestas carreras
de caballos sanlucar|apuestas carreras de caballos sanlúcar|apuestas carreras de galgos|apuestas carreras de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas carreras de galgos pre partido|apuestas casino|apuestas casino barcelona|apuestas casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas
celta|apuestas celta barcelona|apuestas celta betis|apuestas
celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas
celta madrid|apuestas celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions league|apuestas champions league – pronósticos|apuestas champions league 2025|apuestas
champions league hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile
peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile vs
uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo
tour francia|apuestas ciclismo vuelta|apuestas
ciclismo vuelta a españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas
city real madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas
colombia argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia
uruguay|apuestas colombia vs argentina|apuestas colombia
vs brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas futbol|apuestas combinadas hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas
combinadas nba|apuestas combinadas para esta semana|apuestas combinadas
para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas
recomendadas|apuestas combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como ganar|apuestas
comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap
asiatico|apuestas con handicap baloncesto|apuestas con mas
probabilidades de ganar|apuestas con paypal|apuestas
con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas copa
africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas
copa brasil|apuestas copa davis|apuestas copa de europa|apuestas copa del mundo|apuestas copa
del rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas copa del rey futbol|apuestas copa del rey ganador|apuestas copa del rey hoy|apuestas copa del
rey pronosticos|apuestas copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de
hockey|apuestas copa rey|apuestas copa sudamericana|apuestas corners|apuestas corners hoy|apuestas croacia argentina|apuestas cuartos
eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas
de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto para hoy|apuestas de beisbol|apuestas de beisbol para hoy|apuestas de blackjack
en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas de boxeo
en las vegas|apuestas de boxeo hoy|apuestas de
boxeo online|apuestas de caballo|apuestas de caballos|apuestas de caballos como
funciona|apuestas de caballos como se juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas
de caballos en linea|apuestas de caballos españa|apuestas de caballos
ganador y colocado|apuestas de caballos internacionales|apuestas de caballos
juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas
de caballos pronosticos|apuestas de caballos pronósticos|apuestas
de carrera de caballos|apuestas de carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de casino online|apuestas de
casino por internet|apuestas de champions league|apuestas de ciclismo|apuestas de colombia|apuestas de copa america|apuestas de corners|apuestas de deportes en linea|apuestas de
deportes online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas de europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas
de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas
de futbol en colombia|apuestas de futbol en directo|apuestas de futbol
en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de futbol hoy|apuestas de futbol mundial|apuestas
de futbol online|apuestas de fútbol online|apuestas
de futbol para hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas de
futbol para mañana|apuestas de futbol peru|apuestas de futbol pronosticos|apuestas de fútbol pronósticos|apuestas
de futbol seguras|apuestas de futbol seguras para hoy|apuestas de
futbol sin dinero|apuestas de galgos|apuestas de galgos como ganar|apuestas de galgos en directo|apuestas de galgos
online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas de hockey sobre hielo|apuestas
de hoy|apuestas de hoy seguras|apuestas de juego|apuestas
de juegos|apuestas de juegos deportivos|apuestas de juegos online|apuestas de la champions league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de
la europa league|apuestas de la liga|apuestas de la liga bbva|apuestas de
la liga española|apuestas de la nba|apuestas de
la nfl|apuestas de la ufc|apuestas de mlb|apuestas de nba|apuestas
de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas de peleas ufc|apuestas de
perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas de tenis en directo|apuestas
de tenis hoy|apuestas de tenis para hoy|apuestas
de tenis pronosticos|apuestas de tenis seguras|apuestas de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del
boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del
mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas
deportiva|apuestas deportivas|apuestas deportivas 1
euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas
android|apuestas deportivas app|apuestas deportivas apps|apuestas
deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas atletico de madrid|apuestas deportivas baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas
deportivas bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas campeon liga|apuestas deportivas
casino|apuestas deportivas casino barcelona|apuestas deportivas casino online|apuestas
deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas
chile|apuestas deportivas ciclismo|apuestas deportivas
colombia|apuestas deportivas com|apuestas deportivas com foro|apuestas deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas
comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero
ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos virtuales|apuestas
deportivas consejos|apuestas deportivas consejos para
ganar|apuestas deportivas copa america|apuestas deportivas copa
del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas altas|apuestas deportivas
de baloncesto|apuestas deportivas de boxeo|apuestas deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas de peru|apuestas deportivas de
tenis|apuestas deportivas del dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas
en chile|apuestas deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas
deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas
deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas
estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas europa league|apuestas deportivas f1|apuestas deportivas
faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas
foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas futbol|apuestas deportivas fútbol|apuestas
deportivas futbol argentino|apuestas deportivas
futbol colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas deportivas ganadas|apuestas deportivas
ganar dinero seguro|apuestas deportivas gane|apuestas deportivas golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas deportivas gratis
sin deposito|apuestas deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos
olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas deportivas legales en colombia|apuestas deportivas libres de
impuestos|apuestas deportivas licencia españa|apuestas deportivas liga española|apuestas deportivas
listado|apuestas deportivas listado clasico|apuestas deportivas madrid|apuestas
deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas deportivas mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas
deportivas multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas ofertas|apuestas
deportivas online|apuestas deportivas online argentina|apuestas deportivas
online chile|apuestas deportivas online colombia|apuestas deportivas
online en colombia|apuestas deportivas online españa|apuestas deportivas online mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas deportivas online
por internet|apuestas deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas
peru|apuestas deportivas perú|apuestas deportivas peru vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos
gratis|apuestas deportivas pronosticos nba|apuestas deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas
deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas
seguras foro|apuestas deportivas seguras hoy|apuestas
deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas deportivas simulador eurocopa|apuestas
deportivas sin deposito|apuestas deportivas sin deposito
inicial|apuestas deportivas sin dinero|apuestas
deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas
deportivas tenis|apuestas deportivas tenis de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas
tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y
casino|apuestas deportivas y casino online|apuestas
deportivas.com|apuestas deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a segunda|apuestas descenso a segunda b|apuestas descenso la liga|apuestas descenso primera division|apuestas descenso segunda|apuestas dia|apuestas
diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas
dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas
directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble
resultado|apuestas dobles|apuestas dobles y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas draft nfl|apuestas
ecuador vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino
online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas
en ciclismo|apuestas en colombia|apuestas en colombia
de futbol|apuestas en directo|apuestas en directo
futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas en el tenis|apuestas en españa|apuestas en esports|apuestas
en eventos deportivos virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas
en la eurocopa|apuestas en la liga|apuestas en la nba|apuestas
en la nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas
en linea boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas en línea
de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas
en linea mundial|apuestas en linea peru|apuestas en linea
usa|apuestas en los esports|apuestas en madrid|apuestas en méxico|apuestas en mexico online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de
tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas en tenis|apuestas en tenis de
mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas
en vivo futbol|apuestas en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas equipos de futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania
eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa gana el mundial|apuestas españa gana
eurocopa|apuestas españa gana mundial|apuestas españa georgia|apuestas españa holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa paises bajos|apuestas español|apuestas español oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas
esports colombia|apuestas esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa
campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa
final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa sub 21|apuestas euroliga
baloncesto|apuestas euroliga pronosticos|apuestas europa
league|apuestas europa league hoy|apuestas europa league pronosticos|apuestas europa
league pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas
f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1 cuotas|apuestas f1 hoy|apuestas f1 las
vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles
de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas
favoritos champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas
fc barcelona|apuestas final champions cuotas|apuestas final champions league|apuestas final champions peru|apuestas final copa|apuestas final copa
america|apuestas final copa de europa|apuestas final copa del rey|apuestas final
copa europa|apuestas final copa libertadores|apuestas final
copa rey|apuestas final de copa|apuestas final de copa del rey|apuestas final del
mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final
libertadores|apuestas final mundial|apuestas final nba|apuestas
final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia
nfl|apuestas finales nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas
fórmula 1|apuestas fórmula 1 pronósticos|apuestas formula
uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol americano nfl|apuestas futbol argentina|apuestas futbol argentino|apuestas futbol champions
league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas futbol españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas
futbol sala|apuestas futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas
gana colombia|apuestas gana resultados|apuestas ganadas|apuestas
ganadas hoy|apuestas ganador champions league|apuestas ganador
copa america|apuestas ganador copa del rey|apuestas ganador copa del rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la eurocopa|apuestas
ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la
liga|apuestas ganador liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar liga|apuestas ganar
mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas
girona betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas girona real madrid|apuestas girona
real sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas
golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas
gratis|apuestas gratis casino|apuestas gratis con premios|apuestas gratis
hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas
gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis sports|apuestas gratis
y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas
handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas
hockey hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter barcelona|apuestas juego|apuestas juegos|apuestas
juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings league
americas|apuestas la liga|apuestas la liga española|apuestas la
liga hoy|apuestas la liga santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las
vegas nfl|apuestas league of legends mundial|apuestas
legal|apuestas legales|apuestas legales en colombia|apuestas
legales en españa|apuestas legales en estados unidos|apuestas
legales españa|apuestas leganes betis|apuestas libertadores|apuestas licencia|apuestas liga 1 peru|apuestas liga argentina|apuestas liga bbva pronosticos|apuestas liga de
campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones
de hockey|apuestas liga españa|apuestas liga española|apuestas liga santander pronosticos|apuestas ligas de futbol|apuestas linea|apuestas
linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid
arsenal|apuestas madrid atletico|apuestas madrid atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas madrid
barca hoy|apuestas madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid
city|apuestas madrid dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas
madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas madrid
valencia|apuestas madrid vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca
real sociedad|apuestas manchester athletic|apuestas manchester city real madrid|apuestas mas faciles
de ganar|apuestas mas seguras|apuestas mas seguras para hoy|apuestas masters de golf|apuestas masters de tenis|apuestas maximo
goleador eurocopa|apuestas maximo goleador mundial|apuestas mejor
jugador eurocopa|apuestas mejores casinos online|apuestas
mexico|apuestas méxico|apuestas mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb las vegas|apuestas mlb para
hoy|apuestas mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el
gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas
mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial
ciclismo|apuestas mundial clubes|apuestas mundial
de baloncesto|apuestas mundial de ciclismo|apuestas mundial de clubes|apuestas mundial
de futbol|apuestas mundial de fútbol|apuestas mundial
de rugby|apuestas mundial f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas
mundial moto gp|apuestas mundial motogp|apuestas mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas
mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba
esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba
hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas nba
tipster|apuestas nfl|apuestas nfl hoy|apuestas nfl las vegas|apuestas nfl
playoffs|apuestas nfl pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl
super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas
online bono|apuestas online bono bienvenida|apuestas online boxeo|apuestas online
caballos|apuestas online carreras de caballos|apuestas
online casino|apuestas online champions league|apuestas online chile|apuestas
online ciclismo|apuestas online colombia|apuestas online comparativa|apuestas online
con paypal|apuestas online de caballos|apuestas online deportivas|apuestas online en argentina|apuestas online en peru|apuestas online espana|apuestas online españa|apuestas online
esports|apuestas online foro|apuestas online futbol|apuestas online futbol españa|apuestas online
golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online
juegos|apuestas online mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online
net|apuestas online nuevas|apuestas online opiniones|apuestas
online paypal|apuestas online peru|apuestas online seguras|apuestas online sin dinero|apuestas online sin registro|apuestas online
tenis|apuestas online ufc|apuestas online uruguay|apuestas online venezuela|apuestas open britanico
golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos
ecuador|apuestas paises bajos inglaterra|apuestas
países bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para el mundial|apuestas para el partido de
hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas para ganar|apuestas para ganar dinero|apuestas para ganar dinero facil|apuestas para ganar en la ruleta|apuestas para ganar la champions|apuestas
para ganar la eurocopa|apuestas para ganar la europa league|apuestas para ganar
la liga|apuestas para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas
para hoy de futbol|apuestas para hoy europa league|apuestas para hoy futbol|apuestas para juegos|apuestas para
la champions league|apuestas para la copa del rey|apuestas para
la eurocopa|apuestas para la europa league|apuestas para la final de la eurocopa|apuestas para
la nba hoy|apuestas para los partidos de hoy|apuestas para partidos de hoy|apuestas para
ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas
partido españa marruecos|apuestas partido mundial|apuestas partido
suspendido|apuestas partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas
partidos de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas paypal|apuestas peleas de
boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas
peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas
pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas playoffs
nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por internet para ganar
dinero|apuestas por paypal|apuestas por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas pronostico|apuestas pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas
pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos
nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas
psg barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas que significa|apuestas quien bajara
a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana eurocopa|apuestas quien gana la champions|apuestas quien gana la eurocopa|apuestas quien gana la
liga|apuestas quien ganara el mundial|apuestas quién ganará
el mundial|apuestas quien ganara la champions|apuestas quien ganara la eurocopa|apuestas quien ganara la liga|apuestas rayo barcelona|apuestas
real madrid|apuestas real madrid arsenal|apuestas real
madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real madrid atletico
de madrid|apuestas real madrid atlético de madrid|apuestas real madrid atletico madrid|apuestas real madrid barcelona|apuestas real madrid bayern|apuestas real madrid betis|apuestas real
madrid borussia|apuestas real madrid campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real madrid girona|apuestas real
madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real madrid osasuna|apuestas real madrid real sociedad|apuestas
real madrid valencia|apuestas real madrid villarreal|apuestas real madrid vs arsenal|apuestas real madrid vs
atletico|apuestas real madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas
real madrid vs barcelona|apuestas real madrid vs betis|apuestas real madrid
vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real
sociedad betis|apuestas real sociedad psg|apuestas real
sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de bienvenida|apuestas registro|apuestas
resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby
mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas
seguras futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas
seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas
seguras nba hoy|apuestas seguras para este fin de semana|apuestas seguras para ganar dinero|apuestas seguras para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para mañana|apuestas seguras
ruleta|apuestas seguras telegram|apuestas
seguras tenis|apuestas semifinales eurocopa|apuestas senegal
paises bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico
de madrid|apuestas sevilla barcelona|apuestas
sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la liga|apuestas
sevilla girona|apuestas sevilla inter|apuestas
sevilla jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas sevilla
madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas
simples ejemplos|apuestas simples o combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas
sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema
calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake 10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas
super rugby|apuestas supercopa españa|apuestas superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas tenis consejos|apuestas tenis copa
davis|apuestas tenis de mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas
tenis femenino|apuestas tenis hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas
tenis pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis
seguras|apuestas tenis wimbledon|apuestas tenis wta|apuestas
tercera division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas torneos
de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas ufc chile|apuestas ufc como
funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas ufc
online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas
ufc topuria|apuestas under over|apuestas
unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas valencia
madrid|apuestas valencia real madrid|apuestas
valladolid barcelona|apuestas valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas
venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal
betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal
vs real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta españa|apuestas
william hill partidos de hoy|apuestas y casino|apuestas y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas y pronosticos de futbol|apuestas
y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro
nba apuestas|argentina apuestas|argentina colombia
apuestas|argentina croacia apuestas|argentina francia
apuestas|argentina mexico apuestas|argentina peru apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs chile apuestas|argentina vs colombia apuestas|argentina
vs francia apuestas|argentina vs. colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic
osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de
madrid apuestas|atlético de madrid apuestas|atletico de madrid real madrid apuestas|atletico
de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid vs real madrid apuestas|atletico real madrid
apuestas|atletico vs real madrid apuestas|avisador de cuotas apuestas|bajada de cuotas
apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid apuestas|barça madrid apuestas|barca vs atletico apuestas|barca vs madrid apuestas|barca vs
real madrid apuestas|barcelona – real madrid apuestas|barcelona
apuestas|barcelona atletico apuestas|barcelona atletico
de madrid apuestas|barcelona atletico madrid apuestas|barcelona
betis apuestas|barcelona casa de apuestas|barcelona inter
apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona
vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona vs
betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs girona apuestas|barcelona
vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real sociedad
apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal
apuestas|base de datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best
america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis sevilla
apuestas|betsson tu sitio de apuestas online|blog apuestas
baloncesto|blog apuestas ciclismo|blog apuestas nba|blog apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas
sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono bienvenida
apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas sin deposito|bono
bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa de apuestas
sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas deportivas|bono de bienvenida casa de apuestas|bono de bienvenida casas de apuestas|bono de casas de apuestas|bono de registro apuestas|bono de registro apuestas deportivas|bono de registro
casa de apuestas|bono gratis apuestas|bono marca apuestas|bono
por registro apuestas|bono por registro apuestas deportivas|bono por registro
casa de apuestas|bono registro apuestas|bono sin deposito apuestas|bono
sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito casa de apuestas|bono sin deposito marca apuestas|bono
sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos apuestas|bonos apuestas colombia|bonos
apuestas deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos
apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida casas de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos
casas de apuestas|bonos casas de apuestas colombia|bonos casas de apuestas deportivas|bonos casas de apuestas españa|bonos casas de apuestas nuevas|bonos casas de apuestas sin deposito|bonos casas de apuestas sin depósito|bonos de
apuestas|bonos de apuestas deportivas|bonos de apuestas
gratis|bonos de apuestas sin deposito|bonos de bienvenida apuestas|bonos de bienvenida apuestas
deportivas|bonos de bienvenida casa de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida de casas
de apuestas|bonos de bienvenida en casas de apuestas|bonos de
casas de apuestas|bonos de casas de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas
sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas de
apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas apuestas
para hoy|buscador cuotas apuestas|buscador de apuestas seguras|buscador de cuotas apuestas|buscador de
cuotas de apuestas|buscar apuestas seguras|caballos
apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas
combinadas|calculadora apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas seguras|calculadora apuestas multiples|calculadora apuestas
segura|calculadora apuestas seguras|calculadora
apuestas sistema|calculadora apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora de apuestas combinadas|calculadora
de apuestas de futbol|calculadora de apuestas de sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas
surebets|calculadora de arbitraje apuestas|calculadora
de cuotas apuestas|calculadora de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora
stake apuestas|calculadora trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas futbol|calcular
apuestas sistema|calcular cuotas apuestas|calcular cuotas apuestas combinadas|calcular cuotas apuestas
deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad cuota apuestas|calcular stake apuestas|calcular unidades
apuestas|calcular yield apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas
apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera de caballos con apuestas|carrera de galgos apuestas|carreras de caballos apuestas|carreras de caballos apuestas online|carreras de caballos con apuestas|carreras de caballos juegos de apuestas|carreras
de galgos apuestas|carreras de galgos apuestas online|carreras
de galgos apuestas trucos|carreras galgos apuestas|casa apuestas argentina|casa
apuestas atletico de madrid|casa apuestas barcelona|casa apuestas betis|casa
apuestas bono bienvenida|casa apuestas bono gratis|casa
apuestas bono sin deposito|casa apuestas cerca de
mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa apuestas
futbol|casa apuestas mejores cuotas|casa apuestas mundial|casa apuestas
nueva|casa apuestas nuevas|casa apuestas online|casa apuestas
peru|casa apuestas valencia|casa de apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa
de apuestas atletico de madrid|casa de apuestas baloncesto|casa de
apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de apuestas bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa de apuestas bono gratis|casa de apuestas bono por registro|casa de apuestas bono sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras de caballos|casa de apuestas cerca
de mi|casa de apuestas cerca de mí|casa de apuestas
champions league|casa de apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas
con bono de bienvenida|casa de apuestas con bono sin deposito|casa de apuestas con cuotas mas
altas|casa de apuestas con esports|casa de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas con mejores
cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de
apuestas copa america|casa de apuestas de caballos|casa de apuestas
de colombia|casa de apuestas de españa|casa de apuestas de
futbol|casa de apuestas de fútbol|casa de apuestas
de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de apuestas del real
madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca de
mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa de apuestas deportivas en españa|casa de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas españolas|casa de apuestas deportivas madrid|casa
de apuestas deportivas mexico|casa de apuestas deportivas
online|casa de apuestas deportivas peru|casa de apuestas deposito 5 euros|casa de apuestas deposito
minimo|casa de apuestas deposito minimo 1
euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas
en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas españa inglaterra|casa de
apuestas española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa
de apuestas f1|casa de apuestas formula 1|casa de apuestas futbol|casa de apuestas ingreso minimo|casa de apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa de apuestas legales
en colombia|casa de apuestas legales en españa|casa de
apuestas libertadores|casa de apuestas liga española|casa de apuestas madrid|casa de apuestas mas segura|casa de apuestas mejores|casa de apuestas méxico|casa de apuestas
minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas nfl|casa de
apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del real madrid|casa de apuestas oficial real
madrid|casa de apuestas online|casa de apuestas online argentina|casa de apuestas online chile|casa de apuestas online españa|casa de
apuestas online mexico|casa de apuestas online paraguay|casa de apuestas online peru|casa de apuestas online usa|casa de apuestas online venezuela|casa de apuestas pago anticipado|casa de apuestas para boxeo|casa
de apuestas para ufc|casa de apuestas peru|casa de apuestas perú|casa de
apuestas peru online|casa de apuestas por paypal|casa de apuestas
promociones|casa de apuestas que regalan dinero|casa de apuestas real
madrid|casa de apuestas regalo de bienvenida|casa de
apuestas sevilla|casa de apuestas sin dinero|casa de
apuestas sin ingreso minimo|casa de apuestas sin licencia en españa|casa de apuestas sin minimo
de ingreso|casa de apuestas stake|casa de apuestas tenis|casa
de apuestas ufc|casa de apuestas valencia|casa de apuestas
venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de
apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas
apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas
apuestas con licencia|casas apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo
5 euros|casas apuestas legales|casas apuestas legales españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas
apuestas ofertas|casas apuestas online|casas apuestas paypal|casas apuestas
peru|casas apuestas sin licencia|casas apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de
apuestas 5 euros|casas de apuestas app|casas de apuestas argentinas|casas de apuestas asiaticas|casas de
apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono
de bienvenida|casas de apuestas bono por registro|casas de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas
de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas
bonos gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas
caballos|casas de apuestas carreras de caballos|casas de apuestas
casino|casas de apuestas casino online|casas de
apuestas cerca de mi|casas de apuestas champions
league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de
apuestas con apuestas gratis|casas de apuestas con bono|casas de apuestas con bono de bienvenida|casas
de apuestas con bono de registro|casas de apuestas con bono por
registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas
con deposito minimo|casas de apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas de apuestas con licencia en españa|casas de apuestas con licencia españa|casas de
apuestas con licencia española|casas de apuestas con mejores cuotas|casas de apuestas con pago anticipado|casas de apuestas con paypal|casas de
apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa del rey|casas
de apuestas de caballos|casas de apuestas de españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas de apuestas
de peru|casas de apuestas deportivas|casas de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de
apuestas deportivas comparativa|casas de apuestas deportivas con paypal|casas de apuestas deportivas en chile|casas de
apuestas deportivas en españa|casas de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de apuestas
deportivas en mexico|casas de apuestas deportivas en peru|casas
de apuestas deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas
españa|casas de apuestas deportivas españolas|casas de apuestas deportivas legales|casas de apuestas deportivas madrid|casas
de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas de apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas deposito minimo 1 euro|casas de
apuestas depósito mínimo 1 euro|casas de apuestas dinero gratis|casas de apuestas
en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas de
apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa online|casas
de apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas de apuestas en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas de apuestas
en venezuela|casas de apuestas equipos de futbol|casas de apuestas españa|casas de apuestas españa alemania|casas de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas de apuestas españa online|casas de apuestas española|casas de
apuestas españolas|casas de apuestas españolas con licencia|casas de apuestas españolas
online|casas de apuestas esports|casas de apuestas eurocopa|casas de apuestas
eurocopa 2024|casas de apuestas europa league|casas de apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas
fisicas en españa|casas de apuestas formula 1|casas de
apuestas fuera de españa|casas de apuestas futbol|casas de
apuestas fútbol|casas de apuestas futbol españa|casas
de apuestas ganador eurocopa|casas de apuestas gratis|casas
de apuestas ingreso minimo|casas de apuestas ingreso
minimo 1 euro|casas de apuestas ingreso minimo 5
euros|casas de apuestas inter barcelona|casas de
apuestas legales|casas de apuestas legales en colombia|casas
de apuestas legales en españa|casas de apuestas legales en mexico|casas de apuestas legales españa|casas de
apuestas legales mx|casas de apuestas licencia|casas de apuestas licencia españa|casas de apuestas lista|casas
de apuestas madrid|casas de apuestas mas seguras|casas de
apuestas mejores bonos|casas de apuestas mejores cuotas|casas de apuestas mexico|casas de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas de
apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas de apuestas
nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de apuestas ofertas|casas de apuestas
online|casas de apuestas online argentina|casas de apuestas
online colombia|casas de apuestas online deportivas|casas de apuestas online
ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas de apuestas online en colombia|casas de apuestas
online en españa|casas de apuestas online en mexico|casas de apuestas online españa|casas de apuestas online mas fiables|casas de apuestas
online mexico|casas de apuestas online nuevas|casas de apuestas online peru|casas de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago
paypal|casas de apuestas para ufc|c
jp99 online casino http://www.jp99-online.com .
Thanks for taking the time to break this down step-by-step.
The way you write feels personal and authentic.
fichas casino valor fichas casino valor .
оформить перепланировку квартиры цена https://uzakonit-pereplanirovku-cena.ru .
good day 4 play login good day 4 play login .
newsky slot newsky-online.com .
1xbet yeni giri? https://1xbet-7.com .
компании занимащиеся офицально перепланировками квартир http://soglasovanie-pereplanirovki-1.ru .
advista.click – Color palette felt calming, nothing distracting, just focused, thoughtful design.
sure win online http://www.surewin-online.com/ .
beep beep casino bonus http://www.beepbeepcasino-online.com/ .
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas
que significa|1×2 en apuestas|1×2 en apuestas que significa|1×2 que significa en apuestas|5 euros gratis apuestas|9 apuestas
que siempre ganaras|a partir de cuanto se declara apuestas|actividades de juegos
de azar y apuestas|ad apuestas deportivas|aleksandre topuria
ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba
apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas
deportivas android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas deportivas android|aplicaciones
apuestas deportivas gratis|aplicaciones de apuestas android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de
apuestas deportivas peru|aplicaciones de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones de apuestas gratis|aplicaciones de
apuestas online|aplicaciones de apuestas seguras|aplicaciones de apuestas sin dinero|aplicaciones para hacer apuestas|apostar seguro
apuestas deportivas|app android apuestas deportivas|app apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas android|app apuestas
deportivas argentina|app apuestas deportivas colombia|app apuestas
deportivas ecuador|app apuestas deportivas españa|app apuestas deportivas
gratis|app apuestas entre amigos|app apuestas futbol|app apuestas gratis|app apuestas sin dinero|app casa de
apuestas|app casas de apuestas|app control apuestas|app de apuestas|app de apuestas android|app de apuestas casino|app
de apuestas colombia|app de apuestas con bono de bienvenida|app de apuestas de futbol|app de apuestas deportivas|app de apuestas
deportivas android|app de apuestas deportivas argentina|app de apuestas deportivas colombia|app de
apuestas deportivas en españa|app de apuestas deportivas peru|app de apuestas deportivas perú|app de apuestas deportivas sin dinero|app de apuestas ecuador|app de
apuestas en colombia|app de apuestas en españa|app
de apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app de apuestas online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app de apuestas reales|app de casas de apuestas|app marca
apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas
en español|app para ganar apuestas deportivas|app para hacer apuestas|app para hacer apuestas deportivas|app para
hacer apuestas entre amigos|app para llevar control de apuestas|app
pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de
apuestas|apps de apuestas con bono de bienvenida|apps de apuestas de futbol|apps de apuestas deportivas peru|apps de apuestas mexico|apps
para apuestas|aprender a hacer apuestas deportivas|aprender hacer
apuestas deportivas|apuesta del dia apuestas
deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2 division|apuestas 3 division|apuestas a caballos|apuestas a carreras de
caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas a la baja|apuestas a la nfl|apuestas al barcelona|apuestas al dia|apuestas al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz hoy|apuestas alemania españa|apuestas
alonso campeon del mundo|apuestas altas y bajas|apuestas
altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia
argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas
argentina canada|apuestas argentina colombia|apuestas argentina
croacia|apuestas argentina españa|apuestas argentina francia|apuestas argentina francia cuanto
paga|apuestas argentina francia mundial|apuestas argentina gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina
méxico|apuestas argentina mundial|apuestas argentina online|apuestas
argentina paises bajos|apuestas argentina polonia|apuestas argentina uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas
ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas
athletic manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas
athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas
athletic real sociedad final|apuestas athletic roma|apuestas athletic
sevilla|apuestas athletic valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de
liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico
de madrid barcelona|apuestas atletico de madrid gana
la liga|apuestas atletico de madrid real madrid|apuestas atlético de
madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real
madrid|apuestas atletico madrid vs barcelona|apuestas atletico real
madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto
pronostico|apuestas baloncesto pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas
barca athletic|apuestas barca atletico|apuestas barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas barca hoy|apuestas barça hoy|apuestas barca inter|apuestas barca juventus|apuestas barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas barca
vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona
atletico|apuestas barcelona atletico de madrid|apuestas barcelona atlético de
madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona
betis|apuestas barcelona campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas barcelona gana la champions|apuestas barcelona girona|apuestas
barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas
barcelona osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas barcelona real sociedad|apuestas barcelona sevilla|apuestas barcelona valencia|apuestas barcelona villarreal|apuestas barcelona vs atletico madrid|apuestas barcelona vs madrid|apuestas
barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas
béisbol|apuestas beisbol mlb|apuestas beisbol pronosticos|apuestas beisbol
venezolano|apuestas betis|apuestas betis – chelsea|apuestas betis barcelona|apuestas
betis chelsea|apuestas betis fiorentina|apuestas betis
girona|apuestas betis madrid|apuestas betis mallorca|apuestas betis real madrid|apuestas betis real sociedad|apuestas betis sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis
vs valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas billar
online|apuestas bolivia vs colombia|apuestas bono|apuestas bono
bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de
campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas campeón champions|apuestas
campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas
campeon de champions|apuestas campeon de la champions|apuestas campeon de
liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas
campeon europa league|apuestas campeon f1|apuestas campeon f1
2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga
bbva|apuestas campeon liga española|apuestas campeon liga santander|apuestas
campeon motogp 2025|apuestas campeon mundial|apuestas
campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas
campeon roland garros|apuestas campeonato f1|apuestas campeonatos de futbol|apuestas
carrera de caballos|apuestas carrera de caballos hoy|apuestas carrera
de caballos nocturnas|apuestas carrera de galgos fin de semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas carreras caballos|apuestas carreras caballos sanlucar|apuestas carreras de caballos|apuestas carreras de caballos en directo|apuestas carreras de
caballos en vivo|apuestas carreras de caballos españa|apuestas carreras de caballos hoy|apuestas carreras de caballos
nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de caballos
online|apuestas carreras de caballos sanlucar|apuestas
carreras de caballos sanlúcar|apuestas carreras de galgos|apuestas carreras de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas
carreras de galgos pre partido|apuestas casino|apuestas casino
barcelona|apuestas casino futbol|apuestas casino
gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino online argentina|apuestas
casinos|apuestas casinos online|apuestas celta|apuestas celta barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas celta granada|apuestas celta
madrid|apuestas celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions league|apuestas
champions league – pronósticos|apuestas champions league 2025|apuestas champions league
hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas chelsea barcelona|apuestas
chelsea betis|apuestas chile|apuestas chile peru|apuestas chile
venezuela|apuestas chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas
city real madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs brasil|apuestas combinadas|apuestas
combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas combinadas
futbol|apuestas combinadas hoy|apuestas combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas para esta semana|apuestas combinadas para hoy|apuestas combinadas para mañana|apuestas
combinadas pronosticos|apuestas combinadas recomendadas|apuestas
combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para
mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap
asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas
con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa brasil|apuestas copa davis|apuestas
copa de europa|apuestas copa del mundo|apuestas copa del rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas
copa del rey futbol|apuestas copa del rey ganador|apuestas copa del
rey hoy|apuestas copa del rey pronosticos|apuestas copa del rey pronósticos|apuestas
copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial
de hockey|apuestas copa rey|apuestas copa sudamericana|apuestas corners|apuestas corners hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas
cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de
baloncesto para hoy|apuestas de beisbol|apuestas de beisbol para hoy|apuestas de blackjack en linea|apuestas
de boxeo|apuestas de boxeo canelo|apuestas de boxeo en las vegas|apuestas de
boxeo hoy|apuestas de boxeo online|apuestas de caballo|apuestas de caballos|apuestas de caballos como funciona|apuestas de caballos como se
juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas de
caballos en linea|apuestas de caballos españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas de caballos juegos|apuestas de
caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas de caballos
pronosticos|apuestas de caballos pronósticos|apuestas de carrera de caballos|apuestas de carreras de caballos|apuestas de carreras
de caballos online|apuestas de casino|apuestas
de casino online|apuestas de casino por internet|apuestas de champions league|apuestas de ciclismo|apuestas
de colombia|apuestas de copa america|apuestas
de corners|apuestas de deportes en linea|apuestas de deportes online|apuestas de dinero|apuestas de esports|apuestas
de eurocopa|apuestas de europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas de futbol
app|apuestas de futbol argentina|apuestas de futbol
colombia|apuestas de futbol en colombia|apuestas de futbol en directo|apuestas de futbol en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol
gratis|apuestas de futbol hoy|apuestas de
futbol mundial|apuestas de futbol online|apuestas de fútbol online|apuestas de futbol para hoy|apuestas de fútbol para
hoy|apuestas de futbol para hoy seguras|apuestas de futbol para mañana|apuestas
de futbol peru|apuestas de futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas
de futbol seguras para hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas
de galgos como ganar|apuestas de galgos en directo|apuestas de galgos online|apuestas de
galgos trucos|apuestas de golf|apuestas de hockey|apuestas de hockey
sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de
juegos online|apuestas de la champions league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas de la nfl|apuestas de la ufc|apuestas de mlb|apuestas de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas de peleas ufc|apuestas de perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de
sistema como funciona|apuestas de sistema explicacion|apuestas de
sistema explicación|apuestas de tenis|apuestas de tenis de mesa|apuestas
de tenis en directo|apuestas de tenis hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de
tenis seguras|apuestas de todo tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia
de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del mundial|apuestas
del partido de hoy|apuestas del real madrid|apuestas del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10
euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas
android|apuestas deportivas app|apuestas deportivas apps|apuestas
deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas atletico de madrid|apuestas deportivas baloncesto|apuestas deportivas
barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas
bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas
deportivas caballos|apuestas deportivas calculadora|apuestas
deportivas campeon liga|apuestas deportivas casino|apuestas
deportivas casino barcelona|apuestas deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas deportivas
ciclismo|apuestas deportivas colombia|apuestas
deportivas com|apuestas deportivas com foro|apuestas deportivas com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos
gratis|apuestas deportivas con dinero ficticio|apuestas deportivas
con paypal|apuestas deportivas con puntos virtuales|apuestas deportivas consejos|apuestas deportivas
consejos para ganar|apuestas deportivas copa america|apuestas deportivas copa del rey|apuestas
deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas cuotas altas|apuestas
deportivas de baloncesto|apuestas deportivas de boxeo|apuestas
deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas de peru|apuestas deportivas de tenis|apuestas deportivas
del dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas deportivas en español|apuestas
deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas deportivas en sevilla|apuestas deportivas en uruguay|apuestas
deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas
españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias seguras|apuestas deportivas
eurocopa|apuestas deportivas europa league|apuestas deportivas f1|apuestas
deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas foro|apuestas deportivas foro
futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas futbol|apuestas deportivas fútbol|apuestas
deportivas futbol argentino|apuestas deportivas
futbol colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas deportivas
ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas deportivas golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas deportivas gratis hoy|apuestas
deportivas gratis sin deposito|apuestas deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas hoy|apuestas
deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas deportivas
la liga|apuestas deportivas legales|apuestas deportivas
legales en colombia|apuestas deportivas libres de impuestos|apuestas deportivas licencia españa|apuestas
deportivas liga española|apuestas deportivas listado|apuestas
deportivas listado clasico|apuestas deportivas madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas deportivas
mejores|apuestas deportivas mejores app|apuestas deportivas mejores
casas|apuestas deportivas mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas
ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas deportivas online chile|apuestas deportivas online
colombia|apuestas deportivas online en colombia|apuestas deportivas online españa|apuestas deportivas online mexico|apuestas deportivas online paypal|apuestas
deportivas online peru|apuestas deportivas online por internet|apuestas deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas
partido suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas
deportivas perú|apuestas deportivas peru vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas
deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos
gratis|apuestas deportivas pronosticos nba|apuestas deportivas pronosticos tenis|apuestas deportivas
que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas
resultado exacto|apuestas deportivas resultados|apuestas deportivas
rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas
deportivas sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas
deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas
stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas deportivas tenis
de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis
hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas deportivas valencia
barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas
deportivas.com foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas
descenso a segunda|apuestas descenso a segunda b|apuestas descenso la liga|apuestas descenso
primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas
directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas draft nfl|apuestas ecuador vs argentina|apuestas ecuador
vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia
de futbol|apuestas en directo|apuestas en directo futbol|apuestas
en directo pronosticos|apuestas en el futbol|apuestas
en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas
en juegos|apuestas en la champions league|apuestas en la eurocopa|apuestas
en la liga|apuestas en la nba|apuestas en la nfl|apuestas
en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas
en linea chile|apuestas en linea colombia|apuestas en línea de fútbol|apuestas
en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea futbol|apuestas en linea mexico|apuestas
en línea méxico|apuestas en linea mundial|apuestas en linea peru|apuestas
en linea usa|apuestas en los esports|apuestas en madrid|apuestas en méxico|apuestas en mexico online|apuestas en nba|apuestas en partidos de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas
en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas
equipos de futbol|apuestas españa|apuestas españa alemania|apuestas
españa alemania eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa
francia eurocopa|apuestas españa gana el mundial|apuestas españa gana
eurocopa|apuestas españa gana mundial|apuestas españa
georgia|apuestas españa holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa paises bajos|apuestas
español|apuestas español oviedo|apuestas espanyol barcelona|apuestas
espanyol betis|apuestas espanyol villarreal|apuestas esport|apuestas esports|apuestas esports colombia|apuestas esports
españa|apuestas esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa
españa|apuestas eurocopa favoritos|apuestas
eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa
hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa league hoy|apuestas europa league pronosticos|apuestas europa league
pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas
f1 cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles
de ganar|apuestas fáciles de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas fc barcelona|apuestas final champions cuotas|apuestas final champions league|apuestas final
champions peru|apuestas final copa|apuestas final copa america|apuestas final copa
de europa|apuestas final copa del rey|apuestas final copa
europa|apuestas final copa libertadores|apuestas final copa rey|apuestas final de copa|apuestas final de copa del rey|apuestas final del mundial|apuestas final
euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final
rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia
nfl|apuestas finales nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula 1|apuestas fórmula
1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro
nba|apuestas francia argentina|apuestas francia españa|apuestas futbol|apuestas fútbol|apuestas
futbol americano|apuestas futbol americano nfl|apuestas futbol argentina|apuestas
futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol
consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas futbol españa|apuestas futbol español|apuestas fútbol
español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol
foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol telegram|apuestas futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas
galgos trucos|apuestas gana|apuestas gana colombia|apuestas
gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador champions
league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas ganador copa del
rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la eurocopa|apuestas ganador de
la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la liga|apuestas ganador
liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador
nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar liga|apuestas ganar mundial|apuestas ganar nba|apuestas getafe valencia|apuestas ghana
uruguay|apuestas girona|apuestas girona athletic|apuestas girona
betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas
girona real madrid|apuestas girona real sociedad|apuestas goleador
eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas
golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand
slam de tenis|apuestas gratis|apuestas gratis casino|apuestas gratis con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis
sin deposito|apuestas gratis sin depósito|apuestas
gratis sin ingreso|apuestas gratis sports|apuestas
gratis y ganar premios|apuestas grupo a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas
handicap baloncesto|apuestas handicap como funciona|apuestas handicap
nba|apuestas handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas hockey
hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas hoy nba|apuestas
hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas inter
barca|apuestas inter barcelona|apuestas juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos
olimpicos baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings league americas|apuestas la liga|apuestas la liga española|apuestas la liga hoy|apuestas la liga
santander|apuestas las vegas mlb|apuestas las vegas nba|apuestas las vegas
nfl|apuestas league of legends mundial|apuestas legal|apuestas legales|apuestas legales en colombia|apuestas legales
en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas libertadores|apuestas licencia|apuestas liga 1 peru|apuestas liga
argentina|apuestas liga bbva pronosticos|apuestas liga de campeones|apuestas liga de
campeones de baloncesto|apuestas liga de campeones de hockey|apuestas liga
españa|apuestas liga española|apuestas liga santander pronosticos|apuestas ligas
de futbol|apuestas linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas
madrid arsenal|apuestas madrid atletico|apuestas madrid
atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas madrid barca
hoy|apuestas madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid
borussia|apuestas madrid campeon champions|apuestas
madrid celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la
liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas
madrid valencia|apuestas madrid vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas
mas seguras para hoy|apuestas masters de golf|apuestas masters de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador mundial|apuestas
mejor jugador eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas mexico
polonia|apuestas méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas mlb pronosticos|apuestas mlb usa|apuestas mma
ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas mundial 2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial
brasil|apuestas mundial campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas mundial de baloncesto|apuestas mundial de ciclismo|apuestas mundial de clubes|apuestas mundial de futbol|apuestas mundial de fútbol|apuestas
mundial de rugby|apuestas mundial f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial
lol|apuestas mundial moto gp|apuestas mundial motogp|apuestas
mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas
mvp eurocopa|apuestas mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all
star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba
hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online bono|apuestas online
bono bienvenida|apuestas online boxeo|apuestas
online caballos|apuestas online carreras de caballos|apuestas online casino|apuestas online champions
league|apuestas online chile|apuestas online ciclismo|apuestas online colombia|apuestas
online comparativa|apuestas online con paypal|apuestas online de caballos|apuestas online deportivas|apuestas online en argentina|apuestas online
en peru|apuestas online espana|apuestas online españa|apuestas online esports|apuestas
online foro|apuestas online futbol|apuestas online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis
sin deposito|apuestas online juegos|apuestas online mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online
peru|apuestas online seguras|apuestas online sin dinero|apuestas online sin registro|apuestas
online tenis|apuestas online ufc|apuestas online uruguay|apuestas online venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas
over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises
bajos ecuador|apuestas paises bajos inglaterra|apuestas países bajos qatar|apuestas
para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas
para el mundial|apuestas para el partido de hoy|apuestas
para eurocopa|apuestas para europa league|apuestas para futbol|apuestas
para ganar|apuestas para ganar dinero|apuestas para ganar dinero facil|apuestas para ganar
en la ruleta|apuestas para ganar la champions|apuestas para ganar la eurocopa|apuestas para ganar la europa
league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas para
hoy de futbol|apuestas para hoy europa league|apuestas para hoy futbol|apuestas para juegos|apuestas para la champions
league|apuestas para la copa del rey|apuestas para la eurocopa|apuestas para la europa league|apuestas para la final de
la eurocopa|apuestas para la nba hoy|apuestas
para los partidos de hoy|apuestas para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas
partido españa marruecos|apuestas partido mundial|apuestas partido suspendido|apuestas
partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas
partidos de futbol|apuestas partidos de futbol hoy|apuestas
partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas paypal|apuestas peleas de
boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru
uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff
ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por internet para ganar dinero|apuestas por paypal|apuestas por ronda
boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas
pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas pronostico|apuestas pronosticos|apuestas pronosticos
deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas pronosticos tenis|apuestas
prorroga|apuestas psg barca|apuestas psg barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas que
significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana el
mundial|apuestas quien gana eurocopa|apuestas quien gana la champions|apuestas quien gana
la eurocopa|apuestas quien gana la liga|apuestas quien ganara el
mundial|apuestas quién ganará el mundial|apuestas quien ganara la champions|apuestas quien ganara la eurocopa|apuestas quien ganara la liga|apuestas rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real madrid atletico de madrid|apuestas real madrid
atlético de madrid|apuestas real madrid
atletico madrid|apuestas real madrid barcelona|apuestas
real madrid bayern|apuestas real madrid betis|apuestas
real madrid borussia|apuestas real madrid campeon champions|apuestas
real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real madrid
girona|apuestas real madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real madrid osasuna|apuestas real madrid
real sociedad|apuestas real madrid valencia|apuestas real madrid villarreal|apuestas real madrid vs arsenal|apuestas real
madrid vs atletico|apuestas real madrid vs atlético|apuestas real madrid vs
atletico madrid|apuestas real madrid vs barcelona|apuestas real
madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real sociedad barcelona|apuestas real
sociedad betis|apuestas real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas
regalo de bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas
segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas
segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas
seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas
seguras futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras nba|apuestas
seguras nba hoy|apuestas seguras para este
fin de semana|apuestas seguras para ganar dinero|apuestas seguras para hoy|apuestas seguras
para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas
seguras para mañana|apuestas seguras ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises bajos|apuestas sevilla|apuestas sevilla
athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas
sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la liga|apuestas sevilla girona|apuestas sevilla inter|apuestas sevilla jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas
sevilla madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas sevilla
real madrid|apuestas sevilla real sociedad|apuestas sevilla roma|apuestas sevilla
valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas
sin dinero real|apuestas sin empate|apuestas sin empate
que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake 10|apuestas stake
10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis
de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas tenis
itf|apuestas tenis pronosticos|apuestas tenis pronósticos|apuestas tenis retirada|apuestas tenis
roland garros|apuestas tenis seguras|apuestas tenis wimbledon|apuestas
tenis wta|apuestas tercera division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas
tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas
torneos de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas ufc
chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas
ufc ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc
telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas
uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas us
open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia
betis|apuestas valencia madrid|apuestas valencia
real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas
valor app|apuestas valor en directo|apuestas valor galgos|apuestas venezuela|apuestas
venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales sin dinero|apuestas
vivo|apuestas vuelta a españa|apuestas vuelta españa|apuestas
william hill partidos de hoy|apuestas y casino|apuestas y casinos|apuestas y juegos
de azar|apuestas y pronosticos|apuestas y pronosticos
de futbol|apuestas y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina
apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina
peru apuestas|argentina uruguay apuestas|argentina vs bolivia
apuestas|argentina vs chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic osasuna apuestas|athletic real madrid apuestas|atletico
barcelona apuestas|atletico de madrid apuestas|atlético de madrid apuestas|atletico de madrid real madrid
apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs real
madrid apuestas|avisador de cuotas apuestas|bajada de cuotas
apuestas|baloncesto apuestas|barbastro barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid
apuestas|barça madrid apuestas|barca vs atletico apuestas|barca vs madrid
apuestas|barca vs real madrid apuestas|barcelona – real madrid apuestas|barcelona
apuestas|barcelona atletico apuestas|barcelona atletico de
madrid apuestas|barcelona atletico madrid apuestas|barcelona betis apuestas|barcelona casa de
apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona
valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona vs atlético madrid apuestas|barcelona
vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona
vs espanyol apuestas|barcelona vs girona apuestas|barcelona vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal
apuestas|base de datos cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis
apuestas|betis barcelona apuestas|betis chelsea apuestas|betis madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog apuestas baloncesto|blog apuestas
ciclismo|blog apuestas nba|blog apuestas tenis|blog de
apuestas de tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono bienvenida
apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas
españa|bono bienvenida apuestas sin deposito|bono bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono bienvenida marca apuestas|bono casa
apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida apuestas|bono de bienvenida apuestas
deportivas|bono de bienvenida casa de apuestas|bono de bienvenida casas
de apuestas|bono de casas de apuestas|bono de registro apuestas|bono
de registro apuestas deportivas|bono de registro casa de apuestas|bono gratis apuestas|bono marca apuestas|bono por registro apuestas|bono por registro apuestas deportivas|bono por registro
casa de apuestas|bono registro apuestas|bono sin deposito apuestas|bono sin depósito
apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito casa de apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos
apuestas|bonos apuestas colombia|bonos apuestas
deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida casas
de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos casas de
apuestas|bonos casas de apuestas colombia|bonos casas
de apuestas deportivas|bonos casas de apuestas españa|bonos
casas de apuestas nuevas|bonos casas de apuestas sin deposito|bonos
casas de apuestas sin depósito|bonos de apuestas|bonos de apuestas
deportivas|bonos de apuestas gratis|bonos de apuestas sin deposito|bonos de
bienvenida apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida casa de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida de casas de apuestas|bonos de bienvenida en casas de apuestas|bonos
de casas de apuestas|bonos de casas de apuestas sin deposito|bonos en casa de apuestas|bonos en casas
de apuestas sin deposito|bonos gratis apuestas|bonos gratis
apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito
apuestas|bonos paginas de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos
sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de apuestas
deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas apuestas para hoy|buscador cuotas apuestas|buscador de
apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de apuestas|buscar apuestas seguras|caballos apuestas|calculador de apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas
combinadas|calculadora apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas
seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora apuestas
seguras|calculadora apuestas sistema|calculadora apuestas
yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de apuestas|calculadora
de apuestas combinadas|calculadora de apuestas de
futbol|calculadora de apuestas de sistema|calculadora de apuestas
deportivas|calculadora de apuestas multiples|calculadora de
apuestas seguras|calculadora de apuestas sistema|calculadora de
apuestas surebets|calculadora de arbitraje apuestas|calculadora de cuotas apuestas|calculadora de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora
sistema apuestas|calculadora stake apuestas|calculadora trading apuestas|calcular apuestas|calcular apuestas deportivas|calcular apuestas futbol|calcular
apuestas sistema|calcular cuotas apuestas|calcular cuotas
apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias
apuestas deportivas|calcular momios apuestas|calcular probabilidad cuota apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield
apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas apuestas|campeon champions apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera de caballos con apuestas|carrera
de galgos apuestas|carreras de caballos apuestas|carreras de caballos apuestas online|carreras de caballos con apuestas|carreras de caballos
juegos de apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras de galgos
apuestas trucos|carreras galgos apuestas|casa apuestas
argentina|casa apuestas atletico de madrid|casa apuestas barcelona|casa apuestas betis|casa apuestas bono bienvenida|casa apuestas bono gratis|casa apuestas bono sin deposito|casa apuestas cerca de
mi|casa apuestas chile|casa apuestas colombia|casa apuestas con mejores
cuotas|casa apuestas deportivas|casa apuestas españa|casa
apuestas española|casa apuestas eurocopa|casa apuestas futbol|casa apuestas mejores cuotas|casa apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa
apuestas online|casa apuestas peru|casa apuestas valencia|casa de apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de apuestas bono|casa de apuestas bono
bienvenida|casa de apuestas bono de bienvenida|casa de apuestas bono gratis|casa de apuestas bono por
registro|casa de apuestas bono sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa de apuestas carreras de caballos|casa de apuestas cerca de
mi|casa de apuestas cerca de mí|casa de apuestas champions league|casa de apuestas
chile|casa de apuestas ciclismo|casa de apuestas colombia|casa
de apuestas con bono de bienvenida|casa de apuestas
con bono sin deposito|casa de apuestas con cuotas mas altas|casa de apuestas con esports|casa de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa de apuestas copa america|casa de apuestas de caballos|casa de apuestas de colombia|casa
de apuestas de españa|casa de apuestas de futbol|casa de
apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa
de apuestas del madrid|casa de apuestas del real madrid|casa de apuestas deportivas|casa de apuestas deportivas cerca de mi|casa de
apuestas deportivas en argentina|casa de apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa de apuestas deportivas en españa|casa
de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas españolas|casa
de apuestas deportivas madrid|casa de apuestas deportivas mexico|casa de apuestas deportivas online|casa de apuestas deportivas peru|casa de apuestas deposito 5 euros|casa de apuestas deposito minimo|casa de apuestas deposito minimo 1 euro|casa de apuestas
depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas en linea|casa
de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas españa
inglaterra|casa de apuestas española|casa de apuestas españolas|casa de apuestas
esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de apuestas
f1|casa de apuestas formula 1|casa de apuestas futbol|casa de apuestas ingreso
minimo|casa de apuestas ingreso minimo 1 euro|casa de apuestas ingreso
mínimo 1 euro|casa de apuestas legales|casa de apuestas legales en colombia|casa de apuestas legales en españa|casa de apuestas libertadores|casa de apuestas liga
española|casa de apuestas madrid|casa de apuestas mas segura|casa de apuestas mejores|casa de
apuestas méxico|casa de apuestas minimo
5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa
de apuestas nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas
oficial del real madrid|casa de apuestas oficial real madrid|casa de apuestas online|casa de apuestas online argentina|casa de apuestas online chile|casa de apuestas online españa|casa de apuestas online mexico|casa de apuestas online paraguay|casa de apuestas
online peru|casa de apuestas online usa|casa de apuestas online venezuela|casa de apuestas pago anticipado|casa de apuestas para boxeo|casa de apuestas para ufc|casa
de apuestas peru|casa de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa de
apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de bienvenida|casa
de apuestas sevilla|casa de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa
de apuestas sin licencia en españa|casa de apuestas sin minimo de ingreso|casa de apuestas stake|casa de apuestas
tenis|casa de apuestas ufc|casa de apuestas valencia|casa
de apuestas venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas apuestas bonos sin deposito|casas apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas
apuestas deportivas|casas apuestas deportivas
colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas apuestas deportivas nuevas|casas apuestas
españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas legales|casas apuestas legales españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas apuestas
paypal|casas apuestas peru|casas apuestas sin licencia|casas
apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de
apuestas 5 euros|casas de apuestas app|casas de apuestas argentinas|casas
de apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono de bienvenida|casas de apuestas
bono por registro|casas de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas
de apuestas bonos|casas de apuestas bonos de bienvenida|casas de
apuestas bonos gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas
de apuestas caballos|casas de apuestas carreras de
caballos|casas de apuestas casino|casas de apuestas casino
online|casas de apuestas cerca de mi|casas de apuestas champions league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de apuestas con apuestas gratis|casas de apuestas con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono de registro|casas
de apuestas con bono por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas
de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas con deposito minimo|casas de apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas
de apuestas con licencia en españa|casas de apuestas con licencia españa|casas de apuestas
con licencia española|casas de apuestas con mejores cuotas|casas
de apuestas con pago anticipado|casas de apuestas con paypal|casas de apuestas con paypal en perú|casas de
apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa
del rey|casas de apuestas de caballos|casas de apuestas de
españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas
de apuestas de peru|casas de apuestas deportivas|casas de
apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas deportivas
comparativa|casas de apuestas deportivas con paypal|casas de apuestas deportivas
en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de apuestas deportivas en mexico|casas de
apuestas deportivas en peru|casas de apuestas deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de apuestas deportivas españolas|casas de apuestas deportivas legales|casas
de apuestas deportivas madrid|casas de apuestas deportivas
mexico|casas de apuestas deportivas nuevas|casas de apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas
deposito minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de apuestas
dinero gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas
de apuestas en colombia|casas de apuestas en españa|casas de
apuestas en españa online|casas de apuestas en linea|casas de apuestas en madrid|casas de
apuestas en méxico|casas de apuestas en peru|casas de apuestas
en perú|casas de apuestas en sevilla|casas de apuestas en uruguay|casas de apuestas en valencia|casas
de apuestas en venezuela|casas de apuestas equipos de futbol|casas
de apuestas españa|casas de apuestas españa alemania|casas de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas
españa nuevas|casas de apuestas españa online|casas de
apuestas española|casas de apuestas españolas|casas
de apuestas españolas con licencia|casas de apuestas españolas online|casas de apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas de
apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas en españa|casas de apuestas formula 1|casas de apuestas fuera de españa|casas de apuestas futbol|casas de apuestas fútbol|casas de apuestas futbol españa|casas de apuestas ganador eurocopa|casas de apuestas
gratis|casas de apuestas ingreso minimo|casas de apuestas
ingreso minimo 1 euro|casas de apuestas ingreso minimo 5 euros|casas de apuestas inter barcelona|casas
de apuestas legales|casas de apuestas legales en colombia|casas de apuestas
legales en españa|casas de apuestas legales en mexico|casas de apuestas legales españa|casas de apuestas legales mx|casas de apuestas licencia|casas
de apuestas licencia españa|casas de apuestas lista|casas de apuestas madrid|casas de
apuestas mas seguras|casas de apuestas mejores bonos|casas
de apuestas mejores cuotas|casas de apuestas mexico|casas de
apuestas méxico|casas de apuestas minimo 5 euros|casas
de apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas
de apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas
de apuestas nuevas|casas de apuestas nuevas en colombia|casas
de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de apuestas ofertas|casas de apuestas online|casas de
apuestas online argentina|casas de apuestas online colombia|casas de apuestas online deportivas|casas de
apuestas online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas de apuestas online en colombia|casas de apuestas online
en españa|casas de apuestas online en mexico|casas de apuestas online españa|casas de apuestas online mas fiables|casas
de apuestas online mexico|casas de apuestas online nuevas|casas de apuestas online peru|casas
de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas de apuestas
para ufc|casas de apuestas paypal|c
Kazakhstan standards include ST RK (Kazakhstan National Standards) and mandatory Technical Regulations Russian standards in English
https://kra–45cc.ru
growthflow.click – Found practical insights today; sharing this article with colleagues later.
ganabet casino bono ganabet-online.com .
It’s interesting to see how widely used the Rebuy algorithm is, as the article mentions. I found some related information on https://tinyfun.io/game/snapstyle-dress-up that helped me understand the variations a bit better.
Your tips are practical and easy to apply. Thanks a lot!
I enjoyed your perspective on this topic. Looking forward to more content.
jompay99.com casino [url=www.jp99-online.com/]www.jp99-online.com/[/url] .
бти перепланировка квартиры согласование цена http://uzakonit-pereplanirovku-cena.ru .
https://shorturl.fm/zChMo
carnival valor casino games carnival valor casino games .
goodday4play goodday4play .
newsky88 asia http://www.newsky-online.com/ .
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos
para ganar apuestas|15 euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas que significa|1×2 en apuestas|1×2 en apuestas que
significa|1×2 que significa en apuestas|5 euros gratis apuestas|9
apuestas que siempre ganaras|a partir de cuanto se declara apuestas|actividades de juegos de azar y apuestas|ad
apuestas deportivas|aleksandre topuria ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para hacer apuestas de futbol|aplicación para hacer apuestas de fútbol|aplicaciones
apuestas deportivas android|aplicaciones apuestas deportivas gratis|aplicaciones de apuestas
android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones
de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones
de apuestas gratis|aplicaciones de apuestas online|aplicaciones de apuestas seguras|aplicaciones de apuestas sin dinero|aplicaciones
para hacer apuestas|apostar seguro apuestas deportivas|app android apuestas deportivas|app
apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas deportivas
android|app apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app
apuestas deportivas gratis|app apuestas entre amigos|app apuestas
futbol|app apuestas gratis|app apuestas sin dinero|app casa de apuestas|app casas de apuestas|app control apuestas|app de apuestas|app
de apuestas android|app de apuestas casino|app de apuestas colombia|app de apuestas con bono
de bienvenida|app de apuestas de futbol|app de apuestas deportivas|app
de apuestas deportivas android|app de apuestas deportivas argentina|app de apuestas deportivas colombia|app
de apuestas deportivas en españa|app de apuestas deportivas peru|app de
apuestas deportivas perú|app de apuestas deportivas
sin dinero|app de apuestas ecuador|app de apuestas en colombia|app de apuestas en españa|app de
apuestas en venezuela|app de apuestas futbol|app de apuestas gratis|app
de apuestas online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app
de apuestas reales|app de casas de apuestas|app marca
apuestas android|app moviles de apuestas|app para apuestas|app para apuestas de futbol|app para
apuestas deportivas|app para apuestas deportivas en español|app para ganar apuestas deportivas|app para hacer
apuestas|app para hacer apuestas deportivas|app para hacer apuestas entre amigos|app para llevar control de apuestas|app pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de apuestas|apps de
apuestas con bono de bienvenida|apps de
apuestas de futbol|apps de apuestas deportivas peru|apps de
apuestas mexico|apps para apuestas|aprender a hacer apuestas deportivas|aprender hacer apuestas
deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2 division|apuestas 3 division|apuestas a
caballos|apuestas a carreras de caballos|apuestas a colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores
nba|apuestas a la baja|apuestas a la nfl|apuestas al barcelona|apuestas al dia|apuestas al empate|apuestas
al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz
hoy|apuestas alemania españa|apuestas alonso campeon del mundo|apuestas altas y
bajas|apuestas altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas argentina campeon del mundo|apuestas argentina canada|apuestas argentina
colombia|apuestas argentina croacia|apuestas argentina
españa|apuestas argentina francia|apuestas argentina francia cuanto paga|apuestas argentina francia mundial|apuestas argentina
gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina
méxico|apuestas argentina mundial|apuestas argentina online|apuestas
argentina paises bajos|apuestas argentina polonia|apuestas
argentina uruguay|apuestas argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas
athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas athletic manchester united|apuestas athletic osasuna|apuestas athletic real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas athletic real sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic valencia|apuestas atletico|apuestas atletico barcelona|apuestas
atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de liga|apuestas
atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas atletico
de madrid gana la liga|apuestas atletico de madrid real madrid|apuestas atlético de
madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas atletico madrid vs barcelona|apuestas
atletico real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas
baloncesto handicap|apuestas baloncesto hoy|apuestas
baloncesto juegos olimpicos|apuestas baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas
baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas
barca atletico|apuestas barca bayern|apuestas barca
bayern munich|apuestas barca girona|apuestas barca hoy|apuestas
barça hoy|apuestas barca inter|apuestas barca juventus|apuestas barca madrid|apuestas
barça madrid|apuestas barca real madrid|apuestas barca
vs juve|apuestas barca vs madrid|apuestas barca vs
psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona atletico|apuestas
barcelona atletico de madrid|apuestas barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas barcelona
campeon de liga|apuestas barcelona celta|apuestas barcelona espanyol|apuestas
barcelona gana la champions|apuestas barcelona
girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas barcelona
madrid|apuestas barcelona osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas barcelona real sociedad|apuestas barcelona
sevilla|apuestas barcelona valencia|apuestas barcelona villarreal|apuestas
barcelona vs atletico madrid|apuestas barcelona vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol
mlb|apuestas beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas
betis – chelsea|apuestas betis barcelona|apuestas betis chelsea|apuestas betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas betis
real madrid|apuestas betis real sociedad|apuestas betis sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis vs valencia|apuestas betplay
hoy colombia|apuestas betsson peru|apuestas bienvenida|apuestas
billar online|apuestas bolivia vs colombia|apuestas bono|apuestas bono bienvenida|apuestas bono de bienvenida|apuestas bono de bienvenida
sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo
online|apuestas brasil colombia|apuestas brasil peru|apuestas brasil uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos colocado|apuestas caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas
campeon|apuestas campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference
league|apuestas campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas campeon de la
champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa league|apuestas campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas
campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas campeon liga santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas campeón mundial|apuestas campeon mundial
baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas
campeon premier|apuestas campeon premier league|apuestas
campeon roland garros|apuestas campeonato f1|apuestas campeonatos de futbol|apuestas carrera de caballos|apuestas carrera de
caballos hoy|apuestas carrera de caballos nocturnas|apuestas carrera de galgos
fin de semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas carreras caballos|apuestas carreras caballos sanlucar|apuestas carreras de caballos|apuestas carreras de
caballos en directo|apuestas carreras de caballos en vivo|apuestas carreras
de caballos españa|apuestas carreras de caballos
hoy|apuestas carreras de caballos nacionales|apuestas carreras de caballos nocturnas|apuestas carreras de caballos online|apuestas carreras de caballos sanlucar|apuestas carreras de caballos sanlúcar|apuestas carreras de
galgos|apuestas carreras de galgos en vivo|apuestas carreras de
galgos nocturnas|apuestas carreras de galgos pre partido|apuestas casino|apuestas casino barcelona|apuestas casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas casino online|apuestas casino online argentina|apuestas casinos|apuestas casinos online|apuestas
celta|apuestas celta barcelona|apuestas celta betis|apuestas
celta eibar|apuestas celta espanyol|apuestas celta
granada|apuestas celta madrid|apuestas celta manchester|apuestas celta
real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions league|apuestas champions league – pronósticos|apuestas champions league 2025|apuestas champions league hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile
vs uruguay|apuestas ciclismo|apuestas ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo
tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas city real
madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia
argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs
argentina|apuestas colombia vs brasil|apuestas combinadas|apuestas combinadas como funcionan|apuestas combinadas
de futbol|apuestas combinadas de fútbol|apuestas combinadas foro|apuestas
combinadas futbol|apuestas combinadas hoy|apuestas
combinadas mismo partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas
para esta semana|apuestas combinadas para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas
recomendadas|apuestas combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas
seguras para mañana|apuestas como ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero ficticio|apuestas con dinero real|apuestas con dinero
virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas probabilidades de ganar|apuestas con paypal|apuestas con tarjeta de
credito|apuestas con tarjeta de debito|apuestas consejos|apuestas
copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas
copa brasil|apuestas copa davis|apuestas copa de europa|apuestas copa del mundo|apuestas copa
del rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas copa del rey futbol|apuestas copa del rey ganador|apuestas copa del rey hoy|apuestas copa del rey pronosticos|apuestas copa del rey pronósticos|apuestas copa europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de hockey|apuestas copa rey|apuestas copa
sudamericana|apuestas corners|apuestas corners hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto
nba|apuestas de baloncesto para hoy|apuestas de beisbol|apuestas de beisbol para hoy|apuestas de blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas de boxeo en las vegas|apuestas de
boxeo hoy|apuestas de boxeo online|apuestas de caballo|apuestas de caballos|apuestas
de caballos como funciona|apuestas de caballos como se juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas de caballos españa|apuestas de caballos ganador y colocado|apuestas de caballos internacionales|apuestas de caballos
juegos|apuestas de caballos online|apuestas de caballos
online en venezuela|apuestas de caballos por internet|apuestas de caballos pronosticos|apuestas
de caballos pronósticos|apuestas de carrera de caballos|apuestas de
carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de casino online|apuestas de casino
por internet|apuestas de champions league|apuestas de ciclismo|apuestas de colombia|apuestas de copa america|apuestas de corners|apuestas de deportes en linea|apuestas de deportes online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas
de europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas
de fútbol|apuestas de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de futbol en colombia|apuestas de futbol en directo|apuestas de futbol en linea|apuestas
de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de futbol hoy|apuestas de futbol
mundial|apuestas de futbol online|apuestas de fútbol online|apuestas de futbol para hoy|apuestas de fútbol para hoy|apuestas de futbol para hoy seguras|apuestas de futbol
para mañana|apuestas de futbol peru|apuestas de futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas
de futbol seguras para hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas de galgos
como ganar|apuestas de galgos en directo|apuestas
de galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas
de hockey sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de
juegos online|apuestas de la champions league|apuestas de la copa américa|apuestas de la eurocopa|apuestas de la europa league|apuestas de la liga|apuestas de la liga
bbva|apuestas de la liga española|apuestas de
la nba|apuestas de la nfl|apuestas de la ufc|apuestas de mlb|apuestas
de nba|apuestas de nba para hoy|apuestas de partidos|apuestas de partidos de futbol|apuestas de peleas
ufc|apuestas de perros en vivo|apuestas de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema
como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas de tenis
de mesa|apuestas de tenis en directo|apuestas de tenis hoy|apuestas de tenis
para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas de todo tipo|apuestas de
ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas del
clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia de hoy|apuestas del dia
deportivas|apuestas del dia futbol|apuestas del
mundial|apuestas del partido de hoy|apuestas del real madrid|apuestas
del rey|apuestas del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas
deportivas 1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas deportivas android|apuestas
deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas deportivas atletico de madrid|apuestas deportivas
baloncesto|apuestas deportivas barca madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas deportivas bono
bienvenida|apuestas deportivas bono de bienvenida|apuestas deportivas
bono sin deposito|apuestas deportivas bonos de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas campeon liga|apuestas deportivas casino|apuestas
deportivas casino barcelona|apuestas deportivas casino
online|apuestas deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas deportivas ciclismo|apuestas deportivas colombia|apuestas
deportivas com|apuestas deportivas com foro|apuestas deportivas com pronosticos|apuestas
deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas como
se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero ficticio|apuestas deportivas con paypal|apuestas deportivas con puntos
virtuales|apuestas deportivas consejos|apuestas deportivas consejos para ganar|apuestas
deportivas copa america|apuestas deportivas copa del rey|apuestas deportivas
copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas deportivas cual es la mejor|apuestas deportivas
cuotas altas|apuestas deportivas de baloncesto|apuestas deportivas de boxeo|apuestas deportivas de
colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de nhl|apuestas deportivas de peru|apuestas deportivas de tenis|apuestas deportivas del dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas
en argentina|apuestas deportivas en chile|apuestas deportivas
en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas
deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas
deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas estrategias
seguras|apuestas deportivas eurocopa|apuestas deportivas europa league|apuestas
deportivas f1|apuestas deportivas faciles de ganar|apuestas deportivas formula 1|apuestas deportivas
foro|apuestas deportivas foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas
futbol|apuestas deportivas fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas deportivas futbol español|apuestas deportivas gana|apuestas deportivas ganadas|apuestas deportivas ganar dinero seguro|apuestas deportivas gane|apuestas deportivas golf|apuestas deportivas gratis|apuestas deportivas gratis
con premios|apuestas deportivas gratis hoy|apuestas deportivas gratis
sin deposito|apuestas deportivas handicap|apuestas
deportivas handicap asiatico|apuestas deportivas hoy|apuestas deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas deportivas
legales en colombia|apuestas deportivas libres de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga
española|apuestas deportivas listado|apuestas deportivas listado clasico|apuestas deportivas madrid|apuestas deportivas mas seguras|apuestas deportivas mejor pagadas|apuestas deportivas
mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas
deportivas mejores paginas|apuestas deportivas mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas
deportivas multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas
nba hoy|apuestas deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas deportivas online chile|apuestas deportivas online colombia|apuestas deportivas online en colombia|apuestas deportivas online españa|apuestas deportivas
online mexico|apuestas deportivas online paypal|apuestas deportivas online peru|apuestas
deportivas online por internet|apuestas deportivas pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para
hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido
suspendido|apuestas deportivas partidos de hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas deportivas perú|apuestas deportivas peru vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas deportivas pronostico hoy|apuestas deportivas pronosticos|apuestas deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos gratis|apuestas deportivas pronosticos nba|apuestas
deportivas pronosticos tenis|apuestas deportivas que
aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo bienvenida|apuestas deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas
stake 10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas
deportivas tenis de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas deportivas uruguay|apuestas deportivas valencia|apuestas
deportivas valencia barcelona|apuestas deportivas venezuela|apuestas deportivas
virtuales|apuestas deportivas y casino|apuestas deportivas y casino online|apuestas deportivas.com|apuestas deportivas.com
foro|apuestas deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo 1 euro|apuestas descenso a segunda|apuestas descenso a segunda
b|apuestas descenso la liga|apuestas descenso
primera division|apuestas descenso segunda|apuestas dia|apuestas
diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas directo|apuestas directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas
doble resultado|apuestas dobles|apuestas dobles y triples|apuestas dortmund barcelona|apuestas draft nba|apuestas draft nfl|apuestas ecuador
vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas el clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas en casinos|apuestas en casinos online|apuestas
en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas
en directo pronosticos|apuestas en el futbol|apuestas
en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas en golf|apuestas en juegos|apuestas en la champions league|apuestas en la
eurocopa|apuestas en la liga|apuestas en la nba|apuestas
en la nfl|apuestas en las vegas mlb|apuestas en las
vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea argentina|apuestas en linea boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas
en línea de fútbol|apuestas en linea deportivas|apuestas
en linea españa|apuestas en linea estados unidos|apuestas
en linea futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea
peru|apuestas en linea usa|apuestas en los esports|apuestas en madrid|apuestas en méxico|apuestas en mexico online|apuestas
en nba|apuestas en partidos de futbol|apuestas
en partidos de futbol en vivo|apuestas en partidos de tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas en stake|apuestas en tenis|apuestas
en tenis de mesa|apuestas en valencia|apuestas en vivo|apuestas
en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas
en vivo fútbol|apuestas en vivo nba|apuestas en vivo
peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas equipo mbappe|apuestas equipos de futbol|apuestas
españa|apuestas españa alemania|apuestas españa alemania eurocopa|apuestas españa
croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa gana el mundial|apuestas españa gana eurocopa|apuestas españa gana mundial|apuestas españa georgia|apuestas españa
holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas españa mundial|apuestas españa paises bajos|apuestas español|apuestas español oviedo|apuestas espanyol barcelona|apuestas espanyol betis|apuestas espanyol villarreal|apuestas
esport|apuestas esports|apuestas esports colombia|apuestas esports españa|apuestas
esports fifa|apuestas esports gratis|apuestas esports lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas
euro|apuestas euro copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa españa|apuestas eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa sub 21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas europa league|apuestas europa
league hoy|apuestas europa league pronosticos|apuestas
europa league pronósticos|apuestas euros|apuestas f1
abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1
china|apuestas f1 cuotas|apuestas f1 hoy|apuestas
f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas
faciles de ganar|apuestas fáciles de ganar|apuestas faciles para ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas
favoritos eurocopa|apuestas favoritos mundial|apuestas
fc barcelona|apuestas final champions cuotas|apuestas final champions league|apuestas final champions peru|apuestas final copa|apuestas final copa america|apuestas final copa de europa|apuestas final copa del
rey|apuestas final copa europa|apuestas final copa libertadores|apuestas
final copa rey|apuestas final de copa|apuestas final de copa del rey|apuestas
final del mundial|apuestas final euro|apuestas final eurocopa|apuestas
final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia nfl|apuestas finales nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas fórmula 1|apuestas fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas
francia españa|apuestas futbol|apuestas fútbol|apuestas
futbol americano|apuestas futbol americano nfl|apuestas futbol
argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol
chile|apuestas futbol colombia|apuestas futbol consejos|apuestas
futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol
en vivo|apuestas futbol españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol hoy|apuestas futbol
juegos olimpicos|apuestas futbol mexico|apuestas futbol mundial|apuestas futbol online|apuestas futbol
para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol sala|apuestas futbol telegram|apuestas
futbol virtual|apuestas galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas
galgos pronosticos|apuestas galgos trucos|apuestas gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas hoy|apuestas ganador champions league|apuestas
ganador copa america|apuestas ganador copa
del rey|apuestas ganador copa del rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la eurocopa|apuestas ganador de
la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la liga|apuestas ganador liga española|apuestas ganador
mundial|apuestas ganador mundial baloncesto|apuestas ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar liga|apuestas ganar mundial|apuestas
ganar nba|apuestas getafe valencia|apuestas ghana uruguay|apuestas
girona|apuestas girona athletic|apuestas girona betis|apuestas girona campeon de
liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas girona
real madrid|apuestas girona real sociedad|apuestas goleador eurocopa|apuestas goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas gratis|apuestas
gratis casino|apuestas gratis con premios|apuestas gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis
sports|apuestas gratis y ganar premios|apuestas grupo
a eurocopa|apuestas grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas handicap
baloncesto|apuestas handicap como funciona|apuestas
handicap nba|apuestas handicap nfl|apuestas hipicas
online|apuestas hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas
hockey hielo|apuestas hockey patines|apuestas hockey
sobre hielo|apuestas holanda argentina|apuestas holanda vs
argentina|apuestas hoy|apuestas hoy champions|apuestas hoy futbol|apuestas
hoy nba|apuestas hoy pronosticos|apuestas hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas
inter barca|apuestas inter barcelona|apuestas juego|apuestas
juegos|apuestas juegos en linea|apuestas juegos
olimpicos|apuestas juegos olímpicos|apuestas juegos olimpicos baloncesto|apuestas juegos online|apuestas juegos virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings league americas|apuestas
la liga|apuestas la liga española|apuestas la liga hoy|apuestas la liga santander|apuestas las
vegas mlb|apuestas las vegas nba|apuestas
las vegas nfl|apuestas league of legends mundial|apuestas legal|apuestas legales|apuestas legales en colombia|apuestas legales en españa|apuestas
legales en estados unidos|apuestas legales españa|apuestas leganes betis|apuestas
libertadores|apuestas licencia|apuestas liga 1 peru|apuestas
liga argentina|apuestas liga bbva pronosticos|apuestas liga de campeones|apuestas liga de campeones de baloncesto|apuestas liga de campeones de hockey|apuestas liga españa|apuestas
liga española|apuestas liga santander pronosticos|apuestas ligas de
futbol|apuestas linea|apuestas linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas
madrid atletico|apuestas madrid atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas madrid barca hoy|apuestas
madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas
madrid bayern|apuestas madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid
celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la
liga|apuestas madrid gana liga|apuestas madrid hoy|apuestas madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas madrid
valencia|apuestas madrid vs arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester athletic|apuestas manchester city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas
mas seguras para hoy|apuestas masters de golf|apuestas masters
de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador mundial|apuestas mejor jugador eurocopa|apuestas mejores casinos online|apuestas mexico|apuestas méxico|apuestas mexico polonia|apuestas méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb las vegas|apuestas mlb
para hoy|apuestas mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas
mundial 2026|apuestas mundial baloncesto|apuestas mundial balonmano|apuestas mundial brasil|apuestas mundial campeon|apuestas mundial ciclismo|apuestas mundial
clubes|apuestas mundial de baloncesto|apuestas mundial
de ciclismo|apuestas mundial de clubes|apuestas mundial de futbol|apuestas mundial de fútbol|apuestas mundial
de rugby|apuestas mundial f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas
mundial formula 1|apuestas mundial futbol|apuestas mundial ganador|apuestas mundial lol|apuestas mundial
moto gp|apuestas mundial motogp|apuestas mundial rugby|apuestas mundial sub 17|apuestas mundiales|apuestas
mundialistas|apuestas mvp eurocopa|apuestas mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta
noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba
hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba pronosticos|apuestas nba pronósticos|apuestas nba pronosticos hoy|apuestas
nba tipster|apuestas nfl|apuestas nfl hoy|apuestas
nfl las vegas|apuestas nfl playoffs|apuestas nfl pronosticos|apuestas nfl pronósticos|apuestas
nfl semana 4|apuestas nfl super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas online bono|apuestas online bono bienvenida|apuestas online boxeo|apuestas online caballos|apuestas online carreras de caballos|apuestas online casino|apuestas online champions league|apuestas online chile|apuestas online ciclismo|apuestas online colombia|apuestas online comparativa|apuestas online con paypal|apuestas online de caballos|apuestas online
deportivas|apuestas online en argentina|apuestas online en peru|apuestas online espana|apuestas online españa|apuestas online esports|apuestas
online foro|apuestas online futbol|apuestas online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online
juegos|apuestas online mexico|apuestas online
mma|apuestas online movil|apuestas online nba|apuestas online net|apuestas online nuevas|apuestas online opiniones|apuestas online paypal|apuestas online peru|apuestas
online seguras|apuestas online sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online ufc|apuestas online uruguay|apuestas online
venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises
bajos ecuador|apuestas paises bajos inglaterra|apuestas países
bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de hoy|apuestas para el mundial|apuestas para el partido de hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas
para ganar|apuestas para ganar dinero|apuestas para ganar dinero
facil|apuestas para ganar en la ruleta|apuestas para ganar la champions|apuestas
para ganar la eurocopa|apuestas para ganar la europa league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para
hacer|apuestas para hoy|apuestas para hoy de futbol|apuestas
para hoy europa league|apuestas para hoy futbol|apuestas para
juegos|apuestas para la champions league|apuestas para la
copa del rey|apuestas para la eurocopa|apuestas para la europa league|apuestas para la final de la eurocopa|apuestas para la nba hoy|apuestas para los partidos de
hoy|apuestas para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas partido españa
marruecos|apuestas partido mundial|apuestas partido suspendido|apuestas partidos|apuestas
partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos de
futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas paypal|apuestas peleas de
boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas
peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff ascenso|apuestas
playoff ascenso a primera|apuestas playoff nba|apuestas playoff segunda|apuestas playoff segunda b|apuestas playoffs nba|apuestas playoffs nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por internet para ganar
dinero|apuestas por paypal|apuestas por ronda boxeo|apuestas por
sistema|apuestas portugal uruguay|apuestas pre
partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas pronostico|apuestas pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos
futbol|apuestas pronosticos gratis|apuestas pronosticos nba|apuestas
pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas
psg barcelona|apuestas puntos por tarjetas|apuestas puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas que
significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana
eurocopa|apuestas quien gana la champions|apuestas quien gana la eurocopa|apuestas quien gana la liga|apuestas
quien ganara el mundial|apuestas quién ganará el mundial|apuestas quien ganara la champions|apuestas
quien ganara la eurocopa|apuestas quien ganara la
liga|apuestas rayo barcelona|apuestas real madrid|apuestas real madrid arsenal|apuestas real
madrid athletic|apuestas real madrid atletico|apuestas real madrid atletico champions|apuestas real madrid atletico de madrid|apuestas real madrid atlético de
madrid|apuestas real madrid atletico madrid|apuestas real madrid barcelona|apuestas real madrid bayern|apuestas real madrid betis|apuestas real madrid borussia|apuestas real madrid campeon champions|apuestas real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real
madrid girona|apuestas real madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real
madrid osasuna|apuestas real madrid real sociedad|apuestas real madrid valencia|apuestas real madrid
villarreal|apuestas real madrid vs arsenal|apuestas real madrid vs atletico|apuestas real madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas real
madrid vs barcelona|apuestas real madrid vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real
sociedad athletic|apuestas real sociedad barcelona|apuestas real sociedad betis|apuestas real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de bienvenida|apuestas registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas
roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas
segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas
seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas
seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas seguras futbol hoy|apuestas seguras
gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas
seguras nba|apuestas seguras nba hoy|apuestas seguras para
este fin de semana|apuestas seguras para ganar dinero|apuestas
seguras para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para mañana|apuestas seguras
ruleta|apuestas seguras telegram|apuestas seguras tenis|apuestas
semifinales eurocopa|apuestas senegal paises bajos|apuestas
sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas sevilla campeon liga|apuestas sevilla celta|apuestas sevilla gana la liga|apuestas sevilla girona|apuestas sevilla inter|apuestas sevilla
jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas
sevilla madrid|apuestas sevilla manchester united|apuestas sevilla osasuna|apuestas
sevilla real madrid|apuestas sevilla real sociedad|apuestas sevilla roma|apuestas sevilla valencia|apuestas significa|apuestas simples ejemplos|apuestas simples o combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas
sin deposito minimo|apuestas sin dinero|apuestas sin dinero real|apuestas sin empate|apuestas sin empate que
significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas sistema
como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa
del rey|apuestas stake|apuestas stake 10|apuestas stake 10
hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas superliga argentina|apuestas tarjeta
roja|apuestas tarjetas|apuestas tarjetas amarillas|apuestas tenis|apuestas
tenis atp|apuestas tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis de
mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis hoy|apuestas
tenis itf|apuestas tenis pronosticos|apuestas tenis
pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas tenis seguras|apuestas tenis
wimbledon|apuestas tenis wta|apuestas tercera division|apuestas
tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para
hoy|apuestas topuria holloway cuotas|apuestas torneos de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas
uefa europa league|apuestas ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc
ilia topuria|apuestas ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc
topuria|apuestas under over|apuestas unionistas villarreal|apuestas uruguay|apuestas uruguay colombia|apuestas
uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia
barcelona|apuestas valencia betis|apuestas valencia madrid|apuestas
valencia real madrid|apuestas valladolid barcelona|apuestas
valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas
venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas
villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal
bayern|apuestas villarreal betis|apuestas villarreal liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs real
madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales futbol|apuestas virtuales
sin dinero|apuestas vivo|apuestas vuelta a españa|apuestas vuelta
españa|apuestas william hill partidos de hoy|apuestas
y casino|apuestas y casinos|apuestas y juegos de azar|apuestas y pronosticos|apuestas
y pronosticos de futbol|apuestas y pronosticos deportivos|apuestas y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina peru
apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs
chile apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united apuestas|athletic osasuna
apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de madrid apuestas|atlético
de madrid apuestas|atletico de madrid real madrid apuestas|atletico de madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico madrid
vs real madrid apuestas|atletico real madrid apuestas|atletico vs real madrid apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro
barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca madrid apuestas|barça madrid apuestas|barca vs atletico apuestas|barca vs madrid apuestas|barca
vs real madrid apuestas|barcelona – real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona atletico de madrid apuestas|barcelona atletico madrid apuestas|barcelona betis
apuestas|barcelona casa de apuestas|barcelona inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla apuestas|barcelona valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona vs
atlético madrid apuestas|barcelona vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs
girona apuestas|barcelona vs madrid apuestas|barcelona vs real madrid apuestas|barcelona vs real
sociedad apuestas|barcelona vs sevilla apuestas|barcelona vs villarreal apuestas|base de datos cuotas apuestas
deportivas|bayern real madrid apuestas|beisbol apuestas|best
america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea
apuestas|betis apuestas|betis barcelona apuestas|betis chelsea apuestas|betis
madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog apuestas baloncesto|blog apuestas ciclismo|blog apuestas nba|blog apuestas tenis|blog de apuestas de
tenis|bono apuestas|bono apuestas deportivas|bono apuestas deportivas sin deposito|bono
apuestas gratis|bono apuestas gratis sin deposito|bono apuestas sin deposito|bono bienvenida apuestas|bono bienvenida
apuestas deportivas|bono bienvenida apuestas españa|bono
bienvenida apuestas sin deposito|bono bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa
de apuestas|bono bienvenida marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de
bienvenida apuestas|bono de bienvenida apuestas deportivas|bono de bienvenida casa de apuestas|bono de bienvenida casas
de apuestas|bono de casas de apuestas|bono de registro apuestas|bono
de registro apuestas deportivas|bono de registro casa de apuestas|bono gratis apuestas|bono marca
apuestas|bono por registro apuestas|bono por registro apuestas deportivas|bono por
registro casa de apuestas|bono registro
apuestas|bono sin deposito apuestas|bono sin depósito apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas deportivas|bono sin deposito casa de
apuestas|bono sin deposito marca apuestas|bono sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos apuestas|bonos apuestas colombia|bonos apuestas deportivas|bonos apuestas deportivas sin deposito|bonos apuestas gratis|bonos
apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas apuestas|bonos bienvenida
casas de apuestas|bonos casa de apuestas|bonos casas apuestas|bonos casas de apuestas|bonos
casas de apuestas colombia|bonos casas de apuestas deportivas|bonos
casas de apuestas españa|bonos casas de
apuestas nuevas|bonos casas de apuestas
sin deposito|bonos casas de apuestas sin depósito|bonos de
apuestas|bonos de apuestas deportivas|bonos de apuestas gratis|bonos de apuestas sin deposito|bonos de bienvenida
apuestas|bonos de bienvenida apuestas deportivas|bonos de bienvenida
casa de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida
de casas de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de
casas de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos
gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas
de apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos
sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas de apuestas|bot de
apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil
peru apuestas|brasil vs colombia apuestas|buenas apuestas para hoy|buscador cuotas apuestas|buscador de apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de
apuestas|buscar apuestas seguras|caballos apuestas|calculador de
apuestas|calculador de cuotas apuestas|calculadora apuestas|calculadora apuestas combinadas|calculadora apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas deportivas
seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora
apuestas seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora
arbitraje apuestas|calculadora cubrir apuestas|calculadora cuotas apuestas|calculadora de
apuestas|calculadora de apuestas combinadas|calculadora
de apuestas de futbol|calculadora de apuestas de sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora de apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas
surebets|calculadora de arbitraje apuestas|calculadora de
cuotas apuestas|calculadora de cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake
apuestas|calculadora trading apuestas|calcular apuestas|calcular
apuestas deportivas|calcular apuestas futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular
cuotas apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular
momios apuestas|calcular probabilidad cuota apuestas|calcular stake apuestas|calcular unidades apuestas|calcular yield apuestas|calculo
de apuestas|calculo de apuestas deportivas|cambio de
cuotas apuestas|campeon champions apuestas|campeon eurocopa
apuestas|campeon liga apuestas|campeon nba apuestas|canales de
apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera de caballos con apuestas|carrera de galgos apuestas|carreras de caballos apuestas|carreras de caballos apuestas online|carreras de
caballos con apuestas|carreras de caballos juegos de apuestas|carreras de
galgos apuestas|carreras de galgos apuestas online|carreras de galgos
apuestas trucos|carreras galgos apuestas|casa
apuestas argentina|casa apuestas atletico de madrid|casa apuestas barcelona|casa apuestas
betis|casa apuestas bono bienvenida|casa apuestas bono gratis|casa apuestas bono sin deposito|casa apuestas cerca de mi|casa apuestas
chile|casa apuestas colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas española|casa apuestas eurocopa|casa apuestas futbol|casa
apuestas mejores cuotas|casa apuestas mundial|casa apuestas
nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa apuestas valencia|casa de apuestas|casa de apuestas 10 euros gratis|casa de apuestas argentina|casa de apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de apuestas bono|casa de
apuestas bono bienvenida|casa de apuestas bono de
bienvenida|casa de apuestas bono gratis|casa de apuestas bono por
registro|casa de apuestas bono sin deposito|casa de apuestas boxeo|casa de
apuestas caballos|casa de apuestas carreras de caballos|casa de apuestas cerca de mi|casa de apuestas cerca de mí|casa de apuestas champions league|casa de apuestas chile|casa de apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa de apuestas con bono
sin deposito|casa de apuestas con cuotas mas altas|casa de apuestas con esports|casa de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa
de apuestas con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa
de apuestas copa america|casa de apuestas de caballos|casa de apuestas de colombia|casa de
apuestas de españa|casa de apuestas de futbol|casa
de apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de apuestas del real madrid|casa de apuestas
deportivas|casa de apuestas deportivas cerca de mi|casa de apuestas deportivas en argentina|casa de apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa de apuestas deportivas en españa|casa
de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de apuestas deportivas españolas|casa de apuestas deportivas madrid|casa de apuestas deportivas
mexico|casa de apuestas deportivas online|casa de apuestas deportivas peru|casa de apuestas deposito
5 euros|casa de apuestas deposito minimo|casa de apuestas deposito minimo 1 euro|casa
de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas en linea|casa de apuestas en madrid|casa de apuestas
en perú|casa de apuestas en vivo|casa de apuestas españa|casa de apuestas españa inglaterra|casa de apuestas española|casa de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa
de apuestas europa league|casa de apuestas f1|casa de apuestas formula 1|casa
de apuestas futbol|casa de apuestas ingreso minimo|casa de apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa de apuestas
legales en colombia|casa de apuestas legales en españa|casa de apuestas libertadores|casa de apuestas liga
española|casa de apuestas madrid|casa de apuestas mas segura|casa de apuestas mejores|casa de apuestas
méxico|casa de apuestas minimo 5 euros|casa de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas nfl|casa
de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial
del real madrid|casa de apuestas oficial real madrid|casa
de apuestas online|casa de apuestas online argentina|casa de apuestas online chile|casa de apuestas online españa|casa de apuestas online mexico|casa de apuestas online paraguay|casa de apuestas online peru|casa
de apuestas online usa|casa de apuestas online venezuela|casa de apuestas pago anticipado|casa de apuestas para boxeo|casa de apuestas para ufc|casa
de apuestas peru|casa de apuestas perú|casa de apuestas peru
online|casa de apuestas por paypal|casa de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de bienvenida|casa de apuestas sevilla|casa de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa de apuestas sin licencia en españa|casa de apuestas sin minimo de ingreso|casa de apuestas stake|casa de apuestas tenis|casa de apuestas
ufc|casa de apuestas valencia|casa de apuestas venezuela|casa de apuestas
virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del
real madrid|casas apuestas asiaticas|casas apuestas bono sin deposito|casas
apuestas bonos sin deposito|casas apuestas caballos|casas apuestas chile|casas apuestas ciclismo|casas apuestas
con licencia|casas apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas
colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas
ingreso minimo 5 euros|casas apuestas legales|casas apuestas legales españa|casas apuestas licencia|casas apuestas licencia españa|casas apuestas mexico|casas apuestas mundial|casas apuestas nba|casas
apuestas nuevas|casas apuestas nuevas españa|casas apuestas ofertas|casas apuestas online|casas apuestas paypal|casas apuestas peru|casas apuestas sin licencia|casas apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de apuestas 5 euros|casas de apuestas
app|casas de apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas de apuestas barcelona|casas de apuestas bono bienvenida|casas de
apuestas bono de bienvenida|casas de apuestas bono por registro|casas de apuestas bono sin deposito|casas de apuestas bono sin ingreso|casas de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas de
apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas
de apuestas carreras de caballos|casas de apuestas casino|casas de
apuestas casino online|casas de apuestas cerca
de mi|casas de apuestas champions league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas
de apuestas com|casas de apuestas con app|casas de apuestas con apuestas gratis|casas de
apuestas con bono|casas de apuestas con bono de bienvenida|casas de apuestas con bono
de registro|casas de apuestas con bono por registro|casas de apuestas con bono sin deposito|casas de apuestas con bonos|casas
de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas con deposito minimo|casas
de apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas de apuestas con licencia en españa|casas
de apuestas con licencia españa|casas de apuestas con licencia española|casas de apuestas con mejores cuotas|casas de apuestas con pago
anticipado|casas de apuestas con paypal|casas de apuestas con paypal en perú|casas de apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa
del rey|casas de apuestas de caballos|casas
de apuestas de españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas de apuestas de peru|casas de
apuestas deportivas|casas de apuestas deportivas asiaticas|casas de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas de apuestas deportivas con paypal|casas
de apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de apuestas deportivas en mexico|casas de apuestas deportivas en peru|casas de apuestas deportivas en sevilla|casas de
apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de apuestas deportivas españolas|casas
de apuestas deportivas legales|casas de apuestas deportivas madrid|casas de apuestas deportivas mexico|casas de apuestas deportivas nuevas|casas de apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas deportivas perú|casas de apuestas deposito
minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de
apuestas dinero gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas de
apuestas en chile|casas de apuestas en colombia|casas de apuestas
en españa|casas de apuestas en españa online|casas de apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas de apuestas en peru|casas de apuestas en perú|casas de apuestas en sevilla|casas de apuestas en uruguay|casas de
apuestas en valencia|casas de apuestas en venezuela|casas de apuestas equipos de futbol|casas de apuestas españa|casas de
apuestas españa alemania|casas de apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas de apuestas españa online|casas de apuestas española|casas de apuestas españolas|casas de apuestas españolas con licencia|casas de apuestas españolas online|casas de apuestas esports|casas
de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas de apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas
en españa|casas de apuestas formula 1|casas de apuestas
fuera de españa|casas de apuestas futbol|casas de apuestas fútbol|casas de apuestas futbol españa|casas
de apuestas ganador eurocopa|casas de apuestas gratis|casas de apuestas ingreso minimo|casas de apuestas ingreso minimo 1 euro|casas de apuestas ingreso minimo 5 euros|casas de apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales en colombia|casas
de apuestas legales en españa|casas de apuestas
legales en mexico|casas de apuestas legales españa|casas de apuestas legales
mx|casas de apuestas licencia|casas de apuestas licencia españa|casas
de apuestas lista|casas de apuestas madrid|casas de apuestas mas seguras|casas de apuestas mejores bonos|casas de apuestas
mejores cuotas|casas de apuestas mexico|casas de apuestas méxico|casas de apuestas minimo 5 euros|casas de
apuestas mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas mundiales|casas
de apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva
ley|casas de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de
apuestas ofertas|casas de apuestas online|casas de apuestas online argentina|casas de apuestas online colombia|casas de apuestas online deportivas|casas de apuestas online ecuador|casas de apuestas online en argentina|casas de apuestas online en chile|casas de apuestas online en colombia|casas de apuestas online
en españa|casas de apuestas online en mexico|casas de apuestas online españa|casas de apuestas
online mas fiables|casas de apuestas online mexico|casas de apuestas online nuevas|casas de apuestas online peru|casas de apuestas online usa|casas de apuestas online venezuela|casas de apuestas pago
paypal|casas de apuestas para ufc|casas de apuestas paypal|casas
de apuestas peru bono sin deposito|casas de apuestas presenciales en españa|casas de
Je suis emerveille par Lucky 31 Casino, on y trouve une energie contagieuse. La gamme est variee et attrayante, offrant des sessions live palpitantes. Il propulse votre jeu des le debut. Le support est pro et accueillant. Les retraits sont simples et rapides, de temps a autre des offres plus consequentes seraient parfaites. Pour finir, Lucky 31 Casino merite un detour palpitant. Pour completer le site est rapide et style, incite a prolonger le plaisir. Particulierement cool les evenements communautaires dynamiques, offre des bonus constants.
Visiter aujourd’hui|
J’adore le dynamisme de Azur Casino, il procure une sensation de frisson. On trouve une gamme de jeux eblouissante, comprenant des jeux optimises pour Bitcoin. 100% jusqu’a 500 € plus des tours gratuits. Le support est fiable et reactif. Les retraits sont lisses comme jamais, de temps en temps des recompenses additionnelles seraient ideales. Dans l’ensemble, Azur Casino assure un divertissement non-stop. Pour ajouter le design est moderne et energique, ajoute une touche de dynamisme. Un avantage le programme VIP avec des niveaux exclusifs, qui booste la participation.
Plongez-y|
1xbet tr giri? https://www.1xbet-7.com .
J’adore l’ambiance electrisante de Lucky 31 Casino, on y trouve une vibe envoutante. Il y a un eventail de titres captivants, incluant des paris sportifs pleins de vie. Il amplifie le plaisir des l’entree. Le service est disponible 24/7. Les paiements sont securises et rapides, par ailleurs des offres plus consequentes seraient parfaites. Pour finir, Lucky 31 Casino est un must pour les passionnes. En extra la plateforme est visuellement electrisante, amplifie l’adrenaline du jeu. Particulierement attrayant les transactions crypto ultra-securisees, propose des avantages uniques.
Obtenir des infos|
Je suis emerveille par Action Casino, on ressent une ambiance de fete. Le catalogue de titres est vaste, offrant des sessions live immersives. Il booste votre aventure des le depart. Les agents repondent avec rapidite. Le processus est transparent et rapide, par contre des bonus diversifies seraient un atout. En bref, Action Casino merite un detour palpitant. A souligner l’interface est fluide comme une soiree, incite a prolonger le plaisir. Particulierement interessant le programme VIP avec des recompenses exclusives, cree une communaute vibrante.
Aller sur le web|
Je suis enthousiasme par 1xBet Casino, ca invite a plonger dans le fun. Le choix est aussi large qu’un festival, offrant des sessions live immersives. 100% jusqu’a 500 € plus des tours gratuits. Le suivi est impeccable. Les retraits sont simples et rapides, rarement plus de promotions frequentes boosteraient l’experience. Pour conclure, 1xBet Casino est un choix parfait pour les joueurs. De plus le design est tendance et accrocheur, booste l’excitation du jeu. Un point fort les options de paris sportifs variees, qui booste la participation.
Obtenir des infos|
где согласовать перепланировку квартиры http://www.soglasovanie-pereplanirovki-1.ru .
Je suis fascine par Azur Casino, on ressent une ambiance festive. Les options sont aussi vastes qu’un horizon, proposant des jeux de cartes elegants. 100% jusqu’a 500 € plus des tours gratuits. Les agents sont toujours la pour aider. Les gains arrivent sans delai, en revanche des offres plus genereuses rendraient l’experience meilleure. Globalement, Azur Casino est un choix parfait pour les joueurs. A mentionner l’interface est intuitive et fluide, facilite une immersion totale. A noter le programme VIP avec des avantages uniques, qui motive les joueurs.
Voir maintenant|
sure win online casino http://www.surewin-online.com .
beep beep casino регистрация https://beepbeepcasino-online.com/ .
Je suis enthousiaste a propos de Lucky 31 Casino, ca offre un plaisir vibrant. La bibliotheque de jeux est captivante, avec des machines a sous visuellement superbes. 100% jusqu’a 500 € avec des spins gratuits. Le support est rapide et professionnel. Les transactions sont toujours securisees, a l’occasion des recompenses supplementaires seraient parfaites. En resume, Lucky 31 Casino est une plateforme qui fait vibrer. En plus le site est rapide et immersif, ajoute une vibe electrisante. Un element fort les paiements en crypto rapides et surs, renforce la communaute.
http://www.casinolucky31fr.com|
J’adore le dynamisme de 1xBet Casino, on ressent une ambiance de fete. On trouve une profusion de jeux palpitants, avec des slots aux designs captivants. 100% jusqu’a 500 € plus des tours gratuits. Les agents sont toujours la pour aider. Les paiements sont surs et fluides, quelquefois des bonus diversifies seraient un atout. En somme, 1xBet Casino est un lieu de fun absolu. A mentionner le site est rapide et engageant, ajoute une touche de dynamisme. Un bonus les transactions en crypto fiables, cree une communaute soudee.
Plongez-y|
Je suis epate par Action Casino, ca transporte dans un univers de plaisirs. Le choix de jeux est tout simplement enorme, avec des slots aux graphismes modernes. Avec des depots rapides et faciles. Le support est rapide et professionnel. Les paiements sont surs et efficaces, a l’occasion des bonus plus frequents seraient un hit. En bref, Action Casino est une plateforme qui fait vibrer. A mentionner la navigation est intuitive et lisse, ce qui rend chaque session plus excitante. Un atout les evenements communautaires engageants, propose des avantages uniques.
Poursuivre la lecture|
https://shorturl.fm/GjKj6
(10 euros gratis apuestas|10 mejores casas de apuestas|10 trucos para ganar apuestas|15
euros gratis marca apuestas|1×2 apuestas|1×2 apuestas deportivas|1×2 apuestas que significa|1×2 en apuestas|1×2 en apuestas que significa|1×2 que significa en apuestas|5 euros gratis apuestas|9 apuestas que
siempre ganaras|a partir de cuanto se declara apuestas|actividades de juegos de
azar y apuestas|ad apuestas deportivas|aleksandre
topuria ufc apuestas|algoritmo para ganar apuestas deportivas|america apuestas|análisis nba apuestas|aplicacion android apuestas deportivas|aplicacion apuestas deportivas|aplicacion apuestas deportivas android|aplicación de apuestas online|aplicacion para hacer apuestas|aplicacion para hacer apuestas
de futbol|aplicación para hacer apuestas de fútbol|aplicaciones apuestas deportivas android|aplicaciones
apuestas deportivas gratis|aplicaciones de apuestas android|aplicaciones de apuestas de fútbol|aplicaciones de apuestas deportivas|aplicaciones de apuestas deportivas peru|aplicaciones de apuestas deportivas perú|aplicaciones de apuestas en colombia|aplicaciones
de apuestas gratis|aplicaciones de apuestas online|aplicaciones de apuestas seguras|aplicaciones
de apuestas sin dinero|aplicaciones para hacer apuestas|apostar seguro apuestas deportivas|app android apuestas deportivas|app apuestas|app apuestas android|app apuestas de futbol|app apuestas deportivas|app apuestas
deportivas android|app apuestas deportivas argentina|app apuestas deportivas colombia|app apuestas deportivas ecuador|app apuestas deportivas españa|app apuestas deportivas
gratis|app apuestas entre amigos|app apuestas futbol|app apuestas gratis|app
apuestas sin dinero|app casa de apuestas|app casas de apuestas|app control apuestas|app
de apuestas|app de apuestas android|app de apuestas casino|app de
apuestas colombia|app de apuestas con bono de bienvenida|app de apuestas de futbol|app de apuestas deportivas|app de apuestas deportivas android|app de apuestas deportivas argentina|app de apuestas deportivas colombia|app de apuestas deportivas en españa|app de
apuestas deportivas peru|app de apuestas deportivas perú|app de apuestas deportivas sin dinero|app de apuestas ecuador|app de apuestas en colombia|app de apuestas en españa|app de apuestas en venezuela|app de apuestas futbol|app de apuestas
gratis|app de apuestas online|app de apuestas para android|app de apuestas para ganar dinero|app de apuestas peru|app de apuestas reales|app de casas de apuestas|app
marca apuestas android|app moviles de apuestas|app para
apuestas|app para apuestas de futbol|app para apuestas deportivas|app para apuestas deportivas en español|app para ganar apuestas deportivas|app para hacer apuestas|app para
hacer apuestas deportivas|app para hacer apuestas entre amigos|app para llevar control de apuestas|app
pronosticos apuestas deportivas|app versus apuestas|apps apuestas mundial|apps de apuestas|apps de apuestas con bono
de bienvenida|apps de apuestas de futbol|apps de apuestas
deportivas peru|apps de apuestas mexico|apps para apuestas|aprender a hacer
apuestas deportivas|aprender hacer apuestas deportivas|apuesta del dia apuestas deportivas|apuestas 10 euros gratis|apuestas 100 seguras|apuestas 1×2|apuestas 1X2|apuestas 2 division|apuestas 3
division|apuestas a caballos|apuestas a carreras de caballos|apuestas a
colombia|apuestas a corners|apuestas a ganar|apuestas a jugadores nba|apuestas
a la baja|apuestas a la nfl|apuestas al barcelona|apuestas al dia|apuestas
al empate|apuestas al mundial|apuestas al tenis wta|apuestas alaves barcelona|apuestas alcaraz hoy|apuestas alemania españa|apuestas alonso
campeon del mundo|apuestas altas y bajas|apuestas altas y bajas nfl|apuestas ambos equipos marcan|apuestas america|apuestas
android|apuestas anillo nba|apuestas antes del mundial|apuestas anticipadas|apuestas anticipadas nba|apuestas apps|apuestas arabia argentina|apuestas argentina|apuestas argentina campeon del
mundo|apuestas argentina canada|apuestas argentina colombia|apuestas argentina croacia|apuestas argentina españa|apuestas argentina
francia|apuestas argentina francia cuanto paga|apuestas argentina francia mundial|apuestas argentina
gana el mundial|apuestas argentina gana mundial|apuestas argentina holanda|apuestas argentina mexico|apuestas argentina méxico|apuestas argentina
mundial|apuestas argentina online|apuestas argentina paises bajos|apuestas
argentina polonia|apuestas argentina uruguay|apuestas
argentina vs australia|apuestas argentina vs colombia|apuestas argentina vs francia|apuestas argentina vs peru|apuestas argentinas|apuestas arsenal real madrid|apuestas ascenso a primera
division|apuestas ascenso a segunda|apuestas asiaticas|apuestas asiatico|apuestas athletic|apuestas athletic atletico|apuestas athletic barça|apuestas athletic barcelona|apuestas athletic betis|apuestas athletic manchester|apuestas
athletic manchester united|apuestas athletic osasuna|apuestas athletic
real|apuestas athletic real madrid|apuestas athletic real sociedad|apuestas
athletic real sociedad final|apuestas athletic roma|apuestas athletic sevilla|apuestas athletic
valencia|apuestas atletico|apuestas atletico barcelona|apuestas atletico barsa|apuestas atletico campeon champions|apuestas atletico campeon de liga|apuestas atlético copenhague|apuestas atletico de madrid|apuestas atlético de madrid|apuestas atletico de madrid barcelona|apuestas atletico de madrid gana la liga|apuestas atletico de
madrid real madrid|apuestas atlético de madrid real madrid|apuestas atletico de madrid vs barcelona|apuestas atletico madrid|apuestas atletico madrid real madrid|apuestas atletico madrid vs barcelona|apuestas atletico real madrid|apuestas atletico real madrid champions|apuestas atletismo|apuestas bajas|apuestas baloncesto|apuestas baloncesto acb|apuestas
baloncesto handicap|apuestas baloncesto hoy|apuestas baloncesto juegos olimpicos|apuestas
baloncesto nba|apuestas baloncesto pronostico|apuestas baloncesto pronósticos|apuestas baloncesto prorroga|apuestas barca|apuestas barca athletic|apuestas barca atletico|apuestas barca bayern|apuestas barca bayern munich|apuestas barca girona|apuestas barca
hoy|apuestas barça hoy|apuestas barca inter|apuestas barca juventus|apuestas
barca madrid|apuestas barça madrid|apuestas barca real madrid|apuestas barca vs juve|apuestas barca vs madrid|apuestas barca vs psg|apuestas barcelona|apuestas barcelona alaves|apuestas barcelona athletic|apuestas barcelona
atletico|apuestas barcelona atletico de madrid|apuestas
barcelona atlético de madrid|apuestas barcelona atletico madrid|apuestas barcelona bayern|apuestas barcelona betis|apuestas barcelona campeon de liga|apuestas
barcelona celta|apuestas barcelona espanyol|apuestas barcelona gana
la champions|apuestas barcelona girona|apuestas barcelona granada|apuestas barcelona hoy|apuestas barcelona inter|apuestas barcelona madrid|apuestas barcelona osasuna|apuestas barcelona psg|apuestas barcelona real madrid|apuestas barcelona real sociedad|apuestas barcelona sevilla|apuestas
barcelona valencia|apuestas barcelona villarreal|apuestas barcelona vs atletico madrid|apuestas
barcelona vs madrid|apuestas barcelona vs real madrid|apuestas barsa madrid|apuestas basket hoy|apuestas bayern barcelona|apuestas bayern vs barcelona|apuestas beisbol|apuestas béisbol|apuestas beisbol mlb|apuestas
beisbol pronosticos|apuestas beisbol venezolano|apuestas betis|apuestas betis – chelsea|apuestas
betis barcelona|apuestas betis chelsea|apuestas
betis fiorentina|apuestas betis girona|apuestas betis madrid|apuestas betis mallorca|apuestas betis real madrid|apuestas betis real sociedad|apuestas betis sevilla|apuestas betis valencia|apuestas betis valladolid|apuestas betis vs
valencia|apuestas betplay hoy colombia|apuestas betsson peru|apuestas
bienvenida|apuestas billar online|apuestas bolivia vs colombia|apuestas bono|apuestas bono
bienvenida|apuestas bono de bienvenida|apuestas bono de
bienvenida sin deposito|apuestas bono gratis|apuestas bono sin deposito|apuestas bonos sin deposito|apuestas borussia
real madrid|apuestas boxeo|apuestas boxeo de campeonato|apuestas boxeo españa|apuestas boxeo español|apuestas boxeo femenino olimpiadas|apuestas boxeo hoy|apuestas boxeo online|apuestas brasil colombia|apuestas brasil peru|apuestas
brasil uruguay|apuestas brasil vs colombia|apuestas brasil vs peru|apuestas caballos|apuestas caballos
colocado|apuestas caballos españa|apuestas caballos hipodromo|apuestas caballos hoy|apuestas caballos madrid|apuestas caballos
online|apuestas caballos sanlucar de barrameda|apuestas caballos zarzuela|apuestas calculador|apuestas campeon|apuestas campeon champions|apuestas campeón champions|apuestas campeon champions 2025|apuestas campeon champions league|apuestas campeon conference league|apuestas
campeon copa america|apuestas campeon copa del rey|apuestas campeon de champions|apuestas
campeon de la champions|apuestas campeon de liga|apuestas campeon del mundo|apuestas campeon eurocopa|apuestas campeón eurocopa|apuestas campeon europa league|apuestas
campeon f1|apuestas campeon f1 2025|apuestas campeon formula 1|apuestas campeon libertadores|apuestas campeon liga|apuestas campeon liga bbva|apuestas campeon liga española|apuestas campeon liga
santander|apuestas campeon motogp 2025|apuestas campeon mundial|apuestas
campeón mundial|apuestas campeon mundial baloncesto|apuestas campeon nba|apuestas campeón nba|apuestas campeon premier|apuestas campeon premier league|apuestas campeon roland garros|apuestas campeonato f1|apuestas campeonatos de futbol|apuestas carrera
de caballos|apuestas carrera de caballos hoy|apuestas
carrera de caballos nocturnas|apuestas carrera de galgos fin de
semana|apuestas carrera de galgos hoy|apuestas carrera de galgos nocturnas|apuestas carreras caballos|apuestas carreras
caballos sanlucar|apuestas carreras de caballos|apuestas
carreras de caballos en directo|apuestas carreras de
caballos en vivo|apuestas carreras de caballos españa|apuestas carreras de caballos hoy|apuestas
carreras de caballos nacionales|apuestas carreras de caballos
nocturnas|apuestas carreras de caballos online|apuestas carreras
de caballos sanlucar|apuestas carreras de caballos sanlúcar|apuestas
carreras de galgos|apuestas carreras de galgos en vivo|apuestas carreras de galgos nocturnas|apuestas carreras de galgos pre partido|apuestas casino|apuestas casino barcelona|apuestas casino futbol|apuestas casino gran madrid|apuestas casino gratis|apuestas casino madrid|apuestas
casino online|apuestas casino online argentina|apuestas
casinos|apuestas casinos online|apuestas celta|apuestas celta
barcelona|apuestas celta betis|apuestas celta eibar|apuestas celta espanyol|apuestas
celta granada|apuestas celta madrid|apuestas celta manchester|apuestas celta real madrid|apuestas champion league|apuestas champions foro|apuestas champions hoy|apuestas champions league|apuestas champions
league – pronósticos|apuestas champions league 2025|apuestas champions league hoy|apuestas champions league pronosticos|apuestas champions league pronósticos|apuestas
champions pronosticos|apuestas chelsea barcelona|apuestas chelsea betis|apuestas chile|apuestas chile peru|apuestas chile venezuela|apuestas chile vs colombia|apuestas chile vs uruguay|apuestas ciclismo|apuestas
ciclismo en vivo|apuestas ciclismo femenino|apuestas ciclismo tour francia|apuestas ciclismo vuelta|apuestas ciclismo vuelta a
españa|apuestas ciclismo vuelta españa|apuestas city madrid|apuestas city real madrid|apuestas clasico|apuestas clasico español|apuestas clasico real madrid barcelona|apuestas clasificacion mundial|apuestas colombia|apuestas colombia
argentina|apuestas colombia brasil|apuestas colombia paraguay|apuestas colombia uruguay|apuestas colombia vs argentina|apuestas colombia vs brasil|apuestas
combinadas|apuestas combinadas como funcionan|apuestas combinadas de futbol|apuestas combinadas de
fútbol|apuestas combinadas foro|apuestas combinadas futbol|apuestas combinadas hoy|apuestas combinadas mismo
partido|apuestas combinadas mundial|apuestas combinadas nba|apuestas combinadas para esta semana|apuestas combinadas para hoy|apuestas combinadas para mañana|apuestas combinadas pronosticos|apuestas combinadas recomendadas|apuestas combinadas seguras|apuestas combinadas seguras para hoy|apuestas combinadas seguras para mañana|apuestas como
ganar|apuestas comparador|apuestas con bono de bienvenida|apuestas con dinero
ficticio|apuestas con dinero real|apuestas con dinero virtual|apuestas con handicap|apuestas con handicap asiatico|apuestas con handicap baloncesto|apuestas con mas
probabilidades de ganar|apuestas con paypal|apuestas
con tarjeta de credito|apuestas con tarjeta de debito|apuestas consejos|apuestas copa|apuestas copa africa|apuestas copa america|apuestas copa américa|apuestas copa argentina|apuestas copa
brasil|apuestas copa davis|apuestas copa de europa|apuestas copa del
mundo|apuestas copa del rey|apuestas copa del rey baloncesto|apuestas copa del rey final|apuestas copa del rey futbol|apuestas copa del rey ganador|apuestas copa del rey hoy|apuestas copa del rey pronosticos|apuestas copa del rey pronósticos|apuestas copa
europa|apuestas copa italia|apuestas copa libertadores|apuestas copa mundial de hockey|apuestas copa rey|apuestas copa sudamericana|apuestas corners|apuestas
corners hoy|apuestas croacia argentina|apuestas cuartos eurocopa|apuestas cuotas|apuestas cuotas altas|apuestas cuotas bajas|apuestas de 1 euro|apuestas de baloncesto|apuestas de baloncesto hoy|apuestas de baloncesto nba|apuestas de baloncesto para hoy|apuestas
de beisbol|apuestas de beisbol para hoy|apuestas de
blackjack en linea|apuestas de boxeo|apuestas de boxeo canelo|apuestas de boxeo en las vegas|apuestas de boxeo
hoy|apuestas de boxeo online|apuestas de caballo|apuestas
de caballos|apuestas de caballos como funciona|apuestas de caballos como se
juega|apuestas de caballos en colombia|apuestas de caballos en españa|apuestas de caballos en linea|apuestas
de caballos españa|apuestas de caballos ganador y colocado|apuestas de
caballos internacionales|apuestas de caballos
juegos|apuestas de caballos online|apuestas de caballos online en venezuela|apuestas de caballos por internet|apuestas
de caballos pronosticos|apuestas de caballos pronósticos|apuestas de carrera de caballos|apuestas de
carreras de caballos|apuestas de carreras de caballos online|apuestas de casino|apuestas de
casino online|apuestas de casino por internet|apuestas de champions league|apuestas de
ciclismo|apuestas de colombia|apuestas de copa america|apuestas de corners|apuestas de deportes en linea|apuestas de deportes online|apuestas de dinero|apuestas de esports|apuestas de eurocopa|apuestas de
europa league|apuestas de f1|apuestas de formula 1|apuestas de futbol|apuestas de fútbol|apuestas de futbol app|apuestas de futbol argentina|apuestas de futbol colombia|apuestas de futbol en colombia|apuestas
de futbol en directo|apuestas de futbol en linea|apuestas de futbol en vivo|apuestas de futbol español|apuestas de futbol gratis|apuestas de
futbol hoy|apuestas de futbol mundial|apuestas de futbol online|apuestas de fútbol online|apuestas de futbol para hoy|apuestas de fútbol para hoy|apuestas de
futbol para hoy seguras|apuestas de futbol para mañana|apuestas de
futbol peru|apuestas de futbol pronosticos|apuestas de fútbol pronósticos|apuestas de futbol seguras|apuestas de futbol seguras para hoy|apuestas de futbol sin dinero|apuestas de galgos|apuestas
de galgos como ganar|apuestas de galgos en directo|apuestas de
galgos online|apuestas de galgos trucos|apuestas de golf|apuestas de hockey|apuestas
de hockey sobre hielo|apuestas de hoy|apuestas de hoy seguras|apuestas de
juego|apuestas de juegos|apuestas de juegos deportivos|apuestas de juegos online|apuestas de la champions league|apuestas de la copa américa|apuestas de la
eurocopa|apuestas de la europa league|apuestas de la liga|apuestas de la liga bbva|apuestas de la liga española|apuestas de la nba|apuestas de la nfl|apuestas de la ufc|apuestas de mlb|apuestas de nba|apuestas
de nba para hoy|apuestas de partidos|apuestas
de partidos de futbol|apuestas de peleas ufc|apuestas de perros en vivo|apuestas
de perros virtuales|apuestas de peru|apuestas de sistema|apuestas de sistema como funciona|apuestas de sistema explicacion|apuestas de sistema explicación|apuestas de tenis|apuestas
de tenis de mesa|apuestas de tenis en directo|apuestas de tenis hoy|apuestas de tenis para hoy|apuestas de tenis pronosticos|apuestas de tenis seguras|apuestas de todo
tipo|apuestas de ufc|apuestas de ufc hoy|apuestas del boxeo|apuestas del clasico|apuestas
del clasico real madrid barca|apuestas del dia|apuestas del día|apuestas del dia
de hoy|apuestas del dia deportivas|apuestas del dia futbol|apuestas del mundial|apuestas del
partido de hoy|apuestas del real madrid|apuestas del rey|apuestas
del sistema|apuestas deporte|apuestas deportes|apuestas deportiva|apuestas deportivas|apuestas deportivas 1 euro|apuestas deportivas 10 euros gratis|apuestas deportivas 100 seguras|apuestas deportivas 1×2|apuestas
deportivas android|apuestas deportivas app|apuestas deportivas apps|apuestas deportivas argentina|apuestas deportivas argentina futbol|apuestas deportivas argentina legal|apuestas
deportivas atletico de madrid|apuestas deportivas baloncesto|apuestas deportivas barca
madrid|apuestas deportivas barcelona|apuestas deportivas beisbol|apuestas deportivas bono|apuestas
deportivas bono bienvenida|apuestas deportivas bono
de bienvenida|apuestas deportivas bono sin deposito|apuestas deportivas bonos
de bienvenida|apuestas deportivas boxeo|apuestas deportivas caballos|apuestas deportivas calculadora|apuestas deportivas campeon liga|apuestas deportivas casino|apuestas deportivas casino barcelona|apuestas
deportivas casino online|apuestas deportivas cerca de mi|apuestas deportivas champions league|apuestas deportivas chile|apuestas
deportivas ciclismo|apuestas deportivas colombia|apuestas deportivas com|apuestas deportivas com foro|apuestas deportivas
com pronosticos|apuestas deportivas combinadas|apuestas deportivas combinadas para hoy|apuestas deportivas
como se juega|apuestas deportivas comparador|apuestas deportivas con bono gratis|apuestas deportivas con bonos gratis|apuestas deportivas con dinero ficticio|apuestas deportivas con paypal|apuestas
deportivas con puntos virtuales|apuestas deportivas consejos|apuestas deportivas consejos para ganar|apuestas
deportivas copa america|apuestas deportivas copa
del rey|apuestas deportivas copa libertadores|apuestas deportivas copa mundial|apuestas deportivas corners|apuestas
deportivas cual es la mejor|apuestas deportivas cuotas altas|apuestas deportivas
de baloncesto|apuestas deportivas de boxeo|apuestas deportivas de colombia|apuestas deportivas de futbol|apuestas deportivas de nba|apuestas deportivas de
nhl|apuestas deportivas de peru|apuestas deportivas de tenis|apuestas deportivas del
dia|apuestas deportivas dinero ficticio|apuestas deportivas directo|apuestas deportivas doble oportunidad|apuestas deportivas en argentina|apuestas deportivas en chile|apuestas deportivas en colombia|apuestas deportivas en directo|apuestas deportivas en españa|apuestas
deportivas en español|apuestas deportivas en linea|apuestas deportivas en línea|apuestas deportivas en peru|apuestas deportivas en perú|apuestas
deportivas en sevilla|apuestas deportivas en uruguay|apuestas deportivas en vivo|apuestas deportivas
es|apuestas deportivas es pronosticos|apuestas deportivas españa|apuestas deportivas españolas|apuestas deportivas esports|apuestas deportivas estadisticas|apuestas deportivas estrategias|apuestas deportivas
estrategias seguras|apuestas deportivas eurocopa|apuestas deportivas
europa league|apuestas deportivas f1|apuestas deportivas faciles de ganar|apuestas deportivas formula
1|apuestas deportivas foro|apuestas deportivas foro futbol|apuestas deportivas foro tenis|apuestas deportivas francia argentina|apuestas deportivas futbol|apuestas deportivas fútbol|apuestas deportivas futbol argentino|apuestas deportivas futbol colombia|apuestas deportivas futbol español|apuestas deportivas
gana|apuestas deportivas ganadas|apuestas deportivas ganar dinero
seguro|apuestas deportivas gane|apuestas deportivas
golf|apuestas deportivas gratis|apuestas deportivas gratis con premios|apuestas
deportivas gratis hoy|apuestas deportivas gratis sin deposito|apuestas deportivas handicap|apuestas deportivas handicap asiatico|apuestas deportivas hoy|apuestas
deportivas impuestos|apuestas deportivas interior argentina|apuestas deportivas juegos olimpicos|apuestas deportivas la liga|apuestas deportivas legales|apuestas deportivas legales en colombia|apuestas deportivas libres
de impuestos|apuestas deportivas licencia españa|apuestas deportivas liga
española|apuestas deportivas listado|apuestas deportivas
listado clasico|apuestas deportivas madrid|apuestas deportivas
mas seguras|apuestas deportivas mejor pagadas|apuestas deportivas
mejores|apuestas deportivas mejores app|apuestas deportivas mejores casas|apuestas deportivas mejores cuotas|apuestas deportivas mejores paginas|apuestas deportivas
mexico|apuestas deportivas méxico|apuestas deportivas mlb|apuestas deportivas mlb hoy|apuestas deportivas multiples|apuestas deportivas mundial|apuestas deportivas murcia|apuestas deportivas nba|apuestas deportivas nba hoy|apuestas
deportivas nfl|apuestas deportivas nhl|apuestas deportivas nuevas|apuestas deportivas
ofertas|apuestas deportivas online|apuestas deportivas online argentina|apuestas deportivas online
chile|apuestas deportivas online colombia|apuestas deportivas
online en colombia|apuestas deportivas online españa|apuestas
deportivas online mexico|apuestas deportivas online
paypal|apuestas deportivas online peru|apuestas deportivas online por internet|apuestas deportivas
pago paypal|apuestas deportivas para ganar dinero|apuestas deportivas para
hoy|apuestas deportivas para hoy pronosticos|apuestas deportivas partido suspendido|apuestas deportivas partidos
de hoy|apuestas deportivas paypal|apuestas deportivas peru|apuestas deportivas perú|apuestas deportivas
peru vs ecuador|apuestas deportivas predicciones|apuestas deportivas promociones|apuestas deportivas pronostico|apuestas deportivas pronóstico|apuestas deportivas
pronostico hoy|apuestas deportivas pronosticos|apuestas
deportivas pronósticos|apuestas deportivas pronosticos expertos|apuestas deportivas pronosticos gratis|apuestas deportivas pronosticos nba|apuestas deportivas pronosticos tenis|apuestas deportivas que aceptan paypal|apuestas deportivas real madrid|apuestas deportivas regalo
bienvenida|apuestas deportivas resultado exacto|apuestas deportivas resultados|apuestas deportivas
rugby|apuestas deportivas seguras|apuestas deportivas seguras foro|apuestas deportivas seguras hoy|apuestas deportivas seguras para hoy|apuestas deportivas seguras telegram|apuestas deportivas sevilla|apuestas
deportivas simulador eurocopa|apuestas deportivas sin deposito|apuestas deportivas sin deposito inicial|apuestas deportivas sin dinero|apuestas deportivas sin dinero real|apuestas deportivas sin registro|apuestas deportivas stake|apuestas deportivas stake 10|apuestas deportivas telegram españa|apuestas deportivas tenis|apuestas
deportivas tenis de mesa|apuestas deportivas tenis foro|apuestas deportivas tenis hoy|apuestas deportivas tips|apuestas deportivas tipster|apuestas deportivas ufc|apuestas
deportivas uruguay|apuestas deportivas valencia|apuestas deportivas
valencia barcelona|apuestas deportivas venezuela|apuestas deportivas virtuales|apuestas deportivas y casino|apuestas deportivas
y casino online|apuestas deportivas.com|apuestas deportivas.com foro|apuestas
deportivas.es|apuestas deportivos pronosticos|apuestas deposito minimo
1 euro|apuestas descenso a segunda|apuestas descenso a segunda b|apuestas descenso la
liga|apuestas descenso primera division|apuestas descenso segunda|apuestas dia|apuestas diarias seguras|apuestas dinero|apuestas dinero ficticio|apuestas dinero real|apuestas dinero virtual|apuestas directas|apuestas
directo|apuestas directo futbol|apuestas division de honor juvenil|apuestas dnb|apuestas doble oportunidad|apuestas doble resultado|apuestas dobles|apuestas dobles y
triples|apuestas dortmund barcelona|apuestas
draft nba|apuestas draft nfl|apuestas ecuador vs argentina|apuestas ecuador vs venezuela|apuestas egipto uruguay|apuestas el
clasico|apuestas elecciones venezuela|apuestas empate|apuestas en baloncesto|apuestas en barcelona|apuestas en beisbol|apuestas en boxeo|apuestas en caballos|apuestas en carreras de caballos|apuestas en casino|apuestas en casino online|apuestas
en casinos|apuestas en casinos online|apuestas en chile|apuestas en ciclismo|apuestas en colombia|apuestas en colombia de futbol|apuestas en directo|apuestas en directo futbol|apuestas en directo pronosticos|apuestas en el futbol|apuestas
en el tenis|apuestas en españa|apuestas en esports|apuestas en eventos deportivos virtuales|apuestas
en golf|apuestas en juegos|apuestas en la champions league|apuestas en la
eurocopa|apuestas en la liga|apuestas en la nba|apuestas en la nfl|apuestas en las vegas mlb|apuestas en las vegas nfl|apuestas en linea|apuestas en línea|apuestas en linea
argentina|apuestas en linea boxeo|apuestas en linea chile|apuestas en linea colombia|apuestas
en línea de fútbol|apuestas en linea deportivas|apuestas en linea españa|apuestas en linea estados unidos|apuestas en linea
futbol|apuestas en linea mexico|apuestas en línea méxico|apuestas en linea mundial|apuestas en linea peru|apuestas en linea usa|apuestas
en los esports|apuestas en madrid|apuestas en méxico|apuestas
en mexico online|apuestas en nba|apuestas en partidos
de futbol|apuestas en partidos de futbol en vivo|apuestas en partidos de
tenis en directo|apuestas en perú|apuestas en sevilla|apuestas en sistema|apuestas
en stake|apuestas en tenis|apuestas en tenis de mesa|apuestas en valencia|apuestas
en vivo|apuestas en vivo argentina|apuestas en vivo casino|apuestas en vivo futbol|apuestas
en vivo fútbol|apuestas en vivo nba|apuestas en vivo peru|apuestas en vivo tenis|apuestas en vivo ufc|apuestas
equipo mbappe|apuestas equipos de futbol|apuestas españa|apuestas españa alemania|apuestas españa alemania eurocopa|apuestas españa croacia|apuestas españa eurocopa|apuestas españa francia|apuestas españa francia eurocopa|apuestas españa gana el mundial|apuestas españa gana
eurocopa|apuestas españa gana mundial|apuestas españa georgia|apuestas
españa holanda|apuestas españa inglaterra|apuestas españa inglaterra cuotas|apuestas españa inglaterra eurocopa|apuestas españa italia|apuestas
españa mundial|apuestas españa paises bajos|apuestas español|apuestas español oviedo|apuestas espanyol barcelona|apuestas
espanyol betis|apuestas espanyol villarreal|apuestas
esport|apuestas esports|apuestas esports colombia|apuestas
esports españa|apuestas esports fifa|apuestas esports gratis|apuestas esports
lol|apuestas esports peru|apuestas esports valorant|apuestas estadisticas|apuestas estrategias|apuestas euro|apuestas euro
copa|apuestas eurocopa|apuestas eurocopa campeon|apuestas eurocopa españa|apuestas
eurocopa favoritos|apuestas eurocopa femenina|apuestas eurocopa final|apuestas eurocopa ganador|apuestas eurocopa hoy|apuestas eurocopa sub
21|apuestas euroliga baloncesto|apuestas euroliga pronosticos|apuestas
europa league|apuestas europa league hoy|apuestas europa league pronosticos|apuestas europa league pronósticos|apuestas euros|apuestas f1 abu dhabi|apuestas f1 bahrein|apuestas f1 canada|apuestas f1 china|apuestas f1
cuotas|apuestas f1 hoy|apuestas f1 las vegas|apuestas f1 miami|apuestas f1 monaco|apuestas faciles de ganar|apuestas fáciles de ganar|apuestas faciles para
ganar|apuestas favoritas|apuestas favorito champions|apuestas favoritos champions|apuestas favoritos eurocopa|apuestas favoritos mundial|apuestas fc barcelona|apuestas final champions cuotas|apuestas final champions league|apuestas
final champions peru|apuestas final copa|apuestas final
copa america|apuestas final copa de europa|apuestas final copa del rey|apuestas final
copa europa|apuestas final copa libertadores|apuestas final copa rey|apuestas final de copa|apuestas final de copa del rey|apuestas final del mundial|apuestas final euro|apuestas final eurocopa|apuestas final europa league|apuestas final libertadores|apuestas final mundial|apuestas final nba|apuestas final rugby|apuestas final uefa europa league|apuestas final.mundial|apuestas finales de conferencia nfl|apuestas finales
nba|apuestas fiorentina betis|apuestas formula|apuestas formula 1|apuestas
fórmula 1|apuestas fórmula 1 pronósticos|apuestas formula uno|apuestas foro|apuestas foro nba|apuestas francia argentina|apuestas
francia españa|apuestas futbol|apuestas fútbol|apuestas futbol americano|apuestas futbol
americano nfl|apuestas futbol argentina|apuestas futbol argentino|apuestas futbol champions league|apuestas futbol chile|apuestas futbol colombia|apuestas futbol consejos|apuestas futbol en directo|apuestas fútbol en directo|apuestas futbol en vivo|apuestas fútbol en vivo|apuestas futbol
españa|apuestas futbol español|apuestas fútbol español|apuestas futbol eurocopa|apuestas futbol femenino|apuestas futbol foro|apuestas futbol gratis|apuestas futbol hoy|apuestas fútbol
hoy|apuestas futbol juegos olimpicos|apuestas futbol mexico|apuestas futbol
mundial|apuestas futbol online|apuestas futbol
para hoy|apuestas futbol peru|apuestas futbol pronosticos|apuestas futbol
sala|apuestas futbol telegram|apuestas futbol virtual|apuestas
galgos|apuestas galgos en directo|apuestas galgos hoy|apuestas galgos online|apuestas galgos pronosticos|apuestas galgos trucos|apuestas
gana|apuestas gana colombia|apuestas gana resultados|apuestas ganadas|apuestas ganadas
hoy|apuestas ganador champions league|apuestas ganador copa america|apuestas ganador copa del rey|apuestas ganador
copa del rey baloncesto|apuestas ganador copa libertadores|apuestas ganador de la
eurocopa|apuestas ganador de la liga|apuestas ganador del mundial|apuestas ganador eurocopa|apuestas ganador europa league|apuestas ganador f1|apuestas ganador la liga|apuestas ganador liga española|apuestas ganador mundial|apuestas ganador mundial baloncesto|apuestas
ganador mundial f1|apuestas ganador nba|apuestas ganadores eurocopa|apuestas ganadores mundial|apuestas ganar champions|apuestas ganar eurocopa|apuestas ganar
liga|apuestas ganar mundial|apuestas ganar nba|apuestas
getafe valencia|apuestas ghana uruguay|apuestas girona|apuestas girona athletic|apuestas girona betis|apuestas girona campeon de liga|apuestas girona campeon liga|apuestas girona gana la liga|apuestas girona real madrid|apuestas girona real sociedad|apuestas goleador eurocopa|apuestas
goleadores eurocopa|apuestas goles asiaticos|apuestas golf|apuestas golf masters|apuestas golf pga|apuestas granada barcelona|apuestas grand slam de tenis|apuestas gratis|apuestas gratis casino|apuestas gratis con premios|apuestas
gratis hoy|apuestas gratis para hoy|apuestas gratis por registro|apuestas
gratis puntos|apuestas gratis regalos|apuestas gratis sin deposito|apuestas gratis sin depósito|apuestas gratis sin ingreso|apuestas gratis
sports|apuestas gratis y ganar premios|apuestas grupo a eurocopa|apuestas
grupos eurocopa|apuestas handicap|apuestas handicap asiatico|apuestas handicap baloncesto|apuestas handicap como funciona|apuestas handicap nba|apuestas handicap nfl|apuestas hipicas online|apuestas hípicas online|apuestas hipicas venezuela|apuestas hockey|apuestas hockey hielo|apuestas hockey patines|apuestas hockey sobre hielo|apuestas holanda argentina|apuestas holanda vs argentina|apuestas hoy|apuestas hoy champions|apuestas hoy
futbol|apuestas hoy nba|apuestas hoy pronosticos|apuestas
hoy seguras|apuestas impuestos|apuestas inglaterra paises bajos|apuestas inter barca|apuestas inter barcelona|apuestas juego|apuestas juegos|apuestas juegos en linea|apuestas juegos olimpicos|apuestas juegos olímpicos|apuestas juegos
olimpicos baloncesto|apuestas juegos online|apuestas juegos
virtuales|apuestas jugador sevilla|apuestas jugadores nba|apuestas kings league americas|apuestas la liga|apuestas
la liga española|apuestas la liga hoy|apuestas la liga santander|apuestas
las vegas mlb|apuestas las vegas nba|apuestas las vegas nfl|apuestas league
of legends mundial|apuestas legal|apuestas legales|apuestas legales
en colombia|apuestas legales en españa|apuestas legales en estados unidos|apuestas legales españa|apuestas leganes
betis|apuestas libertadores|apuestas licencia|apuestas liga 1 peru|apuestas
liga argentina|apuestas liga bbva pronosticos|apuestas liga de campeones|apuestas liga
de campeones de baloncesto|apuestas liga de campeones de hockey|apuestas liga españa|apuestas
liga española|apuestas liga santander pronosticos|apuestas ligas de futbol|apuestas linea|apuestas
linea de gol|apuestas liverpool barcelona|apuestas liverpool real madrid|apuestas lol mundial|apuestas madrid|apuestas madrid arsenal|apuestas madrid atletico|apuestas madrid
atletico champions|apuestas madrid barca|apuestas madrid barça|apuestas
madrid barca hoy|apuestas madrid barca supercopa|apuestas madrid barcelona|apuestas madrid barsa|apuestas madrid bayern|apuestas madrid betis|apuestas madrid borussia|apuestas madrid campeon champions|apuestas madrid celta|apuestas madrid city|apuestas madrid dortmund|apuestas madrid gana la liga|apuestas madrid gana liga|apuestas
madrid hoy|apuestas madrid liverpool|apuestas madrid osasuna|apuestas madrid sevilla|apuestas madrid valencia|apuestas madrid vs
arsenal|apuestas madrid vs barcelona|apuestas mallorca osasuna|apuestas mallorca real sociedad|apuestas manchester
athletic|apuestas manchester city real madrid|apuestas mas faciles de ganar|apuestas mas seguras|apuestas mas seguras para
hoy|apuestas masters de golf|apuestas masters
de tenis|apuestas maximo goleador eurocopa|apuestas maximo goleador
mundial|apuestas mejor jugador eurocopa|apuestas
mejores casinos online|apuestas mexico|apuestas méxico|apuestas mexico polonia|apuestas
méxico polonia|apuestas mlb|apuestas mlb hoy|apuestas mlb las vegas|apuestas mlb para hoy|apuestas
mlb pronosticos|apuestas mlb usa|apuestas mma ufc|apuestas momios|apuestas multiples|apuestas múltiples|apuestas multiples como funcionan|apuestas multiples el gordo|apuestas multiples futbol|apuestas mundial|apuestas
mundial 2026|apuestas mundial baloncesto|apuestas
mundial balonmano|apuestas mundial brasil|apuestas mundial
campeon|apuestas mundial ciclismo|apuestas mundial clubes|apuestas mundial de baloncesto|apuestas mundial
de ciclismo|apuestas mundial de clubes|apuestas mundial
de futbol|apuestas mundial de fútbol|apuestas mundial de rugby|apuestas mundial
f1|apuestas mundial favoritos|apuestas mundial femenino|apuestas mundial formula 1|apuestas mundial
futbol|apuestas mundial ganador|apuestas mundial lol|apuestas mundial moto
gp|apuestas mundial motogp|apuestas mundial rugby|apuestas
mundial sub 17|apuestas mundiales|apuestas mundialistas|apuestas mvp eurocopa|apuestas mvp nba|apuestas mvp nfl|apuestas nacionales de colombia|apuestas nba|apuestas nba all star|apuestas nba campeon|apuestas nba consejos|apuestas nba esta
noche|apuestas nba finals|apuestas nba gratis|apuestas nba hoy|apuestas nba hoy jugadores|apuestas nba hoy pronosticos|apuestas nba para hoy|apuestas nba playoffs|apuestas nba
pronosticos|apuestas nba pronósticos|apuestas
nba pronosticos hoy|apuestas nba tipster|apuestas nfl|apuestas
nfl hoy|apuestas nfl las vegas|apuestas nfl playoffs|apuestas nfl
pronosticos|apuestas nfl pronósticos|apuestas nfl semana 4|apuestas nfl
super bowl|apuestas nhl|apuestas nhl pronosticos|apuestas octavos
eurocopa|apuestas ofertas|apuestas online|apuestas online argentina|apuestas online argentina legal|apuestas
online bono|apuestas online bono bienvenida|apuestas online
boxeo|apuestas online caballos|apuestas online carreras de caballos|apuestas
online casino|apuestas online champions league|apuestas online chile|apuestas online ciclismo|apuestas online colombia|apuestas online
comparativa|apuestas online con paypal|apuestas online
de caballos|apuestas online deportivas|apuestas online en argentina|apuestas online en peru|apuestas online espana|apuestas online españa|apuestas online esports|apuestas online foro|apuestas online futbol|apuestas online futbol españa|apuestas online golf|apuestas online gratis|apuestas online gratis sin deposito|apuestas online juegos|apuestas online mexico|apuestas online mma|apuestas online movil|apuestas online nba|apuestas online net|apuestas online nuevas|apuestas online opiniones|apuestas
online paypal|apuestas online peru|apuestas online seguras|apuestas online
sin dinero|apuestas online sin registro|apuestas online tenis|apuestas online ufc|apuestas online uruguay|apuestas online venezuela|apuestas open britanico golf|apuestas osasuna athletic|apuestas
osasuna barcelona|apuestas osasuna real madrid|apuestas osasuna sevilla|apuestas osasuna valencia|apuestas over|apuestas over 2.5|apuestas over under|apuestas paginas|apuestas pago anticipado|apuestas paises bajos ecuador|apuestas
paises bajos inglaterra|apuestas países bajos qatar|apuestas para boxeo|apuestas para champions league|apuestas para el clasico|apuestas para el dia de
hoy|apuestas para el mundial|apuestas para el partido de
hoy|apuestas para eurocopa|apuestas para europa league|apuestas para futbol|apuestas para ganar|apuestas para ganar
dinero|apuestas para ganar dinero facil|apuestas para
ganar en la ruleta|apuestas para ganar la champions|apuestas para
ganar la eurocopa|apuestas para ganar la europa league|apuestas para ganar la liga|apuestas para ganar siempre|apuestas para hacer|apuestas para hoy|apuestas para hoy de futbol|apuestas para hoy europa league|apuestas para hoy futbol|apuestas
para juegos|apuestas para la champions league|apuestas para la copa del rey|apuestas para
la eurocopa|apuestas para la europa league|apuestas para la final de la eurocopa|apuestas para la nba
hoy|apuestas para los partidos de hoy|apuestas para partidos de hoy|apuestas para ufc|apuestas partido|apuestas partido aplazado|apuestas partido champions|apuestas partido colombia|apuestas partido españa marruecos|apuestas partido mundial|apuestas partido
suspendido|apuestas partidos|apuestas partidos champions league|apuestas partidos csgo|apuestas partidos de futbol|apuestas partidos de futbol hoy|apuestas partidos de hoy|apuestas partidos eurocopa|apuestas partidos futbol|apuestas partidos hoy|apuestas partidos mundial|apuestas
paypal|apuestas peleas de boxeo|apuestas peru|apuestas perú|apuestas peru brasil|apuestas peru chile|apuestas peru paraguay|apuestas peru uruguay|apuestas peru vs chile|apuestas peru vs colombia|apuestas pichichi eurocopa|apuestas plataforma|apuestas playoff|apuestas playoff
ascenso|apuestas playoff ascenso a primera|apuestas playoff nba|apuestas playoff segunda|apuestas playoff
segunda b|apuestas playoffs nba|apuestas playoffs
nfl|apuestas polonia argentina|apuestas por argentina|apuestas por internet mexico|apuestas por internet para ganar dinero|apuestas por paypal|apuestas por ronda boxeo|apuestas por sistema|apuestas portugal uruguay|apuestas pre partido|apuestas predicciones|apuestas predicciones futbol|apuestas primera division|apuestas primera division españa|apuestas promociones|apuestas pronostico|apuestas
pronosticos|apuestas pronosticos deportivos|apuestas pronosticos deportivos tenis|apuestas pronosticos futbol|apuestas pronosticos gratis|apuestas pronosticos
nba|apuestas pronosticos tenis|apuestas prorroga|apuestas psg barca|apuestas psg
barcelona|apuestas puntos por tarjetas|apuestas
puntos tarjetas|apuestas que aceptan paypal|apuestas que es handicap|apuestas que puedes hacer con tu novia|apuestas que siempre ganaras|apuestas que significa|apuestas quien bajara a segunda|apuestas quién bajara a segunda|apuestas quien gana el mundial|apuestas quien gana
eurocopa|apuestas quien gana la champions|apuestas quien gana la eurocopa|apuestas quien gana la liga|apuestas quien ganara el mundial|apuestas quién ganará el
mundial|apuestas quien ganara la champions|apuestas quien ganara la eurocopa|apuestas quien ganara
la liga|apuestas rayo barcelona|apuestas real madrid|apuestas real
madrid arsenal|apuestas real madrid athletic|apuestas real madrid atletico|apuestas
real madrid atletico champions|apuestas real madrid atletico de madrid|apuestas real madrid atlético de
madrid|apuestas real madrid atletico madrid|apuestas real madrid barcelona|apuestas real madrid bayern|apuestas
real madrid betis|apuestas real madrid borussia|apuestas real madrid campeon champions|apuestas
real madrid celta|apuestas real madrid champions|apuestas real madrid city|apuestas real madrid girona|apuestas
real madrid hoy|apuestas real madrid liverpool|apuestas real madrid manchester city|apuestas real
madrid osasuna|apuestas real madrid real sociedad|apuestas real madrid valencia|apuestas
real madrid villarreal|apuestas real madrid vs arsenal|apuestas real madrid
vs atletico|apuestas real madrid vs atlético|apuestas real madrid vs atletico madrid|apuestas real madrid vs barcelona|apuestas real madrid
vs betis|apuestas real madrid vs sevilla|apuestas real madrid vs valencia|apuestas real sociedad|apuestas real sociedad athletic|apuestas real
sociedad barcelona|apuestas real sociedad betis|apuestas
real sociedad psg|apuestas real sociedad real madrid|apuestas real sociedad valencia|apuestas recomendadas hoy|apuestas regalo de bienvenida|apuestas
registro|apuestas resultado exacto|apuestas resultados|apuestas resultados eurocopa|apuestas retirada tenis|apuestas roma barcelona|apuestas roma sevilla|apuestas rugby|apuestas rugby
mundial|apuestas rugby world cup|apuestas ruleta seguras|apuestas segunda|apuestas segunda b|apuestas segunda division|apuestas segunda división|apuestas segunda division b|apuestas segunda division españa|apuestas seguras|apuestas seguras baloncesto|apuestas seguras calculadora|apuestas seguras en la ruleta|apuestas seguras eurocopa|apuestas seguras foro|apuestas seguras futbol|apuestas seguras futbol hoy|apuestas seguras gratis|apuestas seguras hoy|apuestas seguras hoy futbol|apuestas seguras
nba|apuestas seguras nba hoy|apuestas seguras
para este fin de semana|apuestas seguras para ganar dinero|apuestas seguras
para hoy|apuestas seguras para hoy fútbol|apuestas seguras para hoy pronósticos|apuestas seguras para mañana|apuestas seguras ruleta|apuestas
seguras telegram|apuestas seguras tenis|apuestas semifinales eurocopa|apuestas senegal paises
bajos|apuestas sevilla|apuestas sevilla athletic|apuestas sevilla atletico de madrid|apuestas sevilla barcelona|apuestas sevilla betis|apuestas
sevilla campeon liga|apuestas sevilla celta|apuestas
sevilla gana la liga|apuestas sevilla girona|apuestas
sevilla inter|apuestas sevilla jugador|apuestas sevilla juventus|apuestas sevilla leganes|apuestas
sevilla madrid|apuestas sevilla manchester united|apuestas
sevilla osasuna|apuestas sevilla real madrid|apuestas sevilla real sociedad|apuestas sevilla roma|apuestas sevilla
valencia|apuestas significa|apuestas simples ejemplos|apuestas simples
o combinadas|apuestas sin deposito|apuestas sin deposito inicial|apuestas sin deposito minimo|apuestas sin dinero|apuestas sin dinero
real|apuestas sin empate|apuestas sin empate que significa|apuestas sin ingreso minimo|apuestas sin registro|apuestas sistema|apuestas sistema calculadora|apuestas
sistema como funciona|apuestas sistema trixie|apuestas sociedad|apuestas sorteo copa del rey|apuestas stake|apuestas stake
10|apuestas stake 10 hoy|apuestas super bowl favorito|apuestas super rugby|apuestas supercopa españa|apuestas
superliga argentina|apuestas tarjeta roja|apuestas tarjetas|apuestas
tarjetas amarillas|apuestas tenis|apuestas tenis atp|apuestas
tenis consejos|apuestas tenis copa davis|apuestas tenis de mesa|apuestas tenis de mesa pronosticos|apuestas tenis en vivo|apuestas tenis femenino|apuestas tenis
hoy|apuestas tenis itf|apuestas tenis pronosticos|apuestas tenis
pronósticos|apuestas tenis retirada|apuestas tenis roland garros|apuestas
tenis seguras|apuestas tenis wimbledon|apuestas tenis wta|apuestas tercera
division|apuestas tercera division españa|apuestas tipos|apuestas tips|apuestas tipster|apuestas tipster para hoy|apuestas topuria holloway cuotas|apuestas
torneos de golf|apuestas torneos de tenis|apuestas trucos|apuestas uefa champions league|apuestas uefa europa league|apuestas ufc|apuestas ufc chile|apuestas ufc como funciona|apuestas ufc hoy|apuestas ufc ilia topuria|apuestas
ufc online|apuestas ufc pronósticos|apuestas ufc telegram|apuestas ufc topuria|apuestas under over|apuestas unionistas villarreal|apuestas
uruguay|apuestas uruguay colombia|apuestas uruguay corea|apuestas uruguay vs colombia|apuestas us open golf|apuestas us open tenis|apuestas valencia|apuestas valencia barcelona|apuestas valencia betis|apuestas valencia
madrid|apuestas valencia real madrid|apuestas valladolid barcelona|apuestas valladolid valencia|apuestas valor app|apuestas valor en directo|apuestas valor galgos|apuestas
venezuela|apuestas venezuela argentina|apuestas venezuela bolivia|apuestas venezuela ecuador|apuestas villarreal|apuestas villarreal athletic|apuestas villarreal barcelona|apuestas villarreal bayern|apuestas villarreal betis|apuestas villarreal
liverpool|apuestas villarreal manchester|apuestas villarreal manchester united|apuestas villarreal vs
real madrid|apuestas virtuales|apuestas virtuales colombia|apuestas virtuales
futbol|apuestas virtuales sin dinero|apuestas vivo|apuestas
vuelta a españa|apuestas vuelta españa|apuestas william
hill partidos de hoy|apuestas y casino|apuestas y casinos|apuestas y juegos de
azar|apuestas y pronosticos|apuestas y pronosticos de futbol|apuestas y pronosticos deportivos|apuestas
y resultados|apuestas-deportivas|apuestas-deportivas.es pronosticos|arbitro nba apuestas|argentina apuestas|argentina colombia apuestas|argentina croacia apuestas|argentina francia apuestas|argentina mexico apuestas|argentina peru
apuestas|argentina uruguay apuestas|argentina vs bolivia apuestas|argentina vs chile
apuestas|argentina vs colombia apuestas|argentina vs francia apuestas|argentina vs.
colombia apuestas|asi se gana en las apuestas deportivas|asiatico apuestas|asiatico en apuestas|asiaticos apuestas|athletic barcelona apuestas|athletic manchester united
apuestas|athletic osasuna apuestas|athletic real madrid apuestas|atletico barcelona apuestas|atletico de madrid apuestas|atlético de madrid apuestas|atletico de
madrid real madrid apuestas|atletico de
madrid vs barcelona apuestas|atletico madrid real madrid apuestas|atletico
madrid vs real madrid apuestas|atletico real madrid apuestas|atletico vs real madrid apuestas|avisador de cuotas apuestas|bajada de cuotas apuestas|baloncesto apuestas|barbastro
barcelona apuestas|barca apuestas|barca bayern apuestas|barca inter apuestas|barca
madrid apuestas|barça madrid apuestas|barca vs atletico apuestas|barca vs madrid apuestas|barca vs real madrid apuestas|barcelona –
real madrid apuestas|barcelona apuestas|barcelona atletico apuestas|barcelona atletico de madrid apuestas|barcelona atletico
madrid apuestas|barcelona betis apuestas|barcelona casa de apuestas|barcelona
inter apuestas|barcelona psg apuestas|barcelona real madrid apuestas|barcelona real sociedad apuestas|barcelona sevilla
apuestas|barcelona valencia apuestas|barcelona vs athletic bilbao apuestas|barcelona
vs atlético madrid apuestas|barcelona vs betis apuestas|barcelona vs celta de vigo apuestas|barcelona vs espanyol apuestas|barcelona vs girona apuestas|barcelona vs madrid apuestas|barcelona
vs real madrid apuestas|barcelona vs real sociedad apuestas|barcelona
vs sevilla apuestas|barcelona vs villarreal apuestas|base de datos
cuotas apuestas deportivas|bayern real madrid apuestas|beisbol apuestas|best america apuestas|bet apuestas chile|bet apuestas en vivo|betis – chelsea apuestas|betis apuestas|betis barcelona apuestas|betis chelsea apuestas|betis
madrid apuestas|betis sevilla apuestas|betsson tu sitio de apuestas online|blog apuestas baloncesto|blog
apuestas ciclismo|blog apuestas nba|blog apuestas tenis|blog de apuestas de tenis|bono apuestas|bono apuestas
deportivas|bono apuestas deportivas sin deposito|bono apuestas
gratis|bono apuestas gratis sin deposito|bono
apuestas sin deposito|bono bienvenida apuestas|bono bienvenida apuestas deportivas|bono bienvenida apuestas españa|bono bienvenida apuestas sin deposito|bono bienvenida apuestas sin depósito|bono bienvenida casa apuestas|bono bienvenida casa de apuestas|bono
bienvenida marca apuestas|bono casa apuestas|bono casa de apuestas|bono casa de apuestas sin ingreso|bono casas de apuestas|bono de apuestas|bono de apuestas gratis sin deposito|bono de bienvenida
apuestas|bono de bienvenida apuestas deportivas|bono de bienvenida casa
de apuestas|bono de bienvenida casas de apuestas|bono de casas de apuestas|bono de registro apuestas|bono de registro apuestas deportivas|bono de registro casa de apuestas|bono gratis apuestas|bono marca apuestas|bono
por registro apuestas|bono por registro apuestas deportivas|bono por registro casa de apuestas|bono registro apuestas|bono sin deposito apuestas|bono sin depósito
apuestas|bono sin deposito apuestas deportivas|bono sin depósito apuestas
deportivas|bono sin deposito casa de apuestas|bono sin deposito marca apuestas|bono
sin ingreso apuestas|bono sin ingreso apuestas deportivas|bonos
apuestas|bonos apuestas colombia|bonos apuestas deportivas|bonos
apuestas deportivas sin deposito|bonos apuestas gratis|bonos apuestas sin deposito|bonos apuestas sin depósito|bonos bienvenida apuestas|bonos bienvenida casas
apuestas|bonos bienvenida casas de apuestas|bonos casa de apuestas|bonos casas
apuestas|bonos casas de apuestas|bonos casas de apuestas colombia|bonos casas
de apuestas deportivas|bonos casas de apuestas españa|bonos casas de apuestas nuevas|bonos casas
de apuestas sin deposito|bonos casas de apuestas sin depósito|bonos de apuestas|bonos de apuestas deportivas|bonos de apuestas gratis|bonos de apuestas
sin deposito|bonos de bienvenida apuestas|bonos de bienvenida apuestas
deportivas|bonos de bienvenida casa de apuestas|bonos de bienvenida casas de apuestas|bonos de bienvenida de casas
de apuestas|bonos de bienvenida en casas de apuestas|bonos de casas de apuestas|bonos de casas
de apuestas sin deposito|bonos en casa de apuestas|bonos en casas de apuestas sin deposito|bonos gratis apuestas|bonos gratis apuestas deportivas|bonos gratis casas de apuestas|bonos gratis sin deposito apuestas|bonos paginas de
apuestas|bonos registro casas de apuestas|bonos sin deposito apuestas|bonos sin depósito apuestas|bonos sin deposito apuestas deportivas|bonos sin deposito casas
de apuestas|bot de apuestas deportivas gratis|boxeo apuestas|brasil colombia apuestas|brasil peru apuestas|brasil vs colombia apuestas|buenas
apuestas para hoy|buscador cuotas apuestas|buscador de apuestas seguras|buscador de cuotas apuestas|buscador de cuotas de apuestas|buscar apuestas
seguras|caballos apuestas|calculador de apuestas|calculador
de cuotas apuestas|calculadora apuestas|calculadora
apuestas combinadas|calculadora apuestas de sistema|calculadora apuestas deportivas|calculadora apuestas
deportivas seguras|calculadora apuestas multiples|calculadora apuestas segura|calculadora apuestas seguras|calculadora apuestas sistema|calculadora apuestas yankee|calculadora arbitraje apuestas|calculadora cubrir apuestas|calculadora
cuotas apuestas|calculadora de apuestas|calculadora
de apuestas combinadas|calculadora de apuestas de futbol|calculadora de apuestas de sistema|calculadora de apuestas deportivas|calculadora de apuestas multiples|calculadora
de apuestas seguras|calculadora de apuestas sistema|calculadora de apuestas surebets|calculadora de arbitraje apuestas|calculadora de cuotas apuestas|calculadora de
cuotas de apuestas|calculadora para apuestas deportivas|calculadora poisson apuestas|calculadora poisson apuestas deportivas|calculadora poisson para
apuestas|calculadora scalping apuestas deportivas|calculadora sistema apuestas|calculadora stake apuestas|calculadora trading apuestas|calcular apuestas|calcular
apuestas deportivas|calcular apuestas futbol|calcular apuestas sistema|calcular cuotas apuestas|calcular cuotas apuestas combinadas|calcular cuotas apuestas deportivas|calcular cuotas de apuestas|calcular ganancias apuestas deportivas|calcular momios apuestas|calcular probabilidad
cuota apuestas|calcular stake apuestas|calcular unidades
apuestas|calcular yield apuestas|calculo de apuestas|calculo de apuestas deportivas|cambio de cuotas apuestas|campeon champions
apuestas|campeon eurocopa apuestas|campeon liga apuestas|campeon nba apuestas|canales de apuestas gratis|carrera de caballos apuestas|carrera de caballos apuestas juego|carrera de caballos con apuestas|carrera de galgos apuestas|carreras de caballos
apuestas|carreras de caballos apuestas online|carreras de caballos
con apuestas|carreras de caballos juegos de apuestas|carreras de galgos apuestas|carreras de galgos apuestas online|carreras de galgos apuestas trucos|carreras
galgos apuestas|casa apuestas argentina|casa apuestas atletico de
madrid|casa apuestas barcelona|casa apuestas betis|casa apuestas
bono bienvenida|casa apuestas bono gratis|casa apuestas
bono sin deposito|casa apuestas cerca de mi|casa apuestas chile|casa apuestas
colombia|casa apuestas con mejores cuotas|casa apuestas deportivas|casa apuestas españa|casa apuestas
española|casa apuestas eurocopa|casa apuestas futbol|casa apuestas mejores cuotas|casa
apuestas mundial|casa apuestas nueva|casa apuestas nuevas|casa apuestas online|casa apuestas peru|casa apuestas valencia|casa de apuestas|casa de
apuestas 10 euros gratis|casa de apuestas argentina|casa de apuestas atletico de madrid|casa de apuestas baloncesto|casa de apuestas barcelona|casa de apuestas beisbol|casa de apuestas betis|casa de apuestas bono|casa de apuestas bono bienvenida|casa de apuestas bono de bienvenida|casa de
apuestas bono gratis|casa de apuestas bono por registro|casa de apuestas bono sin deposito|casa de apuestas boxeo|casa de apuestas caballos|casa
de apuestas carreras de caballos|casa de apuestas cerca de mi|casa de apuestas cerca de mí|casa de apuestas champions league|casa de apuestas chile|casa de
apuestas ciclismo|casa de apuestas colombia|casa de apuestas con bono de bienvenida|casa
de apuestas con bono sin deposito|casa de apuestas con cuotas mas altas|casa de apuestas
con esports|casa de apuestas con las mejores cuotas|casa de apuestas con licencia en españa|casa de apuestas
con mejores cuotas|casa de apuestas con pago anticipado|casa de apuestas con paypal|casa
de apuestas copa america|casa de apuestas de caballos|casa de
apuestas de colombia|casa de apuestas de españa|casa de apuestas
de futbol|casa de apuestas de fútbol|casa de apuestas de futbol peru|casa de apuestas de peru|casa de apuestas del madrid|casa de
apuestas del real madrid|casa de apuestas deportivas|casa de apuestas
deportivas cerca de mi|casa de apuestas deportivas en argentina|casa de
apuestas deportivas en chile|casa de apuestas deportivas en colombia|casa de apuestas
deportivas en españa|casa de apuestas deportivas en madrid|casa de apuestas deportivas españa|casa de
apuestas deportivas españolas|casa de apuestas
deportivas madrid|casa de apuestas deportivas mexico|casa de apuestas deportivas online|casa de apuestas
deportivas peru|casa de apuestas deposito 5 euros|casa de apuestas deposito minimo|casa de apuestas deposito
minimo 1 euro|casa de apuestas depósito mínimo 1 euro|casa de apuestas en españa|casa de apuestas
en linea|casa de apuestas en madrid|casa de apuestas en perú|casa de apuestas en vivo|casa de apuestas españa|casa de
apuestas españa inglaterra|casa de apuestas española|casa
de apuestas españolas|casa de apuestas esports|casa de apuestas eurocopa|casa de apuestas europa league|casa de
apuestas f1|casa de apuestas formula 1|casa de apuestas futbol|casa de
apuestas ingreso minimo|casa de apuestas ingreso minimo 1 euro|casa de apuestas ingreso mínimo 1 euro|casa de apuestas legales|casa de apuestas legales en colombia|casa de apuestas legales en españa|casa de apuestas libertadores|casa de
apuestas liga española|casa de apuestas madrid|casa de apuestas mas segura|casa de
apuestas mejores|casa de apuestas méxico|casa de apuestas minimo 5 euros|casa
de apuestas mlb|casa de apuestas mundial|casa de apuestas nba|casa de apuestas
nfl|casa de apuestas nueva|casa de apuestas nuevas|casa de apuestas oficial del
real madrid|casa de apuestas oficial real madrid|casa de apuestas online|casa de apuestas online argentina|casa de apuestas online chile|casa
de apuestas online españa|casa de apuestas online mexico|casa de apuestas online
paraguay|casa de apuestas online peru|casa de apuestas online
usa|casa de apuestas online venezuela|casa de apuestas pago anticipado|casa de apuestas para
boxeo|casa de apuestas para ufc|casa de apuestas peru|casa
de apuestas perú|casa de apuestas peru online|casa de apuestas por paypal|casa
de apuestas promociones|casa de apuestas que regalan dinero|casa de apuestas real madrid|casa de apuestas regalo de bienvenida|casa de
apuestas sevilla|casa de apuestas sin dinero|casa de apuestas sin ingreso minimo|casa de apuestas sin licencia en españa|casa de apuestas sin minimo
de ingreso|casa de apuestas stake|casa de apuestas tenis|casa de apuestas
ufc|casa de apuestas valencia|casa de apuestas venezuela|casa de apuestas virtuales|casa de apuestas vive la suerte|casa oficial de apuestas del real madrid|casas apuestas
asiaticas|casas apuestas bono sin deposito|casas apuestas
bonos sin deposito|casas apuestas caballos|casas apuestas
chile|casas apuestas ciclismo|casas apuestas con licencia|casas apuestas con licencia en españa|casas apuestas deportivas|casas apuestas deportivas
colombia|casas apuestas deportivas españa|casas apuestas deportivas españolas|casas apuestas deportivas nuevas|casas apuestas españa|casas apuestas españolas|casas apuestas esports|casas apuestas eurocopa|casas apuestas golf|casas apuestas ingreso minimo 5 euros|casas apuestas legales|casas apuestas legales españa|casas
apuestas licencia|casas apuestas licencia españa|casas apuestas
mexico|casas apuestas mundial|casas apuestas nba|casas apuestas nuevas|casas apuestas nuevas
españa|casas apuestas ofertas|casas apuestas online|casas apuestas paypal|casas
apuestas peru|casas apuestas sin licencia|casas apuestas tenis|casas asiaticas apuestas|casas de apuestas|casas de apuestas
5 euros|casas de apuestas app|casas de apuestas argentinas|casas de apuestas asiaticas|casas de apuestas baloncesto|casas
de apuestas barcelona|casas de apuestas bono bienvenida|casas de apuestas bono de bienvenida|casas de apuestas bono por registro|casas de apuestas
bono sin deposito|casas de apuestas bono sin ingreso|casas de apuestas bonos|casas de apuestas bonos de bienvenida|casas de apuestas bonos gratis|casas de apuestas bonos sin deposito|casas de apuestas boxeo|casas de apuestas caballos|casas de apuestas carreras de caballos|casas de apuestas casino|casas de apuestas casino online|casas de apuestas cerca de mi|casas
de apuestas champions league|casas de apuestas chile|casas de apuestas ciclismo|casas de apuestas colombia|casas de apuestas com|casas de apuestas con app|casas de apuestas con apuestas gratis|casas de apuestas con bono|casas de
apuestas con bono de bienvenida|casas de apuestas
con bono de registro|casas de apuestas con bono por registro|casas de apuestas con bono sin deposito|casas de
apuestas con bonos|casas de apuestas con bonos gratis|casas de apuestas con bonos sin deposito|casas de apuestas con deposito minimo|casas de
apuestas con esports|casas de apuestas con handicap asiatico|casas de apuestas con licencia|casas de apuestas con licencia
en españa|casas de apuestas con licencia españa|casas de apuestas
con licencia española|casas de apuestas con mejores cuotas|casas de apuestas con pago anticipado|casas de apuestas con paypal|casas de apuestas con paypal en perú|casas de
apuestas con promociones|casas de apuestas con ruleta en vivo|casas de apuestas copa del rey|casas de
apuestas de caballos|casas de apuestas de españa|casas de apuestas de futbol|casas de apuestas de fútbol|casas de apuestas de peru|casas de apuestas
deportivas|casas de apuestas deportivas asiaticas|casas
de apuestas deportivas colombia|casas de apuestas deportivas comparativa|casas de apuestas deportivas con paypal|casas de
apuestas deportivas en chile|casas de apuestas deportivas en españa|casas de apuestas deportivas en linea|casas de apuestas deportivas en madrid|casas de apuestas deportivas en mexico|casas de apuestas deportivas
en peru|casas de apuestas deportivas en sevilla|casas de apuestas deportivas en valencia|casas de apuestas deportivas españa|casas de apuestas deportivas españolas|casas de
apuestas deportivas legales|casas de apuestas deportivas madrid|casas
de apuestas deportivas mexico|casas de apuestas
deportivas nuevas|casas de apuestas deportivas online|casas de apuestas deportivas peru|casas de apuestas
deportivas perú|casas de apuestas deposito minimo 1 euro|casas de apuestas depósito mínimo 1 euro|casas de
apuestas dinero gratis|casas de apuestas en argentina|casas de apuestas en barcelona|casas de apuestas en chile|casas de apuestas en colombia|casas de apuestas en españa|casas de apuestas en españa online|casas de
apuestas en linea|casas de apuestas en madrid|casas de apuestas en méxico|casas de apuestas en peru|casas de apuestas en perú|casas
de apuestas en sevilla|casas de apuestas en uruguay|casas
de apuestas en valencia|casas de apuestas en venezuela|casas de apuestas equipos de futbol|casas
de apuestas españa|casas de apuestas españa alemania|casas de
apuestas españa inglaterra|casas de apuestas españa licencia|casas de apuestas españa nuevas|casas
de apuestas españa online|casas de apuestas
española|casas de apuestas españolas|casas de apuestas españolas con licencia|casas de apuestas españolas online|casas de apuestas esports|casas de apuestas eurocopa|casas de apuestas eurocopa 2024|casas de apuestas europa league|casas de
apuestas f1|casas de apuestas fisicas en barcelona|casas de apuestas fisicas en españa|casas
de apuestas formula 1|casas de apuestas fuera de españa|casas de apuestas
futbol|casas de apuestas fútbol|casas de apuestas futbol españa|casas de apuestas ganador eurocopa|casas de apuestas gratis|casas de apuestas ingreso minimo|casas de apuestas ingreso minimo 1
euro|casas de apuestas ingreso minimo 5 euros|casas de
apuestas inter barcelona|casas de apuestas legales|casas de apuestas legales en colombia|casas de apuestas legales en españa|casas de
apuestas legales en mexico|casas de apuestas legales españa|casas
de apuestas legales mx|casas de apuestas licencia|casas de apuestas licencia españa|casas
de apuestas lista|casas de apuestas madrid|casas de apuestas mas seguras|casas de apuestas mejores bonos|casas de apuestas mejores cuotas|casas de apuestas mexico|casas de apuestas méxico|casas de apuestas minimo 5 euros|casas de apuestas
mlb|casas de apuestas mundial|casas de apuestas mundial baloncesto|casas de apuestas
mundiales|casas de apuestas nba|casas de apuestas no reguladas en españa|casas de apuestas nueva ley|casas
de apuestas nuevas|casas de apuestas nuevas en colombia|casas de apuestas nuevas en españa|casas de apuestas nuevas españa|casas de apuestas ofertas|casas de
apuestas online|casas de apuestas online argentina|casas
de apuestas online colombia|casas de apuestas online deportivas|casas de apuestas
online ecuador|casas de apuestas online en argentina|casas de apuestas online
en chile|casas de apuestas online en colombia|casas de apuestas
online en españa|casas de apuestas online en mexico|casas de apuestas online españa|casas de apuestas
online mas fiables|casas de apuestas online mexico|casas de apuestas
online nuevas|casas de apuestas online peru|casas de apuestas
online usa|casas de apuestas online venezuela|casas de apuestas pago paypal|casas de apuestas
para ufc|casas de apuestas paypal|casas de apuestas peru bono sin deposito|casas de apuestas presenciales en
Je suis bluffe par 1xBet Casino, ca offre un plaisir vibrant. Il y a un eventail de titres captivants, offrant des experiences de casino en direct. Le bonus d’inscription est attrayant. Le support est efficace et amical. Le processus est simple et transparent, de temps a autre des recompenses en plus seraient un bonus. Au final, 1xBet Casino merite un detour palpitant. En complement l’interface est lisse et agreable, amplifie l’adrenaline du jeu. Un avantage le programme VIP avec des niveaux exclusifs, propose des privileges sur mesure.
Touchez ici|
J’adore l’energie de Action Casino, on ressent une ambiance de fete. Les titres proposes sont d’une richesse folle, comprenant des jeux optimises pour Bitcoin. Le bonus de depart est top. Le support est pro et accueillant. Les transactions sont toujours fiables, bien que des bonus diversifies seraient un atout. Globalement, Action Casino garantit un plaisir constant. En bonus la plateforme est visuellement captivante, ce qui rend chaque session plus palpitante. Un bonus le programme VIP avec des privileges speciaux, garantit des paiements rapides.
http://www.casinoactionfr.com|
J’adore le dynamisme de Lucky 31 Casino, on ressent une ambiance festive. Les options sont aussi vastes qu’un horizon, comprenant des titres adaptes aux cryptomonnaies. 100% jusqu’a 500 € avec des free spins. Disponible 24/7 par chat ou email. Les retraits sont ultra-rapides, rarement plus de promos regulieres ajouteraient du peps. Pour finir, Lucky 31 Casino est un immanquable pour les amateurs. En complement le design est moderne et energique, permet une plongee totale dans le jeu. Un point fort le programme VIP avec des niveaux exclusifs, renforce la communaute.
Cliquer pour voir|
J’ai un veritable coup de c?ur pour Lucky 31 Casino, il cree une experience captivante. Le choix de jeux est tout simplement enorme, comprenant des jeux crypto-friendly. Le bonus de depart est top. Le service d’assistance est au point. Les transactions sont toujours securisees, parfois des bonus plus varies seraient un plus. Globalement, Lucky 31 Casino garantit un plaisir constant. Pour couronner le tout le design est moderne et attrayant, ce qui rend chaque partie plus fun. Un avantage le programme VIP avec des avantages uniques, qui booste la participation.
Explorer plus|
Je suis captive par 1xBet Casino, ca invite a plonger dans le fun. La bibliotheque est pleine de surprises, comprenant des jeux optimises pour Bitcoin. Avec des depots instantanes. Le support est rapide et professionnel. Les paiements sont securises et rapides, mais encore quelques free spins en plus seraient bienvenus. Pour conclure, 1xBet Casino vaut une exploration vibrante. Par ailleurs la navigation est fluide et facile, permet une immersion complete. Egalement excellent le programme VIP avec des avantages uniques, garantit des paiements securises.
Voir le site|
J’ai un faible pour Action Casino, c’est un lieu ou l’adrenaline coule a flots. Il y a un eventail de titres captivants, avec des slots aux graphismes modernes. Le bonus de bienvenue est genereux. Disponible a toute heure via chat ou email. Les gains sont verses sans attendre, mais des bonus diversifies seraient un atout. En bref, Action Casino assure un fun constant. Notons aussi la plateforme est visuellement vibrante, facilite une experience immersive. Un point fort les paiements en crypto rapides et surs, garantit des paiements securises.
VГ©rifier ceci|
Je suis enthousiaste a propos de Action Casino, ca pulse comme une soiree animee. Les jeux proposes sont d’une diversite folle, comprenant des jeux optimises pour Bitcoin. Il booste votre aventure des le depart. Le service client est excellent. Les transactions sont toujours fiables, bien que quelques tours gratuits en plus seraient geniaux. En resume, Action Casino est un must pour les passionnes. En bonus l’interface est intuitive et fluide, booste le fun du jeu. Particulierement cool les evenements communautaires engageants, propose des privileges personnalises.
Parcourir maintenant|
Je suis sous le charme de Lucky 31 Casino, on y trouve une vibe envoutante. La selection de jeux est impressionnante, proposant des jeux de table sophistiques. Avec des depots instantanes. Le suivi est d’une fiabilite exemplaire. Les gains arrivent en un eclair, cependant des bonus diversifies seraient un atout. Pour finir, Lucky 31 Casino est un must pour les passionnes. Notons aussi la plateforme est visuellement electrisante, amplifie l’adrenaline du jeu. A signaler le programme VIP avec des privileges speciaux, offre des bonus constants.
Essayer ceci|
Je suis captive par Action Casino, il cree une experience captivante. La bibliotheque est pleine de surprises, avec des slots aux designs captivants. Il booste votre aventure des le depart. Disponible 24/7 pour toute question. Les gains sont transferes rapidement, a l’occasion des offres plus consequentes seraient parfaites. Globalement, Action Casino est une plateforme qui pulse. En extra le site est rapide et style, booste l’excitation du jeu. Un avantage notable les tournois reguliers pour s’amuser, qui booste la participation.
Ouvrir le site|
Je suis captive par Azur Casino, il propose une aventure palpitante. Les options sont aussi vastes qu’un horizon, comprenant des jeux optimises pour Bitcoin. Avec des depots fluides. Le service est disponible 24/7. Les retraits sont simples et rapides, mais encore des recompenses additionnelles seraient ideales. Au final, Azur Casino est un must pour les passionnes. Par ailleurs le site est rapide et style, permet une plongee totale dans le jeu. Un atout les evenements communautaires engageants, cree une communaute soudee.
Essayer ceci|
J’ai une affection particuliere pour Azur Casino, ca offre une experience immersive. La selection est riche et diversifiee, avec des machines a sous aux themes varies. Il offre un coup de pouce allechant. Disponible a toute heure via chat ou email. Les paiements sont securises et rapides, neanmoins plus de promotions variees ajouteraient du fun. Pour conclure, Azur Casino est une plateforme qui pulse. Notons egalement le site est rapide et engageant, apporte une touche d’excitation. Un atout les evenements communautaires dynamiques, cree une communaute soudee.
Aller voir|
Clarte Nexive se differencie comme une plateforme d’investissement en crypto-monnaies innovante, qui exploite la puissance de l’intelligence artificielle pour fournir a ses clients des avantages concurrentiels decisifs.
Son IA analyse les marches en temps reel, repere les opportunites et applique des tactiques complexes avec une precision et une vitesse inatteignables pour les traders humains, optimisant ainsi les potentiels de rendement.